Abstract
Planar Josephson junctions (JJs) made in semiconductor quantum wells with large spin-orbit coupling are capable of hosting topological superconductivity. Indium antimonide (InSb) two-dimensional electron gases (2DEGs) are particularly suited for this due to their large Landé g-factor and high carrier mobility, however superconducting hybrids in these 2DEGs remain unexplored. Here we create JJs in high quality InSb 2DEGs and provide evidence of ballistic superconductivity over micron-scale lengths. A Zeeman field produces distinct revivals of the supercurrent in the junction, associated with a 0−π transition. We show that these transitions can be controlled by device design, and tuned in-situ using gates. A comparison between experiments and the theory of ballistic π-Josephson junctions gives excellent quantitative agreement. Our results therefore establish InSb quantum wells as a promising new material platform to study the interplay between superconductivity, spin-orbit interaction and magnetism.
Similar content being viewed by others
Introduction
Two-dimensional electron gases (2DEGs) coupled to superconductors offer the opportunity to explore a variety of quantum phenomena. These include the study of novel Josephson effects1, superconducting correlations in quantum (spin) Hall systems2,3,4,5,6,7, hybrid superconducting qubits8,9, and emergent topological states in semiconductors with strong spin-orbit interaction (SOI)10,11,12,13. Topological superconductivity in such 2DEGs can be realized using planar Josephson junctions (JJs), where the combined effect of SOI and a Zeeman field is known to significantly alter the current-phase relation14,15,16. In particular, one expects a complete reversal of the supercurrent (i.e., a π–JJ)17,18,19 when the Zeeman and Thouless energy of the system become comparable. It was shown recently that such a 0–π transition in a 2D system is in fact accompanied by a topological phase transition12,13,20,21. This, combined with the promise of creating scalable topological networks22,23,24, provides a strong motivation to study induced superconductivity in 2DEGs.
Key requirements for the semiconductor include low disorder, large SOI and a sizable Landé g-factor, combined with the ability to grow it on the wafer scale. InSb satisfies all of these requirements25,26,27,28 and has emerged as a prime material candidate for engineering topological superconductivity, as evident from nanowire-based systems29,30. However, despite significant progress in the growth of InSb 2DEGs31,32, material challenges have prevented a systematic study of the superconducting proximity effect in these systems.
Here, we overcome these issues and reliably create JJs, thus providing evidence of induced superconductivity in high quality InSb quantum wells. The JJs support supercurrent transport over several microns and display clear signatures of ballistic superconductivity. Furthermore, we exploit the large g-factor and gate tunability of the junctions to control the current-phase relation, and drive transitions between the 0 and π-states. This control over the free energy landscape allows us to construct a phase diagram identifying these 0 and π-regions, in agreement with theory.
Results
Induced superconductivity in InSb 2DEGs
The JJs are fabricated in an InSb 2DEG wafer grown by molecular beam epitaxy, with a nominal electron density n = 2.7 × 1011 cm−2 and mobility μ ≈ 150,000 cm2V−1s−1, which corresponds to a mean free path le ≈ 1.3 μm. Figure 1a shows a cross-sectional illustration and scanning electron micrograph of a typical JJ. Following a wet etch of the 2DEG in selected areas, NbTiN is deposited to create side-contacts to the 2DEG, thus defining a JJ of width W and length L. Prior to sputtering NbTiN, an in-situ argon plasma cleaning of the exposed quantum well is performed in order to obtain good electrical contacts. A metal top-gate, deposited on a thin dielectric layer is used to modify the electron density in the JJ. Details of the device fabrication and wafer growth can be found in the Methods section.
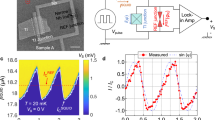
Ballistic superconductivity in InSb 2DEGs. a Cross-sectional schematic and false-colored scanning electron micrograph (along with a measurement schematic) of a top-gated JJ of width W and length L. b Differential resistance, dV/dI, versus perpendicular magnetic field, Bz, and current bias, I, displaying a Fraunhofer-like interference pattern for a JJ with W = 9.7 μm, L = 1.1 μm. White line indicates the magnitude of the switching current, Is, at zero magnetic field. c dV/dI as a function of I and gate voltage, Vg, for the same JJ, showing gate control of Is. d Length dependence of IsRn for JJs on a high mobility (black dots) and low mobility (red dots) wafer, obtained at Vg = 0 V. Dashed lines are 1/L and 1/L2 fits to the data, indicating ballistic and diffusive transport, respectively
The junctions are measured using a quasi-four terminal current-biased circuit (Fig. 1a) at a temperature of 50 mK. We observe a clear supercurrent branch with zero differential resistance, dV/dI, followed by a jump to the resistive branch at switching current, Is. In small perpendicular magnetic fields, Bz, Fraunhofer-like interference patterns are observed, as seen in Fig. 1b. The magnitude of supercurrent is controlled using the gate (Fig. 1c). Lowering the gate voltage, Vg, leads to a reduction of the electron density in the 2DEG and therefore to a suppression of Is and an increase in the normal state resistance, Rn. In addition, we observe multiple Andreev reflections indicating an induced superconducting gap of 0.9 meV, and excess current measurements allow us to estimate transparencies in the range of 0.6–0.7 (representative data are provided in the Supplementary Note 2).
Ballistic superconductivity
Studying JJs of varying lengths (L = 0.7–4.7 μm), we gain insight into the transport regime. These devices fall in the long junction limit, since their lengths exceed the induced superconducting coherence length of around 500 nm (see Supplementary Note 2). In this limit the product of the critical current, Ic, and Rn is proportional to the Thouless energy33, ETh = ℏvFle/2L2, where vF is the Fermi velocity in the 2DEG. Thus, for ballistic (diffusive) transport where le = L (le < L), we expect IcRn to scale as 1/L (1/L2). In our experiments we measure Is, but expect it to be close to Ic, since the Josephson energy (≈20 K) is significantly larger than the fridge temperature (≈50 mK). Figure 1d shows IsRn for a set of JJs. We find a 1/L scaling (black dots) indicative of ballistic superconductivity, with deviations only for the longer (L ≥ 2.7 μm) junctions. Such a 1/L dependence was predicted decades ago34 but has only recently been experimentally observed over micron-scale lengths in clean graphene-based JJs35,36. To confirm the scaling arguments we also include data from a lower mobility wafer (see Supplementary Note 1) with le ≈ 0.5 μm (red dots) and find a 1/L2 scaling, consistent with diffusive behavior. In the remainder of this work we focus on JJs fabricated on the high mobility wafer.
0–π transitions in Josephson junctions
Using these ballistic junctions, we now explore their response to a Zeeman field. The theory of JJs with large SOI subjected to a magnetic field has been discussed extensively14,17,20. Below we briefly describe the essential elements of the physical picture. At zero B the Fermi surfaces are split due to the Rashba SOI (solid lines of Fig. 2a inset). The magnetic field then splits the bands by the Zeeman energy, EZ = gμBB, leading to a shift in the Fermi surfaces by ±δk/2. The depicted shift of the Fermi surfaces assumes that the spin-orbit energy dominates over the Zeeman energy, which is indeed the case for the measured JJs (see Supplementary Note 3 for a detailed discussion). Therefore, Cooper pairs (electrons with opposite momentum and spin) now possess a finite momentum, given by kF ⋅ δk = EZ(m*/ℏ2), where kF is the Fermi momentum and m* the effective mass. This translates to a phase acquired by the superconducting order parameter along the direction of current flow, Ψ(r) ∝ cos(δk ⋅ r)37,38,39. Depending on the length of the Cooper pair trajectories, |r|, the order parameter is either positive or negative, corresponding to the ground state of the JJ being at 0 or π superconducting phase difference, respectively. This oscillation of the order parameter results in a modulation of the critical current Ic ∝ |Ψ|, where a minimum of Ic is expected whenever the order parameter switches sign14,15. Taking only trajectories perpendicular to the contacts \(\left( {\delta {\mathbf{k}} = \delta {{k}}\widehat {\mathbf{x}},{\mathbf{k}}_{\mathrm{F}} = {{k}}_{\mathrm{F}}\widehat {\mathbf{x}}} \right)\), a JJ with length L will display minima in Ic when Lδk = (2N + 1)π/2, with N = 0, 1, 2... The condition for the first minimum (N = 0) can be expressed as a resonance condition in terms of the Zeeman and ballistic Thouless energy as EZ = πETh giving:
Magnetic field-driven 0−π transitions. a Variation of the switching current, Is, with in-plane magnetic field, By, at Vg = 0 V for the same JJ as in Fig. 1b, c. Two distinct revivals of Is are visible at By = 470 mT and 1250 mT, associated with 0−π transitions. The data are from two cool downs (CDs). The momentum shift, δk/2, of the Fermi surfaces due to the Zeeman field is sketched in the inset. The solid (dashed) lines depict the situation at zero (finite) magnetic field, and the arrows represent the spin orientation. b Is as a function of By at Vg = 0 V for four JJs with different lengths. For better visibility, Is is normalized with respect to Is at By = 0 T. Dashed lines indicate B0-π, the field at which the transition occcurs for each length. The inset shows a linear dependence of B0-π on 1/L, in agreement with ballistic transport. c Is vs. By at three different Vg for the JJ with L = 1.1 μm. B0-π shifts to lower values of By with more negative gate voltages. Is vs. Vg at By = 400 mT shows a non-monotonic behavior as displayed in the inset. The length and gate dependence of panel b, c are in qualitative agreement with Eq. (1)
The 0–π transition therefore depends on three experimentally accessible parameters: (1) applied magnetic field, (2) length of the JJ, and (3) carrier density. In the following, we demonstrate independent control of each of these parameters, allowing for a complete study of the free energy landscape of the junctions.
Magnetic field-driven 0–π transitions
We start by varying By, while n (controllable by Vg) and L remain fixed. The orientation of the magnetic field reflects the Fermi surfaces described, and avoids unwanted geometric effects40. Figure 2a shows the expected oscillation of Is with increasing By, displaying two distinct minima at By = 470 mT and By = 1250 mT (see Supplementary Note 4 for details about magnetic field alignment). This behavior is consistent with a magnetic field-driven 0–π transition, as discussed above, where the first (second) minimum corresponds to a transition of the JJ state from 0 to π (π–0). This interpretation is corroborated by the occurrence of the second minimum at a field value, which is approximately three times larger than the first. Note that this is incompatible with a Fraunhofer interference pattern that might arise from the finite thickness of the 2DEG. Furthermore, taking into account the gate dependence of the transition and other geometric considerations (discussed in detail in the Supplementary Note 5) allows us to conclusively rule out such a mechanism for the supercurrent modulation.
Next, we investigate how the length of the JJ influences B0-π, the magnetic field at which the transition occurs. Figure 2b presents the Is oscillation for JJs with four different lengths, showing that B0-π is systematically reduced for increasing L. Plotting B0-π with respect to 1/L (inset of Fig. 2b), we find a linear dependence as expected from Eq. (1). The transition points are therefore determined by the ballistic ETh, consistent with the conclusions from Fig. 1d. Finally, we check the dependence of the transition on the electron density. In Fig. 2c, we plot Is versus By for different gate voltages using a JJ with L = 1.1 μm. As Vg is lowered, B0-π shifts to smaller values, again in qualitative agreement with Eq. (1). Interestingly, above a certain magnetic field the state of the JJ (0 or π) becomes gate-dependent. For example at By = 400 mT, the junction changes from a 0-JJ (Vg = 0 V) to a π-JJ (Vg = −0.4 V), with a transition at Vg = −0.2 V. This indicates the feasibility of tuning the JJ into the π-state using gate voltages, while the magnetic field remains fixed.
Gate-driven 0–π transitions
These gate-driven transitions are demonstrated in Fig. 3a–d, which show a sequence of I–Vg plots for increasing in-plane magnetic fields. At By = 250 mT, Is displays a monotonic reduction with decreasing Vg. At a higher magnetic field, By = 325 mT, Is reveals a markedly different behavior, whereby the supercurrent first decreases and then (at Vg = −0.32 V) shows a clear revival, indicative of a gate-driven 0–π transition, where the resonance condition (EZ = πETh) is achieved by tuning the electron density. Increasing By further, continuously moves the transition point to higher gate voltages (larger density), perfectly in line with expectations for a 0–π transition. Figure 3e shows two line-cuts from Fig. 3d. At zero current bias, dV/dI shows a clear peak, indicative of a re-entrance of the supercurrent due to the the 0–π transition. However, at high bias, dV/dI increases monotonically, similar to the response at zero magnetic field. This eliminates trivial interference effects as an explanation for the supercurrent modulation, where one would expect a correlation between the two curves35,41,42.
Gate-driven 0–π transitions. a–d dV/dI as a function of I and Vg for several By as indicated. From By = 325 mT onward, a gate-driven 0−π transition becomes evident, characterized by a re-emergence of Is with decreasing Vg. As expected, the transition shifts to higher gate voltages with increasing By (see Supplementary Note 6 for sweeps at additional values of the magnetic field). e Line-cuts through panel d at I = 50 nA (black) and I = 0 nA (red). The low bias trace reveals the 0−π transition whereas the high bias trace shows a monotonic behavior
Construction of the 0–π phase diagram
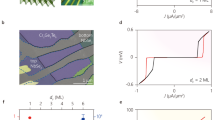
In contrast to the field-driven measurements (Fig. 2), controlling the transition with a gate avoids the need for time-consuming field alignment procedures, thus allowing us to efficiently explore a large parameter space in magnetic field and gate voltage. We now combine these results to construct a 0–π phase diagram of the JJ. The combination of a high quality 2DEG and relatively long devices results in well defined magneto-resistance oscillations, allowing us to directly extract the electron density in the junction. Figure 4a shows the Landau fan diagram in perpendicular magnetic fields, Bz, from which we identify the filling factors, ν = nh/eBz (Fig. 4b), and thereby obtain the n vs. Vg curve (Fig. 4c). We then plot all the transition points in Fig. 4d. The axes represent the two important energy scales in the system (By ∝ EZ and \(\sqrt n \propto E_{{\mathrm{Th}}}\)), thereby highlighting the 0 and π regions in the phase space. Finally, we compare our results with the theory of ballistic JJs represented by Eq. (1). To do so, we independently extract the effective mass (see Supplementary Note 7), m* = (0.022 ± 0.002)me, and fit the data to a single free parameter, gy (the in-plane g-factor), giving gy = 25 ± 3 in good agreement with previous measurements on similar InSb quantum wells28.
0−π phase diagram. a Landau fan diagram for the JJ with L = 1.1 μm, showing the transresistance (dR/dVg) as a function of Bz and Vg. The symbols indicate positions of integer filling factors ν at specific values of Vg. b Dependence of ν on 1/Bz along with linear fits used to extract the electron density, n(Vg), presented in c. d Phase diagram of the 0−π transition as a function of By ∝ EZ and \(\sqrt n \propto E_{{\mathrm{Th}}}\), containing all data points obtained from both field-driven (red) and gate-driven (black) 0−π transitions. For the error analysis, see Supplementary Note 6. We fit the data to Eq. (1) (blue line) with gy as a fitting parameter
Our work provides the first evidence of induced superconductivity in high quality InSb 2DEGs and demonstrates the creation of robust, gate-tunable π-Josephson junctions. We show that the 0–π transition can be driven both by magnetic fields and gate voltages. The significant region of phase space where the π–JJ is stable could prove advantageous in the study of topological superconductivity in planar JJs12,13,20,21. Moreover, these large SOI 2DEGs, in conjunction with our magnetic field compatible superconducting electrodes and clear Landau quantization, would also be excellent candidates to realize topological junctions in the quantum Hall regime7. Finally, the ability to control the ground state between 0 and π states using gates is analogous to recent experimental results in ferromagnetic JJs43, and could possibly serve as a semiconductor-based platform for novel superconducting logic applications44. We therefore establish InSb 2DEGs as a new, scalable platform for developing hybrid superconductor-semiconductor technologies.
Methods
Wafer growth
InSb-based 2DEGs were grown on semi-insulating GaAs (100) substrates by molecular beam epitaxy in a Veeco Gen 930 using ultra-high purity techniques and methods as described in ref. 45. The layer stack of the heterostructure is shown in Supplementary Fig. 1a. The growth has been initiated with a 100 nm thick GaAs buffer followed by a 1 μm thick AlSb nucleation layer. The metamorphic buffer is composed of a superlattice of 300 nm thick In0.91Al0.09Sb and 200 nm thick In0.75Al0.25Sb layers, repeated three times, and directly followed by a 2 μm thick In0.91Al0.09Sb layer. The active region consists of a 30 nm thick InSb quantum well and a 40 nm thick In0.91Al0.09Sb top barrier. The Si δ-doping layer has been introduced at 20 nm from the quantum well and the surface. The InxAl1−xSb buffer, the InSb quantum well and the InxAl1−xSb setback were grown at a temperature of 440 °C under a p(1 × 3) surface reconstruction. The growth temperature was lowered to 340 °C, where the surface reconstruction changed to c(4 × 4), just before the δ-doping layer, to facilitate Si incorporation46. The scanning transmission electron micrograph of Supplementary Fig. 1b reveals the efficiency of the metamorphic buffer to filter the dislocations.
Device fabrication
The devices are fabricated using electron beam lithography. First, mesa structures are defined by etching the InSb 2DEG in selected areas. We use a wet etch solution consisting of 560 ml deionized water, 9.6 g citric acid powder, 5 ml H2O2 and 7 ml H3PO4, and etch for 5 min, which results in an etch depth around 150 nm. This is followed by the deposition of superconducting contacts in an ATC 1800-V sputtering system. Before the deposition, we clean the InSb interfaces in an Ar plasma for 3 min (using a power of 100 W and a pressure of 5 mTorr). Subsequently, without breaking the vacuum, we sputter NbTi (30 s) and NbTiN (330 s) at a pressure of 2.5 mTorr, resulting in a layer thickness of approximately 200 nm. Next, a 45 nm thick layer of AlOx dielectric is added by atomic layer deposition at 105 °C, followed by a top-gate consisting of 10 nm/170 nm of Ti/Au.
Data availability
All data files are available at 4TU.ResearchData repository, https://doi.org/10.4121/uuid:5fab8273-8794-4cd7-96d4-ba8ec00a62cf
References
Riwar, R. P., Houzet, M., Meyer, J. S. & Nazarov, Y. V. Multi-terminal Josephson junctions as topological matter. Nat. Commun. 7, 11167 (2016).
Hart, S. et al. Induced superconductivity in the quantum spin Hall edge. Nat. Phys. 10, 638–643 (2014).
Pribiag, V. S. et al. Edge-mode superconductivity in a two-dimensional topological Insulator. Nat. Nanotech. 10, 593–597 (2015).
Wan, Z. et al. Induced superconductivity in high-mobility two-dimensional electron gas in gallium arsenide heterostructures. Nat. Commun. 6, 7426 (2015).
Amet, F. et al. Supercurrent in the quantum Hall regime. Science 352, 966–969 (2016).
Lee, G.-H. et al. Inducing superconducting correlation in quantum Hall edge states. Nat. Phys. 13, 693–698 (2017).
Finocchiaro, F., Guinea, F. & San-Jose, P. Topological π junctions from crossed Andreev reflection in the Quantum hall regime. Phys. Rev. Lett. 120, 116801 (2018).
Casparis, L. et al. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas. Nat. Nanotech. 13, 915–919 (2018).
Wang, J. I.-J. et al. Coherent control of a hybrid superconducting circuit made with graphene-based van der Waals heterostructures. Nat. Nanotech. 14, 120–125 (2019).
Rokhinson, L. P., Liu, X. & Furdyna, J. K. The fractional a.c. Josephson effect in a semiconductor-superconductor nanowire as a signature of Majorana particles. Nat. Phys. 8, 795–799 (2012).
Nichele, F. et al. Scaling of Majorana zero-bias conductance peaks. Phys. Rev. Lett. 119, 136803 (2017).
Ren, H. et al. Topological superconductivity in a phase-controlled Josephson junction. Nature 569, 93–98 (2019).
Fornieri, A. et al. Evidence of topological superconductivity in planar Josephson junctions. Nature 569, 89–92 (2019).
Bezuglyi, E. V., Rozhavsky, A. S., Vagner, I. D. & Wyder, P. Combined effect of Zeeman splitting and spin-orbit interaction on the Josephson current in a superconductor-two-dimensional electron gas-superconductor structure. Phys. Rev. B 66, 052508 (2002).
Yokoyama, T., Eto, M. & Nazarov, Y. V. Anomalous Josephson effect induced by spin-orbit interaction and Zeeman effect in semiconductor nanowires. Phys. Rev. B 89, 195407 (2014).
Szombati, D. B. et al. Josephson φ 0-junction in nanowire quantum dots. Nat. Phys. 12, 568–572 (2016).
Hart, S. et al. Controlled finite momentum pairing and spatially varying order parameter in proximitized HgTe quantum wells. Nat. Phys. 13, 87 (2017).
Chen, A. Q. et al. Finite momentum Cooper pairing in three-dimensional topological insulator Josephson junctions. Nat. Commun. 9, 3478 (2018).
Li, C. et al. Zeeman-effect-induced 0 − π transitions in ballistic Dirac semimetal Josephson junctions. Phys. Rev. Lett. 123, 026802 (2019).
Pientka, F. et al. Topological superconductivity in a planar Josephson junction. Phys. Rev. X 7, 021032 (2017).
Hell, M., Leijnse, M. & Flensberg, K. Two-dimensional platform for networks of Majorana bound states. Phys. Rev. Lett. 118, 107701 (2017).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Karzig, T. et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 95, 235305 (2017).
Plugge, S., Rasmussen, A., Egger, R. & Flensberg, K. Majorana box qubits. New J. Phys. 19, 012001 (2017).
Gilbertson, A. M. et al. Zero-field spin splitting and spin-dependent broadening in high-mobility InSb/In1−xAlxSb asymmetric quantum well heterostructures. Phys. Rev. B 79, 235333 (2009).
Kallaher, R. L., Heremans, J. J., Goel, N., Chung, S. J. & Santos, M. B. Spin-orbit interaction determined by antilocalization in an InSb quantum well. Phys. Rev. B 81, 075303 (2010).
Nedniyom, B. et al. Giant enhanced g-factors in an InSb two-dimensional gas. Phys. Rev. B 80, 125328 (2009).
Qu, F. et al. Quantized conductance and large g-factor anisotropy in InSb quantum point contacts. Nano. Lett. 16, 7509–7513 (2016).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Zhang, H. et al. Quantized Majorana conductance. Nature 556, 74–79 (2018).
Yi, W. et al. Gate-tunable high mobility remote-doped InSb/In1−xAlxSb quantum well heterostructures. Appl. Phys. Lett. 106, 142103 (2015).
Masuda, T. et al. Transport characteristics of InSb trench-type in-plane gate quantum point contact. Appl. Phys. Lett. 112, 192103 (2018).
Altshuler, B. L. & Spivak, B. Z. Mesoscopic fluctations in a superconductor–normal metal–superconductor junction. Sov. Phys. JETP 65, 343 (1987).
Ishii, C. Josephson currents through junctions with normal metal barriers. Prog. Theor. Phys. 44, 1525 (1970).
Ben Shalom, M. et al. Quantum oscillations of the critical current and high-field superconducting proximity in ballistic graphene. Nat. Phys. 12, 318–322 (2016).
Borzenets, I. V. et al. Ballistic graphene Josephson junctions from the short to the long junction regimes. Phys. Rev. Lett. 117, 237002 (2016).
Bulaevskii, L. N., Kuzii, V. V. & Sobyanin, A. A. Superconducting system with weak coupling to the current in the ground state. JETP Lett. 25, 290 (1977).
Demler, E. A., Arnold, G. B. & Beasley, M. R. Superconducting proximity effects in magnetic metals. Phys. Rev. B 55, 15174–15182 (1997).
Buzdin, A. I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 77, 935–976 (2005).
Suominen, H. J. et al. Anomalous Fraunhofer interference in epitaxial superconductor-semiconductor Josephson junctions. Phys. Rev. B 95, 035307 (2017).
Calado, V. E. et al. Ballistic Josephson junctions in edge-contacted graphene. Nat. Nanotech. 10, 761–764 (2015).
Allen, M. T. et al. Observation of electron coherence and Fabry-Perot standing waves at a graphene edge. Nano. Lett. 17, 7380–7386 (2017).
Gingrich, E. C. et al. Controllable 0–π Josephson junctions containing a ferromagnetic spin valve. Nat. Phys. 12, 564–567 (2016).
Terzioglu, E. & Beasley, M. R. Complementary Josephson junction devices and circuits: a possible new approach to superconducting electronics. IEEE Trans. Appl. Supercond. 8, 48–53 (1998).
Gardner, G. C., Fallahi, S., Watson, J. D. & Manfra, M. J. Modified MBE hardware and techniques and role of gallium purity for attainment of two dimensional electron gas mobility >35 × 106 cm2/V s in AlGaAs/GaAs quantum wells grown by MBE. J. Crys. Growth 441, 71–77 (2016).
Liu, W. K., Goldammer, K. J. & Santos, M. B. Effect of substrate temperature on Si compensation in δ-doped InSb and AlxIn1−xSb grown by molecular beam epitaxy. J. Appl. Phys. 84, 205–208 (1998).
Acknowledgements
We thank Ady Stern, Attila Geresdi, and Michiel de Moor for useful discussions. The research at Delft was supported by the Dutch National Science Foundation (NWO) and a TKI grant of the Dutch topsectoren program. The work at Purdue was funded by Microsoft Quantum.
Author information
Authors and Affiliations
Contributions
C.T.K. and C.M.M. fabricated and measured the devices. C.T., G.C.G. and M.J.M. designed and grew the semiconductor heterostructures. C.T., S.M., C.R.G., R.K., T.W., R.E.D., G.C.G. and M.J.M. characterized the materials. M.L. and G.S. provided the effective mass measurements. C.T.K., C.M.M., F.K.d.V. and S.G. performed the data analysis. The manuscript was written by C.T.K., F.K.d.V., C.M.M. and S.G., with input from all co-authors. S.G. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ke, C.T., Moehle, C.M., de Vries, F.K. et al. Ballistic superconductivity and tunable π–junctions in InSb quantum wells. Nat Commun 10, 3764 (2019). https://doi.org/10.1038/s41467-019-11742-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-11742-4
This article is cited by
-
Magnetically tunable supercurrent in dilute magnetic topological insulator-based Josephson junctions
Nature Physics (2024)
-
Sign reversal of the Josephson inductance magnetochiral anisotropy and 0–π-like transitions in supercurrent diodes
Nature Nanotechnology (2023)
-
Strong and tunable spin–orbit interaction in a single crystalline InSb nanosheet
npj 2D Materials and Applications (2021)
-
Engineered platforms for topological superconductivity and Majorana zero modes
Nature Reviews Materials (2021)
-
Josephson detection of time-reversal symmetry broken superconductivity in SnTe nanowires
npj Quantum Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.