Abstract
Coherence of solid state spin qubits is limited by decoherence and random fluctuations in the spin bath environment. Here we develop spin bath control sequences which simultaneously suppress the fluctuations arising from intrabath interactions and inhomogeneity. Experiments on neutral self-assembled quantum dots yield up to a five-fold increase in coherence of a bare nuclear spin bath. Numerical simulations agree with experiments and reveal emergent thermodynamic behaviour where fluctuations are ultimately caused by irreversible conversion of coherence into many-body quantum entanglement. Simulations show that for homogeneous spin baths our sequences are efficient with non-ideal control pulses, while inhomogeneous bath coherence is inherently limited even under ideal-pulse control, especially for strongly correlated spin-9/2 baths. These results highlight the limitations of self-assembled quantum dots and advantages of strain-free dots, where our sequences can be used to control the fluctuations of a homogeneous nuclear spin bath and potentially improve electron spin qubit coherence.
Similar content being viewed by others
Introduction
The excellent spin–photon interface of confined charges in III–V semiconductor quantum dots (QDs) has recently attracted a lot of attention for potential applications in photon-mediated quantum networks1,2,3. The large optical dipole moment of QDs makes ultrafast optical spin control feasible and permits unrivalled entanglement generation rates4,5,6. On the other hand, the coherence properties of the electron or hole spin qubit are strongly affected by hyperfine interaction with the fluctuating spin bath of the ~105 constituent nuclei of the QD7,8. Although hyperfine-induced qubit dephasing can be reduced using dynamical decoupling9,10, this approach requires a significant number of additional qubit manipulations and rapidly loses efficiency with increasing spin bath inhomogeneity, induced, e.g. by nuclear quadrupolar effects11,12,13,14,15.
There is a complementary pathway of controlling the nuclear spin bath itself with pulsed nuclear magnetic resonance (NMR)16,17. The system of a central (electron) spin qubit coupled to a nuclear spin bath is characterized by a complex hierarchy of interactions and dynamics timescales, meaning that achieving optimal control of the combined electron–nuclear spin coherence is a difficult problem. A simpler starting point is the problem of tailoring the coherence of a bare many-body nuclear spin bath (without a central spin). Examples for controlling spin–spin interactions are found in NMR spectroscopy, where sequences such as WAHUHA18 and MREV19,20 are used to average out dipolar couplings selectively. However, these solid echo sequences do not remove inhomogeneous broadening. By contrast, dynamical decoupling sequences based on π-pulse trains suppress inhomogeneous dephasing21,22,23, but exacerbate dipolar dephasing through the parasitic effect of instantaneous diffusion24,25,26. Thus, a different class of control sequences is required to remove both the effect of inhomogeneity and dipolar interactions.
In this work, we introduce pulse sequences which combine the features of dynamical decoupling with those of solid echoes and are designed to preserve coherence of an arbitrary quantum state of a spin bath. These combined Hahn and solid echo (CHASE) pulse sequences are tested using first-principle quantum mechanical simulations and experiments on neutral InGaAs/GaAs self-assembled QDs, where different isotopes offer access to spin baths with distinct regimes of inhomogeneous broadening and correlations in a many-body system. Even without the electron, the evolution of a bare spin bath reveals unexpected phenomena: in strongly disordered spin baths, where inhomogeneous broadening significantly exceeds the intrabath interactions, the ability to preserve coherence via global control is inherently limited—this case applies to self-assembled QDs, where spin-9/2 indium nuclei with their strong flip-flop coupling impose the ultimate limit on the maximum achievable spin bath coherence. In the case of homogeneous spin baths, we find that cyclic application of CHASE sequences can efficiently suppress spin–spin entanglement, leading to significant extension of coherence times even under nonideal control pulses. This highlights the advantages of spin qubits with homogeneous spin environments, such as dilute donor spins26,27, defect centres28, or strain-free GaAs/AlGaAs quantum dots9,10,29. We show that many-body decoherence emerges naturally under unitary evolution30: similar to the second law of thermodynamics, where useful energy is irreversibly dissipated into wasteful heat, the coherence is irreversibly converted into multipartite spin–spin entanglement. While it is not possible to eliminate spin bath dynamics completely, CHASE control sequences can transform random fluctuations into more deterministic evolution, which can in principle be decoupled from the qubit using standard control schemes17. More broadly, CHASE sequences may be used in quantum thermodynamic applications to preserve coherences, which play an important role in extracting work from nanoscale systems31,32,33.
Results
Design of CHASE pulse sequences
An intuitive approach used previously to extend nuclear spin lifetimes in silicon and diamond27,28 is to combine solid echo π/2-pulse cycles with refocusing π-pulses in order to suppress both the inhomogeneous dephasing and dipolar couplings. Here, we employ a rigorous average Hamiltonian theory (AHT)34, which is a form of perturbation theory based on Magnus expansion35. Using AHT as a benchmark tool (see details in Supplementary Note 1), we systematically analyse various combinations of π- and π/2-pulses to find those that maximise the spin bath coherence while minimising the pulse sequence length. The evolution of a nuclear spin bath Ii is analysed under a given pulse cycle in a strong external magnetic field Bz. We take into account a dipolar coupling term \({\cal{H}}_{\mathrm{d}}^{{\mathrm{zz}}}\) as well as a generic resonance offset Hamiltonian \({\cal{H}}_0^{\mathrm{z}}\), which describes inhomogeneous resonance broadening due to, e.g. chemical shifts or static quadrupolar interaction
where νij is the dipolar coupling constant between two spins Ii and Ij and Δνi denotes the resonance frequency offset of the ith nuclear spin. A larger spread in the Δνi values describes a spin bath with a larger disorder. The free induction decay (FID) of transverse magnetisation under this Hamiltonian is described by a rate \({\mathrm{\Gamma }} \propto 1/T_2^ \ast \propto \sqrt {\langle {\mathrm{\Delta }}\nu _i^2\rangle }\).
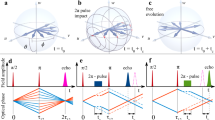
The shortest cycle (CHASE-5) giving a noticeable coherence increase contains only five pulses and is illustrated in Fig. 1a. Assuming infinitely short pulses (tπ → 0), the zeroth-order average Hamiltonian ∝ Γ vanishes. The leading residual contribution to decoherence is a first-order term ∝ ℏtcΓ2 mixing contributions from the inhomogeneous broadening Hamiltonian and the dipolar interaction36,37:
where tc is the full cycle time and \({\cal{H}}_{\mathrm{d}}^{{\mathrm{xx}}}\), \({\cal{H}}_0^{\mathrm{y}}\) are the dipolar and inhomogeneous broadening Hamiltonians acting along orthogonal equatorial axes \(\hat e_{\mathrm{x}}\) and \(\hat e_{\mathrm{y}}\).
Pulse sequences for refocusing inhomogeneous and dipolar broadening. a The combined Hahn and solid echo sequence CHASE-5 with cycle time tc = 3tπ + τevol consisting of the total gate time 3tπ and total free evolution time τevol = 6τ (where τ ≫ tπ is the free evolution time between two pulses). b Extension to CHASE-10, which is less sensitive to finite pulse durations tπ > 0. c Using symmetry considerations, a further optimised sequence CHASE-20 is constructed. d The longest sequence CHASE-34 with a total gate time 20tπ has the best refocusing capability for tπ → 0. The radio frequency (rf) carrier phases are φx = 0, φ−x = π for ±x rotations around the \(\hat e_{\mathrm{x}}\) axis and φy = π/2, φ−y = 3π/2 for ±y rotations around \(\hat e_{\mathrm{y}}\). Narrow pulses indicate π/2-rotations with pulse time tπ/2 and broad pulses correspondingly represent π-rotations with duration tπ
Under realistic experimental conditions, the tπ → 0 assumption is often not justified. For finite pulse durations tπ, the zeroth-order average Hamiltonian does not vanish under CHASE-5. However, we can obtain an average Hamiltonian of the form of Eq. (2) even for finite tπ by extending the cycle to CHASE-10 (Fig. 1b). Furthermore, by adding the pulse block shown in Fig. 1c, we can symmetrise the cycle to CHASE-20 and remove the first-order mixing term, condensing the average Hamiltonian to \(\bar {\cal{H}}_{{\mathrm{CHASE}} - {\mathrm{20}}} \propto {\cal{O}}(\hbar t_{\mathrm{c}}^2{\mathrm{\Gamma }}^3)\) independent of the pulse duration tπ. Finally, we identify the CHASE-34 sequence (Fig. 1d), which reduces the average Hamiltonian to a second-order mixing term for tπ → 0 but has non-vanishing lower-order terms for finite pulse durations. A comprehensive overview of the AHT calculations and residual Hamiltonians can be found in Supplementary Note 1.
CHASE NMR experiments on self-assembled quantum dots
We study the performance of these sequences experimentally on individual charge-free InGaAs QDs with ~105 nuclear spins. The average fractions of the isotopes in a dot are11: 50% (75As), ~24% (69Ga), ~16% (71Ga), ~9.5% (115In) and <0.5% (113In). We follow the ODNMR pump–probe scheme used in ref. 38: the QD sample is kept at low temperature (T = 4.2 K) and is subjected to a strong magnetic field Bz = 8 T. Using a confocal microscopy setup in Faraday configuration, we prepare the nuclear spin bath optically through polarisation-selective pumping of an exciton transition (dynamic nuclear polarisation). In this way, we achieve hyperfine-mediated spin bath polarisation degrees of up to 65%39,40. Radio frequency (rf) fields are coupled to the QD via a multi-winding copper coil in close proximity to the sample. Changes in the final bath polarisation are probed with a weak optical pulse measuring the energy splitting of the neutral exciton Zeeman doublet11.
We perform resonant pulsed NMR measurements on the inhomogeneously broadened central spin transition −1/2 \(\leftrightarrow\) +1/2 of the spin-3/2 75As (inhomogeneous width of \(\Delta \nu _{{\mathrm{inh}}} \sim 40\,{\mathrm{kHz}}\)), spin-3/2 \(^{71}\)Ga \(({\mathrm{\Delta }}\nu _{{\mathrm{inh}}} \sim 10\,{\mathrm{kHz}})\) and spin-9/2 115In \((\Delta \nu _{{\mathrm{inh}}} \sim 30\,{\mathrm{kHz}})\) nuclear ensembles11,38. In each experiment, the population difference of the Iz = ±1/2 states is enhanced via adiabatic rapid passage38,41 and only one isotope is manipulated with rf pulses, while the spins in the |Iz| ≥ 3/2 states as well as other isotopes are left to evolve freely during the pulse sequence. The phases of the π-pulses in all sequences are chosen to produce spin rotations around the \(\hat e_{\mathrm{x}}\) axis of the rotating frame. In each experiment, a π/2-pulse is applied prior to the multipulse cycle to initialise the transverse spin polarisation by converting energy into coherence31. We conduct experiments with initial π/2-rotation around the \(\hat e_{\mathrm{x}}\) axis (Carr–Purcell or CP-like sequences42, denoted as −X) and around the \(\hat e_{\mathrm{y}}\) axis (Carr–Purcell–Meiboom–Gill or CPMG-like sequences43, −Y): in this way, we distinguish between a genuine improvement of the spin coherence and spin locking effects44,45,46, which only stabilise spin magnetisation along a certain direction. A final π/2-pulse is an inverse of the initialisation pulse and projects the spin echo polarisation onto the \(\hat e_{\mathrm{z}}\) axis for optical readout38.
Figure 2 shows representative experimental dependencies of the spin echo amplitude on the total free evolution time τevol over n sequence cycles for 71Ga (a), 75As (b) and 115In (c) nuclei. The decay of the echo measured in terms of hyperfine shift ΔEhf is modeled by a compressed exponential decay function
where β is a compression factor47, T2 describes decoherence of the spin bath during free evolution, while reduction of the echo amplitude ΔEhf(τevol → 0) at short free evolution compared with the initial spin polarisation ΔEhf(t = 0) quantifies the imperfections of pulse spin rotations. The fitted values of T2 and ΔEhf(τevol → 0) are plotted in Fig. 3a–f for the three studied isotopes at different n expressed in terms of the total control gate time in units of tπ. The compression factor β depends on the spectral properties of the random process responsible for the decoherence24. From fitting, we find β≈1.0–2.0 for 71Ga and 75As, agreeing with the values typically found for various spin systems, whereas β≈0.7–1.0 in the case of 115In due to the non-exponential echo decay.
Nuclear spin echoes in a single neutral InGaAs QD. a Decay of the 71Ga NMR spin echo measured via hyperfine shift ΔEhf as a function of the total free evolution time τevol under different control sequences. Symbols mark experimental data and solid lines show best fits with Eq. (3). b, c Results for 75As and 115In, respectively
Experimental nuclear spin decoherence in an InGaAs quantum dot. a–c Dependence of the fitted 71Ga (a), 75As (b) and 115In (c) spin coherence time T2 on the number of sequence cycles n expressed as total rf gate time (in units of tπ). Results are shown for Hahn echo, CP and CHASE pulse sequences. d–f Respective fitted spin echo amplitude ΔEhf(τevol → 0) at short free evolution time τevol → 0 as a function of the total gate time. Error bars mark 90% confidence intervals. The data for one cycle of Hahn echo (HE) and CHASE-10 are combined with the data for integer cycle numbers n of CP and CHASE-20, respectively. The π-pulse durations used in these experiments are tπ = 4.3 μs (71Ga), tπ = 5.7 μs (75As) and tπ = 4.7 μs (115In)
Control of nuclear spin coherence in quantum dots
We start by analysing the common behaviour of all the isotopes under CP-X and CP-Y sequences with an alternating pulse carrier phase (sequence cycle −τ/2 − πx − τ − π−x − τ/2−). For increasing n, the echo amplitude is robust and T2 increases under CP-X (black squares in Fig. 3a–f), whereas under CP-Y (blue circles), the echo amplitude is rapidly reduced, owing to the limited available rf power resulting in deviation from the ideal hard pulses (see Supplementary Note 3). The contrasting behaviour of T2 under alternating phase CP-X/Y has been observed in other systems44,45,46,48 and has been attributed variably to spin locking48,49 or stimulated echoes50. Here, we ascribe the increase of T2 under CP-X to a form of pulsed spin locking arising from dipolar evolution during the finite-duration π-pulses49: our interpretation is based on the observation that the spin lock disappears for small pulse-to-cycle time ratios tπ/tc (see Supplementary Note 2).
We now examine the spin bath coherence under CHASE-10/20 and CHASE-34. Figure 3a–c shows an increase of T2 under CHASE, compared with the Hahn echo T2 for all isotopes. This increase occurs both under −X and −Y initialisation signifying a genuine increase of nuclear spin coherence, as opposed to pulsed spin locking under CP-X. However, the effect of CHASE sequence cycling (increasing n, and correspondingly increasing the total rf gate time) depends strongly on the isotope. For 71Ga, there is a steady increase in T2 up to \(T_2^{{\mathrm{CHASE}} - {\mathrm{Y}} - {\mathrm{20}}} \approx 6.0\,{\mathrm{ms}}\) at n = 16 (compared with Hahn echo \(T_2^{{\mathrm{HE}} - {\mathrm{X}}/{\mathrm{Y}}} \approx 1.0\,{\mathrm{ms}}\), Fig. 3a), revealing the expected convergence of the average Hamiltonian to zero with reducing cycle time tc. The growth of T2 with increasing n is accompanied by a gradual reduction of the echo amplitude (Fig. 3d)—the result of the nonideal (finite-duration) control pulses. By contrast, T2 is nearly constant for 75As (Fig. 3b), and the echo amplitude reduction is more pronounced, owing to the larger inhomogeneous broadening Δνi and limited rf pulse amplitude. While there is no difference for 71Ga, in the case of 75As, CHASE-34 somewhat improves coherence over CHASE-20, showing that with growing inhomogeneous broadening, higher-order Hamiltonian terms have a stronger impact on decoherence than the evolution during nonideal control pulses.
A rather different picture is observed for the spin-9/2 115In: beyond one cycle of CHASE-10, sequence cycling actually reduces T2 (Fig. 3c). Notably, this is not related to imperfect spin rotations, as reduction in echo amplitudes (Fig. 3f) is less pronounced than for 75As (Fig. 3f), suggesting a fundamentally different mechanism.
First-principle numerical simulations
In order to get a better insight into the underlying mechanisms of the many-body spin decoherence, we conduct first-principle quantum mechanical simulations of the nuclear spin bath evolution. We consider an ensemble of 12 dipolar-coupled nuclei with spin I and study the evolution of the Iz = ±1/2 subspace under rf driving of the central transition −1/2↔ +1/2 in the limits of large (Δνi ≫ νij) and vanishing (Δνi ≪ νij) inhomogeneous resonance broadening. Figure 4 shows the fitted coherence times (a, b, c) and echo amplitudes (d, e, f) for simulated spin echo decay curves in the following cases: I = 3/2, Δνi ≪ νij (a, d); I = 3/2, Δνi ≫ νij (b, e); I = 9/2, Δνi ≫ νij (c, f).
Simulated decoherence of a dipolar-coupled nuclear spin ensemble. Numerically simulated spin echo decay under different pulse sequences (see Supplementary Note 4 for representative data and further details) is fitted using Eq. (3) to derive nuclear spin coherence time T2 and the normalised spin echo amplitude 〈Iz(τevol → 0)/Iz(t = 0)〉 for short free evolution. a–c Fitted T2 as a function of the total gate time. d–f Corresponding gate time dependence of the spin echo amplitude. The results are presented for spin-3/2 75As nuclei with small inhomogeneous (quadrupolar) broadening Δνi (a, d), 75As with large Δνi (b, e) and spin-9/2 115In nuclei with large Δνi (c, f). Simulations are done for both infinitely short (tπ → 0, open symbols) and finite pulses (solid symbols, tπ = 5, 10 or 80 μs)
The simulations with Δνi ≫ νij and realistic rf pulse durations (solid symbols) are in very good agreement with the experiments on QDs (Fig. 3). Namely, T2 increases under CP-X (spin locking) and the echo amplitude reduces under CP-Y with growing n. The absolute simulated T2 values are only a factor of ~2 larger than in the experiment (which is due to the limited number of spins in the model, see Supplementary Fig. 5). Under CHASE-10/20, there is a reduction in T2 with increasing n for I = 9/2 spins similar to the 115In experiment (cf. Figs. 3c and 4c); there is a strong reduction of the echo amplitude for spin-3/2 nuclei with Δνi ≫ νij, in agreement with the 75As experiment (cf. Figs. 3b, e and 4b, e). Moreover, the pronounced increase of T2 for 71Ga with its smaller inhomogeneous broadening matches well the simulation with Δνi ≪ νij (cf. Figs. 3a and 4a).
Good agreement with experiments means the simulations are valid and can be used to explore the experimentally inaccessible regimes of ideal (infinitely short tπ → 0) control pulses (open symbols in Fig. 4). We readily find that even with perfect spin rotations (tπ → 0), the T2 of an inhomogeneously broadened (Δνi ≫ νij) spin ensemble under CHASE-10/20 shows a flat region for I = 3/2 (Fig. 4b) and even an initial decrease with growing n for I = 9/2 (Fig. 4c), which is contrary to limn→∞T2 = ∞, expected for the average Hamiltonian converging to zero. This unexpected discrepancy can be understood by noting that the Hahn echo (n = 1/2) coherence \(T_2^{{\mathrm{HE}} - {\mathrm{X}}/{\mathrm{Y}}}\) of spin-3/2 nuclei is ~3 times longer for Δνi ≫ νij due to the freezing of the dipolar spin–spin flip-flops by inhomogeneous broadening38. When n is increased, the CP-X/Y coherence time \(T_2^{{\mathrm{CP}} - {\mathrm{X}}/{\mathrm{Y}}}\) decreases (open squares and circles in Fig. 4b) and asymptotically approaches the \(T_2^{{\mathrm{HE}} - {\mathrm{X}}/{\mathrm{Y}}}\) obtained for Δνi ≪ νij where spin flip-flops are allowed (Fig. 4a). This suggests that the fast spin rotations induced by the high repetition rate train of infinitely short π-pulses effectively reduce the spin lifetime, broaden the homogeneous NMR linewidths and re-enable the frozen dipolar flip-flops in an inhomogeneous spin bath. Further simulations show that restoration of the flip-flops at larger inhomogeneous broadening requires a proportionally larger pulse repetition rate, confirming our interpretation. The ‘heating’ of the spins by frequent control pulses is then also responsible for slow convergence of the average Hamiltonian under CHASE sequences: the growth in T2 can only be achieved when the flip-flops are fully ‘thawed’ (at total gate times ≳200tπ in Fig. 4b, c). When projected to the Iz = ±1/2 states, the dipolar Hamiltonian has the form
so the role of the flip-flops is inherently most pronounced for I = 9/2 nuclei explaining the particularly strong reduction of 115In coherence under long control sequences. Flip-flops in the Iz = ±1/2 subspace are possible only for pairs with opposite spins. Thus, the heating of spins by control pulses will depend on the actual spin state. In other words, under frequent spin rotations, the many-body Hamiltonian itself becomes state-dependent, invalidating the AHT approximation. This mechanism is the main practical limitation in controlling the coherence of a disordered many-body spin system via global spin rotations.
Emergent thermodynamic behaviour in a spin bath
In addition to the measurable transverse spin magnetisation (coherence), numerical simulations permit probing quantities that are not directly observed in experiment. In particular, we now examine the evolution of the multipartite spin–spin quantum entanglement and demonstrate its fundamental role in the decoherence of an interacting spin bath. We quantify entanglement using the basis-independent intrinsic coherence measure CI introduced in ref. 51. Figure 5a shows the simulated time evolution of the transverse spin magnetisation 〈Ix(t)〉 of spin-3/2 nuclei with large inhomogeneous broadening Δνi ≫ νij. The results are averaged over randomly chosen initial eigenstates, and calculations are done for a fixed free evolution time τ between pulses. Figure 5b shows the evolution of the entanglement measure 〈CI(t)〉 for the same simulations, whereas Fig. 5c presents the same results and additional data for a homogeneous bath Δνi ≪ νij and spin-9/2 nuclei as trajectories in the entanglement-coherence 〈CI〉 − 〈Ix〉 phase space.
Simulated evolution of spin coherence and entanglement of a dipolar-coupled nuclear spin bath. Simulations are for the Iz = ±1/2 spin subspace under ideal (tπ → 0, open symbols) and finite (tπ = 10 μs, solid symbols) control pulses. a Time evolution of the average transverse magnetisation 〈Ix(t)〉 normalised by the initial magnetisation 〈Ix(0)〉 for spin-3/2 nuclei with large inhomogeneous broadening Δνi ≫ νij. Simulations are for free induction decay (FID, initialisation π/2-pulse only) and several cyclic pulse sequences. In the case of the cyclic sequences, 〈Ix(t)〉 is plotted only at the times of spin echoes. Note that the results here are simulated with a constant pulse-to-pulse delay τ, whereas the data in Fig. 2a–c are measured with a constant number n of pulse sequence repeats. b Evolution of the averaged spin–spin entanglement 〈CI〉 for the same simulations as in (a). c Trajectories in the 〈CI〉 − 〈Ix〉 phase space for the results of (a) and (b) as well as additional trajectories for small inhomogeneity (Δνi ≪ νij) and spin-9/2 nuclei
Under free induction decay (FID, crosses in Fig. 5), coherence 〈Ix(t)〉 is lost rapidly within ~30 μs, before the onset of entanglement 〈CI〉, which happens within ~3 ms (with some dips arising from the quasiperiodic evolution of a small spin ensemble). Application of the CP-Y sequence with ideal pulses (tπ → 0, open circles) has no effect on entanglement rate but extends coherence decay to the same timescale as entanglement. Going from CP-Y to CHASE-20 (open triangles), we observe a slowdown both in the 〈Ix〉 decay and 〈CI〉 growth, with the actual timescales strongly dependent on τ. The systematic relation between coherence and entanglement is demonstrated in Fig. 5c. Firstly, we find that evolution of the spin ensemble is always accompanied by a nearly monotonic conversion of coherence into entanglement. Secondly, we observe that despite different decoherence and entanglement rates, CP-Y and CHASE-20 with ideal pulses (tπ → 0) result in similar 〈CI〉 − 〈Ix〉 trajectories—extensive simulations for CP-X/Y and CHASE-X/Y show that this similarity holds for a wide range of pulse-to-pulse delays τ and applies to the case of a small inhomogeneity Δνi ≪ νij as well as spin-9/2 nuclei (a limited selection is shown in Fig. 5c to keep the graph readable). This gives an empirical evidence for the existence of a universal optimal trajectory, where 〈Ix〉 has maximal possible value at any given 〈CI〉. Figure 5c reveals the factors leading to suboptimal trajectories: in the absence of pulsed spin control (FID), transverse coherence in an inhomogeneous ensemble (Δνi ≫ νij) is rapidly lost well before emergence of any significant spin–spin entanglement. Furthermore, in an inhomogeneous system under pulsed spin control, going from ideal (tπ → 0, open symbols) to finite (tπ = 10 μs, solid symbols) control pulses, the trajectories become non-ideal with a shift towards the FID trajectory—this is very pronounced in the case of CP-Y (circles), while for CHASE-Y-20 with the same τ≈200 μs, the trajectory is closer to ideal, demonstrating the robustness of the CHASE sequence.
The evolution of coherence and entanglement can be interpreted in the framework of thermodynamics, i.e. without the need to know the exact form of the internal interaction Hamiltonian. The simulation results presented above show that transverse magnetisation 〈Ix〉 (coherence) of the spin system is analogous to work, i.e. a useful resource—in the case of nuclear spins, this work can actually be extracted, e.g. in the form of a current induced in a coil. By contrast, the entanglement 〈CI〉 is analogous to a wasteful heat, which cannot be used to generate coherence or extract work. The true decoherence of the spin ensemble is then associated with the irreversible generation of entanglement 〈CI〉 via the spin–spin interactions52,53. For example, the apparent quick loss of coherence in the FID of an inhomogeneous ensemble (Δνi ≫ νij) does not involve entanglement and in fact can be reversed by applying a π-pulse train (CP sequence). By contrast, once the maximum level of entanglement is reached (〈CI〉≈ 0.67 in Fig. 5c), it is impossible to recover coherence, regardless of the pulse sequence applied. It is important to note that there are no artificial sources of decoherence in the presented simulations, implying the evolution is unitary54 and thus demonstrating that the irreversible loss of coherence due to entanglement emerges naturally30 in a system of just a few dipolar-coupled spins. Entanglement due to the nonideal (finite) control pulses can be understood, since these pulses are equivalent to Hamiltonian quenches, which are generally known to induce irreversible evolution30. The difficulty of improving I = 9/2 indium spin coherence with pulsed control (Figs. 3c and 4c) also finds its explanation within the quantum thermodynamics framework, since stronger spin–spin correlations, which scale as ∝ (I + 1/2)2, generally result in faster entanglement growth53 and more irreversible evolution55.
Discussion
Based on our results, we conclude with the following interpretation of the relation between disorder, coherence and entanglement in dipolar-coupled spin baths. Suppression of spin–spin entanglement growth is required to extend spin coherence. This can be achieved by applying CHASE pulse cycles which converge the spin–spin interaction Hamiltonian to zero with reducing cycle time tc → 0. Realistic (finite-duration) control pulses impose a lower limit on tc. Despite that, the Hamiltonian in a homogeneous spin bath does converge under CHASE, predicting at least a factor of ~100 growth in coherence time under realistic parameters (Fig. 4a). A robust performance under nonideal soft pulses is a unique feature of CHASE distinguishing it from the previously introduced time-suspension sequences28,56,57,58 (see additional simulations in Supplementary Note 5). In a strongly inhomogeneous (disordered) spin bath, the spin–spin interactions are difficult to eliminate, even if ideal control pulses were possible (Fig. 4b, c), as control pulses themselves make the spin–spin interactions state-dependent, disrupting the convergence of the Hamiltonian. Finite control pulses impose further restrictions, limiting the maximum coherence time that can be realistically achieved in an inhomogeneous spin bath.
In the case of bare nuclear spin baths, CHASE can be used, for example, to preserve the quantum information transferred to the nuclei from the electron spin59. Another potential application is for dynamical suppression of the nuclear spin bath decoherence and fluctuations, which limit the electron spin qubit coherence in quantum dots. In order for dynamical suppression to be efficient, a significant fraction of the bath nuclei must be controlled. In self-assembled (InGaAs) quantum dots, the high-spin states |Iz| > 1/2 cannot be manipulated with coherent rf pulses, due to the extreme (few-megahertz) resonance broadening. While this can be overcome by nuclear spin hyperpolarisation29 and a subsequent population transfer38,41 to the |Iz| = 1/2 states, the real fundamental limitation for the InGaAs dots arises from the strongly correlated nature of the indium spin-9/2 subsystem. A more promising area of application are lattice-matched GaAs/AlGaAs quantum dots (both electrostatic15 and epitaxial29) or II–VI quantum dots60, where quadrupolar inhomogeneous broadening is small or absent, enabling significant extension of coherence times and the ability to operate in a wide range of magnetic fields ≳1–10 mT, requiring only that the nuclear Zeeman splitting is larger than the quadrupolar and dipolar nuclear spin interactions.
Interaction with a central (electron) spin complicates the coherent dynamics compared with the bare nuclear spin bath case. For example, the nuclear spin echo coherence in InGaAs electron-charged dots is few tens of microseconds41, but is expected to be longer in GaAs dots, due to the larger number of nuclei and smaller hyperfine interaction per nucleus. Using few microsecond-long rf pulses, it should be possible to examine extension of nuclear spin coherence under CHASE sequences in the presence of an electron. This would be a basis for exploring CHASE control of the nuclei, synchronised with electron spin qubit control, with the aim of creating a deterministically evolving nuclear spin environment and leading to extended electron spin qubit coherence—this approach can compliment existing techniques, such as preparation of the nuclear spin bath in a narrowed state via electron–nuclear feedback61,62.
More broadly, CHASE is promising for dopants and point defects in diamond, silicon and silicon carbide, where it can be applied both to the nuclear spin bath and directly to electron spin qubits to enhance their coherence beyond the limits of standard dynamical decoupling protocols by suppressing the instantaneous spin diffusion16,26 arising from electron–electron dipolar interactions. Further optimisation of spin bath decoherence freezing can be explored using techniques such as optimal control63.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Akopian, N., Wang, L., Rastelli, A., Schmidt, O. G. & Zwiller, V. Hybrid semiconductor-atomic interface: slowing down single photons from a quantum dot. Nat. Photonics 5, 230–233 (2011).
Meyer, H. M. et al. Direct photonic coupling of a semiconductor quantum dot and a trapped ion. Phys. Rev. Lett. 114, 123001 (2015).
Press, D., Ladd, T. D., Zhang, B. & Yamamoto, Y. Complete quantum control of a single quantum dot spin using ultrafast optical pulses. Nature 456, 218–221 (2008).
Delteil, A. et al. Generation of heralded entanglement between distant hole spins. Nat. Phys. 12, 218–223 (2016).
Stockill, R. et al. Phase-tuned entangled state generation between distant spin qubits. Phys. Rev. Lett. 119, 010503 (2017).
Khaetskii, A. V., Loss, D. & Glazman, L. Electron spin decoherence in quantum dots due to interaction with nuclei. Phys. Rev. Lett. 88, 186802 (2002).
Merkulov, I. A., Efros, A. L. & Rosen, M. Electron spin relaxation by nuclei in semiconductor quantum dots. Phys. Rev. B 65, 205309 (2002).
Bluhm, H. et al. Dephasing time of GaAs electron-spin qubits coupled to a nuclear bath exceeding 200 μs. Nat. Phys. 7, 109–113 (2011).
Malinowski, F. K. et al. Notch filtering the nuclear environment of a spin qubit. Nat. Nanotechnol. 12, 16–20 (2017).
Chekhovich, E. A. et al. Structural analysis of strained quantum dots using nuclear magnetic resonance. Nat. Nanotechnol. 7, 646–650 (2012).
Bechtold, A. et al. Three-stage decoherence dynamics of electron spin qubits in an optically active quantum dot. Nat. Phys. 11, 1005–1008 (2015).
Stockill, R. et al. Quantum dot spin coherence governed by a strained nuclear environment. Nat. Commun. 7, 12745 (2016).
Waeber, A. M. et al. Few-second-long correlation times in a quantum dot nuclear spin bath probed by frequency-comb nuclear magnetic resonance spectroscopy. Nat. Phys. 12, 688–693 (2016).
Botzem, T. et al. Quadrupolar and anisotropy effects on dephasing in two-electron spin qubits in GaAs. Nat. Commun. 7, 11170 (2015).
de Lange, G. et al. Controlling the quantum dynamics of a mesoscopic spin bath in diamond. Sci. Rep. 2, 382 (2012).
Perunicic, V. S., Hill, C. D., Hall, L. T. & Hollenberg, L. C. L. A quantum spin-probe molecular microscope. Nat. Commun. 7, 12667 (2016).
Waugh, J. S., Huber, L. M. & Haeberlen, U. Approach to high-resolution NMR in solids. Phys. Rev. Lett. 20, 180–182 (1968).
Rhim, W. K., Elleman, D. D. & Vaughan, R. W. Enhanced resolution for solid state NMR. J. Chem. Phys. 58, 1772–1773 (1973).
Mansfield, P., Orchard, M. J., Stalker, D. C. & Richards, K. H. B. Symmetrized multipulse nuclear-magnetic-resonance experiments in solids: measurement of the chemical-shift shielding tensor in some compounds. Phys. Rev. B 7, 90–105 (1973).
Cywinski, L., Lutchyn, R. M., Nave, C. P. & Das Sarma, S. How to enhance dephasing time in superconducting qubits. Phys. Rev. B 77, 174509 (2008).
Álvarez, G. A., Ajoy, A., Peng, X. & Suter, D. Performance comparison of dynamical decoupling sequences for a qubit in a rapidly fluctuating spin bath. Phys. Rev. A. 82, 042306 (2010).
Ajoy, A., Álvarez, G. A. & Suter, D. Optimal pulse spacing for dynamical decoupling in the presence of a purely dephasing spin bath. Phys. Rev. A. 83, 032303 (2011).
Klauder, J. R. & Anderson, P. W. Spectral diffusion decay in spin resonance experiments. Phys. Rev. 125, 912–932 (1962).
Raitsimring, A. M., Salikhov, K. M., Umanskii, B. A. & Tsvetkov, Y. D. Instantaneous diffusion in the electron spin echo of paramagnetic centers stabilized in a solid host. Sov. Phys. Solid State 16, 492 (1974).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11, 143–147 (2012).
Ladd, T. D., Maryenko, D., Yamamoto, Y., Abe, E. & Itoh, K. M. Coherence time of decoupled nuclear spins in silicon. Phys. Rev. B 71, 014401 (2005).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Chekhovich, E. A. et al. Measurement of the spin temperature of optically cooled nuclei and GaAs hyperfine constants in GaAs/AlGaAs quantum dots. Nat. Mater. 16, 982–986 (2017).
Dorner, R., Goold, J., Cormick, C., Paternostro, M. & Vedral, V. Emergent thermodynamics in a quenched quantum many-body system. Phys. Rev. Lett. 109, 160601 (2012).
Åberg, J. Catalytic coherence. Phys. Rev. Lett. 113, 150402 (2014).
Kammerlander, P. & Anders, J. Coherence and measurement in quantum thermodynamics. Sci. Rep. 6, 22174 (2016).
Vinjanampathy, S. & Anders, J. Quantum thermodynamics. Contemp. Phys. 57, 545–579 (2016).
Haeberlen, U. & Waugh, J. S. Coherent averaging effects in magnetic resonance. Phys. Rev. 175, 453–467 (1968).
Magnus, W. On the exponential solution of differential equations for a linear operator. Commun. Pure Appl. Math. 7, 649–673 (1954).
Rhim, W. K., Elleman, D. D. & Vaughan, R. W. Analysis of multiple pulse NMR in solids. J. Chem. Phys. 59, 3740–3749 (1973).
Burum, D. P. & Rhim, W. K. Analysis of multiple pulse NMR in solids. III. J. Chem. Phys. 71, 944–956 (1979).
Chekhovich, E. A., Hopkinson, M., Skolnick, M. S. & Tartakovskii, A. I. Suppression of nuclear spin bath fluctuations in self-assembled quantum dots induced by inhomogeneous strain. Nat. Commun. 6, 6348 (2015).
Eble, B. et al. Dynamic nuclear polarization of a single charge-tunable InAs/GaAs quantum dot. Phys. Rev. B 74, 081306 (2006).
Puebla, J. et al. Dynamic nuclear polarization in InGaAs/GaAs and GaAs/AlGaAs quantum dots under nonresonant ultralow-power optical excitation. Phys. Rev. B 88, 045306 (2013).
Wüst, G. et al. Role of the electron spin in determining the coherence of the nuclear spins in a quantum dot. Nat. Nanotechnol. 11, 885–889 (2016).
Carr, H. Y. & Purcell, E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 94, 630–638 (1954).
Meiboom, S. & Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 29, 688–691 (1958).
Suh, B. J., Borsa, F. & Torgeson, D. R. Use of an alternating-phase CPMG sequence to avoid spin-locking effects in T 2 measurements in solids. J. Magn. Reson. A 110, 58–61 (1994).
Dementyev, A. E., Li, D., MacLean, K. & Barrett, S. E. Anomalies in the NMR of silicon: unexpected spin echoes in a dilute dipolar solid. Phys. Rev. B 68, 153302 (2003).
Watanabe, S. & Sasaki, S. 29Si nuclear-spin decoherence process directly observed by multiple spin-echoes for pure and carrier-less silicon. Jpn. J. Appl. Phys. 42, L1350–L1352 (2003).
Bar-Gill, N. et al. Suppression of spin-bath dynamics for improved coherence of multi-spin-qubit systems. Nat. Commun. 3, 858 (2012).
Ridge, C. D., O’Donnell, L. F. & Walls, J. D. Long-lived selective spin echoes in dipolar solids under periodic and aperiodic π-pulse trains. Phys. Rev. B 89, 024404 (2014).
Li, D. et al. Intrinsic origin of spin echoes in dipolar solids generated by strong π pulses. Phys. Rev. B 77, 214306 (2008).
Franzoni, M. B. & Levstein, P. R. Manifestations of the absence of spin diffusion in multipulse NMR experiments on diluted dipolar solids. Phys. Rev. B 72, 235410 (2005).
Radhakrishnan, C., Parthasarathy, M., Jambulingam, S. & Byrnes, T. Distribution of quantum coherence in multipartite systems. Phys. Rev. Lett. 116, 150504 (2016).
Bardarson, J. H., Pollmann, F. & Moore, J. E. Unbounded growth of entanglement in models of many-body localization. Phys. Rev. Lett. 109, 017202 (2012).
Serbyn, M., Papić, Z. & Abanin, D. A. Universal slow growth of entanglement in interacting strongly disordered systems. Phys. Rev. Lett. 110, 260601 (2013).
Strasberg, P., Schaller, G., Brandes, T. & Esposito, M. Quantum and information thermodynamics: a unifying framework based on repeated interactions. Phys. Rev. X 7, 021003 (2017).
Lostaglio, M., Jennings, D. & Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 6, 6383 (2015).
Cory, D. G., Miller, J. B. & Garroway, A. N. Time-suspension multiple-pulse sequences: applications to solid-state imaging. J. Magn. Reson. 90, 205–213 (1990).
Moiseev, S. A. & Skrebnev, V. A. Short-cycle pulse sequence for dynamical decoupling of local fields and dipole-dipole interactions. Phys. Rev. A. 91, 022329 (2015).
Moiseev, S. A. & Skrebnev, V. A. Symmetric-cycle pulse sequence for dynamical decoupling of local fields and dipole-dipole interactions. J. Phys. B 48, 135503 (2015).
Taylor, J. M., Marcus, C. M. & Lukin, M. D. Long-lived memory for mesoscopic quantum bits. Phys. Rev. Lett. 90, 206803 (2003).
Ragunathan, G. et al. Direct measurement of hyperfine shifts and radio frequency manipulation of nuclear spins in individual CdTe/ZnTe quantum dots. Phys. Rev. Lett. 122, 096801 (2019).
Stepanenko, D., Burkard, G., Giedke, G. & Imamoglu, A. Enhancement of electron spin coherence by optical preparation of nuclear spins. Phys. Rev. Lett. 96, 136401 (2006).
Vink, I. T. et al. Locking electron spins into magnetic resonance by electron-nuclear feedback. Nat. Phys. 5, 764–768 (2009).
Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrüggen, T. & Glaser, S. J. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson. 172, 296–305 (2005).
Acknowledgements
The authors are grateful to Joseph Maguire and Ian Griffiths for assistance. This work was supported by the EPSRC Programme Grant EP/J007544/1, ITN S3NANO, UK Quantum Technology Hub for Quantum Communications Technologies and EPSRC grant EP/M013472/1. E.A.C. was supported by a University of Sheffield Vice-Chancellor’s Fellowship and a Royal Society University Research Fellowship. Computational resources were provided in part by the University of Sheffield HPC cluster Iceberg.
Author information
Authors and Affiliations
Contributions
M.H., P.S. and D.R. developed and grew the samples. A.M.W. and E.A.C. designed the pulse sequences. A.M.W., G.G. and G.R. conducted the experiments. E.A.C. conducted numerical simulations. A.M.W. and E.A.C. analysed the data. A.M.W., E.A.C. and M.S.S. wrote the paper with input from all authors. E.A.C. coordinated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Waeber, A.M., Gillard, G., Ragunathan, G. et al. Pulse control protocols for preserving coherence in dipolar-coupled nuclear spin baths. Nat Commun 10, 3157 (2019). https://doi.org/10.1038/s41467-019-11160-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-11160-6
This article is cited by
-
Low field slice-selective ZTE imaging of ultra-short \(T_2\) tissues based on spin-locking
Scientific Reports (2023)
-
The squeezed dark nuclear spin state in lead halide perovskites
Nature Communications (2023)
-
Harnessing many-body spin environment for long coherence storage and high-fidelity single-shot qubit readout
Nature Communications (2022)
-
Quantum sensing of a coherent single spin excitation in a nuclear ensemble
Nature Physics (2021)
-
Witnessing quantum correlations in a nuclear ensemble via an electron spin qubit
Nature Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.