Abstract
Transition metal oxides exhibit strong structure-property correlations, which has been extensively investigated and utilized for achieving efficient oxygen electrocatalysts. However, high-performance oxide-based electrocatalysts for hydrogen evolution are quite limited, and the mechanism still remains elusive. Here we demonstrate the strong correlations between the electronic structure and hydrogen electrocatalytic activity within a single oxide system Ti2O3. Taking advantage of the epitaxial stabilization, the polymorphism of Ti2O3 is extended by stabilizing bulk-absent polymorphs in the film-form. Electronic reconstructions are realized in the bulk-absent Ti2O3 polymorphs, which are further correlated to their electrocatalytic activity. We identify that smaller charge-transfer energy leads to a substantial enhancement in the electrocatalytic efficiency with stronger hybridization of Ti 3d and O 2p orbitals. Our study highlights the importance of the electronic structures on the hydrogen evolution activity of oxide electrocatalysts, and also provides a strategy to achieve efficient oxide-based hydrogen electrocatalysts by epitaxial stabilization of bulk-absent polymorphs.
Similar content being viewed by others
Introduction
With the growing concerns about the environmental pollution, global warming and the rapid depletion of petroleum resources, exploiting alternatively sustainable, clean, and renewable energy sources is becoming the most urgent scientific challenge for us in the modern society1,2. Supplying energy without toxic emissions, hydrogen, as a promising energy carrier, is believed to have a crucial role in the future scenario of energy applications3. In the past several decades, numerous efforts have been devoted to developing more sustainable hydrogen-production routes from renewable energy sources3,4. Among them, electrochemical water splitting using the hydrogen evolution reaction (HER, 2H+ + 2e− → H2) is considered as a promising method for hydrogen production3,4,5, owing to its unparalleled capacity and carbon-free nature. Thus, the efficiency of hydrogen production through electrolysis mainly depends on the catalytic performance of the HER electrocatalysts. Currently, the state-of-the-art electrocatalyst for HER is Pt/C, but it suffers from the prohibitive cost and scarcity2. Hence, it is highly desirable to explore new efficient HER electrocatalysts with low-cost and earth-abundant elements.
Transition metal oxides (TMOs) have attracted great interest in both condensed matter physics and materials science due to their fascinating tunable physical and chemical properties with high stability, low cost, and environmental friendliness6,7,8. Titanium dioxide (TiO2) is one of the most studied TMOs, and has been extensively explored as a photocatalyst for water splitting. Its efficiency can be dramatically enhanced by increasing its light absorption via fabricating black hydrogenated TiO2 nanocrystals9,10. The perovskite oxides with a general formula of ABO3 have been well studied as electrocatalysts for water splitting, and high-performance oxygen evolution reaction (OER) was realized in them11,12,13,14. Then, substantial efforts were devoted to understanding its mechanism and investigate the fundamental parameters that govern the catalytic activity15,16,17,18,19,20. Consequently, tuning the electronic structures of the electrocatalysts has been considered as an efficient method to enhance the OER activity of TMOs with stronger metal–oxygen (M–O) hybridization or higher covalency of the M–O bonds12,20,21. For HER, pure oxides were usually inactive, because of the extremely strong hydrogen adsorption on oxygen atoms. Nevertheless, most recently, several oxides (such as Pr0.5(Ba0.5Sr0.5)0.5Co0.8Fe0.2O3-δ2, SrNb0.1Co0.7Fe0.2O3-δ (nanorods)22, and CoO (nanorods)23) were reported to exhibit efficient HER activities. However, the origin of TMO-based HER mechanism with oxides’ characteristics, e.g., metal–oxygen hybridization, and the fundamental parameters that dominate the HER activity still remains unclear.
In this work, we demonstrate the close correlation between the electronic structures and HER catalytic activities in a single-oxide system (Ti2O3) with strongly correlated electrons. Generally, Ti2O3 has a corundum structure24,25 in bulk with an ultra-narrow bandgap (Eg ≈ 0.1 eV), exhibiting excellent photothermal effect26 and mid-infrared photodetection27. Interestingly, a new orthorhombic Ti2O3 polymorph that is absent in bulk was stabilized on Al2O3 single-crystal substrates via epitaxial stabilization, with intriguing emergent properties28,29. Here, extension of the polymorphism of Ti2O3 is further achieved by epitaxially stabilizing a cubic phase, which has not been reported before and is also bulk-absent. Taking advantages of the excellent structural flexibility of Ti2O3, we are able to explore the correlation between the physical electronic structures and HER activities within a single-material system, which provides a more precise understanding on the correlation without disturbance of varied elements. Systematical investigations are performed on the electronic structures, transport properties, and HER activities of three Ti2O3 polymorphs. Evident electronic reconstructions are observed in the epitaxially stabilized orthorhombic and cubic phases with modulated electron–electron interactions and charge-transfer energy. Importantly, smaller charge-transfer energy leads to the stronger hybridization strength of the Ti 3d –O 2p orbitals, which lower the d-band center of Ti and weakens the H adsorption, further resulting in the enhanced HER activity in those epitaxially stabilized polymorphs. This electronic-reconstruction enhanced HER activity, achieved in the structure-tailored Ti2O3, introduces a previously unrecognized route to explore more efficient TMO-based HER electrocatalysts by enhancing the metal–oxygen hybridization via selective stabilization of polymorph phases.
Results
Fabrication and structural characterizations of Ti2O3 polymorphs
Three Ti2O3 polymorphs were successfully fabricated in the epitaxial film form by using the pulsed laser deposition (PLD) technique (Fig. 1a). During the film growth, the same corundum (trigonal) Ti2O3 target was used for stabilizing all Ti2O3 polymorphs. The phase separation was controlled by carefully varying deposition temperature and substrates’ symmetry, which are widely used for the oxides epitaxial stabilization30,31. With the advent of thin-film epitaxial stabilization, new polymorphs that do not exist in bulk could be stabilized on single-crystal substrates28,29,31, resulting in the extension of the oxides’ polymorphism. Polymorphism describes the occurrence of different lattice structures and symmetries in a crystalline material with identical composition, which is a critical and attractive phenomenon in material science and condensed matter physics32,33. Polymorphs would exhibit different physical, chemical, and mechanical properties due to their varied structural characteristics34,35,36,37, e.g., the polymorph-dependent metal–semiconductor transitions in Ti3O538,39.
Fabrication and structural characterizations of the Ti2O3 polymorphs. a Schematic of the PLD chamber where Ti2O3 polymorphs were fabricated using the same (α-Ti2O3) target. b Unit cells for γ-Ti2O3, o-Ti2O3, and α-Ti2O3 polymorphs from top to bottom, respectively. c–e In-plane epitaxial relationships for γ-Ti2O3 on STO, o-Ti2O3, and α-Ti2O3 on Al2O3, respectively. TiO2–STO (001) view refers to view the TiO2-terminated STO (Supplementary Fig. 5) from the < 001 > direction. f HR-XRD patterns of Ti2O3 polymorphs epitaxially stabilized on the single-crystal substrates. Source data are provided as a Source Data file
By recrystallization on the substrates during epitaxial growth (Fig. 1a), three different Ti2O3 polymorphs (Fig. 1b), trigonal (denoted as α-Ti2O3), orthorhombic (denoted as o-Ti2O3), and cubic (denoted as γ-Ti2O3), are obtained on single-crystalline α-Al2O3 and SrTiO3 (STO) substrates. More details of the unit cell parameters for Ti2O3 polymorphs can be found in Supplementary Fig. 1. Both α- and o-Ti2O3 are stabilized on α-Al2O3 (0001) substrates, selected by increasing the deposition temperature from 600 to 900 °C, while cubic γ-Ti2O3 is stabilized on STO substrates at 600 °C. More details for the stabilization of Ti2O3 polymorphs can be found in the Supplementary Fig. 2 and the Supplementary Note 1. Atomic force microscopy (AFM) was used to characterize the surface microstructure and roughness of the Ti2O3 films. As shown in Supplementary Fig. 3, the root mean square (RMS) roughness for all Ti2O3 samples is quite similar and close to 1 nm, which is very small with respect to their thickness (~300 nm), indicating the flat surfaces that are further confirmed by the scanning electron microscopy (SEM) and scanning transmission electron microscopy (STEM) images (Supplementary Fig. 4). Interestingly, unexpected fascinating properties (such as ferromagnetism28 and superconductivity29) were discovered in the o-Ti2O3, demonstrating strong structure–property correlations in Ti2O3, which motivated us to further explore the polymorphism of Ti2O3.
Figure 1c–e shows the in-plane epitaxial relationships for γ-, o-, and α-Ti2O3 film/substrate heterostructures, respectively. The corresponding high-resolution X-ray diffraction (XRD) patterns are shown in Fig. 1f. The epitaxial relations for α- and o-Ti2O3 have been determined to be (0001) α-Ti2O3 || (0001) α-Al2O3 and (011) o-Ti2O3 || (0001) α-Al2O3 by high-resolution STEM and selected area electron diffraction (SAED)29. Since γ-Ti2O3 is a newly stabilized polymorph, we utilized HR-XRD and HR-STEM (Fig. 2) to investigate its epitaxial growth on STO. As shown in Fig. 1f, (004) γ-Ti2O3 was directly grown on (002) STO (Supplementary Fig. 5), indicating a cubic-on-cubic growth. Figure 2a schematically illustrates the epitaxial growth of γ-Ti2O3 on STO, which is further confirmed by in-plane synchrotron-based X-ray φ-scan (Supplementary Fig. 6 and Supplementary Note 2). As isomorphs of γ-Ti2O3, γ-Al2O340,41, and γ-Fe2O342 were also stabilized on STO with the same epitaxial relationship. Moreover, γ-Ti2O3 is also successfully stabilized on LaAlO3 (LAO) substrates, which is identical with that on STO (Supplementary Fig. 6).
Microstructural characterization of the cubic γ-Ti2O3 polymorph. a Sketch of the γ-Ti2O3/STO heterostructure. b Cross-sectional low-resolution STEM image and (c) high-resolution HAADF-STEM image of the γ-Ti2O3/STO interface. d HAADF-STEM image and the corresponding HAADF signal profile obtained along (100) and (001) directions of γ-Ti2O3 from (c)
In-depth STEM measurements were performed to investigate the cubic γ-Ti2O3 on STO. Figure 2b shows the cross-section low-resolution STEM image of the spinel/perovskite γ-Ti2O3/STO heterointerface. The thickness of the γ-Ti2O3 film is about ~300 nm. It needs to be pointed out that the thickness for all Ti2O3 films is fixed at around ~300 nm in order to get the bulk intrinsic properties of these polymorphs. High-resolution high-angle annular dark-field (HAADF) STEM imaging (Fig. 2c) presents the highly crystalline γ-Ti2O3 and the cubic-on-cubic epitaxial growth on STO. The lattice parameters of γ-Ti2O3 measured from the HAADF-STEM signal profiles (Fig. 2d) along (100) and (001) are a = c ≈ 8.5 Å, consistent with the HR-XRD result ((004): 42.35˚ corresponds to c = 8.53 Å). To shed light on the evolution of Ti valence states at the interface, electron energy loss spectroscopy (EELS) line scan was collected across the γ-Ti2O3/STO interface. As shown in Supplementary Fig. 7, the valence state of Ti evolves from 4 + to 3 + crossing the interface from STO to γ-Ti2O3 with obvious variation at the Ti L2,3-edge and O K-edge (Supplementary Note 3). Moreover, the Ti L2,3-edge EELS spectrum collected from γ-Ti2O3 is same as those obtained from α- and o-Ti2O328,43, indicating the same Ti3+ chemical environment. Three Ti2O3 polymorphs with same Ti3+ valence states but different lattice symmetries are identified and confirmed. Subsequently, the electronic band structures of these Ti2O3 polymorphs are carefully investigated by spectroscopic techniques. In order to eliminate the influence of STO substrates with possible oxygen vacancies, formed during the deposition, that would affect that light absorption and conductivity of STO44, the following measurements of γ-Ti2O3 were mainly performed on the γ-Ti2O3/LAO samples.
Determination of electronic reconstructions in Ti2O3 polymorphs
With an unpaired 3d1 election, α-Ti2O3 is regarded as an antiferromagnetic Mott insulator with a unique and broad metal–insulator transition (MIT)45,46,47. In strongly correlated TMO systems, the electron–electron interaction, represented by the on-site Coulomb repulsion U, is significant, and opens the Mott–Hubbard gap inside the transition metal 3d band between the lower Hubbard band (LHB) and upper Hubbard band (UHB). Charge-transfer energy Δ, the energy difference between the oxygen 2p band and transition metal 3d band, is another crucial parameter in determining the physical and chemical properties of TMOs20,48. As illustrated in Fig. 3a, depending on the relative magnitudes of U and Δ, strongly correlated TMOs could be classified into Mott insulators (U < Δ) and charge-transfer insulators (U > Δ). With tunable U and Δ, modulations of the electronic properties that impact on electrochemical activities could be achieved49,50,51.
Electronic reconstructions in Ti2O3 polymorphs. a Schematic energy band diagram for the Mott insulator and charge-transfer insulator. b Proposed electronic structure of Ti2O3 by Goodenough et al.52 c–e Optical conductivity spectra of the α-, o-, and γ-Ti2O3 polymorphs, taken by the ellipsometry at room temperature. Insets are the corresponding absorption coefficient (α) of the Ti2O3 polymorphs, collected by the UV–Vis spectroscopy at room temperature. f Evolution of the U and Δ in Ti2O3 polymorphs. Source data are provided as a Source Data file
Proposed by Goodenough et al.52, the electronic band structure of α-Ti2O3 could be well described using the molecular orbital theory (Fig. 3b). The trigonal crystal field splits Ti 3d t2g orbitals into a pair of \(e_g^\pi\) orbitals and an a1g orbital near the Fermi level. Furthermore, the a1g band splits into the bonding a1g and the antibonding \(a_{1g}^ \ast\) bands, while the \(e_g^\pi\) band splits into the bonding \(e_g^\pi\) and the antibonding \(e_g^{\pi \ast }\) bands, mainly because of the hybridization of the Ti–Ti orbitals. (The \(e_g^\pi\) and \(e_g^{\pi \ast }\) bands are usually located at the same energy level, since the \(e_g^\pi\) − \(e_g^{\pi \ast }\) splitting is very small.) The MIT of Ti2O3 could be explained by the band-crossing scenario53,54. That is, the metallic state emerges when the \(e_g^\pi\) and a1g bands overlap with increased temperature, while the insulating state occurs when a gap arises between the \(e_g^\pi\) and a1g bands with decreased temperature54. At room temperature, the bandgap of insulating α-Ti2O3 is around 0.1 eV, which was verified by both electrical and optical measurements24,28. Based on the above proposed electronic structure, the U and Δ in Ti2O3 could be assigned specifically to the a1g − \(e_g^\pi\) and \(O_{2p}\) − \(e_g^\pi\) transitions, respectively.
To quantify the U and Δ in different Ti2O3 polymorphs, spectroscopic ellipsometry and light absorption measurements were performed at room temperature. Figure 3c–e shows the optical conductivity (σ) of α-, o-, and γ-Ti2O3, respectively, demonstrating the a1g − \(e_g^\pi\) and a1g − \(a_{1g}^ \ast\) interband transitions are located at around 1 and 3 eV55. Concomitant with the different lattice symmetries, substantial electronic reconstructions were observed among the three Ti2O3 polymorphs. Specifically, the U \((a_{1g} - e_g^\pi )\) in α-, o-, and γ-Ti2O3 polymorphs increase from 0.85 eV to 1.01 eV, then to 1.10 eV, respectively, revealing stronger electron–electron interactions. Moreover, typical Drude absorptions are observed in o- and γ-Ti2O3 at low photon energies (ħω), indicating high free electron concentrations in these two polymorphs. This point will be discussed later, combined with the electronic transport results. The Δ \((O_{2p} - e_g^\pi )\) in the Ti2O3 polymorphs were obtained from the UV–Vis light absorption data, which are correspondingly shown as insets of Fig. 3c–e. The absorption coefficients (α) of Ti2O3 polymorphs are in the range of ~0.6 to 2.1 × 105 cm−1 at the UV–Vis range, demonstrating a strong light absorption. In order to extract the energy positions for each optical transitions, Gaussian-fitting analysis was performed. Similarly, the \(a_{1g} - a_{1g}^ \ast\) transitions are still located at around 3 eV, which is consistent with the ellipsometry results. Importantly, the Δ \((O_{2p} - e_g^\pi )\) for α-, o-, and γ-Ti2O3 polymorphs are verified to be 4.78, 4.48, and 4.37 eV, respectively. As a result, the Δ decreases in the Ti2O3 polymorphs with increasing U (Fig. 3f). According to these electronic reconstructions, strong polymorph-dependent properties could be expected in Ti2O3. It is well known that Δ is directly related to the hybridization of M–O orbitals, which would further impact on the conductivity48,49,50 and electrochemical activity20,51.
Hybridization strength of Ti–O orbitals in Ti2O3 polymorphs
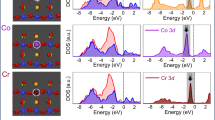
In order to estimate the hybridization of Ti–O orbitals in Ti2O3, synchrotron-based X-ray absorption spectroscopy (XAS) was performed to examine the electronic structures of Ti2O3 polymorphs. The experimental XAS configuration is shown as inset in Fig. 4a. Ti L3 and L2-edge transitions (Fig. 4a) in all Ti2O3 polymorphs are located at ~458.6 eV and ~463.7 eV, respectively, consistent with the bulk Ti2O356. The similar Ti L-edge XAS spectra obtained from the different Ti2O3 polymorphs reveal that they are sharing the same Ti3+ chemical environment as expected. However, distinct variations are observed at the O K-edge XAS spectra. The O K-edge XAS spectrum has been widely utilized to study the hybridization of the M–O orbitals in oxides21,57,58. Notably, the O K-edge pre-edge region near the threshold of the O K-edge XAS demonstrates the hybridization between O 2p and transition metal 3d states21,57. As shown in Fig. 4b, two pre-peaks, located at ~531.7 and ~533.7 eV, are used to evaluate the extent of the hybridization of O 2p with Ti 3d eg and t2g orbitals. Besides the pre-edge, another region of the O K-edge at higher energy range corresponds to O 2p orbitals hybridized with Ti 4 s,4p orbitals. Obviously, hybridization of O 2p with Ti 3d and Ti 4 s,4p orbitals are changed in the Ti2O3 polymorphs duo to their distinct crystal structures.
Hybridization strength of the Ti–O orbitals in different Ti2O3 polymorphs. a Ti L2,3-edge and (b) O K-edge XAS spectra of the Ti2O3 polymorphs, collected in the TEY mode at room temperature. The experimental configuration is shown as inset in (a). The intensity of the O-K edge XAS spectra in (b) are normalized at 547.7 eV. c Fitting and (d) Integrated intensities of the O K-edge pre-edge region (from 528 to 537.2 eV) with subtraction of the linear backgrounds for Ti2O3 polymorphs. The hybridization factor (H.F.) for O2p-eg and O2p-t2g is obtained by calculating the integrated intensities of the fitted eg (blue lines in c) and t2g (red lines in c) curves. Source data are provided as a Source Data file
Integrated intensity of the O K-edge pre-edge region with the subtraction of linear backgrounds is commonly used to quantify the hybridization strength of the M–O orbitals in oxides11,21. Here, we define a hybridization factor (H.F.) as the integrated intensities of the XAS O K-edge pre-edge region (from 528 to 537.2 eV) with the subtraction of the linear backgrounds (shaded area in Fig. 4c). As a consequence, Ti–O hybridization is the strongest in γ-Ti2O3 with the smallest Δ, while that is the weakest in α-Ti2O3 with the largest Δ (Fig. 4d). The same conclusion about the Ti–O hybridization can be obtained by the X-ray photoelectron spectroscopy (XPS) (Supplementary Fig. 8, Supplementary Table 1 and Supplementary Note 4). Stronger Fe 3d –O 2p hybridization was observed in the γ-Fe2O3 than that in the α-Fe2O359, indicating that the stronger M–O hybridization can be induced by the crystal structure and electronic structure of the γ-phase. As we know, smaller Δ with stronger hybridization leads to the delocalization of electrons, and thus increases the conductivity of oxides48,49,50.
Electronic transport properties of Ti2O3 polymorphs
As expected, various electronic transport behaviors (Fig. 5) are observed in the Ti2O3 polymorphs with their electronic reconstructions, revealing strong lattice–charge coupling. As shown in Fig. 5a, all Ti2O3 polymorphs show very low resistivity, and semiconducting behavior is dominant for all below 400 K (except a metal–insulator transition is observed at 360 K for o-Ti2O3). The kink feature in the resistivity of the newly stabilized γ-Ti2O3 at around 140 K reveals a semiconductor–semiconductor transition (SST), which is similar to that of o-Ti2O329 and Mg[Ti2]O460 caused by the instability of Ti–Ti dimerization. Interestingly, α-Ti2O3 shows a nearly flat resistivity below 20 K, while a sudden drop (superconductivity)29 and continuous increase were observed in that of o-Ti2O3 and γ-Ti2O3, respectively (inset of Fig. 5a), indicating the diversity and complexity of Ti2O3. In addition to the electron–electron interaction, the electron–phonon interaction is also an important factor in determining the electronic behaviors of the Ti2O3 polymorphs29,54, which makes Ti2O3 more complicated and interesting. The change of the resistivity from 400 to 2 K in γ-Ti2O3 is more than one order of magnitude, which is larger than that of α-Ti2O3 and o-Ti2O3. Moreover, the transport behavior of γ-Ti2O3 is consistent even when its thickness decreases to 20 nm (Supplementary Fig. 9).
Furthermore, the carrier information of the Ti2O3 polymorphs was investigated by Hall-effect measurement. Interestingly, o-Ti2O3 and γ-Ti2O3 are confirmed to be n-type semiconducting, whereas α-Ti2O3 is a p-type semiconductor. As shown in Fig. 5b, high electron concentrations at the scale of ~1022 cm−3 are observed in o-Ti2O3 and γ-Ti2O3, which could contribute to the strong Drude absorptions in Fig. 3d, e. Surprisingly, an unexpected increase is observed in the carrier concentration of o-Ti2O3 at T < 250 K, while that of γ-Ti2O3 decreases continuously below 400 K. Increase of the carrier concentration in o-Ti2O3 may be correlated to its superconductivity at lower temperatures, which needs further investigations. Lower carrier concentration (~1021 cm−3) is observed in α-Ti2O3, which is about one order of magnitude lower than in o-Ti2O3 and γ-Ti2O3. However, the carrier mobility (>10 cm2 V−1 s−1) in α-Ti2O3 is about one order of magnitude higher than those in o-Ti2O3 and γ-Ti2O3 (Fig. 5c). It should be noted that higher electron concentration leads to more carrier scattering, which results in the lower electron mobility in o-Ti2O3 and γ-Ti2O3. Besides, the more significant change of the resistivity (400–2 K) in γ-Ti2O3 results from the constructive effect between the decreased carrier concentration and mobility, while destructive effects between the carrier concentration and mobility are observed in the α-Ti2O3 and o-Ti2O3 that results in the smaller change of the resistivity (400–2 K). More details are shown in Supplementary Note 5. Notably, the carrier concentrations of Ti2O3 polymorphs at 300 K increases with smaller Δ (Fig. 3f) that result in more delocalized electrons, consistent with the previous scenario48,49,50.
Correlation between HER activity and electronic reconstructions
In order to elucidate the relationship between the electronic reconstructions and HER catalytic activity, Ti2O3 polymorphs were used directly as the working electrodes for HER measurements in 0.5 M H2SO4. The configuration of the HER electrochemical cell is schematically illustrated as the inset of Fig. 6a. Obviously, the electronic reconstructions in Ti2O3 influenced the HER activities significantly, representing strong polymorph dependence. The influence of the surface microstructure or defect on the observed polymorph-dependent HER performance in Ti2O3 is discussed and ruled out in Supplementary Note 6. As shown in Fig. 6a, b, the newly stabilized γ-Ti2O3 has the best activity with the smallest Tafel slope (199 mV dec−1), while the bulk-phase α-Ti2O3 is the least active HER catalyst with the largest Tafel slope (241 mV dec−1). Noticeably, the γ-Ti2O3 displays the smallest overpotential of 271 mV (Fig. 6c) to produce a current density of 10 mA cm−2, which is a ~45% reduction compared with that of the α-Ti2O3 (495 mV). The Tafel plots observed here are a little bit larger than those of the nanostructured oxide samples22,23, which would be caused by the limited surface area of our film samples. Thus, further improvements could be expected by nanostructure-array fabrications on the films with increased surface areas.
Electrocatalytic hydrogen-evolution activities of Ti2O3 polymorphs. a Linear sweep voltammetry (LSV) and (b) corresponding Tafel plots of the LSV curves for α-, o-, and γ-Ti2O3 polymorphs (electrolyte: 0.5 M H2SO4, scan rate: 5 mV s−1). c Overpotential of HER for Ti2O3 polymorphs (@ −10 mA cm−2), deduced from (a). d Correlations between the physical parameters and HER activity in Ti2O3 polymorphs. Source data are provided as a Source Data file
Impressively, the enhanced HER activities are observed in those epitaxially stabilized phases (o- and γ-Ti2O3) that do not exist in bulk form, which may be applicable to other oxide materials. Hence, efficient TMO-based HER catalysts could be achieved by the selective stabilization of bulk-absent polymorphic phases. Most importantly, the HER activity of the Ti2O3 polymorphs are strongly correlated to their electronic structures. As shown in Fig. 6d, the overpotentials of HER decreases with smaller Δ accompanied with stronger Ti–O hybridization, unambiguously demonstrating the HER activity is highly enhanced by the electronic reconstructions. Noteworthily, the Faradaic resistances of Ti2O3 polymorphs, obtained from the electrochemical impendence spectra (Supplementary Fig. 10), do not follow the trend of their HER performances, indicating the enhanced activity is not simply derived from their electrical conductivity, but indeed from the electronic reconstructions. The overall HER catalytic activity of γ-Ti2O3 may not be comparable with those of the state-of-the-art noble metals (e.g., Pt/C), but considering the tiny weight of the γ-Ti2O3 film (~100 μg for 300 nm on 1 × 1 cm substrates), the activity of γ-Ti2O3 is still remarkable as an oxide material. (More discussion is presented in Supplementary Note 7). Moreover, the correlation between the electronic reconstructions and HER activities in the Ti2O3 polymorphs are robust.
Subsequently, the mechanism behind the electronic-reconstruction enhanced HER activity in Ti2O3 is explored. In general, a multi-step electrochemical process would take place, during the HER, on the surface of the electrocatalyst, where gaseous hydrogen (H2) is generated. In acid solution, the HER would proceed via either Volmer–Heyrovsky or Volmer–Tafel pathways61 (Volmer: \({\mathrm{H}}^ + + {\mathrm{M}} + {\mathrm{e}}^ - \leftrightharpoons {\mathrm{M}} - {\mathrm{H}}^ \ast ;\) Heyrovsky: \({\mathrm{M}} - {\mathrm{H}}^ \ast + {\mathrm{H}}^ + + {\mathrm{e}}^ - \leftrightharpoons {\mathrm{M}} + {\mathrm{H}}_2;\) Tafel: 2 \({\mathrm{M}} - {\mathrm{H}}^ \ast \leftrightharpoons 2\,{\mathrm{M}} + {\mathrm{H}}_2\), where H* designates a hydrogen atom chemically adsorbed on the active sites of the electrocatalyst surface (M)). The hydrogen adsorption free energy (ΔGH*) is a well-known descriptor for the HER activity, and its optimal value |ΔGH*| should be zero, indicating the H* adsorption is neither too strong nor too weak61. Because the H* adsorption is excessively strong on the oxygen atoms, TMOs are usually considered to be inactive HER electrocatalysts. However, the H* adsorption on oxides could be weakened by increasing the covalency of the M–O bonds, which results in an activated or enhanced HER efficiency23.
DFT simulations
To gain an in-depth understanding of the observed polymorph-dependent HER in Ti2O3, we conducted the density functional theory (DFT) simulations to calculate the ΔGH* of the Ti sites on the Ti2O3 polymorphs’ surfaces. Since the oxygen atoms cannot provide extra electrons to H, the HER-active sites of Ti2O3 are the Ti sites (Ti3+) with the unpaired 3d1 electrons. The optimized models of H adsorbed on the surfaces of Ti2O3 polymorphs are shown in the Supplementary Fig. 11. H prefers to adsorb at the top site of the Ti atom on the α-Ti2O3 (0001) surface with a bond length of dH−Ti = 1.718 Å, while it prefers to adsorb at the bridge sites of the Ti atoms on the o-Ti2O3 (011) and γ-Ti2O3 (001) surfaces resulting in bond lengths of dH−Ti = 1.908 Å and dH−Ti = 1.915 Å, respectively. The shortest Ti–H bond length on the α-Ti2O3 (0001) surface implies the strongest bond strength among those adsorption surfaces.
We further analyzed the bond formation between the adsorbed H and Ti atoms by calculating the charge accumulation and depletion around H. The charge density difference is determined by using the formula \(\Delta \rho = \rho _{\left( {{\mathrm{H + Ti}}_2{\mathrm{O}}_3} \right)} - ( {\rho _{\mathrm{H}} + \rho _{{\mathrm{Ti}}_2{\mathrm{O}}_3}} )\), where \(\rho _{\left( {{\mathrm{H + Ti}}_2{\mathrm{O}}_3} \right)}\), ρH, and \(\rho _{{\mathrm{Ti}}_2{\mathrm{O}}_3}\) represent the charge density of the H adsorbed on the Ti2O3 surface, isolated H, and the clean Ti2O3 surface, respectively. The calculated charge density difference for H adsorbed on different Ti2O3 polymorphs’ surfaces are shown in Fig. 7a–c, where the magenta regions show the electron accumulation (bonding states) while the yellow regions show electron depletion (antibonding states). As shown in Fig. 7a–c, there is depletion of electron density on the Ti atoms and accumulation of electron density around the H atoms on all Ti2O3 surfaces. That is, there is electron charge transfer from Ti to H. The adsorbed H gains electrons from its bonded Ti atoms, leading to the electron accumulation at H and depletion at Ti atoms. Apparently, more yellow regions (electron depletion) accumulate near the adsorbed H on the γ-Ti2O3 (001) surface (Fig. 7c) than those on the α-Ti2O3 (0001) and o-Ti2O3 (011) surfaces, demonstrating the most antibonding states are generated when H adsorbs on the γ-Ti2O3 (001) surface, which can weaken the adsorption energy of H.
DFT simulations. a–c Electron charge density differences for H adsorbed on the α-Ti2O3 (0001), o-Ti2O3 (011), and γ-Ti2O3 (001) surfaces, respectively. The surface planes for calculations are chosen based on the experimental orientations of the Ti2O3 epitaxial films (Fig. 1f). The red, blue, and green spheres represent oxygen, titanium, and hydrogen atoms, respectively. The isosurface is taken as 0.002 e Å−3. The electron charge accumulation (bonding states) and depletion (antibonding states) are represented by the magenta and yellow regions, respectively. d Calculated Gibbs free energy of H on the surfaces of Ti2O3 polymorphs. Source data are provided as a Source Data file
The top valence band of Ti2O3 (Fig. 3b), just below the Fermi level, is derived from the Ti 3d orbitals (a1g band), whose center is the so called d-band center in the d-band theory62. Based on Hammer et al.’s work62, the energy of the d-band center (Ed) with respect to the Fermi level is the critical factor which determines the strength of the interaction between the metal and the adsorbate. Impressively, the Ed of the H-adsorbed α-Ti2O3 (0001), o-Ti2O3 (011), and γ-Ti2O3 (001) surfaces are calculated to be −1.39, −1.53, and −1.97 eV (Supplementary Fig. 12a), respectively. The difference of the d-band center in Ti2O3 polymorphs can be attributed to their distinct hybridization strength between the Ti 3d and O 2p orbitals. Since the O 2p band is further away from the Fermi level than the Ti 3d (a1g) band (Fig. 3b), stronger Ti–O hybridization could make the d-band center downshift away from the Fermi level. Thus, a lower d-band center (Ed) is achieved with stronger Ti–O hybridization (Supplementary Fig. 12b). Meanwhile, the lowered d-band center will result in an increased filling of the antibonding states63, which weakens the strength of the Ti–H bond and thus decreases the adsorption energy of H.
Finally, the calculated chemisorption energy of H on the γ-Ti2O3 (001) surface is −0.593 eV, while those on the o-Ti2O3 (011) and α-Ti2O3 (0001) surfaces are −0.809 and −0.979 eV, respectively, which is consistent with the results of the optimized Ti–H bond lengths and the d-band center. Considering the correction value of 0.216 eV (ΔEZPE − TΔSH), ΔGH* on the surfaces of Ti2O3 polymorphs are obtained. As shown in Fig. 7d, ΔGH* is −0.376, −0.593, and −0.763 eV on the surfaces of γ-Ti2O3 (001), o-Ti2O3 (011), and α-Ti2O3 (0001), respectively, indicating that H has the strongest chemical bonding on the α-Ti2O3 (0001) surface and the weakest chemical bonding on the γ-Ti2O3 (001) surface. Our theoretical simulations are consistent with the experimental results (Fig. 6c), where it can be found that the overpotential is the smallest (0.271 V) on the γ-Ti2O3 (001) surface and the largest (0.495 V) on the α-Ti2O3 (0001) surface. It should be noted that the difference between theoretical and experimental values may arise from the theoretical perfect surface models without considering any intrinsic defects, whereas experimental samples may contain some intrinsic defects on the surfaces. Nevertheless, our calculated ΔGH* can act as a descriptor for the experimental HER performance of the Ti2O3 polymorphs as they show the same tendency (Table 1).
Discussion
In summary, we systematically studied the strong correlations between the polymorphism (lattice symmetry), electronic structure, and HER activity in the epitaxial Ti2O3 films with three different phases. A bulk-absent cubic Ti2O3 polymorph is successfully grown via epitaxial stabilization using PLD, which further extends the polymorphism of Ti2O3. Distinct polymorph-dependent electronic structures and properties are observed in Ti2O3, indicating strong structure–property correlations. More importantly, the electronic reconstructions (varied U and Δ) observed in the epitaxially stabilized Ti2O3 polymorphs (orthorhombic and cubic) impact significantly on their HER catalytic activities. Decreased Δ leads to a substantial enhancement in the HER performance of γ-Ti2O3, reducing the overpotential by ~45%, with strongest Ti–O hybridization (lowest d-band center). Thus, epitaxial stabilization of bulk-absent polymorphs is demonstrated to be an effective way to discover more efficient HER electrocatalysts in oxides. Moreover, we envision that greater enhancement of the HER activity could be realized by further decreasing the Δ via doping, or increasing the surface area via nanostructure-array fabrications. Our work provides an unambiguous descriptor for the HER activities of Ti2O3 polymorphs, which could be applied to other strongly correlated TMO systems.
Methods
Fabrication of Ti2O3 epitaxial films
All Ti2O3 films were deposited on single-crystal substrates using pulsed laser deposition (PLD), with a 248 -nm Laser (KrF, Coherent). The thickness of the films is ~300 nm. α- and o-Ti2O3 films were deposited on (0001) Al2O3 substrates at 600 °C and 900 °C, respectively29. The phase separation between α- and o-Ti2O3 was controlled by deposition temperature. γ-Ti2O3 films were deposited on (001) SrTiO3 and (001) LAO substrates at 600 °C. The pressure of the PLD chamber was lower than 3.0 × 10−6 Torr. The energy density of the laser on the target was fixed to ~2 J cm−2. The same corundum α-Ti2O3 target (Sigma-Aldrich 99.99%) was used for all films’ deposition.
Structural characterizations
X-ray diffraction patterns were recorded using a Bruker D8 DISCONVER high-resolution diffractometer, which is equipped with Cu Kα radiation source and LynxEye detector. During the measurements, the diffractometer was operated at 35 kV and 50 mA. In-plane φ scans were performed using the synchrotron-based XRD in the Singapore Synchrotron Light Source (SSLS) with a step size of 0.02°. STEM-HAADF images and EELS spectra were collected using the JEOL-ARM200F microscope equipped with an ASCOR aberration corrector, operated at 200 kV. The cross-section TEM samples were prepared by the focused ion beam technique. The EELS line scans were collected with an energy resolution of ~0.1 eV and a spatial resolution of ~0.4 nm.
Synchrotron-based XAS measurements
All the XAS data were taken in an ultra-high-vacuum chamber with a base pressure of ~1 × 10−10 mbar at the Surface, Interface and Nanostructure Science (SINS) beam-line64 of SSLS. The XAS data were obtained by using linear polarized X-rays impinging at an incidence angle of Ѳ = 90° from the sample surface (Fig. 4a) at the Ti L2,3-edge and O K-edge regions. The data were obtained by averaging 20 XAS spectra. All spectra were recorded at room temperature (300 K) using the total electron yield (TEY) mode. The photon energy was calibrated using a standard gold sample in the chamber. In order to record the intrinsic bulk electronic structures of Ti2O3 polymorphs, samples measured by the synchrotron-based XAS were sputter-cleaned before the measurements.
Spectroscopic ellipsometry and light absorption measurements
The ellipsometry parameters Ψ (the ratio between the amplitude of p- and s-polarized reflected light) and Δ (the phase difference between of p- and s-polarized reflected light) were measured using spectroscopic ellipsometer with a photon range of 0.5‒4 eV at incident angles 60°, 65°, and 70° at room temperature. The optical conductivity of Ti2O3 films was extracted from the parameters Ψ and Δ utilizing an air/Ti2O3/Al2O3 (or air/Ti2O3/LaAlO3) multilayer model, where the Ti2O3 films were considered as average homogeneous and uniform mediums. The light absorption of the Ti2O3 films was measured by a UV–Vis spectrophotometer (Shimadzu SolidSpec-3700) in the transmission mode. Backgrounds from the Al2O3 and LaAlO3 substrates were all subtracted.
Electronic transport and electrochemical measurements
The electronic transport properties of the Ti2O3 films were measured in a Quantum Design physical property measurement system (PPMS). The resistivity and Hall effect were collected using the Van der Pauw geometry. The sample size was 5 × 5 mm. Al wires were used to connect the samples and the PPMS puck. The electrochemical measurements were performed in a three-electrode electrochemical cell with a standard VMP3 electrochemical workstation (Bio-logic Inc) at room temperature. During the HER measurements, Hg/HgO and graphite plate were used as the reference and counter electrodes, respectively, while the Ti2O3 polymorphs films on 10 × 10 mm2 single-crystal substrates were acting as the working electrodes directly. The polarization curves were recorded in 0.5 M H2SO4 with a scan rate of 5 mV s−1. All potentials were calibrated with respect to the reversible hydrogen electrode (RHE) using the equation65:
where EvsHg/HgO was the potential measured against the Hg/HgO reference electrode.
First-principles calculations
All the calculations were carried out using DFT + U (Ueff = U − J = 1.9 − 2.3 eV)66 with the generalized Perdew–Burke–Ernzerhof (PBE)67 and the projector augmented-wave (PAW) pseudopotential plane-wave method68 as implemented in the VASP code69. For the PAW pseudopotentials, we considered 1s1 for H, 3d34s1 for Ti, and 2s2sp4 for O. The Monkhorst–Pack (MP) k-point grids of 6 × 6 × 2, 2 × 6 × 8, and 2 × 2 × 1 were used for α-Ti2O3, o-Ti2O3, and γ-Ti2O3 unit cell geometry optimization calculations with a plane-wave basis set with an energy cutoff of 500 eV, respectively. Good convergence was obtained with these parameters, and the total energy was converged to 1.0 × 10−6 eV per atom, as well as the stress exerted on the cell is less than 0.1 kbar and the forces exerted on the atoms are less than 0.01 eV/Å. Optimized unit cells were used to build surface models for H Gibbs free energy calculations (Supplementary Fig. 11). For H adsorption calculations, we cleaved a (0001) slab to build the surface model and expand to 2 × 2 × 1 supercell for α-Ti2O3, a (011) slab to build the surface model and expand to 2 × 2 × 1 supercell for o-Ti2O3, and a (001) slab to build the surface model for γ-Ti2O3 according to the experimental results. All the surface models have a vacuum separation of ~15 Å along the z-direction. We carried out calculations with the van der Waals (vdW) correction by employing optPBE-vdW functional70 using a 2 × 2 × 1 MP k-point grid. The Gibbs free energy of H was calculated by using \(\Delta {\mathrm{G}}_{{\mathrm{H}}^ \ast } = \Delta E_{\mathrm{H}} + \Delta E_{{\mathrm{ZPE}}} - T\Delta S_{\mathrm{H}}\). Hydrogen chemisorption energy ΔEH is computed using \(\Delta E_{\mathrm{H}} = E_{({\mathrm{surface}} + {\mathrm{H}}^ \ast )} - E_{\left( {{\mathrm{surface}}} \right)} - \frac{1}{2}E_{{\mathrm{H}}_2}\), where \(E_{({\mathrm{surface}} + {\mathrm{H}}^ \ast )}\) and \(E_{\left( {{\mathrm{surface}}} \right)}\) are the total energies of the surface with one adsorbed hydrogen atom and the clean surface, respectively, \(E_{{\mathrm{H}}_2}\) is the energy of hydrogen gas phase. \(\Delta E_{{\mathrm{ZPE}}}\) and \(\Delta S_{\mathrm{H}}\) are the differences in zero-point energy (ZPE) and entropy between the adsorbed \({\mathrm{H}}^ \ast\) and gas phase H2. The calculated correction value of \(\Delta E_{{\mathrm{ZPE}}} - T\Delta S_{\mathrm{H}}\) at the temperature (T) of 300 K is ~0.216 eV in this study.
References
Suntivich, J. et al. Design principles for oxygen-reduction activity on perovskite oxide catalysts for fuel cells and metal–air batteries. Nat. Chem. 3, 546–550 (2011).
Xu, X. et al. A perovskite electrocatalyst for efficient hydrogen evolution reaction. Adv. Mater. 28, 6442–6448 (2016).
Zeng, K. & Zhang, D. Recent progress in alkaline water electrolysis for hydrogen production and applications. Prog. Energy Combust. Sci. 36, 307 (2010).
Wang, J. et al. Recent progress in cobalt-based heterogeneous catalysts for electrochemical water splitting. Adv. Mater. 28, 215–230 (2016).
Gong, M. et al. Nanoscale nickel oxide/nickel heterostructures for active hydrogen evolution electrocatalysis. Nat. Commun. 5, 4695 (2018).
Dagotto, E. Complexity in strongly correlated electronic systems. Science 309, 257 (2005).
Kent, P. R. C. & Kotliar, G. Toward a predictive theory of correlated materials. Science 361, 348–354 (2018).
Tokura, Y. & Nagaosa, N. Orbital physics in transition-metal oxides. Science 288, 462 (2000).
Chen, X., Liu, L., Yu, P. Y. & Mao, S. S. Increasing solar absorption for photocatalysis with black hydrogenated titanium dioxide nanocrystals. Science 331, 746 (2011).
Chen, X., Liu, L. & Huang, F. Black titanium dioxide (TiO2) nanomaterials. Chem. Soc. Rev. 44, 1861 (2015).
Grimaud, A. et al. Double perovskite as a family of highly active catalysts for oxygen evolution in alkaline solution. Nat. Commun. 4, 2439 (2013).
Yagi, S. et al. Covalency-reinforced oxygen evolution reaction catalyst. Nat. Commun. 6, 8249 (2015).
Gunkel, F. et al. Ordering and phase control in epitaxial double-perovskite catalysts for the oxygen evolution reaction. ACS Catal. 7, 7029–7037 (2017).
Suntivich, J., May, K. J., Gasteiger, H. A., Goodenough, J. B. & Shao-Horn, Y. A perovskite oxide optimized for oxygen evolution catalysis from molecular orbital principles. Science 334, 1383 (2011).
Grimaud, A. et al. Activating lattice oxygen redox reactions in metal oxides to catalyse oxygen evolution. Nat. Chem. 9, 457–465 (2017).
Cheng, X. et al. Oxygen evolution reaction on La1–xSrxCoO3 perovskites: a combined experimental and theoretical study of their structural, electronic, and electrochemical properties. Chem. Mater. 27, 7662–7672 (2015).
Kim, N. I. et al. Oxygen-deficient triple perovskites as highly active and durable bifunctional electrocatalysts for oxygen electrode reactions. Sci. Adv. 4, 9360 (2018).
Lee, S. A. et al. Enhanced electrocatalytic activity via phase transitions in strongly correlated SrRuO3 thin films. Energy Environ. Sci. 10, 924 (2017).
Mefford, J. T. et al. Water electrolysis on La1-xSrxCoO3-δ perovskite electrocatalysts. Nat. Commun. 7, 11053 (2016).
Hong, W. et al. Charge-transfer-energy-dependent oxygen evolution reaction mechanisms for perovskite oxides. Energy Environ. Sci. 10, 2190 (2017).
Suntivich, J. et al. Estimating hybridization of transition metal and oxygen states in perovskites from O K-edge X-ray absorption spectroscopy. J. Phys. Chem. C. 118, 1856–1863 (2014).
Zhu, Y. et al. A perovskite nanorod as bifunctional electrocatalyst for overall water splitting. Adv. Energy Mater. 7, 1602122 (2017).
Ling, T. et al. Activating cobalt(II) oxide nanorods for efficient electrocatalysis by strain engineering. Nat. Commun. 8, 1509 (2017).
Li, Y. et al. From titanium sesquioxide to titanium dioxide: oxidation-induced dtructural, phase, and property evolution. Chem. Mater. 30, 4383–4392 (2018).
Chambers, S. A. et al. X-ray photoelectron spectra for single-crystal Ti2O3: experiment and theory. Phys. Rev. B 96, 205143 (2017).
Wang, J. et al. High performance photothermal conversion of narrow-bandgap Ti2O3 nanoparticles. Adv. Mater. 29, 1603730 (2017).
Yu, X. et al. Narrow bandgap oxide nanoparticles coupled with graphene for high performance mid-infrared photodetection. Nat. Commun. 9, 4299 (2018).
Li, Y. et al. Orthorhombic Ti2O3: a polymorph-dependent narrow-bandgap ferromagnetic oxide. Adv. Funct. Mater. 28, 1705657 (2018).
Li, Y. et al. Observation of superconductivity in structure-selected Ti2O3 thin films. NPG Asia Mater. 10, 522–532 (2018).
Gorbenko, O. Y., Samoilenkov, S. V., Graboy, I. E. & Kaul, A. R. Epitaxial stabilization of oxides in thin films. Chem. Mater. 14, 4026–4043 (2002).
Lee, J.-H. et al. Epitaxial stabilization of a new multiferroic hexagonal phase of TbMnO3 thin films. Adv. Mater. 18, 3125–3129 (2006).
Mizoguchi, H., Woodward, P. M., Byeon, S.-H. & Parise, J. B. Polymorphism in NaSbO3: structure and bonding in metal oxides. J. Am. Chem. Soc. 126, 3175–3184 (2004).
Wang, Y. et al. Structural phase transition in monolayer MoTe2 driven by electrostatic doping. Nature 550, 487–491 (2017).
Jacobs, I. E. et al. Polymorphism controls the degree of charge transfer in a molecularly doped semiconducting polymer. Mater. Horiz. 5, 655–660 (2018).
Zhang, M., Chen, T. & Wang, Y. Insights into TiO2 polymorphs: highly selective synthesis, phase transition, and their polymorph-dependent properties. RSC Adv. 7, 52755 (2017).
Luo, H. et al. Polytypism, polymorphism, and superconductivity in TaSe2−xTex. Proc. Natl Acad. Sci. USA 112, E1174–E1180 (2015).
Jurchescu, O. D. et al. Effects of polymorphism on charge transport in organic semiconductors. Phys. Rev. B 80, 085201 (2009).
Ohkoshi, S. et al. Synthesis of a metal oxide with a room-temperature photoreversible phase transition. Nat. Chem. 2, 539 (2010).
Shen, Z. et al. Stabilization of microcrystal λ-Ti3O5 at room temperature by aluminum-ion doping. Appl. Phys. Lett. 111, 191902 (2017).
Chen, Y. Z. et al. A high-mobility two-dimensional electron gas at the spinel/perovskite interface of γ-Al2O3/SrTiO3. Nat. Commun. 4, 1371 (2013).
Zhou, R. S. & Snyder, R. L. Structures and transformation mechanisms of the η, γ, and θ transition aluminas. Acta Cryst. B 47, 617–630 (1991).
Li, P. et al. Ultrathin epitaxial ferromagnetic γ-Fe2O3 layer as high efficiency spin filtering materials for spintronics device based on semiconductors. Adv. Funct. Mater. 26, 5679–5689 (2016).
Li, Y. et al. Nanoscale chemical and valence evolution at the metal/oxide interface: a case study of Ti/SrTiO3. Adv. Mater. Interfaces 3, 1600201 (2016).
Lee, S. A. et al. Phase transitions via selective elemental vacancy engineering in complex oxide thin films. Sci. Rep. 6, 23649 (2016).
Morin, F. J. Oxides which show a metal-to-insulator transition at the neel temperature. Phys. Rev. Lett. 3, 34 (1959).
Mott, N. F. On the transition to metallic conduction in semiconductors. Can. J. Phys. 34, 1356 (1956).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039 (1998).
Torrance, J. B., Lacorre, P., Asavaroengchai, C. & Metzger, R. M. Why are some oxides metallic, while most are insulating? Phys. C. 182, 351 (1991).
Zaanen, J., Sawatzky, G. A. & Allen, J. Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 55, 418–421 (1985).
Goodenough, J. B. Covalency criterion for localized vs collective electrons in oxides with the perovskite structure. J. Appl. Phys. 37, 1415 (1966).
Goodenough, J. B. & Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 22, 587–603 (2010).
Van Zandt, L. L., Hoig, J. M. & Goodenough, J. B. Resistivity and magnetic order in Ti2O3. J. Appl. Phys. 39, 594 (1968).
Uchida, M., Fujioka, J., Onose, Y. & Tokura, Y. Charge dynamics in thermally and doping induced insulator-metal transitions of (Ti1-xVx)2O3. Phys. Rev. Lett. 101, 066406 (2008).
Nakatsugawa, H. & Iguchi, E. Transition phenomenon in Ti2O3 using the discrete variational Xα cluster method and periodic shell model. Phys. Rev. B 56, 12931 (1997).
Lu, S. S. M., Pollak, F. H. & Raccah, P. M. Polarization-dependent reflectivity and optical constants of Ti2O3 in the range 0.7−10 eV. Phys. Rev. B 17, 1970 (1978).
Han, K. et al. Controlling kondo-like scattering at the SrTiO3-based interfaces. Sci. Rep. 6, 25455 (2016).
de Groot, F. M. F. et al. Oxygen 1s X-ray-absorption edges of transition-metal oxides. Phys. Rev. B 40, 5715–5723 (1989).
Pedio, M. et al. Covalency in oxygen chemisorption as probed by x-ray absorption. Phys. Rev. B 40, 7924 (1989).
Fujii, T. et al. In situ XPS analysis of various iron oxide films grown by NO2-assisted molecular-beam epitaxy. Phys. Rev. B 59, 3195 (1999).
Zhou, H. D. & Goodenough, J. B. Semiconductor-semiconductor transition in Mg[Ti2]O4. Phys. Rev. B 72, 045118 (2005).
Zheng, Y., Jiao, Y., Jaroniec, M. & Qiao, S. Z. Advancing the electrochemistry of the hydrogen-evolution reaction through combining experiment and theory. Angew. Chem. Int. Ed. 54, 52–65 (2015).
Hammer, B. et al. CO chemisorption at metal surfaces and overlayers. Phys. Rev. Lett. 76, 2141 (1996).
Chen, Z. et al. Tailoring the d-band centers enables Co4N nanosheets to be highly active for hydrogen evolution catalysis. Angew. Chem. Int. Ed. 57, 5076 (2018).
Yu, X. et al. New soft X-ray facility SINS for surface and nanoscale science at SSLS. J. Electron Spectrosc. Relat. Phenom. 144–147, 1031–1034 (2005).
Wang, L. et al. Increasing gas bubble escape rate for water splitting with nonwoven stainless steel fabrics. ACS Appl. Mater. Interfaces 9, 40281 (2017).
Hu, Z. & Metiu, H. Choice of U for DFT+U calculations for titanium oxides. J. Phys. Chem. C. 115, 5841–5845 (2011).
Perdew, J., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Klimeš, J., Bowler, D. R. & Michealides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
Acknowledgements
This work is supported by the Singapore National Research Foundation under CRP Award NRF-CRP10-2012-02, Singapore Ministry of Education under MOE2018-T2-2-043, and AMEIRG18-0022. We acknowledge the Singapore Synchrotron Light Source (SSLS) for providing the facility necessary for conducting the research. The Laboratory is a National Research Infrastructure under the National Research Foundation Singapore. Z.Y. acknowledges supports from the Science and Engineering Research Council of Singapore with Grant no. A1898b0043, and computational resource was provided by A*STAR Computational Resource Centre, Singapore (A*CRC) and the National Supercomputing Centre Singapore (NSCC). X.R.W. acknowledges supports from the Nanyang Assistant Professorship grant from Nanyang Technological University and Academic Research Fund Tier 1 (RG108/17) from Singapore Ministry of Education. We also would like to acknowledge support from the National Research Foundation (NRF) under the Competitive Research Program (NRF-CRP15-2015-01).
Author information
Authors and Affiliations
Contributions
Y.L. and J.S.C. conceived the project. Y.L. designed the experiments, and performed the samples fabrication, characterization, data analysis, and interpretation. L.W. performed the electrochemical measurements. L.M.W., S.W., J.W.C., D.W., and T.V. assisted with the optical measurements. C.S.T., X.M.Y., A.T.S.W., J.W., K.H., and X.R.W. assisted with the XRD measurements. X.J.Y. and M.B.H.B. carried out the XAS measurements. H.W. and S.J.P. assisted with the TEM measurements. Z.G.Y. and Y.W.Z. performed the theoretical calculations. Y.W. and S.D. assisted with the theoretical calculations. Y.L., J.M.X., and J.S.C. discussed the data interpretation. Y.L. and J.S.C. wrote the paper, and all authors commented on the results and the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer Review Information: Nature Communications thanks Min-Rui Gao, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Y., Yu, Z.G., Wang, L. et al. Electronic-reconstruction-enhanced hydrogen evolution catalysis in oxide polymorphs. Nat Commun 10, 3149 (2019). https://doi.org/10.1038/s41467-019-11124-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-11124-w
This article is cited by
-
Stabilizing non-iridium active sites by non-stoichiometric oxide for acidic water oxidation at high current density
Nature Communications (2023)
-
The practically renewable and highly efficient electrocatalysts derived from a newly-designed Mo8Pt polyoxometalate compound
Science China Chemistry (2023)
-
Ultra-flat and long-lived plasmons in a strongly correlated oxide
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.