Abstract
Quantum communication protocols based on nonclassical correlations can be more efficient than known classical methods and offer intrinsic security over direct state transfer. In particular, remote state preparation aims at the creation of a desired and known quantum state at a remote location using classical communication and quantum entanglement. We present an experimental realization of deterministic continuous-variable remote state preparation in the microwave regime over a distance of 35 cm. By employing propagating two-mode squeezed microwave states and feedforward, we achieve the remote preparation of squeezed states with up to 1.6 dB of squeezing below the vacuum level. Finally, security of remote state preparation is investigated by using the concept of the one-time pad and measuring the von Neumann entropies. We find nearly identical values for the entropy of the remotely prepared state and the respective conditional entropy given the classically communicated information and, thus, demonstrate close-to-perfect security.
Similar content being viewed by others
Introduction
In quantum technology, an efficient and secure exchange of quantum information between quantum nodes plays a crucial role1. One of the first protocols realizing such a task was quantum teleportation, where an unknown quantum state is safely transferred from one party to another by using a shared entangled resource and classical feedforward2,3. In a different scenario, where one party has full classical knowledge about a to-be-communicated quantum state, remote state preparation (RSP) can be used to remotely create this quantum state by employing similar tools as in quantum teleportation4,5,6,7. Compared to known classical methods, both protocols provide a quantum advantage as they require a smaller amount of classical information in the feedforward signal in order to communicate a desired quantum state8. However, in contrast to quantum teleportation, RSP allows for a nontrivial trade-off between the amount of classical communication and entanglement necessary for a successful protocol6. Furthermore, the use of an entangled resource allows RSP to operate perfectly secure8. Even though RSP is extensively investigated both theoretically and experimentally for discrete-variable systems9,10,11, deterministic implementations with continuous-variable systems are still lacking12,13. At the same time, quantum communication based on continuous-variables is a field of intense research14,15 investigating, e.g., quantum key distribution16, quantum teleportation17,18, dense coding19, and free-space quantum communication20.
Quantum communication in the microwave domain is motivated by the tremendous progress in the area of quantum information processing with superconducting circuits. In particular, the development of superconducting multi-qubit processors21,22, operated at gigahertz frequencies has been highly successful. We promote an approach of quantum communication directly in the microwave regime based on propagating squeezed states. Since these states have the same frequency and are generated by technology platforms already used for superconducting quantum computers, there is no mismatch between communication and data processing units. This approach is expected to be useful for short and medium distances, where superconducting waveguides can be used.
In this work, we realize deterministic continuous-variable RSP by creating Gaussian squeezed states with tunable squeezing level and squeezing angle over a distance of 35 cm. We investigate the phase space of remotely preparable squeezed states and obtain good agreement with our model calculations based on the input-output formalism. Additionally, we find that our scheme corresponds to an extension of the one-time pad cryptographic protocol23 into the quantum regime which allows for information-theoretic security. In contrast to already demonstrated quantum state transfer protocols between superconducting circuits24,25, our protocol does not directly transmit the target states to the receiving party. Moreover, it can be operated in the continuous regime and utilizes preshared entanglement to enable secure communication between parties. Since the generation and manipulation of Gaussian states is well understood14, they offer a viable option for building future intracity low-temperature quantum networks26.
Results
RSP with squeezed microwaves
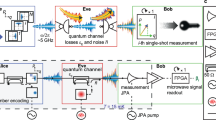
The general idea behind the RSP protocol and our experimental implementation using continuous-variable microwave states are described in Fig. 1. We use flux-driven Josephson parametric amplifiers (JPAs) as the key elements for the generation and manipulation of squeezed microwave states27,28,29 (see Supplementary Note 1 and Supplementary Table 1 for details). We operate all JPAs in the degenerate regime at the frequency f0 = 5.435 GHz with a pump frequency fp = 2f0. The task of JPA 1 and JPA 2 is to generate propagating squeezed states which are incident to an entangling beam splitter. The resulting symmetric two-mode squeezed (TMS)30,31 states have a two-mode squeezing level32 of STMS = 7.1 dB and an entanglement strength characterized by the negativity criterion30,33 of N = 2.2. This number quantifies the strength of nonlocal correlations present between field quadratures of signals propagating along different beam splitter output paths. Additionally, the symmetric TMS states have negligible local squeezing within each path. In other words, the microwave signals propagating on the two paths locally look like thermal states with, nevertheless, strong entanglement between them (see Supplementary Note 2 and Supplementary Fig. 1 for details).
Principle of remote state preparation. a General RSP scheme: Alice remotely prepares a desired state at Bob’s side using a quantum resource and classical communication (feedforward). b Experimentally implemented RSP scheme: a two-mode squeezed state (left) serves as quantum resource and the feedforward to Bob (right) is implemented using JPA 3 and a directional coupler
In the next step, we employ the symmetric propagating TMS states as a resource for remotely preparing the target squeezed microwave states. For this purpose, the TMS states are continuously distributed between two parties, Alice and Bob, who are separated by 35 of superconducting cable. Alice generates a feedforward signal carrying the classical information about her choice on what quantum state is to be remotely prepared at Bob’s side. Finally, Bob displaces his part of the resource state proportionally to the communicated signal by using a directional coupler with a fixed coupling of β ≃ −15 dB34,35. We experimentally implement the feedforward by operating JPA 3 as a phase-sensitive amplifier. Alice uses it to choose and strongly amplify a certain quadrature of the incoming TMS states. Note that, in contrast to the other JPAs, it does not matter whether the outgoing feedforward signal from JPA 3 is squeezed or not (Supplementary Note 5 and Supplementary Fig. 5). The essential classical information, as required for a successful RSP, is encoded in the large instantaneous amplitude of the phase-sensitively amplified field quadrature. For ideal RSP, the coupling β should be vanishingly small. However, since β needs to be approximately compensated by the degenerate gain of JPA 3, we are limited to a certain range of β values due to the noise and gain performance of JPA 3.
Figure 2a shows the experimental performance of the RSP scheme as a function of the JPA 3 degenerate gain Gf for a fixed JPA 3 amplification angle γf = 0°. The latter is defined as the deviation from the angle of the optimal working point at which we achieve the highest purity in the remotely prepared states. We fully characterize these states in terms of their squeezing level Srp, antisqueezing level Arp, and squeezing angle γrp (see “Methods”). We clearly observe squeezing up to Srp = 1.6 ± 0.1 dB in the final states at the output of the displacer near the optimal JPA 3 gain Gf ≃ 13 dB (see Fig. 2b). Srp decreases and the states even become non-squeezed upon deviation from the optimal JPA 3 gain as shown in Fig. 2c. The remotely prepared states can be encoded not only by varying Gf but also by changing γf. The latter leads to a different quadrature in the resource TMS states being projected, and accordingly, to a different state being remotely prepared. The squeezing level and squeezing angle of the remotely prepared states obtained by sweeping both Gf and γf are shown in Fig. 2d, e. The results for the antisqueezing level Arp can be found in Supplementary Fig. 3.
Tomography of remotely prepared states. a Squeezing level Srp (circles), antisqueezing level Arp (diamonds), and squeezing angle γrp (triangles) of remotely prepared states as a function of the JPA 3 degenerate gain Gf at fixed angle γf = 0°. The lines show a fit to the data. The error bars denote the standard error of the mean calculated from multiple repetitions of the protocol. If not shown, the error bars are smaller than the symbol size. b, c Reconstructed Wigner functions of the remotely prepared states for the optimal and one of the non-optimal JPA 3 gains as marked by the dashed lines in panel (a). d, e Srp and γrp of the remotely prepared states as a function of the feedforward parameters. Panels (f), (g) show a joint fit of the three quantities (Srp, Arp, γrp) to the corresponding data in panels (d), (e), respectively (see Supplementary Fig. 3 for the results for Arp). The green lines mark the threshold Srp ≥ 0 dB for squeezing below the vacuum limit. The optimal point is marked by the blue star. The data and fit in panel (a) are marked by dotted lines in panels (d–g)
Model and phase space of prepared states
Our experiment can be theoretically described by a model based on the input-output transformations for every component in the setup including transmission losses. In particular, we define χ1 as the total loss between JPA 1 (or JPA 2) and JPA 3, and χ2 as the total loss between JPA 1 (or JPA 2) and the directional coupler. This definition implies that all path losses between JPA 1 or JPA 2 and any component after the beam splitter are assumed to be equal (Supplementary Fig. 2). Additionally, we assume imperfect JPAs adding a certain amount of noise with mean thermal photon numbers ni (i ∈ {1, 2, f}) to the JPA input signal. Here, nf is the noise photon number of JPA 3. The RSP protocol is expected to work optimally for Gf = τ/(1 − τ) and γf = 0°, where τ = 1 − 10β/10 is the transmissivity of the directional coupler. At this optimal point and under the condition STMS ≥ 3 dB, we obtain the squeezed variance of the remotely prepared state,
In this simplified expression, we assume equal noise photon numbers n1 = n2 = n and squeezing factors r1 = r2 = r of JPA 1 and JPA 2 as well as equal losses χ1 = χ2 = χ (Supplementary Note 3). Equation (1) indicates that the prepared squeezing level Srp at the optimal point is at least 3 dB below the squeezing level of the used resource. In order to correctly model the experiment, we additionally include a finite crosstalk between JPA 3 and the JPAs creating the TMS states as well as asymmetric losses χ1 ≠ χ2 in our data analysis. Figure 2f, g depicts a joint fit to the corresponding data. We observe a very good coincidence between the experimental results and our model for the following parameters (Supplementary Table 2): JPA 1, 2 squeezing levels S = 10.1 dB, n = 0.04, as well as χ1 = 0.22 and χ2 = 0.21 corresponding to losses of 1.1 dB and 1.0 dB, respectively. All values nicely agree with those obtained from independent JPA characterization measurements and loss estimations.
The quantum advantage of the RSP protocol consists in a smaller amount of classical information sent through the feedforward channel in order to prepare a desired state as compared to a purely classical protocol8,36. In the current experiment, this becomes evident by considering that only the amplified quadrature of the feedforward signal will affect the signal at Bob’s side due to the low coupling β ≪ 0 dB of the displacer. Consequently, we only send two real numbers while we are able to prepare different undisplaced mixed squeezed states which are fully described by three real numbers (Srp, Arp, γrp).
The manifold of undisplaced Gaussian states we can prepare is intuitively understood by plotting the results from Fig. 2d, e in the phase space of the prepared squeezing level and angle, as it is shown in Fig. 3 (see Supplementary Note 4 and Supplementary Fig. 4 for details). The purity \(\mu = 1/\left( {4\sqrt {{\mathrm{det}}\,\sigma } } \right)\), where σ is the covariance matrix of the remotely prepared state, incorporates the information about the antisqueezed quadrature and is a measure of how close the state is to a pure state. For application scenarios where pure states are desired, the performance of RSP can be best quantified by the purity. It vanishes for maximally mixed states and is unity for a pure state. We achieve the highest uncorrected purity μ = 0.54 ± 0.01 at the optimal point which is sufficient for many applications of squeezed states such as entanglement generation33, sideband cooling of optomechanical systems37, and quantum illumination38. Using appropriate modeling of our experiment, we are able to investigate the effect of imperfections in different parts of the protocol on the purity of the prepared state at the optimal point. If the resource TMS state is pure and distributed ideally to Alice and Bob, the model predicts an improved purity of 0.60 for otherwise unchanged parameters. Alternatively, ideal operations of Alice and Bob (noiseless JPA 3 combined with no losses on Alice’s and Bob’s sides) with a realistic entangled resource would yield a purity of 0.62. Overall, the observed purity is limited by the added noise of the JPAs and the losses in the setup. Upon reducing the JPA noise photon numbers by one order of magnitude as well as the total losses to χ1 = χ2 = 0.05 (0.2 dB), we expect an optimized purity μopt = 0.80 for the prepared state at the optimal point. The reduction of losses can be achieved by using a superconducting hybrid ring, optimized cable connectors, and improved circulators. In this context, one should remember that our protocol allows for the preparation of continuous-variable squeezed states with a degree of squeezing Srp that is fundamentally related to the initial two-mode squeezing of the resource state. In the current implementation, even for a fixed resource TMS state, Srp and γrp can be changed at the expense of a reduced purity μ. By adding a phase shifter39 on her side, Alice could prepare squeezed states with arbitrary γrp while keeping Srp and μ constant.
Purity of remotely prepared states in phase space. The phase space of the prepared states is spanned by Srp and γrp. The gray area marks squeezing below the vacuum limit. The color code indicates the purity μ of the remotely prepared states. The optimal point is marked by the white star. The inset shows the Wigner function 1/e contours of the experimental state at the optimal point with μ = 0.54 and a pure squeezed state with the same squeezing level. The vacuum 1/e contour is indicated in gray
Quantum one-time pad
Finally, we relate our experimental RSP scheme to the cryptographic protocol known as the one-time pad by extending the latter to the quantum regime8,40. Here, Alice securely sends a quantum state M to Bob over an insecure channel. We identify the transmitted message M as the remotely prepared state on Bob’s side and the openly communicated cipher C as the feedforward signal (see Fig. 4a). The entangled TMS states provide the random key K in the form of quantum fluctuations to both parties. Note that K is essential for the one-time pad since it is used by Alice and Bob to encode and decode M. For secure communication, K needs to be a uniform random variable, such that an eavesdropper with knowledge about C does not gain any information about M41. Formally, we can write
where H(M) is the von Neumann entropy of the remotely prepared state and H(M|C) = H(M, C) − H(C) is the conditional entropy of M given the feedforward signal (Supplementary Note 6). We experimentally investigate the quantum one-time pad by measuring the prepared states as a function of the JPA 3 parameters, while additionally detecting the signal C′ from the second directional coupler output. We compute δ = H(M) − H(M|C′) to verify Eq. (2) under the reasonable approximation C′ ≈ C (due to τ ≃ 1) using state tomography. In Fig. 4b, we observe a decrease in δ when moving towards the optimal point where the smallest value δ = 0.06 ± 0.04 is reached and the entropy of the prepared state is H(M) = 0.80 ± 0.02. The observation \(\delta \ll H(M)\) indicates that the remote preparation of a quantum state on Bob’s side is close to perfect security when approaching the optimal point. At the same time, there is a trade-off between the security and range of prepared states. As previously mentioned, a straightforward extension of the optimal working range of RSP can be realized by adding a phase shifter on Alice’s side. Then, all optimally prepared states would fulfill the security criterion H(M) = H(M|C) for arbitrary squeezing angles while the accessible squeezing level and purity stay unaffected. It is important to note that a potential eavesdropper cannot obtain any information about M by listening exclusively to the TMS resource state since the encoding of M happens later in the protocol. Furthermore, if the eavesdropper completely disentangles the TMS state by its actions, RSP yields no squeezing in the final state which could be exploited to detect the eavesdropper’s presence.
Quantum one-time pad. a Scheme for the interpretation of the RSP setup in terms of the one-time pad. b Entropy difference δ = H(M) − H(M|C′) as a function of the feedforward gain Gf and angle γf. The optimal point is marked by the blue star. It is slightly shifted with respect to the previous measurements due to a modified cryogenic setup
Discussion
To conclude, we have successfully implemented a deterministic RSP protocol over a distance of 35 cm in the microwave regime with continuous variables and explored the influence of different parameters on the remotely prepared states. We have remotely prepared squeezed states with a squeezing level of up to 1.6 dB below the vacuum limit. In our specific RSP implementation, Alice can control the squeezing level and, to some extent, the squeezing angle of the remotely prepared state at the expense of a reduced purity. Additionally, we demonstrate that the protocol can be interpreted as a secure one-time pad near the optimal point. The operational range of both the RSP and quantum one-time pad protocols can be extended to any angle γrp by an additional phase shifter on Alice’s side. The demonstrated protocol opens a way to a multitude of intriguing experiments with quantum microwaves such as probing the Holevo bound limits42, studying the role of quantum discord in quantum communication protocols43, exploring hybrid continuous-discrete schemes of quantum information processing44, and implementing quantum illumination protocols38. Squeezing operations can further be exploited for the preparation of Gottesman-Kitaev-Preskill (GKP) states for continuous-variable quantum error correction45,46. Our experiment proves that prototypical local quantum networks using continuous-variable quantum microwaves are within experimental reach47.
Methods
JPA 1 and JPA 2 perform a squeezing operation \(\hat S(\xi )|0\rangle\), where \(\hat S(\xi ) = {\mathrm{exp}}\left( {\frac{1}{2}\xi ^ \ast \hat a^2 - \frac{1}{2}\xi (\hat a^\dagger )^2} \right)\) is the squeezing operator, \(\hat a^\dagger = \hat q - i\hat p\) and \(\hat a = \hat q + i\hat p\) are the creation and annihilation operators with \(\left[ {\hat a,\hat a^\dagger } \right] = 1\) of the f0 mode with quadratures \(\hat q\) and \(\hat p\), and ξ = reiϕ is the complex squeezing amplitude. Here, the phase ϕ = − 2γ determines the squeezing angle γ between the antisqueezed quadrature and the p-axis in the phase space, while the squeezing factor r parameterizes the amount of squeezing. We define the degree of squeezing in decibels as \(S = - 10{\kern 1pt} \,\log _{10}\left[ {\sigma _{\mathrm{s}}^2/0.25} \right]\), where \(\sigma _{\mathrm{s}}^2\) is the variance of the squeezed quadrature and the vacuum variance is 0.25. Positive values of S indicate squeezing below the vacuum level. The antisqueezing level is defined as \(A = 10\,{\mathrm{log}}_{10}\left[ {\sigma _{\mathrm{a}}^2/0.25} \right]\), where \(\sigma _{\mathrm{a}}^2\) is the variance of the antisqueezed quadrature. We generate symmetric TMS states at the outputs of the hybrid ring by pumping JPA 1 and JPA 2 with strong quasi-continuous microwave drives, so that they produce squeezed states with the same squeezing level and orthogonal squeezing angles γ2 = γ1 + π/2. These angles are stabilized by controlling the respective pump phases employing a phase-locked loop30,34. The stability of these TMS states in terms of two-mode squeezing and symmetry is of paramount importance in our experiments. Only by utilizing the nonclassical correlations between Alice and Bob, it is possible to demonstrate the successful RSP protocol. In order to reconstruct the quantum states in the experiment, we employ a well-tested reference state tomography based on statistical moments of the detected field quadratures32,33.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221 (1997).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Lo, H.-K. Classical-communication cost in distributed quantum-information processing: A generalization of quantum-communication complexity. Phys. Rev. A. 62, 012313 (2000).
Pati, A. K. Minimum classical bit for remote preparation and measurement of a qubit. Phys. Rev. A. 63, 014302 (2000).
Bennett, C. H. et al. Remote state preparation. Phys. Rev. Lett. 87, 077902 (2001).
Paris, M. G. A., Cola, M. & Bonifacio, R. Remote state preparation and teleportation in phase space. J. Opt. B: Quantum Semiclass. Opt. 5, S360 (2003).
Kurucz, Z., Adam, P., Kis, Z. & Janszky, J. Continuous variable remote state preparation. Phys. Rev. A. 72, 052315 (2005).
Dakić, B. et al. Quantum discord as resource for remote state preparation. Nat. Phys. 8, 666–670 (2012).
Peters, N. A., Barreiro, J. T., Goggin, M. E., Wei, T.-C. & Kwiat, P. G. Remote state preparation: Arbitrary remote control of photon polarization. Phys. Rev. Lett. 94, 150502 (2005).
Ye, M.-Y., Zhang, Y.-S. & Guo, G.-C. Faithful remote state preparation using finite classical bits and a nonmaximally entangled state. Phys. Rev. A. 69, 022310 (2004).
Le Jeannic, H., Cavaillès, A., Raskop, J., Huang, K. & Laurat, J. Remote preparation of continuous-variable qubits using loss-tolerant hybrid entanglement of light. Optica 5, 1012–1015 (2018).
Laurat, J., Coudreau, T., Treps, N., Maître, A. & Fabre, C. Conditional preparation of a quantum state in the continuous variable regime: generation of a sub-Poissonian state from twin beams. Phys. Rev. Lett. 91, 213601 (2003).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621 (2012).
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513 (2005).
Jouguet, P., Kunz-Jacques, S., Leverrier, A., Grangier, P. & Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 7, 378–381 (2013).
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706–709 (1998).
Braunstein, S. L. & Kimble, H. J. Teleportation of continuous quantum variables. Phys. Rev. Lett. 80, 869 (1998).
Mattle, K., Weinfurter, H., Kwiat, P. G. & Zeilinger, A. Dense coding in experimental quantum communication. Phys. Rev. Lett. 76, 4656 (1996).
Heim, B. et al. Atmospheric continuous-variable quantum communication. New J. Phys. 16, 113018 (2014).
Neill, C. et al. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science 360, 195–199 (2018).
Córcoles, A. D. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015).
Vernam, G. S. Cipher printing telegraph systems for secret wire and radio telegraphic communications. Trans. Am. Inst. Electr. Eng. 45, 295–301 (1926).
Kurpiers, P. et al. Deterministic quantum state transfer and remote entanglement using microwave photons. Nature 558, 264–267 (2018).
Axline, C. J. et al. On-demand quantum state transfer and entanglement between remote microwave cavity memories. Nat. Phys. 14, 705–710 (2018).
Xiang, Z.-L., Zhang, M., Jiang, L. & Rabl, P. Intracity quantum communication via thermal microwave networks. Phys. Rev. X 7, 011035 (2017).
Yamamoto, T. et al. Flux-driven Josephson parametric amplifier. Appl. Phys. Lett. 93, 042510 (2008).
Pogorzalek, S. et al. Hysteretic flux response and nondegenerate gain of flux-driven Josephson parametric amplifiers. Phys. Rev. Appl. 8, 024012 (2017).
Goetz, J. et al. Photon statistics of propagating thermal microwaves. Phys. Rev. Lett. 118, 103602 (2017).
Fedorov, K. G. et al. Finite-time quantum entanglement in propagating squeezed microwaves. Sci. Rep. 8, 6416 (2018).
Flurin, E., Roch, N., Mallet, F., Devoret, M. H. & Huard, B. Generating entangled microwave radiation over two transmission lines. Phys. Rev. Lett. 109, 183901 (2012).
Eichler, C. et al. Observation of two-mode squeezing in the microwave frequency domain. Phys. Rev. Lett. 107, 113601 (2011).
Menzel, E. P. et al. Path entanglement of continuous-variable quantum microwaves. Phys. Rev. Lett. 109, 250502 (2012).
Fedorov, K. G. et al. Displacement of propagating squeezed microwave states. Phys. Rev. Lett. 117, 020502 (2016).
Di Candia, R. et al. Quantum teleportation of propagating quantum microwaves. EPJ Quantum Technol. 2, 25 (2015).
Killoran, N., Biggerstaff, D. N., Kaltenbaek, R., Resch, K. J. & Lütkenhaus, N. Derivation and experimental test of fidelity benchmarks for remote preparation of arbitrary qubit states. Phys. Rev. A. 81, 012334 (2010).
Clark, J. B., Lecocq, F., Simmonds, R. W., Aumentado, J. & Teufel, J. D. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature 541, 191–195 (2017).
Las Heras, U. et al. Quantum illumination reveals phase-shift inducing cloaking. Sci. Rep. 7, 9333 (2017).
Kokkoniemi, R. et al. Flux-tunable phase shifter for microwaves. Sci. Rep. 7, 14713 (2017).
Leung, D. W. Quantum vernam cipher. Quantum Info. Comput. 2, 14 (2002).
Shannon, C. E. Communication theory of secrecy systems. Bell Syst. Tech. J. 28, 656–715 (1949).
Zwolak, M. & Zurek, W. H. Complementarity of quantum discord and classically accessible information. Sci. Rep. 3, 1729 (2013).
Gu, M. et al. Observing the operational significance of discord consumption. Nat. Phys. 8, 671–675 (2012).
Andersen, U. L., Neergaard-Nielsen, J. S., van Loock, P. & Furusawa, A. Hybrid discrete- and continuous-variable quantum information. Nat. Phys. 11, 713–719 (2015).
Gottesman, D., Kitaev, A. & Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A. 64, 012310 (2001).
Fukui, K., Tomita, A., Okamoto, A. & Fujii, K. High-threshold fault-tolerant quantum computation with analog quantum error correction. Phys. Rev. X 8, 021054 (2018).
Sanz, M., Fedorov, K. G., Deppe, F. & Solano, E. Challenges in open-air microwave quantum communication and sensing. In 2018 IEEE Conference on Antenna Measurements & Applications (CAMA), 1–4 (IEEE, 2018).
Acknowledgements
We acknowledge support by the German Research Foundation through FE 1564/1-1 and Germany’s Excellence Strategy EXC-2111-390814868, Elite Network of Bavaria through the program ExQM, EU Flagship project QMiCS and OpenSuperQ, Spanish MINECO/FEDER FIS2015-69983-P, Basque Government Grant No. IT986-16 and PhD Grant No. PRE-2016-1-0284, projects JST ERATO (Grant No. JPMJER1601) and JSPS KAKENHI (Grant No. 26220601 and Grant No. 15K17731). This material is also based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research (ASCR), under field work proposal number ERKJ335. We would like to thank K. Kusuyama for assistance with part of the JPA fabrication and S. B. Ghaffari for help in early stages of the experiment.
Author information
Authors and Affiliations
Contributions
K.G.F. and F.D. planned the experiment. S.P., M.X., and K.G.F. performed the measurements and analysed the data. M.F. and E.X. contributed to the development of the measurement software. A.P.-R., M.S., and E.S. provided the theory support. K.I. and Y.N. provided the JPA samples. F.D., A.M., and R.G. supervised the experimental part of this work. S.P. and K.G.F. wrote the manuscript. All authors contributed to discussions and proofreading of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks Zachary Dutton, Yvonne Gao and other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pogorzalek, S., Fedorov, K.G., Xu, M. et al. Secure quantum remote state preparation of squeezed microwave states. Nat Commun 10, 2604 (2019). https://doi.org/10.1038/s41467-019-10727-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10727-7
This article is cited by
-
Demonstration of microwave single-shot quantum key distribution
Nature Communications (2024)
-
Quantum Communication Based on Decoherence Suppression Via Weak Measurement and Environment-Assisted Measurement
International Journal of Theoretical Physics (2024)
-
Continuous variable quantum teleportation and remote state preparation between two space-separated local networks
Science China Information Sciences (2024)
-
Scrutinizing joint remote state preparation under decoherence
Scientific Reports (2023)
-
A bidirectional quantum remote state preparation scheme and its performance analysis in noisy environments
Optical and Quantum Electronics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.