Abstract
Being the lightest, most mobile atom that exists, hydrogen plays an important role in the chemistry of hydrocarbons, proteins and peptides and most biomolecules. Hydrogen can undergo transfer, exchange and migration processes, having considerable impact on the chemical behavior of these molecules. Although much has been learned about reaction dynamics involving one hydrogen atom, less is known about those processes where two or more hydrogen atoms participate. Here we show that single and double hydrogen migrations occurring in ethanol cations and dications take place within a few hundred fs to ps, using a 3D imaging and laser pump-probe technique. For double hydrogen migration, the hydrogens are not correlated, with the second hydrogen migration promoting the breakup of the C–O bond. The probability of double hydrogen migration is quite significant, suggesting that double hydrogen migration plays a more important role than generally assumed. The conclusions are supported by state-of-the-art molecular dynamics calculations.
Similar content being viewed by others
Introduction
Intramolecular hydrogen migration is a natural process that plays a crucial role in many biological, chemical, and physical phenomena1,2,3 and is a topic of current research efforts in fuel cells4, proteomics5,6, and combustion chemistry7. Growing in popularity for its success in determining protein structure is hydrogen exchange combined with mass spectroscopy8. In deuterium labeling coupled with mass spectroscopic studies used for determining unknown protein and peptide structures, H/D scrambling or migration induced by the excitation/ionization source can lead to an erroneous interpretation of the measured spectra5,9. Thus, there is an increasing need to combine highly differential experimental measurements with realistic theoretical modeling that can anticipate if hydrogen migration is likely to occur under the chosen experimental conditions.
It is known that hydrogen migration can be induced by exciting a molecule in many ways, as illustrated by mass or luminescence spectra resulting from electron impact ionization10, X-ray absorption11, and ionization following ion collisions12. A key tool for understanding hydrogen migration dynamics, developed over the course of the past few decades is ultrafast, strong-field laser induced ionization and dissociation of small hydrocarbons, including the simplest one, acetylene13,14,15,16,17, and other polyatomic molecules, such as methanol18, ethylene glycol19, and acetonitrile20. Ultrashort VIS/NIR laser pulses with ~1014 W/cm2 intensities can singly or doubly ionize molecules in the gas phase, initiating hydrogen migration. In time-resolved studies, a second laser pulse with variable time delay is used to interrogate the molecular motions by further ionization, leading to Coulomb explosion. Hydrogen migration dynamics are thus revealed through detection of the produced ion fragments. Fast nuclear dynamics such as single hydrogen migration, which unfolds on a time scale ranging from a few tens of fs to several hundreds of fs in simple hydrocarbons, have been resolved using such a pump and probe technique14,15,16.
Several previous studies have considered the formation of H2+ and H3+ from a variety of precursor molecules, which requires the displacement of more than one hydrogen atom19,21,22,23. In many of these cases, the H2+ and H3+ are formed from hydrogen atoms that are close to each other in the molecule (for example, the two or three H atoms bonded to the same atomic center), and therefore are not due to the migration of H atoms from one molecular site to another. Meanwhile, there have been many studies showing that H migration can also play a role in the formation of H2+ and H3+ ions21,24,25. A clear case of this is the observation of H3+ after irradiating allene, which has two H atoms at both ends of the molecule and thus at least one H atom must first migrate across the carbon chain13.
The studies on the molecular hydrogen ion formation have introduced mechanisms classified as roaming and scrambling. Scrambling occurs when two or more H’s exchange bonding sites in the molecule25,26,27. Roaming describes the case when one H or H2 appears to be dissociated from the rest of the molecule, but instead of continuously moving away, it returns. Upon return, it can abstract another H28. The scrambling and roaming mechanisms are energetically unfavorable and kinematically unlikely, as confirmed by applications of the Rice–Ramsperger–Kassel–Marcus (RRKM) theory to small hydrocarbons23,27.
In the present study, we focus on the observation of H2O+ and H3O+ ions, which, in the case of ethanol, are prominently produced and requires the migration of one or two H atoms from the molecular carbon backbone to the OH functional group. Therefore, formation of H2O+ and H3O+ differs from that of molecular hydrogen ions in that not all the H atoms can be originally bonded to the same atomic center. Another interesting point is that they make a new bond with the oxygen, versus with each other, undergoing different transition state(s) to reach the final states. H3O+ ions have already been observed in earlier mass-spectrometry experiments and theory on small alcohols10,29,30,31,32, although the formation of H3O+ was found to be insignificant in methanol21. Thanks to our combination of 3D imaging and fs laser pump-probe technology, here we go a significant step farther and extract temporal information on the formation of these ions, which gives us direct access to the mechanisms of double hydrogen migration and the corresponding time scales. For completeness and as a reference, we also consider the cases where no and single hydrogen migration reactions occur. Apart from its intrinsic interest to understand the mechanisms of double hydrogen migration, ethanol is also important in many everyday applications including, for instance, as an antiseptic cleaning agent, as an additive in gasoline, and consumption in alcoholic beverages. It is also used as a solvent for nanoparticles33 and in fuel cells4.
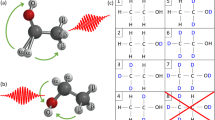
In the following, to track the hydrogen migration reactions that result in H2O+ and H3O+ fragments, we follow the ideas set forth by femtochemistry, and use two ultrashort laser pulses in a pump-probe scheme to time-resolve each migration process34. There are two scenarios on which we focus our studies, outlined in Fig. 1. In the first scenario (Fig. 1a), we track the dynamics occurring mainly in the ethanol cation, which is experimentally monitored (with the probe pulse) via promotion to the dication, leading to Coulomb explosion and the coincident detection of OH+ + C2H5+ (no hydrogen migration, NHM), H2O+ + C2H4+ (single hydrogen migration, SHM), and H3O+ + C2H3+ (double hydrogen migration, DHM). In the second scenario (Fig. 1b), our premise is that the pump laser pulse mainly populates the dication, whose fragmentation dynamics are experimentally probed via the triple coincidence channel H+ + H2O+ + C2H3+. This triple coincidence channel is fed by three possible pathways, as the H+ can be ejected first, come from the C-containing fragment following the formation of the water ion, or come from the O-containing fragment following formation of the hydronium ion. Our experimental approach allows us to disentangle these three paths.
Fragmentation dynamics scenarios. Schematic of the two scenarios investigated with the pump-probe measurements and molecular dynamics calculations, where SHM and DHM leading to H2O+ and H3O+ formation, respectively, in ethanol are involved. In the first scenario (a) the fragmentation dynamics occur in the cation, whereas for the second scenario (b), they occur in the dication. Relative energies for the exit channels are given with respect to the neutral ethanol, computed at the B3LYP/6-31++G(d,p) level of theory
Results
Delay-dependent kinetic energy release
Figure 2a–c shows the dependence of the KER on the pump-probe delay for the NHM, SHM, and DHM double coincidence channels. Figure 2d displays the delay-dependence of the KER for the triple coincidence channel, H+ + H2O+ + C2H3+. Each channel displays KER features that clearly change with the delay. Note that for delays close to 0, the pump and probe pulses overlap, giving rise to interferences in the recorded signal, and therefore are largely excluded from further analysis/interpretation.
Molecular dynamics for the selected channels. Pump-probe delay-dependence of the KER for the channels a OH+ + C2H5+, b H2O+ + C2H4+, c H3O+ + C2H3+, and d H+ + H2O+ + C2H3+. For positive delay, the pump and probe pulses have an intensity of 4.2 × 1014 and 6.7 × 1014 W/cm2, respectively. For the negative delays, the pump and probe pulses reverse roles. The time-independent features at KER ~5 eV for (a–c) and ~13 eV for (d) are mainly due to interaction with only one of the pulses
Double coincidences
The features where the KER for NHM, SHM, and DHM shown in panels a, b, and c of Fig. 2 decrease as the pump-probe delay increases are those that follow scenario 1 (see Fig. 1a). What allows us to state that the two-body coincidences mainly reflect the dynamics of the cation is the statistical analysis of the individual channels compared to their precursor(s), which is elaborated on in the Supplementary information (SI). These time-dependent KER features are then selected to monitor their yield as a function of delay between pump and probe laser pulses. The yield is normalized to the number of pulse pairs for a given delay bin. The resulting curves are presented in Fig. 3a.
Channel yield versus time. Normalized yield as a function of time for the time-dependent features for the a NHM (green, 0–4 eV KER), SHM (red, 0.5–3.6 eV KER), and DHM (blue, 0.5–3.6 eV KER) double coincidence channels and b the triple coincidence channel H+ + H2O+ + C2H3+, split into 0–5 eV KER (blue), 5–13 eV KER, inner arch (red), and 5–13 eV KER, outer arch (purple). Experimental error bars are statistical. Theory (solid lines) is carried out for the cation with 10 eV internal energy in (a) and the dication with 5 eV internal energy in (b)
To get a deeper insight on the H migration mechanisms, we have performed state-of-the-art ab initio molecular dynamics (AIMD) simulations by using the Atom-Centered Density Matrix Propagation35,36,37 method, ADMP, as implemented in the Gaussian09 Package38 (see Methods). Figure 3a shows the calculated number of trajectories as a function of the migration time for ethanol cations with an internal excitation energy of 10 eV for both positive and negative delays. The total number of trajectories in each channel has been scaled such that it matches the measured normalized yield at 1 ps, where it practically reaches its saturation value. We have assigned a migration time to a trajectory that results in H2O+ by identifying the time at which the distance between the migrating H atom and O goes below 1 Å for the first time. Similarly, times for OH+ formation have been assigned whenever the distance between the O atom and the C atom from where it departs is larger than 3 Å. We note that no H3O+ formation (blue symbols in Fig. 1a) is predicted by theory, which is likely due to the limited number of trajectories considered in the cation calculations. From the known excitation energies of ethanol and the AIMD simulations, we estimate that the typical excitation energy of the molecular cation produced by the interaction with the pump pulse should lie between 10 and 15 eV. These numbers agree with those reported in earlier work using similar laser pulses39. The H atoms migrate faster with higher initial internal energy, which should make the single and double H migration timescales a bit shorter for negative delays (the more intense pulse comes first) than for positive delays. We do observe this in the experiment, albeit marginally.
By plotting the ratio of the double coincidence channels, as in Supplementary Fig. 7, we investigate the dependence of the channels on each other. It turns out that the ratios are nearly flat as a function of pump-probe time, with some discrepancies discussed in the SI. This is consistent with a competing reaction model40—where the production of one channel does not depend on the other in a sequential way.
Triple coincidences
To probe the dynamics of the dication in the experiment requires forming the dication with the pump pulse, which means that the probe pulse must further ionize the molecule to the trication, resulting in the three ionic fragments H+ + H2O+ + C2H3+—see scenario 2 presented in Fig. 1b. Strictly speaking one cannot completely discard that the H+ + H2O+ + C2H3+ KER also reflects the dynamics induced by the pump pulse in the singly ionized molecule, since the intensity of the probe pulse is large enough to further ionize the monocation to a triply charged final state. A careful inspection of our pump-only data shows that contribution of the monocation dynamics to the NHM and DHM channels should be at most ∼35%, so that scenario 2 reflects most of the physics discussed below. In contrast, for the SHM channel, our pump-only data suggest that the H+ + H2O+ + C2H3+ KER reflects the dynamics of both the monocation and the dication in almost equal proportions. This should be kept in mind in the discussion of the corresponding mechanisms presented below.
The measured KER as a function of pump-probe delay time is presented in Fig. 2d, which shows two delay-dependent KER features. The lower energy feature (0–5 eV) can be attributed to the case where first H3O+ is formed, and the probe pulse further ionizes and dissociates it into H+ + H2O+. The higher energy feature (5–13 eV) is fed by two precursor channels: one where the H+ comes off first (deprotonation), and one where the H2O+ is formed and the remaining C2H4+ is further ionized and dissociated. We note that, similar to the double coincidence channels, stronger pump pulses (negative delays) ultimately lead to a lower yield of the migration channels. This may be an indication that tunneling ionization prevails over multiphoton ionization or just be the direct effect of having a weaker probe pulse.
The three-body fragmentation channel lends itself to visualizing the fragment momenta in the molecular frame in the form of a Newton plot41, and the energy sharing among the three ions in the form of a Dalitz plot42. The Newton plot coordinates are defined such that the C2H3+ ion is always along the positive x-axis and the H2O+ and H+ are always in the upper and lower half of the plot, respectively. The results are shown in Fig. 4a–l. The H+ momenta \(( - p_ \bot )\) for the high KER feature reveals two distinct contributions, forming an inner and outer arch. These two regions are separated into \(p = \sqrt {p_ \bot ^2 + p_{||}^2}\)< 20 au and >20 au and are plotted individually. While an arch shape in a Newton plot typically represents a sequential fragmentation process, the fact that the H+ can come from six different locations in the molecule jumbles everything, which precludes this interpretation.
Molecular dynamics for H+ + H2O+ + C2H3+. a–l Newton and m–x Dalitz plots for the triple coincidence channel H+ + H2O+ + C2H3+. Panels a–d and m–p are for 0–5 eV KER and e–l and q–x are for 5 to 13 eV KER. The high KER region is split into e–h and q–t which shows the dynamics for the events with p < 20 a.u. and i–l and u–x for the events with p > 20 a.u. The time bins are the same for each column and are from left to right 0–150, 260–410, 460–610, and 660–810 fs (with the center of the time bin denoted). Note that the ellipses are only drawn to help guide the eye, and the color scale, given on the left of the plots range from less counts (bluer) to higher concentration of counts (redder). The blue, green and red shaded boxes show snapshots of the final states reached after the pump step in typical trajectory calculations for the three channels leading to H+ + H2O+ + C2H3+ after the probe step: low KER, high KER inner arch, and high KER outer arch, respectively. Movie frames for the earlier stages of the corresponding fragmentation processes are given in the SI. Panel y shows Dalitz plot simulations considering different breakup mechanisms. Features labeled i (blue), ii (green), and iii (red) are for sequential bond breaking with C2H3+, H2O+, and H+ being the first fragment ejected, respectively, and can be related via color to the first step of the breakup processes shown in the shaded boxes of (b)
The Dalitz plot coordinates are defined as
where Ei (i = C2H3+, H2O+, H+) are the energies of the individual fragments. To interpret the experimental Dalitz plots shown in Fig. 4m–x, we have simulated the different sequential breakup processes by using a random selection of initial conditions and generated the corresponding Dalitz plot by assuming that all these processes contribute equally, displayed in Fig. 4y.
Discussion
The Newton and Dalitz plots show a considerable dependence on the time delay for each of the pathways leading to H+ + H2O+ + C2H3+. The low KER contribution, attributed to DHM, is very small at small time delay (Fig. 4a). As time increases (Fig. 4b–d), the yield increases, but the shape of the momentum distribution and the magnitude of the momentum itself does not change significantly. The corresponding Dalitz plots (Fig. 4m–p) are compatible with a sequential mechanism in which C2H3+ is ejected first leaving H3O+ to further fragment (see process i of Fig. 4y), thus suggesting that the second H migration promotes the breaking of the C–O bond. The energy sharing spreads out with time, indicating that the molecule undergoes significant distortions in its molecular geometry.
For the high KER, inner arch of the Newton plot (Fig. 4e–h), the magnitude of the H+ total momentum decreases with time delay, suggesting that the distance between the ions increases and there is less Coulomb repulsion at the time of the bond breakage (see SI for a more quantitative analysis). The corresponding Dalitz distributions (see Fig. 4q–t) appear in the lower part of the allowed region and are consistent with sequential breakups where C2H3+ is ejected first leaving H3O+ to further fragment (see process i of Fig. 4y) or H2O+ is ejected first leaving C2H4+ to further fragment (see process ii of Fig. 4y). Therefore, this channel can either be attributed to SHM or to DHM, although given the fact that C2H4+ is less bound than the H3O+ fragment, most likely we can attribute this section to SHM where the H2O+ was ejected first. The measured distributions shift to smaller yd as the time delay increases, suggesting that H+ lies between C2H3+ and H2O+ when the molecule breaks.
For the high KER, outer arch of the Newton plot (Fig. 4i–l), the general shape of the H+ momentum distribution remains the same for all time delays, although the peak in the distribution shifts towards negative p||. Furthermore, the H2O+ distribution shows a bifurcation, where part of the distribution seems to remain unchanged, and part of it moves towards positive p||. The corresponding Dalitz distributions (Fig. 4u–x) mainly cover the upper part of the allowed region, which is consistent with process iii (see Fig. 4y) in which H+ is ejected first corresponding to a deprotonation precursor channel. As the time delay increases, the distribution shifts towards larger yd (see SI for a more quantitative analysis) suggesting that the molecular geometry becomes more linear, with either C2H3+ or H2O+ in the middle. The part of the distribution that moves towards positive p|| is consistent with having C2H3+ in the middle, and the part that does not change much with pump-probe delay is consistent with having H2O+ in the middle.
At variance with the ethanol monocation, calculations for the dication do lead to H3O+ fragments. Thus, the calculated trajectories provide information about the three precursor channels and are split accordingly. The calculated yields as functions of migration time are overlaid with the experimental yield, shown in Fig. 3b. Here, the internal energy used in the calculations is 5 eV for both positive and negative delays. The reason why we have chosen a lower value for the internal energy than in the monocation case is that part of the energy provided by the pump laser must be used to eject a second electron from the ethanol molecule. The good agreement between experiment and theory suggests that the most important dynamics are captured by the calculation.
We can now try to answer the question: how does the double H migration unfold? To begin with, we investigate if there is a correlation between H migration times for the first and second individual migrations for those dication trajectories leading to H3O+, as shown in Fig. 5a. The large scatter in the plot suggests that the second H migration takes place rather independently of the first migration. This finding is consistent with the experimentally determined time-independent ratios for the double coincidence channels (see Supplementary Fig. 7).
Theory investigation of correlated motions. Correlation of the H migrations themselves and the C–O bond breaking times for trajectories resulting in H3O+ formation after double ionization. a Second versus first H migration time. b Scheme of ethanol highlighting the C–O distance (black arrow) and the migration of two H atoms from Cα (purple arrow), and Cβ (green arrow). c Correlation between the second H migration and the C–O bond break for H’s originating at the adjacent (Cα, full symbols) or terminal (Cβ, open symbols) carbon atoms
We have also analyzed the AIMD simulation results testing for possible correlations between the time for the first and/or second H migration and the time for the carbon–oxygen bond cleavage (for the trajectories of doubly charged ethanol leading to H3O+). We observe that there is no correlation between the first H migration and the breaking of the C–O bond. However, as shown in Fig. 5c, there is a clear linear correlation between the second H migration and the breaking of the C–O bond. We thus conclude that the second H migration and the C–O break follows a concerted mechanism, that is, the second migration drives the breakup of the C–O bond. This can be understood in terms of Lewis’s octet rule: after migration of the first proton from the molecular backbone to the O atom, which preserves the electronic octet and locates the positive charge around the latter atom, accommodation of a second H atom (proton + electron) is only possible if the C–O bond breaks, so that one electron leaves its place in the O octet to the incoming electron (the one coming with H).
Another interesting finding is that there is no apparent preference whether the second H comes from Cα or Cβ (see Fig. 5b for the distinction between α and β). As can be seen in Fig. 5, the same behaviors are observed for a wide range of internal energies (from 2 to 15 eV), not only for the internal energy used to evaluate the rate presented in Fig. 3. This points to the generality of the above mechanisms, which may be relevant in other contexts, as there are indications that H migration can drive peptide bond breaking in peptide chains43.
In summary, we have combined ultrafast time-resolved imaging techniques and ab-initio molecular dynamics calculations to investigate single and double H migration in ethanol cations and dications. Good agreement between the experimentally measured and calculated yields as a function of pump-probe delay time was achieved, setting a new benchmark standard for studying the ultrafast nuclear dynamics of complex molecules.
The timescales for single and double H migration to form H2O+ and H3O+, respectively, is on the order of several hundred fs to ps under the present conditions of the study. Experimentally measured channel yield ratios as a function of pump-probe delay, as well as the AIMD simulations of the ethanol dication, indicate that the two H migrations needed to form H3O+ are not correlated with each other, and do not show a preference for where they originate from in the molecule. Furthermore, the migration of the second H is concerted with the breaking of the C–O bond.
We hope that our work will help the development of the predictive power necessary to establish routine H migration pathways in complex molecules and contribute new understanding on the timescale of multi-H-migration processes, which are significant for biology, chemistry, and in general for a better understanding of molecular dynamics.
Methods
Experiment
The experiment was carried out utilizing two 730 nm (central wavelength), 9 fs laser pulses in a pump-probe configuration with variable time delay between the arrival of the two pulses. The laser pulses were focused on a thin jet of gas phase ethanol inside a cold target recoil ion momentum spectrometer (COLTRIMS), where a static electric field directs ions and electrons to their respective time- and position-sensitive detectors (see Supplementary Fig. 1a). Each separate pair of laser shots provides a new opportunity for an ethanol molecule in the laser focus to undergo light-induced dynamics. Channel selection is accomplished by plotting a 2D histogram of the time of flights of the first and second ions, shown in Supplementary Fig. 1b, which shows (a subset of) the numerous fragmentation pathways, and gating on the pair(s) of ions that conserve momentum for each corresponding channel.
Theory
Ab initio molecular dynamics (AIMD) simulations were performed by using the Atom-Centered Density Matrix Propagation35,36,37 method, ADMP, as implemented in the Gaussian09 Package38. In this method, electronic structure is described quantum mechanically in the framework of the density functional theory—DFT, in particular by using the B3LYP functional44,45 in combination with the atomic-centered Gaussian basis set 6-31++G(d,p). In contrast, nuclear motion is assumed to be purely classical and is calculated on the fly by using the forces associated with the instantaneous potential created by the electrons. Following previous theoretical work on coupled electron and nuclear dynamics from excited states in molecules of this size (see, for example ref. 46,47,48,49,50,51,52), in this work, we assume that the initial excitation energy has already been relaxed to the ground electronic state, which is a reasonable approximation since the investigated migration dynamics are usually slower than the (non-adiabatic) internal conversion processes leading to such energy relaxation. The simulations were performed for the singly and doubly charged ethanol ions resulting from the vertical ionization of the two known conformers of neutral ethanol. For each value of the excitation energy, randomly distributed among the nuclear degrees of freedom, 1000 trajectories were computed. To ensure the adiabaticity of the dynamics, we have imposed a time step of ∆t = 0.1 fs and a fictitious electron mass of 0.1 amu. The maximum propagation time was 3 ps. More details are given in the SI.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Zhao, J. et al. Intramolecular hydrogen atom migration along the backbone of cationic and neutral radical tripeptides and subsequent radical-induced dissociations. Phys. Chem. Chem. Phys. 14, 8723–8731 (2012).
Breslow, R. & Khanna, P. L. An intramolecular model for the enzymatic insertion of coenzyme B12 into unactivated carbon-hydrogen bonds. J. Am. Chem. Soc. 98, 1297–1299 (1976).
Wasowicz, T. J. & Pranszke, B. Observation of the hydrogen migration in the cation-induced fragmentation of the pyridine molecules. J. Phys. Chem. A 120, 964–971 (2016).
Ni, M., Leung, Y. C. & Leung, M. K. H. A review on reforming bio-ethanol for hydrogen production. Int. J. Hydrog. Energy 32, 3238–3247 (2007).
Bache, N., Rand, K. D., Roepstorff, P., Ploug, M. & Jorgensen, T. J. D. Hydrogen atom scrambling in selectively labeled anionic peptides upon collisional activation by MALDI tandem time-of-flight mass spectrometry. J. Am. Soc. Mass Spectrom. 19, 1719–1725 (2008).
Ledvina et al. Infrared photo-activation reduces peptide folding and hydrogen atom migration following ETD tandem mass spectrometry. Angew. Chem. Int Ed. Engl. 48, 8526–8528 (2009).
Sharma, S., Raman, S. & Green, W. H. Intramolecular hydrogen migration in alkylperoxy and hydroperoxyalkylperoxy radicals: accurate treatment of hindered rotors. J. Phys. Chem. A 114, 5689–5701 (2010).
Englander, S. W. & Krishna, M. M. G. Hydrogen exchange. Nat. Struct. Biol. 8, 741–742 (2001).
Rand, K. D., Adams, C. M., Zubarev, R. A. & Jorgensen, T. J. D. Electron capture dissociation proceeds with a low degree of intramolecular migration of peptide amide hydrogens. J. Am. Chem. Soc. 130, 1341–1349 (2008).
Van Raalte, D. & Harrison, A. G. Energetics and mechanism of hydronium ion formation by electron impact. Can. J. Chem. 41, 3118–3126 (1963).
Liekhus-Schmaltz, C. E. et al. Ultrafast isomerization initiated by X-ray core ionization. Nat. Commun. 6, 8199 (2015).
Jochim, B. et al. Rapid formation of H3 + from ammonia and methane following 4 MeV proton impact. J. Phys. B: . Mol. Opt. Phys. 42, 091002 (2009).
Kuebel, M. et al. Steering proton migration in hydrocarbons using intense few-cycle laser fields. Phys. Rev. Lett. 116, 193001 (2016).
Hishikawa, A., Matsuda, A., Fushitani, M. & Takahashi, E. J. Visualizing recurrently migrating hydrogen in acetylene dication by intense ultrashort laser pulses. Phys. Rev. Lett. 99, 258302 (2007).
Ibrahim, H. et al. Tabletop imaging of structural evolutions in chemical reactions demonstrated for the acetylene cation. Nat. Commun. 5, 4422 (2014).
Burger, C. et al. Visualization of bond rearrangements in acetylene using near single-cycle laser pulses. Faraday Discuss. 194, 495–508 (2016).
DeVine, J. A. et al. Encoding of vinylidene isomerization in its anion photoelectron spectrum. Science 358, 336–339 (2017).
Ando, T. et al. Wave packet bifurcation in ultrafast hydrogen migration in CH3OH+ by pump-probe coincidence momentum imaging with few-cycle laser pulses. Chem. Phys. Lett. 624, 78–82 (2015).
Ekanayake, N. et al. Mechanisms and time-resolved dynamics for trihydrogen cation (H3 +) formation from organic molecules in strong laser fields. Sci. Rep. 7, 4703 (2017).
Hishikawa, A., Hasegawa, H. & Yamanouchi, K. Hydrogen migration in acetonitrile in intense laser fields in competition with two-body Coulomb explosion. J. Electron Spectrosc. Relat. Phenom. 141, 195–200 (2004).
Hoshina, K., Furukawa, Y., Okino, T. & Yamanouchi, K. Efficient ejection of H3 + from hydrocarbon molecules induced by ultrashort intense laser fields. J. Chem. Phys. 129, 104302 (2008).
Rajgara, F. A., Dharmadhikari, A. K., Mathur, D. & Safvan, C. P. Strong fields induce ultrafast rearrangement of H atoms in H2O. J. Chem. Phys. 130, 231104 (2009).
Schirmel, N., Reusch, N., Horsch, P. & Weitzel, K.-M. Formation of fragment ions (H+, H3 +, CH3 +) from ethane in intense femtosecond laser fields – from understanding to control. Faraday Discuss. 163, 461–474 (2013).
Xu, H., Okino, T. & Yamanouchi, K. Ultrafast hydrogen migration in allene in intense laser fields: Evidence of two-body Coulomb explosion. Chem. Phys. Lett. 469, 255–260 (2009).
Okino, T., Watanabe, A., Xu, H. & Yamanouchi, K. Two-body Coulomb explosion in methylacetylene in intense laser fields: double proton migration and proton/deuteron exchange. Phys. Chem. Chem. Phys. 14, 4230–4235 (2012).
Kanya, R. et al. Hydrogen scrambling in ethane induced by intense laser fields: statistical analysis of coincidence events. J. Chem. Phys. 136, 204309 (2012).
Huntress, W. T. Jr. Hydrogen atom scrambling in ion-molecule reactions of methane and ethylene. J. Chem. Phys. 56, 5111–5120 (1972).
Bowman, J. M. & Houston, P. L. Theories and simulations of roaming. Chem. Soc. Rev. 46, 7615–7624 (2017).
Shirota, T., Mano, N., Tsuge, M. & Hoshina, K. Formation of H3O+ from alcohols and ethers induced by intense laser fields. Rapid Commun. Mass Spectrom. 24, 679–686 (2010).
Kotsina, N., Kaziannis, S. & Kosmidis, C. Hydrogen migration in methanol studied under asymmetric fs laser irradiation. Chem. Phys. Lett. 604, 27–32 (2014).
Hoshina, K. & Tsuge, M. Formation of H3O+ from ethanol clusters induced by intense femtosecond laser fields. Chem. Phys. Lett. 489, 154–158 (2010).
Lu, H.-F., Li, F.-Y., Nagaya, K., Hayashi, M. & Lin, S. H. The structures, conversions and fragmentations of C2H6O2+ isomers: An ab initio study. J. Mol. Struct.: THEOCHEM 773, 71–79 (2006).
Khoza, P. B., Moloto, M. J. & Sikhwivhilu, L. M. The effect of solvents, acetone, water, and ethanol, on the morphological and optical properties of ZnO nanoparticles prepared by microwave. J. Nanotechnol. 2012, 195106 (2011).
Zewail, A. H. Femtochemistry: Atomic-scale dynamics of the chemical bond. J. Phys. Chem. A 104, 5660–5694 (2000).
Iyengar, S. S. et al. Ab initio molecular dynamics: propagating the density matrix with Gaussian orbitals. II. Generalizations based on mass-weighting, idempotency, energy conservation and choice of initial conditions. J. Chem. Phys. 115, 10291–10302 (2001).
Schlegel, H. B. et al. Ab initio molecular dynamics: propagating the density matrix with Gaussian orbitals. J. Chem. Phys. 114, 9758–9763 (2001).
Schlegel, H. B. et al. Ab initio molecular dynamics: propagating the density matrix with Gaussian orbitals. III. Comparison with Born-Oppenheimer dynamics. J. Chem. Phys. 117, 8694–8704 (2002).
Gaussian 09, Revision E.01, M. J. Frisch et al. (Gaussian, Inc., Wallingford CT, 2013).
Kling, M. F. et al. Control of electron localization in molecular dissociation. Science 312, 246–248 (2006).
Levine, I. N. Physical Chemistry. sixth edn, 521–526 (McGraw-Hill: New York, 2002).
Muranaka, T. Fragmentation dynamics of triatomic molecules: contribution of geometry. PhD Thesis, (University of Caen, 2007).
Dalitz, R. CXII. On the analysis of τ-meson data and the nature of the τ-meson. Philos. Mag. Ser. 44, 1068–1080 (1953).
Dongre, A. R., Jones, J. L., Somogyi, J. L. & Wysocki, V. H. Influence of peptide composition, gas-phase basicity, and chemical modification on fragmentation efficiency: evidence for the mobile proton model. J. Am. Chem. Soc. 118, 8365–8374 (1996).
Becke, A. D. Density-functional thermochemistry. III. role exact. Exch. J. Chem. Phys. 98, 5648–5652 (1993).
Lee, C., Yang, W. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988).
Capron, M. et al. A Multicoincidence study of fragmentation dynamics in collision of γ aminobutyric acid with low energy ions. Chem. A Eur. J. 18, 9321–9332 (2012).
Maclot, S. et al. Dynamics of glycine dications in the gas phase: ultrafast intramolecular hydrogen migration versus Coulomb repulsion. J. Phys. Chem. Lett. 4, 3903–3909 (2013).
Ha, D. T. et al. Fragmentation dynamics of doubly charged methionine in the gas phase. J. Phys. Chem. A 118, 1374–1383 (2014).
Kukk, E. et al. Internal energy dependence in X-ray-induced molecular fragmentation: an experimental and theoretical study of thiophene. Phys. Rev. A 91, 043417 (2015).
Piekarski, D. G. et al. Unusual hydroxyl migration in the fragmentation of β-alanine dication in the gas phase. Phys. Chem. Chem. Phys. 17, 16767–16778 (2015).
Maclot, S. et al. Determination of energy-transfer distributions in ionizing ion-molecule collisions. Phys. Rev. Lett. 117, 073201 (2016).
Piekarski, D. G. et al. Production of doubly-charged highly reactive species from the long-chain amino acid GABA initiated by Ar9+ ionization. Phys. Chem. Chem. Phys. 19, 19609–19618 (2017).
Acknowledgements
This work was funded by the National Science Foundation under award No. 1700551, the MINECO projects FIS2016-77889-R and CTQ2016- 76061-P, ‘Severo Ochoa’ Programme for Centres of Excellence in R&D (SEV-2016-0686) and ‘María de Maeztu’ Programme for Units of Excellence in R&D (MDM-2014-0377). We acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). S.D.-T. gratefully acknowledges the “Ramón y Cajal” program (RYC-2010-07019) of the Spanish Ministerio de Educación y Ciencia. We thank Todd Martinez and Daniel Rolles for helpful discussions.
Author information
Authors and Affiliations
Contributions
N.K. and N.B. conceived the experimental study, S.T. and F.M. conceived and carried out the theoretical study. N.K., R.O., and M.S. acquired experimental data. N.K. performed experimental data analysis. N.K., M.R.D., H.X., M.S., S.D.K., M.D., P.D., A.C., and T.O. all contributed to the experimental setup. N.K., F.M., S.T., and N.B. wrote the first draft of the manuscript. All authors contributed to the interpretation of the data, as well as edited and approved the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications would like to thank the anonymous reviewers for their contribution to the peer review of this journal.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kling, N.G., Díaz-Tendero, S., Obaid, R. et al. Time-resolved molecular dynamics of single and double hydrogen migration in ethanol. Nat Commun 10, 2813 (2019). https://doi.org/10.1038/s41467-019-10571-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10571-9
This article is cited by
-
Direct tracking of H2 roaming reaction in real time
Nature Communications (2024)
-
Initial-site characterization of hydrogen migration following strong-field double-ionization of ethanol
Nature Communications (2024)
-
Hydrogen migration in inner-shell ionized halogenated cyclic hydrocarbons
Scientific Reports (2023)
-
H2 formation via non-Born-Oppenheimer hydrogen migration in photoionized ethane
Nature Communications (2023)
-
Formation of H3+ from ethane dication induced by electron impact
Communications Chemistry (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.