Abstract
Co-intercalation reactions make graphite as promising anodes for sodium ion batteries, however, the high redox potentials significantly lower the energy density. Herein, we investigate the factors that influence the co-intercalation potential of graphite and find that the tuning of the voltage as large as 0.38 V is achievable by adjusting the relative stability of ternary graphite intercalation compounds and the solvent activity in electrolytes. The feasibility of graphite anode in sodium ion batteries is confirmed in conjunction with Na1.5VPO4.8F0.7 cathodes by using the optimal electrolyte. The sodium ion battery delivers an improved voltage of 3.1 V, a high power density of 3863 W kg−1both electrodes, negligible temperature dependency of energy/power densities and an extremely low capacity fading rate of 0.007% per cycle over 1000 cycles, which are among the best thus far reported for sodium ion full cells, making it a competitive choice in large-scale energy storage systems.
Similar content being viewed by others
Introduction
Driven by the concerns of limited and unevenly distributed lithium resources, sodium ion battery (SIB) technologies have taken the privilege over lithium ion batteries (LIBs) on meeting the emerging and demanding applications of large-scale energy storage systems, because of the abundant sodium resources in the earth crust and sea water1,2,3. During the past few years, great efforts have been devoted to exploring suitable electrode materials to take advantage of the cost-effective sodium-rechargeable battery chemistry4,5. In the endeavor, metal alloys/oxides/chalcogenides, phosphorus, and carbonaceous materials have been extensively studied as potential anodes for SIBs, showing great promises6,7,8,9,10,11. In particular, materials undergoing alloying and/or conversion reactions could present high sodium storage capacities and low operation potential, which could benefit the energy density of SIBs. Moreover, traditional carbonaceous materials such as hard carbon were capable of delivering a respectable cyclic stability with high capacities of ~300 mAh g−1 12,13. Nevertheless, the drastic volume changes that are typically accompanied in the alloying or conversion reactions cause the structural degradation of electrode materials, leading to a relatively fast capacity fading9,10. Regarding the use of the hard carbon anode, the low redox voltage close to that of the sodium metal plating12 would induce serious concerns on the safety issues.
Graphite has been recently revisited as a potential anode material for SIBs. At the early stage of the research, it was often demonstrated that only a negligible amount of sodium ions can be intercalated into the graphite structure (i.e., 30 mAh g−1), which was attributed to the thermodynamic instability of the binary Na-intercalated graphite compound (b-GIC) based on computational studies14,15. Meanwhile, it was revealed by Jache et al.16 and our group17 that sodium can be reversibly stored in graphite through co-intercalation reactions, where solvated sodium ions are intercalated into the galleries of graphite, forming a ternary graphite intercalation compound (t-GIC). Co-intercalation reactions endowed graphite electrodes with a remarkable reversibility and fast sodium intercalation kinetics, opening the new avenue toward exploiting graphite as a promising anode for advanced SIBs.
Motivated by these findings, the electrochemical performance of the graphite anode and its intrinsic reaction mechanisms have been extensively investigated in recent years. Yoon et al.18 and Jung et al.19 described the specific conditions that trigger the co-intercalation reactions in the electrochemical cells based on density functional theory (DFT) calculations. Goktas et al.20 found that several solvents like crown ether that were unsuitable for the co-intercalation reaction at room temperature could be activated at elevated temperatures. It was also unveiled that the co-intercalation in graphite occurs via a fast staging process21,22, with the growth of a very thin solid electrolyte interphase (SEI) layer. The structural stability and the fast kinetics led to the experimental realizations that the graphite anodes consistently display the cyclic stability up to thousands of cycles and high rate capabilities23,24. When assembled in the sodium ion full cell using Na0.7CoO2 as a cathode, it could still retain a high-power capability of 300 W kg−1 and long cycle life of 1000 cycles25. Nonetheless, one of the grand challenges in exploiting the graphite anode till now has been its relatively high co-intercalation redox potential. According to the sodium ion full cell demonstrated by Hasa et al.25, the output voltage was only 2.2 V due to the high potential exhibited by graphite anode (i.e., 0.77 V), which led to an unsatisfactory energy density of 60 Wh kg−1, far from sufficient to meet the requirement for practical applications. In other series of reports, the sodium co-intercalation voltages were also identified in the range of 0.6−0.8 V vs. Na+/Na using various ether-based electrolytes21,22,26. These values are far higher than the ~0.15 V vs. Li+/Li for the conventional intercalation reactions of lithium to the graphite anode in LIBs. How to tailor the co-intercalation potential for SIBs with high output voltage that can lead to high energy and power densities still remains an open question.
In this work, we aim to tune the sodium intercalation potential in graphite by systematically investigating the correlations among the co-intercalation voltage, the solvent species, the concentrations of sodium ions in the electrolytes, and the temperatures. It is found that the relative stability of the ternary graphite intercalation compounds and the free solvent activity are one of the most dominant factors determining the sodium storage voltage. Following these insights, a large tuning range of 380 mV is obtained with the lowest reaction voltage of 0.43 V for graphite-based half-cells. When coupling the graphite anodes with Na1.5VPO4.8F0.7 cathodes and an optimal electrolyte, we attain Na-ion full cells presenting one of the highest power densities with the output voltages of 3.1 V and impressive capacity retention at a wide range of temperature (from 0 to 60 °C), which are among the best thus far reported for Na-ion full batteries, promoting the practical application of secondary Na-ion batteries with feasible graphite anodes.
Results
Co-intercalation voltage of graphite anode in SIB
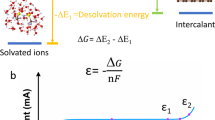
In tailoring the co-intercalation reaction potential, it is necessary to recall the relevant reaction processes involving sodium, solvent, and graphite. The electrode reactions for a half-cell of graphite|| 1 M NaPF6 diethylene glycol dimethyl ether (G2)|| sodium can be described as follows:
where [Na − G2]+ refers to the solvated Na ions and [Na − G2]Cx is the t-GIC (Fig. 1a). Based on Eqs. (1) and (2), the co-intercalation reaction voltage (V) can be expressed as
where \(E_{t - {\mathrm{GIC}}}^0,\) \(E_{{\mathrm{Na}}}^0,\) R, T, F, and \(a_{{\mathrm{G2}}}\) denote the standard electrode potentials of t-GIC and Na metal, gas constant, absolute temperature, Faraday constant, and the solvent activity, respectively. Accordingly, the co-intercalation voltage depends on the standard formation potential of t-GIC \(\left( {E_{t - {\mathrm{GIC}}}^0} \right)\) and the activity of free solvent molecules (aG2).
Solvent dependency of co-intercalation voltage. a Schematic illustration of solvated Na ion co-intercalating into graphite galleries. b dQ/dV plots of graphite electrodes cycled in 1 M NaPF6 G1, G2, G4, Gn–250, and Gn–500 electrolytes, respectively. c Plot of normalized repulsion energy as a function of interlayer distance to elucidate the correlation between Na storage potential in graphite and ethers used in electrolytes
Relative stability of ternary GIC
In order to understand the effect of these energetics, we conducted a series of co-intercalation experiments using six different linear solvent species with increasing average chain lengths (i.e., dimethyl ether (G1), G2, triethylene glycol dimethyl ether (G3), tetraethylene glycol dimethyl ether (G4), and poly (ethylene glycol) dimethyl ether (Gn-250 with Mw ≈ 250, and Gn-500 with Mw ≈ 500)). Supplementary Fig. 1 presents the charge/discharge profiles of graphite cycled in 1 M NaPF6 electrolytes with the respective solvents at 50 mA g−1 in the voltage range of 0.1–2.0 V. The shape of the charge/discharge profiles and the Na storage capacities in G1, G2, G4, and Gn systems are similar, where the specific capacities are in the range of 105–120 mAh g−1. It is noted that the co-intercalation of graphite in G3 system is only partly reversible; thus, we will exclude the G3 system in the following discussion on electrochemical performance22. Figure 1b illustrates the differential capacity versus voltage (dQ/dV) curves derived from the charge/discharge profiles. It clearly presents that the average Na co-intercalation voltage alters systematically from 0.60, 0.66, 0.77, and 0.78 to 0.81 V for G1, G2, G4, Gn-250, and Gn-500-based electrolytes, respectively. It suggests an increase of the average co-intercalation voltage, as the chain length of the solvent increases. Note that the average co-intercalation voltage is determined from dQ/dV curves by the dashed lines located between discharge and charge plateau potentials (Fig. 1b), similar with previous studies16,17,20. Also note that the average co-intercalation voltages are consistent with the values calculated by the method of dividing the energy density into specific capacity.
The \(E_{t - {\mathrm{GIC}}}^0\) depends on the thermodynamic stability of t-GICs, which can be considered with respect to the following interactions, namely, (i) the interaction between the intercalants and graphene layers, (ii) the repulsion among positively charged intercalants, and (iii) the effective repulsion among negatively charged graphene layers27. As the chain length of the ether solvent increases, it is expected that the Na ions are more efficiently shielded in the solvated structure; therefore, the unfavorable interaction between the Na intercalant and the graphite, which has prevented the intercalation of the bare Na ion in the graphite structure18,27, would be significantly weakened. It would lead to the stabilization of the t-GIC structure, and accordingly, the average co-intercalation voltage would increase with longer ether solvent molecules. As the Na ions are better shielded in the solvated structure, the repulsion among positively charged intercalants is also expected to decrease as well, which aids in the further stabilization of the t-GICs21. Finally, the repulsive interaction between the negatively charged graphene layers would be mitigated by the larger interlayer distances offered by the co-intercalation. The interlayer distances calculated from XRD patterns of the fully sodiated graphite (Supplementary Fig. 2) present the values of about 11.6, 11.8, 12.01 12.2, and 12.5 Å for G1, G2, G4, Gn-250, and Gn-500 systems, respectively22. When the relative stabilities of the graphite host are estimated as a function of interlayer distance from the DFT calculations as depicted in Fig. 1c and Supplementary Fig. 2, it is observed that the repulsion energy decreases with the distance between graphene layers. We would like to note that the amount of charge transferred from the intercalants to graphene layers is almost identical among co-intercalated t-GICs, because of their similar reversible capacities (Supplementary Fig. 1) and Bader charges of intercalants (Supplementary Table 1). This allows us to compare the repulsive interactions of all compounds in a single curve in Fig. 1c. As indicated with stars in the dashed line, the weaker repulsion between graphene layers stabilizes the t-GIC structure, resulting in higher intercalation potentials, with the longer chain of the ether solvents. It illustrates the efficacy of regulating the co-intercalation potential by a proper selection of solvents.
Solvent activity dependency of co-intercalation voltage
To further investigate the effect of solvent, we systematically altered the solvent activity (aG2 of a specific solvent (G2-based electrolyte)) by preparing a series of electrolytes with different salt concentrations (NaPF6 from 0.05 to 3 M). The charge/discharge profiles of graphite electrodes cycled in these electrolytes at 50 mA g−1 are presented in Supplementary Fig. 3. Figure 2a depicts that the Na storage voltages are apparently shifted to lower values, as the concentration of electrolytes increases. The correlation between the concentration and the Na half-cell voltage is more clearly displayed in Fig. 2b. In the relatively diluted region from 0.05 to 1.0 M, only a slight shift of the co-intercalation voltage is observed from 0.630 to 0.622 V. On the other hand, a more abrupt change in the voltage is accompanied with the concentration increase from 1.0 to 3.0 M, suggesting the efficacy of highly concentrated electrolytes to tune the voltage.
Co-intercalation voltage change with electrolyte concentrations. a dQ/dV curves of graphite anodes cycled in NaPF6 G2 electrolytes with concentrations from 0.05 to 3 M at 35 °C. b Average co-intercalation voltages in Na half-cells derived from (a) plotted as a function of electrolyte concentration. c Deconvoluted Raman spectra of electrolytes for different concentrations. The peak at ~738 cm−1 that corresponds to the P–F bond from PF6− anion increases in the intensity monotonously with the salt concentration, implying that the electrolytes were well prepared for targeted compositions. d Intensity ratio of Raman peak between solvated solvent to free solvent and the molar ratio of G2 solvent to NaPF6 salt. e 23Na NMR spectra of electrolytes as a function of concentration
In order to elucidate the negative shift and the better efficacy in higher concentrations, the structure of electrolytes was first examined by Raman. Figure 2c shows Raman spectra of the electrolytes with concentrations from 0.05 to 3 M (the full spectra are presented in Supplementary Fig. 4). By dissolving NaPF6 salt in G2 solvent, two new peaks at 839 and 867 cm−1 referring to solvation of Na+ by G2 gradually appear, while the intensities of the free G2 solvent peaks at 805, 825, and 850 cm−1 decrease, implying the increased ratio of coordinated solvents28. The intensity ratios of coordinated solvent to free solvent molecules (ISolvated/IFree) are plotted as a function of the concentration in Fig. 2d. It illustrates that the ratio increases from 0.04 (at 0.05 M) to 0.23 (at 1.5 M) and 15.7 (at 3 M), while molar ratios of G2 solvent to NaPF6 salt drastically decrease from 142 (at 0.05 M) to 4.7 (at 1.5 M) and 2.3 (at 3 M). Both results suggest that a significant reduction of free solvent molecules takes place, particularly at a highly concentrated electrolyte above 1.5 M29. Fourier-transform infrared (FTIR) spectra in Supplementary Fig. 4 also support the similar trend of the decrease of the free solvent, consistent with the Raman analyses. In addition, the local environment of Na+ in G2 with different concentrations probed by 23Na nuclear magnetic resonance (NMR) in Fig. 2e indicates the 23Na chemical shift from −8.11 to −6.39 ppm when the concentration increased from 0.05 to 3 M. It is attributable to the increased intensity of contact ion pairs between the negative \({\mathrm{PF}}_6^ -\) anion and the Na+ cation in the concentrated electrolyte30, leading to a lower electron density of the Na+ nucleus. These results consistently suggest the substantial reduction in the amount of free solvent molecules for concentrated NaPF6-G2 electrolytes.
Inspired by this, we estimated the activities (or activity co-efficiencies) of G2 solvent in the concentrated electrolytes. The electromotive force (EMF) was measured by recording the potential difference between two Na metal specimens in the sample electrolytes and the reference electrolyte (1 M NaPF6 G2), which were connected by a vycor glass30. The EMF increased linearly with logarithmic concentration \(({\mathrm{log}}c_{{\mathrm{Na}}^ + })\) below 1 M (Supplementary Fig. 5), as predicted by the Nernst equation. However, in the high-concentration region from 1 to 3 M, we found that the EMF increased more rapidly and was about 150 mV higher in the 3 M electrolyte than that for the reference. To interpret this notably high potential difference, we turned to the electrode potential (ENa) of Na metal with solvation/desolvation reactions (see Eq. (1)):
where \(E_{{\mathrm{Na}}}^0\) is the standard electrode potential, \(a_{[{\mathrm{Na}} - {\mathrm{G}}2]^ + }\) and aG2 refer to the activities of [Na-G2]+ and free G2, respectively. Based on the Raman and FTIR analyses, the amount of free G2 is extremely low in high-concentration electrolytes, yielding the aG2 effectively near to zero. In Eq. (4), the logarithm diverges to an infinite value if aG2 = 0, thus qualitatively explaining the sharp increase of the electrode potential in the concentrated regime30,31,32. By combining these results, we can postulate that the free solvent activity in the electrolyte can be significantly reduced by preparing highly concentrated electrolytes, which in turn would decrease the average voltage for the co-intercalation reactions (see Eq. (3)). In order to support this, we additionally carried out similar sets of experiments using other electrolyte systems, i.e., NaPF6 dissolved in G1 from 0.1 to 2 M, NaClO4 dissolved in G2 from 0.5 to 3 M, and NaCF3SO3 dissolved in G2 from 0.1 to 2 M (Supplementary Fig. 6). All exhibited a consistent trend of the negative shift of the co-intercalation voltage, with the increase of the salt concentration in electrolytes, further verifying the effectiveness of tailoring the co-intercalation voltage by regulating the solvent activity, particularly at high concentrations. Note that the co-intercalation voltage change could be related to the potential changes of both graphite electrode and Na metal electrode (see the detailed discussion in Supplementary Note 1).
Temperature dependency of co-intercalation voltage
We observed an apparent negative shift of the electrode potentials for co-intercalation, when the graphite-based half-cells were cycled at elevated temperatures from 25, 35, and 45 °C to 60 °C (marked with black arrows in Fig. 3a). Figure 3b more clearly displays a temperature dependence of the co-intercalation voltage, which appears to be a linear relationship with negative slopes. The temperature coefficients (ΔE/ΔT) were calculated to be about −2.85 mV K−1 for dilute electrolytes (0.1–1 M) and ` −1.6 mV K−1 for high-concentration electrolytes (2 M and 3 M), respectively. The difference in the temperature coefficient for each electrolyte system is attributed to the low activity of free G2 solvent, according to the following equation derived from Eq. (3):
Temperature dependency of co-intercalation voltage and optimal conditions for low co-intercalation voltage. a Galvanostatic discharge/charge profiles of graphite anodes in 1 M NaPF6 G2 electrolyte at different temperatures. b Na co-intercalation voltage in graphite anodes at different concentrations of G2-based electrolytes plotted as a function of operating temperature. c Summary of Na co-intercalation voltage at different temperatures in different electrolytes. d Discharge/charge voltage profiles. e Cyclic capacities and f rate capabilities of graphite anodes cycled in 1 M G4 and 2 M G1-based electrolytes
In a viewpoint of classical thermodynamics, the temperature coefficient can be also expressed with entropy changes (ΔS) of the co-intercalation reactions as follows:
Compared with the temperature coefficient for lithium ion intercalation reaction in graphite (−0.0512 mV K−1)33,34, the ΔE/ΔT values in this work are orders of magnitudes greater, suggesting the higher-entropy changes of sodium co-intercalation reaction over the conventional ion intercalation reactions. It is attributable to the generally greater difference in the entropy when involving liquid or gas-phase reactant in the overall reaction, such as solvent molecules in this case. Nevertheless, further studies are needed to elucidate the origin of the distinct ΔS behavior, depending on the intercalation mechanisms.
In Fig. 3c, we summarized the variations of the co-intercalation potentials for graphite electrode, considering solvent species, salt concentrations, and temperatures. It indicates that a substantial co-intercalation voltage tuning as much as 380 mV is possible by properly adjusting the components of electrolytes and the operation temperatures. It is worth noting that the shift of co-intercalation potential is present by the plateau voltage change in half-cells. It is also worthwhile to note that the discernible shift of the redox potential is not generally achievable for conventional intercalation reactions. When the similar changes in the conditions are applied for the graphite electrode in the conventional lithium intercalation, no noticeable change in the intercalation potential was observed as demonstrated in Supplementary Fig. 7, suggesting that it is a unique property for the co-intercalation reactions. In Fig. 3d, as one of the examples of the combined effect of solvent species and the concentration, we comparatively display the electrochemical profiles of the graphite electrodes, using 2 M NaPF6 G1- and 1 M NaPF6 G4-based electrolytes at room temperature. It reveals that the average co-intercalation voltage is about 0.56 V in 2 M G1-based electrolyte, which is notably lower than 0.78 V in 1 M G4-based electrolyte in the same operating conditions. Despite the change in the redox potential, there was no noticeable difference either in sodium storage capacity or cycle stability for these two electrolyte systems as shown in Fig. 3e. However, it was found that the cell in 2 M G1-based electrolyte exhibited a better power capability than that in 1 M G4-based electrolyte (Fig. 3f). It is probably due to the lower viscosity (3.1 cp vs. 7.5 cp for G4-based electrolyte) and higher ionic conductivity (16.6 mS vs. 2.3 mS for G4-based electrolyte) of the 2 M G1-based electrolyte. It is worth noting that we also prepared G1-based electrolyte with higher concentrations (i.e., 2.5 and 3 M) to explore the limit of using a highly concentrated electrolyte to further decrease co-intercalation voltage. However, electrodes cycled in 2.5 and 3 M G1-based electrolytes presented inferior rate capabilities (Supplementary Fig. 8), due to the high viscosity of the electrolytes. In total, 2 M G1-based electrolyte was thus identified as close to the sweet spot for further electrochemical evolutions. We additionally conducted analogous experiments at 60 °C as presented in Supplementary Fig. 9, which showed similar results that the combined effects of the solvent species, concentrations, and temperature can cumulatively alter the redox potential, without the significant alternation in other electrochemical properties.
Electrochemical performance of Na-ion full batteries
To estimate the electrochemical performance of graphite in Na-ion full cells, Na1.5VPO4.8F0.7 was prepared and used as a cathode (the details on the sample characterizations can be found in Supplementary Fig. 10)35,36. In a selected 2 M G1-based electrolyte, the Na1.5VPO4.8F0.7 cathode presented a reversible capacity of ~120 mAh g−1, an average Na storage potential of 3.8 V (vs. Na+/Na), and a respectable cyclic reversibility for 150 cycles at 50 mA g−1 (Fig. 4a). The Na1.5VPO4.8F0.7 cathodes were also tested in 1 M G1, G2, and G4-based electrolytes at room temperature (25 °C) and 2 M G1-based electrolyte at 60 °C, respectively (Supplementary Fig. 11). No apparent differences in charge/discharge capacities or average redox potentials were observed, indicating the independence of sodium storage behaviors for Na1.5VPO4.8F0.7 cathodes on the electrolyte systems. In addition, the electrochemical stability of electrolytes used in this work was examined in Supplementary Fig. 12, which indicated that no significant oxidative reaction was observed up to 4.5 V37,38, ensuring their suitable application in Na-ion full batteries.
Electrochemical performance of Na ion full cells. a First ten cycles discharge/charge profiles, and the cyclic capacities, Coulombic efficiencies for Na1.5VPO4.8F0.7 cathodes for 150 cycles in 2 M NaPF6 G1 electrolyte at 100 mA g−1. b and c The 1st, 2nd, 10th, 20th, and 50th charge/discharge profiles of Na ion full cells in 2 M NaPF6 G1 and 1 M NaPF6 G4 electrolytes. d Rate performance of Na ion full cells in 2 M NaPF6 G1 and 1 M NaPF6 G4 electrolytes. e, f Comparison of current Na ion full cells with those recently reported in literatures25,39,40,41,42,43,44,45,46,47. g Long-term cycling performance of Na ion full cells at 1 A g−1 for 1000 cycles. The schematic inset (g) illustrates the kinetics of solvated Na ions between two electrodes during cycling
The Na-ion full cells were assembled by using graphite anodes and Na1.5VPO4.8F0.7 cathodes with optimal mass ratios. Pre-cycling of the electrodes was conducted before testing39. The full cells cycled in 2 M G1-based electrolyte delivered a capacity of ~120 mAg h−1 based on the mass of an anode, with an average voltage of ~3.1 V at 100 mA g−1 (Fig. 4b), leading to a high-energy density of 149 Wh kg−1 based on the total mass of anode and cathode active materials. The well-defined high-voltage plateaus could be stably maintained over cycles with a respectable cyclic retention performance. On the other hand, graphite||Na1.5VPO4.8F0.7 full cells cycled in 1 M G4-based electrolyte presented a much lower average output voltage of 2.78 V (Fig. 4c), due to the relatively higher co-intercalation potential of graphite in the half-cell. The full cells were further cycled in other electrolyte systems or operating conditions such as 1 M G2-based electrolytes at room temperature and 2 M G1-based electrolyte at 60 °C (Supplementary Fig. 13). They presented average output voltages of 2.9 and 3.2 V, respectively, further evidencing the feasibility in engineering the output voltage of Na-ion full cells.
Figure 4d presents rate performance of the Na-ion full cells with 2 M G1- or 1 M G4-based electrolyte at current densities from 0.05, 0.1, 0.2, 0.5, 1, and 2 to 4 A g−1. Approximately 80% of the capacity still could be retained even when the current density increased by 80-folds from 0.05 to 4 A g−1 for the case of the 2 M G1-based electrolyte. The high rate capability renders a remarkably high-power density of 3863 W g−1 with an energy density of 112 Wh kg−1 (based on the total mass of electrode materials). An impressive capacity retention of 93% was also obtained after 1000 cycles, with an unprecedentedly low capacity decay rate of 0.007% per cycle (Fig. 4g), which records one of the lowest among the reported Na full cells to date25,39,40,41,42,43,44,45,46,47. The Coulombic efficiencies after ten cycles are about 99.99% (inset Fig. 4g), thus supporting their suitability to serve as energy storage devices in practical applications. To estimate the standing of our graphite||Na1.5VPO4.8F0.7 (anode||cathode) full cell, we summarized the electrochemical performance of recently reported full cell configurations in terms of sodium storage capacity, output voltage, cycle life, specific energy densities, and power densities in Fig. 4e, f and Supplementary Table 2. It clearly illustrates that the graphite||Na1.5VPO4.8F0.7 full cells in this work outperformed all the peers, with regard to cyclability and high-power densities, which can be attributed to the fast and stable co-intercalation reactions of graphite anodes, as well as the improved voltage by using optimal electrolytes. It is worth noting that the specific energy density of current graphite-based full cell is lower than the widely studied hard carbon-based full cell, for example, 210 Wh kg−1 for hard carbon||Na0.9[Cu0.22Fe0.3Mn0.48]O248, due to the larger Na storage capacity in hard carbon than that in graphite with co-intercalation reaction. However, the power density of 3863 W kg−1 for the graphite||Na1.5VPO4.8F0.7 full cell far excels the ~815 W kg−1 for hard carbon||Na0.9[Cu0.22Fe0.3Mn0.48]O2 full cell. Considering the primary applications of the secondary SIBs for large-scale stationary energy storage, the low cost of raw materials, long cycle life, and high-power capability for fast charge/discharge would be essential parameters40, making the graphite||Na1.5VPO4.8F0.7 chemistry in this work one of the most appealing choices.
The electrochemical performance and safety of secondary batteries have been demonstrated to be greatly affected by the operation temperatures49,50. To this end, we further evaluated the temperature dependency of cyclic capacities and rate capability of optimal graphite||Na1.5VPO4.8F0.7 full cells at various temperatures. The reversible capacities at 0.1 A g−1 were determined to be 109, 120, 121, 123, 122, and 112 mAh g−1 at 0, 10, 25, 35, 45, and 60 °C (Supplementary Fig. 14), respectively, rendering exceptionally low-capacity variations. It is noted that the low-temperature performance of the full cell as low as 0 °C is remarkable, which is hardly achievable with conventional battery chemistry51, possibly due to the fast reaction kinetics of co-intercalation22 and the beneficial properties from the very thin and stable SEI layer on graphite surface (Supplementary Fig. 15)52. In addition, the cyclic capacities measured from 0.05 to 4 A g−1 at different temperatures (Fig. 5a) present a similarly outstanding high rate capability, while some noticeable capacity loss was observed for the case at 0 °C above 1 A g−1. The energy and power densities of the full cells cycled at different temperatures were further evaluated, based on the total mass of the anode and cathode materials in the Ragone plot (Fig. 5b). It shows that, even under the harsh conditions of a low temperature below 10 °C, respectably high-power densities of above 1000 W kg−1 could be successfully maintained. The outstanding temperature-dependent performance of this system would be one of the practical merits for the large-scale applications that may be exposed to the frequent change of the temperature around the year.
We have successfully developed high-energy and high-power SIBs with excellent cyclic and temperature-dependent performance by systematically investigating the systems for co-intercalation reactions. The unique solvent-involved co-intercalation reactions require an extra solvent, potentially increasing the electrolyte/electrode mass ratio in real batteries. The ultimate electrolyte/graphite mass ratio was calculated to be 0.55 for 2 M G1-based electrolyte, with a theoretical energy density of 146 Wh kg−1, based on the total mass of anode, cathode, and the least amount of electrolyte (see detailed calculation in Supplementary Note 2). Indeed, more efforts are needed to optimize the electrolyte/electrode ratio to approach the high theoretical energy density. In addition, the optimization of a highly concentrated electrolyte would be necessary in the future for commercialization of SIBs, considering that the highly concentrated electrolyte may induce high cost. One promising attempt to mitigate this issue is to use cheap sodium salt, such as NaClO4 (Supplementary Fig. 16). Another issue that needs to be taken into account for practical SIBs is the large-volume variation of graphite electrodes during cycling (Supplementary Fig. 17). Potential strategies, such as increasing the anode porosity, rationally limiting the co-intercalation capacity, and designing new cell configurations53, are suggested.
Discussion
We successfully tailored the co-intercalation potential of graphite anodes for Na-ion batteries with high output voltages, high energy, and power densities. By systematically investigating the factors affecting the thermodynamics of co-intercalation reactions, we demonstrated that a large tuning range of 380 mV can be achievable by adjusting the parameters of the solvent species, the concentration of electrolyte, and the temperature. Na-ion full cells with graphite anodes, Na1.5VPO4.8F0.7 cathodes, and an optimal ether-based electrolyte presented an outstanding electrochemical performance, with one of the highest voltages of about 3.1 V and the competitive high-energy density of 149 Wh kg−1both electrodes. Specifically, the power density, low-temperature performance, and cycle life achievable in current Na-ion full cells is among the best thus far reported for SIBs. Moreover, the temperature-dependent charge/discharge tests exhibited excellent energy/power-density retentions at a wide temperature range of 0–60 °C. These findings support that the Na ion full cells with graphite anodes exploiting the co-intercalation are promising for large-scale energy storage system applications.
Methods
Preparation and characterization of electrolytes
Electrolytes were prepared in an Ar-filled glove box at low moisture content (H2O < 20 ppm) and oxygen content (O2 < 0.5 ppm). Sodium salts and molecular sieves were dried in vacuum oven overnight at 180 °C, before dissolving in G1, G2, G3, G4, Gn-250 (Mw ≈ 250 g mol−1), and Gn-500 (Mw ≈ 50 mol−1) solvents at different concentrations in the glove box. Note that more information about Gn-250 and Gn–500 (supplied by Sigma Aldrich) is provided in Supplementary Fig. 18. All the solutions were strongly stirred at 50 °C for 8 h in a glove box, and then molecular sieves were added to remove the residual H2O in electrolytes.
The structure of the electrolytes was studied by Raman (LabRAM HV Evolution, HORIBA, Japan) spectroscopy using a 521-nm laser at a scan range of 200–1000 cm−1. FTIR (FT-IR-4200, JASCO, Japan) equipped with an attenuated total reflectance (ATR) was employed to examine the chemical structure of various electrolytes. The physiochemical properties of electrolytes were evaluated by using a viscosity meter (SV-10 viscometer, A&D Company Ltd., Japan) and a portable ionic conductivity meter (Model CON 610, Oakton, Singapore). A NMR spectrometer (Avance 600, Bruker, Germany) was used to study the 23Na NMR spectra of the electrolyte at room temperature, by using a liquid NMR tube. NMR spectra were recorded at 23Na frequency of 158.7 MHz, with an accumulation of 256 transients and a repetition time of 1.45 s for each sample (acquisition time for 0.45 s and relaxation delay for 1 s) for complete relaxation. All chemical shifts of 23Na NMR spectra were referenced to a standard solution of 1 M NaCl aqueous solution.
Electrode preparation and electrochemical characterizations
The graphite anodes were prepared by mixing natural graphite powders (average size ≈100 µm) and a polyvinylidene fluoride (PVDF) binder with a mass ratio of 9:1, using N-methyl-2-pyrrolidone (NMP) solvent. The uniform slurry was then cast on Cu foil and dried at 70 °C overnight in a vacuum oven. The average electrode thickness and active material loading were ~40 µm and ~3 mg cm−2, respectively. The Na1.5VPO4.8F0.7 cathode materials were synthesized according to our previous work35. Specifically, a stoichiometric amount of V2O5 (Sigma Aldrich, 99%) and NH4H2PO4 (Sigma Aldrich, 99%) were blended by ball milling and annealing at 750 °C for 4 h in Ar atmosphere to obtain VOPO4 powder. To synthesize VPO4 powder, a stoichiometric amount of V2O5 and NH4H2PO4 was mixed together and ball milled with 20 mol% super P, and then heat-treated at 850 °C for 2 h in Ar atmosphere. VOPO4, VPO4, NaF (Sigma Aldrich, 99%), and Na2CO3 (Sigma Aldrich, 99%) precursors were later mixed with a molar ratio of 8:2:7:4. Blending of the precursors was conducted by high-energy ball milling at 300 rpm for 24 h; the resulting mixture was heat-treated at 750 °C for 1.5 h under flowing Ar. The Na1.5VPO4.8F0.7 cathodes were fabricated by mixing 80 wt% Na1.5VPO4.8F0.7 powders, 10 wt% super P, and 10 wt% PVDF binder in NMP solvent. The loadings of the active materials on the electrodes were ~3 mg cm−2 for half-cell tests.
Sodium ion half-cells were assembled in a glove box into a two-electrode configuration, using the working electrodes, sodium metal as the counter electrode, glass fiber (GF/F, Whatman, USA) as a separator, and 100-µl electrolyte. Graphite||Na1.5VPO4.8F0.7 full cells were fabricated by using graphite anodes and Na1.5VPO4.8F0.7 cathodes, with an optimal mass ratio of 1:1.5 of active materials. For full cell measurement, the loadings of the graphite anode were about 6 mg cm−2, on the same scale with the literature48. The cathode pellet is slightly larger than the anode (2/3 inch for cathode and 1/2 inch for anode, respectively). The energy and power densities for full cells were calculated based on the total mass of active materials, excluding masses of other components such as separator, electrolyte, and coin cell components42,43,44,45,46,47,48,49,50. It is noted that pre-sodiation for anodes was performed to activate the material and stabilize the electrode surface. The electrochemical performance of as-prepared coin cells was measured on a multichannel potentio-galvanostat (Won A Tech, Korea) at different current densities. The voltage windows for half-cells with graphite anodes, half-cells with Na1.5VPO4.8F0.7 cathodes, and the full cells were set as 0.1 –2.0 V, 2.0–4.3 V, and 0.7–3.8 V, respectively.
Calculations
To estimate the repulsion energy between negatively charged graphene layers, density functional theory calculations were conducted. It is noted that the amount of charge injected in graphene layers was also properly determined, based on the reversible capacity of different GICs, similar to our previous work27. See Supplementary Information for detailed computational methods.
Data availability
The data that support the findings of this study are in the paper and/or the Supplementary Information. Additional data are available from the authors on reasonable request.
References
Kim, S. W., Seo, D. H., Ma, X., Ceder, G. & Kang, K. Electrode materials for rechargeable sodium-ion batteries: potential alternatives to current lithium-ion batteries. Adv. Energy Mater. 2, 710–721 (2012).
Xu, Z. L., Liu, X., Luo, Y., Zhou, L. & Kim, J. K. Nanosilicon anodes for high performance rechargeable batteries. Prog. Mater. Sci. 90, 1–44 (2017).
Hwang, J. Y., Myung, S. T. & Sun, Y. K. Sodium-ion batteries: present and future. Chem. Soc. Rev. 46, 3529–3614 (2017).
He, X. et al. Durable high-rate capability Na0.44MnO2 cathode material for sodium-ion batteries. Nano Energy 27, 602–610 (2016).
Lu, Y., Li, L., Zhang, Q., Niu, Z. & Chen, J. Electrolyte and interface engineering for solid-state sodium batteries. Joule 2, 1747–1770 (2018).
Sun, Y. et al. Direct atomic-scale confirmation of three-phase storage mechanism in Li4Ti5O12 anodes for room-temperature sodium-ion batteries. Nat. Commun. 4, 1810–1870 (2013).
Xu, Z. L., Park, J., Yoon, G., Kim, H. & Kang, K. Graphitic carbon materials for advanced sodium-ion batteries. Small Methods 8, 1800227 (2018).
Xu, Z. L., Yao, S., Cui, J., Zhou, L. & Kim, J. K. Atomic scale, amorphous FeOx/carbon nanofiber anodes for Li-ion and Na-ion batteries. Energy Storage Mater. 8, 10–19 (2017).
Hu, Z., Liu, Q., Chou, S. L. & Dou, S. X. Advances and challenges in metal sulfides/selenides for next-generation rechargeable sodium-ion batteries. Adv. Mater. 29, 1700606 (2017).
Lao, M. et al. Alloy-based anode materials toward advanced sodium-ion batteries. Adv. Mater. 29, 1700622 (2017).
Lu, Y., Lu, Y., Niu, Z. & Chen, J. Graphene-based nanomaterials for sodium-ion batteries. Adv. Energy Mater. 4, 1702469 (2018).
Stevens, D. A. & Dahn, J. R. The mechanisms of lithium and sodium insertion in carbon materials. J. Electrochem. Soc. 148, A803–A811 (2001).
Yun, Y. S. et al. Sodium-ion storage in pyroprotein-based carbon nanoplates. Adv. Mater. 27, 6914–6921 (2015).
Moriwake, H., Kuwabara, A., Fisher, C. A. J. & Ikuhara, Y. Why is sodium-intercalated graphite unstable? RSC Adv. 7, 36550–36554 (2017).
Liu, Y., Merinov, B. V. & Goddard, W. A. Origin of low sodium capacity in graphite and generally weak substrate binding of Na and Mg among alkali and alkaline earth metals. Proc. Natl Acad. Sci. USA 113, 3735–3739 (2016).
Jache, B. & Adelhelm, P. Use of graphite as a highly reversible electrode with superior cycle life for sodium-ion batteries by making use of co-intercalation phenomena. Angew. Chem. Int. Ed. 53, 10169–10173 (2014).
Kim, H. et al. Sodium storage behavior in natural graphite using ether-based electrolyte systems. Adv. Funct. Mater. 25, 534–541 (2015).
Yoon, G., Kim, H., Park, I. & Kang, K. Conditions for reversible Na intercalation in graphite: theoretical studies on the interplay among guest ions, solvent, and graphite host. Adv. Energy Mater. 7, 1601519 (2017).
Jung, S. C., Kang, Y. J. & Han, Y. K. Origin of excellent rate and cycle performance of Na+-solvent cointercalated graphite vs. poor performance of Li+-solvent case. Nano Energy 34, 456–462 (2017).
Goktas, M., Akduman, B., Huang, P., Balducci, A. & Adelhelm, P. Temperature-induced activation of graphite co-intercalation reactions for glymes and crown ethers in sodium-ion batteries. J. Phys. Chem. C. 122, 26816–26824 (2018).
Kim, H. et al. Sodium intercalation chemistry in graphite. Energy Environ. Sci. 8, 2963–2969 (2015).
Seidl, L. et al. Intercalation of solvated Na-ions into graphite. Energy Environ. Sci. 10, 1631–1642 (2017).
Zhu, Z., Cheng, F., Hu, Z., Niu, Z. & Chen, J. Highly stable and ultrafast electrode reaction of graphite for sodium ion batteries. J. Power Sources 293, 626–634 (2015).
Cohn, A. P., Share, K., Carter, R., Oakes, L. & Pint, C. L. Ultrafast solvent-assisted sodium ion intercalation into highly crystalline few-layered graphene. Nano. Lett. 16, 543–548 (2016).
Hasa, I. et al. A sodium-ion battery exploiting layered oxide cathode, graphite anode and glyme-based electrolyte. J. Power Sources 310, 26–31 (2016).
Kim, H. et al. Exploiting lithium-ether co-intercalation in graphite for high-power lithium-ion batteries. Adv. Energy Mater. 7, 1700418 (2017).
Kim, H., Yoon, G., Lim, K. & Kang, K. A comparative study of graphite electrodes using the co-intercalation phenomenon for rechargeable Li, Na and K batteries. Chem. Commun. 52, 12618–12621 (2016).
Yamada, Y., Yaegashi, M., Abe, T. & Yamada, A. A superconcentrated ether electrolyte for fast-charging Li-ion batteries. Chem. Commun. 49, 11194 (2013).
Yamada, Y. & Yamada, A. Review—superconcentrated electrolytes for lithium batteries. J. Electrochem. Soc. 162, A2406–A2423 (2015).
Moon, H. et al. Solvent activity in electrolyte solutions controls electrochemical reactions in Li-ion and Li-sulfur batteries. J. Phys. Chem. C. 119, 3957–3970 (2015).
Moon, H. et al. Mechanism of Li ion desolvation at the interface of graphite electrode and glyme-Li salt solvate ionic liquids. J. Phys. Chem. C. 118, 20246–20256 (2014).
Ueno, K. et al. Li+ solvation in glyme–Li salt solvate ionic liquids. Phys. Chem. Chem. Phys. 17, 8248–8257 (2015).
Egorkina, O. Y. & Skundin, A. M. The effect of temperature on lithium intercalation into carbon materials. J. Solid State Electrochem. 2, 216–220 (1998).
Yazami, R., Zaghib, K. & Deschamps, M. Carbon fibers and natural graphite as negative electrodes for lithium ion type batteries. J. Power Sources 52, 55–59 (1994).
Park, Y. U. et al. A family of high-performance cathode materials for Na-ion batteries, Na3(VO1-xPO4)2F1+2x (0 ≤ x ≤ 1): Combined first-principles and experimental study. Adv. Funct. Mater. 24, 4603–4614 (2014).
Qi, Y. et al. Scalable room-temperature synthesis of multi-shelled Na3(VOPO4)2F microsphere cathodes. Joule 3, 1–16 (2018).
Xu, Z. L. et al. Engineering solid electrolyte interphase for pseudocapacitive anatase TiO2 anodes in sodium ion batteries. Adv. Funct. Mater. 8, 1802099 (2018).
Wang, C., Wang, L., Li, F., Cheng, F. & Chen, J. Bulk bismuth as a high-capacity and ultralong cycle-life anode for sodium-ion batteries by coupling with glyme-based electrolytes. Adv. Mater. 29, 1702212 (2017).
Li, H. et al. An advanced high-energy sodium ion full battery based on nanostructured Na2 Ti3O7/VOPO4 layered materials. Energy Environ. Sci. 9, 3399–3405 (2016).
Guo, S. et al. A high-voltage and ultralong-life sodium full cell for stationary energy storage. Angew. Chem. - Int. Ed. 54, 11701–11705 (2015).
Liang, L. et al. Large-scale highly ordered Sb nanorod array anodes with high capacity and rate capability for sodium-ion batteries. Energy Environ. Sci. 8, 2954–2962 (2015).
Xiong, H., Slater, M. D., Balasubramanian, M., Johnson, C. S. & Rajh, T. Amorphous TiO2 nanotube anode for rechargeable sodium ion batteries. J. Phys. Chem. Lett. 2, 2560–2565 (2011).
Wang, Y., Xiao, R., Hu, Y.-S., Avdeev, M. & Chen, L. P2-Na0.6[Cr0.6Ti0.4]O2 cation-disordered electrode for high-rate symmetric rechargeable sodium-ion batteries. Nat. Commun. 6, 6954 (2015).
Sheng, M., Zhang, F., Ji, B., Tong, X. & Tang, Y. A novel Tin-graphite dual-ion battery based on sodium-ion electrolyte with high energy density. Adv. Energy Mater. 7, 1601963 (2017).
Li, Z., Young, D., Xiang, K., Carter, W. C. & Chiang, Y. M. Towards high power high energy aqueous sodium-ion batteries: the NaTi2(PO4)3/Na0.44MnO2 system. Adv. Energy Mater. 3, 290–294 (2013).
Wang, L. et al. Rhombohedral Prussian white as cathode for rechargeable sodium-ion batteries. J. Am. Chem. Soc. 137, 2548–2554 (2015).
Wang, N., Bai, Z., Qian, Y. & Yang, J. Double-walled Sb@TiO2-x nanotubes as a superior high-rate and ultralong-lifespan anode material for Na-ion and Li-ion batteries. Adv. Mater. 28, 4126–4133 (2016).
Mu, L. et al. Prototype sodium-ion batteries using an air-stable and Co/Ni-free O3-layered metal oxide cathode. Adv. Mater. 27, 6928–6933 (2015).
Liao, L. et al. Effects of temperature on charge/discharge behaviors of LiFePO4 cathode for Li-ion batteries. Electrochim. Acta 60, 269–273 (2012).
Ji, Y., Zhang, Y. & Wang, C. Y. Li-ion cell operation at low temperatures. J. Electrochem. Soc. 160, A636–A649 (2013).
Rustomji, C. S. et al. Liquefied gas electrolytes for electrochemical energy storage devices. Science 356, eaal4263 (2017).
Goktas, M. et al. Graphite as cointercalation electrode for sodium-ion batteries: electrode dynamics and the missing solid electrolyte interphase (SEI). Adv. Energy Mater. 17, 1702724 (2018).
Luo, F. et al. Nano-silicon/carbon composite anode materials towards practical application for next generation Li-ion batteries. J. Electrochem. Soc. 162, A2509–A2528 (2015).
Acknowledgements
This work was financially supported by Samsung Research Funding Center of Samsung Electronics under project No. SRFC-TA1603-03 and the Creative Materials Discovery Program through the National Research Foundation of Korea (NRF) under project No. NRF-2017M3D1A1039553. Z.L.X. acknowledges the Korea Research Fellowship (KRF) Program through the National Research Foundation of Korea funded by the Ministry of Science and ICT (Project No. 2017H1D3A1A01013931).
Author information
Authors and Affiliations
Contributions
K.K. and Z.L.X. conceived the original idea. Z.L.X. designed the experiments with help from K.Y.P., H.P., O.T., S.J.K. and W.M.S. The computations were performed by G.Y. K.K. revised the paper prepared by Z.L.X. All authors discussed the results and contributed to the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks Lukas Seidl and other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, ZL., Yoon, G., Park, KY. et al. Tailoring sodium intercalation in graphite for high energy and power sodium ion batteries. Nat Commun 10, 2598 (2019). https://doi.org/10.1038/s41467-019-10551-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10551-z
This article is cited by
-
Molybdenum Oxynitride Atomic Nanoclusters Bonded in Nanosheets of N-Doped Carbon Hierarchical Microspheres for Efficient Sodium Storage
Nano-Micro Letters (2022)
-
Nitrogen-doped porous carbon nanofoams with enhanced electrochemical kinetics for superior sodium-ion capacitor
Rare Metals (2022)
-
Effect of ionotropic gelation of COOH-functionalized polymeric binders in multivalent ion batteries
Journal of Solid State Electrochemistry (2022)
-
Recent Advances on Electrospun Nanofiber Materials for Post-lithium Ion Batteries
Advanced Fiber Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.