Abstract
The oil and gas (O&G) sector represents a large source of greenhouse gas (GHG) emissions globally. However, estimates of O&G emissions rely upon bottom-up approaches, and are rarely evaluated through atmospheric measurements. Here, we use aircraft measurements over the Canadian oil sands (OS) to derive the first top-down, measurement-based determination of the their annual CO2 emissions and intensities. The results indicate that CO2 emission intensities for OS facilities are 13–123% larger than those estimated using publically available data. This leads to 64% higher annual GHG emissions from surface mining operations, and 30% higher overall OS GHG emissions (17 Mt) compared to that reported by industry, despite emissions reporting which uses the most up to date and recommended bottom-up approaches. Given the similarity in bottom-up reporting methods across the entire O&G sector, these results suggest that O&G CO2 emissions inventory data may be more uncertain than previously considered.
Similar content being viewed by others
Introduction
The objective of limiting the increase in global temperature to <1.5 °C this century is dependent upon reducing anthropogenic greenhouse gas (GHG) emissions to net zero1. Identifying mitigation potentials to achieve this goal and assessing GHG reductions relies upon accurate emission estimates of anthropogenic sources, which inform national and international climate policies. Consequently, participating countries in the United Nations Framework Convention on Climate Change (UNFCCC) are required to submit sector-based emissions data in an annual national GHG inventory report (NIR)2,3. Such anthropogenic GHG emission data ultimately underpin carbon pricing and trading policies.
The global energy industry alone accounts for ≈35% of anthropogenic GHG emissions (using a 100-year global warming potential (GWP))4, a significant portion of which are attributed to the global upstream oil and gas (O&G) sector. It is estimated that the global O&G sector (which is included in NIRs) contributes ~10% of anthropogenic GHG emissions4, using GHG emission estimates that are derived primarily through complex calculations based upon UNFCCC inventory guidelines5. The estimation of anthropogenic GHG emissions in NIRs from stationary sources in the energy sector (including the O&G sector) is primarily a bottom–up exercise, where GHG emissions from individual sources within a given facility are added together, as outlined in UNFCCC protocols5. These estimates have varying degrees of accuracy (i.e., Tier 1–3)5 but fundamentally rely on emission factors and associated activity data (e.g., production and consumption intensity), which in some cases may be outdated or assumed to be homogeneous across the world. In general, Tier 3 approaches are considered to use the best available data specific to the industry and should provide improved emissions estimates relative to Tier 1 and Tier 2 methods.
The large contribution of the O&G sector to global GHG emissions underscores the need for accurate sectoral GHG emissions in national inventories. This is particularly relevant since studies have indicated discrepancies between top–down and bottom–up estimates of O&G methane (CH4)6,7,8,9,10,11,12, many of which having shown that official inventories or industrial reports underestimate emissions. However, few atmospheric measurement-based evaluations have been performed for O&G carbon dioxide (CO2) emission inventories, despite CO2 emissions being significantly larger than CH4. This may be in part because uncertainties in emission factors and activity data used in bottom–up CO2 estimates for this sector are considered small (<10%)5 compared to CH4 (50–150%)5. Nonetheless, small uncertainties in CO2 emission estimates have the potential to result in large unaccounted for CO2 based upon the magnitude of the CO2 emitted compared to CH4.
Evaluating GHG emissions reported to inventories for the O&G sector is especially important now, with global fossil fuel production and demand at an all-time high13. Such evaluations are highly important for countries with resource-based economies such as Canada, where O&G activities account for ≈26% of national GHG emissions and oil sands (OS) production in particular ≈10%14. In general, CO2 emissions from the O&G sector (including the Canadian OS sector) are derived for inventories using an Intergovernmental Panel on Climate Change (IPCC) Tier 3 approach15 and following the UNFCCC protocols16. However, estimates of the emission intensity (kg CO2e per barrel of oil) of OS operations and of their absolute GHG emissions are not derived from direct measurements of CO2. Aircraft measurements over large-scale O&G emission sources can provide a top–down assessment of these bottom–up reported GHG estimates.
Here the utility of a top–down measurement approach is demonstrated below for the Canadian OS surface mining operations (one of the largest single O&G sources of GHGs in Canada). The results indicate that overall, OS GHG emissions may be underestimated and suggests that reporting that follows this Tier 3 approach (or less accurate Tier 1 and Tier 2 approaches) may universally underestimate CO2 emissions. This highlights the potential need for updated IPCC inventory guidelines that include atmospheric measurement-based evaluations of CO2 emissions, for an improved assessment of the O&G contribution to the global anthropogenic GHG burden.
Results
Hourly emission rates
Thirteen aircraft flights around the OS surface mining facilities in Alberta (Supplementary Table 1) were conducted in the summer of 2013, with virtual polygon flight boxes surrounding a given facility that encompassed all CO2 emission sources, including mining, processing, upgrading, and tailings release17 (Supplementary Fig. 1a–c). Approximately 5–12 different altitudes were flown for each box, depending upon the facility. Background subtracted CO2 data from these flights were used as inputs into a Top–down Emissions Rate Retrieval Algorithm (TERRA)18 (see Methods), from which hourly CO2 emission rates were derived. For the OS surface mining facilities, an example virtual box is shown in Fig. 1 for the Suncor (SUN) facility and the resultant hourly CO2 emissions for all facilities in the inset table. The downwind side of the virtual box of Fig. 1 demonstrates the complexity of CO2 plumes from this facility including emissions from both ground sources and elevated stacks, which can be quantified separately. Based on these flights, the largest hourly CO2 emissions are associated with Syncrude Mildred Lake (SML; 1650 ± 134 t h−1) and SUN (1220 ± 138 t h−1) facilities, followed by Canadian National Resources Ltd Horizon (CNRL; 538 ± 68 t h−1) and Shell Albian and Jackpine (SAJ, now part of CNRL, 423 ± 55 t h−1), all of which are dominant compared to CO2 from local transportation within the virtual box (see Supplementary Note 1). Propagated uncertainties (see Methods) associated with hourly emission rates for single flights were small (≈8–26%; Supplementary Table 1), with emission rates consistent between flights (relative standard error (RSE) ≈ 8–13%; Fig. 1) despite being conducted on various days spanning approximately 1 month.
Measured CO2 from flight 15 around the SUN facility. Mass emission rates have been determined for this facility using the TERRA algorithm, where elevated and surface emissions can be quantified separately. The mean hourly CO2 emission rates (t h−1) during all flights covering the four major surface mining operations in the oil sands are shown in the inset table. Uncertainties represent the standard error \(\left( {\frac{\sigma }{{\sqrt N }}} \right)\) for the multiple flights over a facility. Map data: Google, Image Landsat, CNES/Airbus, Digital Globe 2017. Source data for the inset table are provided in Supplementary Data 1
Emission intensities
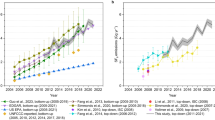
For each surface mining facility, the CO2 emission intensity \(( {I_{{\mathrm{CO}}_2}} )\), in units of \({\mathrm{kg}}_{{\mathrm{CO}}_2}{\mathrm{barrel}}^{ - 1}\) of synthetic crude oil (SCO), is shown in Fig. 2a. The \(I_{{\mathrm{CO}}_2}\) is derived by upscaling the hourly CO2 emissions (Fig. 1, Supplementary Table 1) to monthly values (see Methods) and dividing by known monthly facility production volumes of SCO19. The overall lifecycle GHG emission intensity for any petroleum source is dominated by the combustion of its end product (e.g., gasoline), which is relatively constant and accounts for 70–80% of the total GHG emission20. Hence, to compare the GHG emission across various petroleum sources, estimates typically only include processes occurring from the well to the refinery gate (WTRG) and are based on quantities derived from various emission models21,22,23. The current results are the first top–down WTRG estimates of \(I_{{\mathrm{CO}}_{2}}\) for the OS using direct CO2 measurements, thus providing a benchmark for the assessment of previous model estimates of \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) (which include CH4). Such model estimates are known to be highly variable, due mainly to the types of sources included in the model, uncertainties in fuel-related assumptions, and other methodological challenges20,24,25,26. The derived \(I_{{\mathrm{CO}}_2}\) here ranged from 44.3 ± 6.8 to 245 ± 25.4 \({\mathrm{kg}}_{{\mathrm{CO}}_2}{\mathrm{barrel}}^{ - 1}\) (Fig. 2a and Supplementary Table 2) for the 4 major surface mining facilities in operation in 2013. Including measurement-based CH4 emissions reported previously12 in the present CO2 emissions results in \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) ranging from 47.6 ± 7.6 to 267 ± 31 \({\mathrm{kg}}_{{\mathrm{CO}}_{2{\mathrm{eq}}}}{\mathrm{barrel}}^{ - 1}\), which is dominated by the contribution from CO2 (see Methods). With the exception of SML (which includes emissions of SAU), the measured \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) are somewhat larger than the \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) calculated using overall industry average inputs from up to 6 years earlier (77–122 \({\mathrm{kg}}_{{\mathrm{CO}}_2}{\mathrm{barrel}}^{ - 1}\) SCO)25. However, the measured \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\)here does not include the emissions associated with transport of SCO to the refinery gate. Including such emissions would make the actual \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) even larger than industry average model values20,25,26. The difference between estimated and reported intensities is even larger when comparing the currently estimated \(I_{{\mathrm{CO}}_2}\) (or \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\)) with those reported for specific facilities in the same year (2013). In this case, the estimated \(I_{{\mathrm{CO}}_2}\) are 13–123% larger than those calculated using CO2 emissions reported to Environment and Climate Change Canada’s GHG reporting program (GHGRP)15 and reported production volumes19 (see Methods). The measurement-based \(I_{{\mathrm{CO}}_2}\) values are similarly larger than the \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) provided directly by industry27,28 for 2013 (Fig. 2a). The estimated \(I_{{\mathrm{CO}}_2}\) for SUN is in reasonable agreement with the calculated estimates shown in Fig. 2a, being only 13% higher and within the measurement uncertainty. In contrast, estimates of the mean \(I_{{\mathrm{CO}}_2}\) for CNRL, SAJ, and SML/SAU are 36%, 38%, and 123% greater than those calculated using publicly available data15,19 and larger than the facility-specific \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) modeled in recent studies24,25,26.
CO2 emission intensities and total emissions. a Aircraft measurement derived (mean) and calculated well to the refinery gate CO2 emission intensities \((I_{{\mathrm{CO}}_2})\) for the 4 major surface mining operations in the oil sands in 2013 (n = 3–6). Calculated emission intensities use publically available data from the GHG reporting program (GHGRP) for the same facilities (2013). Opaque data points represent facility-specific model calculation of \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) in the literature and open symbols represent \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) reported directly by the industry for 2013. SAJ (now part of CNRL) does not upgrade to synthetic crude oil on site, hence its intensity is per barrel of bitumen. The \(I_{{\mathrm{CO}}_2}\) for SML includes emissions from SAU. b Annual emissions of CO2 measured for the four major surface mining facilities in 2013 compared to those reported by industry to the GHGRP. Error bars in a, b represent the propagated uncertainty of the mean value. Source data are provided in Supplementary Data 1
Annual emission estimates
Based upon the aircraft-estimated \(I_{{\mathrm{CO}}_2}\), the annual CO2 emissions for each facility are estimated (see Methods) and shown in Fig. 2b, together with the CO2 emissions reported by industry to the GHGRP for 2013. The aircraft measurement-based annual CO2 emissions from the 4 major OS facilities ranged from 3.9 ± 0.6 to 25 ± 3 Mt. These emissions are higher than the reported CO2 emissions, reflecting the differences in the aircraft measurement-estimated vs facility-estimated \(I_{{\mathrm{CO}}_2}\), with the largest statistically significant difference (see Methods) of 13 Mt year−1 for SML/SAU (123%) and the smallest for SUN (13%).
The differences between aircraft-estimated and facility-reported CO2 emissions for SML and SUN are further validated through a separate approach using measurements of sulfur dioxide (SO2) and reported mined OS ore volumes19 as tracers for stack and ground-based CO2 emissions, respectively (see Methods). For these two facilities, the emissions of SO2 are associated with bitumen upgrading and are generally confined to elevated stack outflows only, leading to elevated SO2 plumes downwind (Fig. 3a, Supplementary Fig. 2). Hence, CO2 plumes from both these facilities are clearly split into an elevated stack plume that is closely associated with the SO2 plume and a ground-based plume (Fig. 3b). Multiplying the CO2 to SO2 emission ratios in the elevated plumes (Fig. 3a, c) with measured annual SO2 emissions29 provides an alternative means to determine annual stack CO2 emissions specifically (Fig. 3d) (See Methods and Supplementary Note 2). Similarly, a ground-based emission ratio was estimated by normalizing the TERRA-derived ground-based emissions by the monthly volume of mined OS ore (see Methods). Using these approaches, the separated annual CO2 emissions from stacks and ground emissions at SML are estimated at 14.2 ± 1.3 and 8.1 ± 1.0 Mt, respectively (Fig. 3d). This result is consistent with that derived using TERRA specifically for elevated plumes (Fig. 3d) and indicates that stack CO2 emissions alone are ~29% greater than the reported facility total CO2 emissions for SML/SAU (all sources; Fig. 3d). Furthermore, the combined emissions (stacks + ground based; 22.3 ± 3.5 Mt) for SML are in agreement with the facility total derived above through the use of \(I_{{\mathrm{CO}}_2}\) (24.5 ± 3.0 Mt, which includes SAU; Fig. 2b), supporting the discrepancy between total aircraft measurement-based estimated and total reported CO2 emissions for this facility (Fig. 2b). In contrast, stack CO2 emissions estimated for SUN are ~20% lower than the reported facility total CO2 emissions (all sources; Fig. 3d), while the total measured stack (6.4 ± 0.4 Mt)+ground CO2 emissions (4.8 ± 0.7 Mt) are only slightly higher than the reported CO2 emissions of Fig. 2b. Based on Fig. 3d, it is estimated that stack CO2 emissions for SML and SUN account for 61 ± 12% and 67 ± 13% of their respective total emissions, in relative agreement with available model estimates20,24.
Emissions of CO2 for upgrading operations and ground-based sources in the oil sands. a Background subtracted SO2 in elevated plumes from OS upgrading emissions during flight 18 derived with TERRA. b Background subtracted CO2 in the same elevated plumes of flight 18. c Direct correlation between background subtracted CO2 and SO2 within plumes. d Annual emissions of CO2 from upgrading stacks for SML and SUN derived using the CO2:SO2 emission ratios measured in plume (green bars; see Methods). Orange and gray bars represent upgrading and ground-based emissions, respectively, derived using TERRA directly and up-scaled as described in Methods. Dashed lines represent total facility-reported CO2 emissions to the GHG reporting program. Error bars in Fig. 2a, b represent the propagated uncertainty of the mean value. Source data are provided in Supplementary Data 1
The overall impact of the differences between measured and reported GHG emissions found here is large. Put into context, the unaccounted emissions represent a total CO2e (100-year GWP timescale) emission increase of ~64% (or 17 Mt year−1) over that reported for OS surface mining operations (Fig. 4) and a ~30% increase for the entire OS (including reported in situ emissions) (Fig. 4). Such an absolute emission quantity (17 Mt year−1 CO2e) is similar to the GHG emissions from a metropolitan area the size of Seattle30 or Toronto31. Additionally, GHG emission reports from OS in situ extraction facilities have yet to be evaluated using atmospheric measurements. This suggests that the potential exists for further unaccounted GHG emissions, as partially demonstrated by Lagrangian flights that show hourly CO2 emissions downwind that are larger than the sum of individual facility emission rates (see Supplementary Note 3).
Total oil sands (OS) annual greenhouse gas (GHG) emissions compared to those reported to the GHG reporting program. Methane emissions from Baray et al.12 are added to the surface mining CO2 measured here, to be comparable to reported \({\mathrm{CO}}_2{\mathrm{e}}\). A global warming potential (GWP) of 25 is used for methane. Blue bars include in-surface and in situ OS extraction. Revised estimate for total OS emissions includes the measured surface mining emissions determined in this study and the reported emissions from in situ operations. Errors associated with annual CO2 (Fig. 2b) and CH4 estimates have been added in quadrature: \(\delta = \sqrt {\delta _{{\mathrm{CO}}_2}^2 + \delta _{{\mathrm{CH}}_4}^2}.\) Source data are provided in Supplementary Data 1
Discussion
There are important implications associated with the current findings. Since many stationary combustion sources in the O&G sector derive their emissions using similar Tier 1–3 protocols5, this issue may not be unique to the OS or to CO2. Indeed, the Tier 3 approach (and other provincial reporting regulations) used for the OS is considered to utilize the best possible data, and yet top–down and bottom–up results here remain significantly different. This may suggest that other GHG sources or industries in other regions, which use less accurate bottom–up methods (i.e., Tier 1) could exhibit similar discrepancies between top–down and bottom–up estimates. The results here further suggest that top–down emission estimates can be used to inform the development of federal and provincial emission regulations and highlights the value of atmospheric measurements in tracking and/or monitoring progress in terms of emission reduction targets. Equally important is that the underlying data used in reporting to the GHGRP are also used in formulating OS GHG emission estimates in Canada’s NIR to the UNFCCC16. Both the GHG emission estimates in the GHGRP and NIR are considered Tier 3 according to the IPCC as they use the best available information specific to the industry and provide the highest possible accuracy5,16. As a result, the GHGRP and NIR emission data vary little from each other for specific facilities, with uncertainties associated with OS fugitive CO2 emissions16, overall emissions for the Canadian energy sector16, and stationary combustion emission factors5 reported as approximately ±6%, ±3%, and ±< 10%, respectively. However, the top–down measurement results here indicate that the total inventory GHG estimates for the OS sector may need to be revised upward by at least 30%. Most importantly, the results imply that complex emission factors and activity data used in NIRs should be periodically re-assessed and highlights the potential need for new IPCC guidelines for atmospheric measurement-based validation of emissions. Such guidelines are particularly important since atmospheric measurements are now recognized for their ability to systematically monitor GHG emissions in support of the Paris Agreement32. Finally, this type of atmospheric observation can directly inform stakeholders at the subnational scale about unknown or poorly quantified GHG sources at the facility level, as a contribution to the recently adopted integrated global GHG Information System33 of the World Meteorological Organization and United Nations Environment Program.
Methods
Aircraft measurements
Aircraft measurements of CO2 and CH4 over the Athabasca OS region of northern Alberta were performed from August 13 to September 7, 2013 as part of an intensive field campaign. Details of the study objectives, aircraft implementation, and other technical aspects have been described previously17,34. During the study, 22 flights totaling 84 h were conducted over individual facilities of the OS and downwind of the facilities at distances up to 120 km. The flight patterns have been shown previously17, 13 of which were used to quantify primary emissions from individual OS facilities, and 4 conducted to quantify their transformation downwind. Emission quantification flights were conducted by flying a 4- or 5-sided polygon, at multiple altitudes, resulting in 21 separate virtual boxes encompassing 7 OS facilities. Results from 17 flights were used in the current analysis, while the others were excluded because of highly variable wind speeds and direction and/or the presence of confounding pollutant interferences from adjacent OS facilities. The specific facilities studied and their corresponding flight numbers are given in Supplementary Table 1. Three of the flights (F7, F19, and F20) examined the photo-chemical transformation of pollutants downwind of the OS facilities34 and are used here to quantify total emissions from all OS surface mining facilities (for comparison to the sum of individual emission flights), as they encompass the majority of emissions from the region. These transformation flights were designed as Lagrangian, such that the same air parcel in the OS plumes was sampled successively, 1 h apart, in virtual screens constructed from level flight tracks at multiple altitudes (Supplementary Fig. 3, Supplementary Table 1). There were no industrial emissions between the screens of each flight.
Gas, particle, meteorological, and aircraft state measurements were made during flights, with a detailed description provided elsewhere17,34,35. The current work makes use of a subset of these measurements specifically for the quantitation of CO2 and SO2 gases. CO2 was measured using a Picarro model G2401-m instrument (http://www.picarro.com/products_solutions/gas_analyzers/flight_co_co2_ch4_h2o) with a time resolution of 2 s12. The instrument sampled ambient air through a 6.35-mm (1/4 inch) diameter perfluoroalkoxy, backwards facing sampling line with a residence time of ~2 s. Calibrations were performed before, during, and after the field campaign using a range of mixing ratios from NIST certified standard cylinders (350–450 ppm). The precision of the CO2 measurements in flight were estimated to be <100 ppb. SO2 was measured using a Thermo Scientific 43iTLE analyzer with a time resolution of 1 s. The SO2 instrument was calibrated with NIST certified standard cylinders over a range of 0–400 ppb. The standard deviation of the calibration slopes was 0.9% and the average standard deviation of the 1-s data during calibrations was 1.99 ppb18. The time delay for the SO2 measurement, due to the gas traversing the length of the inlet, was ≈6 s and was corrected for in the data. NO and NO2 measurements were made using two Thermo Scientific 42iTLE analyzers at 1 Hz (NOX averaged to 2 s) with a sample residence time of ≈3–4 s. Each instrument was calibrated with NIST standard cylinders of NO. High frequency wind data were averaged to 1 or 2 s for subsequent analysis in the emission rate algorithm.
Top–down emission rate retrieval algorithm analysis
CO2 emission rates for each OS surface mining facility and for the entire OS region were derived using an algorithm designed to estimate pollutant transfer rates through the virtual boxes/screens of aircraft measurements. The algorithm is based on the Divergence Theorem to resolve mass balance (TERRA)18 and has been used extensively for determining emission rates of volatile organic compounds (VOCs), black carbon, CH4, secondary organic aerosol (SOA), organic/inorganic acids, and SO217,18,34,36 Emissions are derived with the TERRA algorithm by combining box-like aircraft flight patterns with pollutant concentration measurements at high time resolution and wind speed and direction data. The algorithm applies simple kriging18 to the data to produce virtual walls of gridded 20 × 40 m2 mesh on the virtual box, resolves the air mass balance within the virtual box, and determines the mass transfer rates across the walls (including the top of the box) to derive a net emission rate for a pollutant. In the case of virtual screens (rather than boxes), TERRA quantifies the mass transfer rate of a pollutant (kg h−1) through the virtual screens, in the same manner as it does for a single wall of a virtual box flight34,36.
The use of the standard TERRA to estimate emissions accounts for incoming and outgoing air mass advective and turbulent fluxes within a volume, including the top of the virtual box, and is ideal for species that have little background contribution to the measured concentration. However, in the case of CO2 that has a large background concentration, this approach can introduce large uncertainties if even a small portion of the measured CO2 is calculated to leave through the top of the box. To address this uncertainty, a background CO2 is subtracted prior to the use of TERRA, such that the transfer rate through any one outgoing side of a box (or single screen) represents the facility emission rate. This approach has been used successfully for CH412, VOCs35,36, and SOAs34 and is similar to other single screen approaches37,38. Background CO2 was determined using upwind measurements for box flights and screen flights (where available). For screen flights where upwind measurements were not conducted, the levels at the edges of the screen were used as background. The background between upwind data was linearly interpolated and box-car smoothed within a 20–40-min moving window to derive a variable baseline CO2 for the entire 2–3 h flight. Examples of the derived CO2 baseline are shown in Supplementary Fig. 3. The uncertainty added to the final emission rate for each flight contributed by the baseline estimation method was examined by varying the derived CO2 baseline by the standard deviation of the upwind data (±0.5–3 ppm CO2), followed by input into TERRA. This baseline CO2 sensitivity analysis resulted in CO2 emission rates that varied by 1–33% (δB; Supplementary Table 1). This relatively small variation in emission rates caused by the background CO2 is due to the short duration of the flights, which were flown during an established planetary boundary layer and because there was significant enhancement of plume CO2 of up to >80 ppm above background. In general, a changing boundary layer depth could in principle introduce additional uncertainty in the emission results from TERRA. However, the flights were intentionally conducted during mid-afternoon hours, when the boundary layer was constant. This was assessed through vertical profiles performed before and after the emission estimation portions of the flights. Under conditions where boundary layer depth was stable, real-time vertical profile data (pollutants, water vapor, temperature) from the flights were used to ensure that the highest flight track was always above the top of the boundary layer, hence ensuring that the entire plume from the various facilities was contained within the specific flight box or within the flight screen.
It has been demonstrated previously that extrapolation of pollutant concentrations from the lowest flight level to the ground is the main source of uncertainty in TERRA, with an overall uncertainty in the derived emission rates of approximately 20%18. This was determined previously18 through a sensitivity analysis in a series of closed-loop numerical experiments. In such experiments, a simulated Gaussian plume driven by a known emission flux was created and sampled with the TERRA algorithm, while also using various forms of extrapolation to the ground (i.e., linear to the ground, exponential, constant, linear to zero). A similar analysis was performed in the current study, with the differences in extrapolations also resulting in a <20% difference in final estimated emissions. For pollutant sources that are entirely above the lowest flight level, extrapolation to the ground is not relevant and the associated uncertainty in the TERRA-derived emissions has been demonstrated to be ≈ 4%18. This was determined by comparing the TERRA-derived emissions of SO2 with continuous emissions monitoring system (CEMS) data for the same facility stack (CNRL) and for the exact hour of the flight. We note that CEMS data are regularly audited and mandated to be accurate to within 10%. Further comparisons of TERRA-derived SO2 stack emission rates with those concurrently measured with CEMS indicate that this uncertainty may be even smaller (<1%) as shown in Supplementary Fig. 4a. However, the larger 4% uncertainty for elevated stack emissions is used in this analysis. The excellent agreement between TERRA emissions and the audited CEMS data provide confidence that uncertainties associated with possible under sampling are negligible. The uncertainties for stack and ground-based emissions (i.e., 4% and 20%) are applied separately in cases where low level and elevated stack sources are clearly spatially differentiated, which are further propagated with the uncertainties associated with the background CO2 determination described above. The overall propagated uncertainty associated with the hourly emission rates derived for individual facilities ranged from 8% to 28% \((\Delta E_{{\mathrm{CO}}_2})\) for facility flights and from 24% to 38% for downwind transformation flights as shown in Supplementary Table 1. In contrast to the emission box flights, the largest uncertainty in the transfer rates through the downwind screens arises from the background subtraction of CO2 (δB in Eq. 9 below) due to the higher variability in background CO2 over a typically longer flight time. Such uncertainties are included in the emission results from TERRA and reported separately in Supplementary Table 1.
Upscaling OS emissions
The hourly emissions of CO2 derived with TERRA in Fig. 1 and Supplementary Table 1 are used to calculate the CO2 emission intensity \(\left( {I_{{\mathrm{CO}}_2}} \right)\) for individual facilities (\({\mathrm{kg}}_{{\mathrm{CO}}_2}{\mathrm{barrel}}^{ - 1}\) SCO) as a first step to estimating annual CO2 emissions. This emission intensity is derived as
where \(E_{{\mathrm{M}}_{{\mathrm{CO}}_2}}\) is the measured emission rate of CO2 for a given facility scaled to a month and PSCO is the reported monthly production volume of SCO in units of barrels (reported to the Alberta Energy Regulator (AER)). Since production volumes are reported as monthly totals19, the measured hourly emission rates (\(E_{{\mathrm{CO}}_2}\)) must be scaled up to a month to be used in the above equation (see below). The fact that the relative standard deviation between flights for a single facility spanning a period of a month was <10% supports this monthly upscaling of emission rates. Alternatively, production volumes and hourly CO2 emissions can both be scaled to daily values. For simplicity, we have chosen to only scale the emissions measurements to monthly values; however, scaling both the emissions up and the production down to 1 day results in the same CO2 intensities (within <1%).
Scaling the hourly CO2 emissions to daily or monthly values with a simple 24 h (i.e., 1 day) or 744 h (i.e., 1 month) scaling factor may overestimate the total emissions during that time period. Rather, we have used an approach described previously for VOC emissions17. As described in Li et al., the TERRA-derived hourly emission rates are converted to daily (or monthly) emission rates based on the diurnal (or monthly) changes in bitumen production. This approach is ideally suited to CO2 as it is not likely to have the added complexity of temporally/temperature-dependent emissions from non-combustion sources, which may not scale with production. For combustion-based emissions, the hourly emission rate (Em) is related to the average hourly emission rate (\(\overline {E_{\mathrm{m}}}\)), the hourly bitumen production q at the hour of measurement, and the 24-h production p.
Since combustion and thus production is accompanied by NOX emissions, the ratio q/p may be derived as
where \(E_{{\mathrm{NO}}_X}\) is the hourly emission rate during aircraft measurement, and \(\mathop {\sum }\nolimits E_{{\mathrm{NO}}_X}\) is the daily NOX emission rate. Thus a factor Cdaily, for converting hourly to daily emission rates, can be expressed as
Similarly, a scaling factor to convert hourly to monthly emission rates is derived as
where \({\sum} {E_{{\mathrm{NO}}_X}}\) is the monthly emission rate. Using NOX as an indicator of production is convenient since hourly, daily, and monthly NOX emission rates are available from CEMS measurements. The underlying assumption is that both CO2 and NOX emissions are proportional to SCO production, which is consistent with the fundamental assumptions for emission factor-based emission reporting, and consistent with the empirical relationship between CO2 and NOX observed here (Supplementary Fig. 4b). Although various in-plant sources of combustion exist, each with a different NOX/CO2 ratio, this assumption requires the aggregate NOX emissions (sum of all CEMS data) to vary with production. While SO2 was chosen previously as a surrogate for production17, we have chosen to use NOX, as the CEMS data for NOX is more likely to include other stack combustion sources in addition to the upgrader stacks, which are the main source of SO2. While it is not known whether the NOX/CO2 ratios from different sources within a facility are temporally invariant, the standard deviation of the slope of the empirical relationships in Supplementary Fig. 4b are used as a measure of the potential error introduced by variable NOX/CO2 ratios during the study (δV). The CEMS data for \(E_{{\mathrm{NO}}_X}\) from the facilities are reported to be accurate to within 10%39 (δCEM). The uncertainty in each Cmonthly scaling factor per flight (δC) is then derived as
and ranged from ≈14% to 15%. The mean scaling factor Cmonthly is derived to be 0.83 ± 0.05, 1.00 ± 0.07, and 0.89 ± 0.06 for SML, SUN, and CNRL, respectively. For other facilities where no CEMS data were available, the average of the terms above is used to calculate Cmonthly (0.91 ± 0.13). The monthly CO2 emission rates (\(E_{{\mathrm{M}}_{{\mathrm{CO}}_2}}\)) for a given facility are then derived as
where \(E_{{\mathrm{CO}}_2}\) is the TERRA-derived hourly emission rate (720/Cmonthly is used for September). This is subsequently used to compute the CO2 emission intensities \(( {I_{{\mathrm{CO}}_2}} )\) via Eq. (1) above and shown in Fig. 2a and Supplementary Table 2.
Annual OS CO2 estimates and uncertainties
Annual CO2 emissions (Eannual) for individual facilities are derived by multiplying the top–down derived CO2 emission intensities (Supplementary Table 2), by the reported annual SCO production volumes for the year 201319:
The derived annual CO2 emissions have an overall relative error (δE) with contributions from the errors associated with the application of TERRA (δT ≈ 7–20%), the baseline CO2 estimation (δB ≈ 1–20%), the hourly to monthly scaling factor (δC ≈ 14–15%; above), the relative measured variability in TERRA-derived emissions from multiple flights per facility (standard error; δD ≈ 4–10%), and the reported production volumes of SCO (δP ≈ 1%). The overall relative uncertainty in the annual emission rate (δE = ΔEannual/Eannual) can hence be calculated as
for each flight and ranged from 17% to 32% depending on the facility (Supplementary Table 2). The mean annual emissions (across individual flights) for each facility is shown in Fig. 2b, with the error bars representing the propagated uncertainty of the mean (see Supplementary Table 2).
The uncertainty associated with the calculated emission intensities \(( {I_{{\mathrm{CO}}_2}} )\) of Fig. 2a are also derived with Eq. (9), but using a value of δP (≈ 1%) for monthly reported production (rather than annual production). This also results in a calculated uncertainty in \(I_{{\mathrm{CO}}_2}\) of 17–32%. The absolute uncertainties in \(I_{{\mathrm{CO}}_2}\) derived for each individual facility flight are provided in Supplementary Table 2 and ranged from ±10 to ±76 kg CO2 barrel−1, with a propagated error in the mean \(I_{{\mathrm{CO}}_2}\) for each facility ranging from ±7 to ±26 kg CO2 barrel−1 (see Supplementary Table 2). It is expected that applying the emission intensities \(( {I_{{\mathrm{CO}}_2}} )\) derived for 1 month in this study across the entire year to determine annual emissions is significantly more accurate than attempting to scale the measured CO2 emissions from these flights directly to a full year. This intrinsically assumes that the measured emission rates are more representative of a month than they are to a full year and only requires \(( {I_{{\mathrm{CO}}_2}} )\) to be relatively constant from month to month (see other considerations and assumptions section).
Annual CH4 emissions used in Fig. 4 were taken directly from previous work12. Deriving an emission intensity for methane (to be included in the total \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\)) using similar upscaling factors as was done for CO2 may not be fully appropriate for CH4, as most CH4 in the OS is not derived via combustion. Hence \(I_{{\mathrm{CO}}_{2{\mathrm{eq}}}}\) for CH4 specifically was derived by dividing previously reported annual CH412 by annual production volumes of SCO19. Regardless, applying the upscaling approach for CO2 described above to hourly CH4 resulted in CH4 emission intensities that differed by <5% and remain a small contributor to overall OS GHG emissions (using 100-year GWP).
The statistical significance of the differences between reported annual CO2 emissions and those derived here (Fig. 2b) are investigated through the use of a single-sample t test, since as with all reported emissions there is only a single reported value for each facility. This analysis tests the null hypothesis that can be stated as: \(\bar M\) = μo, i.e., the mean of all aircraft measurement results for a given facility (\(\bar M\)) equals the reported value (μo). Consequently, the t statistic can be given as:
where \(\bar M\) is the sample mean, μo is the reported value, X are the aircraft-based emission rates from all flights of a facility, and N is the number of flights for each facility, with a degree of freedom of N − 1. Using this test for the SML facility results in a t = 8.4, which translates into a p value of 0.0004. This indicates that the aircraft measurement-based emission results for SML are statistically and significantly different from the reported emission at the 99.9% confidence level. The results for other facilities resulted in t values of 1.95, 2.32, and 2.69 for SUN, CNRL, and SAJ, respectively. This corresponds to means that are different than reported values at p < 0.2, <0.1 and <0.1 (i.e., ~80–90% confidence level).
Other considerations and assumptions
There are potentially additional considerations that should be noted with respect to the estimated emission intensities and annual emissions particularly when compared to traditional bottom–up approaches. Such bottom–up approaches rely upon accurate and detailed knowledge of: the technology in use, emission factors, fuel mixture data, operating conditions, quality of maintenance, control technologies in use, carbon content data, and the lower or higher heating values (LHV vs HHV) of the process. These items can have a degree of uncertainty associated with them and do not include the potential for unintentional errors or omissions of sources (among the very many bottom–up sources that exist). While aircraft measurements of CO2 concentrations and associated top–down methodologies are also subject to a range of quantifiable uncertainties, the approach provides a useful and complimentary dataset to bottom–up methods, which can identify when further investigation into emissions is required, particularly when discrepancies exist. While it is not possible to unequivocally determine the root causes of the observed discrepancies here, it is speculated that that they may arise from a combination of factors, including outdated emission factors and activity data, unknown/poorly updated fuel carbon content data, poorly quantified area sources, and human error. Such difficulties are expected to be faced by various O&G and other industries, suggesting the potential for universal differences between top–down and bottom–up emission estimation methods.
Some additional uncertainties for the top–down methodology (those not already stated in methods) are also possible. For example, the aircraft measurements were performed over the course of a month and appropriately scaled, taking into account monthly production to derive emission intensity. A seasonal change in emission intensity during non-sampled months is possible, although we expect that this should be minimal (<15%) as noted previously26, particularly since seasonal emissions of CO2 from fugitive sources such as tailing ponds are small contributors to overall CO2 emissions40. Since much of the CO2 is a result of combustion, it expected that increased energy/heat would be required during the winter, potentially resulting in increased emission intensities compared to the summer. In addition, changes in the fuel mixture used within facilities over the year can influence the derived emission intensities. For example, increased use of pet coke as fuel (which is known to emit more CO2) during the month of this study could bias the derived emission intensities high compared to other months. The underlying assumption in this regard is that the relative proportion of fuel types used during the aircraft flights was similar to other months. This is supported by OS plant statistics19, which show that the fraction of pet coke used varied by <10% month to month in 2013 for SML. Regardless, the carbon content of pet coke is only 10–15% higher than that of natural gas and process gas used for fuel and would only apply to 60–70% of total facility emissions (i.e., not from the mining process).
Other end products arising from OS operation (i.e., not SCO) are also possible, which could introduce some uncertainty into the emission intensity estimates that use SCO production in the denominator of the equation for \(I_{{\mathrm{CO}}_2}\). This is also expected to be relatively small as SML and SUN generally produce ~90% SCO26. Regardless, using an alternative emission factor approach (i.e., CO2/SO2 or CO2/ore mined) results in very similar annual emissions compared to the emission intensity approach. The results from these independent approaches are good evidence that they are valid and support the underlying assumption that NOX emissions on aggregate are proportional to SCO production (see Methods). Regardless, provided that the product mixture does not change significantly from month to month, the derived \(I_{{\mathrm{CO}}_2}\) remains a valid emission factor that can be used to calculate annual emissions. The OS plant statistics19 support the assumption of a constant product mixture as it varies by <10% month to month. Finally, the possibility of unforeseen facility maintenance, open burning of overburden, or increased flaring resulting in increased CO2 emissions cannot be ruled out. However, there was no evidence of maintenance or burning occurring during this study, and flaring is expected to account for a very small fraction of the overall CO2 emissions. Regardless, such events are unlikely to have occurred systematically across the exact days of study during the months of August and September.
Reporting summary
Further information on experimental design is available in the Nature Research Reporting Summary linked to this article.
Data availability
All data used in this publication are freely available on the Canada-Alberta Oil Sands Environmental Monitoring Information Portal: http://donnees.ec.gc.ca/data/air/monitor/ambient-air-quality-oil-sands-region/pollutant-transformation-summer-2013-aircraft-intensive-multi-parameters-oil-sands-region/?lang = en The source data underlying Figs. 1–4, Supplementary Figs. 2b, c, 3d, 4b, and Tables 1 and 2 are provided as a Source Data file.
Code availability
All the computer code associated with the TERRA algorithm, including for the kriging of pollutant data, a demonstration dataset and associated documentation is freely available upon request. The authors request that future publications which make use of the TERRA algorithm cite Gordon et al.18, Liggio et al.34, or Li et al.17 publications as appropriate.
References
IPCC. Global Warming of 1.5°C: An IPCC Special Report on the Impacts of Global Warming of 1.5°C above Pre-industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty (World Meteorological Organization, Geneva, 2018). https://www.ipcc.ch/sr15/
UNFCCC. GHG Data Interface. https://unfccc.int/process/transparency-and-reporting/greenhouse-gas-data/ghg-data-unfccc# (2015).
UNFCCC. National Inventory Submissions 2017. https://unfccc.int/process/transparency-and-reporting/reporting-and-review-under-the-convention/greenhouse-gas-inventories-annex-i-parties/submissions/national-inventory-submissions-2017 (2017).
Stocker, T. F. Climate Change 2013: The Physical Science Basis (Cambridge University Press, New York, 2014).
IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories: Volume 2 - Energy, Chapter 2 - Stationary Combustion. https://www.ipcc-nggip.iges.or.jp/public/2006gl/pdf/2_Volume2/V2_2_Ch2_Stationary_Combustion.pdf (2006).
Höglund-Isaksson, L. Bottom-up simulations of methane and ethane emissions from global oil and gas systems 1980 to 2012. Environ. Res. Lett. 12, https://doi.org/10.1088/1748-9326/aa583e (2017).
Ren, X. et al. Methane emissions from the Marcellus Shale in southwestern Pennsylvania and northern West Virginia based on airborne measurements. J. Geophys. Res. 122, 4639–4653 (2017).
Zavala-Araiza, D. et al. Reconciling divergent estimates of oil and gas methane emissions. Proc. Natl Acad. Sci. USA 112, 15597–15602 (2015).
Roscioli, J. R. et al. Characterization of methane emissions from five cold heavy oil production with sands (CHOPS) facilities. J. Air Waste Manag. Assoc. 68, 671–684 (2018).
Johnson, M. R., Tyner, D. R., Conley, S., Schwietzke, S. & Zavala-Araiza, D. Comparisons of airborne measurements and inventory estimates of methane emissions in the alberta upstream oil and gas sector. Environ. Sci. Technol. 51, 13008–13017 (2017).
Alvarez, R. A. et al. Assessment of methane emissions from the U.S. oil and gas supply chain. Science 361, 186–188 (2018).
Baray, S. et al. Quantification of methane sources in the Athabasca Oil Sands Region of Alberta by aircraft mass balance. Atmos. Chem. Phys. 18, 7361–7378 (2018).
BP. Statistical Review of World Energy. https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (2017).
Environment and Climate Change Canada. Canadian Environmental Sustainability Indicators: Greenhouse Gas Emissions. www.ec.gc.ca/indicateurs-indicators/default.asp?lang=En&n=FBF8455E-1 (2017).
Environment and Climate Change Canada. Greenhouse Gas Reporting program (2017). https://www.canada.ca/en/environment-climate-change/services/climate-change/greenhouse-gas-emissions/facility-reporting.html
Environment and Climate Change Canada. 1990-2013: Greenhouse gas sources and sinks in Canada National Inventory Report (2015). http://www.publications.gc.ca/site/eng/9.506002/publication.html
Li, S.-M. et al. Differences between measured and reported volatile organic compound emissions from oil sands facilities in Alberta, Canada. Proc. Natl. Acad. Sci. USA 114, E3756–E3765, https://doi.org/10.1073/pnas.1617862114 (2017).
Gordon, M. et al. Determining air pollutant emission rates based on mass balance using airborne measurement data over the Alberta oil sands operations. Atmos. Meas. Tech. 8, 3745–3765 (2015).
Alberta Energy Regulator, Alberta Mineable Oil Sands Plant Statistics. https://www.aer.ca/data-and-publications/statistical-reports/st39 (2013).
Cai, H. et al. Well-to-wheels greenhouse gas emissions of canadian oil sands products: implications for U.S. petroleum fuels. Environ. Sci. Technol. 49, 8219–8227 (2015).
Argonne National Laboratory. GREET model-the greenhouse gases, regulated emissions, and energy use in transportation model. https://greet.es.anl.gov (2017).
S&T Squared. GHGenius: a model for Lifecycle assessment of transporttaion fuels. https://www.ghgenius.ca/ (2018).
Stanford School of Earth, Energy & Environmental Sciences. OPGEE: the Oil Production Greenhouse Gas Emissions Estimator. https://eao.stanford.edu/research-areas/opgee (2018).
Brandt, A. R. Variability and uncertainty in life cycle assessment models for greenhouse gas emissions from Canadian Oil sands production. Environ. Sci. Technol. 46, 1253–1261 (2012).
Charpentier, A. D., Bergerson, J. A. & MacLean, H. L. Understanding the Canadian oil sands industry’s greenhouse gas emissions. Environ. Res. Lett. 4, https://doi.org/10.1088/1748-9326/4/1/014005 (2009).
Englander, J. G. et al. Oil sands energy intensity assessment using facility-level data. Energy Fuels 29, 5204–5212 (2015).
Syncrude Canada. Syncrude Sustainability: climate change. http://syncrudesustainability.com/2016/environment/climate-change.html (2018).
Suncor Energy Inc. Suncor Sustainability Report 2016. http://sustainability.suncor.com/2016/en/environment/2015-ghg-performance.aspx (2016).
Environment and Climate Change Canada. National Pollution Release Inventory. https://www.canada.ca/en/services/environment/pollution-waste-management/national-pollutant-release-inventory.html (2013).
Hillman, T. & Ramaswami, A. Greenhouse gas emission footprints and energy use benchmarks for eight U.S. cities. Environ. Sci. Technol. 44, 1902–1910 (2010).
CDP. Citywide GHG Emissions. https://data.cdp.net/Cities/2016-Citywide-GHG-Emissions/dfed-thx7/data (2016).
UNFCCC. Research and systematic observation; Draft conclusions proposed by the Chair of Subsidiary Body for Scientififc and Technological Advice. https://unfccc.int/resource/docs/2017/sbsta/eng/l21.pdf (2017).
DeCola, P. An Integrated Global Greenhouse Gas Information System (IG3IS); WMO Bulletin 66 (2017). https://public.wmo.int/en/resources/bulletin/integrated-global-greenhouse-gas-information-system-ig3is
Liggio, J. et al. Oil sands operations as a large source of secondary organic aerosols. Nature 534, 91–94 (2016).
Liggio, J. et al. Understanding the primary emissions and secondary formation of gaseous organic acids in the oil sands region of Alberta, Canada. Atmos. Chem. Phys. 17, 8411–8427 (2017).
Liggio, J. et al. Quantifying the primary emissions and photochemical formation of isocyanic acid downwind of oil sands operations. Environ. Sci. Technol. 51, 14462–14471 (2017).
Cambaliza, M. O. L. et al. Assessment of uncertainties of an aircraft-based mass balance approach for quantifying urban greenhouse gas emissions. Atmos. Chem. Phys. 14, 9029–9050 (2014).
Walter, D. et al. Flux calculation using CARIBIC DOAS aircraft measurements: SO2 emission of Norilsk. J. Geophys. Res. 117, https://doi.org/10.1029/2011JD017335 (2012).
Alberta Environment and Parks. Continuous emissions monitoring system (CEMS) code. http://aep.alberta.ca/air/reports-data/continuous-emissions-monitoring/documents/ContinuousEmissionMonitoringSystem-1998.pdf (1998).
Small, C. C., Cho, S., Hashisho, Z. & Ulrich, A. C. Emissions from oil sands tailings ponds: review of tailings pond parameters and emission estimates. J. Petrol. Sci. Eng. 127, 490–501 (2015).
Acknowledgements
We thank the National Research Council (NRC) of Canada flight crew of the Convair-580, the technical support staff of AQRD, Dr. Stewart Cober for the management of the study and the community of Fort McKay and Alberta Energy and Parks (AEP) for useful discussions. The project was supported by the Environment and Climate Change Canada Air Pollution program and the Oil Sands Monitoring program (OSM).
Author information
Authors and Affiliations
Contributions
J.L., S.-M.L., R.S., K.H., A.D., R.L.M., J.O., M.W., and R.M. all contributed to the collection of aircraft observations in the field. R.S., R.M., R.L.M., and K.H. made the CO2 and CH4 measurements and subsequent QA/QC of data. A.D. contributed to the development of TERRA. J.O. made measurements of NOX and subsequent QA/QC of data. D.W. and F.V. provided GHG inventory information. J.L. and S.-M.L. wrote the paper with input from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liggio, J., Li, SM., Staebler, R.M. et al. Measured Canadian oil sands CO2 emissions are higher than estimates made using internationally recommended methods. Nat Commun 10, 1863 (2019). https://doi.org/10.1038/s41467-019-09714-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-09714-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.