Abstract
Although CDW correlations are a ubiquitous feature of the superconducting cuprates, their disparate properties suggest a crucial role for pinning the CDW to the lattice. Here, we report coherent resonant X-ray speckle correlation analysis, which directly determines the reproducibility of CDW domain patterns in La1.875Ba0.125CuO4 (LBCO 1/8) with thermal cycling. While CDW order is only observed below 54 K, where a structural phase transition creates inequivalent Cu-O bonds, we discover remarkably reproducible CDW domain memory upon repeated cycling to far higher temperatures. That memory is only lost on cycling to 240(3) K, which recovers the four-fold symmetry of the CuO2 planes. We infer that the structural features that develop below 240 K determine the CDW pinning landscape below 54 K. This opens a view into the complex coupling between charge and lattice degrees of freedom in superconducting cuprates.
Similar content being viewed by others
Introduction
Holes doped into the Mott insulating parent compounds of the high-temperature superconducting cuprates experience strong interactions with the antiferromagnetic background and with each other, as well as with the lattice in which they reside1. The Hubbard Hamiltonian, often used to model the cuprates, predicts that charge density wave (CDW) fluctuations are an intrinsic property of strongly interacting electrons in pristine, undistorted 2D square lattices2,3. CDWs have indeed been observed in essentially all hole-doped cuprates, but with distinct transition temperatures, correlation lengths, and wavevectors4,5,6,7,8,9,10,11. This is epitomized by comparing two very similar cuprates that have slightly different low-temperature crystal structures: La1.875Sr0.125CuO4 (LSCO 1/8) and LBCO 1/8. LSCO 1/8 has weak CDW correlations and is a bulk superconductor below its transition temperature of Tc = 28 K8,12,13,14; whereas LBCO 1/8 has well-correlated CDW order that almost completely suppresses bulk superconductivity into what is proposed to be a 2D superconducting pair density wave state15,16,17,18,19. As the main difference between these compounds is a subtle change in the crystal structure20, it is evident the lattice that hosts the CDW correlations has a dramatic influence on the properties of the CDW and the superconducting ground state.
Multiple types of lattice deformation or disorder are present in cuprates including that of interstitial oxygen atoms, chemical substitutions, as well as local and long-range tilting of the Cu–O octahedra, all of which have been proposed as possible CDW pinning features that stabilize CDW order4,21,22,23,24,25,26,27. One widely discussed lattice deformation in this context is the LTT phase in LBCO, in which octahedral tilts define a preferential direction for stripe pinning within each CuO2 plane4,20,22. While the LTO phase transition is common for both LBCO and LSCO, the LTT structural transition is a special feature in LBCO that coincides with the CDW formation. Fully understanding this process is, however, hampered by a lack of experimental techniques that are sensitive to the spatial distribution of the CDW order parameter.
This article reports our implementation of coherent resonant X-ray speckle correlation analysis as a tool for probing CDW domain pinning in the cuprates, choosing LBCO 1/8 as the model system due to its LTT structure and particularly large CDW correlation length. We discover strikingly reproducible CDW domain formation upon repeated thermal cycling well above its transition temperature and show that the CDW pinning memory is defined by structures that form at the LTO transition at 236(5) K rather than disorder or the LTT transition at 54(1) K that appears alongside CDW order.
Results
Experimental setup
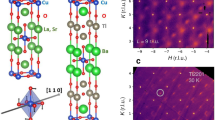
Although CDW pinning has potential to dramatically change the superconducting ground state, directly observing CDW pinning and tracking its changes with temperature are very challenging tasks. Much of the difficulty is that one must combine a technique that is sensitive enough to detect the CDW domain spatial arrangement, which we will call “texture”, with the ability to reproducibly illuminate the same sample volume over a wide temperature range. Figure 1 shows how we have addressed the problem using coherent resonant X-ray diffraction: a scattering method that measures the interference between scattering from different domains in the CDW texture as a “speckle” pattern. Our innovation, reported here, is to attach a mask with a microscopic pinhole to the sample, which we overfill with the coherent X-ray beam to ensure we illuminate the same sample volume despite possible temperature-induced drifts of the sample position.
Experimental setup. a The scattering geometry in which coherent X-rays illuminate the masked LBCO 1/8 sample and the CDW Bragg peak is measured on a CCD detector. b A SEM image of the LBCO 1/8 single crystal with a Au mask fixed on top. Numbers 1–16 indicate the 16 pinholes drilled in the Au mask using a focused ion beam (FIB) prior to being fixed on the crystal. The white scale bar represents 50 μm. c A zoomed SEM image of pinhole #10, through which most of our data were taken. The white scale bar represents 5 μm
CDWs in cuprates modulate the in-plane valance charge density with a period of ~3–4 lattice units along the Cu–O bond direction, and tend to stack out-of-phase from plane-to-plane leading to CDW propagation vectors of (H, 0, 0.5) or (0, K, 0.5), where H = K ≈ 0.2–0.35. For these experiments we chose an LBCO 1/8 single crystal which has one of the strongest CDW intensities of any cuprate and aligned it to its Bragg condition at wavevector Q = (0.236, 0, 1.5) (see Methods). We furthermore tuned the X-ray energy to the Cu L3-edge resonance around 931 eV in order to enhance our sensitivity to the weak CDW. In this condition the incident X-ray angle is θi = 88° with respect to the [001] sample surface and the detector angle is 2θ = 119°. Such an approach has been used extensively to study the average CDW properties5,6,7,8,9,28,29,30. The very high coherent flux (1013 photons/s) at the 23-ID-1 beamline at the National Synchrotron Light Source II (NSLS II) opens up the possibility of observing coherent interference between the domains of a weakly scattering order parameter, such as that of cuprate CDWs31,32. This was configured to produce a beam of ~20 μm at the sample overfilling the 10 μm pinhole in the Au mask attached to the sample (see Methods).
Pinned domains within the ordered state
Figure 2a plots a detector image at the CDW Bragg condition, which is zoomed in panels b–g. The extent of the observed peak (in this case ~4 × 10−3 Å−1) is inversely proportional to the CDW correlation length (or domain size) similar to what is seen in conventional scattering. The speckle modulations on top of the peak envelope arise from coherent interference between different CDW domains. The average size and elongated shape of the speckles on the detector is determined primarily by the geometry of the experiment and the extent of the illuminated sample volume, which is fixed by the 10 μm pinhole and ~100 nm X-ray penetration depth (Fig. 1a) (see refs. 31,32 for a detailed discussion of the speckle shape and speckle visibility). Therefore, while the full speckle distribution contains information about the real-space domain distribution, the average speckle size and shape do not immediately provide information on the sample properties. The speckle locations, however, are highly sensitive to the CDW domain positions and can therefore be used to test for changes in the CDW domain texture as a function of temperature33,34,35. We note that while phase retrieval algorithms can in-principle reconstruct real-space images, the complexity of the domain pattern in this case makes this process intractable in practice36.
Temperature dependence of the CDW speckle positions within the ordered state. a A detector image of the LBCO 1/8 CDW Bragg peak at 24 K at Q = (0.236, 0, 1.5). The color-bar denotes intensity in photons s−1, and the white bar at the bottom indicates 100 detector pixels (0.0025 r.l.u). b–g The temperature dependence of speckle positions as the temperature was raised from 24 to 46 K. Zoomed-in speckle images are taken from the same detector area indicated by the red box in (a). Despite the broadening and weakening of the CDW Bragg peak, the speckles tend to persist in similar locations to 46 K, above which the speckle intensity becomes too low and noise dominates the signal
In LBCO 1/8, static CDW order exists at low temperatures with a correlation length of 240 Å. This can be directly verified with X-rays by noting that the speckle pattern does not vary as a function of time as reported previously31,32. With increasing temperature the CDW correlation length decreases and the CDW Bragg peak disappears coincident with TLTT = 54 K28,29,31,37,38,39. (The temperature dependence of the CDW peak intensity is explicitly compared with the LTT to LTO structural phase transition in Fig. 3a later in the manuscript.) We measured a range of temperatures from 24 up to 46 K (the highest temperature for which we have sufficient CDW signal in order to observe the speckle locations). At all temperatures, the speckle locations were found to persist as illustrated in Fig. 2b–g.
CDW and structural phases in LBCO 1/8 compared to speckle memory. a Temperature dependence of normalized CDW peak intensity (blue) and lattice parameters reproduced from ref. 49 (orange). The CDW transition coincides with the LTT structural transition at TLTT. A second lattice transition occurs at TLTO. The inset images represent the octahedral tilts associated with the LTT, LTO, and HTT phases. b CDW speckle images taken at 24 K. The black arrows indicate the temperature cycling between images. Tcycle indicates the highest temperature that sample was brought to during a temperature cycle
CDW domain memory
Speckle images were taken at 24 K successively before and after the sample temperature was cycled to Tcycle as we illustrate in Fig. 3b (see Supplementary Fig. 7 for a larger field of view). After cycling to Tcycle = 180 K, a temperature well above the CDW transition temperature, the speckle patterns are strikingly similar [see panels (i) and (ii)]. However, as the sample was heated to higher temperatures, the degree of reproducibility dropped, and by Tcycle = 320 K, their positions completely changed as seen in panels (ii) to (iv).
In order to compare speckle positions quantitatively, and identify the onset temperature of this change, we calculated the normalized cross-correlation function. Speckle images were background subtracted as described in Supplementary Note 1. These images are then represented as M × N matrices Am,n and Bm,n where m and n are row-column indices. Cross-correlations matrices are calculated via
Here, Am,n and Bm,n were taken to be M = 200 × N = 200-pixel images under the CDW peak measured before and after thermally cycling the sample, which include ~30–50 speckles. When Am,n and Bm,n have the same or similar speckle patterns, the correlated intensity features a peak that we sum over to obtain a single normalized speckle cross-correlation coefficient33,34,35
In this equation, \(\mathop {\sum}\nolimits_{{\mathrm{speckle}}}\) denotes summing over the peak in the cross-correlation matrix, corresponding to just over one speckle (~4 × 16 pixels) in size. The value is normalized by dividing by the auto-correlations of Am,n and Bm,n, such that two identical images have ξ = 1. In Fig. 4, we show ξ for various cycle temperatures showing a transition from high to low speckle reproducibility well above the CDW ordering temperature. We fit ξ versus Tcycle using an error function, which provides a reasonable phenomenological description of the shape of the transition. The onset temperature of de-correlation was 240(3) K, which coincides with the LTO structural phase transition at TLTO = 236(5) K37. This transition involves rotations of the Cu–O octahedra around the 〈110〉HTT direction and since nearest-neighbor octahedra rotate in opposite directions, the unit cell volume increases by a factor of two, with \(a_{\mathrm{o}} \approx b_{\mathrm{o}} \approx \sqrt 2 a\). Below this threshold the majority of the speckles reproduce with ξ = 0.84(9); above the transition ξ = 0.21(4), which corresponds to the value expected in a random domain distribution (Supplementary Note 2). We further confirmed that different regions within the speckle pattern shown in Fig. 2a and data taken through another pinhole reproduce the same phenomenology within error bars.
CDW memory. Normalized speckle cross-correlation coefficient, ξ, of data before and after temperature cycling to different values of Tcycle. Images of 200 × 200 detector pixels were used for this calculation. An error function fit gives a de-correlation onset temperature of 240(3) K, which coincides with the LTO structural phase transition. The red box indicates 24 K the temperature where all the speckle images were sampled for this figure. Error bars are estimated by taking the standard deviation of repeated, nominally equivalent, measurements
Discussion
These data establish that the CDW domains are strikingly reproducible upon temperature cycling well above the LTT and CDW transitions. The CDW is pinned at low temperatures, which is the usual behavior for a system with a long CDW correlation length as this can be accomplished by even a weak pinning force. This is, however, not a priori certain and the CDW in chromium has been reported to be dynamic down to low temperatures40. It further appears that the reproduciblity threshold here is associated with the LTO transition. This differs from what might have been anticipated based on the fact that the CDW appears at the LTT transition temperature4,29,38,41, which would suggest the reproduciblity threshold should match this temperature. We go on to discuss this intriguing result.
An analysis of hard X-ray Bragg diffraction data suggests that the typical LTO domain width is ~700 nm (Supplementary Note 3); we expect the LTT domain width to be comparable. In these experiments we illuminate a ~10 × 10 μm2 area of the sample with coherent X-rays, which will contain of order 200 LTT domains. All the CDW signal from this area contributes to the interference that determines the speckles. Within a given CuO2 layer, only half of the twin domains will contribute to a given CDW diffraction peak because of the unidirectional ordering within the LTT structure; the other half of the twin domains will contribute to a CDW peak rotated by 90°, i.e. at (0, 0.23, 1.5) rather than (0.23, 0, 1.5). Hence, in order for the speckle pattern to reproduce after cycling through the LTO-LTT transition, the domain pattern must reproduce precisely.
Now, the speckle pattern reproduces with cycling, but only if we use Tcycle < 240(3) K. This temperature matches the LTO–HTT transition. So if we cycle into the HTT phase, the resulting CDW speckle pattern in the LTT phase changes. This indicates that LTO domain boundaries play a crucial role in propagating the CDW domain memory.
How does the CDW domain memory created at LTO–HTT transition translate through LTT? Based on strain considerations, LTO domain boundaries are expected to occur along the 〈100〉HTT lattice directions, as confirmed by TEM imaging42,43,44. Early structural studies of LBCO demonstrated that the LTT and LTO tilt patterns can be conceptualized as superpositions of one-another20,45. Such superposition-based arguments naturally justified the observation that LTT-like tilts occur at LTO domain boundaries in the cuprates42,43,44. Moreover, this supports the idea that LTT twin boundary locations can be inherited from the LTO twin boundary configuration. From the experimental results and the discussion above, we infer that the LTO twin domain pattern must change in a significant way on cycling into the HTT phase and that this process limits the observed CDW memory effect.
This is a remarkable result, but it is just the start. One might have expected a random nucleation of CDW domains on each cycling, which would change the speckles. The CDW order, with a period of ~4a, has a four-fold degeneracy with respect to how it aligns within a CuO2 layer of the LTT structure. The experiment, on the other hand, shows that the phase of the CDW order with respect to the lattice must be reproduced precisely each time. The CDW correlation length is just 24 nm (at low temperature), which is much smaller than the structural domain size. That implies that defects within a structural domain must locally pin the phase of the CDW order. Disorder and structural distortions are present in almost all cuprates and have been discussed extensively in connection with CDW pinning in the cuprates4,21,22,23,24,25,26,27,46. In La2−xBaxCuO4 the most prominent form of disorder is La/Ba cation substitution, with locations that are independent of temperature. This may act in concert with the domain boundaries to pin the local CDW phase.
Another significant observation is that, within the CDW phase, the speckle locations do not change with temperature (see Fig. 2), despite the fact that the CDW correlation length varies with temperature10,29,37,38,41. This can be explained by uniform expansion of CDW domains around their pinning centers on cooling, as speckle locations are primarily dependent on the locations of the domains and largely insensitive to their size (Supplementary Note 4).
Almost all cuprates show some form of orthorhombic structural symmetry breaking, so the CDW memory effects discovered here may well be shared by many different cuprate species. Testing whether other cuprates, including those without a LTT phase, show similar behavior, and whether lattice pinning and the stability of CDW ordering are related will be important in future work. We further emphasize that the experimental configuration presented here, in which sample drift problems are avoided by attaching a mask directly to the sample, is also applicable to applied current or laser excitation, as well as to the magnetic field-dependent behavior studied previously in magnetic alloys33,34,35. This complements what can be achieved with scanning tunneling spectroscopy, which has superior spatial resolution, but is limited to cleaved surfaces23. The use of coherence and resonant X-ray scattering further opens the possibility to study charge, spin and orbital order parameters in other quantum materials with better resolution than is possible with current microdiffraction techniques26.
In conclusion, we present the first application of coherent resonant soft X-ray speckle correlation analysis to study the CDW domain hysteresis in LBCO 1/8. We uncover remarkably reproducible CDW domain formation upon temperature cycling far above the 54 K CDW transition, before the CDW pattern is almost completely reconfigured by cycling above 240(3) K. The CDW order, which is associated with the dramatic suppression of superconductivity in this sample, experiences a pinning landscape that is determined by structural domains that form at the LTO phase transition. Our results open a new route to study the complex interplay between lattice and charge degrees of freedom in quantum materials at cryogenic temperatures.
Methods
Sample preparation
Single crystals of LBCO 1/8 were grown using the floating zone method, and characterized extensively in previous studies10,11,29,39,47, all indicating excellent sample quality. A 2 μm gold (Au) film was evaporated onto a free-standing 200 nm Si3N4 membrane. Arrays of 10 μm asymmetric pinholes were drilled into the film using a focused ion beam yielding the shape shown in Fig. 1c. Although any stable shape is adequate for speckle correlation analysis, we chose to make a two-lobe structure. This decision was taken to break circular symmetry, which should improve the prospects for obtaining real-space images via Bragg coherent diffractive imaging in the future. Such attempts have thus far been unsuccessful. This assembly was pressed onto the LBCO single crystal with poly methyl methacrylate (PMMA) as a glue. The excess PMMA that filled in the pinholes was then removed using reactive ion etching. The resulting sample was imaged in a JEOL 7600F scanning electron microscope (Fig. 1b, c). In this paper, we index the crystal using the HTT unit cell where a = b = 3.78 and c = 13.28 Å. Correlation length here is defined as a/HWHM where HWHM is the half width at half maximum of the peak in reciprocal lattice units (r.l.u.).
Coherent X-ray scattering
Data were taken at the Coherent Soft X-Ray (CSX) 23-ID-1 beamline at the NSLS II which is optimized to deliver high coherent flux at the sample. The beam was energy-dispersed in the vertical plane with a grating and focused onto a 20 μm pinhole ~5 mm from the sample to which the Au mask with a 10 μm pinhole was attached. In this configuration, the transverse coherence of the beam is greater than the extent of the illuminated region of the sample and the longitudinal coherence of the beam is of order 2 μm. The X-ray energy was further tuned to the Cu L3 absorption edge around 931 eV to enhance the signal from the CDW peak. The positions of the pinholes were determined by scanning the sample through the X-ray beam using the LBCO Cu fluorescent yield. We typically performed multiple measurements at each temperature to ensure that the cryostat was fully stable during the data collection. It typically required ~1 h to fully stabilize the cryostat at each temperature. Data were collected using a fast CCD48 with a 30 × 30 μm2 pixel size placed 340 mm from the sample. Images were read out every 5 s for a total collection time of ~10 min. A temperature ramp rate of 3 K min−1 was used for all the temperature cycles with an average waiting time of 5 min at the cycling temperature.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Keimer, B., Kivelson, S., Norman, M., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Zheng, B.-X. et al. Stripe order in the underdoped region of the two-dimensional hubbard model. Science 358, 1155–1160 (2017).
Huang, E. W. et al. Numerical evidence of fluctuating stripes in the normal state of high-c cuprate superconductors. Science 358, 1161–1164 (2017).
Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y. & Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 375, 561–563 (1995).
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x. Science 337, 821–825 (2012).
Comin, R. et al. Charge order driven by fermi-arc instability in Bi2Sr2−xLaxCuO6+δ. Science 343, 390–392 (2014).
da Silva Neto, E. H. et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science 343, 393–396 (2014).
Thampy, V. et al. Rotated stripe order and its competition with superconductivity in La1.88Sr0.12CuO4. Phys. Rev. B 90, 100510 (2014).
Tabis, W. et al. Charge order and its connection with fermi-liquid charge transport in a pristine high-T c cuprate. Nat. Commun. 5, 5875 (2014).
Miao, H. et al. High-temperature charge density wave correlations in La1.875Ba0.125CuO4 without spin–charge locking. Proc. Natl. Acad. Sci. USA 114, 12430–12435 (2017).
Miao, H. et al. Incommensurate phonon anomaly and the nature of charge density waves in cuprates. Phys. Rev. X 8, 011008 (2018).
Croft, T. P., Lester, C., Senn, M. S., Bombardi, A. & Hayden, S. M. Charge density wave fluctuations in La2−xSrxCuO4 and their competition with superconductivity. Phys. Rev. B 89, 224513 (2014).
Christensen, N. et al. Bulk charge stripe order competing with superconductivity in La2−xSrxCuO4 (x = 0.12). arXiv preprint arXiv:1404.3192 (2014).
Wu, H.-H. et al. Charge stripe order near the surface of 12-percent doped La2−xSrxCuO4. Nat. Commun. 3, 1023 (2012).
Moodenbaugh, A. R., Xu, Y., Suenaga, M., Folkerts, T. J. & Shelton, R. N. Superconducting properties of La2−xBaxCuO4. Phys. Rev. B 38, 4596–4600 (1988).
Li, Q., Hücker, M., Gu, G. D., Tsvelik, A. M. & Tranquada, J. M. Two-dimensional superconducting fluctuations in stripe-ordered La1.875Ba0.125CuO4. Phys. Rev. Lett. 99, 067001 (2007).
Berg, E. et al. Dynamical layer decoupling in a stripe-ordered high-T c superconductor. Phys. Rev. Lett. 99, 127003 (2007).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium : theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Xu, Z. et al. Neutron-scattering evidence for a periodically modulated superconducting phase in the underdoped cuprate La1.905Ba0.095CuO4. Phys. Rev. Lett. 113, 177002 (2014).
Axe, J. D. et al. Structural phase transformations and superconductivity in La2−xBaxCuO4. Phys. Rev. Lett. 62, 2751–2754 (1989).
Božin, E., Billinge, S., Kwei, G. & Takagi, H. Charge-stripe ordering from local octahedral tilts: Underdoped and superconducting La2−xSrxCuO4 (0 ≤ x ≤ 0.30). Phys. Rev. B 59, 4445 (1999).
Kivelson, S. A. et al. How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 75, 1201–1241 (2003).
Hanaguri, T. et al. A ‘checkerboard’ electronic crystal state in lightly hole-doped Ca2−xNaxCuO2Cl2. Nature 430, 1001–1005 (2004).
Vojta, M. Lattice symmetry breaking in cuprate superconductors: stripes, nematics, and superconductivity. Adv. Phys. 58, 699–820 (2009).
Nie, L., Tarjus, G. & Kivelson, S. A. Quenched disorder and vestigial nematicity in the pseudogap regime of the cuprates. Proc. Natl. Acad. Sci. USA 111, 7980–7985 (2014).
Campi, G. et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-T c superconductor. Nature 525, 359–362 (2015).
Wu, T. et al. Incipient charge order observed by NMR in the normal state of YBa2Cu3Oy. Nat. Commun. 6, 6438 (2015).
Abbamonte, P. et al. Spatially modulated ‘Mottness' in La2−xBaxCuO4. Nat. Phys. 1, 155–158 (2005).
Wilkins, S. B. et al. Comparison of stripe modulations in La1.875Ba0.125CuO4 and La1.48Nd0.4Sr0.12CuO4. Phys. Rev. B 84, 195101 (2011).
Hashimoto, M. et al. Direct observation of bulk charge modulations in optimally doped Bi1.5Pb0.6Sr1.54CaCu2O8+δ. Phys. Rev. B 89, 220511 (2014).
Chen, X. M. et al. Remarkable stability of charge density wave order in La1.875Ba0.125CuO4. Phys. Rev. Lett. 117, 167001 (2016).
Thampy, V. et al. Static charge-density-wave order in the superconducting state of La2−xBaxCuO4. Phys. Rev. B 95, 241111 (2017).
Pierce, M. S. et al. Quasistatic X-ray speckle metrology of microscopic magnetic return-point memory. Phys. Rev. Lett. 90, 175502–175504 (2003).
Chesnel, K., Nelson, J., Wilcken, B. & Kevan, S. D. Mapping spatial and field dependence of magnetic domain memory by soft X-ray speckle metrology. J. Synchrotron Radiat. 19, 293–306 (2012).
Chesnel, K., Safsten, A., Rytting, M. & Fullerton, E. E. Shaping nanoscale magnetic domain memory in exchange-coupled ferromagnets by field cooling. Nat. Commun. 7, 11648 (2016).
Miao, J., Ishikawa, T., Robinson, I. K. & Murnane, M. M. Beyond crystallography: Diffractive imaging using coherent x-ray light sources. Science 348, 530–535 (2015).
Hücker, M. et al. Stripe order in superconducting La2−xBaxCuO4 (0.095 ≤ x ≤ 0.155). Phys. Rev. B 83, 104506 (2011).
Hücker, M. et al. Enhanced charge stripe order of superconducting La2−xBaxCuO4 in a magnetic field. Phys. Rev. B 87, 014501 (2013).
Dean, M. P. M. et al. Magnetic excitations in stripe-ordered La1.875Ba0.125CuO4 studied using resonant inelastic x-ray scattering. Phys. Rev. B 88, 020403 (2013).
Shpyrko, O. et al. Direct measurement of antiferromagnetic domain fluctuations. Nature 447, 68–71 (2007).
Fujita, M., Goka, H., Yamada, K., Tranquada, J. M. & Regnault, L. P. Stripe order, depinning, and fluctuations in La1.875Ba0.125CuO4 and La1.875Ba0.075Sr0.050CuO4. Phys. Rev. B 70, 104517 (2004).
Zhu, Y. et al. Tetragonal-orthorhombic structural modulation at low temperature in La2−xBaxCuO4. Phys. Rev. Lett. 73, 3026–3029 (1994).
Chen, C., Cheong, S., Werder, D., Cooper, A. & Rupp, L. Low temperature microstructure and phase transitions in La2−xSrxCuO4 and La2−xBaxCuO4. Physica C 175, 301–309 (1991).
Chen, C., Cheong, S.-W., Werder, D. & Takagi, H. Microstructural changes induced by lattice instabilities in La2−xBaxCuO4 (x = 0.125) and Nd2NiO4. Physica C 206, 183–194 (1993).
Hücker, M. Structural aspects of materials with static stripe order. Physica C 481, 3–14 (2012).
Alloul, H., Bobroff, J., Gabay, M. & Hirschfeld, P. J. Defects in correlated metals and superconductors. Rev. Mod. Phys. 81, 45–108 (2009).
Thampy, V. et al. Comparison of charge modulations in La1.875Ba0.125CuO4 and YBa2Cu3O6.6. Phys. Rev. B 88, 024505 (2013).
Doering, D. et al. Development of a compact fast ccd camera and resonant soft x-ray scattering endstation for time-resolved pump-probe experiments. Rev. Sci. Instrum. 82, http://scitation.aip.org/content/aip/journal/rsi/82/7/10.1063/1.3609862 (2011).
Bozin, E. S. et al. Reconciliation of local and long-range tilt correlations in underdoped La2−xBaxCuO4 (0 ≤ x ≤ 0.155). Phys. Rev. B 91, 1–13 (2015).
Acknowledgements
We thank Derek Meyers for useful comments. The work at Brookhaven National Laboratory was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under Contract no. DE-SC0012704. This research used resources 23-ID-1 beamline of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract no. DE-SC0012704. The sample pattern was performed at the Center for Functional Nanomaterials, which is a U.S. DOE Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. Work at Argonne National Laboratory was supported by the US Department of Energy, Office of Basic Energy Sciences, under Contract no. DE-AC0206CH11357.
Author information
Authors and Affiliations
Contributions
S.B.W., M.P.M.D. and I.K.R. initiated and managed the project. X.M.C., C.M., Y.C., V.T., A.M.B., W.H., T.A.A., H.M., G.F., M.P.M.D., S.B.W. and I.K.R. prepared and performed the x-ray experiment. X.M.C., M.L. and G.D.G. prepared the sample. X.M.C., C.M., Y.C., V.T., J.M.T., M.P.M.D., S.B.W. and I.K.R. analyzed and interpreted the results. X.M.C., J.M.T., M.P.M.D. and I.K.R. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks Giacomo Ghiringhelli and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, X.M., Mazzoli, C., Cao, Y. et al. Charge density wave memory in a cuprate superconductor. Nat Commun 10, 1435 (2019). https://doi.org/10.1038/s41467-019-09433-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-09433-1
This article is cited by
-
Tuning of charge order by uniaxial stress in a cuprate superconductor
Communications Physics (2024)
-
Coherent correlation imaging for resolving fluctuating states of matter
Nature (2023)
-
Molecular interactions induced collapse of charge density wave quantum states in 2H tantalum disulfide nanosheets
Nano Research (2023)
-
Ultrafast X-ray imaging of the light-induced phase transition in VO2
Nature Physics (2022)
-
Charge density waves in cuprate superconductors beyond the critical doping
npj Quantum Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.