Abstract
The nature of Fermi surface defines the physical properties of conductors and many physical phenomena can be traced to its shape. Although the recent discovery of a current-dependent nonlinear magnetoresistance in spin-polarized non-magnetic materials has attracted considerable attention in spintronics, correlations between this phenomenon and the underlying fermiology remain unexplored. Here, we report the observation of nonlinear magnetoresistance at room temperature in a semimetal WTe2, with an interesting temperature-driven inversion. Theoretical calculations reproduce the nonlinear transport measurements and allow us to attribute the inversion to temperature-induced changes in Fermi surface convexity. We also report a large anisotropy of nonlinear magnetoresistance in WTe2, due to its low symmetry of Fermi surfaces. The good agreement between experiments and theoretical modeling reveals the critical role of Fermi surface topology and convexity on the nonlinear magneto-response. These results lay a new path to explore ramifications of distinct fermiology for nonlinear transport in condensed-matter.
Similar content being viewed by others
Introduction
Layered transition metal dichalcogenides are an emerging class of materials with novel physical phenomena and a wide range of potential applications1,2. Among them, semimetal tungsten ditelluride (WTe2) especially showed an extremely large and unsaturated magnetoresistance (MR)3, which was attributed to a Fermi surface with perfectly compensated electron and hole pockets3,4,5. Up to now, the MR investigated in WTe2 appears in the linear region and the exploration of a current-dependent nonlinear magnetoresistance is lacking. In this context, a nonlinear magnetoresistance (NLMR) that scales linearly with the applied electric and magnetic fields has been recently discovered independently in a polar semiconductor6 and a topological insulator7 with spin-momentum locked bands, and has led to a surge of interest within condensed-matter physics toward understanding its underlying mechanisms8,9,10. In WTe2, the large spin-orbit coupling (SOC) and broken inversion symmetry lift the spin degeneracy, as observed in spin- and angle-resolved photoemission spectroscopy (ARPES)11,12,13. Taking advantage of the large SOC and low crystalline symmetry, WTe2 was recently demonstrated as an intriguing spin-source for generating out-of-plane anti-damping torques to an adjacent magnetic material14. To further explore ramifications of the spin-polarized bands in WTe2, and their interplay with the richly structured Fermi surface15,16,17, we investigate in detail the spin-dependent nonlinear magnetotransport.
WTe2 exhibits properties remarkably sensitive to temperature as a combined result of nearly perfect carrier compensation at low temperatures with a hole-suppressing Lifshitz transition at ~ 160 K18. Accordingly, small temperature variations cause essential changes in the Fermi surface, as revealed by ARPES5,18. In addition, WTe2 undergoes a topological transition from a Weyl to a topologically trivial semimetal at ~ 70 K17,19. While an understanding of the Fermi surface is critical to describe and explore many technologically promising physical phenomena, such as the oscillatory exchange coupling or superconductivity20, and even though previous studies investigated the role of spin textures in both k and real spaces6,7,9,10, the fermiological implications and opportunities remain unexplored in the context of nonlinear magnetotransport. With such a rich and easily tunable Fermi surface, WTe2 is an excellent platform to investigate these questions.
In this work, we report the observation of a current-dependent NLMR in WTe2 that scales with the first power of both the applied electric current and magnetic field6,7. This is in striking contrast with the conventional (linear) MR so far characterized in WTe2, which is current-independent and quadratic in the magnetic field3,4. Interestingly, the NLMR shows a temperature-driven inversion and a significant anisotropy along different crystallographic axes. Our experimental results are reproduced qualitatively by theoretical modeling that combines ab-initio band structure calculations with a semiclassical calculation of the magneto-response. The calculations reveal that the spin-polarized electronic structure evolves with the magnetic field, giving rise to the measured spin-dependent NLMR. Furthermore, we establish that the inversion of NLMR arises from a transition in the Fermi contours from convex to concave, whereas the giant anisotropy is due to the low symmetry of the Fermi surface. Therefore, we establish here a close relationship between Fermi surface topology, convexity and the nonlinear magnetotransport response. These results also demonstrate that fine tuning of the Fermi level is critical in controlling the nonlinear magnetotransport in semimetals.
Results
Sample and characterization
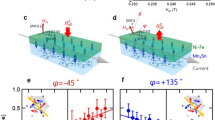
At ambient conditions, bulk WTe2 is in the orthorhombic Td phase21 where, as a result of strong octahedral distortions and the displacement of the metal within each octahedron, the W ions organize as effective zigzag chains along the a axis and sandwiched between Te layers as shown in Fig. 1a. The band structure calculated from the density functional theory (DFT) is plotted in Fig. 1b, and agrees with previous calculations18,22. In Fig. 1c, we show a schematic representation of the Fermi surface with only electron pockets at different carrier filling that illustrates how the sign of the NLMR depends on whether the Fermi surface consists of a concave set or a convex set. In bulk WTe2, the Fermi surface at 0 K consists of multiple hole and electron pockets, which can be seen below.
Crystal and band structures and nonlinear magnetotransport in WTe2. a Crystal structure of the layered WTe2 and its crystalline directions. b The calculated band structure of bulk WTe2, where the high symmetry k points are indicated in the 3D Brillouin zone sketched underneath. A magnified plot of the band dispersion is also shown to emphasize details of the electron and hole pockets. c Schematic Fermi surfaces at two representative Fermi energies illustrating the distinct convexity (see Fig. 4b for the full realistic Fermi surfaces and contours of bulk WTe2 at T = 0 K). Under a magnetic field H perpendicular to the applied electric field E (along b axis), a nonlinear charge current density \(J_{bb}^{(2)}\) at the second-order in E is generated along the b direction. \(J_{bb}^{(2)}\) has opposite sign at the two Fermi energies. d Temperature-dependent resistivity ρ with a thickness of 34 nm WTe2. e A typical optical image of Hall bar devices. f Schematic of harmonic magnetoresistance (MR) measurements while rotating H in the xy plane at an angle φ with the current
Our WTe2 flakes were obtained by mechanical exfoliation on Si/SiO2 substrates and subsequently patterned into Hall devices for transport measurements (see Methods). Multiple devices were prepared with the current channels (that define our x direction) designed along different crystallographic directions of the underlying WTe2. The typical temperature dependence of their resistivity (ρ) is shown in Fig. 1d, and is consistent with previous reports3,13. To first order in the applied current I, the longitudinal resistance R can be expressed as R = R0 + R′I, where R0 is the current-independent (linear) resistance and R′I is the current-dependent (nonlinear) resistance. In order to study the nonlinear magnetotransport, a low-frequency a.c. current Iω = I sin(ωt) was applied through the devices (Fig. 1e, f), and we recorded the second-harmonic longitudinal voltage \(V_{2\omega }{\mathrm{ = }}\frac{1}{2}R{\prime}I^2\sin (2\omega t - \pi /2)\) using lock-in techniques. The second-harmonic resistance R2ω (\(R_{2\omega } \equiv \frac{1}{2}R{\prime}I\)), equivalent to half of the nonlinear resistance R′I, is used to quantify the nonlinear magnetotransport response (which we verified to be independent of the driving frequency)23. The measurements were performed while rotating the applied magnetic field H in the xy plane of the film (out-of-plane misalignment evaluated to be <1°) at an angle φ with the current direction, as illustrated in Fig. 1f. We note that, unlike the colossal linear MR, which is the strongest under perpendicular fields3,4,5, the nonlinear magneto-response is maximized under in-plane fields due to the planar spin texture of bulk WTe2, as we discuss below.
Nonlinear magnetoresistance in WTe2
We observe a sinusoidal dependence of the second-harmonic resistance R2ω on the angle φ between the magnetic field and the current direction. Figure 2a shows that the period is 360° with a maximum when the field is orthogonal to the current (φ = 90° or 270°), and approaches zero when they are collinear (φ = 0° or 180°). Hence, unlike the first harmonic resistance Rω (see Supplementary Fig. 1), R2ω changes sign upon reversal of the magnetic field. To further characterize the NLMR, R2ω was measured at different I and H at 300 K, and the same dependence R2ω = −ΔR2ω sin φ was observed. Figure 2b shows that the extracted amplitude ΔR2ω increases linearly with I and, at the same time, scales linearly with H, as plotted in Fig. 2c (the behavior shown in Fig. 2a–c persists down to 2 K). This contrasts with the field dependence of the linear resistance Rω, which grows quadratically with H (Supplementary Fig. 1)3. These observations extend the class of systems bearing current-dependent nonlinear magnetotransport to the layered semimetal WTe2, where it is observable at room temperature.
Nonlinear magnetoresistance with a temperature-driven inversion in WTe2. a Angular-dependent second-harmonic resistance R2ω measured at T = 300 K for a 34 nm thick WTe2 device with the current applied at 45° from the a axis of WTe2 crystal. The solid line is a sinusoidal fit (−ΔR2ωsinφ) to the data. A vertical offset was subtracted for clarity. b, c Current I (b) and magnetic field H (c) dependence of the sinusoidal amplitude ΔR2ω at room temperature. The solid lines are linear fits to the data. d ΔR2ω extracted at different temperatures under H = 14 T and I = 1 mA. The insets illustrate the position of the Fermi level in different temperature ranges. ‘e’ and ‘h’ indicates the electron and hole pocket, respectively. e Field dependence of the Hall resistance Rxy at three representative temperatures (red lines are to guide the eye). f Experimental temperature dependence of the electron ne and hole nh densities (points, bottom and left axes), overlaid with the Fermi level dependence of ne and nh as calculated ab-initio (lines, top and right axes)
Temperature-driven inversion of the nonlinear magnetoresistance
Motivated by the strong temperature dependence of its other known transport properties5,17,18,19, we study in detail the NLMR of WTe2. Measurements of the φ-dependent R2ω at different temperatures (Supplementary Fig. 2) reveal that, upon lowering T from room temperature, the initially positive amplitude ΔR2ω undergoes a gradual reduction until it reaches zero at T ≈ 140 K, at which point it changes sign and progressively increases to large negative values as the temperature reduces. This behavior is shown in Fig. 2d, which is distinct from that of the linear MR (see Supplementary Fig. 1). We note that the inversion in R2ω occurs at a temperature close to that of the reported Lifshitz transition in bulk WTe218, where the Fermi surface topology changes. In order to evaluate changes of the electronic structure with temperature18,19, we measure the Hall resistance Rxy in Fig. 2e, which displays a gradual deviation from the linear field dependence at low temperatures. By fitting Rxy (H) according to a two-carrier model19, we extract the hole (electron) density, which increases (decreases) upon lowering the temperature (Fig. 2f). This is consistent with the strong sensitivity of the chemical potential to temperature changes in WTe25,18. As we show below, the temperature-driven changes in the chemical potential are reflected not only in variations of the size of the electron and hole pockets5,18, as schematically shown in the inset of Fig. 2d, but also in the convexity of the Fermi contours. The latter effect turns out to be crucial to drive the inversion of the NLMR.
Giant crystal anisotropy of nonlinear magnetoresistance
The strong local distortion of the W ions in the Td structure causes them to arrange along one-dimensional zigzag chains parallel to the a axis within each monolayer, and this imparts a strong electronic anisotropy3,5. To investigate its consequences in the NLMR R2ω, we pattern circular Hall devices as shown in Fig. 3a, in which currents can be applied along different crystallographic directions of the same WTe2 device. One of the current channels is chosen parallel to the a axis of WTe2 (Fig. 1a), as identified by polarized Raman spectra24 (see Supplementary Fig. 3). The longitudinal (linear) resistivity ρ is plotted in Fig. 3b and, as expected, is anisotropic with values along the a axis ~ 3 times lower than those along b25. The behavior of the second-harmonic R2ω is, however, more interesting as plotted in Fig. 3c for the four different directions of current flow. The magnitude of R2ω is much stronger along b compared to that of the a direction, with a b/a magnitude ratio ~18 at 2 K and ~5 at 300 K. Moreover, the sign-change in R2ω is also sensitive to the current direction in relation to the crystallographic axes: the sign inversion with temperature is clear when the current flows along the b axis, and inversion is absent when it flows parallel to a. We define χ = 2 R2ω/(Rω I H), which characterizes the NLMR under unit electric voltage and magnetic field shown in Fig. 3d, and note that χ reaches up to 0.04 and −0.22 Ω V−1 T−1 (or A−1 T−1) along the a and b directions at 2 K, respectively. Such a large anisotropy in the NLMR constitutes a record, and has not been observed in other materials6,7,9,10. The discovery of this giant anisotropy from a nonlinear magnetotransport perspective enriches our understanding of the anisotropic Fermi surface in WTe2 as we discuss below.
Crystal anisotropy of nonlinear magnetoresistance. a Optical image of a circular Hall bar device with a flake thickness of 13.6 nm with arrows indicating the a and b directions. b Temperature dependence of the channel resistivity ρ along different crystallographic directions. c, d Temperature dependence of the nonlinear magnetoresistance R2ω (at φ = 270°) normalized under unit current and magnetic field (c) and normalized under unit electric voltage and magnetic field (d) along different crystallographic orientations
Theoretical nonlinear charge current and Fermi surface. a Calculated longitudinal second-order current density \(J_{bb}^{(2)}\) versus Fermi level µ for current flowing along the b axis with a Zeeman energy of 0.1 meV. b, c Calculated Fermi surfaces of bulk WTe2 at µ = 0 and 120 meV, respectively, with three horizontal cuts shown underneath. ‘e’ and ‘h’ indicates the electron and hole pocket, respectively. Based on the result of Fig. 2f, these two chemical potentials correspond to T = 0 K and 300 K, respectively. d Temperature dependence of the ratio \(- J_{ii}^{(2)}/\left[ {J_{ii}^{(1)}} \right]^2 \propto \chi\) for the current applied along the a and b axes. The T axis takes into account both the thermal broadening by the Fermi-Dirac distribution and the Fermi level shift. e, f Variation of the calculated \(J_{bb}^{(2)}\) at 300 K with magnetic field angle φ (e) and with the field intensity at φ = 90° (f). Dashed lines are, respectively, the function sin(φ) and a linear fit to the calculated points. The above results in a–f are calculated based on the Wannier Hamiltonian of bulk WTe2, which reproduces the density functional theory (DFT) band structure shown in Fig. 1b. g The calculated second-order current density \(J_{bb}^{(2)}\) versus the Fermi level µ for the simplified quasi-bulk tight-binding model. h, i The energy dispersion and Fermi surfaces at µ = 200 and 75 meV, respectively, which correspond to the values marked by the vertical dashed lines in g. Calculated currents are presented in arbitrary units in all panels (Supplementary Note 1)
Theoretical modeling
To gain insight into the observed NLMR in WTe2, we calculated the longitudinal second-order current density, \(J_{xx}^{(2)}\), in the presence of an external magnetic field H perpendicular to E (Supplementary Note 1), and use the fact that \(J_{xx}^{(2)} \propto - R_{2\omega }\) (see Supplementary Note 2). The calculation relies on a Wannier tight-binding Hamiltonian that reproduces all the details of the DFT band structure of bulk WTe2 given in Fig. 1b, including the relative positions of hole and electron pockets, as well as the flat bands immediately below the Fermi energy that were discussed in ref. 5. It is important to note that, in semimetallic WTe2, the Fermi level µ is known to change by ~ 50 meV between 40 and 160 K18. To corroborate this, we have calculated the hole (nh) and electron (ne) densities at different µ (Supplementary Note 3), which are shown with the experimental ones in Fig. 2f. We establish the relation between T (bottom axis in Fig. 2f) and µ (top axis in Fig. 2f) by comparing the calculated ne and nh with the experimental data.
Figure 4a displays the dependence of calculated J(2) on µ at different temperatures for current flowing along the b direction. The sign of \(J_{bb}^{(2)}\) changes from positive to negative with increasing µ, and the inversion threshold is mostly insensitive to the thermal broadening. This indicates that the experimentally observed inversion in R2ω is primarily due to changes in the Fermi level. For a direct comparison, we plotted in Fig. 4d the calculated ratio \(J_{ii}^{(2)}/[J_{ii}^{(1)}]^2 \propto - \chi\) (Supplementary Note 2) versus T for the current along the a and b axes (i = a, b). The calculated result captures the overall qualitative behavior of the experimental data in Fig. 3d, with the sign inversion and large crystalline anisotropy. In addition, the theoretical J(2) in Fig. 4e reproduces the experimental sinusoidal dependence on φ (Fig. 2a), and the linearity of J(2) in Fig. 4f with respect to the magnetic field (Fig. 2c). Another significant implication from the calculations is that the sign inversion of \(J_{bb}^{(2)}\) is dominated by the electron carriers as can be seen from the carrier-resolved \(J_{bb}^{(2)}\) in Supplementary Fig. 4. This indicates that the electron pockets are responsible for the sign-change.
We now discuss the role of the Fermi surface topology to understand the non-trivial transport phenomena, NLMR in WTe2. The calculated Fermi contours are plotted in Fig. 4b, c at two Fermi levels associated with opposite J(2) in Fig. 4a. In addition to the suppression of hole pockets, we find a distinctive change in the three-dimensional (3D) convexity of the Fermi surface: the Fermi contours contain portions with a concave (CC) shape at µ = 0 (Fig. 4b), which evolves into entirely convex (CV) contours at µ = 120 meV (Fig. 4c). As J(2) is governed by both the local band velocity and curvature, the Fermi surface convexity should determine the sign of the nonlinear current. To further illustrate this characteristic observed consistently both in the experiments and the calculations, we build a simplified quasi-bulk model Hamiltonian26 based on symmetry (see Supplementary Fig. 7 and Supplementary Note 4). Reflecting what is seen in the DFT-derived band structure (Fig. 4b, c), this model yields electron pockets whose Fermi surface convexity changes with the chemical potential. We calculate \(J_{bb}^{(2)}\) based on this simpler, stripped-down Hamiltonian and see the same sign inversion at a threshold µ, as is clear from Fig. 4g. Moreover, the inversion threshold is directly correlated to the transition of the Fermi contour from CV to CC, as illustrated in Fig. 4h, i, whereas at low µ (Fig. 4i) the longitudinal dispersion is parabolic, at higher µ (Fig. 4h) it becomes shaped like a Mexican hat, a direct manifestation of the CC of the Fermi contour. Thus, it can be concluded that a transition from CV to CC is a necessary condition for the observation of a sign inversion in J(2), as intuitively expected from the analytical expression for \(J_{bb}^{(2)}\), which depends on the effective mass only along the b direction (see Supplementary Note 5).
This establishes the convexity of the Fermi surface as the driving mechanism behind the sign inversion in J(2) with temperature and indicates that the NLMR is a simple transport observable to electrically monitor the variation of the Fermi level with temperature in this system. Overall, our results confirm the critical role of topology and convexity of the Fermi surface on the exotic nonlinear magnetotransport of WTe2.
Discussion
In semimetallic WTe2, we have demonstrated that it exhibits a NLMR at room temperature, which is sensitive to temperature including a sign reversal, and strongly anisotropic. These properties critically depend on the Fermi surface morphology. In WTe2, the strong temperature dependence arises from an unusually large thermal shift of the chemical potential.
Nonlinear magneto-currents associated with strong SOC and Fermi surfaces with non-trivial spin textures are a nascent field of research. Here, we have shown the ability to control their magnitude, and especially their sign, with either magnetic fields, or temperature in WTe2. In addition, doping22, pressure27, electrostatic gating15,28,29, and film thickness30,31,32 are known to be effective to tune the Fermi surface of WTe2. Reducing the thickness was found to modify the electronic structure of WTe2 films32, and flakes with different thicknesses display different R2ω inversion temperatures (Supplementary Fig. 9). The extreme case of monolayer 1 T’-WTe2 was recently shown to be a two-dimensional topological insulator with an insulating bulk and a topologically non-trivial metallic edge26,33,34,35, although the nonlinear magnetotransport at the monolayer edge is still an open question. On the other hand, bulk WTe2 was predicted to be a type-II Weyl semimetal36, but the nonlinear magneto-response when the Fermi energy of a Weyl semimetal is tuned to the Weyl nodes remains unknown.
All these factors suggest ample space for further tunability and possibly even richer nonlinear, spin-dependent features in the charge and spin transport of WTe2. Moreover, changes in the topology and convexity of the Fermi surface are widely observed in other materials, such as the Dirac semimetal ZrTe537 and LaAlO3/SrTiO338 at the Lifshitz transition. Details of the Fermi surface are also very sensitive to the strength of SOC in Weyl semimetals of the transition metal monopnictide family39, such as TaAs40, TaP41, and NbP39. We anticipate the existence of a NLMR in these materials as well which, if confirmed, could establish this effect as a transport-only probe of topological and other types of Fermi surface transitions.
Methods
Sample preparation
WTe2 thin film flakes with different thicknesses were cleaved from a bulk WTe2 single crystal (HQ Graphene) by mechanical exfoliation onto a 300 nm Si/SiO2 substrate with alignment markers. Subsequently, a capping layer of SiO2 (4 nm) was deposited on them as a protection layer to eliminate material degradation during subsequent fabrication processes. Hall bar devices with a conventional rectangular (as well as radial multi-terminal) geometry were fabricated using the standard photolithography (E-beam lithography) method and Ar+-milling. Prior to the Cr (30 nm)/Au (60 nm) electrode deposition using magnetron-sputtering, the contact regions were treated with Ar+-etching to remove the SiO2. Ohmic contacts were confirmed by I–V measurements. The crystallographic direction of the current channel was confirmed by performing polarized Raman measurements with a misalignment < ± 5°. The flake thickness and surface morphology were measured by an atomic force microscope.
Electrical measurements
Hall bar devices were wire-bonded to a rotatable sample holder and installed in a physical property measurement system (PPMS, Quantum Design) for transport measurements in the temperature range 2–300 K. We performed the measurements of a.c. harmonic resistances using a Keithley 6221 current source and Stanford Research SR830 lock-in amplifiers. During the measurements, a constant amplitude sinusoidal current with a frequency of 21 Hz was applied to the devices, and the in-phase (0°) first harmonic Vω and out-of-phase (−90°) second-harmonic V2ω longitudinal voltage signals were measured simultaneously by two lock-in amplifiers.
Theoretical modeling
The starting point for our calculations of the carrier density (Fig. 2f) and nonlinear current (Fig. 4a–f) is the electronic band structure of bulk WTe2 obtained within DFT. From the ab-initio results, we obtain an accurate Wannier tight-binding Hamiltonian representation that describes the electronic structure of this system, and which is subsequently used in our transport-related calculations. We used the DFT-derived tight-binding that has been previously employed to predict Fermi arcs in this material in ref. 22. The observable transport properties are calculated from Boltzmann response theory using the tight-binding Hamiltonian (Supplementary Note 1). In order to isolate analytically the Fermi surface convexity as the underlying cause of the sign-change in the nonlinear MR, we also considered the effective k · p Hamiltonian dictated by symmetry for this system, as described in Supplementary Notes 4 and 5. The results shown in Fig. 4g–i have been obtained with this approximated Hamiltonian; all other calculations are based on the full DFT-derived tight-binding Hamiltonian.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotech. 7, 699 (2012).
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V. & Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mat. 2, 17033 (2017).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2. Nature 514, 205 (2014).
Cai, P. L. et al. Drastic pressure effect on the extremely large magnetoresistance in WTe2: quantum oscillation study. Phys. Rev. Lett. 115, 057202 (2015).
Pletikosić, I., Ali, M. N., Fedorov, A. V., Cava, R. J. & Valla, T. Electronic structure basis for the extraordinary magnetoresistance in WTe2. Phys. Rev. Lett. 113, 216601 (2014).
Ideue, T. et al. Bulk rectification effect in a polar semiconductor. Nat. Phys. 13, 578–583 (2017).
He, P. et al. Bilinear magnetoelectric resistance as a probe of three-dimensional spin texture in topological surface states. Nat. Phys. 14, 495–499 (2018).
Wakatsuki, R. & Nagaosa, N. Nonreciprocal current in noncentrosymmetric Rashba superconductors. Phys. Rev. Lett. 121, 026601 (2018).
He, P. et al. Observation of out-of-plane spin texture in a SrTiO3(111) two-dimensional electron gas. Phys. Rev. Lett. 120, 266802 (2018).
Yokouchi, T. et al. Electrical magnetochiral effect induced by chiral spin fluctuations. Nat. Commun. 8, 866 (2017).
Feng, B. et al. Spin texture in type-II Weyl semimetal WTe2. Phys. Rev. B 94, 195134 (2016).
Das, P. K. et al. Layer-dependent quantum cooperation of electron and hole states in the anomalous semimetal WTe2. Nat. Commun. 7, 10847 (2016).
Jiang, J. et al. Signature of strong spin-orbital coupling in the large nonsaturating magnetoresistance material WTe2. Phys. Rev. Lett. 115, 166601 (2015).
MacNeill, D. et al. Control of spin–orbit torques through crystal symmetry in WTe2/ferromagnet bilayers. Nat. Phys. 13, 300 (2016).
Wang, Y. et al. Gate-tunable negative longitudinal magnetoresistance in the predicted type-II Weyl semimetal WTe2. Nat. Commun. 7, 13142 (2016).
Li, P. et al. Evidence for topological type-II Weyl semimetal WTe2. Nat. Commun. 8, 2150 (2017).
Lv, Y. -Y. et al. Experimental observation of anisotropic Adler-Bell-Jackiw anomaly in Type-II Weyl semimetal WTe1.98 crystals at the quasiclassical regime. Phys. Rev. Lett. 118, 096603 (2017).
Wu, Y. et al. Temperature-induced Lifshitz transition in WTe2. Phys. Rev. Lett. 115, 166602 (2015).
Luo, Y. et al. Hall effect in the extremely large magnetoresistance semimetal WTe2. Appl. Phys. Lett. 107, 182411 (2015).
Dugdale, S. B. Life on the edge: a beginner’s guide to the Fermi surface. Phys. Scr. 91, 053009 (2016).
Zhou, Y. et al. Pressure-induced Td to 1T’ structural phase transition in WTe2. AIP Adv. 6, 075008 (2016).
Chang, T. -R. et al. Prediction of an arc-tunable Weyl Fermion metallic state in MoxW1−xTe2. Nat. Commun. 7, 10639 (2016).
Avci, C. O. et al. Unidirectional spin Hall magnetoresistance in ferromagnet/normal metal bilayers. Nat. Phys. 11, 570–575 (2015).
Kong, W. -D. et al. Raman scattering investigation of large positive magnetoresistance material WTe2. Appl. Phys. Lett. 106, 081906 (2015).
Zhao, Y. et al. Anisotropic magnetotransport and exotic longitudinal linear magnetoresistance in WT2 crystals. Phys. Rev. B 92, 041104 (2015).
Qian, X., Liu, J., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347 (2014).
Pan, X. -C. et al. Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805 (2015).
Fatemi, V. et al. Magnetoresistance and quantum oscillations of an electrostatically tuned semimetal-to-metal transition in ultrathin WTe2. Phys. Rev. B 95, 041410 (2017).
Zhang, E. et al. Tunable positive to negative magnetoresistance in atomically thin WTe2. Nano Lett. 17, 878–885 (2017).
MacNeill, D. et al. Thickness dependence of spin-orbit torques generated by WTe2. Phys. Rev. B 96, 054450 (2017).
Xiang, F. -X. et al. Thickness dependent electronic structure in WTe2 thin films. Phys. Rev. B 98, 035115 (2018).
Wang, L. et al. Tuning magnetotransport in a compensated semimetal at the atomic scale. Nat. Commun. 6, 8892 (2015).
Tang, S. et al. Quantum spin Hall state in monolayer 1T’-WTe2. Nat. Phys. 13, 683 (2017).
Fei, Z. et al. Edge conduction in monolayer WTe2. Nat. Phys. 13, 677 (2017).
Wu, S. et al. Observation of the quantum spin Hall effect up to 100 kelvin in a monolayer crystal. Science 359, 76–79 (2018).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495 (2015).
Zhang, Y. et al. Electronic evidence of temperature-induced Lifshitz transition and topological nature in ZrTe5. Nat. Commun. 8, 15512 (2017).
Nandy, S., Mohanta, N., Acharya, S. & Taraphder, A. Anomalous transport near the Lifshitz transition at the LaAlO3/SrTiO3 interface. Phys. Rev. B 94, 155103 (2016).
Liu, Z. K. et al. Evolution of the Fermi surface of Weyl semimetals in the transition metal pnictide family. Nat. Mater. 15, 27 (2015).
Xu, S. -Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Xu, S. -Y. et al. Experimental discovery of a topological Weyl semimetal state in TaP. Sci. Adv. 1, e1501092 (2015).
Acknowledgements
The work was partially supported by the National Research Foundation (NRF), Prime Minister’s Office, Singapore, under its Competitive Research Program (CRP award no. NRFCRP12-2013-01). Numerical calculations were performed at the HPC facilities of the NUS Center for Advanced 2D Materials.
Author information
Authors and Affiliations
Contributions
P.H., S.S. and H.Y. designed the experimental study. S.S. and P.H. fabricated devices, P.H. performed the transport measurements and analyzed the data. K.C., J.Y.W, Q.W. and G.E. helped in sample characterization. C.-H.H., V.M.P. and H.L. designed the theoretical methodology with C.H.H performing all the numerical calculations. All authors discussed the results. P.H., C.-H.H., V.M.P. and H.Y. wrote the manuscript. H.Y. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal Peer Review Information: Nature Communications thanks Prabhat Mandal, and other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
He, P., Hsu, CH., Shi, S. et al. Nonlinear magnetotransport shaped by Fermi surface topology and convexity. Nat Commun 10, 1290 (2019). https://doi.org/10.1038/s41467-019-09208-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-09208-8
This article is cited by
-
Observation and enhancement of room temperature bilinear magnetoelectric resistance in sputtered topological semimetal Pt3Sn
npj Spintronics (2024)
-
Observation of giant non-reciprocal charge transport from quantum Hall states in a topological insulator
Nature Materials (2024)
-
Strong modulation of carrier effective mass in WTe2 via coherent lattice manipulation
npj 2D Materials and Applications (2022)
-
Nonreciprocal charge transport up to room temperature in bulk Rashba semiconductor α-GeTe
Nature Communications (2021)
-
Room-temperature nonlinear Hall effect and wireless radiofrequency rectification in Weyl semimetal TaIrTe4
Nature Nanotechnology (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.