Abstract
Twisted bilayer graphene (tBLG) is a metallic material with two degenerate van Hove singularity transitions that can rehybridize to form interlayer exciton states. Here we report photoluminescence (PL) emission from tBLG after resonant 2-photon excitation, which tunes with the interlayer stacking angle, θ. We spatially image individual tBLG domains at room-temperature and show a five-fold resonant PL-enhancement over the background hot-electron emission. Prior theory predicts that interlayer orbitals mix to create 2-photon-accessible strongly-bound (~0.7 eV) exciton and continuum-edge states, which we observe as two spectral peaks in both PL excitation and excited-state absorption spectra. This peak splitting provides independent estimates of the exciton binding energy which scales from 0.5–0.7 eV with θ = 7.5° to 16.5°. A predicted vanishing exciton-continuum coupling strength helps explain both the weak resonant PL and the slower 1 ps−1 exciton relaxation rate observed. This hybrid metal-exciton behavior electron thermalization and PL emission are tunable with stacking angle for potential enhancements in optoelectronic and fast-photosensing graphene-based applications.
Similar content being viewed by others
Introduction
The interlayer orbital overlap in twisted bilayer graphene (tBLG) produce sharp optical absorption resonances that tune with the layer-stacking angle, θ1,2,3,4,5. Currently, there are two prevailing models explaining resonant light absorption in tBLG: the free-electron van Hove singularity (vHs) model, and the strongly bound-interlayer exciton model1,6. Figure 1b sketches the vHs model as two optically-allowed, degenerate transitions X13, and X24 between anticrossing regions of band-structure. This band-flattened region of tBLG has recently been associated with many surprising many-body electronic effects, such as exciton effects, θ-tunable superconductivity, and metal-insulator phase transitions6,7,8. In this work, we use 2-photon resonant excitation to find resonant PL emission from similar flattened-band interlayer states in tBLG.
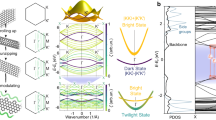
θ-tunable photoluminescence. a Setup for 2-photon PL microscopy on tBLG with filters passing E ≥ \(E_{X_S}\). The delayed pulse, t is used only for transient absorption confirmation of the exciton binding energy. b Anticrossing band regions give two degenerate interlayer vHs transitions, X13 and X24. In an exciton model (lower panel): rehybridized transitions give a symmetric, bright (XS) and a 2-photon accessible antisymmetric (XA) states. c PLE peaks (circles) tune with θ = 11.2°, 11.5°, and 16.3°, and suggests 2-photon states, XA lying δ-below dashed linear absorption peaks, XS
Near tBLG band-structure anticrossing regions, theory predicts strongly enhanced electron-hole interactions from interlayer orbital mixing6. The lower panel of Fig. 1b outlines this alternative bound-exciton model with the renormalized vHs labelled as unbound, degenerate exciton transitions, X13 and X24. Symmetric and antisymmetric mixing of these two transitions is predicted to yield hybridized interlayer exciton states; specifically, an optically bright state, XS and a strongly bound state, labeled XA. Using Bethe–Salpeter equation (BSE) simulations, Liang et al. predicted that the lower-lying exciton state, XA is strongly bound, optically dark with vanishing exciton to graphene continuum coupling strength, \(H_{X_A,k}\) (see Fig. 1b)6. To search for such optically dark interlayer exciton states in tBLG, we loosely assume parity-based optical selection rules from the hydrogenic exciton model and detect photoluminescence (PL) and excited-state absorption (ESA) signals generated via resonant 2-photon excitation9,10,11.
Using 2-photon PL, we can differentiate between the prevailing vHs model and the bound-interlayer exciton model in Fig. 1b. The vHs model for tBLG predicts only non-resonant hot-electron and blackbody PL emission because interlayer optical excitations thermalize rapidly (~10–20 fs) by the efficient electron-electron scattering in graphene12. We further estimate exciton binding energy, Eb using both 2-photon PL excitation (PLE) spectra and excited-state absorption (ESA) transient spectra methods. These figures of merit directly impact recent optoelectronic applications of tBLG such as chiral-light sensitive photosensors and light-induced metal-insulator phase transitions13,14.
Results
Weak θ-tunable interlayer PL emission
Non-resonant hot-electron and blackbody PL from both graphene and tBLG have been recently reported15,16. Unexpectedly, we observe PL emitted from tBLG domains after resonant 2-photon excitation. This weak emission is θ-tunable and independent of substrates and preparation method. To clearly observe resonant PL emission, we employ 2-photon excitation to remove the non-resonant scattering background with shortpass or bandpass optical filter stacks. The basic experimental setup showing a modified scanning confocal microscope is outlined in Fig. 1a. PL spatial maps and transient dynamics of single-domain tBLG were collected over our 0.3–1.8 eV laser tuning range. Both PL maps were acquired by raster scanning a ~1 μm wavelength-tunable laser spot across tBLG supported on silicon nitride or fused silica. The filtered 2-photon PL is collected with a back-illuminated electron-multiplying CCD camera or a photomultiplier tube (PMT) and lock-in amplifier.
Figure 1c (circles) plots PLE spectra collected after 2-photon excitation and the associated θ-tunable linear absorption spectra (dashed lines). The PLE spectrum is plotted after subtracting the non-resonant background signals such as blackbody emission15,16. Gaussian fits of the 2-photon PLE spectrum (solid lines) are peaked at XA ≅ 2.61, 1.73, and 1.67 eV for the 16.3°, 11.5°, and 11.2° domains, respectively. Selective 10 nm wide bandpass filters were applied to confirm that the resonant PL emission was centered near ~2.7, 2.1, and 2.0 eV respectively. The domain angles were assigned by 1-photon linear absorption spectra which spectrally overlap with the corresponding 2-photon PLE peaks in Fig. 1c. Like PLE, the linear absorption spectra tune with stacking angle, θ but are blue shifted by an energy δ. In Fig. 1c, the 2-photon PLE and 1-photon absorption peak energies have a splitting, δ that is θ-tunable, ranging from δ = 160 to 380 meV (see Table 1). The absorption spectra after background-subtraction (σtBLG − 2σG) are also used to assign the θ-orientation of the tBLG domains with about ±0.2° precision (see Supplementary Figs. 1–3)4.
2-photon PL spatial maps of tBLG domains
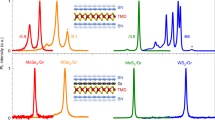
The PL and absorption spectra plotted in Fig. 1c were compiled from full-frame spatial maps collected over spectrally tuned 1- and 2-photon excitation energies. For example, Fig. 2a shows a linear absorption contrast map with the 18.3° domains resonantly excited4. Figure 2b shows the corresponding tBLG spatial PL map collected at 1.26 eV excitation to search for allowed 2-photons transitions. Strikingly, two 17.5° domains show a ~5× enhancement of PL relative to the background hot-electron PL from the neighboring tBLG domains in Fig. 2b. Contributions below 2.65 eV were removed with an OD >6 filter stack. Selective bandpass optical filtering confirmed that emission energy matches the 1-photon absorption XS resonance of the 17.5° domain at ~2.8 eV. This process showing resonant emission is detailed in Fig. 2c on 20 μm wide θ ~ 14° domain. This suggests that the resonant emission relies on electronic thermalization with the spectrally overlapping dark XA state, as sketched in Fig. 3a. This bright–dark state splitting δ, was >150 meV, making tBLG emission inherently very weak.
Maps of tBLG absorption and PL. a Linear absorption map taken at 2.9 eV excitation shows 20% resonant absorption enhancement of the 18.3° domains. b Scanning PL map of tBLG show resonant PL emission enhancement after 2-photon excitation (2 × 1.26 eV) of the 17.5° domains. The PL detection window is E > 2.65 eV. c PL emission wavelength is verified using bandpass filters to compare on-resonance PL (left, PL from XS) to off-resonance hot-PL (right) under identical excitation conditions
Interlayer exciton binding energy and PLE spectra. a Exciton model diagram showing emission of the XS state after 2-photon excitation of XA or continuum edge state, XS + Δ. b Spatial PL map of CVD tBLG shows enhanced emission from the 16.3° domain and adjacent spectrally overlapping 15.2° domains after 2-photon excitation at 2 × 1.3 eV. c Extended range 2-photon PLE spectrum (black squares) fits to bimodal Gaussian peaks straddling the 1-photon linear absorption spectrum (green line). The total peak splitting δ + Δ, suggests Eb ≅ 0.5 eV. (Inset) 3D PL map showing ~5× PL resonant enhancement of the θ = 16.3° domain
Verification of PL origin
To verify the signals in Figs. 1–3 are θ-tunable PL emitted from interlayer excitons, we must exclude any contributions or leaks from other resonantly-enhanced 2-photon scattering processes such as second harmonic generation (SHG) or 2-photon resonant Raman. 1-photon resonant Raman is well-documented in tBLG for G-band splitting with an energy of ~0.2 eV4,17. The unexpected Gaussian-like lineshapes of these early Raman studies provided the early clues that excitons may be involved in tBLG photophysics4,18,19. For Raman, the G-band spectral Stokes and anti-Stokes energies need to be a θ-independent3,20,21. However, our peak splitting energies vary strongly with θ from δ = 0.16–0.38 eV, ruling out a 2-photon resonant Raman signal origin.
Previously observed hot-electron PL was also excluded as the signal origin15. Such thermally drivenc emission produces a broadband blackbody emission spectrum, whereas we show in Figs. 2b and 3b that there is a ~5× PL enhancement over the non-resonant background signal collected from bilayer graphene. In Fig. 2c, we show that the PL emission collected with resonant vs. non-resonant bandpass (BP) filters give starkly contrasting emission instensity for large θ = 14° domain after resonant excitation. We conclude the majority of the photons are emitted resonantly rather than hot-electron or blackbody emission. Further examples of PL maps are in the Supplementary Figs. 3–5.
Both resonant 2-photon PL and transient absorption (TA) signals show a counter-intuitive linear trend with laser fluence. This trend is expected based on our concurrently measured 1-photon spectra showing clear square root (\(\sqrt n\)) pump-fluence dependence on carrier density, n (see Supplementary Fig. 7 for detailed fluence-dependent measurements). This square root is functionally distinct from graphene’s sub-linear Fermi-filling dependence22. Instead, \(\sqrt n\) results from Auger or exciton–exciton annihilation. The net result requires a linear 2-photon PL flux-dependence, \(I(n_{2ph}) \propto \sqrt {n_{2ph}^2}\) where n2ph is proportional to the incident laser flux, which is typically 2 × 1014 photons/cm2 during 2-photon PL collection. As a control, we show in the supplement that our setup in Fig. 1a gives the typical 2-photon PL quadratic (I ∝ \(n_{2ph}^2\)) pump-power dependence when CdSe quantum dots were measured under identical experimental conditions. We further confirmed that the 1-photon TA signal in tBLG has a clear square root dependence, \(I(n_{1ph}) \propto \sqrt {n_{1ph}}\) (see Supplementary Fig. 8)23,24. Very similar trends are reported for closely analogous materials such as carbon nanotubes (CNTs)24,25,26,27,28,29. This fluence dependence shows evidence that resonantly excited interlayer carriers undergo exciton–exciton annihilation.
Estimates of interlayer exciton binding energy, E b
Using established 2-photon PL and intraband TA methods, we estimate Eb in resonantly excited tBLG10,11. Figure 3a shows how we measured Eb by expanding our energy range to include higher-lying 2-photon states predicted to cluster near the continuum edge for a hydrogenic exciton model. Upon 2-photon excitation at energy, Δ above the XS absorption resonance with Epump2, the carriers will relax to the lower-lying dark state XA. 2-photon excitation at either Epump1 or Epump2 results in PL emission from the bright XS state as the dark XA and XS state in Fig. 3c overlap spectrally. This bright–dark state splitting, δ quenches PL emission. A similar low-lying dark state is also thought to quench PL in CNTs30.
Figure 3b plots the 2-photon PL microscopy map of tBLG domains grown by chemical vapor deposition (CVD) and subsequently transferred to silicon nitride. Similar to the single-layer dry transfer tBLG in Fig. 2, we also show resonantly-enhanced PL (localized to the 16.3° domain). A partially overlapping absorption resonance results in the similarly stacked 15.2° domain emitting slightly-weaker PL. In Fig. 3c, the PLE spectral fits (magenta lines) for the 16.3° domain shows a bimodal distribution with two peaks spanning the 2.76 eV (green) absorption resonance at 2.61 and 3.10 eV. This spectral splitting energy is Δ ~ 0.34 eV, and this 2-photon PLE peak has almost twice the spectral width compared to the XS or XA peaks. This peak broadening may imply continuum edge mixing, suggesting we can estimate a lower bound for the exciton binding energy as Eb ≅ δ + Δ = 0.51 eV for the 16.3° domain shown. We summarize the θ–dependent peak splitting and Eb estimates in Table 1 below:
Verifying E b using ultrafast intraband ESA
The hot-electron vHs model in Fig. 1b has sufficiently predicted scattering resonances in Raman and circular dichroism2,19,31,32. For example,scattering in tBLG Raman and ARPES experiments do not optically populate interlayer excitons. Resonant PL emission is not conventionally observed for metallic materials because of strong screening of electron-hole pair interactions, and fast thermalization with continuum states. For resonant optical absorption, strong electron-hole interactions are already well-accepted in graphene-based systems. For example in single-layer graphene, there is ~0.4 eV red-shift in the absorption resonance about the M saddle-point owning to band renormalization from strong exciton effects33,34. Likewise, Ju et al. recently showed that 0° Bernal stacked bilayer graphene enables a bandgap of strongly bound interlayer excitons under high-fields and low-temperatures8. 1D metallic CNTs also have bound excitons with Eb ≥ 50 meV35,36.
Pump-probe kinetic studies and lineshape analysis of absorption and Raman spectra offered the early experimental motivation to search for interlayer exciton states in tBLG6,17,23. BSE simulations by Liang et al. support a strongly bound-exciton model for tBLG6. Theory simulates that the bound-exciton state, XA has effectively zero electronic coupling with the lower metallic graphene continuum states6. Historically, such dark exciton states with \(H_{X_A,k}\) = 0 (see Fig. 1b), have been termed ghost Fano resonances and observed in selected systems including some quantum dots6,23,37.
In Fig. 4, we plot the transient spectra and exciton relaxation dynamics of a 7.9° tBLG domain by raster scanning two collinear ~160 fs pump and probe pulses. By measuring the differential TA of the probe pulse, we plot the full transient spectra at t = 0.5 ps in Fig. 4b. The corresponding relaxation kinetics are shown in Fig. 4c. To spectrally resolve the intraband exciton transition (dashed blue arrows in Fig. 4a), the pump beam was optically resonant at \(E_{X_S}\) = 1.54 eV and the near-IR probe energy was scanned from 0.4–1.2 eV. The dynamics intrinsic to the interlayer states are isolated by subtracting the graphene 0° bilayer TA contribution (ΔσB) from the tBLG TA response (ΔσT) for both Fig. 4b, c4.
TA spectrum estimates of exciton binding energy. a Two measures methods of Eb, blue arrows: pump XS, with probe ESA to intraband exciton band-edge states near the e-h continuum. gray arrows: 2-photon pump, probe at XS. (right inset) Equivalent experiments in a vHs model. b Blue and gray TA spectra independently estimate Eb at ~0.7 eV for θ = 7.9°. tBLG absorption spectra is in green. c Interlayer relaxation kintetics for both intraband and interband probe are delayed relative to the faster thermalization rate of 0° bilayer graphene shown in gray
Transient spectra in Fig. 4b provide a secondary, independent estimate of Eb. In analogous systems like CNTs, the exciton binding energy is estimated by an ESA spectrum of intraband exciton state transitions (see Fig. 4a, blue arrow)38. ESA transient absorption microscopy uses a NIR probe pulse to promote an exciton to the continuum band edge. The 2-photon selection rules are relaxed as this is an intraband transition within an exciton band of states11. In Fig. 4b, the TA spectrum (blue circles) is positively peaked at 0.7 eV, an ESA response. This suggests an intraband transition to the continuum edge-states illustrated in Fig. 4a, and that Eb ~ 0.7 eV for θ = 7.9° tBLG.
We verified the intraband ESA estimate of Eb by checking it with 2-photon TA microscopy (gray circles). Specifically, we scanned the 2-photon pump energy across the XA and XS + Δ state regions and probed the transient interband optical conductivity of the bright state XS. The resulting 2-photon absorption spectrum is shown in Fig. 4b (gray line). Two ground state bleach peaks are centered at 1.18 and 1.82 eV (gray line) and they straddle the 1-photon absorption peak at 1.54 eV (green line). Like the PLE in Fig. 3, the binding energy is estimated by the peak splitting, δ + Δ ≅ 0.69 meV. Both measurements methods shown in blue and gray in Fig. 4c gaive very similar estimates of Eb. Our θ-tunable exciton binding energies are summarized in Table 1 and they are similar to the theoretically simulated binding energy value of 0.7 eV for a 21° tBLG domain6. Such large values from Eb are comparable to analogous semiconducting 1D and 2D excitonic materials36,39,40,41,42.
Delayed thermalization of interlayer excitons
Lastly, we measure the interlayer carrier lifetimes in tBLG. In Fig. 4c, a least squares method is used to fit the decay of blue line to obtain an intraband lifetime of 1.05 ps that we associate with the exciton lifetime XA. The resonant interband (green line) tBLG carrier relaxation dynamics have been previously reported23. Comparing the two TA decay rates plotted in Fig. 4c (after subtraction of the much weaker, non-resonant 0° TA graphene response, ΔσB), we note the absence of the fast initial electronic thermalization component typical for graphene (gray line). This suggests that interlayer XA excitons may thermalize by exciton–exciton or exciton-phonon assisted processes, rather than by scattering from the electronic continuum22. Our observations of delayed thermalization of resonantly excited interlayer carriers for both the interband and the intraband kinetics supports the theoretical prediction that the bound-exciton has weak coupling to metallic continuum state (\(H_{X_A,k} \cong 0\))6. Long lifetimes and predicted weak exciton-continuum coupling both suggests interlayer excitons may thermalize slower than they would in single-layer graphene.
Discussion
In summary, we observe resonant, θ-tunable emission of PL upon direct 2-photon excitation of tBLG interlayer electronic states. Assuming hydrogenic exciton selection rules loosely apply, two-photon excitation was employed to optically excite dark exciton states10. Figures 2 and 3 show a ~5x resonant PL enhancement that we justify using a strongly bound-interlayer exciton model. This observation of resonant PL conflicts with the vHs model, as here electrons will thermalize rapidly to lower metallic continuum states by electron-electron scattering. Both CVD bilayer growths and dry-transferred stacked tBLG show similar PL emission in Figs. 2 and 3 for both the silicon nitride and fused silica substrates used. The PL is not surface quenched, suggesting it is emitted from protected interlayer electronic states.
As a 2D metal, tBLG interlayer excitons differ from excitons in similar materials like CNTs. For 2D metallic systems, unbound excitonic effects near the graphene M-point are well-known31,32. For tBLG, we suggest excitation of bound excitons are possible by mixing the two degenerate interlayer Fano resonances illustrated in Fig. 1b. Our estimates of the tBLG exciton binding energies are summarized in Table 1. We obtained Eb, from the spectral peak splitting in both near-IR intraband TA and 2-photon PLE microscopy. The exciton binding energy scales with θ increasing from ~0.5 eV at 16.3° to 0.69 at 7.9°. This first measurement of Eb agrees with ~0.7 eV predictions from prior theory6. BSE theory predicts zero exciton-continuum coupling after the two interlayer degenerate transitions rehybridize. In accord, Fig. 4c (blue line) shows that interlayer excitons have much slower thermalization rate compared to 0° bilayer graphene (gray line). The ability to optically prepare interlayer excitons suggests tBLG is a 2D hybrid material with bound excitons coexisting alongside the metallic continuum states before decaying on a ~1.1 ps timescale. This unusual metal-exciton character of tBLG may enable stacking angle tunable materials applications from optically induced metal-insulator transitions to efficiency enhancements in graphene photosensing.
Methods
tBLG sample characterization
PL was observed from tBLG prepared both by CVD and the manual layer stacking by the dry transfer method43,44. The substrates were silicon nitride and fused silica and measurements were generally performed in ambient under a continuous nitrogen purge. 2-photon PL was observed for both the stacking methods and substrates used. The stacking angles of individual tBLG domains were assigned primarily with hyperspectral linear absorption microscopy after subtraction of the non-resonance graphene background (σG)4. θ–stacking assignments were further verified by transient absorption (TA) and dark-field TEM5,17,23.
2-photon PL measurements
For the 2-photon PL and interband ESA measurements, we use a Coherent Chameleon (80 MHz, 140 fs) pumping an APE Compact optical parametric oscillator (OPO) with wavelength range 680–4000 nm. For the 2-photon PL microscopy measurements, the pump beam was generated by the OPO. The beam is then raster scanned by the piezo-scanning mirror and the 1-photon back reflection off the sample on an InGaAs detector provided a way to map the 2-photon and 1-photon responses concurrently. Total beam flux was 2 to 4 × 1014 photons/cm2. The emitted photoluminescence was measured with a TE cooled, back-illuminated EMCCD camera (ProEm HS, Princeton Instruments, 95% QE) and a Hamamatsu Si PMT as a secondary detection confirmation (with lock-in amplifier). To exclude scattered laser light from Rayleigh, Raman and residual second harmonic generation (SHG), collection of photons with energy less than twice the 2-photon excitation energy were excluded, calibrated Chroma or Thorlabs shortpass and bandpass optical filters stacks were used in front of the camera for emission detection to maintain an OD > 6 blockage throughout. All the measurements were performed at 295 K unless specified, in a nitrogen-purged box to minimize the chance of sample damage by oxidation.
ESA and 2-photon transient absorption spectra
ESA TA experiments were used to probe intraband exciton transitions (Fig. 4, blue lines) using confocal transient absorption microscopy23. The pump beam was modulated at 1 MHz with an AO-modulator. Pump fluences were on average at ~1014 photons/cm2 with fluence dependence showing a square root exciton–exciton annihilation trend (see Supplementary Figs. 7 and 8).
Rigorous power normalization curves were taken in-situ for all spectrally resolved measurements. This includes the microscope objective transmission corrections, the spectral response of the detection system, and spectral characteristics of the optical filters were taken into account for each wavelength.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Li, G. et al. Observation of van hove singularities in twisted graphene layers. Nat. Phys. 6, 109113 (2010).
Luican, A. et al. Single-layer behavior and its breakdown in twisted graphene layers. Phys. Rev. Lett. 106, 126802 (2011).
Wu, J.-B. et al. Resonant raman spectroscopy of twisted multilayer graphene. Nat. Commun. 5, 5309 (2014).
Havener, R. W., Zhuang, H., Brown, L., Hennig, R. G. & Park, J. Angle-resolved raman imaging of interlayer rotations and interactions in twisted bilayer graphene. Nano Lett. 12, 3162–3167 (2012).
Havener, R. W. et al. Hyperspectral imaging of structure and composition in atomically thin heterostructures. Nano Lett. 13, 3942–3946 (2013).
Liang, Y. et al. Strongly bound excitons in gapless two dimensional structures. Phys. Rev. B 90, 115418 (2014).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Ju, L. et al. Tunable excitons in bilayer graphene. Science 358, 907910 (2017).
Cao, T., Wu, M. & Louie, S. G. Unifying optical selection rules for excitons in two dimensions: band topology and winding numbers. Phys. Rev. Lett. 120, 087402 (2018).
Wang, F., Dukovic, G., Brus, L. E. & Heinz, T. F. The optical resonances in carbon nanotubes arise from excitons. Science 308, 838841 (2005).
Wang, J., Graham, M. W., Ma, Y., Fleming, G. R. & Kaindl, R. A. Ultrafast spectroscopy of midinfrared internal exciton transitions in separated single-walled carbon nanotubes. Phys. Rev. Lett. 104, 177401 (2010).
Kim, R., Perebeinos, V. & Avouris, P. Relaxation of optically excited carriers in graphene. Phys. Rev. B 84, 075449 (2011).
Cao, Y. et al. Correlated insulator behaviour at halffilling in magic-angle graphene superlattices. Nature 556, 8084 (2018).
Kim, C.-J. et al. Chiral atomically thin films. Nat. Nanotechnol. 11, 520–524 (2016).
Alencar, T. V. et al. Twisted bilayer graphene photoluminescence emission peaks at van hove singularities. J. Phys. Condens. Matter 30, 175302 (2018).
Lui, C. H. et al. Ultrafast photoluminescence from graphene. Phys. Rev. Lett. 105, 127404 (2010).
Havener, R. W., Liang, Y., Brown, L., Yang, L. & Park, J. Van hove singularities and excitonic effects in the optical conductivity of twisted bilayer graphene. Nano Lett. 14, 3353–3357 (2014).
Carozo, V. et al. Resonance effects on the raman spectra of graphene superlattices. Phys. Rev. B 88, 085401 (2013).
Ni, Z. et al. G-band raman double resonance in twisted bilayer graphene: evidence of band splitting and folding. Phys. Rev. B 80, 125404 (2009).
Jorio, A. et al. Optical-phonon resonances with saddlepoint excitons in twisted-bilayer graphene. Nano Lett. 14, 5687–5692 (2014).
Souza Filho, A. et al. Stokes and anti-stokes raman spectra of small-diameter isolated carbon nanotubes. Phys. Rev. B 69, 115428 (2004).
Graham, M. W. et al. Transient absorption and photocurrent microscopy show that hot electron supercollisions describe the rate-limiting relaxation step in graphene. Nano Lett. 13, 54975502 (2013).
Patel, H. et al. Tunable optical excitations in twisted bilayer graphene form strongly bound excitons. Nano Lett. 15, 5932–5937 (2015).
Ma, Y.-Z. et al. Ultrafast carrier dynamics in singlewalled carbon nanotubes probed by femtosecond spectroscopy. J. Chem. Phys. 120, 3368–3373 (2004).
Wang, F., Dukovic, G., Knoesel, E., Brus, L. E. & Heinz, T. F. Observation of rapid auger recombination in optically excited semiconducting carbon nanotubes. Phys. Rev. B 70, 241403 (2004).
Wang, F., Wu, Y., Hybertsen, M. S. & Heinz, T. F. Auger recombination of excitons in one-dimensional systems. Phys. Rev. B 73, 245424 (2006).
Sun, D. et al. Observation of rapid exciton–exciton annihilation in monolayer molybdenum disulfide. Nano Lett. 14, 5625–5629 (2014).
Mouri, S. et al. Nonlinear photoluminescence in atomically thin layered wse 2 arising from diffusion-assisted exciton-exciton annihilation. Phys. Rev. B 90, 155449 (2014).
Yan, T., Yang, S., Li, D. & Cui, X. Long valley lifetime of free carriers in monolayer wse2. Phys. Rev. B 95, 241406 (R) (2017).
Srivastava, A., Htoon, H., Klimov, V. I. & Kono, J. Direct observation of dark excitons in individual carbon nanotubes: Inhomogeneity in the exchange splitting. Phys. Rev. Lett. 101, 087402 (2008).
Kim, K. et al. Raman spectroscopy study of rotated double-layer graphene: misorientation-angle dependence of electronic structure. Phys. Rev. Lett. 108, 246103 (2012).
Ni, Z., Wang, Y., Yu, T., You, Y. & Shen, Z. Reduction of fermi velocity in folded graphene observed by resonance raman spectroscopy. Phys. Rev. B 77, 235403 (2008).
Mak, K. F., Shan, J. & Heinz, T. F. Seeing many-body effects in single- and few-layer graphene: observation of two-dimensional saddle-point excitons. Phys. Rev. Lett. 106, 046401 (2011).
Chae, D.-H. et al. Excitonic fano resonance in freestanding graphene. Nano Lett. 11, 1379–1382 (2011).
Spataru, C. D., Ismail-Beigi, S., Benedict, L. X. & Louie, S. G. Excitonic effects and optical spectra of single-walled carbon nanotubes. Phys. Rev. Lett. 92, 077402 (2004).
Wang, F. et al. Observation of excitons in onedimensional metallic single-walled carbon nanotubes. Phys. Rev. Lett. 99, 227401 (2007).
Guevara, M., Claro, F. & Orellana, P. Ghost Fano resonance in a double quantum dot molecule attached to leads. Phys. Rev. B 67, 195335 (2003).
Zhou, Y. et al. Probing dark excitons in atomically thin semiconductors via near-field coupling to surface plasmon polaritons. Nat. Nanotechnol. 12, nnano.2017.106 (2017).
Deslippe, J., Spataru, C. D., Prendergast, D. & Louie, S. G. Bound excitons in metallic single-walled carbon nanotubes. Nano Lett. 7, 1626–1630 (2007).
Ma, Y.-Z., Valkunas, L., Bachilo, S. M. & Fleming, G. R. Exciton binding energy in semiconducting single-walled carbon nanotubes. J. Phys. Chem. B 109, 15671–15674 (2005).
Hanbicki, A., Currie, M., Kioseoglou, G., Friedman, A. & Jonker, B. Measurement of high exciton binding energy in the monolayer transition-metal dichalcogenides ws 2 and wse 2. Solid State Commun. 203, 16–20 (2015).
Ye, Z. et al. Probing excitonic dark states in single layer tungsten disulfide. Nature 513, 214–218 (2014).
Li, X. et al. Large-area graphene single crystals grown by low-pressure chemical vapor deposition of methane on copper. J. Am. Chem. Soc. 133, 2816–2819 (2011).
Brown, L. et al. Polycrystalline graphene with single crystalline electronic structure. Nano Lett. 14, 5706–5711 (2014).
Acknowledgements
This research was supported by the Spectroscopy Society of Pittsburgh and AFOSR (FA 9550-10-1-0410) grant.
Author information
Authors and Affiliations
Contributions
The experiment was performed by H.P. Twisted bilayer graphene was grown by L.H., C.-J.K. and J.P. Data analysis was performed by H.P. and M.G. Manuscript was written by H.P. and M.G.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks Marcos Pimenta and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Patel, H., Huang, L., Kim, CJ. et al. Stacking angle-tunable photoluminescence from interlayer exciton states in twisted bilayer graphene. Nat Commun 10, 1445 (2019). https://doi.org/10.1038/s41467-019-09097-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-09097-x
This article is cited by
-
Waveguide-integrated twisted bilayer graphene photodetectors
Nature Communications (2024)
-
Nonlinear physics of moiré superlattices
Nature Materials (2024)
-
In-situ twistable bilayer graphene
Scientific Reports (2022)
-
Electronic Thermal Properties of Twisted Bigraphene
Russian Physics Journal (2022)
-
Enhanced third-harmonic generation by manipulating the twist angle of bilayer graphene
Light: Science & Applications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.