Abstract
The thermoelectric effect is attracting a renewed interest as a concept for energy harvesting technologies. Nanomaterials have been considered a key to realize efficient thermoelectric conversions owing to the low dimensional charge and phonon transports. In this regard, recently emerging two-dimensional materials could be promising candidates with novel thermoelectric functionalities. Here we report that FeSe ultrathin films, a high-Tc superconductor (Tc; superconducting transition temperature), exhibit superior thermoelectric responses. With decreasing thickness d, the electrical conductivity increases accompanying the emergence of high-Tc superconductivity; unexpectedly, the Seebeck coefficient α shows a concomitant increase as a result of the appearance of two-dimensional natures. When d is reduced down to ~1 nm, the thermoelectric power factor at 50 K and room temperature reach unprecedented values as high as 13,000 and 260 μW cm−1 K−2, respectively. The large thermoelectric effect in high Tc superconductors indicates the high potential of two-dimensional layered materials towards multi-functionalization.
Similar content being viewed by others
Introduction
Two-dimensional (2D) materials are expanding their arena in terms of richness in material type, properties, and functions, which range from electronic devices to catalysts and medicines1,2. Thermoelectric generation is one of the physical functions in which 2D materials are anticipated to be superior in comparison with their bulk counterparts. The density of states (DOS) in 2D semiconductors is considerably different from that of three-dimensional (3D) materials at the band edge singularity3. As the Seebeck coefficient α is related to the profile of the DOS at the Fermi energy, 2D or low dimensional structures are considered to be advantageous for enhancing thermoelectric performance. Such a concept was proposed originally for semiconductor quantum wells and superlattices;4 however, recently emerging 2D-layered materials provide naturally formed atomic layers and their hetero-structures5, which are an ideal platform to elicit their intrinsic 2D nature. For characterization of thermoelectric properties of nanomaterials, on-chip device measurements have been often utilized6,7,8. Although the device configuration used for the measurements is not directly adapted to practical applications, it is highly powerful for realizing ideal conditions including the structures free from significant disorder and the tunable carrier density and thus for elucidating the intrinsic performance of materials. This method also fits the thermoelectric characterization of 2D materials in the present study.
The performance of thermoelectric semiconductors is measured by the figure of merit ZT = α2Τ/ρκ (where ρ is the electrical resistivity, κ is the thermal conductivity, and T is the absolute temperature). Therefore, materials with the large power factor α2/ρ can be candidates for high ZT. In order to maximize α2/ρ, we propose to extensively investigate recent 2D layered materials. In addition to the possible enhancement of the Seebeck effect in 2D DOS, an important characteristic of the recent 2D materials is their excellent crystallinity, which is preferable for keeping a large conductivity even in nano-thick monolayers.
For our purpose, 3d transition-metal-based compounds should be more favorable than 4d and 5d counterparts because the wave functions of 3d-based compounds are more localized, generally causing a larger effective mass m* and thus the larger DOS. Among 3d-based materials, we chose FeSe, first because a relatively large m* ranging from 2 to 4 me has been reported in heavily electron-doped regions9,10, where me is the free electron mass. The physical properties of ultrathin FeSe have attracted much attention because of the appearance of the unexpected high-Tc superconducting phase by reducing the film thickness down to a monolayer, the Tc of which reaches 65 K11,12 or 100 K13. Surprisingly, the high conductivity value survives even in monolayer FeSe;11,14,15 this is in stark contrast to conventional semiconductor thin films, where the resistance increases with reducing the thickness.
Here we report simultaneous measurements of α and ρ while controlling the thickness d of FeSe films on SrTiO3 (001) substrates in an electric double-layer transistor configuration16. In previous studies, we succeeded in optimization of α2/ρ with controlling n through the gate bias VG and applied this technique to various materials16 (see Methods). When VG is applied at ~220 K, which is just above the glass transition temperature of the ionic liquid used in this study (see Methods), the cations or anions are self-aligned on the surface of FeSe; thus, charge carriers are electrostatically accumulated to form the electric double layer17,18. On the other hand, when a certain level of VG is applied at higher temperatures such as ~245 K or above, an electrochemical reaction takes place at the liquid–solid interface, and the topmost FeSe layer dissolves into the ionic liquid in a pseudo layer-by-layer manner15. Therefore, systematic investigation of the thermoelectric properties from bulk to ultrathin FeSe now becomes possible at a wide temperature range from 10 K to around room temperature. We found that the thermoelectric effect is dramatically enhanced with reducing d down to ~1 nm and thermoelectric power factor at 50 K and room temperature reach unprecedented values as high as 13,000 and 260 μW cm−1 K−2, respectively. The coexistence of giant thermoelectric power factor and high-Tc superconductivity indicates the high potential of 2D layered materials towards multi-functionalization.
Results
Electrochemically enhanced Seebeck effect in FeSe thin film
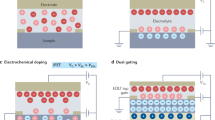
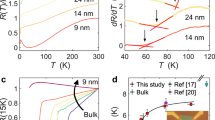
Dimensionality is a possible key factor to induce the evolution of the thermoelectric response owing to the characteristic DOS (Fig. 1a, b). The electric double layer transistor configuration shown in Fig. 1c enables us to control the film thickness d through the electrochemical etching on the surface of the FeSe films (Fig. 1d). Figure 2a shows the thermoelectric voltage ΔV as a function of the temperature difference ΔT between two thermocouples (see Fig. 1c) in Sample A at VG = 5 V. Here, it is noted that the application of VG not only induces the electrochemical etching of the thin films but also accumulates the electron carriers on the top surface. The thermoelectric measurement was done at 200 K; possible conduction paths through the ionic liquid are completely eliminated. The device was cooled down to 200 K for the measurement at each thickness d after electrochemical etching at higher temperatures15. All the ΔV plots for different d’s linearly depended on ΔT, securing the accurate characterization of the Seebeck effect. At 200 K, ΔV was dramatically enhanced across the sign change with decreasing d from ~18 nm to ~1 nm. Figure 2b plots the d dependence of α (= −ΔV/ΔT) at 200 K for VG = 5 V. A very small α of +3.8 μV K−1 at d ~18 nm is consistent with the reported values on bulk FeSe19,20, where such a small α value reflects the semimetallic electronic structure21. With the thickness reduction, on the other hand, the absolute value of α was surprisingly enhanced by two orders of magnitude up to |−454 μV K−1|.
Schematic device structure for thermoelectric measurement. a Schematic illustration of the electronic density of states (DOS) for three-dimensional (3D) and two-dimensional (2D) electrons. b The large effective mass m* enhances the DOS, which is favorable to the enhancement of the Seebeck effect. c Device structure for thermoelectric measurement. VSD and VG stand for the source (S)−drain (D) voltage and the gate bias voltage, respectively. When VG is applied to the Pt plate, ions in the ionic liquid are redistributed, forming an electric double layer on the surface of the FeSe film. d Enlarged illustration of the ionic liquid/FeSe interface. Under the positive gate bias, N,N-diethyl-N-(2-methoxyethyl)-N-methylammonium cations, DEME + , align on the surface of FeSe. The thickness d of the FeSe thin film was tuned by electrochemical etching15. See Methods for details of the device structure and fabrication
Thinning-induced enhancement of thermoelectric effect. a Thermoelectric voltage ΔV under temperature difference ΔT in an FeSe thin film, Sample A. The thermoelectric measurements were performed at 200 K with VG = 5 V. The value of ΔV changed its sign and dramatically increased with decreasing thickness d from ~18 nm to ~1 nm. b Thickness d dependence of the Seebeck coefficient α. The values of α were estimated from the slope of the ΔV−ΔT plot in a as α = −ΔV/ΔT. The inset shows the temperature T dependence of the normalized sheet resistance ρ2D with respect to 200 K. Superconductivity appeared when VG = 5 V was applied. c Variation of sheet resistance ρ2D200 K at 200 K as a function of d. The value of ρ2D200 K for VG = 5 V showed a weak d dependence (blue circles), whereas that for VG = 0 V increased with decreasing d (gray circles). d Thickness d dependence of thermoelectric power factor α2/ρ exhibiting anomalous enhancement in the ultrathin limit. Here, ρ is the electrical resistivity, which is estimated as ρ = ρ2D × d. The value of α2/ρ at 200 K in the thick region is comparable to that in bulk FeSe19, whereas α2/ρ increased with decreasing d because of the double-digit increase of α in ultrathin regions in b. The error bar of d corresponds to ~ ± 0.5 nm, which was estimated from the surface roughness of the initial thin film15
It should be noted that the parasitic conduction of the SrTiO3 substrate is ruled out because the gate electric field on SrTiO3 through the FeSe thin films is negligible in the present configuration owing to the screening effect in the metallic conducting FeSe and also the formation of the Schottky barrier at the FeSe/SrTiO3 interface22,23,24 (see Supplementary Figure 1, Supplementary Figure 2, and Supplementary Note 1). The existence of an oxygen deficient layer at the surface of SrTiO3 substrate as a source of the large Seebeck response is also definitely ruled out as the large α is observed only under gate bias and is suppressed to bulk-like small values by switching off VG to 0 V, as seen in the main panel of Fig. 2b. Importantly, the high-Tc superconductivity appears by applying VG = 5 V and disappears by removing VG15,17,18, as shown in the inset of Fig. 2b. The simultaneous emergence of the giant thermoelectric response and the high-Tc superconductivity proves that these two transport properties arise from the same electronic state of FeSe thin films.
Another noticeable feature of FeSe thin films is the low electrical resistance realized even in ultrathin regions. Figure 2c shows the 2D sheet resistance ρ2D of Sample A for VG = 0 V (gray circles) and 5 V (blue circles) as a function of d. When starting from the initial state with d ~18 nm, the sheet resistance at 200 K, ρ2D200 K, first increased with decreasing d for both VG = 0 V and 5 V. With further decreasing d, ρ2D200 K at VG = 5 V showed a small peak at around d ~11 nm and kept small values down to d ~1 nm because the gated topmost layer of FeSe and the charge transfer layer at the FeSe/SrTiO3 interface dominate the electrical transport of the thin film (see Supplementary Figure 3 and Supplementary Note 2 for the details of the d dependence of ρ2D200 K). Such a low electrical resistance irrespective of the film thickness is consistent with the previous studies; for example, the resistivity of monolayer or few layer MBE-grown FeSe11,14 is comparable to that of 10 nm thick (~15 layers) FeSe17,18 owing to the interface or surface electron doping. Actually, ρ2D200 K ~1 kΩ at VG = 5 V in the thin limit (Fig. 2c) is close to that in doped FeSe monolayers11,14,15. On the other hand, the small α and high ρ2D200 K at VG = 0 V indicate that the charge transfer layer does not produce the enhanced values of α. Consequently, the thermoelectric power factor α2/ρ at 200 K achieved a dramatic development in Fig. 2d owing to the enhancement of α and the concomitant reduction of electrical resistivity ρ = ρ2D × d, which rarely occurs in the framework of conventional material design and fabrication. Along with the reduction of d from 18 nm to 1 nm, α2/ρ kept increasing and finally reached ~1500 μW cm−1K−2.
Temperature-thickness mapping of thermoelectric response
Figures 3a, b display the temperature T—thickness d mappings of the absolute value of α (i.e., |α|) and α2/ρ, respectively, for another FeSe thin film, Sample B. The values of |α| and α2/ρ showed dramatic developments in the nanometer-thick region, which agrees well with the results for Sample A (see Figs. 2b, c). Moreover, the enhancement for both |α| and α2/ρ covers a wide temperature range from 50 K (just above Tc) to 280 K. Figure 3c summarizes α2/ρ for representative thermoelectric materials that possess high α2/ρ values (see Supplementary Table 1). The values of α2/ρ for the FeSe ultrathin film increased from ~260 μW cm−1 K−2 at 280 K up to ~13,000 μW cm−1 K−2 at 50 K, being the largest among existing bulk materials reported so far. Assuming the thermal conductivity for bulk Fe-based superconductors25,26, κ ~5 W m−1 K−1, the dimensionless figure of merit ZT of the FeSe ultrathin film reaches as large as ~1.5 at 280 K.
Giant thermoelectric response in ultrathin FeSe. a Mapping of Seebeck coefficient α of FeSe (Sample B) against temperature T and thickness d. Here, the absolute value of α (i.g., |α|) for VG = 3.95 V was plotted. The white circles correspond to the onset temperature Tc of the superconducting transition. b Evolution of thermoelectric power factor α2/ρ of FeSe (Sample B) above Tc. The value of α2/ρ increased with decreasing d, mainly owing to the large enhancement of α shown in a. c Comparison of temperature dependence of α2/ρ among representative thermoelectric materials. The values of α2/ρ in the FeSe ultrathin film were larger than any existing bulk materials reported so far in a wide temperature range (see Supplementary Table 1 for the reference of the experimental values). The data point for Sample A at 200 K (open circle) shows fair reproducibility
Common trend of Seebeck effect in Fe-based superconductors
The detailed temperature dependence of α for different d’s is presented in Fig. 4a to show the unusual thermoelectric response in FeSe. Except for the initial thickness (19.1 nm) with moderate temperature dependence, α for Sample B showed a peak at around ~200 K, which follows neither the T-linear behavior expected in conventional metals nor the phonon drag thermopower (see Supplementary Figure 1 and Supplementary Note 1). Actually, the temperature dependence of α in the FeSe thin film is qualitatively similar to that in bulk Fe-based high-Tc superconductors such as Ba(Fe0.9Co0.1)2As227, LaFeAs(O0.9F0.1)28, and La(Fe0.9Co0.1)AsO29, as shown in Fig. 4b. This trend can be seen even more clearly in Fig. 4c, where the data in Fig. 4a, b are normalized by the peak value αpeak of each sample. These similarities further prove that α observed in Fig. 4a is attributed to FeSe itself rather than other artifacts such as substrates and ionic liquids. The characteristic temperature dependence of α/αpeak in Fig. 4c is considered unique to Fe-based superconductors and has been discussed in the context of quantum criticality30,31,32 or the two carrier model27,33. For example, it was reported that |α|/T in Ba(Fe0.9Co0.1)2As227 shows a divergence above Tc and a strong enhancement when in proximity to the quantum critical point.
Temperature dependence of Seebeck coefficient. a Seebeck coefficient α vs. temperature T in FeSe thin film (Sample B). The values of α were enhanced by the thickness reduction in all temperature regions. b α−T curves in representative Fe-based high-Tc superconductors. Ba(Fe0.9Co0.1)2As227, LaFeAs(O0.9F0.1)28, and La(Fe0.9Co0.1)AsO29 show the peak behavior at ~150 K, in a similar manner to the FeSe thin film in a. c Temperature dependence of α normalized by the peak value αpeak for FeSe thin films and bulk materials in b. Overall temperature variation of α is seemingly common for Fe-based superconductors
Electronic band structure in gated FeSe thin film
The transfer characteristics (the VG dependence of resistance) of a FeSe thin film (see Supplementary Figure 4 and Supplementary Note 3) indicates that the dominant carriers change from holes to electrons with reducing the thickness. This behavior is consistent with the band structure evolution derived from the angle-resolved photoemission spectroscopy (ARPES)12,34,35,36 in monolayer FeSe on SrTiO3 and in K-coated FeSe thin films, which clarified that the hole pocket at the Γ-point disappears and a gap of ~60 meV is opened at the M-point34 owing to the thinning and concomitant electron doping. The present ion-gated FeSe thin films should have a similar band structure because the electron density accumulated by the ionic gating, ~1014 cm−2, is comparable to that of the charge transfer from SrTiO3 substrate and of surface K coating. This band structure of FeSe monolayer should be beneficial for the enhancement of |α|. We calculated the Seebeck coefficient for the undoped bulk FeSe and electron-doped monolayer FeSe at T = 280 K (see Supplementary Figure 5 and Supplementary Note 4), and obtained α values as + 5 μV K−1 and −200 μV K−1 for the bulk and the monolayer FeSe, respectively. These estimations reasonably explain the experimental values of α at 280 K: + 17 μV K−1 and −245 μV K−1 (Fig. 3a) for the initial (d ~19.1 nm) and final (d ~1 nm) thicknesses, respectively. On the other hand, our calculation based on the Fermi liquid picture predicts T-linear behavior and does not explain the non-monotonous temperature dependence of α in ultrathin FeSe. The experimentally observed broad peak in α located at ~200 K (Fig. 4a) is suggestive of a crucial role of electronic correlations in the Seebeck response of ultrathin FeSe; in fact, the recent ARPES studies pointed out a strong electronic correlation9 in the high-Tc phase of FeSe. A quantitative theoretical analysis of this effect remains to be performed.
Discussion
Nanostructures or low-dimensional structures have been a powerful guideline for the exploration of high-performance thermoelectric materials8,37,38,39,40. The present results show that further enhancement of thermoelectric properties should be possible, if peculiar band structures of nano-structured systems including 2D layered materials are combined with additional ingredients such as strong electronic correlations. The unprecedented coexistence of giant thermoelectric power factor and high-Tc superconductivity in ultrathin FeSe exemplifies that there may exist unknown multifunctional materials waiting to be disclosed in extreme conditions, illuminating a next research direction of functional thermoelectric materials.
Methods
Device fabrication
We fabricated ion-gated devices based on FeSe-thin films on SrTiO3 substrates15 with channel size of 1.2 × 2 mm2. The details of the thin-film preparation were reported in our previous study15. The device structure used in this study is schematically shown in Fig. 1c. The FeSe thin films were patterned by using a laser cutter to perform four-terminal resistance measurements. The gold wires were attached at both edges of the patterned film, working as a drain terminal D and a source terminal S. An ionic liquid, which worked as a gate dielectric, was placed on the FeSe surface. We used N,N-diethyl-N-(2-methoxyethyl)-N-methylammonium bis-(trifluoromethylsulfonyl)-imide (DEME-TFSI) as the ionic liquid. A Pt plate was placed on top of them, working as a gate electrode.
Thermoelectric measurements under gate biases
As shown in Fig. 1c, a heater and a heat sink were attached to either side of the ion-gated device to produce a thermal gradient. The type E thermocouples were attached to monitor the temperature difference ΔT and the thermoelectric voltage ΔV. The thermocouples were also used for the four-terminal resistance measurements. The temperature difference ΔT (0–1 K) and the voltage ΔV between the thermocouples were measured, and the values of α were evaluated from the slope of the ΔV−ΔT plots (See Fig. 2a). This device configuration allows us to measure α and ρ simultaneously. The thermoelectric measurements with solid41,42,43,44,45,46,47 and ionic gate dielectrics48,49,50,51,52,53,54,55,56,57 are widely accepted as a method to evaluate the thermoelectric properties of semiconductors with changing the carrier densities.
Calculations
We performed first-principles band structure calculations using the Perdew-Burke-Ernzerhof parameterization of the generalized gradient approximation58 and the full-potential (linearized) augmented plane-wave method, with the inclusion of spin-orbit coupling as implemented in the wien2k code59. Muffin-tin radii (RMT) of 2.38 and 2.11 Bohr were used for Fe and Se, respectively. The maximum modulus for the reciprocal vectors Kmax was chosen such that RMTKmax = 7.0 and a 10 × 10 × 10 k-mesh in the first Brillouin zone was used. The tight-binding Hamiltonian for the 3d orbitals of the Fe atom was constructed with Wannier9060 and wien2wannier61.
Data availability
The authors declare that all data supporting the findings of this study are available within the paper and its Supplementary Information or from the authors upon reasonable request.
References
Fiori, G. et al. Electronics based on two-dimensional materials. Nat. Nanotechnol. 9, 768–779 (2014).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Dresselhaus, M. S. et al. New directions for low-dimensional thermoelectric materials. Adv. Mater. 19, 1043–1053 (2007).
Hicks, L. D. & Dresselhaus, M. S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 47, 12727–12731 (1993).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Venkatasubramanian, R., Siivola, E., Colpitts, T. & O’Quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 413, 597–602 (2001).
Harman, T. C., Taylor, P. J., Walsh, M. P. & La Forge, B. E. Quantum dot superlattice thermoelectric materials and devices. Science 297, 2229–2232 (2002).
Ohta, H. et al. Giant thermoelectric Seebeck coefficient of a two-dimensional electron gas in SrTiO3. Nat. Mater. 6, 129–134 (2007).
Wen, C. H. P. et al. Anomalous correlation effects and unique phase diagram of electron-doped FeSe revealed by photoemission spectroscopy. Nat. Commun. 7, 10840 (2016).
Seo, J. J. et al. Superconductivity below 20 K in heavily electron-doped surface layer of FeSe bulk crystal. Nat. Commun. 7, 11116 (2016).
Wang, Q.-Y. et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 29, 037402 (2012).
Liu, D. et al. Electronic origin of high-temperature superconductivity in single-layer FeSe superconductor. Nat. Commun. 3, 931 (2012).
Ge, J.-F. et al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nat. Mater. 14, 285–289 (2014).
Sun, Y. et al. High temperature superconducting FeSe films on SrTiO3 substrates. Sci. Rep. 4, 6040 (2014).
Shiogai, J., Ito, Y., Mitsuhashi, T., Nojima, T. & Tsukazaki, A. Electric-field-induced superconductivity in electrochemically etched ultrathin FeSe films on SrTiO3 and MgO. Nat. Phys. 12, 42–46 (2016).
Bisri, S. Z., Shimizu, S., Nakano, M. & Iwasa, Y. Endeavor of iontronics: from fundamentals to applications of ion-controlled Electronics. Adv. Mater. 29, 1607054 (2017).
Lei, B. et al. Evolution of high-temperature superconductivity from a low T c phase tuned by carrier concentration in FeSe thin Flakes. Phys. Rev. Lett. 116, 077002 (2016).
Hanzawa, K., Sato, H., Hiramatsu, H., Kamiya, T. & Hosono, H. Electric field-induced superconducting transition of insulating FeSe thin film at 35 K. Proc. Natl. Acad. Sci. USA 113, 3986–3990 (2016).
McQueen, T. M. et al. Extreme sensitivity of superconductivity to stoichiometry in Fe1+δSe. Phys. Rev. B 79, 014522 (2009).
Song, Y. J. et al. Superconducting properties of a stoichiometric FeSe compound and two anomalous features in the normal State. J. Korean Phys. Soc. 59, 312–316 (2011).
Nakayama, K. et al. Reconstruction of band structure induced by electronic nematicity in an FeSe superconductor. Phys. Rev. Lett. 113, 237001 (2014).
Wu, C. T. et al. Heterojunction of Fe(Se 1−xTex) superconductor on Nb-doped SrTiO3. Appl. Phys. Lett. 96, 122506 (2010).
Zhang, W. et al. Interface charge doping effects on superconductivity of single-unit-cell FeSe films on SrTiO3 substrates. Phys. Rev. B 89, 060506(R) (2014).
Zhang, H. et al. Origin of charge transfer and enhanced electron-phonon coupling in single unit-cell FeSe films on SrTiO3. Nat. Commun. 8, 214 (2017).
Machida, Y. et al. Possible sign-reversing s-wave superconductivity in co-doped BaFe2As2 proved by thermal transport measurements. J. Phys. Soc. Jpn. 78, 073705 (2009).
Checkelsky, J. G. et al. Thermal hall conductivity as a probe of gap structure in multiband superconductors: the case of Ba1-xKxFe2As2. Phys. Rev. B 86, 180502(R) (2012).
Arsenijević, S. et al. Pressure effects on the transport coefficients of Ba(Fe1-xCox)2As2. Phys. Rev. B 84, 075148 (2011).
Zhu, Z. W. et al. Nernst effect of a new iron-based superconductor LaO1-xFxFeAs. New J. Phys. 10, 063021 (2008).
Kondrat, A., Behr, G., Büchner, B. & Hess, C. Unusual Nernst effect and spin density wave precursors in superconducting LaFeAsO1-xFx. Phys. Rev. B 83, 092507 (2011).
Gooch, M., Lv, B., Lorenz, B., Guloy, A. M. & Chu, C. W. Critical scaling of transport properties in the phase diagram of iron pnictide superconductors KxSr1−xFe2As2 and KxBa1−xFe2As2. J. Appl. Phys. 107, 09E145 (2010).
Maiwald, J., Jeevan, H. S. & Gegenwart, P. Signatures of quantum criticality in hole-doped and chemically pressurized EuFe2As2 single crystals. Phys. Rev. B 85, 024511 (2012).
Arsenijević, S. et al. Signatures of quantum criticality in the thermopower of Ba(Fe1-xCox)2As2. Phys. Rev. B 87, 224508 (2013).
Sales, B. C., McGuire, M. A., Sefat, A. S. & Mandrus, D. A semimetal model of the normal state magnetic susceptibility and transport properties of Ba(Fe1-xCox)2As2. Phys. C. 470, 304–308 (2010).
He, S. et al. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nat. Mater. 12, 605–610 (2013).
He, J. et al. Electronic evidence of an insulator-superconductor transition in single-layer FeSe/SrTiO3 films. Proc. Natl Acad. Sci. USA 111, 18501–18506 (2014).
Miyata, Y., Nakayama, K., Sugawara, K., Sato, T. & Takahashi, T. High-temperature superconductivity in potassium-coated multilayer FeSe thin films. Nat. Mater. 14, 775–779 (2015).
Choi, W. S., Ohta, H., Moon, S. J., Lee, Y. S. & Noh, T. W. Dimensional crossover of polaron dynamics in Nb:SrTiO3/SrTiO3 superlattices: Possible mechanism of thermopower enhancement. Phys. Rev. B 82, 024301 (2010).
Ohta, H. et al. Field-induced water electrolysis switches an oxide semiconductor from an insulator to a metal. Nat. Commun. 1, 118 (2010).
Ohta, H. et al. Unusually large enhancement of thermopower in an electric field induced two-dimensional electron gas. Adv. Mater. 24, 740–744 (2012).
Zhang, Y. et al. Double thermoelectric power factor of a 2D electron system. Nat. Commun. 9, 2224 (2018).
Zavaritsky, N. V. Phonon drag in two-dimensional electron systems. Phys. B+C. 126, 369–376 (1984).
Gallagher, B. L., Gibbings, C. J., Pepper, M. & Cantrell, D. G. The thermopower of Si inversion layers. Semicond. Sci. Technol. 2, 456–459 (1987).
Small, J., Perez, K. & Kim, P. Modulation of thermoelectric power of individual carbon nanotubes. Phys. Rev. Lett. 91, 256801 (2003).
Yoshikawa, A. et al. Electric-field modulation of thermopower for the KTaO3 field-effect transistors. Appl. Phys. Express 2, 121103 (2009).
Checkelsky, J. & Ong, N. Thermopower and Nernst effect in graphene in a magnetic field. Phys. Rev. B 80, 081413 (2009).
Zuev, Y., Chang, W. & Kim, P. Thermoelectric and magnetothermoelectric transport measurements of graphene. Phys. Rev. Lett. 102, 096807 (2009).
Ohta, H. et al. Field-modulated thermopower in SrTiO3-based field-effect transistors with amorphous 12CaO・7Al2O3 glass gate insulator. Appl. Phys. Lett. 95, 113505 (2009).
Shimizu, S., Ono, S., Hatano, T., Iwasa, Y. & Tokura, Y. Enhanced cryogenic thermopower in SrTiO3 by ionic gating. Phys. Rev. B 92, 165304 (2015).
Yoshida, M. et al. Gate-optimized thermoelectric power factor in ultrathin WSe2 single crystals. Nano. Lett. 16, 2061–2065 (2016).
Shimizu, S. et al. Enhanced thermopower in ZnO two-dimensional electron gas. Proc. Natl Acad. Sci. USA 113, 6438–6443 (2016).
Shimizu, S. et al. Thermoelectric detection of multi-subband density of states in semiconducting and metallic single-walled carbon nanotubes. Small 12, 3388–3392 (2016).
Yanagi, K. et al. Tuning of the thermoelectric properties of one-dimensional materials networks by electric double layer techniques using ionic liquids. Nano. Lett. 14, 6437 (2014).
Takayanagi, R., Fujii, T. & Asamitsu, A. Simultaneous control of thermoelectric properties in p- and n-type materials by electric double-layer gating: New design for thermoelectric device. Appl. Phys. Express 8, 051101 (2015).
Chien, Y.-Y., Yuan, H. T., Wang, C.-R. & Lee, W.-L. Thermoelectric power in bilayer graphene device with ionic liquid gating. Sci. Rep. 6, 20402 (2016).
Kawasugi, Y. et al. Simultaneous enhancement of conductivity and Seebeck coefficient in an organic Mott transistor. Appl. Phys. Lett. 109, 233301 (2016).
Pu, J. et al. Enhanced thermoelectric power in two-dimensional transition metal dichalcogenide monolayers. Phys. Rev. B 94, 014312 (2016).
Kawai, H. et al. Thermoelectric properties of WS2 nanotube networks. Appl. Phys. Express 10, 015001 (2017).
Perdew, J. P., Bruke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blaha, P., Schwarz, K., Madsen, G., Kvasnicka, D. & Luitz, J. WIEN2k, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties. (Tech. Univ, Wien, 2001).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Kuneš, J. et al. Wien2wannier: From linearized augmented plane waves to maximally localized Wannier functions. Comput. Phys. Commun. 181, 1888–1895 (2010).
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers JP25000003, JP16H00923 (SATL), JP16H06345, JP17H02928, JP17K19060.
Author information
Authors and Affiliations
Contributions
S.Sh. and J.S. equally contributed to this work. S.Sh., J.S., T.N., A.T. and Y.I. conceived and designed this work. S.Sh., N.T., S.Sa., A.T. and Y.I. wrote the paper. S.Sh. and J.S. performed all the measurements, and N.T., S.Sa., H.I. and R.A. conducted the calculations. All authors contributed to discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shimizu, S., Shiogai, J., Takemori, N. et al. Giant thermoelectric power factor in ultrathin FeSe superconductor. Nat Commun 10, 825 (2019). https://doi.org/10.1038/s41467-019-08784-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-08784-z
This article is cited by
-
Capillary compression induced outstanding n-type thermoelectric power factor in CNT films towards intelligent temperature controller
Nature Communications (2024)
-
Anomalous enhancement of thermoelectric power factor in multiple two-dimensional electron gas system
Nature Communications (2024)
-
Enhanced performance of Pb/FeSe2 interfaces designed for electrical applications
Applied Physics A (2024)
-
Heat-fueled enzymatic cascade for selective oxyfunctionalization of hydrocarbons
Nature Communications (2022)
-
Oxidation-induced thermopower inversion in nanocrystalline SnSe thin film
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.