Abstract
Controlling the group velocity of an optical pulse typically requires traversing a material or structure whose dispersion is judiciously crafted. Alternatively, the group velocity can be modified in free space by spatially structuring the beam profile, but the realizable deviation from the speed of light in vacuum is small. Here we demonstrate precise and versatile control over the group velocity of a propagation-invariant optical wave packet in free space through sculpting its spatio-temporal spectrum. By jointly modulating the spatial and temporal degrees of freedom, arbitrary group velocities are unambiguously observed in free space above or below the speed of light in vacuum, whether in the forward direction propagating away from the source or even traveling backwards towards it.
Similar content being viewed by others
Introduction
The publication of Einstein’s seminal work on special relativity initiated an investigation of the speed of light in materials featuring strong chromatic dispersion1. Indeed, the group velocity vg of an optical pulse in a resonant dispersive medium can deviate significantly from the speed of light in vacuum c, without posing a challenge to relativistic causality when vg > c because the information speed never exceeds c1,2. Modifying the temporal spectrum in this manner is the basic premise for the development of the so-called slow light and fast light3 in a variety of material systems including ultracold atoms4, hot atomic vapors5,6, stimulated Brillouin scattering in optical fibers7, and active gain resonances8,9. Additionally, nanofabrication yields photonic systems that deliver similar control over the group velocity through structural dispersion in photonic crystals10, metamaterials11, tunneling junctions12, and nanophotonic structures13. In general, resonant systems have limited spectral bandwidths that can be exploited before pulse distortion obscures the targeted effect, with the pulse typically undergoing absorption, amplification, or temporal reshaping, but without necessarily affecting the field spatial profile.
In addition to temporal spectral modulation, it has been recently appreciated that structuring the spatial profile of a pulsed beam can impact its group velocity in free space14,15,16. In a manner similar to pulse propagation in a waveguide, the spatial spectrum of a structured pulsed beam comprises plane wave contributions tilted with respect to the propagation axis, which undergo larger delays between two planes than purely axially propagating modes. A large-area structured beam (narrow spatial spectrum) can travel for longer distances before beam deformation driven by diffraction and space-time coupling, but its group velocity deviates only slightly from c; whereas a narrow beam deviates further from c, but travels a shorter distance. Consequently, vg is dependent on the size of the field spatial profile, and the maximum group delay observable is limited by the numerical aperture. Only velocities slightly lower than c (≈0.99999c) have been accessible in the experiments performed to date with maximum observed group delays of ~30fs, corresponding to a shift of ~10 μm over a distance of 1 m (or 1 part in 105).
Another potential approach to controlling the group velocity of a pulsed beam in free space relies on sculpting the spatio-temporal profile of propagation-invariant wave packets17,18. Instead of manipulating separately the field spatial or temporal degrees of freedom and attempting to minimize unavoidable space-time coupling, tight spatio-temporal correlations are intentionally introduced into the wave packet spectrum, thereby resulting in the realization of arbitrary group velocities: superluminal, luminal, or subluminal, whether in the forward direction propagating away from the source or in the backward direction traveling toward it. The group velocity here is the speed of the wave packet central spatio-temporal intensity peak, whereas the wave packet energy remains spread over its entire spatio-temporal extent. Judiciously associating each wavelength in the pulse spectrum with a particular transverse spatial frequency traces out a conic section on the surface of the light-cone while maintaining a linear relationship between the axial component of the wave vector and frequency19,20. The slope of this linear relationship dictates the wave packet group velocity, and its linearity eliminates any additional dispersion terms. The resulting wave packets propagate free of diffraction and dispersion17,18,19,20,21,22, which makes them ideal candidates for unambiguously observing group velocities in free space that deviate substantially from c.
There have been previous efforts directed at producing optical wave packets endowed with spatio-temporal correlations. Several strategies have been implemented to date, which include exploiting the techniques associated with the generation of Bessel beams, such as the use of annular apertures in the focal plane of a spherical lens23 or axicons24,25,26, synthesis of X-waves27 during nonlinear processes such as second-harmonic generation28 or laser filamentation29,30, or through direct filtering of the requisite spatio-temporal spectrum31,32. The reported superluminal speeds achieved with these various approaches in free space have been to date 1.00022c25, 1.00012c26, 1.00015c33, and 1.111c in a plasma24. Reports on measured subluminal speeds have been lacking17 and limited to delays of hundreds of femtoseconds over a distance of 10 cm34,35, corresponding to a group velocity of ≈0.999c. There have been no experimental reports to date on negative group velocities in free space.
Here, we synthesize space-time (ST) wave packets20,36,37 using a phase-only spatial light modulator (SLM) that efficiently sculpts the field spatio-temporal spectrum and modifies the group velocity. The ST wave packets are synthesized for simplicity in the form of a light sheet that extends uniformly in one transverse dimension over ~25 mm, such that control over vg is exercised in a macroscopic volume of space. We measure vg in an interferometric arrangement utilizing a reference pulsed plane wave and confirm precise control over vg from 30c in the forward direction to −4c in the backward direction. We observe group delays of ~±30 ps (three orders-of-magnitude larger than those in refs. 14,15), which is an order-of-magnitude longer than the pulse width, and is observed over a distance of only ~10 mm. Adding to the uniqueness of our approach, the achievable group velocity is independent of the beam size and of the pulse width. All that is needed to change the group velocity is a reorganization of the spectral correlations underlying the wave packet spatio-temporal structure. The novelty of our approach is its reliance on a linear system that utilizes a phase-only spatio-temporal Fourier synthesis strategy, which is energy efficient and precisely controllable20. Our approach allows for endowing the field with arbitrary, programmable spatio-temporal spectral correlations that can be tuned to produce—smoothly and continuously—any desired wave packet group velocity. The versatility and precision of this technique with respect to previous approaches is attested by the unprecedented range of control over the measured group velocity values over the subluminal, superluminal, and negative regimes in a single optical configuration. Crucially, while distinct theoretical proposals have been made previously for each range of the group velocity (e.g., subluminal38,39,40, superluminal41, and negative42 spans), our strategy is—to the best of our knowledge—the only experimental arrangement capable of controlling the group velocity continuously across all these regimes (with no moving parts) simply through the electronic implementation of a phase pattern imparted to a spectrally spread wave front impinging on a SLM.
Results
Concept of space-time wave packets
The properties of ST light sheets can be best understood by examining their representation in terms of monochromatic plane waves \(e^{i(k_xx + k_zz - \omega t)}\), which are subject to the dispersion relationship \(k_x^2 + k_z^2 = ({\textstyle{\omega \over c}})^2\) in free space; here, kx and kz are the transverse and longitudinal components of the wave vector along the x and z coordinates, respectively, ω is the temporal frequency, and the field is uniform along y. This relationship corresponds geometrically in the spectral space \((k_x,k_z,{\textstyle{\omega \over c}})\) to the surface of the light-cone (Fig. 1). The spatio-temporal spectrum of any physically realizable optical field compatible with causal excitation must lie on the surface of the light-cone with the added restriction kz > 0. For example, the spatial spectra of monochromatic beams lie along the circle at the intersection of the light-cone with a horizontal iso-frequency plane, whereas the spatio-temporal spectrum of a traditional pulsed beam occupies a two-dimensional (2D) patch on the light-cone surface.
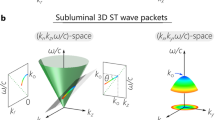
Spatio-temporal spectral engineering for arbitrary group velocity control. a–c Conic-section trajectories at the intersection of the free space light-cone with a spectral hyperplane \({\cal P}(\theta )\) are spatio-temporal spectral loci of space-time (ST) wave packets with tunable group velocities vg in free space: a subluminal, b superluminal, and c negative-superluminal vg. For each case we plot the projection of the spatio-temporal spectrum onto the (kx, kz) plane restricted to kz > 0 (white curve). d Projections of the spatio-temporal spectra from (a–c) onto the \((k_z,{\textstyle{\omega \over c}})\) plane. The slope of each projection determines the group velocity of each ST wave packet along the axial coordinate z, vg = ctanθ
The spectra of ST wave packets do not occupy a 2D patch, but instead lie along a curved one-dimensional trajectory resulting from the intersection of the light-cone with a tilted spectral hyperplane \({\cal P}(\theta )\) described by the equation \({\textstyle{\omega \over c}} = k_{\mathrm{o}} + (k_z - k_{\mathrm{o}}){\mathrm{tan}}\theta\), where \(k_{\mathrm{o}} = {\textstyle{{\omega _{\mathrm{o}}} \over c}}\) is a fixed wave number20, and the ST wave packet thus takes the form
Therefore, the group velocity along the z-axis is \(v_{\mathrm{g}} = {\textstyle{{\partial \omega } \over {\partial k_z}}} = c\,{\mathrm{tan}}\,\theta\), and is determined solely by the tilt of the hyperplane \({\cal P}(\theta )\). In the range 0 < θ < 45°, we have a subluminal wave packet vg < c, and \({\cal P}(\theta )\) intersects with the light-cone in an ellipse (Fig. 1a). In the range 45° < θ < 90°, we have a superluminal wave packet vg > c, and \({\cal P}(\theta )\) intersects with the light-cone in a hyperbola (Fig. 1b). Further increasing θ reverses the sign of vg such that the wave packet travels backwards towards the source vg < 0 in the range 90° < θ < 180° (Fig. 1c). These various scenarios are summarized in Fig. 1d.
Experimental realization
We synthesize the ST wave packets by sculpting the spatio-temporal spectrum in the \((k_x,{\textstyle{\omega \over c}})\) plane via a 2D pulse shaper20,43. Starting with a generic pulsed plane wave, the spectrum is spread in space via a diffraction grating before impinging on a SLM, such that each wavelength λ occupies a column of the SLM that imparts a linear phase corresponding to a pair of spatial frequencies ±kx that are to be assigned to that particular wavelength, as illustrated in Fig. 2a; see Methods. The retro-reflected wave front returns to the diffraction grating that superposes the wavelengths to reconstitute the pulse and produce the propagation-invariant ST wave packet corresponding to the desired hyperplane \({\cal P}(\theta )\). Using this approach we have synthesized and confirmed the spatio-temporal spectra of 11 different ST wave packets in the range 0° < θ < 180° extending from the subluminal to superluminal regimes. Figure 3a shows the measured spatio-temporal spectral intensity \(|\tilde E(k_x,\lambda )|^2\) for a ST wave packet having θ = 53.2° and thus lying on a hyperbolic curve on the light-cone corresponding to a positive superluminal group velocity of vg = 1.34c. The spatial bandwidth is Δkx = 0.11 rad/μm, and the the temporal bandwidth is Δλ ≈ 0.3 nm. This spectrum is obtained by carrying out an optical Fourier transform along x to reveal the spatial spectrum. Our spatio-temporal synthesis strategy is distinct from previous approaches that make use of Bessel-beam-generation techniques and similar methodologies23,24,25,26,41, nonlinear processes28,29,30, or spatio-temporal filtering31,32. The latter approach utilizes a diffraction grating to spread the spectrum in space, a Fourier spatial filter then carves out the requisite spatio-temporal spectrum, resulting in either low throughput or high spectral uncertainty. In contrast, our strategy exploits a phase-only modulation scheme that is thus energy-efficient and can smoothly and continuously (within the precision of the SLM) tune the spatio-temporal correlations electronically with no moving parts, resulting in a corresponding controllable variation in the group velocity.
Synthesizing space-time (ST) wave packets and measuring their group velocity. a A pulsed plane wave is split into two paths: in one path the ST wave packet is synthesized using a two-dimensional pulse shaper formed of a diffraction grating (G), cylindrical lens (L), and spatial light modulator (SLM), while the other path is the reference. BS beam splitter, CCD charge-coupled device, DL delay line. The insets provide the spatio-temporal profile of a ST wave packet with a Gaussian spectrum, the reference pulsed plane wave, and their interference. See Methods and Supplementary Fig. 1 for details. b The reference and the ST wave packets are superposed, and the shorter reference pulse probes a fraction of the longer ST wave packet. Maximal interference visibility is observed when the selected delays L1 and L2 cause their peaks to coincide; see Methods and Supplementary Figs 2,3
Spatio-temporal measurements of space-time (ST) wave packets. a, b Spatio-temporal a spectrum \(|\tilde E(k_x,\lambda )|^2\) and b intensity profile I(x, 0, τ) for a ST wave packet with superluminal group velocity vg = 1.34c, corresponding to a spectral hyperplane with θ = 53.2°. b The yellow and orange lines depict the pulse profile at x = 0, I(0, 0, τ), and beam profile at τ = 0, I(x, 0, 0), respectively. The inset shows the spatio-temporal intensity profile after propagating for z = 10 mm confirming the self-similar evolution of the ST wave packet. On the right, the normalized time-integrated beam profile \(I(x,0) = {\int} {\mathrm{d}}\tau I(x,0,\tau )\) is given
To map out the spatio-temporal profile of the ST wave packet I(x, z, t) = |E(x, z, t)|2, we make use of the interferometric arrangement illustrated in Fig. 2a. The initial pulsed plane wave (pulse width ~100 fs) is used as a reference and travels along a delay line that contains a spatial filter to ensure a flat wave front (see Methods and Supplementary Fig. 1). Superposing the shorter reference pulse and the synthesized ST wave packet (Eq. 1) produces spatially resolved interference fringes when they overlap in space and time—whose visibility reveals the spatio-temporal pulse profile (Fig. 2a and Supplementary Fig. 2). The measured intensity profile I(x, 0, τ) = |E(x, 0, τ)|2 of the ST wave packet having θ = 53.2° is plotted in Fig. 3b; τ is the delay in the reference arm. Plotted also are the pulse profile at the beam center I(0, 0, τ) = |E(x = 0, 0, τ)|2 whose width is ≈4.2 ps, and the beam profile at the pulse center I(x, 0, 0) = |E(x, 0, τ = 0)|2 whose width is ≈16.8 μm. Previous approaches for mapping out the spatio-temporal profile of propagation-invariant wave packets have made use of strategies ranging from spatially resolved ultrafast pulse measurement techniques26,34,35 to self-referenced interferometry31.
Controlling the group velocity of a space-time wave packet
We now proceed to make use of this interferometric arrangement to determine vg of the ST wave packets as we vary the spectral tilt angle θ. The setup enables synchronizing the ST wave packet with the luminal reference pulse while also uncovering any dispersion or reshaping in the ST wave packet with propagation. We first synchronize the ST wave packet with the reference pulse and take the central peak of the ST wave packet as the reference point in space and time for the subsequent measurements. An additional propagation distance L1 is introduced into the path of the ST wave packet, corresponding to a group delay of τST = L1/vg≫Δτ that is sufficient to eliminate any interference. We then determine the requisite distance L2 to be inserted into the path of the reference pulse to produce a group delay τr = L2/c and regain the maximum interference visibility, which signifies that τST = τr. The ratio of the distances L1 and L2 provides the ratio of the group velocity to the speed of light in vacuum L1/L2 = vg/c.
In the subluminal case vg < c, we expect L1 < L2; that is, the extra distance introduced into the path of the reference traveling at c is larger than that placed in the path of the slower ST wave packet. In the superluminal case vg > c, we have L1 > L2 for similar reasons. When considering ST wave packets having negative-vg, inserting a delay L1 in its path requires reducing the initial length of the reference path by a distance −L2 preceding the initial reference point, signifying that the ST wave packet is traveling backwards towards the source. As an illustration, the inset in Fig. 3b plots the same ST wave packet shown in the main panel of Fig. 3b observed after propagating a distance of L1 = 10 mm, which highlights the self-similarity of its free evolution20. The time axis is shifted by τr ≈ 24.88 ps, corresponding to vg = (1.36 ± 4 × 10−4)c, which is in good agreement with the expected value of vg = 1.34c.
The results of measuring vg while varying θ for the positive-vg ST wave packets are plotted in Fig. 4 (see also Supplementary Table 1). The values of vg range from subluminal values of 0.5c to the superluminal values extending up to 32c (corresponding to values of θ in the range 0° < θ < 90°). The case of a luminal ST wave packet corresponds trivially to a pulsed plane wave generated by idling the SLM. The data are in excellent agreement with the theoretical prediction of vg = ctanθ. The measurements of negative-vg (90° < θ < 180°) are plotted in Fig. 4, inset, down to vg ≈ −4c, and once again are in excellent agreement with the expectation of vg = ctanθ.
Measured group velocities for space-time (ST) wave packets. By changing the tilt angle θ of the spectral hyperplane \({\cal P}(\theta)\), we control vg of the synthesized ST wave packets in the positive subluminal and superluminal regimes (corresponding to 0 < θ < 90°). We plot vg on a logarithmic scale. Measurements of ST wave packets with negative-vg (corresponding to θ > 90°) are given as points in the inset on a linear scale. The data in the main panel and in the inset are represented by points and both curves are the theoretical expectation vg = ctanθ. The error bars are obtained from the standard error in the slope resulting from linear regression fits (see Methods and Supplementary Fig. 4). The error bars for the measurements are too small to appear, and are provided in Supplementary Table 1
Discussion
An alternative understanding of these results makes use of the fact that tilting the plane \({\cal P}(\theta )\) from an initial position of \({\cal P}(0)\) corresponds to the action of a Lorentz boost associated with an observer moving at a relativistic speed of vg = ctanθ with respect to a monochromatic source (θ = 0)21,22,43. Such an observer perceives in lieu of the diverging monochromatic beam a non-diverging wave packet of group velocity vg44. Indeed, at θ = 90° a condition known as time diffraction is realized where the axial coordinate z is replaced with time t, and the usual axial dynamics is displayed in time instead21,43,45,46. In that regard, our reported results here on controlling vg of ST wave packets is an example of relativistic optical transformations implemented in a laboratory through spatio-temporal spectral engineering.
Note that it is not possible in any finite configuration to achieve a delta-function correlation between each spatial frequency kx and wavelength λ; instead, there is always a finite spectral uncertainty δλ in this association. In our experiment, δλ ~ 24 pm (Fig. 3a), which sets a limit on the diffraction-free propagation distance over which the modified group velocity can be observed36. The maximum group delay achieved and the propagation-invariant length are essentially dictated by the spectral uncertainty δλ (see ref. 36 for details). The finite system aperture ultimately sets the lower bound on the value of δλ. For example, the size of the diffraction grating determines its spectral resolving power, the finite pixel size of the SLM further sets a lower bound on the precision of association between the spatial and temporal frequencies, whereas the size of the SLM active area determines the maximum temporal bandwidth that can be exploited. Of course, the spectral tilt angle θ determines the proportionality between the spatial and temporal bandwidths Δkx and Δλ, respectively, which then links these limits to the transverse beam width. However, ST wave packets having the same spatial transverse width will propagate for different distances depending on the spectral uncertainty associated with each. The confluence of all these factors determine the maximum propagation-invariant distance and hence the maximum achievable group delays. Careful design of the experimental parameters helps extend the propagation distance47, and exploiting a phase plate in lieu of a SLM can extend the propagation distance even further48. Note that we have synthesized here optical wave packets where light has been localized along one transverse dimension but remains extended in the other transverse dimension. Localizing the wave packet along both transverse dimensions would require an additional SLM to extend the spatio-temporal modulation scheme into the second transverse dimension that we have not exploited here.
Finally, another strategy that also relies on spatio-temporal structuring of the optical field has been recently proposed theoretically49 and demonstrated experimentally50 that makes use of a so-called flying focus, whereupon a chirped pulse is focused with a lens having chromatic aberrations such that different spectral slices traverse the focal volume of the lens at a controllable speed, which was estimated by means of a streak camera.
We have considered here ST wave packets whose spatio-temporal spectral projection onto the \((k_z,{\textstyle{\omega \over c}})\) plane is a line. A plethora of alternative curved projections may be readily implemented to explore different wave packet propagation dynamics and to accommodate the properties of material systems in which the ST wave packet travels. Our results pave the way to novel schemes for phase matching in nonlinear optical processes51,52, new types of laser-plasma interactions53,54, and photon-dressing of electronic quasiparticles55.
Methods
Determining conic sections for the spatio-temporal spectra
The intersection of the light-cone \(k_x^2 + k_z^2 = ({\textstyle{\omega \over c}})^2\) with the spectral hyperplane \({\cal P}(\theta )\) described by the equation \({\textstyle{\omega \over c}} = k_{\mathrm{o}} + (k_z - k_{\mathrm{o}})\,{\mathrm{tan}}\,\theta\) is a conic section: an ellipse (0° < θ < 45° or 135° < θ < 180°), a tangential line (θ = 45°), a hyperbola (45° < θ < 135°), or a parabola (θ = 135°). In all cases vg = ctanθ. The projection onto the \((k_x,{\textstyle{\omega \over c}})\) plane, which the basis for our experimental synthesis procedure, is in all cases a conic section given by
where k1, k2, and k3 are positive-valued constants: \({\textstyle{{k_1} \over {k_{\mathrm{o}}}}} = \left| {{\textstyle{{{\mathrm{tan}}\theta } \over {1 + {\mathrm{tan}}\theta }}}} \right|\), \({\textstyle{{k_2} \over {k_{\mathrm{o}}}}} = {\textstyle{1 \over {|1 + {\mathrm{tan}}\theta |}}}\), and \({\textstyle{{k_3} \over {k_{\mathrm{o}}}}} = \sqrt {|{\textstyle{{1 + {\mathrm{tan}}\theta } \over {1 - {\mathrm{tan}}\theta }}}|}\). The signs in the equation are (−, +) in the range 0 < θ < 45° (an ellipse), (−,−) in the range 45° < θ < 90°, and (+, −) in the range 90° < θ < 135°.
In the paraxial limit where \(k_x^{{\mathrm{max}}} \ll k_{\mathrm{o}}\), the conic section in the vicinity of kx = 0 can be approximated by a section of a parabola,
whose curvature is determined by θ through the function f(θ) given by
Spatially resolved interference to obtain intensity profiles
We take the ST wave packet to be \(E(x,z,t) = e^{i(k_{\mathrm{o}}z - \omega _{\mathrm{o}}t)}\psi (x,z - v_{\mathrm{g}}t)\) as provided in Eq. (1), and that of the reference plane wave pulse to be \(E_{\mathrm{r}} = e^{i(k_{\mathrm{o}}z - \omega _{\mathrm{o}}t)}\psi _{\mathrm{r}}(z - ct)\). We have dropped the x-dependence of the reference and ψr(z) is a slowly varying envelope. Superposing the two fields in the interferometer after delaying the reference by τ results in a new field ∝E(x, z, t) + Er(x, z, t − τ), whose time-average I(x, τ) is recorded at the output,
We make use of the following representations of the fields for the ST wave packet and the reference pulse:
We set the plane of the detector at z = 0 (CCD1 in our experiment; see Supplementary Fig. 1), from which we obtain the spatio-temporal interferogram
where
where we have made the simplifying assumption that the spatial spectrum of the ST wave packet is an even function, \(\tilde \psi (k_x) = \tilde \psi ( - k_x)\). This assumption is applicable to our experiment and does not result in any loss of generality. Note that IST(x) corresponds to the time-averaged transverse spatial intensity profile of the ST wave packet, as would be registered by a charge-coupled device (CCD), for example, in the absence of an interferometer. Similarly, Ir is equal to the time-averaged reference pulse and represents constant background term. Note that z could be set at an arbitrary value because both the reference pulse and the ST wave packet are propagation invariant.
The cross-correlation function \(R(x,\tau ) = |R(x,\tau )|e^{i\varphi _{\mathrm{R}}(x,\tau )}\) is given by
Taking the integral over time t produces
where ω is no longer an independent variable, but is correlate to the spatial frequency kx through the spatio-temporal curve at the intersection of the light-cone with the hyperspectral plane \({\cal P}(\theta )\). Because the reference pulse is significantly shorter that the ST wave packet, the spectral width of \(\tilde \psi _{\mathrm{r}}\) is larger than that of \(\tilde \psi\), so that one can ignore it, while retaining its amplitude,
Note that the spectral function \(\tilde \psi (k_x)\) of the ST wave packet determines the coherence length of the observed spatio-temporal interferogram, which we thus expect to be on the order of the temporal width of the ST wave packet itself.
The visibility of the spatially resolved interference fringes (Supplementary Fig. 2) is given by
The squared visibility is then given by
where the last approximation requires that we can ignore IST(x) with respect to the constant background term Ir stemming from the reference pulse.
Synthesis of ST wave packets
The input pulsed plane wave is produced by expanding the horizontally polarized pulses from a Ti:sapphire laser (Tsunami, Spectra Physics) having a bandwidth of ~8.5 nm centered on a wavelength of 800 nm, corresponding to pulses having a width of ~100 fs. A diffraction grating having a ruling of 1200 lines/mm and area 25 × 25 mm2 in reflection mode (Newport 10HG1200-800-1) is used to spread the pulse spectrum in space and the second diffraction order is selected to increase the spectral resolving power, resulting in an estimated spectral uncertainty of δλ ≈ 24 pm. After spreading the full spectral bandwidth of the pulse in space, the width size of the SLM (≈16 mm) acts as a spectral filter, thus reducing the bandwidth of the ST wave packet below the initial available bandwidth and minimizing the impact of any residual chirping in the input pulse. An aperture A can be used to further reduce the temporal bandwidth when needed. The spectrum is collimated using a cylindrical lens L1−y of focal length f = 50 cm in a 2f configuration before impinging on the SLM. The SLM imparts a 2D phase modulation to the wave front that introduces controllable spatio-temporal spectral correlations. The retro-reflected wave from is then directed through the lens L1−y back to the grating G, whereupon the ST wave packet is formed once the temporal/spatial frequencies are superposed; see Supplementary Fig. 1. Details of the synthesis procedure are described elsewhere20,43,47,48.
Spectral analysis of ST wave packets
To obtain the spatio-temporal spectrum \(|\tilde E(k_x,\lambda )|^2\) plotted in Fig. 3a in the main text, we place a beam splitter BS2 within the ST synthesis system to sample a portion of the field retro-reflected from the SLM after passing through the lens L1−y. The field is directed through a spherical lens L4−s of focal length f = 7.5 cm to a CCD camera (CCD2); see Supplementary Fig. 1. The distances are selected such that the field from the SLM undergoes a 4f configuration along the direction of the spread spectrum (such that the wavelengths remain separated at the plane of CCD2), while undergoing a 2f system along the orthogonal direction, thus mapping each spatial frequency kx to a point.
Reference pulse preparation
The reference pulse is obtained from the initial pulsed beam before entering the ST wave packet synthesis stage via a beam splitter BS1. The beam power is adjusted using a neutral density filter, and the spatial profile is enlarged by adding a spatial filtering system consisting of two lenses and a pinhole of diameter 30 μm. The spherical lenses are L5−s of focal length f = 50 cm and L6−s of focal length f = 10 cm, and they are arranged such that the pinhole lies at the Fourier plane. The spatially filtered pulsed reference then traverses an optical delay line before being brought together with the ST wave packet.
Beam analysis
The ST wave packet is imaged from the plane of the grating G to an output plane via a telescope system comprising two cylindrical lenses L2−x and L3−x of focal lengths 40 cm and 10 cm, respectively, arranged in a 4f system. This system introduced a demagnification by a factor 4×, which modifies the spatial spectrum of the ST wave packet. The phase pattern displayed by the SLM is adjusted to pre-compensate for this modification. The ST wave packet and the reference pulse are then combined into a common path via a beam splitter BS3. A CCD camera (CCD1) records the interference pattern resulting from the overlap of the ST wave packet and reference pulse, which takes place only when the two pulses overlap also in time; see Supplementary Fig. 2.
Group velocity measurements
Moving CCD1 a distance Δz introduces an extra common distance in the path of both beams. However, since the ST wave packet travels at a group velocity vg and the reference pulse at c, a relative group delay of \(\Delta \tau = \Delta z({\textstyle{1 \over c}} - {\textstyle{1 \over {v_{\mathrm{g}}}}})\) is introduced and the interference at CCD1 is lost if \({\mathrm{\Delta }}\tau \gg {\mathrm{\Delta }}T\), where ΔT is the width of the ST wave packet in time. The delay line in the path of the reference pulse is then adjusted to introduce a delay τ = Δτ to regain the interference. In the subluminal case vg < c, the reference pulse advances beyond the ST wave packet, and the interference is regained by increasing the delay traversed by the reference pulse with respect to the original position of the delay line. In the superluminal case vg > c, the ST wave packet advances beyond the reference pulse, and the interference is regained by reducing the delay traversed by the reference pulse with respect to the original position of the delay line. When vg takes on negative values, the delay traversed by the reference pulse must be reduced even further. Of course, in the luminal case the visibility is not lost by introducing any extra common path distance Δz. See Supplementary Fig. 3 for a graphical depiction.
From this, the group velocity is given by
For a given value of Δz, we fit the temporal profile I(0, 0, τ) to a Gaussian function to determine its center from which we estimate Δτ. For each tilt angle θ, we repeat the measurement for three different values of Δz and set one of the positions as the origin for the measurement set: 0 mm, 2 mm, and 4 mm in positive subluminal case (Supplementary Fig. 4a); 0 mm, 5 mm, and 10 mm in the positive superluminal case (Supplementary Fig. 4b); and 0 mm, −5 mm, and −10 mm in the negative-vg case (Supplementary Fig. 4c). Finally, we fit the obtained values to a linear function, where the slope corresponds to the group velocity. The uncertainty in estimating the values of vg (Δvg in Supplementary Table 1 and error bars for Fig. 4) are obtained from the standard error in the slope resulting from the linear regression.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Brillouin, L. Wave Propagation and Group Velocity (Academic Press, New York, 1960).
Schulz-DuBois, E. O. Energy transport velocity of electromagnetic propagation in dispersive media. Proc. IEEE 57, 1748–1757 (1969).
Boyd, R. W. & Gauthier, D. J. Controlling the velocity of light pulses. Science 326, 1074–1077 (2009).
Hau, L. V., Harris, S. E., Dutton, Z. & Behroozi, C. Light speed reduction to 17 m per second in an ultracold atomic gas. Nature 397, 594–598 (1999).
Kash, M. M. et al. Ultraslow group velocity and enhanced nonlinear optical effects in a coherently driven hot atomic gas. Phys. Rev. Lett. 82, 5229–5232 (1999).
Wang, L. J., Kuzmich, A. & Dogariu, A. Gain-assisted superluminal light propagation. Nature 406, 277–279 (2000).
Song, K. Y., Herráez, M. G. & Thévenaz, L. Gain-assisted pulse advancement using single and double Brillouin gain peaks in optical fibers. Opt. Express 13, 9758–9765 (2005).
Casperson, L. & Yariv, A. Pulse propagation in a high-gain medium. Phys. Rev. Lett. 26, 293–295 (1971).
Gehring, G. M., Schweinsberg, A., Barsi, C., Kostinski, N. & Boyd, R. W. Observation of backward pulse propagation through a medium with a negative group velocity. Science 312, 895–897 (2005).
Baba, T. Slow light in photonic crystals. Nat. Photon. 2, 465–473 (2008).
Dolling, G., Enkrich, C., Wegener, M., Soukoulis, C. M. & Linden, S. Simultaneous negative phase and group velocity of light in a metamaterial. Science 312, 892–894 (2005).
Steinberg, A. M., Kwiat, P. G. & Chiao, R. Y. Measurement of the single-photon tunneling time. Phys. Rev. Lett. 71, 708–711 (1993).
Tsakmakidis, K. L., Hess, O., Boyd, R. W. & Zhang, X. Ultraslow waves on the nanoscale. Science 358, eaan5196 (2017).
Giovannini, D. et al. Spatially structured photons that travel in free space slower than the speed of light. Science 347, 857–860 (2015).
Bouchard, F., Harris, J., Mand, H., Boyd, R. W. & Karimi, E. Observation of subluminal twisted light in vacuum. Optica 3, 351–354 (2016).
Lyons, A. et al. How fast is a twisted photon? Optica 5, 682–686 (2018).
Turunen, J. & Friberg, A. T. Propagation-invariant optical fields. Prog. Opt. 54, 1–88 (2010).
Hernández-Figueroa, H. E., Recami, E. & Zamboni-Rached, M (eds). Non-Diffracting Waves (Wiley-VCH, Weinheim, 2014)
Donnelly, R. & Ziolkowski, R. Designing localized waves. Proc. R. Soc. Lond. A 440, 541–565 (1993).
Kondakci, H. E. & Abouraddy, A. F. Diffraction-free space-time beams. Nat. Photon. 11, 733–740 (2017).
Longhi, S. Gaussian pulsed beams with arbitrary speed. Opt. Express 12, 935–940 (2004).
Saari, P. & Reivelt, K. Generation and classification of localized waves by Lorentz transformations in Fourier space. Phys. Rev. E 69, 036612 (2004).
Saari, P. & Reivelt, K. Evidence of X-shaped propagation-invariant localized light waves. Phys. Rev. Lett. 79, 4135–4138 (1997).
Alexeev, I., Kim, K. Y. & Milchberg, H. M. Measurement of the superluminal group velocity of an ultrashort Bessel beam pulse. Phys. Rev. Lett. 88, 073901 (2002).
Bonaretti, F., Faccio, D., Clerici, M., Biegert, J. & Di Trapani, P. Spatiotemporal amplitude and phase retrieval of Bessel-X pulses using a Hartmann-Shack sensor. Opt. Express 17, 9804–9809 (2009).
Bowlan, P. et al. Measuring the spatiotemporal field of ultrashort Bessel-X pulses. Opt. Lett. 34, 2276–2278 (2009).
Lu, J.-Y. & Greenleaf, J. F. Nondiffracting X waves – exact solutions to free-space scalar wave equation and their finite aperture realizations. IEEE Trans. Ultrason. Ferroelec. Freq. Control 39, 19–31 (1992).
Di Trapani, P. et al. Spontaneously generated X-shaped light bullets. Phys. Rev. Lett. 91, 093904 (2003).
Faccio, D. et al. Conical emission, pulse splitting, and X-wave parametric amplification in nonlinear dynamics of ultrashort light pulses. Phys. Rev. Lett. 96, 193901 (2006).
Faccio, D. et al. Spatio-temporal reshaping and X wave dynamics in optical filaments. Opt. Express 15, 13077–13095 (2007).
Dallaire, M., McCarthy, N. & Piché, M. Spatiotemporal bessel beams: theory and experiments. Opt. Express 17, 18148–18164 (2009).
Jedrkiewicz, O., Wang, Y.-D., Valiulis, G. & Di Trapani, P. One dimensional spatial localization of polychromatic stationary wave-packets in normally dispersive media. Opt. Express 21, 25000–25009 (2013).
Kuntz, K. B. et al. Spatial and temporal characterization of a bessel beam produced using a conical mirror. Phys. Rev. A 79, 043802 (2009).
Lõhmus, M. et al. Diffraction of ultrashort optical pulses from circularly symmetric binary phase gratings. Opt. Lett. 37, 1238–1240 (2012).
Piksarv, P. et al. Temporal focusing of ultrashort pulsed Bessel beams into Airy-Bessel light bullets. Opt. Express 20, 17220–17229 (2012).
Kondakci, H. E. & Abouraddy, A. F. Diffraction-free pulsed optical beams via space-time correlations. Opt. Express 24, 28659–28668 (2016).
Parker, K. J. & Alonso, M. A. The longitudinal iso-phase condition and needle pulses. Opt. Express 24, 28669–28677 (2016).
Liu, Z. & Fan, D. Propagation of pulsed zeroth-order Bessel beams. J. Mod. Opt. 45, 17–21 (1998).
Sheppard, C. J. R. Generalized Bessel pulse beams. J. Opt. Soc. Am. A 19, 2218–2222 (2002).
Zapata-Rodríguez, C. J., Porras, M. A. & Miret, J. J. Free-space delay lines and resonances with ultraslow pulsed Bessel beams. J. Opt. Soc. Am. A 25, 2758–2763 (2008).
Valtna, H., Reivelt, K. & Saari, P. Methods for generating wideband localized waves of superluminal group velocity. Opt. Commun. 278, 1–7 (2007).
Zapata-Rodríguez, C. J. & Porras, M. A. X-wave bullets with negative group velocity in vacuum. Opt. Lett. 31, 3532–3534 (2006).
Kondakci, H. E. & Abouraddy, A. F. Airy wavepackets accelerating in space-time. Phys. Rev. Lett. 120, 163901 (2018).
Bélanger, P. A. Lorentz transformation of packetlike solutions of the homogeneous-wave equation. J. Opt. Soc. Am. A 3, 541–542 (1986).
Porras, M. A. Gaussian beams diffracting in time. Opt. Lett. 42, 4679–4682 (2017).
Porras, M. A. Nature, diffraction-free propagation via space-time correlations, and nonlinear generation of time-diffracting light beams. Phys. Rev. A 97, 063803 (2018).
Bhaduri, B., Yessenov, M. & Abouraddy, A. F. Meters-long propagation of diffraction-free space-time light sheets. Opt. Express 26, 20111–20121 (2018).
Kondakci, H. E. et al. Synthesizing broadband propagation-invariant space-time wave packets using transmissive phase plates. Opt. Express 26, 13628–13638 (2018).
Sainte-Marie, A., Gobert, O. & Quéré, F. Controlling the velocity of ultrashort light pulses in vacuum through spatio-temporal couplings. Optica 4, 1298–1304 (2017).
Froula, D. H. et al. Spatiotemporal control of laser intensity. Nat. Photon. 12, 262–265 (2018).
Averchi, A. et al. Phase matching with pulsed Bessel beams for high-order harmonic generation. Phys. Rev. A 77, 021802(R) (2008).
Bahabad, A., Murnane, M. M. & Kapteyn, H. C. Quasi-phase-matching of momentum and energy in nonlinear optical processes. Nat. Photon. 4, 570–575 (2010).
Turnbull, D. et al. Raman amplification with a flying focus. Phys. Rev. Lett. 120, 024801 (2018).
Turnbull, D. et al. Ionization waves of arbitrary velocity. Phys. Rev. Lett. 120, 225001 (2018).
Byrnes, T., Kim, N. Y. & Yamamoto, Y. Exciton-polariton condensates. Nat. Phys. 10, 803–813 (2014).
Acknowledgements
We thank D. N. Christodoulides and A. Keles for helpful discussions. This work was supported by the U.S. Office of Naval Research (ONR) under contract N00014-17-1-2458.
Author information
Authors and Affiliations
Contributions
A.F.A. and H.E.K. developed the concept, designed the experiment, and wrote the paper. H.E.K. carried out the experimental work and the data analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journol peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kondakci, H.E., Abouraddy, A.F. Optical space-time wave packets having arbitrary group velocities in free space. Nat Commun 10, 929 (2019). https://doi.org/10.1038/s41467-019-08735-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-08735-8
This article is cited by
-
Spatiotemporal hologram
Nature Communications (2024)
-
Optical spatiotemporal vortices
eLight (2023)
-
Elusive phase wave caught
Nature Physics (2023)
-
The propagation speed of optical speckle
Scientific Reports (2023)
-
Nonlocal flat optics
Nature Photonics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.