Abstract
Studies on quantum critical points (QCP) have focused on magnetic QCPs to date. Remarkable phenomena such as superconductivity due to avoided criticality have been discovered, but we focus here on the non-magnetic counterpart, i.e., the superconductivity of SrTiO3 regarded as being close to a ferroelectric QCP. Here we prepare high-quality Sr1−xLaxTi(16O1−z18Oz)3 single crystals without localisation at low temperatures, which allow us to systematically investigate the La substitution of Sr as an alternative to introducing oxygen vacancies. Analysis of our data based on a theoretical model predicts an appearance of the ferroelectric QCP around 3 × 1018 cm−3. Because of the QCP, the superconducting dome of Sr1−xLaxTiO3 can be raised upwards. Furthermore, remarkable enhancement of Tc (~0.6 K) is achieved by 18O exchange on the Sr1−xLaxTiO3 crystals. These findings provide a new knob for observing intriguing physics around the ferroelectric QCP.
Similar content being viewed by others
Introduction
SrTiO3 is one of the most studied transition-metal oxides in the history of condensed matter physics. It is a simple band insulator with a band gap of ~3.3 eV between the Ti 3d and O 2p bands but exhibits various unique and interesting properties and thus remains at the centre of ardent research1,2. SrTiO3 undergoes an antiferrodistortive phase transition at ~105 K due to the staggered rotations of TiO6 octahedra around the [001] axis. Many studies suggest that this antiferrodistortive transition suppresses the ferroelectric (FE) phase transition3,4 at relatively high temperatures, and this scenario is supported by first-principles calculations5. However, it remains unclear why the ferroelectricity is suppressed down to very low temperatures (at least 350 mK6) despite its phonon structure with polar soft modes remaining. Because of this missing ferroelectricity, a huge static dielectric constant ε ~ 24,000 is observed at low temperatures, resulting in a very large effective Bohr radius of ~0.5 µm. Thus, slight carrier doping of even 2 × 1016 cm−3 leads to the appearance of an extraordinary dilute metallic state7. It is generally believed that the missing ferroelectricity, even at low temperatures, is entirely due to quantum fluctuations: i.e., zero-point motion preventing the complete softening of the transverse optic phonons6,8. The low-temperature phase is positioned close to a quantum critical point (QCP), where different phases compete (such as paraelectric, antiferrodistortive, and FE states with similar energies9,10,11). Near the QCP, any residual interactions may drive the system to a superconducting state8,12,13.
Electron-doped SrTiO3 is one of the most dilute superconductors14 and has been known for more than half a century; however, its mechanism is poorly understood15,16. Several theoretical ideas linking the superconductivity of SrTiO3 to low-temperature instabilities have been proposed. One typical idea is that a soft phonon mode associated with the antiferrodistortive rotation may play a crucial role in the formation of Cooper pairs17. Another representative idea involves quantum fluctuations of the FE ordering6,18,19. Systematic experimental studies are needed to clarify the mechanism.
Here, we start by demonstrating an appearance of the superconducting dome; i.e., the dome-shaped evolution of Tc as a function of n, achieved by La substitution of Sr in SrTiO3 single crystals. Then, we demonstrate the further enhancement of Tc by oxygen isotope (18O) exchange of the La-substituted SrTiO3 single crystals. It should be noted here that La-substituted SrTiO3 single crystals have never been studied systematically nor in detail to date. In this work, the optimal Tc reaches 0.44 K at a carrier density n of ~5.9 × 1019 cm−3. Moreover, for the 18O-exchanged La-substituted SrTiO3 single crystals, the maximum Tc is enhanced to 0.55 K at almost the same n of ~6.0 × 1019 cm−3. These values of n are slightly lower than n ~ 1 × 1020 cm−3, at which SrTiO3−δ exhibits the optimal Tc (δ is the amount of oxygen off-stoichiometry that provides two electrons per δ in a formula unit.)20,21. These enhancements of Tc are investigated in this work, and the results suggest a hidden QCP even in a metallic region which may contribute to the Tc enhancement.
Results
Resistivity and superconductivity for La-doped SrTiO3
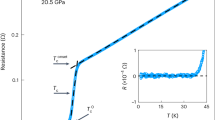
The temperature dependences of the resistivity ρ for the single crystals of Sr1−xLaxTiO3 (x ~ 0.0003, 0.0005, 0.001, 0.003, 0.005, and 0.007) are presented in Fig. 1a. Each value of x is a nominal value, which was used to prepare each sample (see Methods). As shown in the inset of Fig. 1a, each nominal value of x is almost identical to the number of carriers per Ti site, which was deduced from Hall effect measurements (see Supplementary Figure 7). It is widely accepted that in the oxygen deficient SrTiO3−δ, the carrier doping δ is directly related to the defect formation on the Ti–O bond of SrTiO3, whereas in Sr1−xLaxTiO3, the A-site substitution of the ABO3 perovskite-type structure does not directly introduce disorder to the Ti–O conduction paths22. At least for the relatively larger carrier-doping region, La substitution would be an ideal method to investigate the carrier-doping-dependent phenomena of SrTiO3. On the other hand, the disturbance due to the oxygen defects appears to be less significant in the extremely dilute doping region7,14,23, where the La substitution is not easily controlled. It should be noted, in passing, that the ideal thin film of Sr1−xLaxTiO3 fabricated by the molecular beam epitaxy method, the mobility reaches 30,000 cm2 V−1 s−1,24. But both this large mobility as well as that of our Sr1−xLaxTiO3 single crystals fit to the general trend of mobility vs. carrier concentration seen in n-doped SrTiO325 (see Supplementary Note 3).
Resistivity and superconductivity of Sr1-xLaxTiO3 single crystals. a Temperature dependence of resistivity in Sr1−xLaxTiO3 single crystals with nominal values of x ~ 0.0003, 0.0005, 0.001, 0.003, 0.005, and 0.007 with which we substituted La for Sr in the raw material. The inset shows that the number of electrons per Ti site determined using the Hall effect measurements was almost identical to the nominal value of x. b, c Resistivity in a re-plotted vs. T2. The straight dotted lines represent the best fits to the data below 40 K. As x increases, the slope gradually decreases, and the deviation point of the straight line from the real data shifts to higher temperatures. d Resistivity measured using a 3He/4He dilution refrigerator plotted against T below 1 K for the same samples shown in a. With increasing La substitution, the residual resistivity decreases monotonously, whereas the value of Tc increases up to x ~ 0.003 and decreases for x ~ 0.007
As apparent from Fig. 1a, the resistivity decreases with increasing La substitution. At 5 K, the resistivity is ~3 × 10−4 Ωcm for x ~ 0.0005, which changes to ~1.6 × 10−4 Ωcm for x ~ 0.007. These behaviours appear to reflect that of a conventional metal. The resistivity is plotted as a function of T2 in Fig. 1b and c. Although the T2 dependence of the resistivity is in general a representation of a three-dimensional Fermi liquid26, it should be noted that the ρ ~ AT2 behaviour of the conventional Fermi liquid requires Umklapp scattering, for which the smallest reciprocal lattice vector must not exceed four times the Fermi wave vector23. The smallest carrier density that satisfies this condition is greater than 2 × 1020 cm−3. Therefore, the carrier density of our Sr1−xLaxTiO3 is too small for Umklapp scattering, indicating that the ρ ~ AT2 behaviour up to high temperatures may be related to other mechanisms15. However, it is very intriguing that the behaviour of the coefficient A appears to reflect the Lifshitz transition, which is the change of the number of Fermi surfaces that occurs by changing the carrier density. This means the value of A is related to the fermiology of SrTiO3. It should be noted that this does not underpin the observed ρ ~ AT2 due to the Umklapp scattering in the conventional Fermi liquid. We will discuss this issue later.
Figure 1d shows the temperature dependences of the resistivity below 1 K for the same samples in Fig. 1a measured using a 3He/4He dilution refrigerator. Notably, no upturn in resistivity was observed upon decreasing the temperature for any of the samples with different x values, which differs from the reported weak localisation27 or charge Kondo effect observed in Sr1−xCaxTiO3−δ28. The resistive superconducting transitions are clearly observed. In this study, we define the superconducting transition temperature Tc which gives the mid-point of the resistivity during the resistance drop for the superconductivity as described in the Supplementary Note 4. The values of Tc increase from 0.26 K for x ~ 0.0005 to 0.41 K for x ~ 0.003. As x increases further, Tc decreases to 0.34 K for x ~ 0.007. All the results are summarised in Table 1.
Comparison between 18O-exchanged and 18O-free Sr1-xLaxTiO3
As described in the Methods section, we prepared two Sr1−xLaxTiO3 single-crystal rods with the same value of x, one of which was 18O exchanged. For each of the 18O-exchanged single crystals, the amount of 18O (the value of z) was evaluated from the Raman scattering (see Supplementary Figure 1). The temperature dependences of the resistivity for Sr1−xLaxTi(16O1−z18Oz)3 with (x, z) = (~0.002, 0), (~0.002, 0.57), (~0.0035, 0), (~0.0035, 0.57), (~0.01, 0), and (~0.01, 0.60) are plotted in Fig. 2a. The z = 0.57 and z = 0.60 samples are denoted hereafter as z = 0.6 for convenience. Apparent T2 dependence up to high temperatures was also observed in these samples, as shown in Fig. 2b.
Resistivity and superconductivity of Sr1−xLaxTi(16O1−z18Oz)3 single crystals. a Temperature dependence of resistivity for 18O-exchanged Sr1−xLaxTi(16O1−z18Oz)3 with (x, z) = (~0.002, 0.57), (~0.0035, 0.57), and (~0.01, 0.60) (blue lines) compared with that for Sr1−xLaxTiO3 with x ~ 0.002, 0.0035, and 0.01 (red lines). b Resistivity ρ vs. T2. The dotted lines represent ρ ~AT2 relations to fit the experimental data. The coefficient A increases with 18O exchange, indicating mass enhancement of the carriers. c Logarithmic plot of A as a function of carrier density n for all our Sr1−xLaxTi(16O1−z18Oz)3 samples in Fig. 1a and a with the data in the literature: SrTiO3–δ23 (open circles), SrTi1−xNbxO315 (crosses), and Sr1−xLaxTiO326 (triangles). The straight lines are guides to the eye. A two-orders-of-magnitude drop of A for increasing n is observed, and a kink appears at n ~ 4 × 1019 cm−3 near the critical value for the Lifshitz transition15,30,31. d–f Residual resistivity ρ0 and superconducting transition temperatures Tc measured using a 3He/4He dilution refrigerator below 1 K for the same samples shown in a
Figure 2c shows the behaviour of the coefficient A of ρ ~ AT2 for all the Sr1−xLaxTi(16O1−z18Oz)3 samples in Fig. 1a and Fig. 2a as a function of the carrier density n. We deduced the value of A by fitting the resistances of all the samples below 40 K (see Fig. 1b and c) to distinguish the low-temperature T2 behaviour from the high-temperature T3 behaviour29. The obtained value of A decreased drastically by approximately two orders of magnitude with increasing carrier density, and a kink was observed near n ~ 3.9 × 1019 cm−3. This value of n for the kink is close to the critical carrier density of the Lifshitz transition (n ~ 4.4 × 1019 cm−3 by a band calculation15, and ~3 × 1019 cm−3 by a quantum oscillation measurement30,31), where the Fermi energy enters the third t2g band. Lin et al. reported a similar kink for A in their SrTiO3−δ samples when the second t2g band starts to be filled23. As mentioned above, the coincidence of the kink of A and the Lifshitz transition is not easily acceptable. This is because the ρ ~ AT2 without the Umklapp scattering cannot be explained by the conventional Fermi liquid theory, and thus A is not necessary to reflect the topology of the Fermi surface. Furthermore, our Sr1−xLaxTiO3 does not show anomaly of Tc at the Lifshitz transition although the density of states as a function of n may have a rapid change at this transition point. These are interesting future problems, which would be a clue for understanding a superconductivity of this system.
Through the 18O exchange, the values of A become larger than those of the corresponding 18O-free ones. If we accept the Fermi liquid-like understanding of A, this result indicates that the effective mass of an electron may become larger32,33, possibly resulting from enhancement of the electron–phonon interactions. Because of the large electron–phonon interactions, the resistivity in the entire temperature range as well as the superconducting Tc are enhanced.
Figure 2d–f shows the temperature dependence of the resistivity below 1 K for the same single crystals shown in Fig. 2a. The superconducting transition temperatures of the 18O-exchanged and 18O-free samples were compared for the x ~ 0.002, 0.0035, and 0.01 samples. All the experimentally deduced parameters for Fig. 2 are summarised in Table 2.
Superconducting dome for Sr1−xLaxTi(16O1−z 18Oz)3
In Fig. 3a, Tc is plotted as a function of n for our Sr1−xLaxTi(16O1−z18Oz)3 single crystals prepared using the floating zone (FZ) method. For the z = 0.4 samples, see the Supplementary Note 4. In addition to our data, reported values of Tc for SrTiO3−δ21,28,31 and SrTi1−xNbxO3 single crystals31,34 as well as La-substituted SrTiO3 single crystals27 are also included in the plot; all of these reported samples in the literature were prepared using the Verneuil method. Despite the different crystal growth procedures (FZ or Verneuil), the values of Tc for all the La-substituted SrTiO3 single crystals (z = 0) comply with a single superconducting dome. At x ~ 0.0035 (n ~ 6 × 1019 cm−3), the dome reached a maximum Tc of ~0.44 K.
Evolution of the superconducting dome with La substitution and 18O exchange. a Tc vs. n plot for the Sr1−xLaxTi(16O1−z18Oz)3 single crystals shown in Figs. 1a and 2a. The upper and lower error bars are determined from the onset and end temperatures of the superconductivity (see Supplementary Figure 4). Tc for SrTiO3−δ21,28,31, SrTi1−xNbxO331,34, and La-substituted SrTiO327 are also plotted. b The lines were obtained from calculations based on the model in ref. 18, which are compared with some of the experimental data in a. c Tunnelling energy Γ vs. Fermi temperature TF deduced from the experimental values of Tc and n using Supplementary Equations 1 and 2: Sr1−xLaxTiO3 (red squares) and Sr1−xLaxTi(16O1−z18Oz)3 (z = 0.6; x ~ 0.002, 0.0035, and 0.01) (blue squares) from this study; SrTiO3−δ (black circles) from the literature21. The experimental data were fitted by the lines of Γ = A + BTF + CTF2. From these fitting results for Γ, we obtained the Tc vs. n relation represented by the lines in b. d The blow-up of c to emphasise where the Γ crosses Γ = 1 line
Discussion
FE fluctuations in SrTiO3 with zone-centre soft-mode optical phonons (either longitudinal or transverse) have been considered to play some relevant roles in the mechanism of the superconductivity16,35,36,37,38,39. As the FE fluctuations are clearly suppressed with increasing carrier density n (as the system becomes more metallic), the concomitant disappearance of the superconductivity for the overdoped region (n ≳ 2 × 1020 cm−3) may be an implication of the superconductivity driven by the ferroelectricity. On the other hand, in the underdoped region (n ≲ 1 × 1020 cm−3), the FE fluctuations are enhanced by the decrease of n. However, if n is too small, the superconductivity is depressed, as the carrier density is not sufficient to provide robust superconductivity. The formation of the superconducting dome can be explained in this way, though there is room for argument.
What is prominent in Fig. 3a is not only the elucidation of the superconducting dome of Sr1−xLaxTiO3 but also the large enhancement of its Tc by the 18O exchange. As described above, there are many models of the mechanism of superconductivity in SrTiO3−δ; however, most of these models cannot be simply applied to our experimental data to provide insight into the enhancement by the 18O exchange. A recent theoretical approach proposed by Edge et al.18 is one of the most tractable approaches, such that we attempted to compare this model to our data as follows. It should be noted here that we do not rule out any other theories which may explain the rise of the superconducting dome.
We calculated the theoretical Tc vs. n curve applying the model in ref. 18 to the reported21 and our experimental Tc vs. n data. In Fig. 3b, the curves (solid and partially dashed lines) are plotted with the experimental data points. The black line is for SrTiO3−δ, the red line is for Sr1−xLaxTiO3, and the blue line is for Sr1−xLaxTi(16O0.418O0.6)3. Details of the calculation steps are provided in Supplementary Note 7. The model explains fairly well the observed superconducting dome of Sr1−xLaxTiO3.
The Tc vs. n lines in Fig. 3b are based on the Γ vs. TF plots in Fig. 3c. Here, Γ is the tunnelling energy of the double-well potential18 in analogy with that of magnetic phase transitions, and TF is the Fermi energy but we used the value of TF deduced from the carrier density by assuming a free electron gas without mass enhancement. The Γ vs. TF plot was obtained directly from the experimental Tc vs. n data, as described in the Supplementary Note 7. Then, we fit the data using a power expansion of Γ in TF such as Γ = A + BTF + CTF2, where A, B, and C are fitting parameters. The QCP, i.e., the divergence of λ, corresponds to the point at which Γ = 1. It should be noted that our systematic investigation of La substitution made a reliable fitting possible. Then, it has finally elucidated that Γ < 1 below n < nc in Sr1−xLaxTiO3 as seen in Fig. 3b (the blow-up is plotted in Fig. 3d); this means the model predicts the appearance of a QCP at n = nc ~ 3 × 1018 cm−3.
At n = nc, the superconductivity coupling constant λ diverges, and Tc at the QCP becomes unpredictable18. Our own numerical calculations following the model produced an exponential enhancement of Tc at n = nc (dotted lines in Fig. 3b). It has been suggested that if QCP is above around 1 × 1018 cm−3, Tc goes up when the system approaches the QCP40. However, the validity of this divergence is controversial. The value of Tc might be suppressed to zero because the model is not simply applicable in the vicinity of QCP. Unfortunately, for our Sr1−xLaxTiO3 system, it is difficult to explore such an extremely dilute region, where the system actually crosses the QCP. This is an important problem to be clarified by more detailed experimental investigation, such as the application of tensile stress, which is considered to shift the QCP towards the higher doping region leading to a drastic enhancement of Tc at the QCP41,42 or the isostatic pressure to diminish the QCP40,43 and suppress Tc.
We further attempted to fit the Γ vs. TF data of Sr1−xLaxTi(16O1−z18Oz)3 (z = 0.6) using Γ = A + BTF + CTF2 with the same B and C values as those for Sr1−xLaxTiO3 (blue dashed line in Fig. 3b). Although this assumption is naive, we do not think that it is unreasonable, because in principle 18O exchange does not affect TF. Because our experimental data are only three points, the fitting was not very good. We understand that nc increased; i.e., the QCP shifts towards larger carrier density with the 18O exchange. The observed further enhancement of Tc (blue line in Fig. 3a) can be explained in this way by the shift of QCP.
It should be mentioned that the SrTiO3−δ data21 in Fig. 3b cannot be simply fitted by the same model in ref. 18. It seems that the data might be separated into at least two parts: a smaller carrier-density region below ~5 × 1019 cm−3, and a larger carrier-density region above it. The fitting of the experimental data in the larger carrier-density region (dash-dotted line in Fig. 3b) suggests there is QCP even for SrTiO3−δ at almost the same carrier density as that of Sr1-xLaxTiO3 (see the Γ = 1 point of the red solid line and the dash-dotted line in Fig. 3c and d). On the other hand, in the small carrier-density region, although the data of SrTiO3−δ are almost identical to those of Sr1−xLaxTiO3, the two additional points in the lowest carrier density make the fitting worse (see the black solid and dotted line). The analysis predicts the QCP may be close to 2 × 1018 cm−3.
Figure 4 presents schematic diagrams showing the evolution of the FE QCP in the metallic region. The planes are spanned by the horizontal axes of carrier density and the vertical axes of ferroelectricity. The FE state must be rapidly suppressed by the screening due to mobile carriers; however, a certain ordered state was considered to remain even in the metallic phase for very small n18,28. Hence, the boundary of the ordered FE state is assumed to penetrate into the carrier doped region as shown in Fig. 418.
Schematic diagrams of La substitution and 18O exchange. Schematic explanation of the evolution of QCP in the metallic state, carrier doping by oxygen defects (red arrows), 18O exchange and Ca substitution toward ferroelectricity (blue arrows), as well as the La substitution (green arrow) on the “ferroelectricity” vs. “carrier density” plane. The corresponding Tc vs. n schematics are also shown. a α) SrTi(16O1−z18Oz)3−δ44 and β) Sr1−xCaxTiO3−δ28, b Sr1−xLaxTiO3, and c Sr1−xLaxTi(16O1−z18Oz)3. QCP corresponds to the white portion of the arrow at which the behaviour of Tc becomes unpredictable18. However, the shift of QCP towards larger carrier-density region is expected to raise the superconducting dome upwards18,31,42
In the literature, there were two types of investigations of the superconductivity on this plane (Fig. 4a). One is to do 18O exchange (blue vertical arrow) and to dope carriers by oxygen-defect creation (red horizontal arrow)44. The other is to do Ca2+ substitution for Sr2+ (blue vertical arrow) and to dope carriers by oxygen-defect creation (red horizontal arrow)28. The former did not actually cross the QCP but an enhancement of Tc was observed. The latter crossed the QCP but there was no anomaly in the Tc vs. n behaviour at QCP, contradicting to the theoretical models18,42. However, in these systems, the values of Tc are relatively large even in the small carrier-density region. There must be a non-negligible contribution of the latent ferroelectricity in the metallic state to the enhancement of the superconductivity.
The La substitution process can be expressed as the diagonal line (Fig. 4b). As discussed in the Supplementary Note 6, if we consider a virtual “La2+” substitution as an analogy of Sr1−xBaxTiO3 and Sr1−xCaxTiO3, it is reasonable to assume that the La substitution process can be decomposed into 1) SrTiO3 to Sr1−x“La2+”xTiO3 process (light blue vertical arrow) and 2) Sr1−x“La2+”xTiO3 to Sr1−xLaxTiO3 process (light red horizontal arrow). Therefore, the actual La substitution process is represented by the diagonal green arrow. (This green arrow is not necessary to be the straight one but for simplicity we consider it is a simple straight arrow.) Since there is no experimental evidence, we are not sure the diagonal line crosses the border of the FE metal and the normal metal (i.e., the so-called quantum critical line QCL), but the analysis of our experimental data with the theoretical model18 has predicted the appearance of QCP. Although the figure is schematic, we can assume the crossing point (or the point where the diagonal line is in the vicinity of the border line) is located in the low carrier-density region.
The SrTi(16O1−z18Oz)3 exhibits ferroelectricity at z = 0.36 (refs. 45. and 46). Then, the La substitution process for Sr1−xLaxTi(16O1−z18Oz)3 (z > 0.36) corresponds to the green diagonal line in Fig. 4c. This diagonal line is sure to cross the border of the FE metal and the normal metal. The important argument in this schematic diagram is that the crossing point for Sr1−xLaxTi(16O1−z18Oz)3 (z > 0.36) should appear at larger n than that of Sr1−xLaxTiO3, explaining why Tc of Sr1−xLaxTi(16O1−z18Oz)3 (z > 0.36) is higher than that of Sr1−xLaxTiO3. It is clearly demonstrated that diagonal La substitution x in Sr1−xLaxTi(16O1−z18Oz)3 is much more effective for increasing Tc than the simple horizontal oxygen-defect doping δ in SrTi(16O1−z18Oz)3−δ.
In summary, we prepared high-quality Sr1−xLaxTi(16O1−z18Oz)3 single crystals in the low doping region (0.0003 ≲ x ≲ 0.01) with oxygen-isotope exchange. La substitution is an ideal method to introduce carriers into SrTiO3; our samples do not show tendencies of localisation at low temperatures. The carrier density is too small for Umklapp scattering23; however, the ρ ~ AT2 behaviour is seen and the coefficient A reflects the topological change of the Fermi surface, suggesting that the Sr1−xLaxTiO3 system cannot be simply understood by a conventional Fermi liquid theory. The superconducting Tc exhibits a dome shape similar to that of SrTiO3−δ. The values of Tc were remarkably enhanced to 0.55 K for Sr1−xLaxTi(16O1−z18Oz)3 (x ~ 0.0035 and z ~ 0.6). Although the mechanism of the superconductivity in SrTiO3−δ and related materials remains a controversial topic, we demonstrated reasonable agreement of our experimental data with the hidden FE QCP model; i.e., the QCP is located in a region where the system is already metallic and will contribute to the Tc enhancement.
Ferroelectricity is a state of broken inversion symmetry. If we can prepare a sample within the QCP of Sr1−xLaxTi(16O1−z18Oz)3, it may be a novel realisation of noncentrosymmetric superconductivity47, which is currently under intensive study, as it may hold mixed-parity pairing mechanisms with topological aspects to their superconducting states. Such a sample will possibly incubate extremely large and highly anisotropic upper critical fields and topologically protected spin currents48,49. Our findings will add another page to current research on the FE QCP and associated superconductivity.
Methods
Synthesis of Sr1−xLaxTiO3 single crystals
Mixed powders of SrCO3, La2O3, and TiO2 in a ratio of 1−x:x/2:1 were calcined at 500 °C in air for 2–3 h. The calcined powders were sintered at 1000 °C in air for 5 h. Then, the powders were pulverised and formed into a rod with a diameter of approximately 4 mm and length of approximately 60 mm. The rod was fired at 1300 °C–1380 °C for 5 h in a flowing argon gas atmosphere. The crystal growth of Sr1−xLaxTiO3 was performed with a conventional FZ method. In this method, we use a furnace equipped with double hemi-ellipsoidal mirrors coated with gold. Two halogen incandescent lamps were used as heat sources. The crystals were grown in a stream of argon gas, and the growth rate was set at 10–15 mm per hour.
Synthesis of Sr1−xLaxTi(16O1−z 18Oz)3 single crystals
Because the oxygen diffusion in La-substituted single crystals is extremely slow50, the oxygen isotope (18O) exchange was fulfilled for the mixed powders of SrTiO3, La2O3, and TiO2. We first prepared the SrTiO3 powders. The mixed powder of SrCO3 and TiO2 with a molar ratio of 1:1 was calcined at 500 °C for 2–3 h. The calcined powders were sintered at 1280 °C for 30 h in air to synthesise the polycrystalline powders of SrTiO3. Then, we mixed the powders of SrTiO3, La2O3, and TiO2 in a ratio of 1−x:x/2:x and formed them into a rod with a diameter of 4 mm and length of 60 mm. The rod was sintered at 1000 °C in air for 5 h. The sintered rod was then divided into two rods. In a furnace equipped with double sapphire tubes, one rod was placed in the tube with flowing 16O2/18O2 mixed gas atmosphere to exchange the 16O atoms with 18O ones. The other rod was placed in the other tube in a flowing oxygen (16O) atmosphere as a reference. The temperature of the furnace was then increased to 1000 °C to promote the 16O/18O exchange. The annealing at 1000 °C was continued until the equilibrium concentration of the 16O2/18O2 atmosphere was reached. The amount of 18O atoms absorbed into the rod was by first estimated from the weight change of the rod and then from the amount of 18O2 gas in the atmosphere of the furnace, which was determined using a quadrupole mass analyser. These two values matched very well, which indicated that the 18O-exchange was sufficiently controlled in our experiments. Both the 18O-free and 18O-exchanged feed rods were used for the single crystal growth, the procedure for which was the same as described in the previous section. The amount of 18O atoms in the grown crystals was finally determined from the frequency shift of the Raman scattering (Supplementary Figure 1).
Resistivity measurements
The formation of a single crystal was confirmed using the reflection Laue method. Several pieces were cut from the single crystal rod along the [100] direction of the cubic indices. The pieces were further formed into a rectangular shape with the longest dimension parallel to the [100] direction of the cubic indices. The typical dimensions were 0.5 × 0.3 × 7 mm3. The d.c. resistivity ρ and Hall resistivity ρH for 5 K ≤ T ≤ 300 K were measured in a cryostat equipped with a superconducting magnet (Physical Property Measurement System (PPMS), Quantum Design Inc.). The resistivity down to 50 mK was measured using an a.c. resistance bridge (LR700, Linear Research Inc.) in a cryostat with a 3He/4He dilution refrigerator (µ dilution, Taiyo-Toyo Sanso Inc.). The electrodes were prepared using ultrasonic indium soldering. The transport current was injected parallel to the [100] direction of the cubic indices.
Data availability
The data that support the plots within this paper and other findings of this study are available in figshare with the digital object identifier https://doi.org/10.6084/m9.figshare.7434221 (ref. 51). Further data and resources in support of the findings of this study are available from the corresponding authors upon reasonable request.
References
Lemanov, V. V. Improper ferroelastic SrTiO3 and what we know today about its properties. Ferroelectrics 265, 1–21 (2011).
Chandra, P., Lonzarich, G. G., Rowley, S. E. & Scott, J. F. Prospects and applications near ferroelectric quantum phase transitions: a key issues review. Rep. Prog. Phys. 80, 112502 (2017).
Yamanaka, A. et al. Evidence for competing orderings in strontium titanate from hyper-Raman scattering spectroscopy. Europhys. Lett. 50, 688–694 (2000).
Aschauer, U. & Spaldin, N. Competition and cooperation between antiferrodistortive and ferroelectric instabilities in the model perovskite SrTiO3. J. Phys. Condens. Matter 26, 122203 (2014).
Zhong, W. & Vanderbilt, D. Competing structural instabilities in cubic perovskites. Phys. Rev. Lett. 74, 2587–2590 (1995).
Müller, K. A. & Burkard, H. SrTiO3: An intrinsic quantum paraelectric below 4 K. Phys. Rev. B 19, 3593–3602 (1979).
Spinelli, A., Torija, M. A., Liu, C., Jan, C. & Leighton, C. Electronic transport in doped SrTiO3: conduction mechanisms and potential applications. Phys. Rev. B 81, 155110 (2010).
Gabay, M. & Triscone, J.-M. Superconductivity: ferroelectricity woos pairing. Nat. Phys. 13, 624–625 (2017).
Saifi, M. A. & Cross, L. E. Dielectric properties of strotium titanate at low temperatures. Phys. Rev. B 2, 677–684 (1970).
Zhong, W. & Vanderbilt, D. Effect of quantum fluctuations on structural phase transitions in SrTiO3 and BaTiO3. Phys. Rev. B 53, 5047–5050 (1996).
Hemberger, H. et al. Quantum paraelectric and induced ferroelectric states in SrTiO3. J. Phys.: Condens. Matrer 8, 4673–4690 (1996).
Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1998).
Coleman, P. & Schofield, A. J. Quantum criticality. Nature 433, 226–229 (2005).
Lin, X., Zhu, Z., Fauqué, B. & Behnia, K. Fermi surface of the most dilute superconductor. Phys. Rev. X 3, 021002 (2013).
van der Marel, D., van Mechelen, J. L. M. & Mazin, I. I. Common Fermi-liquid origin of T 2 resistivity and superconductivity in n-type SrTiO3. Phys. Rev. B 84, 205111 (2011).
Gor’kov, L. P. Phonon mechanism in the most dilute superconductor n-type SrTiO3. Proc. Natl Acad. Sci. USA 113, 4646–4651 (2016).
Appel, J. Soft-mode superconductivity in SrTiO3−x. Phys. Rev. 180, 508–515 (1969).
Edge, J. M., Kedem, Y., Aschauer, U., Spaldin, N. A. & Balatsky, A. V. Quantum critical origin of the superconducting dome in SrTiO3. Phys. Rev. Lett. 115, 247002 (2015).
Rowley, S. E. et al. Ferroelectric quantum criticality. Nat. Phys. 10, 367–372 (2014).
Koonce, C. S., Cohen, M. L., Schooley, J. F., Hosler, W. R. & Pfeiffer, E. R. Superconducting transition temperatures of semiconducting SrTiO3. Phys. Rev. 163, 380–390 (1967).
Schooley, J. F. et al. Dependence of the superconducting transition temperature on carrier concentration in semiconducting SrTiO3. Phys. Rev. Lett. 14, 305–307 (1965).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Lin, X., Fauque, B. & Behnia, K. Scalable T 2 resistivity in a small single-component Fermi surface. Science 349, 945–948 (2015).
Son, J. et al. Epitaxial SrTiO3 films with electron mobilities exceeding 30,000 cm2V-1s-1. Nat. Mater. 9, 482–484 (2010).
Behnia, K. On mobility of electrons in a shallow Fermi sea over a rough seafloor. J. Phys. Condens. Matter 27, 375501 (2015).
Okuda, T., Nakanishi, K., Miyasaka, S. & Tokura, Y. Large thermoelectric response of metallic perovskites: Sr1−xLaxTiO3 (0≤x≤0.1). Phys. Rev. B 63, 113104 (2001).
Suzuki, H. et al. Superconductivity in single-crystalline Sr1−xLaxTiO3. J. Phys. Soc. Jpn. 65, 1529–1532 (1996).
Rischau, C. W. et al. A ferroelectric quantum phase transition inside the superconducting dome of Sr1−xCaxTiO3−δ. Nat. Phys. 13, 643–648 (2017).
Lin, X. et al. Metallicity without quasi-particles in room-temperature strontium titanate. npj Quantum Mater. 2, 41 (2017).
Lin, X. et al. Critical doping for the onset of a two-band superconducting ground state in SrTiO3−δ. Phys. Rev. Lett. 112, 207002 (2014).
Collignon, C., Lin, X., Rischau, C. W., Fauque, B. & Behnia, K. Metallicity and superconductivity in doped strontium titanate. Ann. Rev. Cond. Mat. Phys. 10, 13–43 (2018).
Kadowaki, K. & Woods, S. B. Universal relationship of the resistivity and specific heat in heavy-fermion compounds. Solid State Commun. 58, 507–509 (1986).
Hussey, N. E. Non-generality of the Kadowaki-Woods ratio in correlated oxides. J. Phys. Soc. Jpn. 74, 1107–1110 (2005).
Lin, X. et al. Multiple nodeless superconducting gaps in optimally doped SrTi1−xNbxO3. Phys. Rev. B 90, 140508(R) (2014).
de Lima, B. S. et al. Interplay between antiferrodistortive, ferroelectric, and superconducting instabilities in Sr1−xCaxTiO3−δ. Phys. Rev. B 91, 045108 (2015).
Gurevich, L., Larkin, A. & Firsov, Y. On the possibility of superconductivity in sermiconductors. Sov. Phys. Solid State 4, 131–135 (1962).
Takada, Y. Theory of superconductivity in polar semiconductors and its application to N-type semiconducting SrTiO3. J. Phys. Soc. Jpn. 49, 1267–1275 (1980).
Bussmann-Holder, A., Simon, A. & Büttner, H. Possibility of a common origin to ferroelectricity and superconductivity in oxides. Phys. Rev. B 39, 207–214 (1989).
Lin, X., Rischau, C. W., van der Beek, C. J., Fauqué, B. & Behnia, K. s-wave superconductivity in optimally doped SrTi1−xNbxO3 unveiled by electron irradiation. Phys. Rev. B 92, 174504 (2015).
Rowley, S. E., et al. Superconductivity in the vicinity of a ferroelectric quantum phase transition. http://arxiv.org/abs/1801.08121 (2018).
Herrera, C., Cerbin, J., Dunnett, K., Balatsky, A. V. & Sochnikov, I. Strain-engineered interaction of quantum polar and superconducting phases. http://arxiv.org/abs/1808.03739 (2018).
Dunnett, K., Narayan, A., Spaldin, N. A. & Balatsky, A. V. Strain and ferroelectric soft-mode induced superconductivity in strontium titanate. Phys. Rev. B 97, 144506 (2018).
Coak, M. J. et al. Dielectric response of quantum critical ferroelectric as a function of pressure. Sci. Rep. 8, 14936 (2018).
Stucky, A. et al. Isotope effect in superconducting n-doped SrTiO3. Sci. Rep. 6, 37582 (2016).
Itoh, M. et al. Ferroelectricity induced by oxygen isoope exchange in strontium titanate perovskite. Phys. Rev. Lett. 82, 3540–3543 (1999).
Itoh, M. & Wang, R. Quantum ferroelectricity in SrTiO3 induced by oxygen isotope exchange. Appl. Phys. Lett. 76, 221–223 (2000).
Kanasugi, S. & Yanase, Y. Spin-orbit-coupled ferroelectric superconductivity. Phys. Rev. B 98, 024521 (2018).
Bauer, E. & Sigrist, M. Non-centrosymmetric Superconductors: Introduction and Overview. (Springer, Berlin, 2012).
Yip, S. Noncentrosymmetric superconductors. Ann. Rev. Condens. Matter Phys. 5, 15–33 (2014).
Paladino, A. E., Rubin, L. G. & Waugh, J. S. Oxygen ion diffusion in single crystal SrTiO3. J. Phys. Chem. Solids 26, 391–397 (1965).
Inoue, I. Enhanced superconductivity close to a non-magnetic quantum critical point in electron-doped strontium titanate: replication dataset. Figshare Digital Repository https://doi.org/10.6084/m9.figshare.7434221 (2019).
Acknowledgements
This study was supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant No. 17684020 (Young Scientists A) and Grant Nos. 24244062, 15H02113, and 18H03686 (Category A). The authors would like to thank Yoshihiro Aiura and the late Hiroshi Bando for use of their patented isotope-gas-circulating furnace before the patent was filed and for helping us adapt the equipment for this research project. The authors are also grateful to Jun’ya Tsutsumi and Nao Takeshita for their help with the experiments and to Yasuhiro Tada, Masaki Oshikawa, Justin Ye, Akihito Sawa, Izumi Hase, Matthew Coak, Alexander Balatsky, and Kamran Behnia for fruitful discussions.
Author information
Authors and Affiliations
Contributions
The single crystal growth and resistivity measurements were performed by Y.T. Oxygen isotope substitution was performed by I.H.I. The 3He/4He dilution refrigerator was set up by N.S., and all the measurements below 1 K were conducted by Y.T. and N.S. Raman scattering spectra were measured and analysed by K.S. All the authors discussed the results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tomioka, Y., Shirakawa, N., Shibuya, K. et al. Enhanced superconductivity close to a non-magnetic quantum critical point in electron-doped strontium titanate. Nat Commun 10, 738 (2019). https://doi.org/10.1038/s41467-019-08693-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-08693-1
This article is cited by
-
Stoichiometric control of electron mobility and 2D superconductivity at LaAlO3-SrTiO3 interfaces
Communications Physics (2024)
-
Superconductivity enhancement in polar metal regions of Sr0.95Ba0.05TiO3 and Sr0.985Ca0.015TiO3 revealed by systematic Nb doping
npj Quantum Materials (2022)
-
Superconductivity from energy fluctuations in dilute quantum critical polar metals
Nature Communications (2022)
-
A large modulation of electron-phonon coupling and an emergent superconducting dome in doped strong ferroelectrics
Nature Communications (2021)
-
Study of Carrier Transfer Mechanism When Substituting Strontium at Barium Sites in CuTl-1223 Superconducting Phase
Journal of Electronic Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.