Abstract
Microcombs provide a path to broad-bandwidth integrated frequency combs with low power consumption, which are compatible with wafer-scale fabrication. Yet, electrically-driven, photonic chip-based microcombs are inhibited by the required high threshold power and the frequency agility of the laser for soliton initiation. Here we demonstrate an electrically-driven soliton microcomb by coupling a III–V-material-based (indium phosphide) multiple-longitudinal-mode laser diode chip to a high-Q silicon nitride microresonator fabricated using the photonic Damascene process. The laser diode is self-injection locked to the microresonator, which is accompanied by the narrowing of the laser linewidth, and the simultaneous formation of dissipative Kerr solitons. By tuning the laser diode current, we observe transitions from modulation instability, breather solitons, to single-soliton states. The system operating at an electronically-detectable sub-100-GHz mode spacing requires less than 1 Watt of electrical power, can fit in a volume of ca. 1 cm3, and does not require on-chip filters and heaters, thus simplifying the integrated microcomb.
Similar content being viewed by others
Introduction
Optical frequency combs have revolutionized time-keeping and frequency metrology over the past two decades, and have found a wide variety of applications1,2. Microresonator-based Kerr frequency combs (Kerr microcombs) have provided a route to compact chip-scale optical frequency combs, with broad optical bandwidth and repetition rates in the microwave to terahertz domain (10 GHz−1 THz)3,4. Their compact and low-power nature could enable utilization in mobile or airborne applications beyond research laboratories, including operation in space5. The observation that such microcombs can be operated in the dissipative Kerr soliton (DKS) regime (soliton microcombs) has enabled fully coherent microcombs6,7. DKS exhibits a rich set of nonlinear optical phenomena such as soliton Cherenkov radiation (also known as dispersive waves), which can extend the spectral bandwidth of the frequency comb8. Soliton microcombs have been applied in counting of the cycles of light9, coherent communication10, ultrafast ranging11,12, dual-comb spectroscopy13, low-noise microwave generation14, and optical frequency synthesis15. The full photonic integration of soliton microcombs in a single, compact, and electrically driven package would allow mass-manufacturable devices compatible with emerging high-volume applications such as laser-based ranging, or sources for dense wavelength division multiplexing for data center-based optical interconnects. Via advances in silicon photonics, such level of integration has been achieved for lasers16, modulators17, and a wide range of passive and active elements, which are already commercially available. Photonic integration of soliton microcombs requires not only the integration of nonlinear high-Q microresonators on chip but also an on-chip solution for the narrow linewidth seed lasers with output power levels that are sufficient for soliton initiation, as well as any laser tuning mechanism used in the soliton excitation process7,8,18,19. On one hand, photonic integration of high-Q microresonators suitable for the soliton formation has advanced significantly, in particular using Si3N4—a CMOS-compatible material used as a capping layer20. The platform possesses several advantageous properties, including a high Kerr nonlinearity, large flexibility for dispersion engineering, outer-space compatibility5, and a large bandgap (~5 eV), thus free from two-photon absorption in the telecommunication band. All these advantages facilitate soliton formation in Si3N4 microresonators8. In a related effort, ultrahigh-Q SiO2 air-clad microresonators have recently been integrated with Si3N4 waveguides for soliton generation21. On the other hand, efforts to combine integrated photonic microresonators with chip-scale lasers, such as those developed in silicon photonics, have recently been made15. Yet, these and other approaches are still optically pumped with stand-alone bulk laser modules, and typically employ additional amplifiers for soliton initiation to overcome coupling losses and the low Q-factors of integrated photonic resonators. Likewise, the use of silicon photonics-based lasers is presently compounded since the threshold of soliton formation usually exceeds the laser’s output power (few-mW scale). Recent advances in fabrication of high-Q Si3N4 photonic integrated microresonators (intrinsic Q0 > 1 × 107)22,23,24 suggest that electrically driven microcombs that employ chip-scale laser diodes—compatible with scalable manufacturing—may become viable.
Here we demonstrate an electrically driven, and current-initiated, soliton microcomb significantly simplifying photonic integration. The integrated device has a volume of ca. 1 cm3, and uses a commercially available semiconductor laser diode chip. This device consumes less than 1 Watt of electrical power and produces a soliton microcomb with sub-100-GHz line spacing. By using high-Q (Q0 > 1 × 107) photonic chip-scale Si3N4 microresonators fabricated using the photonic Damascene reflow process24,25, in conjunction with a multiple-longitudinal-mode (multi-frequency) Fabry–Pérot InP laser diode chip, we observe self-injection locking26,27 in a regime where solitons are formed concurrently. Such self-injection locking with concurrent soliton formation has recently been demonstrated for bulk ultrahigh-Q crystalline MgF2 resonators14,28. We observe that the current tuning of the laser diode can induce transitions from the injection-locking-based single-longitudinal-mode lasing (×1000-fold reduction of linewidth) to Kerr frequency combs, breather soliton formation, followed by stable multiple and single DKS formation in the integrated microresonator. Heterodyne measurements demonstrate the low-noise nature of the generated soliton states. Such an electrically driven photonic chip-based soliton microcomb demonstrated here provides a solution for integrated, unprecedentedly compact optical comb sources suitable for high-volume applications. In comparison with a concurrent report of integrated soliton microcomb29, our scheme alleviates the need for on-chip Vernier filters, as well as for thermal heaters for soliton tuning30, which avoids extra power consumption (30 mW per heater29) and the complexity in both the fabrication process and the process of soliton initiation.
Results
Experimental setup and technique
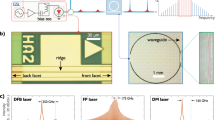
Figure 1 illustrates the approach taken in this work. A multi-frequency Fabry–Pérot laser diode chip (InP) is directly butt-coupled to a Si3N4 photonic chip (Fig. 1a, b). The butt-coupling scheme gives an overall insertion loss of ~6 dB (diode-chip-lensed fiber), with a double-inverse tapered structure for the light input/output coupling31. When the frequency of the light emitted from the laser diode coincides with a high-Q resonance of the Si3N4 microresonator, laser self-injection locking can take place. The process occurs due to the bulk and surface Rayleigh scattering in the microresonator, which injects a fraction of light back into the diode27. This provides a frequency-selective optical feedback to the laser, leading to single-frequency operation with a significant reduction of the laser linewidth.
Principle of an ultra-compact, laser injection-locked soliton Kerr frequency comb. a Close-range photo of the experimental setup, in which the laser diode chip is butt-coupled to a Si3N4 photonic chip, which contains several microresonators. b Schematic representation of the laser injection-locked soliton Kerr frequency comb. An InP multi-frequency laser diode chip is directly butt-coupled to a Si3N4 photonic chip with a microresonator. c An optical image of the InP laser diode chip showing the magnified view. d Sketch of the experimental setup. The microresonator device output is characterized both in the optical domain using an optical spectral analyzer and in the radio frequency (RF) domain using an electrical-signal spectral analyzer. In addition, to assess the coherence of the frequency comb, we employ a heterodyne beatnote measurement to a selected comb tooth with a narrow linewidth reference laser. TC: temperature control module; CC: current control module; AFG: arbitrary function generator; OSA: optical spectral analyzer; OSC: oscilloscope; ESA: electrical-signal spectral analyzer. e False-colored scanning electron micrograph (SEM) image of the waveguide cross-section. The Si3N4 waveguide (blue) has no top SiO2 cladding but only side and bottom SiO2 cladding (red)
A key step for our approach is to match the optical power requirement for soliton generation to that of the laser diode. This is achieved by employing high-Q Si3N4 microresonators fabricated using the photonic Damascene process, featured with a novel and critical reflow step24, allowing for ultra-smooth waveguide sidewalls that enable high-Q-factors (Q0 > 1 × 107) across the entire L-band (cf. Methods).
The Fabry–Pérot laser diode we employ in the experiments is centered at 1530 nm, and its emission spectrum without self-injection locking is shown in Fig. 2b. The mode spacing is 35 GHz, determined by the Fabry–Pérot cavity length. The overall maximum optical output power is ~100 mW when applying a current of ~350 mA to the diode. The electrical power consumed by the laser diode is less than 1 W. Figure 2c shows the heterodyne beatnote of the free running laser diode mode with a reference laser (Toptica CTL1550, short-time linewidth ~10 kHz), which is fitted with the Voigt profile (cf. discussions in the following and Methods), revealing both a Gaussian linewidth of 60 MHz and an estimated short-time linewidth of 2 MHz.
Electrically pumped soliton microcomb via laser injection-locked soliton formation. a Transmission spectrum of a Si3N4 microresonator of 1.02 THz free spectral range (FSR), featuring two sets of resonances: the fundamental transverse electric (TE) mode family (marked by red circles) and one high-order TE mode family. b The laser spectrum of the multi-frequency laser diode chip used in this experiment, corresponding to state i in g. c Measured and fitted heterodyne beat signal between the free running laser diode and a narrow linewidth reference laser (Toptica CTL1550, short-time linewidth ~10 kHz), showing 60 MHz full-width at half-maximum (FWHM) of Voigt profile. d (state ii in g): Spectra of single longitudinal mode that is injection locked to a selected resonance of the microresonator. f (state iii in g): Spectrum of the Kerr frequency comb that stems from the laser injection locking. Inset: One resonance of the fundamental TE mode showing mode splitting due to backscattering, with the estimated 118 MHz coupling strength \(\left( {\frac{\gamma }{{2\pi }}} \right)\) between the forward and backward propagating modes. e Heterodyne beat signal between the injection-locked laser and a narrow linewidth reference laser. The measured beat signal is fitted with Voigt profile with FWHM ~186 kHz (cf. Methods). RBW: Resolution bandwidth. g Typical transmitted power trace measured at the chip output facet, by current modulation imposed on the laser diode, in which different states are marked: (i) noisy, multi-frequency lasing without injection locking; (ii) laser injection locking to a microresonator resonance, and simultaneous formation of low-noise single-longitudinal-mode lasing (the orange region); (iii) formation of Kerr frequency comb (the green region)
Self-injection locking phenomena
We first studied self-injection locking of the laser diode chip to the photonic chip-based microresonator. This is achieved by tuning the current of the laser diode, which not only changes the optical output power but also shifts the lasing frequency via the carrier dispersion effect. Initially, the laser diode coupled to the Si3N4 chip operates multi-frequency (Fig. 2b), a regime where none of the high-Q microresonator modes is frequency-matched with the multi-mode laser emission from the diode. By shifting the lasing frequency of the diode via current tuning, we observe that the initially multi-frequency emission spectrum switches to single mode operation, indicative of self-injection locking. Figure 2d demonstrates that the lasing frequency coincides with a selected resonance of the microresonator, and we also observe injection locking occurring for several resonances32. We note that all resonances, which give rise to the laser self-injection locking, feature mode splitting as a result of backscattering (cf. the inset in Fig. 2d). The back-coupling rate for the measured resonance, extracted from its mode-splitting profile, is γ/2π = 118 MHz (cf. Methods). The presence of this back-coupling leads to an amplitude reflection coefficient (r) from the passive microresonator on resonance:
where η = κex/κ characterizes coupling efficiency (κ = κ0 + κex, with η = 1/2 corresponding to critical coupling, and η ≈ 1 corresponding to strong overcoupling), and Γ = γ/κ is the normalized mode-coupling parameter that describes the visibility of the resonance split. According to ref. 33 this reflection can initiate self-injection locking, and give rise to a narrow linewidth of:
where Q = ω/κ is the microresonator quality factor, ω/2π is the light frequency, and δωfree/2π is the linewidth of the free running laser. The phase-amplitude coupling factor αg is the linewidth enhancement factor, given by the ratio of the variation of the real refractive index to the imaginary refractive index of the laser diode-active region in response to a carrier density fluctuation34 and takes typical values from 1.6 to 7. The InGaAsP/InP multiple quantum well laser diode has αg = 2.5. The laser diode quality factor QLD can be estimated as \(Q_{{\mathrm{LD}}} \approx \frac{{\omega \tau _{\mathrm{d}}R_{\mathrm{o}}}}{{1 - R_{\mathrm{o}}^2}},\) where Ro is the amplitude reflection coefficient of the output laser mirrors and τd is the laser cavity round trip. The reflection coefficient is a parameter of the laser diode and is given by the laser diode manufacturer as \(R_{\mathrm{o}} = \sqrt {0.05}\) as well as αg = 2.5. Other experimentally determined parameters are κ/2π ≈ 110 MHz, γ/2π ≈ 118 MHz, η ≈ 0.64, Γ ≈ 1, and τd = 1/FSRdiode = 1/(35 GHz) = 28.6ps. The theoretical estimation for the narrowed linewidth is δω/2π~0.1 kHz. We next compare these theoretical estimates of the self-injectioned locked linewidth to experiments. The linewidth of the self-injection-locked single-longitudinal-mode laser is measured by a heterodyne measurement (see Fig. 2e). The lineshape is fitted with a Voigt profile, which represents a convolution of Lorentzian and Gaussian lineshape (cf. Methods), yielding a Gaussian contribution to the linewidth of 186 kHz. The estimated Lorentzian contribution amounts to 0.7 kHz, describing the wings of the measured beatnote. Self-injection locking leads to a narrowing of the white noise of the laser diode (Eq. 2)33. Therefore, this value should be compared with the Lorentzian contribution in the Voigt profile (i.e., 0.7 kHz) corresponding to a more than 1000-fold reduction in the linewidth.
Injection locking occurs also in the case where the laser cavity and microresonator are detuned from each other due to “injection pulling,” and as outlined below, is imperative to generate DKS using self-injection locking. Injection pulling is a result of a slight phase difference between the laser emission and its feedback, leading to imperfect locking33. The locking range is defined as the frequency range over which the laser diode emission self-injection locks to the high-Q microresonator resonance and follows the expression33:
The theoretically estimated locking range exceeds Δωlock/2π ≈ 30 GHz.
Kerr frequency comb generation via self-injection locking
Experimentally, we can access injection pulling by tuning the current of the laser diode, allowing the laser frequency to be changed concurrently with the self-injection locking, providing thereby a frequency scan over the resonance—a prerequisite for DKS formation7. Figure 2g shows the optical output power (transmission) trace as a function of the current tuning, where self-injection locking is deterministically observed. An initial chaotic power trace (state (i) in Fig. 2g) is switched to a step-like pattern (state (ii) in Fig. 2g, the orange marked region). The average output power reduces during the switching since the self-injection leads to single-longitudinal-mode operation, with enhanced power being coupled into the high-Q resonance of the Si3N4 microresonator. Most significantly, upon further tuning the current, a second step-like pattern in the power trace is observed (state (iii) in Fig. 2g, the green marked region), corresponding to the formation of a (low noise) Kerr frequency comb. Indeed, at high optical power levels (typically setting the current to be ~300 mA), Kerr comb generation was observed upon tuning the current, as shown in Fig. 2f. This phenomenon relies critically on the Q-factor of the Si3N4 microresonator, allowing sub-mW threshold power for parametric oscillations (cf. Methods).
DKS with an electronically detectable mode spacing
We next investigated if self-injection locking can also be observed in devices with an electronically detectable mode spacing (149 and <100 GHz), and critically if it can also enable operation in a regime where DKS are formed concurrently. Figure 3a shows the self-injection-locked Kerr comb generation in a microresonator with a free spectral range (FSR) of 149 GHz. Significantly, not only were Kerr combs observed but also switching into the DKS regime7. Upon self-injection locking, and via current tuning we first excite a Kerr comb in a low-coherence state, as evidenced by the noise in the low-frequency radio frequency (RF) spectrum (inset in Fig. 3a). We emphasize that for such low repetition rates the amplitude noise is still a valid indicator of the frequency comb’s coherence, in contrast to terahertz mode spacing resonators where the noise can be located at high RF frequencies (>1 GHz)35. Importantly, we observe, that upon increasing the current to the diode further (\({\cal O}\)(mA)), which leads to a laser detuning increase by injection pulling, the low-coherence comb state is turned into an intermediate oscillatory state. That can be identified as a breather DKS (Fig. 3b)36, where the soliton exhibits periodic oscillations both in the power and in the pulse duration. The RF spectrum shows the breathing frequency at ~490 MHz exhibiting harmonics, see inset in Fig. 3b. Such soliton breathing dynamics (breather solitons) have been studied previously36, and in particular the feature that breathing frequency depends on the laser detuning is also observed in the present work via the current tuning scheme. The observation of a DKS breathing state demonstrates that the injection pulling enables operation in the effectively red detuned regime, required for soliton generation. Further increasing the laser current, we observe a transition to a low-noise comb state, demonstrating the formation of stable DKS as shown in Fig. 3c. The spectral envelope of the frequency comb exhibits a secant-squared profile, corresponding to a single soliton circulating in the resonator, with the breathing oscillations absent from the RF spectrum (inset in Fig. 3c). This transition, which we induce here by current tuning only, has been achieved in previous work by tuning the laser over the resonance from the blue to the effectively red detuned side7. Most significantly, to corroborate operation in the soliton state we verify the coherence via a heterodyne beatnote measurement2. The heterodyne beatnote of a soliton comb tooth with a narrow linewidth reference laser is shown in Fig. 4c. The measured heterodyne beatnote linewidth is comparable to that of the injection-locked laser (cf. Figure 2e), that is, the Gaussian linewidth is 201 kHz and the estimated short-time Lorentzian linewidth (that describes the wings of the beatnote only) is 1 kHz. These values indicate no degradation of the coherence during the process of soliton comb generation via laser self-injection locking.
Soliton comb generation with self-injection locking. Evolution of Kerr frequency comb in the regime of laser self-injection locking, from noisy state in the operation regime of modulation instability (MI) (a) to breathing state (b), and eventually to a low-noise state (c) showing the formation of a dissipative Kerr soliton (DKS) in the microresonator, where the spectrum is a hyperbolic secant envelope (green-solid line showing the fitting of the spectral envelope). Each inset shows the low-frequency radio frequency (RF) spectrum corresponding to each state. The current imposed to the diode is initially set ~300 mA and the increase to evoke the transitions is within 1 mA. The Si3N4 microresonator in this measurement has a free spectral range (FSR) of 149 GHz
Laser injection-locked multiple breathing and dissipative Kerr solitons. a Measured and fitted dispersion landscape in a Si3N4 microresonator (cross-section 1.58 × 0.75 μm2) (cf. Methods), which has the FSR = 92.4 GHz, and the second-order dispersion element indicating the anomalous group velocity, D2/2π ≈ 1.56 MHz. b Histogram of resonance linewidths that are ~110 MHz, corresponding to a loaded Q-factor ~1.8 × 106. c Heterodyne beat signal between the sideband of soliton Kerr frequency comb and the narrow linewidth reference laser. The measured beat signal is fitted with Voigt profile with full-width at half-maximum (FWHM) ~201 kHz (cf. Methods). RBW: Resolution bandwidth. d, e Showcase of multiple dissipative solitons formed in Si3N4 microresonators, in the breathing state (d) as well as in the low-noise stable soliton state (e), the fitting of the spectrum envelope (green-solid lines) further shows the relative position of solitons circulating in the micro-ring cavity (schematic insets). The low-frequency RF spectra corresponding to breather solitons are also shown as insets. Spectra in d and e are generated in Si3N4 microresonators with a free spectral range (FSR) of ~88 and ~92 GHz, respectively
DKS formation via laser self-injection locking was also observed in Si3N4 microresonators with FSRs below 100 GHz, an electronically detectable repetition rate, where due to the high Q-factors (Q0 ~ 8 × 106) enabled by the photonic Damascene reflow process, soliton combs could still be generated25. Figure 4a, b show a dispersion measurement of the microresonator (cf. Methods), where the FSR is read as 92.4 GHz. The parabolic dispersion profile shows quadratic contribution from an anomalous group velocity dispersion (GVD) to be: D2/2π ≈ 1.56 MHz, centered at a wavelength ~1540 nm. The loaded resonance linewidth κ/2π is ca. 110 MHz (Fig. 4b), corresponding to an over-coupled regime of the microresonator (the intrinsic loss rate is κ0/2π < 30 MHz). In these type of microresonators, multiple dissipative solitons are observed, shown in Fig. 4d, e, not only in the breathing state but in the low-noise stable soliton state as well. The spectral envelope reveals a multi-soliton state as a result of interfering Fourier components of the solitons. By fitting these spectral envelopes (cf. Methods), we can resolve the number of solitons and estimate their relative positions, illustrated as insets in Fig. 4d, e. The overall transmitted optical power, consisting of both the comb power and the residual pump power, is measured ~11 mW (cf. Methods).
Discussion
In summary, we have demonstrated a route to an ultra-compact, cost-effective soliton frequency comb in photonic integrated Si3N4 microresonators, via laser self-injection-locking with off-the-shelf laser diodes. Self-injection-locking leads to a significant stabilization of a laser diode, eliminates the need for complicated soliton generation methods. We observed power-efficient soliton combs in microresonators with different FSRs, particularly for FSR below 100 GHz. This approach offers a dramatic reduction in size, cost, and weight, and also offers simplified heterogeneous integration, in particular as no wafer bonding is required unlike for silicon photonic III–V lasers. This approach provides a route to scalable manufacturing of soliton microcombs for future high-volume applications.
Methods
Fabrication and characterization of Si3 N 4 microresonator chip
The photonic integrated Si3N4 chips are fabricated using the photonic Damascene reflow process. Waveguide and resonator patterns were defined by deep-ultraviolet (DUV) stepper lithography and transferred to the SiO2 preform via dry etching. A preform reflow step was used to reduce the waveguide sidewall roughness caused by dry etching24,37, allowing for ultra-smooth waveguides and leading to high-Q-factors for the microresonators. Optimized chemical mechanical polishing (CMP) allows precise control of the waveguide height to 750 ± 20 nm, measured over the full 4-in. wafer scale. No top cladding was deposited onto the Si3N4 waveguides. The precise dimension control by both the lithography (mainly in the waveguide width) and CMP (in the height) enables samples of the same design to have the identical geometry at different positions on the wafer.
The microresonator is coupled to the bus waveguide on the chip through the evanescent field. Light is coupled onto the Si3N4 chip via double inverse nanotapers31 on the bus waveguides at both the input and output facets, that is, from the laser diode chip to the microresonator chip and from the microresonator chip to a lensed fiber which collects the comb spectrum. In addition, the bus waveguide’s geometry is designed to achieve a high coupling ideality with reduced parasitic losses38.
The microresonator dispersion can be extracted by measuring the transmission spectrum, which is calibrated by a standard optical frequency comb39,40. The dispersion of the microresonator is represented in terms of resonant frequency deviation with respect to a linear grid, namely:
where ωμ is the physical resonant frequencies of the microresonator. A central resonance (to which the laser is injection locked) is given the index μ = 0. D1 = 2π × FSR is the repetition frequency. The second-order element D2 is the GVD of the microresonator and D2 > 0 represents the anomalous GVD. When the dispersion is described to the second order, the dissipative and nonlinear optical resonator can be described by the Lugiato–Lefever equation41, which is equivalent to the coupled mode equation. Each resonance is fitted using the model based on coupled mode theory42,43 from the transmission spectrum. The resonance linewidth reflects the total loss rate (κ) of the microresonator, which consists of both the intrinsic loss rate (κ0) and the external coupling rate κex, that is, κ = κ0 + κex. To extract the intrinsic Q-factor (Q0), highly under-coupled microresonators are measured, that is, κex → 0.
In this work, there are three sets of Si3N4 microresonators in terms of different FSRs: ~1 THz, ~150 GHz, and <100 GHz. The microresonator corresponding to results shown in Fig. 2f has: Q0 ≈ 6 × 106, FSR = 1.02 THz, D2/2π ≈ 188 MHz, for fundamental TE mode. The microresonator width is 1.53 μm. The microresonator corresponding to results shown in Fig. 3 has: Q0 ≈ 6.5 × 106, FSR = 149 GHz, D2/2π ≈ 3.90 MHz (fundamental TE mode), the microresonatore width is 1.58 μm. The microresonators corresponding to results shown in Fig. 4 have: Q0 ≈ 8.2 × 106; (for Fig. 4d) FSR = 88.6 GHz, D2/2π ≈ 1.10 MHz (fundamental TE mode), the microresonator width is 1.58 μm; (for Fig. 4e) FSR = 92.4 GHz, D2/2π ≈ 1.56 MHz (fundamental TE mode), the microresonator width is 1.58 μm.
Such high Q-factors have already enabled direct soliton comb generation in microresonators without amplification of the seed laser25. The threshold power for parametric oscillation can be as low as sub-milli-Watt (critical coupled), which is calculated as:
where n is the refractive index, Veff indicates the effective modal volume, ω is the angular frequency of light, c the speed of light in vacuum, and n2 is the nonlinear refractive index. For Si3N4 microresonators with FSR ~1 THz, we have n ≈1.9, Veff ≈1.5 × 10−16 μm3, and n2 ≈2.4 × 10−19 m2/W. Hence, the threshold power is as low as Pth ≈ 0.62 mW.
DKS comb power
Multiple DKS in the microresonator with FSR ~92.4 GHz are generated when applying a current ~280 mA to the diode chip, corresponding to an optical output power of ~50 mW. The output power is measured as ~11 mW, collected by using a lensed fiber at the output chip facet, indicating a coupling efficiency of ~22% (overall insertion loss −6.6 dB). The optical power in the bus waveguide is estimated to be ~23.5 mW, which has been demonstrated to be sufficient to excite DKS in high-Q Si3N4 microresonators25.
Heterodyne beat signal and fitting function
The heterodyne measurement is used to assess the coherence of the generated soliton comb, as its lineshape reveals the frequency noise spectral density with respect to the reference laser. In fact, the frequency noise may consist of both the white noise (resulting in a Lorenztian lineshape) and the flicker noise (corresponding to a Gaussian lineshape). Therefore, we employ the Voigt profile44 to fit the beat signal, which represents the convolution of the Lorenztian (L(f)) and the Gaussian (G(f)) lineshapes, that is:
where f indicates the frequency shift with respect to the center of the beat signal, in the radio frequency domain, and σ and ψ scale the linewidth. To initiate the fitting we assume that, on the wings of the beat profile, the signal is mostly contributed by the white noise that determines the intantaneous linewidth described by ψ. In contrast, around the center of the beat profile, the signal is also contributed by flicker noise depending on, for example, the acquisition time of the electrical-signal spectral analyzer (ESA), as well as the stability of current or temperature controller. This part of noise is scaled by σ. The full-width at half-maximum (FWHM) of the Gaussian lineshape is then ΔfG = 2σ and ΔfL = 2ψ for the Lorentzian.
DKS comb spectral fitting
It is known that N identical solitons circulating in the resonator produce a spectral interference on the single soliton spectrum:7,8
Here ϕi ∈ [0, 2π] is the position of the ith pulse along the cavity round trip, μ is the comb mode index relative to the pump laser frequency and S(1)(μ) is the spectral envelope of a single soliton following an approximate secant hyperbolic squared:
where A is the power of the comb lines near the pump, Δμ is the spectral width of the comb (in unit of comb lines) and μc is the central mode of the soliton (to account for soliton recoil or self-frequency shift). Knowing the comb repetition rate fr, the spectral width (or pulse duration) can be retrieved: Δf = frΔμ.
The spectral envelope of the single or multiple soliton states are fitted using the following procedure: first, the peaks \(\tilde S(\mu )\) constituting the frequency comb are detected and labeled with their relative mode index from the pump μ, and the pump mode is rejected. The number of solitons N is estimated by taking the inverse Fourier transform of this spectrum, which yields the autocorrelation of the intracavity waveform, and detecting its peaks8. The set of fitting parameters {A, Δμ, μc, ϕi|i ∈ [2, N]} is defined accordingly (the position of one soliton is arbitraly set to zero) and the expression (9) is fitted to the experimental points \(\tilde S(\mu )\). When N solitons are perfectly equi-spaced, the repetition is multiplied by N and the single soliton expression can be fitted on every N line.
Data availability
The code and data used to produce the plots within this paper are available at 10.5281/zenodo.2203625. All other data used in this study are available from the corresponding authors upon reasonable request.
Change history
03 April 2019
The original version of this Article contained an error in the first sentence of the Acknowledgements, which incorrectly read ‘This publication was supported by Contract HR0011-15-C-0055 (DODOS) from the Defense Advanced Research Projects Agency (DARPA), Defense Sciences Office (DSO).’ The correct version states ‘Microsystems Technology Office (MTO)’ in place of ‘Defense Sciences Office (DSO)’. This has been corrected in both the PDF and HTML versions of the Article.
References
Udem, T., Holzwarth, R. & Hänsch, T. W. Optical frequency metrology. Nature 416, 233 (2002).
Cundiff, S. T. & Ye, J. Colloquium: femtosecond optical frequency combs. Rev. Mod. Phys. 75, 325–342 (2003).
Del’Haye, P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214 (2007).
Kippenberg, T. J., Holzwarth, R. & Diddams, S. A. Microresonator-based optical frequency combs. Science 332, 555–559 (2011).
Brasch, V., Chen, Q.-F., Schiller, S. & Kippenberg, T. J. Radiation hardness of high-Q silicon nitride microresonators for space compatible integrated optics. Opt. Express 22, 30786–30794 (2014).
Leo, F. et al. Temporal cavity solitons in one-dimensional Kerr media as bits in an all-optical buffer. Nat. Photonics 4, 471–476 (2010).
Herr, T. et al. Temporal solitons in optical microresonators. Nat. Photonics 8, 145–152 (2014).
Brasch, V. et al. Photonic chip-based optical frequency comb using soliton Cherenkov radiation. Science 351, 357–360 (2016).
Jost, J. D. et al. Counting the cycles of light using a self-referenced optical microresonator. Optica 2, 706–711 (2015).
Marin-Palomo, P. et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 546, 274 (2017).
Trocha, P. et al. Ultrafast optical ranging using microresonator soliton frequency combs. Science 359, 887–891 (2018).
Suh, M.-G. & Vahala, K. J. Soliton microcomb range measurement. Science 359, 884–887 (2018).
Suh, M.-G., Yang, Q.-F., Yang, K. Y., Yi, X. & Vahala, K. J. Microresonator soliton dual-comb spectroscopy. Science 354, 600–603 (2016).
Liang, W. et al. High spectral purity Kerr frequency comb radio frequency photonic oscillator. Nat. Commun. 6, 7957 (2015).
Spencer, D. T. et al. An optical-frequency synthesizer using integrated photonics. Nature 557, 81–85 (2018).
Fang, A. W. et al. Electrically pumped hybrid AlGaInAs-silicon evanescent laser. Opt. Express 14, 9203–9210 (2006).
Green, W. M. J., Rooks, M. J., Sekaric, L. & Vlasov, Y. A. Ultra-compact, low RF power, 10 Gb/s silicon Mach-Zehnder modulator. Opt. Express 15, 17106–17113 (2007).
Stone, J. R. et al. Thermal and nonlinear dissipative-soliton dynamics in kerr-microresonator frequency combs. Phys. Rev. Lett. 121, 063902 (2018).
Brasch, V., Geiselmann, M., Pfeiffer, M. H. P. & Kippenberg, T. J. Bringing short-lived dissipative Kerr soliton states in microresonators into a steady state. Opt. Express 24, 29312 (2016).
Levy, J. S. et al. CMOS-compatible multiple-wavelength oscillator for on-chip optical interconnects. Nat. Photonics 4, 37–40 (2010).
Yang, K. Y. et al. Bridging ultrahigh-Q devices and photonic circuits. Nat. Photonics 12, 297 (2018).
Xuan, Y. et al. High-Q silicon nitride microresonators exhibiting low-power frequency comb initiation. Optica 3, 1171–1180 (2016).
Ji, X. et al. Ultra-low-loss on-chip resonators with sub-milliwatt parametric oscillation threshold. Optica 4, 619–624 (2017).
Pfeiffer, M. H. P. et al. Ultra-smooth silicon nitride waveguides based on the damascene reflow process: fabrication and loss origins. Optica 5, 884–892 (2018).
Liu, J. et al. Ultralow-power chip-based soliton microcombs for photonic integration. Optica 5, 1347–1353 (2018).
Dahmani, B., Hollberg, L. & Drullinger, R. Frequency stabilization of semiconductor lasers by resonant optical feedback. Opt. Lett. 12, 876–878 (1987).
Vassiliev, V. V. et al. Narrow-line-width diode laser with a high-Q microsphere resonator. Opt. Commun. 158, 305–312 (1998).
Pavlov, N. G. et al. Narrow-linewidth lasing and soliton Kerr microcombs with ordinary laser diodes. Nat. Photonics 12, 694 (2018).
Stern, B., Ji, X., Okawachi, Y., Gaeta, A. L. & Lipson, M. Battery-operated integrated frequency comb generator. Nature 562, 401 (2018).
Joshi, C. et al. Thermally controlled comb generation and soliton modelocking in microresonators. Opt. Lett. 41, 2565–2568 (2016).
Liu, J. et al. Double inverse nanotapers for efficient light coupling to integrated photonic devices. Opt. Lett. 43, 3200–3203 (2018).
Galiev, R. R. et al. Spectrum collapse, narrow linewidth, and bogatov effect in diode lasers locked to high-q optical microresonators. Opt. Express 26, 30509–30522 (2018).
Kondratiev, N. M. et al. Self-injection locking of a laser diode to a high-Q WGM microresonator. Opt. Express 25, 28167–28178 (2017).
Henry, C. Theory of the linewidth of semiconductor lasers. IEEE J. Quantum Electron. 18, 259–264 (1982).
Pfeiffer, M. H. P. et al. Octave-spanning dissipative kerr soliton frequency combs in Si3N4 microresonators. Optica 4, 684–691 (2017).
Lucas, E., Karpov, M., Guo, H., Gorodetsky, M. L. & Kippenberg, T. J. Breathing dissipative solitons in optical microresonators. Nat. Commun. 8, 736 (2017).
Pfeiffer, M. H. P. et al. Photonic damascene process for integrated high-Q microresonator based nonlinear photonics. Optica 3, 20–25 (2016).
Pfeiffer, M. H., Liu, J., Geiselmann, M. & Kippenberg, T. J. Coupling ideality of integrated planar High-Q microresonators. Phys. Rev. Appl. 7, 024026 (2017).
Del’Haye, P., Arcizet, O., Gorodetsky, M. L., Holzwarth, R. & Kippenberg, T. J. Frequency comb assisted diode laser spectroscopy for measurement of microcavity dispersion. Nat. Photonics 3, 529–533 (2009).
Liu, J. et al. Frequency-comb-assisted broadband precision spectroscopy with cascaded diode lasers. Opt. Lett. 41, 3134–3137 (2016).
Lugiato, L. A. & Lefever, R. Spatial dissipative structures in passive optical systems. Phys. Rev. Lett. 58, 2209–2211 (1987).
Gorodetsky, M. L., Pryamikov, A. D. & Ilchenko, V. S. Rayleigh scattering in high-Q microspheres. JOSA B 17, 1051–1057 (2000).
Kippenberg, T. J., Spillane, S. M. & Vahala, K. J. Modal coupling in traveling-wave resonators. Opt. Lett. 27, 1669–1671 (2002).
Stéphan, G. M., Tam, T. T., Blin, S., Besnard, P. & Têtu, M. Laser line shape and spectral density of frequency noise. Phys. Rev. A 71, 043809 (2005).
Acknowledgements
This publication was supported by Contract HR0011-15-C-0055 (DODOS) from the Defense Advanced Research Projects Agency (DARPA), Microsystems Technology Office (MTO). This work was supported by funding from the Swiss National Science Foundation under grant agreement no. 163864 (Swiss-Russian JRP), Russian Science Foundation (RSF) (17-12-01413) and EU H2020 FET OPTIMISM (grant no. 801352). H.G. acknowledges support by funding from the European Unions Horizon 2020 research and innovation program under Marie Sklodowska-Curie IF grant agreement no. 709249. M.K. and E.L. acknowledge the support from the European Space Technology Center with ESA Contract No. 4000116145/16/NL/MH/GM and 4000118777/16/NL/GM, respectively. All samples were fabricated in the Center of MicroNanoTechnology (CMi) at EPFL. We acknowledge Bahareh Ghadiani for the assistance in sample fabrication. We thank M.H. Anderson for useful discussion and assistance in manuscript preparation.
Author information
Authors and Affiliations
Contributions
A.S.R., A.S.V., H.G., S.E.A., J.D.J., A.S.G., N.G.P. and M.K. setup the experiment and performed measurements. J.L. designed and fabricated the Si3N4 microresonator samples. A.S.R. and J.L. characterized and analyzed the Q and dispersion of the Si3N4 microresonator samples. A.S.R., H.G., A.S.V., A.E.S., J.L., E.L. and R.R.G. processed and analyzed the data. T.J.K., H.G., A.S.R., A.S.V., M.K. and J.L. wrote the manuscript with input from all authors. M.L.G. initiated the project and supervised the project from the Russian side. T.J.K. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Raja, A.S., Voloshin, A.S., Guo, H. et al. Electrically pumped photonic integrated soliton microcomb. Nat Commun 10, 680 (2019). https://doi.org/10.1038/s41467-019-08498-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-08498-2
This article is cited by
-
Scalable and efficient grating couplers on low-index photonic platforms enabled by cryogenic deep silicon etching
Scientific Reports (2024)
-
Nonlinear and quantum photonics using integrated optical materials
Nature Reviews Materials (2024)
-
Advances in resonator-based Kerr frequency combs with high conversion efficiencies
npj Nanophotonics (2024)
-
Electrically empowered microcomb laser
Nature Communications (2024)
-
Phase-stabilised self-injection-locked microcomb
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.