Abstract
Uranium compounds can manifest a wide range of fascinating many-body phenomena, and are often thought to be poised at a crossover between localized and itinerant regimes for 5f electrons. The antiferromagnetic dipnictide USb2 has been of recent interest due to the discovery of rich proximate phase diagrams and unusual quantum coherence phenomena. Here, linear-dichroic X-ray absorption and elastic neutron scattering are used to characterize electronic symmetries on uranium in USb2 and isostructural UBi2. Of these two materials, only USb2 is found to enable strong Hund’s rule alignment of local magnetic degrees of freedom, and to undergo distinctive changes in local atomic multiplet symmetry across the magnetic phase transition. Theoretical analysis reveals that these and other anomalous properties of the material may be understood by attributing it as the first known high temperature realization of a singlet ground state magnet, in which magnetism occurs through a process that resembles exciton condensation.
Similar content being viewed by others
Introduction
Uranium compounds can feature a fascinating interplay of strongly correlated and itinerant electronic physics, setting the stage for emergent phenomena such as quantum criticality, heavy fermion superconductivity, and elusive hidden order states1,2,3,4,5,6,7,8,9,10,11,12,13. The isostructural uranium dipnictides UX2 (X = As, Sb, Bi) present a compositional series in which high near-neighbor uranium-uranium coordination supports robust planar antiferromagnetism (TN~200K, see Fig. 1a, b)7,8. Of these, the USb2 variant has received close attention due to the discovery of several unexplained low temperature quantum coherence phenomena at T < 100K7,9,10,11, and a remarkably rich phase diagram incorporating quantum critical and tricritical points as a function of pressure and magnetic field12,13. However, the effective valence state of uranium and the resulting crystal field state basis defining the f-electron component of local moment and Kondo physics have not been identified.
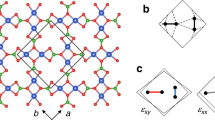
Singlet ground state magnetism and the ligand cage of U(Bi/Sb)2. a, b The U(Sb/Bi)2 crystal structure is shown with spins indicating the antiferromagnetic structure in UBi2 (TN~180 K) and USb2 (TN~203 K). The uranium atoms have 9-fold ligand coordination with base (S1), middle (S2), and pinnacle (S3) ligand layers as labeled in a with respect to the central uranium atom. c, d In-plane ferromagnetic nucleation regions are circled in c doublet and d singlet ground state magnetic systems. The singlet crystal field ground state has no local moment, causing much of the lattice to have little or no magnetic polarization
Here, X-ray absorption (XAS) at the uranium O-edge and numerical modeling are used to evaluate the low energy atomic multiplet physics of USb2 and UBi2, revealing only USb2 to have significant Hund’s rule correlations. These investigations yield the prediction that USb2 must be a uniquely robust realization of a singlet-ground-state magnet, in which magnetic moments appear via the occupation of low-energy excited states on a non-magnetic background (Fig. 1c). The evolution of crystal field symmetries and magnetic ordered moment across the antiferromagnetic phase transition is measured with linear dichroism (XLD) and elastic neutron scattering, confirming that the magnetic transition in USb2 occurs through an exotic process that resembles exciton condensation.
Results
Electron configuration of uranium in UBi2 and USb2
Unlike the case with stronger ligands such as oxygen and chlorine, there is no unambiguously favored effective valence picture for uranium pnictides. Density functional theory suggests that the charge and spin density on uranium are significantly modified by itinerancy effects14,15 (see also Supplementary Note 1), as we will discuss in the analysis below, making it difficult to address this question from secondary characteristics such as the local or ordered moment. However, analyses in 2014–2016 have shown that resonant fine structure at the O-edge (5d→5 f transition) provides a distinctive fingerprint for identifying the nominal valence state and electronic multiplet symmetry on uranium16,17,18,19. X-ray absorption spectra (XAS) of UBi2 and USb2 were measured by the total electron yield (TEY) method, revealing curves that are superficially similar but quantitatively quite different (Fig. 2a). Both curves have prominent resonance features at hυ~100 and ~113 eV that are easily recognized as the ‘R1’ and ‘R2’ resonances split by the G-series Slater integrals16. Within models, these resonances are narrowest and most distinct for 5 f0 systems, and merge as 5f electron number increases, becoming difficult to distinguish beyond 5f2 (see Fig. 2a (bottom) simulations). The USb2 sample shows absorption features that closely match the absorption curve of URu2Si216, and are associated with the J = 4 ground states of a 5f2 multiplet. This correspondence can be drawn with little ambiguity by noting a one-to-one feature correspondence with the fine structure present in a second derivative analysis (SDI, see Fig. 2b).
XAS fine structure and valence of UBi2 and USb2. a The x-ray absorption of UBi2 and USb2 on the O-edge of uranium is compared with (bottom) multiplets simulations for 5 f1 (U5+), 5f2 (U4+), and 5f3 (U3+). b A negative second derivative (SDI) of the XAS data and simulated curves, with drop-lines showing feature correspondence. Noise in the SDI has an amplitude comparable to the plotted line thickness, and all features identified with drop-lines were consistently reproducible when moving the beam spot. Prominent absorption features are labeled peak-A (UBi2, hυ = 99.2 eV), peak-B (USb2, hυ = 98.2 eV), and peak-C (USb2, hυ = 100.8 eV). Source data are provided as a Source Data file
The R1 and R2 resonances of UBi2 are more broadly separated than in USb2, and the lower energy R1 feature of UBi2 is missing the prominent leading edge peak at hυ~98.2 eV (peak-B), which is a characteristic feature of 5f2 uranium16,17. The UBi2 spectrum shows relatively little intensity between R1 and R2, and the higher energy R2 resonance has a much sharper intensity onset. All of these features are closely consistent with expectations for a 5f1 multiplet, and the SDI curve in Fig. 2b reveals that the R1 fine structure of UBi2 is a one-to-one match for the 5f1 multiplet. We note that a close analysis is not performed for R2 as it is influenced by strong Fano interference (see Supplementary Note 2). The lack of prominent 5f2 multiplet features suggests that the 5f1 multiplet state is quite pure, and the measurement penetration depth of several nanometers (see Methods) makes it unlikely that this distinction between UHV-cleaved UBi2 and USb2 originates from surface effects. However, the picture for UBi2 is complicated by a very rough cleaved surface, which our STM measurements (see Supplementary Note 3) find to incorporate at least two non-parallel cleavage planes. Surface oxidation in similar compounds is generally associated with the formation of UO2 (5f2) and does not directly explain the observation of a 5f1 state.
We note that even with a clean attribution of multiplet symmetries, it is not at all clear how different the f-orbital occupancy will be for these materials, or what magnetic moment should be expected when the single-site multiplet picture is modified by band-structure-like itinerancy10,11 (see also Supplementary Note 1). The effective multiplet states identified by shallow-core-level spectroscopy represent the coherent multiplet (or angular moment) state on the scattering site and its surrounding ligands, but are relatively insensitive to the degree of charge transfer from the ligands20.
Nonetheless, the 5f1 and 5f2 nominal valence scenarios have very different physical implications. A 5f1 nominal valence state does not incorporate multi-electron Hund’s rule physics21,22 (same-site multi-electron spin alignment), and must be magnetically polarizable with non-zero pseudospin in the paramagnetic state due to Kramer’s degeneracy (pseudospin ½ for the UBi2 crystal structure). By contrast in the 5f2 case one expects to have a Hund’s metal with strong alignment of the 2-electron moment (see dynamical mean field theory (DFT + DMFT) simulation below), and the relatively low symmetry of the 9-fold ligand coordination around uranium strongly favors a non-magnetic singlet crystal electric field (CEF) ground state with Γ1 symmetry, gapped from other CEF states by roughly 1/3 the total spread of state energies in the CEF basis (see Table 1). The Γ1 state contains equal components of diametrically opposed large-moment |mJ = + 4 > and |mJ = -4 > states, and is poised with no net moment by the combination of spin-orbit and CEF interactions. This unusual scenario in which magnetic phenomena emerge in spite of a non-magnetic singlet ground state has been considered in the context of mean-field models23,24,25,26, and appears to be realized at quite low temperatures (typically T < ~10 K) in a handful of rare earth compounds. The resulting magnetic phases are achieved by partially occupying low-lying magnetic excited states, and have been characterized as spin exciton condensates23.
Multiplet symmetry from XLD versus temperature
To address the role of low-lying spin excitations, it is useful to investigate the interplay between magnetism and the occupied multiplet symmetries by measuring the polarization-resolved XAS spectrum as a function of temperature beneath the magnetic transition. Measurements were performed with linear polarization set to horizontal (LH, near z-axis) and vertical (LV, a–b plane) configurations. In the case of UBi2, the XAS spectrum shows little change as a function of temperature from 15 to 210K (Fig. 3a, b), and temperature dependence in the dichroic difference (XLD, Fig. 3b) between these linear polarizations is inconclusive, being dominated by noise from the data normalization process (see Methods and Supplementary Note 4). This lack of temperature dependent XLD is consistent with conventional magnetism from a doublet ground state. The XLD matrix elements do not distinguish between the up- and down-moment states of a Kramers doublet, and so strong XLD is only expected if the magnetic phase incorporates higher energy multiplet symmetries associated with excitations in the paramagnetic state.
Temperature dependence of occupied f-electron symmetries. a The R1 XAS spectrum of UBi2 is shown for linear horizontal (LH) and vertical (LV) polarizations. b The dichroic difference (LH-LV) is shown with temperature distinguished by a rainbow color order (15K (purple), 40K (blue), 80K (green), 120K (yellow), and 210K (red)). c, d Analogous spectra are shown for USb2. Arrows in d show the monotonic trend direction on the peak-B and peak-C resonances as temperature increases. e, f Simulations for 5f2 with mean-field magnetic interactions. g A summary of the linear dichroic difference on the primary XAS resonances of USb2, as a percentage of total XAS intensity at the indicated resonance energy (hυ = 98.2 eV for peak-B, and hυ = 100.8 eV for peak-C). Error bars represent a rough upper bound on the error introduced by curve normalization. h The linear dichroic difference trends from the mean field model. Source data are provided as a Source Data file. Shading in g, h indicates the onset of a magnetic ordered moment
By contrast, the temperature dependence of USb2 shows a large monotonic progression (Fig. 3c, d), suggesting that the atomic symmetry changes significantly in the magnetic phase. The primary absorption peak (hυ~98.2 eV, peak-B) is more pronounced under the LH-polarization at low-temperature, and gradually flattens as temperature increases. The LV polarized spectrum shows the opposite trend, with a sharper peak-B feature visible at high temperature, and a less leading edge intensity at low temperature. This contrasting trend is visible in the temperature dependent XLD in Fig. 3d, as is a monotonic progression with the opposite sign at peak-C (hυ~100.8 eV).
Augmenting the atomic multiplet model for 5f2 uranium with mean-field magnetic exchange (AM + MF) aligned to match the TN~203K phase transition (see Methods) results in the temperature dependent XAS trends shown in Fig. 3e. The temperature dependent changes in peak-B and peak-C in each linear dichroic curve match the sign of the trends seen in the experimental data, but occur with roughly twice the amplitude, as can be seen in Fig. 3d, f. No attempt is made to precisely match the T > 200K linear dichroism, as this is influenced by itinerant and Fano physics not considered in the model. The theoretical amplitude could easily be reduced by adding greater broadening on the energy loss axis or by fine tuning of the model (which has been avoided – see Methods). However, it is difficult to compensate for a factor of two, and the discrepancy is likely to represent a fundamental limitation of the non-itinerant mean field atomic multiplet model. Indeed, when the competition between local moment physics and electronic itinerancy is evaluated for USb2 with dynamical mean field theory (DFT + DMFT), we find that the uranium site shows a non-negligible ~25% admixture of 5f1 and 5f3 configurations (Fig. 4a).
Electronic symmetry convergence in USb2. a The partial multiplet state occupancy on uranium in USb2 from DFT + DMFT numerics, with Hund-aligned symmetries highlighted in bold (3H4 and 4I9/2). b Temperature dependence of the partial occupancy of different multiplet states within a 5f2 mean field model. In spite of a magnetic transition above 200K, roughly 1/3rd of the ground state convergence occurs in the range from 30–100K. The labeled CEF symmetries are only fully accurate in the high temperature paramagnetic state. Beneath the Néel temperature, the Γ1 ground state is magnetically polarized by admixture with Γ2. Shading indicates the onset of a magnetic ordered moment. c The ordered magnetic moment of (red circles) USb2 and (black circles) UBi2 from elastic neutron scattering. The mean field multiplet model for USb2 is shown as a solid blue curve, and critical exponent trends near the phase transition are traced with dashed black lines representing m(T) = mmax(1-T/TN)β. The USb2 data are overlaid with a steep critical exponent trend of β = 0.19 indicating strong fluctuations, and the UBi2 data are overlaid with the conventional 3D Ising critical exponent (β = 0.327). d The Néel temperature as a function of doping level in U1-xThxSb2 (red circles), and the simulated ordered moment in Bohr magnetons (renormalized to 62% as described in Methods; red-hot shading). Source data for all curves are provided as a Source Data file
Magnetic ordered moment and the nature of fluctuations
Compared with conventional magnetism, the singlet ground state provides a far richer environment for low temperature physics within the magnetic phase. In a conventional magnetic system, the energy gap between the ground state and next excited state grows monotonically as temperature is decreased beneath the transition, giving an increasingly inert many-body environment. However, in the case of singlet ground state magnetism, the ground state is difficult to magnetically polarize, causing the energy gap between the ground state and easily polarized excited states to shrink as temperature is lowered and the magnetic order parameter becomes stronger. Consequently, within the AM + MF model, many states keep significant partial occupancy down to T < 100K, and the first excited state (derived from the Γ5 doublet) actually grows in partial occupancy beneath the phase transition (see Fig. 4b). Of the low energy CEF symmetries (tracked in Fig. 4b), Γ5 and Γ2 are of particular importance, as Γ5 is a magnetically polarizable Ising doublet, and Γ2 is a singlet state that can partner coherently with the Γ1 ground state to yield a z-axis magnetic moment (see Supplementary Note 5). These non-ground-state crystal field symmetries retain a roughly 1/3rd of the total occupancy at T = 100K, suggesting that a heat capacity peak similar to a Schottky anomaly should appear at low temperature, as has been observed at T < ~50K in experiments (see the supplementary material of ref. 10). Alternatively, when intersite exchange effects are factored in, the shrinking energy gap between the Γ1 and Γ5 CEF states at low temperature will enable Kondo-like resonance physics and coherent exchange effects that are forbidden in conventional magnets.
Critical behavior at the Néel transition should also differ, as the phase transition in a singlet-ground-state magnet is only possible on a background of strong fluctuations. Measuring the ordered moment as a function of temperature with elastic neutron scattering (Fig. 4c) reveals that the UBi2 moment follows a trend that appears consistent with the β = 0.327 critical exponent for a 3D Ising system27. The order parameter in USb2 has a sharper onset that cannot be fitted sufficiently close to the transition point due to disorder, but can be overlaid with an exponent of β~0.19, and may resemble high-fluctuation scenarios such as tricriticality (β = 0.2528,29). This sharp onset cannot be explained from the AM + MF model (blue curve in Fig. 4c), as mean field models that replace fluctuations with a static field give large critical exponents such as β = 0.5 and unphysically high transition temperatures in systems where fluctuations are important. Another approach to evaluate the importance of fluctuations is to lower the Néel temperature by alloying with non-magnetic thorium (Th), as U1-xThxSb2 (see Fig. 4d), thus quenching thermal fluctuations at the phase transition. Performing such a growth series reveals that the magnetic transition can be suppressed to TN~100 K, but is then abruptly lost at x~0.7, consistent with the need for fluctuations across a CEF gap of kBTN~10 meV, which matches expectations from theory for the energy separation between Γ1 and Γ5 (see Table 1 and Methods).
Discussion
In summary, we have shown that the USb2 and UBi2 O-edge XAS spectra represent different nominal valence symmetries, with USb2 manifesting 5f2 moments that are expected to create a Hund’s metal physical scenario, and UBi2 showing strong 5f1 –like symmetry character. The CEF ground state of a paramagnetic USb2 Hund’s metal is theoretically predicted to be a robust non-magnetic singlet, creating an exotic setting for magnetism that resembles an exciton condensate, and is previously only known from fragile and low temperature realizations. The temperature dependence of XLD measurements is found to reveal a symmetry evolution consistent with singlet-based magnetism. Neutron diffraction measurements show a relatively sharp local moment onset at the transition, consistent with the importance of fluctuations to nucleate the singlet-based magnetic transition, and suppressing thermal fluctuations in a doping series is found to quench magnetism beneath TN < ~100K.
Taken together, these measurements are consistent with a singlet-based magnetic energy hierarchy that yields an anomalously large number of thermally accessible degrees of freedom at low temperature (T < 100K), and provides a foundation for explaining the otherwise mysterious coherence effects found in previous transport, heat capacity, and ARPES measurements at T < 100K7,9,10,11. The interchangeability of elements on both the uranium (demonstrated as U1-xThxSb2) and pnictogen site suggests UX2 as a model system for exploring the crossover into both Hund’s metal and singlet-ground-state magnetic regimes.
Methods
Experiment
The samples of UBi2 and USb2 were top-posted in a nitrogen glove-box and then transferred within minutes to the ultra high vacuum (UHV) environment. The samples were cleaved in UHV and measured in-situ, with initial U O-edge spectra roughly 30 minutes after cleavage. The UV-XAS measurements were performed in the MERIXS (BL4.0.3) in the Advanced Light Source with base pressure better than 4 × 10−10 Torr. The switch between linear horizontal polarization (LH-pol) and linear vertical polarization (LV-pol) is controlled by an elliptically polarizing undulator (EPU) and keep precisely the same beam spot before and after the switch. The incident angle of the photon beam was 30°, which gives a 75% out-of-plane E-vector spectral component under the LH-pol condition and 100% in-plane E-vector under the LV-pol condition. The XAS signal was collected by the total electron yield (TEY) method. The penetration depth of VUV and soft X-ray XAS measured with the TEY method is generally in the 2–4 nm range set by the mean free path of low energy (E < ~10 eV) secondary electrons created in the scattering process30, making it a much more bulk sensitive technique than single-particle techniques such as angle resolved photoemission.
Air-exposed UBi2 can degrade rapidly due to oxidization. No evidence of a large volume fraction of oxide or other phases was found from neutron scattering data for USb2 and UBi2. Possible sample oxidation was surveyed by measuring oxygen L1-edge XAS via TEY for both USb2 and UBi2 during the uranium O-edge XAS experiments. An oxygen L1-edge signal was visible at the cleaved surface of both samples, and found to have similar intensity for both USb2 and UBi2 samples (Supplementary Note 6).
The O-edge XAS curves observed under LH-pol and LV-pol polarization are normalized by assigning constant intensity to the integrated area of the R1 region. Spectral intensity was integrated between featureless start (95 eV) and end points (102 eV) for both UBi2 and USb2. The linear dichroism of the XAS in the main text is defined as:
where ILH(max) is the XAS intensity maximum under LH-pol condition within R1 region. The monotonic temperature linear dichroism of USb2 in the main text is a solid result under different data normalization process but linear dichroic rate can be influenced by some factors, for example the irreducible background in ILH(max). In the simulation, tuning the broadening factor is also easy to change simulated linear dichroic rate which make seriously quantitative comparison of the linear dichroism between experiment and the simulation meaningless.
Neutron diffraction measurements were performed on single crystals at the BT-7 thermal triple axis spectrometer at the NIST Center for Neutron Research31 using a 14.7 meV energy and collimation: open - 25′ - sample - 25′ - 120′. For USb2, the magnetic intensity at the (1, 0, 0.5) peak was compared to the nuclear intensity at the (1, 0, 1) peak, while the temperature dependence of the (1 1, 0.5) peak was used to calculate an order parameter. For UBi2, the temperature-dependent magnetic intensity at the (1, 1, 1) peak was compared to nuclear intensity at (1, 1, 1) peak at 200K, above the Néel temperature. In both cases, an f2 magnetic form factor was assumed32.
Atomic multiplet + mean field model (AM + MF)
Atomic multiplet calculations were performed as in ref. 16, describing 5d105 fn → 5d95 fn+1 X-ray absorption in the dipole approximation. Hartree-Fock parameters were obtained from the Cowan code33, and full diagonalization of the multiplet Hamiltonian was performed using LAPACK drivers34. Hartree-Fock parameters for 5f multipole interactions renormalized by a factor of β = 0.7 for UBi2, and a more significant renormalization of β = 0.55 was found to improve correspondence for USb2. This difference matches the expected trend across a transition between 5f2 and 5f1 local multiplet states. Core-valence multipole interactions renormalized by βC = 0.55, consistent with other shallow core hole actinide studies35. The 5f spin orbit is not renormalized in USb2 but renormalized by a factor of 1.15 in UBi2 due to the much larger spin orbit coupling on bismuth. A detailed comparison of simulation results generated from two sets of Hartree-Fock parameters is included in Supplementary Note 7.
Total electron yield is dominated by secondary electrons following Auger decay of the primary scattering site. We have assigned core hole lifetime parameters to describe this decay, and adopted the common approximation that the number of secondary electrons escaping from the material following each core hole decay event is independent of the incident photon energy. For the 5f1 simulation, the core hole inverse lifetime is Γ = 1.4 eV at hυ < 100 eV, Γ = 1.8 eV at 100 eV < hυ < 108.5 eV, and 6.5 eV at hυ > 108.5 eV. For 5f2 and 5f3 simulations, feature widths were obtained from a core hole inverse lifetime set to Γ = 1.3 eV (hυ < 99 eV), Γ = 1.5 eV (99 eV < hυ < 103.5 eV), and 6.5 eV (hυ > 103.5 eV). In the 5f3 simulation, assigning the 103 eV XAS feature to R1 (longer lifetime) as in the Fig. 2 makes it more prominent than if it is assigned to R2 (shorter lifetime). It is also worth noting that scenarios intermediate to 5f2 and 5f3 do not necessarily closely resemble the 5f3 endpoint, and spectral weight in the 103 eV 5f3 XAS peak may depend significantly on local hybridization. However, in real materials, 5f3 character is associated with a downward shift in the R1 resonance onset energy that is opposite to what is observed in our data36.
The mean field model was implemented by considering the USb2 uranium sublattice with Ising exchange coupling between nearest neighbors:
where A,i is the 5f2 single-atom multiplet Hamiltonian, Ji,k is an exchange coupling parameter with distinct values for in-plane versus out-of-plane nearest neighbors, and Sz,i is the z-moment spin operator acting on site i. Mean field theory allows us to replace one of the spin interaction terms (Sz,k) with a temperature-dependent expectation value, and describe the properties of the system in terms of a thermally weighted single-atom multiplet state ensemble. The specific values of individual Ji,k terms are unimportant in this approximation, however their signs must match the antiferromagnetic structure in Fig. 1, and the sum of the absolute value of near-neighbor terms must equal Jeff = ∑<k> |Jn,k| = 43 meV to yield a magnetic transition at TN = 203 K. When considering the doped case of U1-xThxSb2, the expectation value < Sz,k > is effectively reduced by weighting in the appropriate density of 0-moment 5f0 Th sites.
The CEF energy hierarchy has not been fine tuned. Perturbation strengths are scaled to set the lowest energy excitation to 10 meV, a round number that roughly matches the lowest kBTN value at which a magnetic transition is observed in U1-xThxSb2. This assignment gives a total energy scale for crystal field physics that is approximately comparable to room temperature (ΔCEF~kBTN), as expected for this class of materials, and the associated orbital energies were found to correspond reasonably (within <~30%) with coarse estimates from density functional theory. The crystal field parameters are listed in the first column of Table 1.
The low temperature ordered moment of M = 1.90 μB seen by neutron scattering is matched by downward-renormalizing the moment calculated in the mean field model to 62% (see Fig. 4d shading). Within density functional theory (DFT) models, the consideration of itinerant electronic states provides a mechanism to explain most of this discrepancy. In DFT simulations, the spin component of the magnetic moment is enhanced to MS~2 μB14,15, larger than the maximal value of MS~1.4 μB that we find in the 5 f2 (J = 4) atomic multiplet picture. This larger DFT spin moment is directly opposed to the orbital magnetic moment, resulting in a smaller overall ordered moment. The ordered moment in the multiplet simulation could alternatively be reduced by strengthening the crystal field, but this is challenging to physically motivate, and has the opposite effect of reducing the spin moment to MS < 1 μB.
Density functional theory + dynamical mean field theory (DFT + DMFT)
The combination of density functional theory (DFT) and dynamical mean-field theory (DMFT)37, as implemented in the full-potential linearized augmented plane-wave method38,39, was used to describe the competition between the localized and itinerant nature of 5f-electron systems. The correlated uranium 5f electrons were treated dynamically by the DMFT local self-energy, while all other delocalized spd electrons were treated on the DFT level. The vertex corrected one-crossing approximation38 was adopted as the impurity solver, in which full atomic interaction matrix was taken into account. The Coulomb interaction U = 4.0 eV and the Hund’s coupling J = 0.57 eV were used for the DFT + DMFT calculations.
Code availability
Though the source code used for these multiplet calculations is not publicly available, there are excellent options with equivalent capabilities such as CTM4XAS (http://www.anorg.chem.uu.nl/CTM4XAS/) and Quanty (http://www.quanty.org).
Data availability
All relevant data of this study are available from the corresponding author upon reasonable request.
References
Palstra, T. T. M. et al. Superconducting and magnetic transitions in the heavy-fermion system URu2Si2. Phys. Rev. Lett. 55, 2727–2730 (1985).
Maple, M. B. et al. Partially gapped Fermi surface in the heavy-electron superconductor URu2Si2. Phys. Rev. Lett. 56, 185–188 (1986).
Schlabitz, W. J. et al. Superconductivity and magnetic order in a strongly interacting fermi-system: URu2Si2. Z. Phys. B 62, 171–177 (1986).
Fisher, R. A. et al. Specific heat of URu2Si2: effect of pressure and magnetic field on the magnetic and superconducting transitions. Phys. B 163, 419–423 (1990).
Pfleiderer, C. Superconducting phases of f-electron compounds. Rev. Mod. Phys. 81, 1551–1624 (2009).
Moore, K. T. & van der Laan, G. Nature of the 5f states in actinide metals. Rev. Mod. Phys. 81, 235–298 (2009).
Aoki, D. et al. Cylindrical Fermi surfaces formed by a fiat magnetic Brillouin zone in uranium dipnictides. Philos. Mag. B 80, 1517–1544 (2004).
Leciejewicz, J., Troć, R., Murasik, A. & Zygmunt, A. Neutron‐diffraction study of antiferromagnetism in USb2 and UBi2. Phys. Status Solidi B 22, 517–526 (1967).
Wawryk, R. Magnetic and transport properties of UBi2 and USb2 single crystals. Philos. Mag. 86, 1775–1787 (2006).
Qi, J. et al. Measurement of two low-temperature energy gaps in the electronic structure of antiferromagnetic USb2 using ultrafast optical spectroscopy. Phys. Rev. Lett. 111, 057402 (2013).
Xie, D. H. et al. Direct measurement of the localized-itinerant transition, hybridization and antiferromagnetic transition of 5f electrons. Preprint at https://arxiv.org/abs/1611.08059 (2016).
Stillwell, R. L. et al. Tricritical point of the f -electron antiferromagnet USb2 driven by high magnetic fields. Phys. Rev. B 95, 014414 (2017).
Jeffries, J. R. et al. Emergent ferromagnetism and T -linear scattering in USb2 at high pressure. Phys. Rev. B 93, 184406 (2016).
Lebègue, S., Oppeneer, P. M. & Eriksson, O. Ab initio study of the electronic properties and Fermi surface of the uranium dipnictides. Phys. Rev. B 73, 045119 (2006).
Ghasemikhah, E., Jalali Asadabadi, S., Ahmad, I. & Yazdani-Kacoeia, M. Ab initio studies of electric field gradients and magnetic properties of uranium dipnicties. RSC Adv. 5, 37592 (2015).
Wray, L. A. et al. Spectroscopic determination of the atomic f-electron symmetry underlying hidden order in URu2Si2. Phys. Rev. Lett. 114, 236401 (2015).
Butorin, S. M. Resonant inelastic X-ray scattering as a probe of optical scale excitations in strongly electron-correlated systems: quasi-localized view. J. Electron Spectrosc. Relat. Phenom. 110-111, 213–223 (2000).
Sundermann, M. et al. Direct bulk-sensitive probe of 5f symmetry in URu2Si2. Proc. Natl Acad. Sci. USA 113, 13989–13994 (2016).
Kvashnina, K. O. & de Groot, F. M. F. Invisible structures in the X-ray absorption spectra of actinides. J. Electron Spectrosc. Relat. Phenom. 194, 88–93 (2014).
Augustin, E. et al. Charge transfer excitations in VUV and soft x-ray resonant scattering spectroscopies. J. Electron Spectrosc. Relat. Phenom. 220, 121–124 (2017).
Haule, K. & Kotliar, G. Coherence–incoherence crossover in the normal state of iron oxypnictides and importance of Hund’s rule coupling. New J. Phys. 11, 025021 (2009).
Georges, A., de’ Medici, L. & Mravlje, J. Strong correlations from Hund’s coupling. Annu. Rev. Condens. Matter Phys. 4, 137–178 (2013).
Wang, Y.-L. & Cooper, B. R. Collective excitations and magnetic ordering in materials with singlet crystal-field ground state. Phys. Rev. 172, 539 (1968).
Cooper, B. & Vogt, O. Singlet ground state magnetism. J. De. Phys. Colloq. 32, C1–958 (1971).
Lindgard, P.-A. & Schmid, B. Theory of singlet-ground-state magnetism: Application to field-induced transitions, in CsFeCl3 and CsFeBr3. Phys. Rev. B 48, 13636–13646 (1993).
Haule, K. & Kotliar, G. Arrested Kondo effect and hidden order in URu2Si2. Nat. Phys. 5, 796–799 (2009).
Campostrini, M., Pelissetto, M., Rossi, P. & Vicari, E. 25th-order high-temperature expansion results for three-dimensional Ising-like systems on the simple-cubic lattice. Phys. Rev. E 65, 066127 (2002).
Landau, L. D. On the theory of specific heat anomalies. Phys. Z. Sowjetunion 8, 113 (1935).
Huang, K. Statistical Mechanics. 2nd ed (Wiley, New York, 1987).
Stöhr, J. . NEXAFS Spectroscopy. 1st ed, (Springer, Berlin, 1992). Corr. 2nd ed. 2003.
Lynn, J. W. et al. Double-focusing thermal triple-axis spectrometer at the NCNR. J. Res. Natl Inst. Stand. Technol. 117, 61–79 (2012).
Freeman, A. J., Desclaux, J. P., Lander, G. H. & Faber, J. Jr. Neutron magnetic form factors of uranium ions. Phys. Rev. B 13, 1168–1176 (1976).
Robert D. Cowan’s Atomic Structure Code https://www.tcd.ie/Physics/people/Cormac.McGuinness/Cowan/ (2009).
Anderson, E. et al. LAPACK User’s Guide. 3rd ed., (SIAM, Philadelphia, 1999).
Gupta, S. S. et al. Coexistence of bound and virtual-bound states in shallow-core to valence x-ray spectroscopies. Phys. Rev. B 84, 075134 (2011).
Kotani, A. & Ogasawara, H. Theory of core-level spectroscopy in actinide systems. Phys. B. 186–188, 16–20 (1993).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5. Phys. Rev. B 81, 195107 (2010).
Blaha, P., Schwarz, K., Madsen, G., Kvasnicka, D. & Luitz, J. WIEN2k: An Augmented Plane Wave + LO Program for Calculating Crystal Properties. (TU Wien, Vienna, 2001).
Acknowledgements
We are grateful for discussions with S. Roy and L. Klein. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. Work at NYU was supported by the MRSEC Program of the National Science Foundation under Award Number DMR-1420073. P.A. acknowledges funding from the U.S. National Science Foundation CAREER under award No. NSF-DMR 1654482. The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology. G.K. and C.-J.K. are supported by DOE BES under grant no. DE-FG02-99ER45761. G.K. carried out this work during his sabbatical leave at the NYU Center for Quantum Phenomena, and gratefully acknowledges NYU and the Simons foundation for sabbatical support. Y.W. was supported by the US Department of energy, Office of Science, Basic Energy Sciences as a part of the Computational Materials Science Program through the Center for Computational Design of Functional Strongly Correlated Materials and Theoretical Spectroscopy.
Author information
Authors and Affiliations
Contributions
L.M., R.B., Y.X., E.K., and H.H. carried out the XAS experiments with support from J.D.D., Y.-D.C., and J.R.J.; neutron measurements were performed by S.R. and N.P.B. with support from Y.Z., Z.X., and J.W.L.; STM measurements were performed by I.G., with guidance from P.A.; high quality samples were synthesized by S.R. and S.R.S. with guidance from N.P.B.; multiplet simulations were performed by L.M. with guidance from L.A.W., and DFT + DMFT simulations were performed by C.-J.K. with assistance from Y.W. and guidance from G.K.; L.M., R.B., Y.X., P.A., N.P.B., and L.A.W participated in the analysis, figure planning, and draft preparation; L.A.W. was responsible for the conception and the overall direction, planning, and integration among different research units.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miao, L., Basak, R., Ran, S. et al. High temperature singlet-based magnetism from Hund’s rule correlations. Nat Commun 10, 644 (2019). https://doi.org/10.1038/s41467-019-08497-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-08497-3
This article is cited by
-
Breakdown of the scaling relation of anomalous Hall effect in Kondo lattice ferromagnet USbTe
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.