Abstract
Ambient electrochemical N2 reduction is emerging as a highly promising alternative to the Haber–Bosch process but is typically hampered by a high reaction barrier and competing hydrogen evolution, leading to an extremely low Faradaic efficiency. Here, we demonstrate that under ambient conditions, a single-atom catalyst, iron on nitrogen-doped carbon, could positively shift the ammonia synthesis process to an onset potential of 0.193 V, enabling a dramatically enhanced Faradaic efficiency of 56.55%. The only doublet coupling representing 15NH4+ in an isotopic labeling experiment confirms reliable NH3 production data. Molecular dynamics simulations suggest efficient N2 access to the single-atom iron with only a small energy barrier, which benefits preferential N2 adsorption instead of H adsorption via a strong exothermic process, as further confirmed by first-principle calculations. The released energy helps promote the following process and the reaction bottleneck, which is widely considered to be the first hydrogenation step, is successfully overcome.
Similar content being viewed by others
Introduction
Known as the most common industrial chemical, ammonia (NH3) is provoking much attention as a highly efficient energy carrier with low liquefying pressure and high hydrogen density1. Its synthesis from the hydrogenation of atmospheric nitrogen (N2), however, is extremely difficult due to the inherent nature of the N–N triple bond2. Industrially, NH3 manufacture is still dominated by the long-standing Haber–Bosch process under harsh conditions, which consumes more than 1% of the energy supply on earth3. However, this energy-intensive process can only achieve a relatively low conversion ratio due to the unfavorable chemical equilibrium4. Therefore, to alleviate these conditions, it is of great significance to develop alternative routes for more efficient N2 fixation under milder conditions. In response, a worldwide gold rush has been triggered, and many pioneering methods have been reported, including biological catalysis5,6, photocatalysis7,8, and electrocatalysis9,10.
The electrochemical N2 reduction reaction (NRR) is emerging as a highly promising choice since it can be performed at atmospheric pressure and moderate temperature using a renewable electricity source11,12. From the thermodynamic view, the electrochemical NRR usually proceeds at similar potential to that required by the hydrogen evolution reaction (HER)13. In this case, the selectivity challenge comes from the competition between the binding of N2 (N2 + * → *N2) and H (H+ + e− +* → *H), where * indicates the active site of the catalyst. Unfortunately, at relatively large applied potentials, most electrons and protons contribute to evolving hydrogen, accounting for the very low selectivity towards artificial synthesis of NH3 (ref. 14). To increase the NH3 selectivity, it would be desirable to fabricate an electrocatalytic system that could lower the free energy barrier of *N2 to compete with H for active sites and thus promote the NRR at low overpotentials. Once adsorbed N2 preoccupies the active sites instead of the undesirable coverage of hydrogen, the protons and electrons tend to attack the bound N2, leading to its hydrogenation and, finally, the synthesis of ammonia13. To date, although some catalysts have been synthesized to improve nitrogen adsorption and alleviate reaction barriers15,16,17, they still cannot efficiently separate the NRR from the HER and once the two reactions blur into each other, the Faradaic efficiency remains at very low levels. Accordingly, further efforts are needed to widen the potential gap between the NRR and the HER and to boost the NRR kinetics at low overpotentials to obtain reasonable performances.
Herein, we propose and demonstrate that a highly efficient and selective electrochemical NRR is indeed possible under ambient conditions by positively shifting the reaction potential. Starting with an onset potential of 0.193 V vs. reversible hydrogen electrode (RHE), the single-atom catalyst endowed the NRR with a superior Faradaic efficiency (56.55%) and a desirable yield rate (7.48 μg h−1 mg−1) at 0 V vs. RHE. An isotopic labeling experiment using 15N2 as the feeding gas was carried out and only a doublet coupling representing 15NH4+ was observed in the spectra, confirming that the produced NH3 entirely comes from the electroreduction of N2. Such excellent performance is a joint effect of a suppressed HER and an enhanced NRR. Molecular dynamics (MD) simulations suggest only a small energy barrier of 2.38 kJ mol−1 for the access of the N2 molecule to the single-atom Fe, benefiting efficient N2 delivery. The following adsorption is a strong exothermic reaction, as confirmed by density functional theory (DFT) calculations, and the energy released in this process could contribute to lowering the free energy barrier of the following hydrogenation, thus overcoming the reaction bottleneck of the whole process. On the other hand, considerably high energy barriers for *H adsorption as well as its conversion into H2 are observed in the catalytic system, indicating inferior HER activity.
Results
Synthesis and characterization of the FeSA–N–C catalyst
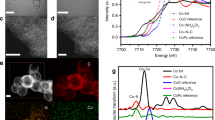
The proof-of-concept single-atom dispersed Fe–N–C (FeSA–N–C) catalyst was prepared by optimized modulation of the polypyrrole–iron coordination complex. Supplementary Fig. 1 and Fig. 1a indicate a graphene-like morphology of FeSA–N–C, with no observable nanoparticle phase of iron. Aberration-corrected high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) with subangstrom resolution was then conducted to elucidate the existing forms of Fe atoms. A large number of bright dots could be discerned in Fig. 1b, suggesting isolated iron atoms. The representative mapping images of the FeSA–N–C sample in Fig. 1c further verify the uniform distribution of Fe atoms over the entire architecture along with N, which acted as anchor points for the Fe18. The Fe content is approximately 1.09 wt%, determined by inductively coupled plasma optical emission spectrometry analysis.
Physical characterization. a Transmission electron microscopy (TEM) image of single-atom dispersed Fe–N–C (FeSA–N–C). Scale bar, 50 nm. b High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of FeSA–N–C. Single Fe atoms are highlighted by red circles. Scale bar, 2 nm. c High-resolution TEM (HRTEM) image and corresponding element maps showing the distribution of C (red), N (orange), and Fe (green). Scale bar, 50 nm. d X-ray absorption near-edge structure (XANES) spectra and e Fourier transform spectra at the Fe K-edge of FeSA–N–C and Fe foil
To further investigate the state of the Fe species at the atomic level, X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) analyses were carried out, with Fe foil as reference. In Fig. 1d, the absorption edge of FeSA–N–C situates at more positive energy than does that of the Fe foil, implying that the isolated Fe single atoms bear positive charges. The Fourier transformed EXAFS curve of FeSA–N–C only shows one distinct peak at approximately 1.44 Å, corresponding to the Fe–N scattering paths. Moreover, no obvious Fe–Fe peak (2.2 Å) or other peaks are observed (Fig. 1e). Iron atoms in FeSA–N–C are thus confirmed to be stabilized by N atoms and atomically dispersed on the supports19. To probe the specific role of single Fe atoms, metal-free nitrogen-doped carbon (N–C) was synthesized for comparison (Supplementary Fig. 2). X-ray diffraction (XRD) patterns show no distinct differences between FeSA–N–C and N–C, with two broad peaks assignable to the (002) and (101) planes of graphitic carbon (Supplementary Fig. 3a), which can also be verified by the ID/IG value in Raman spectra (Supplementary Fig. 3b). Notably, no peaks related to metallic Fe or other Fe species are observed in the XRD pattern of FeSA–N–C, further indicating the single-atomic nature of Fe.
Electroreduction of N2 to NH3 on the FeSA–N–C catalyst
The electrochemical measurements were conducted under ambient conditions using a gas-tight electrocatalytic system, wherein the Nafion membrane separated the two parts of the cell (Supplementary Fig. 4). To evaluate the electrocatalytic performance of the catalysts for the NRR, linear sweep voltammograms were first measured in an Ar- or N2-saturated solution. For this, 0.1 M KOH was chosen as the electrolyte. The HER in alkaline solution requires extra energy to break the water molecule, namely the strong covalent H–O–H bond, prior to hydrogen adsorption. Such an additional water dissociation step would make the entire process difficult to achieve at low overpotentials20. In an N2 environment, the current density of N–C increases obviously when the potential is more negative than −0.018 V vs. RHE, indicating the initiated NRR. For FeSA–N–C, its onset potential shifted markedly to a more positive potential of 0.193 V vs. RHE, suggesting that FeSA–N–C is much more active than is N–C for the NRR.
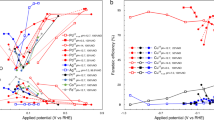
The NRR activity of FeSA–N–C was then systematically studied in 0.1 M KOH with continuous N2 bubbling at various potentials (Supplementary Fig. 5). The indophenol blue method was used to detect the produced ammonia. To avoid production loss by N2 blowing during the test, another glass tube filled with 0.001 M H2SO4 as the gas absorption liquid was set at the end of the cell. The total NH3 production yield was the summation of NH3 in the 0.1 M KOH and 0.001 M H2SO4 (Supplementary Figs. 6 and 7). Hydrazine was another possible product and was detected by the Watt and Chrisp method (Supplementary Figs. 8 and 9), but no hydrazine was produced in our work. The average ammonia yields and corresponding Faradaic efficiencies of FeSA–N–C are plotted in Fig. 2b. Strikingly, the highest Faradaic efficiency of 56.55% with a yield rate of 7.48 μg h−1 mg−1 was achieved at 0 V vs. RHE. With negatively moving the applied potential, the adsorption of hydrogen species gradually outcompeted nitrogen on the electrode surface, leading to the HER as the primary reaction in the catalytic system. As a result, the Faradaic efficiency and the yield rate were cast into shade. To the best of our knowledge, such selectivity at 0 V vs. RHE is the highest among previously reported works under similar conditions (Supplementary Table 1).
Electroreduction of N2 to NH3 at ambient conditions. a Linear sweep voltammograms of single-atom dispersed Fe–N–C (FeSA–N–C) and nitrogen-doped carbon (N–C) in Ar-saturated (dashed line) or N2-saturated (solid line) 0.1 M KOH solution with a scan rate of 50 mV s−1. b NH3 Faradaic efficiencies and mass-normalized yield rates at each given potential of FeSA–N–C. c NH3 Faradaic efficiencies and mass-normalized yield rates at each given potential of N–C. d Surface-area-normalized yield rate of NH3 production at different applied potentials on FeSA–N–C and N–C. e H2 selectivity of FeSA–N–C and N–C at different potentials. The error bars correspond to the standard deviations of measurements over three separately prepared samples under the same conditions. f Surface-area-normalized yield rate of H2 production at different applied potentials on FeSA–N–C and N–C
To attest the superiority of FeSA–N–C, the potentiostatic NRR tests for N–C were also conducted at the same potentials (Supplementary Fig. 10). As shown in Fig. 2c, for N–C, the highest NRR Faradaic efficiency is only 9.34%, which is a sixth of that of FeSA–N–C. The double-layer capacitance (Cdl) was calculated to determine the electrochemical active surface area (ECSA) of each sample (Supplementary Fig. 11). The surface-area-normalized yield rate of NH3 on FeSA–N–C shows a greater advantage over the mass-normalized activity, corresponding to a 2.6-fold improvement compared with N–C towards the NRR (Fig. 2d). The hydrogen evolution selectivity was tested to support this huge performance gap (Fig. 2e). For FeSA–N–C, with single-atom dispersed iron serving as active sites with a high selectivity of N2 adsorption with respect to H adsorption, inferior hydrogen evolution is observed at 0 vs. RHE. For N–C, its activity towards nitrogen reduction is relatively weak based on the narrow gap in the LSV curves of N2 and Ar-saturated environments, and most protons and electrons tend to evolve hydrogen. The surface-area-normalized activity of the HER was further calculated and compared in Fig. 2f. An H2 yield rate of 0.0029 μg h−1 cmECSA−2 was obtained on FeSA–N–C at 0 vs. RHE, which is less than a fourth of that on N–C (0.0125 μg h−1 cmECSA−2), indicating that single Fe atoms could indeed retard the HER process. Based on the above results, we can conclude that the superior NRR activity of FeSA–N–C derives from a joint effect of enhanced nitrogen reduction and suppressed hydrogen evolution.
As a further proof that the produced NH3 originated from the feeding N2, 15N (99 atom% 15N) isotope labeling experiments were conducted21. Obviously, when 15N2 was supplied, no labeled ammonia was produced in the absence of an applied potential (Supplementary Fig. 12). After electrolysis at 0 vs. RHE, only doublet peaks representing 15NH4+ were observed in the 1H nuclear magnetic resonance (1H NMR) spectra of the electrolyte, while no triple coupling indicating 14NH4+ could be detected (Fig. 3a). Moreover, the measured Faradaic efficiency and yield rate match well with that determined using 14N2 as the feeding gas (Fig. 3b), confirming that the produced NH3 in our study entirely comes from the electroreduction of N2 catalyzed by FeSA–N–C. In addition, control experiments without the FeSA–N–C catalyst and with an Ar-saturated electrolyte were also performed as an alternative analytical method. As shown in Supplementary Fig. 13, the corresponding ultraviolet–visible (UV–vis) absorption spectra obtained using the indophenol blue method exhibit no apparent NH3 when using bare carbon paper as the working electrode. Similarly, upon conducting electrolysis on FeSA–N–C-coated carbon paper in an Ar-saturated solution, no NH3 was detected, further indicating a reliable NH3 production data. The stability of the catalyst is important for practical use, and it was investigated by consecutive recycling electrolysis at 0 V vs. RHE. For FeSA–N–C, no obvious change could be observed in the total current density during 15 consecutive cycles (Supplementary Fig. 14) nor in the ammonia Faradaic efficiency and yield rate (Fig. 3c), suggesting its excellent stability for ambient ammonia synthesis. Careful examination of SEM, TEM, and HAADF-STEM images of FeSA–N–C show that the atomically dispersed Fe atoms were still anchored the N-doped carbon nanosheet without any agglomeration (Supplementary Figs. 15 and 16). The catalyst phase property also shows no obvious change, as confirmed by further characterization with XRD (Supplementary Fig. 17), indicating the robustness of FeSA–N–C towards ammonia synthesis.
15N isotope labeling experiment and stability test. a 15N isotope labeling experiment. b Comparison of the Faradaic efficiency and ammonia yield rate using different feeding gases for the NRR at 0 V vs. reversible hydrogen electrode (RHE). The error bars correspond to the standard deviations of measurements over three separately prepared samples under the same conditions. c Faradaic efficiencies and NH3 yield rates of the single-atom dispersed Fe–N–C (FeSA–N–C) calculated after consecutive recycling electrolysis in N2-saturated 0.1 M KOH at 0 V vs. RHE for 1 h
Discussion
Emerging cutting-edge operando techniques are considered critical for giving insight into the intrinsic mechanism of catalytic processes compared with ex-situ measurements. In-situ XANES with ultrasensitivity to the electronic properties of the metal was thus conducted under operation conditions to probe if single-atom Fe was the actual active phase for the NRR (Supplementary Fig. 18). Potentiostatic testing was carried out at 0 V vs. RHE and the XANES results of the Fe K-edge were collected at different times, as shown in Supplementary Fig. 19. Obviously, once the reaction proceeds, the white-line peak shifted from 7133 eV to a lower energy of 7131 eV after 15 min, suggesting a decreased valence state of Fe. During the NRR process, N2 molecules are fixed to bond with Fe sites by donating electrons to the unoccupied d orbitals of Fe22,23, thus accounting for the negative shift of its energy position. As the reaction goes on, the adsorption of nitrogen and the desorption of ammonia constantly occur and reach a dynamic balance; thus, the adsorption edge of Fe shows no distinct change from 15 to 30 min. The XANES and EXAFS profiles obtained after the NRR remain almost the same as those obtained before the reaction (Supplementary Fig. 20), which is consistent with the lack of change in the HAADF-STEM images and XRD patterns of the fresh and spent electrocatalysts, again confirming the stability of the single-atom Fe.
Computational studies were performed to understand the unique activity of the NRR on the FeSA–N–C catalyst in alkaline medium (Supplementary Fig. 21). The adsorption behavior of N2 towards single-atom Fe was first explored by MD simulations. Umbrella sampling was performed to quantify the free energy barrier of N2 access (Supplementary Fig. 22), and the potential of the mean force (PMF) as a function of the distance is shown in Fig. 4a. Clearly, starting from a distance of 1.5 nm, there is only a small energy barrier of 2.38 kJ mol−1 at approximately 0.54 nm for the approaching of N2 molecule. As a result, the N2 molecules tend to accumulate at approximately 0.45 nm away from the Fe site, leading to a localized high concentration, which would facilitate the following adsorption and thus benefit the whole NRR process. The competing adsorption between *N2 and *H was then evaluated by DFT calculations in Fig. 4b. In our case, *H comes from water dissociation and the energy barrier of this step is as high as 2.91 eV, representing negligible *H adsorption. Even if *H is adsorbed, its desorption to form H2 is still an endothermic reaction, with a much stronger Gibbs free energy change than those of common transition and noble metals24, as shown in Supplementary Fig. 23. Therefore, the HER kinetics are particularly sluggish on the FeSA–N–C surface. In contrast, it was found that nitrogen adsorption undergoes a downhill process and the binding Gibbs free energy of *N2 is as low as −0.28 eV, suggesting a significantly exothermic process. The usual weakness of the low absorbability of nitrogen is thus overcome25.
Computational studies. a Potential of the mean force (PMF) for N2 adsorption on the single-atom dispersed Fe–N–C (FeSA–N–C) in 0.1 M KOH, inset: Molecular dynamics (MD) simulation snapshots at 0.45 and 1.5 nm, with N2, blue spheres; H2O, gray dots; OH−, red and white sticks; K+, purple spheres. b Calculated energy barriers of the adsorption of hydrogen and nitrogen. c Free energy diagram for the nitrogen reduction reaction (NRR) on the FeSA–N–C catalyst at U = 0 V. Inset models represent the corresponding adsorbates. The orange, blue, red, green, and gray spheres represent C, N, O, Fe, and H atoms, respectively
Notably, considering the experimental environment of N2-saturated 0.1 M KOH, the solvent effect on NRR cannot be ignored and the adsorption energies of *H2O, *N2, *OH−, and *K+ (Supplementary Fig. 24) are compared in Supplementary Table 3. It turns out that *OH− is the easiest to adsorb onto FeSA–N–C; thus, the Gibbs free energy for each step of the NRR was calculated based on the Fe-*OH− structure. The computed energy profiles are depicted in Fig. 4c, and the alternating pathway (Supplementary Fig. 25) is more feasible than the distal pathway (Supplementary Fig. 26), as hydrogenation occurs preferentially between the two N atoms. The hydrogen tends to first attack the adsorbed *OH− and the reaction process from *OH− to *H2O-N2 is completely barrier-less (Fig. 4c). This thermodynamically favorable process could contribute to the activation of the following hydrogenation steps. According to the so-called hot atom mechanism, the molecule’s vibrational energy level can be enhanced by the energy released in the nitrogen adsorption process26. As a result, the reaction barrier of the following nitrogen activation is reduced. The reaction Gibbs free energy of the first hydrogenation step (*H2O-N2 + H+ + e− → *H2O-NNH), which is usually considered the rate-determining step of the whole process, is calculated to be only 0.28 eV uphill after nitrogen adsorption, which is much lower than that of the previously reported noble metal catalyst11. The reaction bottleneck is shifted to the last step (*OH-NH3 + NH3 + H+ + e− → *OH + 2NH3) and the overall reaction barrier is dramatically reduced. The DFT-calculated free energetics of the HER and NRR rationalize the electrochemical measurements and we can conclude that the desirable performance derives from the preferential nitrogen adsorption and its exothermic effect on the following nitrogen activation.
In summary, we have shown that positively shifting the reaction potential of the NRR enabled a single-atom dispersed Fe–N–C catalyst to achieve a Faradaic efficiency of 56.55% and a desirable yield rate of 7.48 μg h−1 mg−1 under ambient conditions. Comparative experiments indicate both enhanced NRR and suppressed HER performance. The promoted NRR process starts with a very positive onset potential of 0.193 V vs. RHE and achieves the best performance at 0 V vs. RHE. To determine reliability of the NH3 production data, an 15N isotopic labeling experiment using 15N2 as the feeding gas was carried out, and all the produced NH3 were confirmed to come from the electroreduction of N2 catalyzed by FeSA–N–C. In addition, during consecutive recycling, no obvious change can be observed in the ammonia Faradaic efficiency and yield rate, indicating the excellent stability of the catalyst. The specific mechanism of this excellent activity is unveiled by the MD and DFT calculations. The FeSA–N–C structure could effectively attract the access of nitrogen molecules, with a small energy barrier of 2.38 kJ mol−1. The obtained localized high concentration of N2 would favor the following adsorption with a particularly low binding Gibbs free energy of −0.28 eV. Moreover, such an exothermic process could provide energy for the following hydrogenation, as suggested by the hot atom hypothesis. As a result, the overall reaction barrier is dramatically reduced, and a highly selective ammonia synthesis is realized.
Methods
Reagents
Pyrrole (C4H5N, 98%) was purchased from Sigma-Aldrich. Ferrous chloride tetrahydrate (FeCl2·4H2O, ≥99.0%), hydrogen peroxide solution (H2O2, 30 wt% in H2O), sodium chloride (NaCl, 99.5%), ammonium persulfate ((NH4)2S2O8, ≥ 98%), potassium hydroxide (KOH, 95%), phenol (C6H6O, ≥99.5%), sodium nitroferricyanide dihydrate (C5FeN6Na2O·2H2O, 99.0%), sodium citrate dehydrate (C6H5Na3O7·2H2O, 99.0%), sodium hydroxide (NaOH, 96%), salicylic acid (C7H6O3, 99.5%), sodium hypochlorite solution (NaClO, available chlorine≥5.0%), ammonium chloride (NH4Cl, 99.5%), p-dimethylaminobenzaldehyde (C9H11NO, 99%) were purchased from Aladdin. Hydrochloric acid (HCl, 36.0–38.0%), sulfuric acid (H2SO4, 95.0–98.0%), ethyl alcohol (C2H5OH, 75%), hydrazine monohydrate (N2H4·H2O, ≥85.0%) were purchased from Sinopharm Chemical Reagent Co., Ltd. All chemical reagents were used without further purification.
Catalyst preparation
To prepare FeSA–N–C, 2 ml pyrrole was adequately dispersed in deionized water by ultrasonic vibration. Excess ferrous chloride and hydrogen peroxide were added, and the reaction lasted several hours until a bright yellow and transparent solution was obtained. Sodium chloride was further dissolved in the solution to be used as a template. The product was collected by freeze-drying to obtain brown powders. The material was then placed in a ceramic boat and carbonized at 600 °C for 2 h under argon protection. After removing the salt templates through sufficient washing with a lot of water and ethanol, the products were dried in a vacuum at 60 °C overnight prior to use. To prepare N–C, 2 ml pyrrole was adequately dispersed in deionized water by ultrasonic vibration. Sodium chloride was dissolved in the solution, followed by the addition of 1 ml 1 M HCl. Then, (NH4)2S2O8 solution was dropwise added into the system under vigorous stirring to start the pyrrole polymerization. The solution was freeze-dried after the reaction and was kept in an ice/water bath for 24 h. The obtained material was placed in a ceramic boat and carbonized at 600 °C for 2 h under argon protection. After removing the salt templates through sufficient washing with a lot of water and ethanol, the samples were dried in a vacuum at 60 °C overnight to obtain black powders.
Physical characterization
The morphology was studied via a field emission scanning electron microscope (FESEM, SU8010, Japan) and a field emission transmission electron microscope (FETEM, FEI Tecnai G2 F20 S-TWIN TMP, Hongkong). The dispersion of single Fe atoms was characterized by atomic-resolution high-angle annular dark-field scanning transmission electron microscopy on a JEOL JEM-ARM200F instrument equipped with a probe spherical aberration corrector. The iron concentrations of the samples were determined via inductively coupled plasma atomic emission spectroscopy. The EXAFS spectra (Fe K-edge) were collected at 1W1B station in the Beijing Synchrotron Radiation Facility (BSRF). The storage rings of BSRF were operated at 2.5 GeV with a maximum current of 250 mA. Using an Si (111) double-crystal monochromator, data collection was carried out in transmission mode using the ionization chamber for the Fe foil and in fluorescence excitation mode using a Lytle detector for FeSA–N–C. All spectra were collected in ambient conditions. The composition of the catalysts was characterized by XRD patterns (D8 Advance, Bruker) and Raman spectroscopy (HR evolution, Horiba Jobin Yvon, France).
Cathode preparation
Typically, 1 mg of catalyst and 5 μl of Nafion solution (Alfa Aesar, 5 wt%) were dispersed in 100 μl of ethanol by sonicating for at least 1 h to form a homogeneous ink. Then, the catalyst ink was loaded onto carbon paper with an area of 1 × 1 cm2 and dried in N2 atmosphere at 80 °C for 1 h. The obtained mass loading was 1 mg cm−2.
Electrochemical NRR measurements
The reduction of N2 gas was performed in a two-compartment cell at room temperature, which was separated by a Nafion 211 membrane (DuPont). Before the NRR tests, the Nafion membrane was pretreated by successive heating in H2O2 (5%) aqueous solution at 80 °C for 1 h and in ultrapure water at 80 °C for another 1 h. A conventional three-electrode system in an electrochemical workstation was used to conduct electrochemical measurements, with FeSA–N–C or N–C as the working electrode, Pt foil as the counter electrode, and Ag/AgCl (4 M KCl) as the reference electrode. All potentials were converted to the RHE scale via calibration. Pure N2 was continuously fed into the cathodic compartment, with a properly positioned sparger to ensure that the entire cathode was hit by the N2 gas bubbles during the experiments. The electrochemical NRR was tested in N2-saturated 0.1 M KOH (30 ml in each cell compartment) at ambient temperature and pressure. The linear sweep voltammetry was scanned at a rate of 50 mV s−1. The potentiostatic tests were tested at different potentials including 0.1, 0, −0.1, −0.2, −0.3, and −0.4 V vs. RHE. To avoid the loss of produced NH3 by N2 blowing during the test, another glass tube filled with 0.001 M H2SO4 (30 ml) as the gas absorption liquid was set at the end of the cell. The total NH3 production yield was the summation of the NH3 in the 0.1 M KOH and 0.001 M H2SO4. After the electrochemical reduction reaction, the electrolyte and gas absorption liquid were both collected and analyzed by chromogenic reactions for qualitative measurements. For comparison, potentiostatic tests in Ar-saturated 0.1 M KOH were also conducted in this work.
Determination of the produced ammonia
The concentration of the produced ammonia in the 0.1 M KOH and 0.001 M H2SO4 was determined by the indophenol blue method7. For the 0.1 M KOH case, 10 ml of the electrolyte after the NRR potentiostatic test was taken out, and 0.4 ml of the solution containing 5 g of phenol in 50 ml of ethanol, and 0.4 ml of 0.5 wt% C5FeN6Na2O (sodium nitroferricyanide) was successively added. Then, 1 ml of oxidizing solution containing 10 g of sodium citrate dehydrate, 0.5 g of sodium hydroxide and 10 ml of sodium hypochlorite in 50 ml of Millipore water was also added into the above solution. For the 0.001 M H2SO4 case, 2 ml of the electrolyte after the NRR potentiostatic test was taken out. Next, 2 ml of a 1 M NaOH solution containing salicylic acid and sodium citrate dehydrate was added. Then, 1 ml of 0.05 M NaClO and 0.2 ml of 1 wt% C5FeN6Na2O (sodium nitroferricyanide) were also added into the above solution. The UV–Vis absorption spectrum was measured after the mixture was stored in darkness at room temperature for 3 h. The concentration of indophenol blue was measured according to the absorbance at a wavelength of 655 nm. Standard NH4Cl solutions at a series of concentrations in 0.1 M KOH and 0.001 M H2SO4 were prepared to build the calibration curves and quantify the produced ammonia.
Determination of the produced hydrazine
The concentration of the produced hydrazine in the 0.1 M KOH and 0.001 M H2SO4 was determined by the Watt and Chrisp method27. In both cases, a mixture of ethanol (300 ml), HCl (concentrated, 30 ml), and p-dimethylaminobenzaldehyde (5.99 g) was used as a color reagent. For this, 5 ml of the residual electrolyte after the NRR potentiostatic test was taken out, and 5 ml of the above-prepared color reagent was successively added. The resulting solution was stirred for 10 min, and its absorbance was measured at a wavelength of 455 nm. Standard hydrazine monohydrate solutions at a series of concentrations in 0.1 M KOH and 0.001 M H2SO4 were prepared to build the calibration curves and quantify the produced hydrazine.
Determination of the HER productions
The H2 was manually sampled and analyzed by gas chromatography (GC, Agilent 7890B).
Calculation of the equilibrium potential
The standard potential for the NRR in alkaline medium was calculated from the standard Gibbs energy of formation at 298.15 K.
where n is the number of transferred electrons (6) and F is the Faraday constant (96,485 C mol−1).
The thermodynamic equilibrium potential under the reaction conditions was calculated according to the Nernst equation, assuming 1 atm of N2 in the solution.
where R is the gas constant (8.314 J mol−1 K−1), T is the temperature in Kelvin (298.15 K), F is the Faraday constant (96,485 C mol−1), c(OH−) is the hydroxide concentration (0.1 M), and the pH is 13. Assuming a c(NH4OH) of 10−7 M in the solution, the corresponding thermodynamic equilibrium potentials is determined to be 0.227 V vs. RHE.
Faradaic efficiency and the yield rate
The Faradaic efficiency (FE) and mass-normalized yield rate of NH3 were calculated as below:
where F is the Faraday constant (96,485 C mol−1), t is the electrolysis time (1 h), m is the loading mass of the catalysts (1 mg), Q is the total charge passed through the electrode, V is the volume of the electrolyte, and c(NH3) is the measured ammonia concentration.
The electrochemical double-layer capacitance (Cdl) of the materials was measured to determine their electrochemical surface area (ECSA) using the cyclic voltammograms (CVs) in a small potential range with no faradic processes between 0.9 and 1.0 V vs. RHE. The plotted current density against scan rate has a liner relationship and its slope is twice the Cdl. The ECSA can then be calculated as below:
The surface-area-normalized activity of NH3 was calculated as below:
The Faradaic efficiency of H2 was calculated as below:
where v(H2) is the volume concentration of H2 in the exhaust gas from the electrochemical cell (GC data), G is the gas flow rate (ml min−1 at room temperature and ambient pressure), itotal is the steady-state cell current, p0 = 1.01 × 105 Pa, and R = 8.314 J mol−1 K−1.
The surface-area-normalized activity of H2 was calculated as below:
where Mr(H2) is the relative molecular mass of H2, e is the electron charge (1.602 × 10−19 C), and NA is the Avogadro constant (6.02 × 1023 mol−1).
15N isotopic labeling experiment
15N2 (Wuhan Newradar Special Gas Co. Ltd 99 atom% 15N) was used as the feeding gas in the labeling experiment. A low-velocity gas flow system was adopted due to the limited supply and expense of 15N2. After electrolysis at 0 V vs. RHE for 10 h, 10 ml of the electrolyte was taken out, and its pH was adjusted to 3 by adding 0.5 M H2SO4. Then, the solution was concentrated to 2 ml and 0.9 ml of the resulting liquid was taken out, followed by adding 0.1 ml of D2O as an internal standard. The produced ammonia was quantified using 1H nuclear magnetic resonance measurements (1H NMR; Agilent 600 MHz).
In-situ XAS characterization for NRR
In-situ and ex-situ XAS data were collected at room temperature at the BL14W1 beamline of Shanghai Synchrotron Radiation Facility (SSRF). Energy calibration was carried out with a Fe foil standard using transmission mode, while the Si (111) monochromator scanned the incident X-ray photon energy through the Fe K absorption edge. All spectra of the samples were measured in fluorescence mode. The special three-electrode system was assembled using a tailor-made mold with a window for X-ray penetration. The working electrode was prepared by casting FeSA–N–C onto carbon paper. A graphite rod was used as the counter electrode, and Ag/AgCl (4 M KCl) was used as the reference electrode. The electrolyte was N2-saturated 0.1 M KOH. Potentiostatic testing at 0 V vs. RHE was used for in-situ XAS characterization using the CHI660E (Shanghai Chenhua instrument Co., Ltd) electrochemical workstation.
Computational method and model
The umbrella-sampling method was used to calculate the PMF for the adsorption of nitrogen molecules onto FeSA–N–C. The FeSA–N–C was placed at the center of a simulation box (4 nm × 4 nm × 6 nm) and perpendicular to the z-axis, with one N2 molecule right above the center Fe atom at a distance of 1.5 nm. Then, the box was solvated with KOH solution (containing 6 K+, 6 OH– and 3000 water molecules). The entire system was energy-minimized (EM) and NPT-equilibrated (constant number of atoms, pressure, and temperature) at 298 K and 1 bar for 1 ns.
Subsequently, the N2 molecule was pulled towards the Fe atom along the z-axis at a rate of 0.01 nm ps–1 with a force constant of 105 kJ mol–1 nm–2. The trajectory was extracted, and a series of configurations was picked out, with the center of mass position of the N2 molecule in adjacent configurations at 0.03 nm. These consecutive configurations were used as windows for umbrella sampling for 8 ns at NPT (298 K, 1 bar). The temperature and pressure were controlled by the Nose-Hoover thermostat and Parrinello-Rahman barostat, respectively.
A harmonic force constant of 104 kJ mol–1 nm–2 in all directions was employed to restrain the FeSA–N–C. For the N2 molecule, a harmonic force constant of 106 kJ mol–1 nm–2 was employed during EM and NPT equilibration in all directions but only in the x–y directions during pulling and umbrella sampling. During umbrella sampling, a harmonic force constant of 105 kJ mol–1 nm–2 was employed in the z-direction. The weighted histogram analysis method was used to obtain the PMF curve.
The DFT calculations were conducted based on the Cambridge Sequential Total Energy Package (CASTEP). The exchange-correlation function under the generalized gradient approximation (GGA) with norm-conserving pseudopotentials and the Perdew–Burke–Ernzerhof function was adopted to describe the electron–electron interaction. An energy cutoff of 750 eV was used, and a k-point sampling set of 5 × 5 × 1 was tested to be converged. A force tolerance of 0.01 eV Å−1, an energy tolerance of 5.0 × 10−7 eV per atom, and a maximum displacement of 5.0 × 10−4 Å were considered. Each atom in the storage models is allowed to relax to the minimum enthalpy without any constraints. The vacuum space along the z-direction is set to be 15 Å. The intermediates have been absorbed onto the Fe atom of the substrate.
The complete linear and quadratic synchronous transit method search protocol, the self-consistent field tolerance of 5.0 × 10−7 eV, and root mean square convergence of 0.02 eV/Å were set for transition states.
The adsorption energy ΔE of the A group on the surface of the substrates was defined as
where *A and * denote the adsorption of the A group onto the substrates and the bare substrates and, EA denotes the energy of the A group.
The Gibbs free energy change (ΔG) of each chemical reaction is calculated by
where E, ZPE, T, and S denote the calculated total energy, zero-point energy, temperature, and entropy, respectively. ΔGU = –eU (U is the potential measured against a normal hydrogen electrode) and ΔGpH = –kBTln(10) × pH. Here, T = 300 K and pH = 13 are considered.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Gruber, N. & Galloway, J. N. An Earth-system perspective of the global nitrogen cycle. Nature 451, 293–296 (2008).
Pool, J. A., Lobkovsky, E. & Chirik, P. J. Hydrogenation and cleavage of dinitrogen to ammonia with a zirconium complex. Nature 427, 527–530 (2004).
Erisman, J. W., Sutton, M. A., Galloway, J., Klimont, Z. & Winiwarter, W. How a century of ammonia synthesis changed the world. Nat. Geosci. 1, 636–639 (2008).
van der Ham, C. J. M., Koper, M. T. M. & Hetterscheid, D. G. H. Challenges in reduction of dinitrogen by proton and electron transfer. Chem. Soc. Rev. 43, 5183–5191 (2014).
Liu, C., Sakimoto, K. K., Colon, B. C., Silver, P. A. & Nocera, D. G. Ambient nitrogen reduction cycle using a hybrid inorganic biological inorganicbiological system. Proc. Natl. Acad. Sci. USA 114, 6450–6455 (2017).
Shanmugam, K. T. & Valentine, R. C. Microbial production of ammonium ion from nitrogen. Proc. Natl. Acad. Sci. USA 72, 136–139 (1975).
Zhu, D., Zhang, L. H., Ruther, R. E. & Hamers, R. J. Photo-illuminated diamond as a solid-state source of solvated electrons in water for nitrogen reduction. Nat. Mater. 12, 836–841 (2013).
Ali, M. et al. Nanostructured photoelectrochemical solar cell for nitrogen reduction using plasmon-enhanced black silicon. Nat. Commun. 7, 11335 (2016).
Pickett, C. J. & Talarmin, J. Electrosynthesis of ammonia. Nature 317, 652–653 (1985).
Kyriakou, V., Garagounis, I., Vasileiou, E., Vourros, A. & Stoukides, M. Progress in the electrochemical synthesis of ammonia. Catal. Today 286, 2–13 (2017).
Bao, D. et al. Electrochemical reduction of N2 under ambient conditions for artificial N2 fixation and renewable energy storage using N2/NH3 Cycle. Adv. Mater. 29, 1604799 (2017).
Shi, M. -M. et al. Au sub-nanoclusters on TiO2 toward highly efficient and selective electrocatalyst for N2 conversion to NH3 at ambient conditions. Adv. Mater. 29, 1606550 (2017).
Singh, A. R. et al. Electrochemical ammonia synthesis—the selectivity challenge. ACS Catal. 7, 706–709 (2017).
Kordali, V., Kyriacou, G. & Lambrou, C. Electrochemical synthesis of ammonia at atmospheric pressure and low temperature in a solid polymer electrolyte cell. Chem. Commun. 0, 1673–1674 (2017).
Li, S. –J. et al. Amorphizing of Au nanoparticles by CeOx–RGO hybrid support towards highly efficient electrocatalyst for N2 reduction under ambient conditions. Adv. Mater. 29, 1700001 (2017).
Shi, M. -M. et al. Anchoring PdCu amorphous nanocluster on graphene for electrochemical reduction of N2 to NH3 under ambient conditions in aqueous solution. Adv. Energy Mater. 8, 1800124 (2018).
Lv, C. et al. An amorphous noble-metal-free electrocatalyst that enables nitrogen fixation under ambient conditions. Angew. Chem. Int. Ed. 130, 6181–6184 (2017).
Chen, Y. et al. Isolated single iron atoms anchored on N-doped porous carbon as an efficient electrocatalyst for the oxygen reduction reaction. Angew. Chem. 129, 7041–7045 (2017).
Xiao, M. et al. Microporous framework induced synthesis of single-atom dispersed Fe-N-C acidic ORR catalyst and its in situ reduced Fe-N4 active site identification revealed by X-ray absorption spectroscopy. ACS Catal. 8, 2824–2832 (2018).
Mahmood, N. et al. Electrocatalysts for hydrogen evolution in alkaline electrolytes: mechanisms, challenges, and prospective solutions. Adv. Sci. 5, 1700464 (2018).
Wang, J. et al. Ambient ammonia synthesis via palladium-catalyzed electrohydrogenation of dinitrogen at low overpotential. Nat. Commun. 9, 1795–1801 (2018).
Wang, P. et al. Breaking scaling relations to achieve low-temperature ammonia synthesis through LiH-mediated nitrogen transfer and hydrogenation. Nat. Chem. 9, 64–70 (2017).
Légaré, M. A. et al. Nitrogen fixation and reduction at boron. Science 359, 896–900 (2018).
Nørskov, J. K. et al. Trends in the exchange current for hydrogen evolution. J. Electrochem. Soc. 152, J23–J26 (2005).
Suryanto, B. H. R. et al. Rational electrode−electrolyte design for efficient ammonia electrosynthesis under ambient conditions. ACS Energy Lett. 3, 1219–1224 (2018).
Gong, Y. et al. Ternary intermetallic LaCoSi as a catalyst for N2 activation. Nat. Catal. 1, 178–185 (2018).
Watt, G. W. & Chrisp, J. D. Spectrophotometric method for determination of hydrazine. Anal. Chem. 24, 2006–2008 (1952).
Acknowledgements
We acknowledge the support from the National Natural Science Foundation of China (No. 51622208, No. 21703149, and No. 51872193). We also appreciate Shanghai Synchrotron Radiation Facility (SSRF) and Taiwan Light Source (TLS) for the support of XAS experiments.
Author information
Authors and Affiliations
Contributions
C.Y. and T.Q. conceived and designed this work. M.W. and S.L. prepared materials and performed the material characterization and electrochemical measurement. H.J. conducted the theoretical calculation. J. Zhou, J.L., J.X., and J. Zhong offered help in the material characterization. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks Hong Jin Fan and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, M., Liu, S., Qian, T. et al. Over 56.55% Faradaic efficiency of ambient ammonia synthesis enabled by positively shifting the reaction potential. Nat Commun 10, 341 (2019). https://doi.org/10.1038/s41467-018-08120-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-08120-x
This article is cited by
-
Achieving green synthesis of high-value-added chemicals via N-integrated CO2 co-reduction: a review
Rare Metals (2024)
-
Selective Pathway of Nitrogen Reduction Controlled by Symmetry Breaking in BiErRu2O7 Pyrochlores
Catalysis Letters (2024)
-
The reformation of catalyst: From a trial-and-error synthesis to rational design
Nano Research (2024)
-
Prospects and challenges of green ammonia synthesis
Nature Synthesis (2023)
-
Effective Descriptor for Nitrogen Reduction on Atomic Catalysts
Catalysis Letters (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.