Abstract
Plasmons, collective oscillations of electron systems, can efficiently couple light and electric current, and thus can be used to create sub-wavelength photodetectors, radiation mixers, and on-chip spectrometers. Despite considerable effort, it has proven challenging to implement plasmonic devices operating at terahertz frequencies. The material capable to meet this challenge is graphene as it supports long-lived electrically tunable plasmons. Here we demonstrate plasmon-assisted resonant detection of terahertz radiation by antenna-coupled graphene transistors that act as both plasmonic Fabry-Perot cavities and rectifying elements. By varying the plasmon velocity using gate voltage, we tune our detectors between multiple resonant modes and exploit this functionality to measure plasmon wavelength and lifetime in bilayer graphene as well as to probe collective modes in its moiré minibands. Our devices offer a convenient tool for further plasmonic research that is often exceedingly difficult under non-ambient conditions (e.g. cryogenic temperatures) and promise a viable route for various photonic applications.
Similar content being viewed by others
Introduction
Selective detection and spectroscopy of THz fields is a challenging task in modern optoelectronics offering a wide range of applications: from security and medical inspection to radio astronomy and wireless communications1,2. Among the variety of available detection principles2, one elegant proposal has always stood out and remained intriguing for more than two decades. The idea is to compress incident radiation into highly-confined two-dimensional plasmons propagating in the field effect transistor (FET) channel and to rectify the induced ac potential using the same device3. The FET channel, in this case, acts as a tunable plasmonic cavity with a set of resonant frequencies defined by its length and the density of charge carriers. The implementation of such resonant devices has promised on-chip selective sensing, spectroscopy, mixing, and modulation of THz fields below the classical diffraction limit3. However, despite decades-long experimental efforts, the excitation of long-lived plasma oscillations in conventional FETs has proven challenging4,5,6,7,8,9 and little evidence of resonant THz detection has been found so far10,11,12,13,14.
Graphene has recently demonstrated great promise for mid- and far-infrared plasmonics15,16,17,18,19,20,21,22 and attracted a great deal of attention as a platform for plasmonic radiation detectors19,23. With lowering the operation frequency down to the THz domain, the resonant excitation of plasmons becomes exceedingly difficult and can only be achieved if the momentum relaxation rate is below the plasmon frequency, which, in turn, requires ultra-high electron mobility. For this reason, in all graphene-based far-field THz detectors reported so far, the plasma waves—if any—were overdamped, and the devices exhibited only a broadband (non-resonant) photoresponse5,6,7,8,9,24,25. As a result, numerous applications relying on resonant plasmon excitation (see e.g. refs. 3,26,27,28,29) remain experimentally yet unrealized.
In this work, we demonstrate this long-sought resonant regime using FETs based on high-quality van der Waals heterostructures. In particular, we employ graphene encapsulated between hexagonal boron nitride (hBN) crystals which have been shown to provide the cleanest environment for long-lived graphene plasmons20,22. Antenna-mediated coupling of such FETs to free-space radiation results in the emergence of dc photovoltage that peaks when the channel hosts an odd number of plasmon quarter-wavelengths. Exploiting the gate-tunability of plasmon velocity, we switch our detectors between more than 10 resonant modes, and use this functionality to measure plasmon wavelength and lifetime. Thanks to the far-field radiation coupling, our compact devices offer a convenient tool for studies of plasmons in two-dimensional electron systems under non-ambient conditions (e.g. cryogenic environment and high magnetic fields) where other techniques may be arduous. As an example, we apply our approach to probe plasmons in graphene/hBN superlattices and unveil collective modes of charge carriers in moiré minibands.
Results
Graphene-based THz detectors
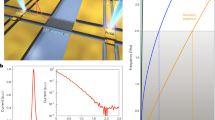
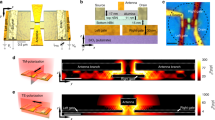
There are three crucial steps to consider in the design of resonant photodetectors. First, the incoming radiation needs to be efficiently compressed into plasmons propagating in the FET channel. Second, the channel should act as a high-quality plasmonic cavity, where constructive interference of propagating plasma waves leads to the enhancement of the field strength. Third, the high-frequency plasmon field needs to be rectified into a dc photovoltage. To meet these hard-to-satisfy5,6,7,8 requirements, we fabricated proof-of-concept detectors using high-mobility bilayer graphene (BLG) FETs. To this end, we first applied a standard dry transfer technique to encapsulate BLG between two relatively thin (d ≈ 80 nm) slabs of hBN30. The heterostructure had side contacts (Fig. 1a) which were extended to the millimeter scale and one of them served as a sleeve of the broadband antenna, Fig. 1c and Supplementary Fig. 3a, b (see Methods). Another antenna sleeve was connected to the top gate covering the FET channel (inset of Fig. 1d). In this coupling geometry, the incident radiation induces high-frequency modulation of the gate-to-channel voltage thereby launching plasma waves from the source terminal3. The detector was assembled on a THz–transparent Si wafer attached to a Si lens focusing the incident radiation onto the antenna (Fig. 1b).
Graphene-based THz detectors. a Schematics of the encapsulated BLG FET used in this work. b 3D rendering of our resonant photodetector. THz radiation is focused to a broadband bow-tie antenna by a hemispherical silicon lens yielding modulation of the gate-to-source voltage, as indicated in a. c Optical photograph of one of our photodetectors. Scale bar is 200 μm. d Conductance of one of our BLG FETs as a function of the gate voltage Vg, measured at a few selected temperatures. Inset: zoomed-in photograph of c showing a two-terminal FET with gate and source terminals connected to the antenna. Scale bar is 10 μm
We studied four BLG FETs, from 3 to 6 μm in length L and from 6 to 10 μm in width W, all exhibiting typical field-effect behavior as seen from measurements of the conductance G (Fig. 1d and Supplementary Fig. 3e). In particular, G is minimal at the charge neutrality point and rises with increasing Vg. The mobility of our devices at the characteristic carrier density n = 1012 cm−2 exceeded 10 m2/Vs and remained above 2 m2/Vs at temperatures T = 10 K and 300 K, respectively, as determined from the characterization of a multiterminal Hall bar produced under identical protocol reported in Methods (Supplementary Note 1 and Supplementary Fig. 1).
Broadband operation
We intentionally start the photoresponse measurements at the low end of the sub-THz domain, where the plasma oscillations are overdamped (see below). This allows us to compare the performance of our detectors with previous reports5,6,7,8,23. Figure 2a shows an example of the responsivity Ra = ΔU/P, where ΔU is the emerging source-to-drain photovoltage and P is the incident radiation power, as a function of the top gate voltage Vg under irradiation with frequency f = 0.13 THz in one of our BLG detectors (see Methods). In good agreement with the previous studies, the Ra(Vg) dependence follows the evolution of the FET-factor \(F = - {\textstyle{1 \over \sigma }}{\textstyle{{d\sigma } \over {dV_{\mathrm{g}}}}}\), shown in the inset of Fig. 2a. In particular, Ra increases in magnitude upon approaching the charge neutrality point (NP) where it flips sign because of the change in charge carrier type.
Plasmon-assisted THz photodetection. a Responsivity measured at f = 130 GHz and three representative temperatures. Orange rectangle highlights an offset stemming from the rectification of incident radiation at the p-n junction between the p-doped graphene channel and the n-doped area near the contact. Upper inset: FET-factor F as a function of Vg at the same T. Lower inset: maximum Ra as a function of T. b Gate dependence of responsivity recorded under 2 THz radiation. The upper inset shows a zoomed-in region of the photovoltage for electron doping. Resonances are indicated by black arrows. Lower inset: resonant responsivity at liquid-nitrogen temperature
We have studied the operation of our detectors at different temperatures and found that Ra grows with decreasing T (bottom inset of Fig. 2a) and reaches its maximum Ra ≈ 240 V/W at T = 10 K due to a steeper F(Vg) at this T (top inset of Fig. 2a). At large positive Vg, Ra approaches zero at all T, whereas at negative Vg, a positive offset is observed (orange rectangle in Fig. 2a). This behavior is common for this type of devices and is related to additional rectification by p–n junctions at the boundaries between the p-doped graphene channel and the n-doped contact regions24,31,32.
The overall broadband responsivity of our BLG detectors is further improved in transistors with stronger nonlinearity, which can be conveniently parametrized by the FET-factor introduced above. To this end, we took advantage of the gate-tunable band structure of BLG and fabricated a dual-gated photodetector. Simultaneous action of the two gates results in a band gap opening and a steep F(Vg) dependence that, in turn, causes a drastic enhancement of Ra (Supplementary Note 2). The latter exceeded 3 kV/W for a weak displacement field D of 0.1 V/nm (Supplementary Fig. 2b). This translates to the noise equivalent power (NEP) of about 0.2 pW/Hz1/2, estimated using the Johnson-Nyquist noise spectral density obtained for the same D. The observed performance of our detectors makes them competitive not only with other graphene-based THz detectors operating in the broadband regime23, but also with some commercial superconducting and semiconductor bolometers operating at the same f and T (Supplementary Table 1).
Resonant operation
The response of our photodetectors changes drastically as the frequency of incident radiation is increased. Figure 2b shows the gate voltage dependence of Ra recorded in response to 2 THz radiation. In stark contrast to Fig. 2a, Ra exhibits prominent oscillations, despite the fact that F as a function of Vg is featureless (black curve in Fig. 2b). The oscillations are clearly visible for both electron and hole doping and display better contrast on the hole side, likely because of the aforementioned p–n junction rectification. Resonances are well discerned at 10 K, although they persist up to liquid-nitrogen T, especially for Vg < 0. A further example of resonant operation of another BLG device is shown in Supplementary Note 3.
We have also studied the performance of our detectors at intermediate frequencies and found that the resonant operation of our devices onsets in the middle of the sub-THz domain (Supplementary Note 4). In particular, we have found that at f = 460 GHz, the resonances are already well-developed (Supplementary Fig. 4). At such low f, only two peaks in the photoresponse (one for electrons and one for holes) are observed for the same gate voltage span as in Fig. 2b along with an apparent increase of their full width at half-height. These observations are in full agreement with the plasmon-assisted photodetection model discussed below.
Plasmon resonances in graphene FETs
We argue that the observed peaks in the photoresponse emerge as a result of plasmon resonance in the FET channel. To this end, we model our FET as a plasmonic Fabry-Perot cavity endowed with a rectifying element. This results in responsivity given by
where R0 is a smooth function of carrier density n and frequency f that depends on the microscopic rectification mechanism, rs and rd are the wave reflection coefficients from the source and drain terminals, respectively, and q is the complex wave vector governing the wave propagation in the channel (Supplementary Note 5). In gated 2D electron systems, the relation between the frequency ω and the real part of the wave vector q′ is linear, ω = sq′, where the plasmon phase velocity is
Here m and e are the effective mass of carriers and the elementary charge respectively, vF and \(k_{\mathrm{F}} = \sqrt {\pi n}\) are the Fermi velocity and the Fermi wave vector, d is the distance to the gate, αc = e2/(4πεzε0ħvF) is the dimensionless coupling constant and εz is the out-of-plane dielectric permittivity33,34. We further note that Eq. (2) is valid for monolayer graphene upon replacement of the effective mass m with the cyclotron mass, m → ħkF/vF (see Supplementary Note 6). The latter increases with gate-induced carrier density n, thereby limiting the tuning range of s for a given voltage span. In contrast, in the case of BLG, m is nearly constant (≈0.036me) for experimentally accessible values of Vg, a feature that allows us to vary s over a wider range and thus switch the detector between multiple modes, as we now proceed to show.
It follows from Eq. (1), that the responsivity of our Fabry–Perot rectifier is expected to peak whenever the denominator in Eq. (1) approaches zero. In our devices, the source potential is clamped to antenna voltage, and no ac current flows into the drain, therefore rsrd ≈ −1 (refs. 3,32). The resonances should therefore occur whenever the real part of the wave number is quantized according to
The quantization rule (3) combined with Eq. (2) predicts a linear dependence of the mode number k on \(| {V_{\mathrm{g}}} |^{ - 1/2}\) which may serve as a benchmark for plasmon resonances in the FET channel. This is indeed the case of our photodetector, as shown in Fig. 3a, e and Supplementary Fig. 3c. The slope of the experimental \(k( {| {V_{\mathrm{g}}} |^{ - 1/2}} )\) dependence in Fig. 3a matches well the theoretical expectation for a BLG Fabry-Perot cavity of length L = 6 μm. At large \(| {V_{\mathrm{g}}} |^{ - 1/2}\), we find a slight upward trend in the experimental data with respect to the linear dependence. We attribute this trend to deviations of the plasmon dispersion from the linear law at short wavelengths which stem from the non-local relation between electric potential and carrier density33. Note that the known non-parabolicity of the BLG spectrum35 resulting in an increase of m at large density n would bend the dependence in Fig. 3a in the opposite direction.
Plasmon resonances in encapsulated graphene FET. a Mode number k as a function of \(V_{\mathrm{g}}^{ - 1/2}\) (symbols). Solid line: theoretical dependence for L = 6 μm, m = 0.036me, and f = 2 THz. The first mode supported by our Fabry-Pérot plasmonic cavity corresponds to kmin = 3; the fundamental mode with k = 0 is beyond the accessible gate voltages. b Examples of high-frequency potential distribution in the plasmon mode (real part) under resonant conditions for given k. Brown and blue colors represent positive and negative values of electrical potential, respectively. S, G, and D stand for source, gate, and drain terminals, respectively. c Experimental (symbols) and calculated (solid line) plasmon wavelengths λp as a function of carrier density, as obtained from a. The corresponding value of the inverse compression ratio, λ0/λp, for f = 2 THz is given on the right axis. d Plasmon lifetime τp and quality factor Q as obtained from the width of the resonances shown in e. Error bars stem from the fitting procedure. e Experimental and calculated responsivities as functions of \(V_{\mathrm{g}}^{ - 1/2}\), normalized to the effective antenna impedance \(Z = V_{\mathrm{a}}^2{\mathrm{/}}P\) relating the incident power to the resulting gate-to-channel voltage Va. The theoretical Dyakonov-Shur dependence (Supplementary Note 9) was obtained by using characteristic τp = 0.6 ps from d. Inset: normalized responsivity Ra/Z after the subtraction of a smooth non-oscillating background. The solid blue line is the best Lorentzian fit to the data, with δ = 0.1 V−1/2, which translates to τp = 0.5 ps
Photovoltage-based spectroscopy of 2D plasmons
The resonant gate-tunable response of our detectors offers a convenient tool to characterize plasmon modes in graphene channels. From Eq. (3) it follows that resonances occur if L = (2k + 1)λp/4, where λp = 2π/q′ is the plasmon wavelength (Fig. 3b). Using the experimentally observed peak positions, we have determined the density dependence of λp, shown in Fig. 3c, which flaunts excellent agreement with theory (Supplementary Note 5). The compression ratio λp/λ0 between the plasmon and free-space wavelength (λ0 = c/f and c the speed of light in vacuum) ranges between 1/50 and 1/150, highlighting the ultra-strong confinement of THz fields enabled by graphene plasmons, matching the record value known in the literature20.
Apart from λp, the resonant responsivity carries information about another valuable characteristic of plasmons, namely, their lifetime, τp. The latter is related to the peak width at half-height δ via (Supplementary Note 7)
Using Lorentzian fits to the photoresponse curves (inset of Fig. 3e), we have extracted τp as a function of n, shown in Fig. 3d. The lifetime was found to range between ≈0.3 and ≈0.9 ps, which is slightly shorter than the transport time τtr ≈ 2 ps as extracted from the mobility, τtr = mμ/e (Supplementary Note 1). The corresponding quality factor, Q = 2πfτp, was found to vary between 4 and 11 for f = 2 THz, and between 0.2 and 0.7 for f = 0.13 THz, see Fig. 3d. The latter implies that it is unreasonable to expect resonant photoresponse of such detectors in the GHz range, and they can only operate in the broadband (non-resonant) regime, in accordance with the data in Fig. 2a. On the contrary, the resonant responsivity should become more profound at higher frequencies of the THz window and can be further enhanced in graphene FETs of higher quality, such as those using graphite gates to screen remote charge impurities36.
Miniband plasmons in graphene/hBN superlattices
The approach demonstrated above is universal and can be applied to studies of plasmons in arbitrary high-mobility 2D systems embedded in FET channels, as we now proceed to show for the case of devices made of BLG/hBN moiré superlattices37.
Figure 4b and Supplementary Fig. 3c show examples of Ra as a function of Vg recorded in our superlattice devices in response to 2 THz radiation. As in the case of plain BLG, the overall evolution of the superlattice responsivity Ra (Vg) follows that of the FET-factor (black curve) modulated by the plasmon resonances. Note the total number of resonances is smaller due to the shorter FET channel (cf. Supplementary Fig. 3c) and they are visible only for Vg < 0, presumably due to a stronger nonlinearity in this detector for negative doping (in another superlattice FET, the resonances were well-observed for both Vg polarities as shown in Supplementary Fig. 3c). Importantly, the FET-factor in these devices is, in turn, a more complex function of Vg (cf. inset of Fig. 2a) due the presence of secondary neutrality points (sNP) stemming from a peculiar band structure of the BLG/hBN superlattice. The latter is characterized by narrow minibands emerging in the vicinity of the \(\tilde K{\mathrm{/}}\tilde K\prime\)-points of the superlattice Brillouin zone37 (Fig. 4c). The sNPs are clearly visible as peaks in the FET resistance which appear around Vg = ±10 V (Fig. 4a).
Miniband plasmons in BLG/hBN moiré superlattices. a Two-terminal resistance of one of our BLG/hBN superlattice devices as a function of Vg measured at given T. Inset: illustration of the BLG/hBN superlattice demonstrating a mismatch between graphene and hBN lattice constants. For simplicity, only one graphene layer is shown. b Normalized responsivity (red) and the FET-factor (black) as a function of Vg measured in the same device as in a. Dashed lines trace Vg where the FET-factor reaches extreme values in the vicinity of the sNP. Pink (blue) arrows point to the resonant peaks near the secondary (main) NP. L = 3 μm. c Schematic representation of the BLG/hBN superlattice band structure. In the vicinity of the \({\tilde{\mathrm \Gamma }}\)-point (blue), BLG supports propagation of the ordinary plasma waves. Miniband THz plasmons emerge when the chemical potential approaches the sNP (pink)
A striking feature of the superlattice photoresponse is the resonances appearing when the Fermi level is brought close to the sNP (pink arrows in Fig. 4b). The resonances are of opposite sign with respect to those observed near the main NP (blue arrows), which indicates that they originate from the plasmons supported by the charge carriers of the opposite type (cf. Fig. 2b). Since the latter are hosted by the minibands near the \(\tilde K{\mathrm{/}}\tilde K{\prime}\)-points of the superlattice Brillouin zone (Fig. 4c), our measurements provide evidence for miniband plasmons that were long identified theoretically38 but remained elusive in experiment. To date, the experimental studies of superlattice plasmons have been only performed at room temperature using scattering-type scanning near field microscopy operating in the mid-IR domain39. The mid-IR excitation energy (10 μm ≈ 120 meV) is high enough to induce interband absorption close to the sNP, which hampers the observation of plasmons in superlattice minibands39. In contrast, our approach relies on the low-energy excitations (2 THz ≈ 8 meV), is applicable at cryogenic temperatures, and, therefore, paves a convenient way for further studies of miniband plasmonics.
Discussion
Resonant responsivity is a universal phenomenon in ultra-clean graphene devices and is expected to be independent of the physical mechanisms behind the rectification of the ac field into a dc photovoltage. Nevertheless, it is important to establish possible nonlinearities responsible for the rectification, for example, in order to be able to increase the magnitude of responsivity.
We first note that the aforementioned asymmetry in Ra (Vg) between electron and hole doping indicates rectification at the p–n junction formed in vicinity of the contacts. This rectification usually appears due to the thermoelectric effect arising as a result of non-uniform sample heating and the difference between the Seebeck coefficients in the graphene channel and contact regions21,24,32,40 (Supplementary Note 8). However, Ra remains finite even for Vg > 0, where both channel and contact areas are n-doped. This indicates that alternative rectification mechanisms are also involved.
Another commonly accepted mechanism is the rectification arising as a result of the simultaneous action of longitudinal high-frequency field and modulation of channel conductivity, also known as resistive self-mixing2. The latter can be enhanced by the dc photovoltage that balances the difference between electron kinetic energies at the source and drain terminals2,3, similar to Bernoulli’s law for classical fluids. Both mechanisms are combined into so-called Dyakonov-Shur (DS) rectification3 and result in R0 proportional to the sensitivity of the conductivity to the gate voltage variation4, given by the F-factor introduced above (Supplementary Note 9). In Fig. 3e we compare the resonant photoresponse of our BLG photodetector with the responsivity expected from the DS model3 assuming an average \(\tau _{\mathrm{p}}\sim 0.6\,{\mathrm{ps}}\), as found from Fig. 3d, and using the effective antenna impedance Z as the only fitting parameter. The two curves show the same functional behavior and match quantitatively for the n-doped case (where the p–n junction is absent) and Z ≈ 74 Ω, a value close to that expected from the equivalent circuit design32. We further note, that although the original DS proposal was based on the hydrodynamic electron transport41,42, an identical photoresponse is expected outside the hydrodynamic window as it follows from the analysis of graphene’s nonlinear conductivity43.
Last but not least, we note that while the overall trend of the responsivity is well-described by the model introduced above, the values of τp extracted from the peak width at half-height are found to be below the momentum relaxation time. This suggests that other mechanisms of resonance broadening are also involved. In particular, leakage of plasma waves into metal contacts44 and electromagnetic dissipation in antenna may also contribute to the apparent resonance width. We have found that respective contributions to \(\tau _{\mathrm{p}}^{ - 1}\) are most pronounced at large carrier densities and small harmonic numbers (Supplementary Figs. 6 and 7), in agreement with experimental data in Fig. 3d. Elimination of these damping channels, e.g. with Schottky/tunnel contacts and low-impedance antennas, may extend the resonant detection down to tens of gigahertz45. Other dissipation channels such as electron viscosity46,47 and interband absorption18 should be most pronounced at higher-order harmonics and in the vicinity of the NP, as opposed to the data in Fig. 3d, and are unlikely relevant to the present study.
In conclusion, we have shown that high-mobility graphene FETs exploiting far-field coupling to incoming radiation can operate as resonant THz photodetectors. In addition to their potential applications in high-responsivity detection and on-chip spectroscopy of the THz radiation, our devices also represent a convenient tool to study plasmons under conditions where other approaches may be technically challenging. Due to their compact size and far-field coupling, our photodetectors can easily be employed to carry out plasmonic experiments in extreme cryogenic environments and in strong magnetic fields, as well in studies of more complex van der Waals heterostructures. As an example, we have demonstrated the use of our approach to reveal low-energy plasmons hosted by moiré minibands in BLG/hBN superlattices. The method has a strong potential for studies of collective modes in magnetic minibands which have recently gained a great level of attention48.
Methods
Device fabrication
All our devices were made of BLG. BLG was first encapsulated between relatively thick hBN crystals using the standard dry-peel technique30. The thickness of the top hBN was measured by atomic force microscopy. The stack was then deposited either directly on top of a low-conductivity boron-doped silicon wafer capped with a thin oxide layer (500 nm) or on a predefined back gate electrode. The resulting van der Waals heterostructure was patterned using electron beam lithography to define contact regions. Reactive ion etching was then used to selectively remove the areas unprotected by a lithographic mask, resulting in trenches for depositing electrical leads. Metal contacts to graphene were made by evaporating 3 nm of Cr and 60 nm of Au. Afterwards, a second e-beam lithography was used to design the top gate. The graphene channel was finally defined by a third round of e-beam lithography, followed by reactive ion etching etching using Poly(methyl methacrylate) and gold top gate as the etching mask. Finally, we used optical photolithography to pattern large antenna (spiral or bow-tie) sleeves connected to the source and the top-gate terminals, followed by evaporation of 3 nm of Cr and 400 nm of Au. Antennas were designed to operate at an experimentally accessible frequency range.
Photoresponse measurements
Photoresponse measurements were performed in a variable temperature optical cryostat equipped with a polyethylene window that allowed us to couple the photodetector to incident THz radiation. The latter was focused to the device antenna by a silicon hemispherical lens attached to the silicon side of the chip (Fig. 1b). The transparency of the chips to THz radiation over the entire temperature and frequency range was verified in transmission experiments using a home-made optical cryostat coupled to the THz spectrometer. Photovoltage measurements were performed using either a standard lockin amplifier synchronized with a chopper rotating at 1 kHz frequency, positioned between the radiation source and the cryostat window, or by a home-made measurement board.
In order to study the photoresponse of our detectors at different frequencies, we used three radiation sources. Sub-THz radiation was provided by two backward wave oscillators (BWO) generating f = 0.13 THz and f = 0.46 THz. For higher frequencies, a quantum cascade continues wave laser based on a GaAs/Al0.1Ga0.9As heterostructure emitting f = 2.026 THz radiation was used.
The responsivity of our devices was calculated assuming that the full power delivered to the device antenna funnelled into the FET channel. The as-determined value provides the lower bound for our detectors’ responsivity and is usually referred to as extrinsic. The calculation procedure consisted of a few steps. First the source-to-drain voltage Udark was measured as a function of Vg in the dark. Then, the dependence of the source-to-drain voltage USD on Vg was recorded under illumination with THz radiation. The difference ΔU = USD − Udark formed the photovoltage. At the next stage, we measured the full power Pfull delivered to the cryostat window using Golay cell. The responsivity was then calculated as Ra = ΔU/P, where P ≈ Pfull/3.5 is the power delivered to the device antenna after accounting for losses in the silicon lens and the cryostat optical window (≈5.5 dB). All the measurements reported above were performed in the linear-in-P regime. The performance of our detectors outside the linear regime is discussed in Supplementary Note 10 and reported in Supplementary Fig. 8.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Dhillon, S. S. et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 50, 043001 (2017).
Daryoosh, S. Handbook of Terahertz Technology For Imaging, Sensing And Communications (Woodhead Publishing, Cambridge, 2013).
Dyakonov, M. & Shur, M. Detection, mixing, and frequency multiplication of terahertz radiation by two-dimensional electronic fluid. IEEE Trans. Electron Devices 43, 380–387 (1996).
Knap, W. et al. Field effect transistors for terahertz detection: physics and first imaging applications. J. Infrared Millim. Terahertz Waves 30, 1319–1337 (2009).
Vicarelli, L. et al. Graphene field-effect transistors as room-temperature terahertz detectors. Nat. Mater. 11, 865–871 (2012).
Spirito, D. et al. High performance bilayer-graphene Terahertz detectors. Appl. Phys. Lett. 104, 061111 (2014).
Tong, J., Muthee, M., Chen, S. Y., Yngvesson, S. K. & Yan, J. Antenna enhanced graphene THz emitter and detector. Nano Lett. 15, 5295–5301 (2015).
Qin, H. et al. Room-temperature, low-impedance and high-sensitivity terahertz direct detector based on bilayer graphene field-effect transistor. Carbon 116, 760–765 (2017).
Generalov, A. A., Andersson, M. A., Yang, X., Vorobiev, A. & Stake, J. A 400-GHz graphene FET detector. IEEE Trans. Terahertz Sci. Technol. 7, 614–616 (2017).
Peralta, X. G. et al. Terahertz photoconductivity and plasmon modes in double-quantum-well field-effect transistors. Appl. Phys. Lett. 81, 1627–1629 (2002).
Knap, W., Deng, Y., Rumyantsev, S. & Shur, M. S. Resonant detection of subterahertz and terahertz radiation by plasma waves in submicron field-effect transistors. Appl. Phys. Lett. 81, 4637–4639 (2002).
Teppe, F. et al. Room-temperature plasma waves resonant detection of sub-terahertz radiation by nanometer field-effect transistor. Appl. Phys. Lett. 87, 85–88 (2005).
Muravev, V. M. & Kukushkin, I. V. Plasmonic detector/spectrometer of subterahertz radiation based on two-dimensional electron system with embedded defect. Appl. Phys. Lett. 100, 082102 (2012).
Giliberti, V. et al. Downconversion of terahertz radiation due to intrinsic hydrodynamic nonlinearity of a two-dimensional electron plasma. Phys. Rev. B 91, 165313 (2015).
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 6, 630–634 (2011).
Yan, H. et al. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol. 7, 330–334 (2012).
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 486, 82–85 (2012).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Grigorenko, A., Polini, M. & Novoselov, K. Graphene plasmonics. Nat. Photonics 6, 749–758 (2012).
Woessner, A. et al. Highly confined low-loss plasmons in graphene-boron nitride heterostructures. Nat. Mater. 14, 421–425 (2015).
Alonso-González, P. et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotechnol. 12, 31–36 (2016).
Ni, G. et al. Fundamental limits to graphene plasmonics. Nature 557, 530–533 (2018).
Koppens, F. H. L. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 9, 780–793 (2014).
Cai, X. et al. Sensitive room-temperature terahertz detection via the photothermoelectric effect in graphene. Nat. Nanotechnol. 9, 814–819 (2014).
Auton, G. et al. Terahertz detection and imaging using graphene ballistic rectifiers. Nano Lett. 17, 7015–7020 (2017).
Otsuji, T., Hanabe, M., Nishimura, T. & Sano, E. A grating-bicoupled plasma-wave photomixer with resonant-cavity enhanced structure. Opt. Express 14, 4815–4825 (2006).
Tomadin, A., Tredicucci, A., Pellegrini, V., Vitiello, M. S. & Polini, M. Photocurrent-based detection of terahertz radiation in graphene. Appl. Phys. Lett. 103, 211120 (2013).
Ryzhii, V., Otsuji, T., Ryzhii, M. & Shur, M. S. Double graphene-layer plasma resonances terahertz detector. J. Phys. D Appl. Phys. 45, 302001 (2012).
Fateev, D. V., Mashinsky, K. V. & Popov, V. V. Terahertz plasmonic rectification in a spatially periodic graphene. Appl. Phys. Lett. 110, 061106 (2017).
Kretinin, A. V. et al. Electronic properties of graphene encapsulated with different two-dimensional atomic crystals. Nano Lett. 14, 3270–3276 (2014).
Ryzhii, V. & Shur, M. S. Resonant terahertz detector utilizing plasma oscillations in two-dimensional electron system with lateral schottky junction. Jpn J. Appl. Phys. 45, L1118 (2006).
Bandurin, D. A. et al. Dual origin of room temperature sub-terahertz photoresponse in graphene field effect transistors. Appl. Phys. Lett. 112, 141101 (2018).
Chaplik, A. Possible crystallization of charge carriers in low-density inversion layers. JETP 35, 395 (1972).
Tomadin, A. & Polini, M. Theory of the plasma-wave photoresponse of a gated graphene sheet. Phys. Rev. B 88, 205426 (2013).
Zou, K., Hong, X. & Zhu, J. Effective mass of electrons and holes in bilayer graphene: Electron-hole asymmetry and electron-electron interaction. Phys. Rev. B 84, 085408 (2011).
Zibrov, A. A. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017).
Mucha-Kruczyński, M., Wallbank, J. & Fal’Ko, V. Heterostructures of bilayer graphene and h-BN: Interplay between misalignment, interlayer asymmetry, and trigonal warping. Phys. Rev. B 90, 205418 (2013).
Tomadin, A., Guinea, F. & Polini, M. Generation and morphing of plasmons in graphene superlattices. Phys. Rev. B 90, 161406(R) (2014).
Ni, G. et al. Plasmons in graphene moiré superlattices. Nat. Mater. 14, 1217–1222 (2015).
Jung, M., Rickhaus, P., Zihlmann, S., Makk, P. & Schonenberger, C. Microwave photodetection in an ultraclean suspended bilayer graphene p-n junction. Nano Lett. 16, 6988–6993 (2016).
Bandurin, D. et al. Fluidity onset in graphene. Nat. Commun. 9, 4533 (2018).
Berdyugin, A. et al. Measuring hall viscosity of graphene’s electron fluid. Preprint at https://arxiv.org/abs/1806.01606 (2018).
Principi, A., Bandurin, D., Rostami, H. & Polini, M. Pseudo-Euler equations from nonlinear optics: plasmon-assisted photodetection beyond hydrodynamics. Preprint at https://arxiv.org/abs/1811.06540 (2018).
Satou, A., Ryzhii, V., Mitin, V. & Vagidov, N. Damping of plasma waves in two-dimensional electron systems due to contacts. Phys. Status Solidi (B) 246, 2146–2149 (2009).
Graef, H. et al. Ultra-long wavelength Dirac plasmons in graphene capacitors. J. Phys. Mater. 1, 01LT02 (2018).
Kumar, R. K. et al. Superballistic flow of viscous electron fluid through graphene constrictions. Nat. Phys. 13, 1182–1185 (2017).
Svintsov, D. Hydrodynamic-to-ballistic crossover in Dirac materials. Phys. Rev. B 97, 121405 (2018).
Krishna Kumar, R. et al. High-temperature quantum oscillations caused by recurring Bloch states in graphene superlattices. Science 357, 181–184 (2017).
Acknowledgments
Device fabrication and Manchester’s part of the work was supported by the European Research Council, the Graphene Flagship and Lloyd’s Register Foundation. The work at the MSPU (Photoresponse measurements) has been carried out with the support of the Russian Science Foundation (project No. 17-72-30036). D.A.B. acknowledges financial support from Leverhulme Trust. Experimental work of M.M. (transport measurements) was supported by Russian Science Foundation (Grant 18-72-00234). M.P. was supported by the European Union’s Horizon 2020 research and innovation program under grant agreement No. 785219 - GrapheneCore2. Modelling of antenna electrodynamics was supported by RFBR (Project 18-29-20116). Theoretical work of D.S. was supported by the grant 16-19-10557 of the Russian Science Foundation. Photoresponse measurements have been performed using quantum cascade laser fabricated by A. Valavanis in the group of Prof. Dragan Indjin at the University of Leeds (UK). We thank A. Tomadin, R. Krishna Kumar, A. Berdyugin, L. Levitov, and V. Fal’ko for fruitful discussions.
Author information
Authors and Affiliations
Contributions
D.A.B. and G.F. designed and supervised the project. S.G.X. and I.G. fabricated the devices. Photoresponse measurements were carried out by I.G., M.M., and D.A.B. Data analysis was performed by D.A.B. and D.S. Theory analysis was done by D.S. The manuscript was written by D.A.B. and D.S. with input from I.V.G., M.P., A.P., and A.K.G. Experimental support was provided by I.T., D.Y., S.Z., and G.G.; T.T. and K.W. grew the hBN crystals. All authors contributed to discussions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contributions to the peer review of this work. Peer Reviewer Reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bandurin, D.A., Svintsov, D., Gayduchenko, I. et al. Resonant terahertz detection using graphene plasmons. Nat Commun 9, 5392 (2018). https://doi.org/10.1038/s41467-018-07848-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-07848-w
This article is cited by
-
Tamm-cavity terahertz detector
Nature Communications (2024)
-
The rise of semi-metal electronics
Nature Reviews Electrical Engineering (2024)
-
Complete electromagnetic consideration of plasmon mode excitation in graphene rectangles by incident terahertz wave
Scientific Reports (2024)
-
Impact of device resistances in the performance of graphene-based terahertz photodetectors
Frontiers of Optoelectronics (2024)
-
Two-dimensional materials for future information technology: status and prospects
Science China Information Sciences (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.