Abstract
Impact-induced erosion is the ablation of matter caused by being physically struck by another object. While this phenomenon is known, it is empirically challenging to study mechanistically because of the short timescales and small length scales involved. Here, we resolve supersonic impact erosion in situ with micrometer- and nanosecond-level spatiotemporal resolution. We show, in real time, how metallic microparticles (~10-μm) cross from the regimes of rebound and bonding to the more extreme regime that involves erosion. We find that erosion in normal impact of ductile metallic materials is melt-driven, and establish a mechanistic framework to predict the erosion velocity.
Similar content being viewed by others
Introduction
The combination of high pressures, temperatures, and deformation rates that occur during an impact can evoke many unusual materials responses. These include crater formation1,2,3, solid state splashing4, impact bonding5, peculiar phase transformations6, nanocrystallization7, and chemical reactions8. Among the most extreme of such phenomena lies impact-induced erosion that often occurs at the micron scale whether in space9, on the ground10, or beneath11. At the micron scale, metallic microparticles change their interaction with metallic targets as impact velocity increases. In the limit of extremely weak impact (<~0.1 m/s), an elastic response occurs; the particles rebound with their initial kinetic energy recovered12. At higher impact velocities (~10 m/s), impacting microparticles bounce off with a fraction of their initial kinetic energy while plastically deforming themselves and the target13. At even higher impact velocities (~100 m/s) the incoming microparticles can adhesively bond to the target (substrate in this case) and additively build-up coatings or bulk components14,15,16. In neither of these first regimes, i.e., rebound nor bonding, is material lost from the microparticle or the substrate. At higher impact velocities in the third regime, on the other hand, material loss can occur; velocities of ~km/s cause impact damage to, for instance, space vehicles and satellites9,17,18. However, such high-velocity erosion has been historically studied by post-mortem analysis only19,20. Without direct observation, there remain many fundamental questions pertaining to the mechanisms of impact-induced erosion, and conditions required to even trigger erosion are not resolved.
Here, we conduct in situ single microparticle supersonic impacts aimed at systematically elucidating erosion with micron scale and nanosecond level spatiotemporal resolution. Furthermore, we establish a mechanistic framework to predict the erosion velocity.
Results
In situ and post-mortem measurements
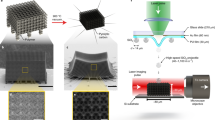
We choose tin as a model material for its low melting temperature and specific heat. As schematically shown in Fig. 1a, micron-sized particles are initially dispersed on a launching pad assembly, a stack comprising a glass substrate, a thin layer of gold, and a layer of elastomeric polyurea film. Microparticles are launched by focusing a laser excitation pulse, thereby ablating the gold film, and causing rapid expansion of the polyurea film4,5,21,22. The particle interaction with a substrate is recorded in real time using a high-frame-rate camera and a synchronized quasi-cw laser imaging pulse for illumination. The exposure was set to be 5 ns for all frames, and the interframe time was adjusted depending on the impact velocity from 50 to 150 ns. Details regarding the launching pad preparation are described elsewhere4,5,23.
In situ observation of microparticle supersonic impact. a Experimental platform for microparticle impact test and real-time imaging. b–e Multi–frame sequences with 5 ns exposure times showing (b) 9 µm, (c) 9 µm, (d) 10 µm, and (e) 10 µm tin particles arriving from the top of the field of view and impacting tin substrates at velocities of (b) 336, (c) 374, (d) 678, and (e) 1067 m/s, spanning from the rebound regime to the bonding and the erosion regimes. The scale bar is 50 μm. (f) Coefficient of restitution, vr/vi, of the rebounding tin particles and fragments. The coefficient of restitution is equal to zero in the bonding regime, and it is non-zero in the rebound and erosion regimes. The size of the data points on the plot is proportional to the ratio of the fragment and particle diameters. We also color-coded volume fraction, i.e., volume of the rebounding particle/fragment divided by the volume of the incoming particle
Figure 1b–e show some exemplar snapshots capturing tin microparticles impacting tin substrates. We explored the interaction between particle and substrate at various impact velocities, from 100 to 1100 m/s, and observed four distinct behaviors. First, at low impact velocity, the particle bounces off the substrate as shown in Fig. 1b (336 m/s). Second, with increasing impact velocity (374 m/s), the particle in Fig. 1c no longer rebounds, but instead bonds to the substrate adhesively. Third, increasing the impact velocity further to 678 m/s leads to a material splash involving ejected fragmented pieces of material (Fig. 1d). Fourth, at the high-end of our velocity scale at 1067 m/s we observe only a stark splash, with no discernible individual fragments in the cloud of ejecta (Fig. 1e). These image sequences have been montaged into Supplementary Movies 1-4 and are available in the Supplementary Information.
We measured the impact velocity, rebound velocity, size of the impacting particle, and size of the rebounding particle (or fragments of it) for 68 experiments. Figure 1f shows how the coefficient of restitution (the ratio of rebound, vr, and impact, vi, velocities), varies with impact velocity. We observe an apparent linear decrease in vr/vi for the impact velocity range of 100–350 m/s, which is the regime where the particle bounces. The sharp decrease in this ratio to zero at ~350 m/s identifies the transition from rebound to bonding. In our previous work we have measured this critical velocity for bonding for a number of metals4. New to the present work is the observation of a second transition at around 450 m/s, to a third regime of behavior where there is material ejection from the impact with non-zero vr/vi values; the quantitative values reported in Fig. 1f correspond to the ejection velocities of the small fragments that could be discerned in our photographs. As splash and fragmentation lead to material loss, we refer to this regime as the erosion regime. A scanning electron micrograph of a crater left behind after an impact in the erosion regime, as well as its reconstruction using 3D surface profilometry, are shown in Fig. 2a, b respectively. Crater and pileup can be observed in Fig. 2c in a profile across the line shown in the inset. An impact involving particle deposition would create more pileup volume than crater volume. By contrast, our analysis of Fig. 2b shows that the crater volume is 116 μm3 larger than the pileup volume. Considering that there may still be some material deposition from the particle, our analysis confirms that at least a material volume of 116 μm3 is lost from the substrate.
Surface profilometry of a typical impact in the erosion regime. (a) Scanning electron micrograph, (b) laser confocal image of the impact area, and (c) a typical surface profile after a 10-µm tin particle impacted the tin substrate at 1036 m/s velocity. The color bar in (b) represents surface height. While the apparent crater volume is 742 μm3, the pileup volume is 626 μm3 confirming that at least a volume of 116 μm3 is lost from the substrate during impact. The scale bars are 10 μm
Another interesting feature of Fig. 1f is that the erosion regime involves a wide range of ejection velocities, owing to the ejecta comprising a variety of small fragments. We have elected to scale the size of particles/ejecta with the size of the data points and represent the volume fraction (of the ejecta of each size) with the color scale in Fig. 1f, which helps visualize the distribution of different particles and their velocities during the erosion event. In general, the larger volumes of ejecta tend to travel more slowly. What is more, it is possible to distinguish a further, more subtle transition within the erosion regime. In the first sub-regime, from ~450 to ~900 m/s, solid fragments are easily discerned and significantly contribute to the total material loss. As impact velocity increases, fragment sizes tend to decrease to the point where no significant individual fragment can be observed. For any impact velocity higher than ~900 m/s we observe that material is almost entirely lost in an ejecta cloud which we interpret to be liquid splashing, as further developed below.
Post-mortem observations of the impact sites confirm these four behavioral regimes identified in situ above. In the rebound regime, an indentation such as shown in Fig. 3a is left behind on the substrate. Particles exceeding the critical bonding velocity, such as the one in Fig. 3b, adhere to the substrate without substantial material loss. At higher velocities where erosion sets on, impacts leave residue behind. Figure 3c at 580 m/s exhibits two different morphologies, one indicated by black arrows that appears formed by solid plasticity, and a second indicated by white arrows that is rounded and smooth and suggestive of melting and resolidification. This type of residue is consistent with our in situ observations in that some large solid fragments might be seen to form from plastic deformation and fracture, while a fine spray of ejecta could be a result of impact melting and splashing. Finally, in the highest speed regime, where we exclusively see splashes without discernible fragments, the impact site appears to be a completely melted and resolidified crater, as shown in Fig. 3d. Although we cannot directly discern melting in the substrate from the post-mortem observations in Fig. 3c, d, we note that both particle and substrate have the same material properties and undergo a conformal plastic deformation as confirmed by the surface profile in Fig. 2c. Therefore, melting in the particle can be a reasonable indictor of melting in the substrate.
Post-mortem observations of impact area. Scanning electron micrographs of the impact areas after (a) 9 µm, (b) 9 µm, (c) 10 µm, (d) 10 µm tin particles impacted the tin substrate at (a) 184, (b) 374, (c) 580, and (d) 1108 m/s velocities, showing (a) rebound, (b) bonding, (c) partial melt, and (d) full melt. Corresponding in situ observations confirm material loss in (c) and (d). The scale bar is 5 μm
Erosion mechanism
A critical conclusion that emerges by combining our postmortem and in situ observations is that significant material loss and melting emerge concurrently at the transition velocity between the bonding and the erosion regimes. In other words, erosion appears to be melt-driven in the present case. This is mechanistically unforeseen based on prior work on erosion, although the significance of plasticity-induced heating and melting upon impact, especially at velocities on the order of 1 km/s has been pointed out recently24,25. The conventional wisdom about impact erosion of ductile metallic materials is based upon eroding metallic surfaces by a large number of particle impacts in a fluid stream26,27,28,29,30,31. In such conditions, material loss is mechanistically attributed to either a cutting action11,32 or a combined forging–extrusion action33,34,35 of the eroding particles. In the former, which is mostly relevant to oblique impacts, particles penetrate the substrate, translate along the surface and plow material ahead of them. In the latter, which is more relevant to normal-incidence impacts, small highly distressed platelets of the substrate material are envisioned to result at a first impact site, which can then be flaked off the surface by a subsequent impact. The cutting mechanism cannot be the predominant factor for material loss in the present normal-incidence impacts, and there is no succeeding particle to remove platelets formed by previous impacts as envisioned with the forging–extrusion mechanism.
Thus, we see our observation of melt-driven erosion as a departure from previously established erosion mechanisms. This is reasonable in light of two significant distinctions between our work and the studies of impact erosion cited above. First, our impact velocities are higher by a large factor, up to an order of magnitude with respect to some studies. Second, most studies employ particles significantly harder than the substrate they are eroding, while we have used a matched pair. Delineating property and velocity regimes in which different mechanisms are dominant may become possible if quantitative mechanistic models are developed; we pursue this in what follows for melt-based erosion.
Discussion
As a starting point we take our experimental observation that melting and erosion appear to set on together at a single critical velocity in tin; predicting erosion thus hinges on assessing when an impact can trigger melting. In what follows we develop a first-order analysis in the spirit of prior analogous works from other domains8,36, so that we can map the most critical physics of the process across many possible materials. During a normal-incidence impact of a microparticle, the plastic work dissipates as heat, and in turn only a fraction of the kinetic energy of the impacting particle causes plastic work. At the onset of melt-driven erosion we can balance the input kinetic energy thusly dissipated with the energy required to heat and melt an affected volume of material:
where β is the fraction of plastic work dissipated as heat, α is the fraction of the initial kinetic energy of the particle deposited into the substrate, mp is the mass of the particle, vi,e is the impact velocity at the erosion onset, ρ is the density, Vaff is the affected volume over which the temperature rises from its initial value T0 to the melting temperature Tm, Cp is the specific heat, and Hf is the enthalpy of fusion. For a first-order approximation, we assume that temperature is uniformly distributed in the affected volume. For simplicity we can take the affected volume as the product of the contact area of the impact, Ac, and the distance, dth, heat is conducted during the contact time, \(t_{\mathrm {c}} \approx d/v_{{\mathrm {i,e}}}\), where d is the particle diameter assuming that the affected volume can approximate the volume in which the inelastic heat is generated. We calculate the thermal distance using \(d_{{\mathrm {th}}} = \sqrt {\left( {\frac{k}{{\rho C_{\mathrm {p}}}}} \right) \times t_{\mathrm {c}}}\) with k being the thermal conductivity. In order to estimate the contact area, we assume that upon impact a spherical particle transforms to a half-ellipsoid with a height equal to the particle radius. Conserving the volume then leads to \(A_{\mathrm {c}} = \pi d^2/2\). Substituting these relations into Eq. (1) and re-arranging it yields:
While the left-hand side of Eq. (2) is an impact-dependent term, the right-hand side can be regarded as the product of two material parameters, i.e, the thermal effusivity, \(e_{{\mathrm {th}}} = ( {\rho kC_p} )^{1/2}\), and what we define as a melting index, \(I_{{\mathrm {melt}}} = T_{\mathrm {m}} - T_0 + \frac{{H_{\mathrm {f}}}}{{C_p}}\). A fine estimation of the physical parameters α and β needs devoted case-by-case studies. Considering the uncertainty associated with the inelastic heat fraction, β can be treated as a calibration factor with a physical meaning. However, for a first-order approximation, we set a median value of β = 0.6 for the fraction of plastic work dissipated as heat in dynamic deformation37,38, and assume the initial energy is partitioned equally between the particle and the substrate (α = 0.5), especially for the present case where the particle and substrate materials are matched. Thus, we propose the threshold impact velocity that marks the onset of erosion should be approximately given by:
While this analysis is a simple energy-balance with many approximations, Eq. (3) is nontrivial and presents an opportunity to test the hypothesis that melting controls erosion. Interestingly, a more physically based thermomechanical argument developed in Supplementary Note 1 implicitly supports the notion that erosion velocity is related to eth × Imelt. However, we highlight that neither in the energy-balance approach here nor in the thermomechanical approach developed in Supplementary Note 1, have we considered material strength effects. Strength effects are expected to be non-negligible when the deformation is not purely hydrodynamic. Thus, in what follows we limit ourselves to situations where hydrodynamic conditions would prevail, i.e., for conditions with relatively higher velocities, smaller particles, and softer metals.
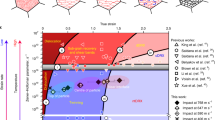
Figure 4 shows a map constructed based on Eq. (3) for 10-μm particles, in which we suggest the use of particle properties on the y-axis and substrate properties on the x-axis. By fixing particle diameter for this presentation, we are left with density on the y-axis to locate the particle material. The x-axis is the product of effusivity and the melting index, and can be used to locate the substrate material, when material loss from the substrate is concerned. Thus, for a given particle (horizontal line) and substrate (vertical line) there is an intersection position that is associated with a critical erosion velocity. The range of erosion velocities is represented by a series of contours in the present map.
Melt-driven erosion map. Impact velocity at which melt-driven erosion is triggered for different combinations of particle/substrate materials. Particle material is populated on the y-axis. Material of interest in which erosion occurs (primarily substrate in the present context) is located on the x-axis. The intersecting point on the map determines the erosion velocity. The black diamond is the real-time measurement of tin erosion velocity with 4% uncertainty. The white diamonds are approximations of erosion velocity based on a limited number of site-specific impact experiments, and thus involve higher uncertainties
We superimpose our in situ measurement of erosion velocity for tin particles impacting a tin substrate onto the map with a black diamond, and note a good agreement with the experimental critical erosion velocity of ~450 m/s lying on the correct theoretical contour line of the same velocity. To further confirm the versatility of the map, we conducted a limited number of site-specific impact experiments with zinc particles impacting zinc, bismuth particles impacting bismuth, and titanium particles impacting titanium (see Supplementary Figures 2–4). We estimate the lower bound erosion velocity based on the post-mortem observations of localized melting in the Supplementary Figures 2–4. All these cases are superimposed onto the map with white diamonds next to which the experimental erosion velocities are reported. Overall, we observe good agreement between the predictions of the map and the experimental measurements for different material pairs. This is a demonstration of the strength of the simple, but mechanistic, Eq. (3), and the introduction of eth × Imelt as a material index to rank substrate materials can help advance materials design against erosion.
While our results are in good agreement with available estimations of erosion velocity39 for tin and zinc, both our experiment and theory predict erosion in titanium initiating at lower impact velocity than estimated previously. What is more, we do not see a major constraint in using Eq. (3) to predict erosion at larger scales. For example, measurements of mass gain after impacts of a 20-mm copper ball on a steel substrate show39 erosion at ~1000 m/s, and the emergence of material loss between ~350 and ~600 m/s. Eq. (3) predicts ~245 m/s to be the threshold velocity for melting for the same size copper ball impacting copper, which we interpret as being associated with the emergence of material loss. Underestimation of the erosion velocity by Eq. (3) compared to such macroscale experimental measurements can be attributed to two factors. First, the substrate in those experiments39 was much harder than copper while Eq. (3) predicts the velocity at which erosion would have emerged in a copper substrate. Second, at larger scales where the impact is more adiabatic, thermal conduction may be less significant in dictating the affected volume.
As a final note, and a direction for future studies, we highlight that as the impact velocity is increased, the erosion regime does not necessarily follow the bonding regime for all materials. For example, for bismuth impacts on bismuth (Supplementary Figure 2) we noted that rebound directly gives way to erosion, with no appreciable solid-state bonding in between. This can be justified by the fact that the two phenomena of bonding and erosion are governed by different mechanisms. Bonding is associated with solid-state hydrodynamic jetting4,16 whereas melt-driven erosion is governed by thermal properties of materials, as suggested by Eq. (3). Therefore, while Eq. (3) is the lower bound for melt-driven erosion, it can also be regarded as an upper bound velocity if an ideal impact-induced solid state bonding is sought.
To summarize, we have presented nanosecond and microscale in situ observations that span a broad range of possible regimes in matched materials impact. By extending the current understanding of microparticle impact from rebound and bonding to now include direct observations of erosion, we have provided the mechanistic insight that for normal-incidence microparticle impacts, such erosion in ductile materials is melt-driven. Simple mechanistic frameworks considering the conversion of impact kinetic energy into heat adequately capture the impact velocity at the onset of erosion. It also offers a material parameter that should prove useful for the design of materials to withstand erosive impacts, or for the design of additive manufacturing processes that rely on impact-bonding where the erosion regime must be avoided.
Methods
Materials and sample preparation
Tin, zinc, and bismuth powder particles with nominal particle sizes of -325 mesh, 6–9 μm, -100 mesh, as well as a tin plate with 3.2 mm thickness and a bismuth rod with 11 mm diameter were purchased from Alfa Aesar (Ward Hill, USA). A batch of titanium powder particles with nominal particle size of -325 mesh was purchased from AP&C (Quebec, Canada). A titanium plate and a zinc plate with 3.175 mm thickness were purchased from OnlineMetals (Seattle, USA). Supplementary Figure 1 shows the shape and the morphology of the powder particles. We used a diamond blade on a precision cutter to extract 12 × 12 mm plates for use as the targets for the impact experiments. Each target surface was ground and polished to nominally 0.04 µm mirror finish prior to the impact experiments. While impact of tin, zinc, and titanium particles is technologically relevant to cold spray coating/additive manufacturing14,15,40,41,42, bismuth enables us to explore impact-induced erosion of a metal with extremely low e×Imelt.
Single particle impact experiments
Single particle impact experiments were conducted using an in-house-designed all-optical microballistic platform. An intense laser pulse (pulsed Nd:YAG, 10-ns duration, 532-nm wavelength, pulse energy up to 60 mJ) is focused onto a launching assembly that consists of a glass substrate (210-μm thickness), a gold layer (60-nm thickness), and a polyurea film (30-μm thickness) on top of which metallic microparticles are dispersed. Following laser ablation of the gold film and rapid expansion of the polyurea film, the microparticles are accelerated toward the target. The particle speed is controlled by adjusting the laser energy (from 2 to 60 mJ). The laser pulse is focused into a 50-μm diameter spot size on the gold film using a 30-mm focal length lens. The distance between the launching pad and the target is typically 1 mm. The impact events are captured in real time using a μs laser pulse (10 μs duration, 640 nm wavelength) for illumination and a high-speed camera (SIMX 16, Specialized Imaging) that can acquire 16 frame videos with a rate up to 109 fps and nanosecond time resolution. More details can be found elsewhere4,5,22,23.
During the impact experiments both particles and substrates are exposed to air. Thus, although we have not characterized surface oxide explicitly, we expect to have a typical native oxide of a few nm being present on both surfaces.
Impact and rebound velocities are determined by measuring the distance traveled by the particles in a few snapshots divided by the total interframe time between those snapshots. Particle velocities are extracted with an uncertainty of 4% taking into account the uncertainty in particle localization (±3 pixels corresponding to 1 μm) and in timing (±1 ns). More details on the uncertainties can be found elsewhere21. For each impact, the particle diameter was extracted from the image sequence. The average diameter for tin particles used in the impact experiments is 10 ± 1 µm. The particle size for each particle used in the site-specific impact experiments with bismuth, zinc, and titanium is reported in the captions of Supplementary Figures 2–4. Post-mortem observations of the impact residue were performed with Zeiss Merlin high-resolution scanning electron microscope. We conducted surface profilometry using a 3D laser scanning confocal microscope (VK-X200 series, Keyence), and measured the crater and pileup volumes accordingly.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information file.
References
Richardson, J. E., Melosh, H. J. & Greenberg, R. Impact-induced seismic activity on asteroid 433 Eros: a surface modification process. Science 306, 1526–1529 (2004).
Katsuragi, H. & Durian, D. J. Unified force law for granular impact cratering. Nat. Phys. 3, 420–423 (2007).
Malin, M. C., Edgett, K. S., Posiolova, L. V., McColley, S. M. & Dobrea, E. Z. N. Present-day impact cratering rate and contemporary gully activity on Mars. Science 314, 1573–1577 (2006).
Hassani-Gangaraj, M., Veysset, D., Nelson, K. A. & Schuh, C. A. In-situ observations of single micro-particle impact bonding. Scr. Mater. 145, 9–13 (2018).
Hassani-Gangaraj, M., Veysset, D., Nelson, K. A. & Schuh, C. A. Melting can hinder impact-induced adhesion. Phys. Rev. Lett. 119, 175701 (2017).
Xue, S. et al. High-velocity projectile impact induced 9R phase in ultrafine-grained aluminium. Nat. Commun. 8, 1653 (2017).
Thevamaran, R. et al. Dynamic creation and evolution of gradient nanostructure in single-crystal metallic microcubes. Science 354, 312–316 (2016).
Humphry-Baker, S. A., Garroni, S., Delogu, F. & Schuh, C. A. Melt-driven mechanochemical phase transformations in moderately exothermic powder mixtures. Nat. Mater. 15, 1280–1286 (2016).
Berthoud, L. & Mandeville, J. C. Material damage in space from microparticle impact. J. Mater. Sci. 32, 3043–3048 (1997).
Zhou, Q. et al. Analysis of water drop erosion on turbine blades based on a nonlinear liquid–solid impact model. Int. J. Impact Eng. 36, 1156–1171 (2009).
Finnie, I. Erosion of surfaces by solid particles. Wear 3, 87–103 (1960).
Johnson, K. Contact Mechanics (Cambridge University Press, Cambridge, 1987).
Hassani-Gangaraj, S. M., Cho, K. S., Voigt, H.-J. L., Guagliano, M. & Schuh, C. A. Experimental assessment and simulation of surface nanocrystallization by severe shot peening. Acta Mater. 97, 105–115 (2015).
Assadi, H., Kreye, H., Gärtner, F. & Klassen, T. Cold spraying—a materials perspective. Acta Mater. 116, 382–407 (2016).
Moridi, A., Hassani-Gangaraj, S. M., Guagliano, M. & Dao, M. Cold spray coating: review of material systems and future perspectives. Surf. Eng. 30, 369–395 (2014).
Hassani-Gangaraj, M., Veysset, D., Champagne, V. K., Nelson, K. A. & Schuh, C. A. Adiabatic shear instability is not necessary for adhesion in cold spray. Acta Mater. 158, 430–439 (2018).
Bernhard, R. P., Christiansen, E. L., Hyde, J. & Crews, J. L. Hypervelocity impact damage into space shuttle surfaces. Int. J. Impact Eng. 17, 57–68 (1995).
Christiansen, E. L., Hyde, J. L. & Bernhard, R. P. Space shuttle debris and meteoroid impacts. Adv. Space Res. 34, 1097–1103 (2004).
Hirai, T. et al. Microparticle impact calibration of the Arrayed Large-Area Dust Detectors in INterplanetary space (ALADDIN) onboard the solar power sail demonstrator IKAROS. Planet. Space Sci. 100, 87–97 (2014).
Kearsley, A. T., Burchell, M. J., Hörz, F., Cole, M. J. & Schwandt, C. S. Laboratory simulation of impacts on aluminum foils of the Stardust spacecraft: calibration of dust particle size from comet Wild-2. Meteorit. Planet. Sci. 41, 167–180 (2006).
Veysset, D. et al. Dynamics of supersonic microparticle impact on elastomers revealed by real-time multi-frame imaging. Sci. Rep. 6, 25577 (2016).
Veysset, D., Hsieh, A. J., Kooi, S. E. & Nelson, K. A. Molecular influence in high-strain-rate microparticle impact response of poly(urethane urea) elastomers. Polymer 123, 30–38 (2017).
Hassani-Gangaraj, M., Veysset, D., Nelson, K. A. & Schuh, C. A. Supersonic impact of metallic micro-particles. Preprint at arXiv:1612.08081 (2016).
Kurosawa, K. & Genda, H. Effects of friction and plastic deformation in shock-comminuted damaged rocks on impact heating. Geophys. Res. Lett. 45, 620–626 2018.
Melosh, H. J. & Ivanov, B. A. Slow impacts on strong targets bring on the heat. Geophys. Res. Lett. 45, 2597–2599 2018.
Tilly, G. P. A two stage mechanism of ductile erosion. Wear 23, 87–96 (1973).
Desale, G. R., Gandhi, B. K. & Jain, S. C. Particle size effects on the slurry erosion of aluminium alloy (AA 6063). Wear 266, 1066–1071 (2009).
Oka, Y. I., Okamura, K. & Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 1: Effects of impact parameters on a predictive equation. Wear 259, 95–101 (2005).
Oka, Y. I. & Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 2: Mechanical properties of materials directly associated with erosion damage. Wear 259, 102–109 (2005).
Smeltzer, C. E., Gulden, M. E. & Compton, W. A. Mechanisms of metal removal by impacting dust particles. J. Basic Eng. 92, 639–652 (1970).
Levy, A. V. & Chik, P. The effects of erodent composition and shape on the erosion of steel. Wear 89, 151–162 (1983).
Bitter, J. G. A. A study of erosion phenomena part I. Wear 6, 5–21 (1963).
Bellman, R. & Levy, A. Erosion mechanism in ductile metals. Wear 70, 1–27 (1981).
Hutchings, I. M. A model for the erosion of metals by spherical particles at normal incidence. Wear 70, 269–281 (1981).
Sundararajan, G. & Shewmon, P. G. A new model for the erosion of metals at normal incidence. Wear 84, 237–258 (1983).
Schwarz, R. B. & Koch, C. C. Formation of amorphous alloys by the mechanical alloying of crystalline powders of pure metals and powders of intermetallics. Appl. Phys. Lett. 49, 146–148 (1986).
Knysh, P. & Korkolis, Y. P. Determination of the fraction of plastic work converted into heat in metals. Mech. Mater. 86, 71–80 (2015).
Rittel, D., Zhang, L. H. & Osovski, S. The dependence of the Taylor–Quinney coefficient on the dynamic loading mode. J. Mech. Phys. Solids 107, 96–114 (2017).
Schmidt, T., Gärtner, F., Assadi, H. & Kreye, H. Development of a generalized parameter window for cold spray deposition. Acta Mater. 54, 729–742 (2006).
Hussain, T., McCartney, D. G. & Shipway, P. H. Impact phenomena in cold-spraying of titanium onto various ferrous alloys. Surf. Coat. Technol. 205, 5021–5027 (2011).
Maledi, N. B. et al. Influence of cold spray parameters on the microstructures and residual stress of Zn coatings sprayed on mild steel. Surf. Coat. Technol. 318, 106–113 (2017).
Legoux, J.-G., Irissou, E. & Moreau, C. Effect of substrate temperature on the formation mechanism of cold-sprayed aluminum, zinc and tin coatings. J. Therm. Spray. Technol. 16, 619–626 (2007).
Acknowledgements
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-SC0018091. Supported was also provided through the U.S. Army Research Office under Contract No. W911NF-13-D-0001 and W911NF-18-2-0048. Support for equipment was provided through the Office of Naval Research DURIP Grant No. N00014-13-1-0676.
Author information
Authors and Affiliations
Contributions
M.H.-G., D.V., K.N., and C.S. designed the research. M.H.-G. and D.V. conducted the experiments. M.H.-G. developed the theory. All authors analyzed the data and co-wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hassani-Gangaraj, M., Veysset, D., Nelson, K.A. et al. Melt-driven erosion in microparticle impact. Nat Commun 9, 5077 (2018). https://doi.org/10.1038/s41467-018-07509-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-07509-y
This article is cited by
-
Metals strengthen with increasing temperature at extreme strain rates
Nature (2024)
-
Molecular dynamics and experimental studies of the dependence of strain rate on the indentation deformation of polycarbonate
Journal of Polymer Research (2023)
-
Quantification of the Kinetic Energy Conversion to Temperature Increase in Metal-on-Metal Impacts up to Hypervelocity Conditions by Molecular Dynamics Simulation
Journal of Dynamic Behavior of Materials (2023)
-
Numerical and Experimental Analysis of the Deformation Behavior of CoCrFeNiMn High Entropy Alloy Particles onto Various Substrates During Cold Spraying
Journal of Thermal Spray Technology (2022)
-
Cold Spray: Over 30 Years of Development Toward a Hot Future
Journal of Thermal Spray Technology (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.