Abstract
Nuclear magnetic resonance (NMR) spectroscopy is a powerful method for analyzing the chemical composition and molecular structure of materials. At the nanometer scale, NMR has the prospect of mapping the atomic-scale structure of individual molecules, provided a method that can sensitively detect single nuclei and measure inter-atomic distances. Here, we report on precise localization spectroscopy experiments of individual 13C nuclear spins near the central electronic sensor spin of a nitrogen-vacancy (NV) center in a diamond chip. By detecting the nuclear free precession signals in rapidly switchable external magnetic fields, we retrieve the three-dimensional spatial coordinates of the nuclear spins with sub-Angstrom resolution and for distances beyond 10 Å. We further show that the Fermi contact contribution can be constrained by measuring the nuclear g-factor enhancement. The presented method will be useful for mapping atomic positions in single molecules, an ambitious yet important goal of nanoscale nuclear magnetic resonance spectroscopy.
Similar content being viewed by others
Introduction
One of the visionary goals of nanoscale quantum metrology with NV centers is the structural imaging of individual molecules, for example proteins, that are attached to the surface of a diamond chip1. By adapting and extending measurement techniques from nuclear magnetic resonance (NMR) spectroscopy, the long-term perspective is to reconstruct the chemical species and three-dimensional location of the constituent atoms with sub-Angstrom resolution2,3. In contrast to established structural imaging techniques like X-ray crystallography, cryo-electron tomography, or conventional NMR, which average over large numbers of target molecules, only a single copy of a molecule is required. Conformational differences between individual molecules could thus be directly obtained, possibly bringing new insights about their structure and function.
In recent years, first experiments that address the spatial mapping of nuclear and electron spins with NV-based quantum sensors have been devised. One possibility is to map the position into a spectrum, as it is done in magnetic resonance imaging. For nanometer-scale imaging, this requires introducing a nanomagnet4,5,6. Another approach is to exploit the magnetic gradient of the NV center’s electron spin itself, whose dipole field shifts the resonances of nearby nuclear spins as a function of distance and internuclear angle. Refinements in quantum spectroscopic techniques have allowed the detection of up to 8 individual nuclear spins7,8 as well as of spin pairs9,10,11 for distances of up to ~30 Å12,13. Due to the azimuthal symmetry of the dipolar interaction, however, these measurements can only reveal the radial distance r and polar angle θ of the inter-spin vector r = (r, θ, ϕ), but are unable to provide the azimuth ϕ required for reconstructing three-dimensional nuclear coordinates. One possibility for retrieving ϕ is to change the direction of the static external field12, however, this method leads to a mixing of the NV center’s spin levels which suppresses the ODMR signal14 and shortens the coherence time15. Other proposed methods include position-dependent polarization transfer16 or combinations of microwave and radio-frequency fields17,18,19.
Here we demonstrate three-dimensional localization of individual, distant nuclear spins with sub-Angstrom resolution. To retrieve the missing angle ϕ, we combine a dynamic tilt of the quantization axes using a high-bandwidth microcoil with high resolution correlation spectroscopy20,21. Our method provides the advantage that manipulation and optical readout of the electronic spin can be carried out in an aligned external bias field. This ensures best performance of the optical readout and the highest magnetic field sensitivity and spectral resolution of the sensor.
Results
Theory
We consider a nuclear spin I = 1/2 located in the vicinity of a central electronic spin S = 1 with two isolated spin projections mS = {0, −1}. The nuclear spin experiences two types of magnetic field, a homogeneous external bias field B0 (aligned with the quantization axis ez of the electronic spin), and the local dipole field of the electronic spin. Because, the electronic spin precesses at a much higher frequency than the nuclear spin, the latter only feels the static component of the electronic field, and we can use the secular approximation to obtain the nuclear free precession frequencies,
Here, γn is the nuclear gyromagnetic ratio and
is the secular hyperfine vector of the hyperfine tensor \(\underline {\underline {\bf{A}} } ({\bf{r}})\) that gives rise to the hyperfine magnetic field mSAz(r)/γn (see Fig. 1b).
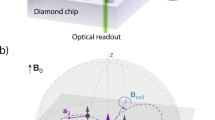
Coordinate systems for spins and magnetic fields. a Reference frame of the central nitrogen-vacancy (NV) sensor spin (red) with a nuclear spin (blue) located at the three-dimensional position r = (r, θ, ϕ). The quantization axis of the NV center defines the z-axis. The hyperfine field of the NV spin (red field lines) provides the magnetic field gradient for imaging. b Sketch of two nuclear spins I1 and I2 experiencing the same hyperfine interaction (red) [Eq. (2)]. Application of a transverse field ΔB (purple) reduces (I1) or increases (I2) the total magnetic field \({\bf{B}}_{{\mathrm{tot}}}^\prime\) (blue) experienced by the nuclear spins depending on the ϕ angle, allowing us to discriminate the nuclear locations. B0 is the static external field (green). c Geometry of the experimental setup in the laboratory frame of reference. A small solenoid on top of the diamond chip provides a rapidly switchable magnetic field ΔB. To change the vector orientation of ΔB, we translate the coil over the diamond
To obtain information about the distance vector r, a standard approach is to measure the parallel and transverse components of the hyperfine vector, a|| = Azz and \(a_ \bot = \left( {A_{xz}^2 + A_{yz}^2} \right)^{1/2}\), and to relate them to the field of a point dipole,
where μ0 = 4π × 10−7 TmA−1 is the vacuum permeability, ħ = 1.054 × 10−34 Js is the reduced Planck constant, |γe| = 2π × 28 GHz T−1 is the electron gyromagnetic ratio, and where we have included a Fermi contact term aiso (set to zero for now) for later discussion. Experimentally, the parallel projection a|| can be inferred from the precession frequencies \(f_{m_S}\) using Eq. (1), and the transverse projection a⊥ can be determined by driving a nuclear Rabi rotation via the hyperfine field of the central spin and measuring the rotation frequency21. Once a|| and a⊥ are known, Eqs. (3) and (4) can be used to extract the distance r and polar angle θ of the distance vector r = (r, θ, ϕ). Due to the rotational symmetry of the hyperfine interaction, however, knowledge of a|| and a⊥ is insufficient for determining the azimuth ϕ.
To break the rotational symmetry and recover ϕ, we apply a small transverse magnetic field ΔB during the free precession of the nuclear spin. Application of a transverse field tilts the quantization axes of the nuclear and electronic spins. The tilting modifies the hyperfine coupling parameters a|| and a⊥ depending on the angle between ΔB and Az, which in turn shifts the nuclear precession frequencies \(f_{m_S}\). To second-order in perturbation theory, the mS-dependent precession frequencies are given by:22
where α(mS) is a small enhancement of the nuclear g-factor. The enhancement results from non-secular terms in the Hamiltonian that arise due to the tilting of the electronic quantization axis, and is given by22
Here D = 2π × 2.87 GHz is the ground-state zero-field splitting of the NV center. By measuring the shifted frequencies \(f_{m_S}\) and comparing them to the theoretical model of Eqs. (5) and (6), we can then determine the relative ϕ angle between the hyperfine vector and ΔB.
Experimental setup
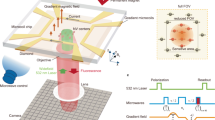
We experimentally demonstrate three-dimensional localization spectroscopy of four 13C1–4 nuclei adjacent to three distinct NV centers. NV1 is coupled to two 13C spins, while NV2 and NV3 are each coupled to a single 13C spin. For readout and control of the NV center spin, we use a custom-built confocal microscope that includes a coplanar waveguide and a cylindrical permanent magnet for providing an external bias field of B0 ~ 10 mT applied along the NV center axis ez. Precise alignment of the bias field is crucial for our experiments and is better than 0.3° (Methods section).
To dynamically tilt the external field we implement a multi-turn solenoid above the diamond surface (Fig. 1d). The coil produces ~2.5 mT field for 600 mA of applied current and has a rise time of ~2 μs. We calibrate the vector magnetic field of the coil with an absolute uncertainty of less than 15 μT in all three spatial components using two other nearby NV centers with different crystallographic orientations (ref. 23 and Methods section).
Mapping of r and θ
We begin our 3D mapping procedure by measuring the parallel and perpendicular hyperfine coupling constants using conventional correlation spectroscopy21 with no coil field applied, ΔB = 0 (Fig. 2). The parallel coupling a|| is determined from a free precession experiment (sequence 1 in Fig. 2) yielding the frequencies f0 and f−1 (Fig. 2b). The coupling constant is then approximately given by a||/(2π) ≈ f−1 − f0. The transverse coupling a⊥ is obtained by driving a nuclear Rabi oscillation via the NV spin, using sequence 2, and recording the oscillation frequency fR, where a⊥/(2π) ≈ πfR (Fig. 2c). Because, the Zeeman and hyperfine couplings are of similar magnitude, these relations are not exact and proper transformation must be applied to retrieve the exact coupling constants a|| and a⊥ (ref. 21 and Methods section). Once the hyperfine parameters are known, we can calculate the radial distance r = 8.58(1) Å and the polar angle θ = 52.8(1)° of the nuclear spin by inverting the point-dipole formulas (Eqs. 3, 4). The measurement uncertainties in r and θ are very small because correlation spectroscopy provides high precision estimates of both a|| and a⊥.
Implementation of three-dimensional localization spectroscopy. a Correlation spectroscopy protocol. By correlating two phase measurements we trace out the precession of the target nuclear spin(s) under different NMR sequences. Phase measurements are implemented by a Carr–Purcell–Meiboom–Gill (CPMG) train of microwave π pulses applied to the central electronic spin, where τ ≈ [2(f0 + f−1)]−1. Laser pulses are used to polarize and readout the electronic spin. Repetitions are N = 4–8 and M = t/τ. Experimental parameters for all measurements are collected in Supplementary Tables 2–9. b Free precession signal of the nuclear spin as a function of time t, using sequence 1. Right panel shows the corresponding power spectrum. The two frequencies f0 and f−1 are approximately equal to γnB0/(2π) and (γnB0 + a||)/(2π), respectively, see text. c Application of periodic π pulses on the NV center during t (sequence 2) causes a Rabi nutation of the nuclear spin, whose oscillation frequency fR is approximately equal to (a⊥/π)/(2π). d Activation of a transverse microcoil field ΔB during the nuclear precession (sequence 3) leads to shifted frequencies \(f_0^\prime\) and \(f_{ - 1}^\prime\). All measurements were conducted on 13C1. Extracted frequencies are listed in Table 1
Mapping of ϕ
In a second step, we repeat the free precession measurement with the coil field turned on (sequence 3), yielding a new pair of frequency values \(f_0^\prime\), \(f_{ - 1}^\prime\) (Fig. 2d). We then retrieve ϕ by computing theoretical values for \(f_0^{{\mathrm{(th)}}}\), \(f_{ - 1}^{{\mathrm{(th)}}}\) based on Eq. (5) and the calibrated fields in Table 1, and minimizing the cost function
with respect to ϕ. To cancel residual shifts in the static magnetic field and improve the precision of the estimates, we compare the frequency difference between mS states rather than the absolute precession frequencies.
In Fig. 3a, we plot |ξ(ϕ)| for three different coil positions and opposite coil currents for 13C1. We use several coil positions because a single measurement has two symmetric solutions for ϕ, and also because several measurements improve the overall accuracy of the method. The best estimate ϕ = 239(2)° is then given by the least squares minimum of the cost functions (dash-dotted line in Fig. 3a). To obtain a confidence interval for ϕ, we calculate a statistical uncertainty for each measurement by Monte Carlo error propagation taking the calibration uncertainties in B0 and ΔB, as well as the measurement uncertainties in the observed precession frequencies into account (Methods section). Values for all investigated 13C nuclei are collected in Supplementary Tables 2–9.
Determination of azimuth angle ϕ and Fermi contact contribution aiso for 13C1. a Cost function |ξ(ϕ)| between observed and predicted precession frequencies, as defined in Eq. (7). Here aiso = 0. Six measurements are shown for three spatial coil positions (solid curves) and opposite polarities of the coil current. The estimate for ϕ is given by the minimum of the squared cost functions \({\sum} \left| {\xi (\phi )} \right|^2\) of the six measurements (dash-dotted curve). b Scatter plot of maximum likelihood estimates of ϕ and aiso obtained by Monte Carlo error propagation. The plot is generated from 4 × 104 scatter points, where each point is the result of minimizing \({\sum} \left| {\xi \left( {\phi ,a_{{\mathrm{iso}}}} \right)} \right|^2\) for a different Monte Carlo sampling. Histograms for ϕ (bottom) and aiso (right) are obtained by integrating the 2D scatter plot along the vertical or horizontal direction, respectively. Corresponding plots for 13C2–4 are given in Supplementary Figs. 3–5
Fermi contact interaction
Thus far we have assumed that the central electronic spin generates the field of a perfect point dipole. Previous experimental work22,24 and density functional theory (DFT) simulations25,26, however, suggest that the electronic wave function extends several Angstrom into the diamond host lattice. The finite extent of the spin density leads to two deviations from the point dipole model: modified hyperfine coupling constants Aij, and a non-zero Fermi contact term aiso. In the remainder of this study we estimate the systematic uncertainty to the localization of the nuclear spins due to deviations from the point dipole model.
We first consider the influence of the Fermi contact interaction, which arises from a non-vanishing NV spin density at the location of the nuclear spin. The Fermi contact interaction adds an isotropic term to the hyperfine coupling tensor, A + aiso1, which modifies the diagonal elements Axx, Ayy, and Azz. DFT simulations25,26 indicate that aiso can exceed 100 kHz even for nuclear spins beyond 7 Å. It is therefore important to experimentally constrain the size of aiso.
To determine aiso, one might consider measuring the contact contribution to the parallel hyperfine parameter a||, which is equal to Azz. This approach, however, fails because a measurement of a|| cannot distinguish between dipolar and contact contributions. Instead, we here exploit the fact that the gyromagnetic ratio enhancement α depends on Axx and Ayy, and hence aiso. To quantify the Fermi contact coupling we include aiso as an additional free parameter in the cost function (7). By minimizing ξ(ϕ, aiso) as a joint function of ϕ and aiso and generating a scatter density using Monte Carlo error propagation, we obtain maximum likelihood estimates and confidence intervals for both parameters (Fig. 3b). The resulting contact coupling and azimuth for nuclear spin 13C1 are aiso/(2π) = 9(8) kHz and ϕ = 238(2)°, respectively; data for 13C2–4 are collected in Table 2. Because the gyromagnetic ratio enhancement α is only a second-order effect, our estimate is poor, but it still allows us constraining the size of aiso. By subtracting the Fermi contact contribution from a||, we further obtain refined values for the radial distance and polar angle, r = 8.3(2) Å and θ = 58(4)°. Note that introducing aiso as a free parameter increases the uncertainties in the refined r and θ, because the error in aiso is large. This leads to disproportionate errors for distant nuclei where aiso is small. Once nuclei are beyond a certain threshold distance, which we set to r = 10 Å in Table 2, it therefore becomes more accurate to constrain aiso = 0 and apply the simple point dipole model.
Extended electronic wave function
The second systematic error in the position estimate results from the finite size of the NV center’s electronic wave function. Once the extent of the wave function becomes comparable to r, the anisotropic hyperfine coupling constants Aij are no longer described by a point dipole, but require integrating a geometric factor over the sensor spin density25. While we cannot capture this effect experimentally, we can estimate the localization uncertainty from DFT simulations of the NV electron spin density. Following ref. 26, we convert the calculated DFT hyperfine parameters of 510 individual lattice sites to (r, θ) positions using the point-dipole formula (Eqs. 3, 4), and compute the difference to the DFT input parameters (rDFT, θDFT). The result is plotted in Fig. 4a. We find that the difference 〈Δr〉 = r − rDFT decreases roughly exponentially with distance, and falls below 0.2 Å when r > 10 Å (gray dots and curve).
Three-dimensional localization of four 13C nuclear spins. a Average localization uncertainty 〈Δr〉 as a function of radial distance r to the central spin. Gray dots represent the systematic error of the point-dipole approximation (see text), extracted for all lattice sites reported in the DFT calculation of ref. 26. Blue curve is an exponential fit to the median values (gray circles) of the gray dots in intervals of 2 Å. Black curves show the uncertainty of the frequency measurement, assuming a precision of 100 Hz (solid line, this study) and of 3 Hz11, 38, 39 (dashed line). Dotted horizontal line is one-half the diamond C–C bond length of aC−C = 1.54 Å. b Reconstructed locations of the four distant nuclear spins 13C1–4. Shaded regions mark the 2σ-confidence area of the localization projected onto (xy, yz, xz)-planes of the coordinate system. Gray points represent carbon lattice positions projected onto the same planes. The origin is set to the expected center of gravity of the spin density at 2.29 Å from the nitrogen nucleus on the NV symmetry axis25, 26. Due to the inversion symmetry of the hyperfine interaction, our method cannot distinguish between sites in the upper and lower hemisphere; all 13C are therefore plotted in the upper hemisphere
Discussion
Figure 4b summarizes our study by plotting the reconstructed locations for all four carbon atoms in a combined 3D chart. The shaded regions represent the confidence areas of the localization, according to Table 2, projected onto the Cartesian coordinate planes. We note that the DFT simulations are in good agreement with our experimental results.
The accuracy of our present experiments is limited by deviations from the point-dipole model, which dominate for small r (Fig. 4a). For larger r ≳ 1 nm, this systematic uncertainty becomes negligible, and the localization imprecision is eventually dictated by the NMR frequency measurement. In the present study, which probed isolated 13C nuclei with a narrow intrinsic line-width, the frequency precision was limited by the accuracy of our detection protocol to ~100 Hz. This corresponds to a radial localization error of ~0.75 Å at a distance of r = 3 nm (solid black line in Fig. 4a and Supplementary Fig. 6). Improving the frequency precision to 3 Hz11,27 would extend this distance to r ~ 7 nm (dashed black line).
Our work demonstrates a basic strategy for mapping spatial positions of single nuclei in 3D with high precision. Extending these experiments to single molecules outside a diamond chip poses a number of additional challenges, and overcoming them will require the combination of several strategies. To isolate single molecules, they can be embedded in a spin-free matrix layer deposited on the diamond surface28 or immobilized by a linker chemistry29. Nuclear dipole interactions can be suppressed using homo- and heteronuclear decoupling13, taking advantage of the existing microcoil. Line-widths and spectral complexity can be further reduced by polarizing the constituent nuclei, and by spin dilution and isotope labeling of molecules30. Alternatively, measurements of inter-spin couplings will allow constraining the structure and size of molecules31. To sensitively detect very weakly coupled nuclei in distant molecules, spin precession can be recorded by repetitive weak measurements32,33. Further improvement of sensitivity is possible by optimizing the optical detection efficiency compared to our present setup34, and possibly by cryogenic operation11. How well these strategies will work we do not know at present, but we believe that the prospect of a general single-molecule MRI technique, which will have many applications in structural biology and chemical analytics, provides sufficient motivation to warrant these efforts.
Methods
Diamond sample
Experiments were performed on a bulk, electronic-grade diamond crystal from ElementSix with dimensions 2 × 2 × 0.5 mm with \(\left\langle {110} \right\rangle\) edges and a \(\left\langle {100} \right\rangle\) front facet. The diamond was overgrown with a layer structure of 20 nm enriched 12C (99.99%), 1 nm enriched 13C (estimated in-grown concentration ~5–10%) and a 5 nm cap layer of again enriched 12C (99.99%). Nitrogen-vacancy (NV) centers were generated by ion-implantation of 15N with an energy of 5 keV, corresponding to a depth of ~5–10 nm. After annealing the sample for NV formation, we had to slightly etch the surface (at 580 °C in pure O2) to remove persistent surface fluorescence. The intrinsic nuclear spin of the three NV centers studied in our experiments were confirmed to be of the 15N isotope. Further characterizations and details on the sample can be found in a recent study (sample B in ref. 35).
Coordinate systems
In Supplementary Fig. 2a both laboratory and NV coordinate system are shown in a combined schematic. The laboratory coordinate system (xLab, yLab, zLab) is defined by the normal vectors to the diamond faces, which lie along \(\left\langle {110} \right\rangle\), \(\left\langle {\bar 110} \right\rangle\) and \(\left\langle {001} \right\rangle\), respectively. The reference coordinate system of the NV center is defined by its quantization direction, which is labeled zNV and lies along \(\left\langle {111} \right\rangle\). The xNV- and yNV-axis are pointing along the \(\left\langle {11\bar 2} \right\rangle\) and \(\left\langle {\bar 110} \right\rangle\) direction, respectively.
Experimental apparatus
A schematic of the central part of the experimental apparatus is shown in Supplementary Fig. 1. The diamond sample is glued to a 200 μm thick glass piece and thereby held above a quartz slide with incorporated microwave transmission line for electron spin control. Below the quartz slide we placed a high numerical aperture (NA = 0.95) microscope objective for NV excitation with a 532 nm laser and detection using a single photon counting module (SPCM). We applied static, external magnetic bias fields with a cylindrical NdFeB permanent magnet (not shown in Supplementary Fig. 1). The magnet is attached to a motorized, three-axis translation stage. The NV control pulses were generated by an arbitrary waveform generator (Tektronix, AWG5002C) and upconverted by I/Q mixing with a local oscillator to the desired ~2.6 GHz.
Planar, high-bandwidth coil
The planar coil is positioned directly above the diamond sample and attached to a metallic holder, which can be laterally shifted to translate the coil. Due to the thickness of the diamond (500 μm) and the glass slide the minimal vertical stand-off of the coil to the NV centers is ~700 μm. Design parameters of the planar coil, used in our experiments, are listed in Supplementary Table 1. These were found by numerically maximizing the magnetic field at the position of the NV center, located at a planned vertical stand-off of ~700–1000 μm (Supplementary Fig. 1). The coil had an inductance of ≤2.5 μH and a resistance of ≤0.5 Ω. The coil was manufactured by Sibatron AG (Switzerland) and it is mounted onto a copper plate that acts as a heat-sink, using thermally conducting glue. For the coil control, a National Instruments NI PCI 5421 arbitrary waveform generator was used, to generate voltage signals that controlled a waveform amplifier (Accel Instruments TS-250) which drives the coil current.
Calibration of the coil field ΔB
We calibrated the vector field generated by the coil ΔB using the target NV, coupled to nuclear spins of interest, and two auxiliary NV centers with different crystallographic orientation. All three NV centers were located in close proximity to each other, with a distance of typically ≤5 μm (Supplementary Fig. 2c). Over this separation the magnetic field of the coil can be assumed to be homogeneous. We determined the orientation of the symmetry axis of many NV centers by moving the permanent magnet over the sample and observing the ODMR splitting. The azimuthal orientation of the target NVs defines the x-axis in the laboratory and NV frame (ϕ = 0). This orientation was the same for all target NV centers investigated in this work. The auxiliary NV centers were selected to be oriented along ϕa,1 = 90° and ϕa,2 = 270° (Supplementary Fig. 2b). To calibrate the coil field, we removed the permanent magnet and recorded ODMR spectra for the target NV center and both auxiliary NV centers with the field of the coil activated. In this way, we record in total 6 ODMR lines, with 2 lines per NV center.
A numerical, nonlinear optimization method was used to determine the magnetic field ΔB from these ODMR resonances. For each of the three NV centers we simultaneously minimized the difference between the measured ODMR lines and the eigenvalues of the ground-state Hamiltonian:
Here, the magnetic field (ΔB)i acting onto the specific NV center is obtained by a proper rotation of ΔB into the respective reference frame.
Precise alignment of the bias field B 0
Precise alignment of the external bias field to the quantization axis of the NV center (z-axis) is critical for azimuthal localization measurements, because residual transverse fields of B0 modify the precession frequencies in the same way as the field of the coil. The coarse alignment of the magnet and a rough adjustment of the magnitude of the field, to ~10 mT, was achieved by recording ODMR spectra of the target NV center for different (x, y, z)-positions of the magnet. Afterwards, we iteratively optimized the alignment of the magnet. In each iteration, we reconstructed the vector field B0 acting on the target NV centers using the method used for the calibration of ΔB. Subsequently, we moved the magnet in the lateral (x, y)-plane of the laboratory frame. The direction and step size was determined from a field map of the permanent magnet and the residual transverse components of the field B0. We terminated this iterative process when the residual transverse field components were smaller than 50 μT.
Determination of hyperfine couplings (a ||, a ⊥) from (f 0, f −1, f R)
The hyperfine couplings a|| and a⊥ in the limit \(2\pi f_0 \gg a_{||},a_ \bot\) are given by:
In our experiments the hyperfine couplings and the nuclear Larmor frequency f0 were of similar magnitude, and we used the following transformations21 to obtain the hyperfine couplings.
Monte Carlo error propagation
Confidence intervals for ϕ and aiso were obtained using standard Monte Carlo error propagation36. The Monte Carlo simulation took calibration uncertainties in the external fields B0, ΔB and in the observed precession frequencies \(f_{m_s}\) into account. All parameters subject to uncertainty were assumed to follow a normal distribution. Precession frequencies were determined using a nonlinear, least-squares fitting algorithm and their measurement uncertainties were obtained from the fit error21. The uncertainty in the magnetic field components was estimated from the residuals between calculated and measured ODMR lines in the calibration method for B0, ΔB.
Nuclear g-factor enhancement
The nuclear g-factor enhancement factor α(mS) given in Eq. (6) of the main text is based on the approximation of small external bias fields \(D \gg \gamma _{\mathrm{e}}B_0\). More generally the mS-dependent enhancement factors are given by37:
which is also valid in the limit of large magnetic fields \(\gamma _{\mathrm{e}}B_0 \gg D\) and provides, in principle, more accurate theory values for small B0. We have analyzed our experimental data using this expression and found deviations to Eq. (6) that are smaller than the frequency resolution in our experiments.
Code availability
Custom code was programmed to perform the Monte Carlo simulations. The code is available from the corresponding author upon request.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Shi, F. et al. Single-protein spin resonance spectroscopy under ambient conditions. Science 347, 1135 (2015).
Ajoy, A., Bissbort, U., Lukin, M. D., Walsworth, R. L. & Cappellaro, P. Atomic-scale nuclear spin imaging using quantum-assisted sensors in diamond. Phys. Rev. X 5, 011001 (2015).
Perunicic, V. S., Hill, C. D., Hall, L. T. & Hollenberg, L. A quantum spin-probe molecular microscope. Nat. Commun. 7, 12667 (2016).
Degen, C. L., Poggio, M., Mamin, H. J., Rettner, C. T. & Rugar, D. Nanoscale magnetic resonance imaging. Proc. Natl Acad. Sci. USA 106, 1313 (2009).
Grinolds, M. S. et al. Subnanometre resolution in three-dimensional magnetic resonance imaging of individual dark spins. Nat. Nano 9, 279–284 (2014).
Lazariev, A. & Balasubramanian, G. A nitrogen-vacancy spin based molecular structure microscope using multiplexed projection reconstruction. Sci. Rep. 5, 14130 (2015).
Taminiau, T. H. et al. Detection and control of individual nuclear spins using a weakly coupled electron spin. Phys. Rev. Lett. 109, 137602 (2012).
Schirhagl, R., Chang, K., Loretz, M. & Degen, C. L. Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 65, 83 (2014).
Shi, F. et al. Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 10, 21–25 (2014).
Reiserer, A. et al. Robust quantum-network memory using decoherence-protected subspaces of nuclear spins. Phys. Rev. X 6, 021040 (2016).
Abobeih, M. H. et al. One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 9, 2552 (2018).
Zhao, N. et al. Sensing single remote nuclear spins. Nat. Nano 7, 657 (2012).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Epstein, R. J., Mendoza, F. M., Kato, Y. K. & Awschalom, D. D. Anisotropic interactions of a single spin and dark-spin spectroscopy in diamond. Nat. Phys. 1, 94 (2005).
Stanwix, P. L. et al. Coherence of nitrogen-vacancy electronic spin ensembles in diamond. Phys. Rev. B 82, 201201 (2010).
Laraoui, A., Pagliero, D. & Meriles, C. A. Imaging nuclear spins weakly coupled to a probe paramagnetic center. Phys. Rev. B 91, 205410 (2015).
Wang, Z.-Y., Haase, J. F., Casanova, J. & Plenio, M. B. Positioning nuclear spins in interacting clusters for quantum technologies and bioimaging. Phys. Rev. B 93, 174104 (2016).
Sasaki, K., Itoh, K. M. & Abe, E. Determination of the position of a single nuclear spin from free nuclear precessions detected by a solid-state quantum sensor. Phys. Rev. B 98, 121405 (2018).
Zopes, J., Herb, K., Cujia, K. S. & Degen, C. L. Three-dimensional nuclear spin positioning using coherent radio-frequency control. Phys. Rev. Lett. 121, 170801 (2018).
Laraoui, A. et al. High-resolution correlation spectroscopy of c-13 spins near a nitrogen-vacancy centre in diamond. Nat. Commun. 4, 1651 (2013).
Boss, J. M. et al. One- and two-dimensional nuclear magnetic resonance spectroscopy with a diamond quantum sensor. Phys. Rev. Lett. 116, 197601 (2016).
Childress, L. et al. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 314, 281 (2006).
Steinert, S. et al. High sensitivity magnetic imaging using an array of spins in diamond. Rev. Sci. Instrum. 81, 43705 (2010).
Smeltzer, B., Childress, L. & Gali, A. 13C hyperfine interactions in the nitrogen-vacancy centre in diamond. New J. Phys. 13, 025021 (2011).
Gali, A., Fyta, M. & Kaxiras, E. Ab initio supercell calculations on nitrogen-vacancy center in diamond. Phys. Rev. B 77, 155206 (2008).
Nizovtsev, A. P. et al. Non-flipping 13C spins near an nv center in diamond: hyperfine and spatial characteristics by density functional theory simulation of the C510[NV]H252 cluster. New J. Phys. 20, 023022 (2018).
Glenn, D. R. et al. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 555, 351 (2018).
Mamin, H. J., Sherwood, M. H. & Rugar, D. Detecting external electron spins using nitrogen-vacancy centers. Phys. Rev. B 86, 195422 (2012).
Sushkov, A. O. et al. All-optical sensing of a single-molecule electron spin. Nano. Lett. 14, 6443–6448 (2014).
Loquet, A., Lv, G., Giller, K., Becker, S. & Lange, A. 13C spin dilution for simplified and complete solid-state nmr resonance assignment of insoluble biological assemblies. J. Am. Chem. Soc. 133, 4722–4725 (2011).
Ernst, R. R., Bodenhausen, G. & Wokaun, A. Principles of nuclear magnetic resonance in one and two dimensions. (International Series of Monographs on Chemistry, Clarendon Press, New York, 1990).
Gefen, T., Khodas, M., McGuinness, L. P., Jelezko, F. & Retzker, A. Quantum spectroscopy of single spins assisted by a classical clock. Phys. Rev. A. 98, 013844 (2018).
Cujia, K. S., Boss, J. M., Zopes, J. & Degen, C. L. Watching the precession of a single nuclear spin by weak measurements. arXiv:1806.08243 (2018). https://arxiv.org/abs/1806.08243.
Wan, N. H. et al. Efficient extraction of light from a nitrogen-vacancy center in a diamond parabolic reflector. Nano Lett. 18, 2787 (2018).
Unden, T. et al. Coherent control of solid state nuclear spin nano-ensembles. npj Quant. Inf. 4, 39 (2018).
Alper, J. S. & Gelb, R. I. Standard errors and confidence intervals in nonlinear regression: comparison of monte carlo and parametric statistics. J. Phys. Chem. 94, 4747–4751 (1990).
Maze, J. Quantum manipulation of nitrogen-vacancy centers in diamond: From basic properties to applications. Ph.D. thesis (Harvard University, New York, 2010). http://www.fis.puc.cl/jmaze/MazeHUThesis.pdf
Rosskopf, T., Zopes, J., Boss, J. M. & Degen, C. L. A quantum spectrum analyzer enhanced by a nuclear spin memory. npj Quant. Inf. 3, 33 (2017).
Zaiser, S. et al. Enhancing quantum sensing sensitivity by a quantum memory. Nat. Commun. 7, 12279 (2016).
Acknowledgements
The authors thank Jyh-Pin Chou, Adam Gali, A. Nizovtsev, and Fedor Jelezko for sharing DFT data, and Julien Armijo, Kevin Chang, Nils Hauff, Konstantin Herb, Takuya Segawa, and Tim Taminiau for helpful discussions. This work was supported by Swiss NSF Project Grant 200021_137520, the NCCR QSIT, and the DIADEMS 611143 and ASTERIQS 820394 programs of the European Commission. The work at Keio has been supported by JSPS KAKENHI (S) No. 26220602, JSPS Core-to-Core, and Spin-RNJ.
Author information
Authors and Affiliations
Contributions
C.L.D. initiated the project. J.Z. conceived the microcoil. J.Z. performed the experiments with the help of J.M.B., K.S. and K.S.C. J.Z. and C.L.D. analyzed the data and co-wrote the paper with the help of K.M.I. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zopes, J., Cujia, K.S., Sasaki, K. et al. Three-dimensional localization spectroscopy of individual nuclear spins with sub-Angstrom resolution. Nat Commun 9, 4678 (2018). https://doi.org/10.1038/s41467-018-07121-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-07121-0
This article is cited by
-
Correlated sensing with a solid-state quantum multisensor system for atomic-scale structural analysis
Nature Photonics (2024)
-
Three-dimensional magnetic resonance tomography with sub-10 nanometer resolution
npj Quantum Information (2024)
-
Coherent optical two-photon resonance tomographic imaging in three dimensions
Communications Physics (2023)
-
Quantum Memory on 13C–13C Dimers in Diamond with NV Centers: Simulation by Quantum Chemistry Methods
Journal of Applied Spectroscopy (2023)
-
Vector Magnetometry Using a Single NV–13C Complex in Diamond
Journal of Applied Spectroscopy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.