Abstract
Neuromorphic networks of artificial neurons and synapses can solve computationally hard problems with energy efficiencies unattainable for von Neumann architectures. For image processing, silicon neuromorphic processors outperform graphic processing units in energy efficiency by a large margin, but deliver much lower chip-scale throughput. The performance-efficiency dilemma for silicon processors may not be overcome by Moore’s law scaling of silicon transistors. Scalable and biomimetic active memristor neurons and passive memristor synapses form a self-sufficient basis for a transistorless neural network. However, previous demonstrations of memristor neurons only showed simple integrate-and-fire behaviors and did not reveal the rich dynamics and computational complexity of biological neurons. Here we report that neurons built with nanoscale vanadium dioxide active memristors possess all three classes of excitability and most of the known biological neuronal dynamics, and are intrinsically stochastic. With the favorable size and power scaling, there is a path toward an all-memristor neuromorphic cortical computer.
Similar content being viewed by others
Introduction
The gap between artificial intelligence (AI) and mammal-level intelligence lies in both the architecture and the building blocks. It is unlikely that AI implemented on conventional computing platforms will eventually fill both gaps. Even if the brain’s connectivity were reproduced, artificial neurons and synapses built with non-biomimetic complementary metal-oxide-semiconductor (CMOS) circuits are not capable of emulating the rich dynamics of biological counterparts without sacrificing the energy consumption and size. CMOS-based neuromorphic computing (NMC) hardware suffer from the cost-fidelity dilemma i.e., scalability and biological fidelity are not simultaneously achievable. Although spike domain algorithms are energy savvy, their performance is handicapped by the poor scalability of neuron and synapse building blocks. A survey of chip-scale deep-learning image inference (See Supplementary Fig. 1) reveals that graphic processing units (GPUs) are the state-of-the-art (SOA) in throughput. However, the higher throughput comes at the cost of lower energy efficiency (EE). By contrast, NMC processors are the SOA in EE, but their throughput is much lower than GPUs’. Regardless of architecture, a universal boundary looks to exist for the throughput·EE product of all CMOS processors, which is likely limited by the CMOS device physics.
Memristors provide an alternative approach to advance NMC. The nonvolatile, stochastic, and adaptive passive memristor offers an electronic analog to biological synapses. The superb scalability of memristor crossbars projects towards the synapse density of the brain (1010 cm−2)1,2. Recently, biologically plausible self-learning and spike-timing dependent plasticity (STDP) were demonstrated3,4. A complementary device, the active memristor, can be used to construct an electronic equivalent of biological neurons. Active memristors show volatile resistive switching and are locally active within a hysteretic negative differential resistance (NDR) regime in current-voltage characteristics. The NDR provides signal gain needed for signal processing. Recently, active memristor based spiking neurons were demonstrated5 with biomimetic properties such as all-or-nothing spiking, refractory period, and tonic spiking and bursting. However, these demonstrations were interpreted by leaky integrate-and-fire (LIF) models6. LIF neurons possess much fewer neuro-computational properties7 than biologically-accurate models, e.g., the Hodgkin Huxley (HH) model8. Network-wise, most of the prior art pursued hybrid approaches that combine passive memristors with software neurons or CMOS neurons9,10,11,12. Such hybrid approaches promise bio-competitive synaptic scalability, but still suffer the poor size and power scalability of Si neurons (See Supplementary Fig. 2). The lack of built-in stochasticity for CMOS neurons is a handicap for achieving complex computational tasks, e.g., Bayesian inference, that require stochastic neuronal populations13.
In this article, using scalable vanadium dioxide (VO2) active memristors, we show that memristor neurons possess most of the known biological neuronal dynamics. Twenty three types of biological neuronal behaviors are experimentally demonstrated, including tonic spiking and bursting, phasic spiking (Class 3 excitability) and bursting, mixed-mode spiking, spike frequency adaptation, Class 1 and Class 2 excitabilities, spike latency, subthreshold oscillations, integrator, resonator, rebound spike and burst, threshold variability, bistability, depolarizing after-potential, accommodation, inhibition-induced spiking and bursting, all-or-nothing firing, refractory period, and excitation block. The built-in stochasticity is demonstrated by stochastic phase-locked firing, aka skipping. Finally, our simulations show that the dynamic and static power scaling of memristor neurons project toward biologically competitive neuron density and EE.
Results
Locally active memristors
Chua’s memristive theorem14 proves that a pinched hysteresis in the I–V (I: current, V: voltage) loci is the only required fingerprint of a memristor. Although a canonical memristor is a passive one-port (two-terminal) circuit element, the same theorem can be applied to a class of one-port devices that exhibit a hysteretic negative differential resistance (NDR, i.e., \(\frac{\mathrm{d}V}{\mathrm{d}I} \,< \, 0\)) in certain region of the I–V loci. If the circuit operating point lies within the NDR regime, e.g., when a resistor load line intersects with the I–V of the nonlinear device in the NDR regime, the device becomes locally active (see Fig. 1e). A locally active (active hereinafter) memristor can produce an a.c. signal gain greater than 1 and serve as an amplifier, or excite oscillations in appropriate circuits having reactive elements (see Supplementary Fig. 3 and Note 1). Therefore, active memristors can be used as scalable gain elements in information processing. Local activity, together with edge of chaos, are two basic properties for neurons. Chua showed that the locally active domain in the activity diagram of a HH cell is the origin of spikes15, and it is derived from the locally active regime in the I–V loci of voltage-gated ion channels.
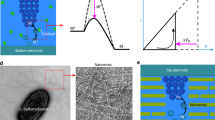
Circuit diagram of a biomimetic active memristor neuron and active memristor device characteristics. a Schematic structure of a biological neuron, showing that an action potential is fired near the axon hillock (under sufficient input stimulus) and propagates along the cell axon towards the output synapses. b Mechanism of voltage-gated Na+ and K+ ion flows across the cell membrane that accounts for the action potential generation and repetition across the nodes of Ranvier (myelin-sheath gaps). A similar mechanism exists in neurons that lack a myelin sheath. c Basic circuit topology of a two-channel active memristor neuron to emulate the neuronal dynamics in (b). A voltage-gated Na+ (K+) channel is emulated by a negatively (positively) d.c. biased active memristor device, which is closely coupled with a local membrane capacitor C1 (C2) and a series load resistor RL1 (RL2). d Schematic structure and a scanning electron micrograph of a typical VO2 active memristor nano-crossbar device (X1 or X2 in (c)). Scale bar: 100 nm. e Typical two-terminal quasi d.c. voltage-controlled (force V) and current-controlled (force I) I–V characteristics of a VO2 active memristor device. A wide hysteresis loop exists in the voltage-controlled mode due to the Mott transitions (blue arrows). The same Mott transitions are manifested by an “S” shaped negative differential resistance (NDR) regime (highlighted by cyan color) with a much narrower hysteresis (red arrows) in the current-controlled mode. In its resting state, the resistor load line for memristor X1 (or X2) intersects with its I–V loci outside the NDR regime (green dotted line). An input current or voltage stimulus can shift the load line into the NDR regime (green dashed line) and elicit an action potential generation (spiking)
We limit the discussions to active memristors that show current-controlled NDR (“S”-shaped I–V loci in current sweeps), since they are at a high-resistance state when powered off, thus offering low standby power dissipation. Not every hysteretic NDR device is an active memristor, though. A counter example is silicon thyristor, which exhibits a hysteretic NDR but the I–V loci does not pass through the origin (not “pinched”), and therefore it is not a genuine memristor16. In contrast to a passive memristor, in an active memristor the hysteresis collapses before the external voltage is removed, therefore the memory effect is transient. Several mechanisms can produce “S”-NDR. It may show up in the electroforming of a passive oxide memristor17 due to self-heating induced conductivity instability. However, such an NDR is irreversible and vanishes after the device is electroformed. Ovonic threshold switches (OTS) made of amorphous chalcogenides have reversible “S”-NDR18,19, which can be explained by trap-limited conduction that increases exponentially under high electric field20. OTS are being exploited as an access selector device in memristor crossbars to mitigate the sneak-path issue19, but their endurance is limited by material degradation due to field stress. A more promising class of “S”-NDR devices is Mott memristors based on thermodynamically-driven Mott insulator-to-metal transition (IMT) in certain transition metal oxides. Mott memristors are more robust since there is no high field or chemical redox reaction involved in the quantum phase transition. Nanoscale niobium dioxide (NbO2) Mott memristor electroformed from amorphous niobium pentoxide (Nb2O5) was reported21. However, we found that such an electroforming process, in our case forming VO2 from amorphous vanadium pentoxide (V2O5), produced void in the oxide film and electrode damage, likely due to O2 gas released in the reduction of V2O5. Electroformed VO2 devices showed poor yield and large variations in switching characteristics, and hence are impractical for circuit applications22. In this work, we have developed electroforming-free VO2 active memristors on CMOS-compatible SiNx-coated silicon substrates with typical yield > 98% (See Methods and Supplementary Figs. 4–8). These electroforming-free VO2 nano-crossbar devices show low device-to-device variability with < 13% coefficient of variation in switching threshold voltage for devices with critical dimension from 50–600 nm, and high switching endurance of > 26.6 million cycles without discernible change in device I–V characteristics. The electroforming-free VO2 device technology expedited the development of active memristor neuron circuitries that can emulate most of the known neuronal dynamics and cleared the path toward large-scale integrated circuit (IC) implementations. Moreover, VO2 is a superior Mott memristor than NbO2 in both switching speed and switching energy. Simulated Mott transition in VO2 is 100 times faster than in NbO2, and only consumes about one-sixth (16%) of the energy (See Supplementary Fig. 9, Table 1, Note 1 and Note 2).
Circuit topology and spiking behaviors of VO2 neurons
Schematic structure and action potential generation mechanism in a biological neuron is shown in Fig. 1a, b. The basic circuit topology of a single-compartment VO2 active memristor neuron is shown in Fig. 1c. The prototype circuit consists of two resistively coupled relaxation oscillators, each having a d.c.-biased active memristor (X1 or X2), a parallel membrane capacitor (C1 or C2), and a load resistor (RL1 or RL2). The oppositely-energized (polarized) memristors X1 and X2 emulate the voltage-gated Na+ and K+ membrane protein ion channels, respectively. Similar circuit concepts emerged in early 1960s, e.g., the “Neuristor” axon first proposed by H. Crane23,24, but the scalability of these early proposals were poor due to the needs of either inductors25 or bipolar thyristors26. Scalable Neuristor circuitries can be realized by Mott memristors due to their superior 4F2/N (F: half pitch, N: number of stacked layers) scalability5. In our design, the two membrane capacitors are grounded instead of d.c. biased5, so that the voltages across them are the actual local membrane potential across the nerve cell membrane. This is consistent with the original HH neuron model, except that the single membrane capacitor is divided into two, each closely coupled with a voltage-gated membrane ion channel. Unbiased capacitors also offer more flexibility in IC design. The two-stage circuit has the same dimensionality as the HH model. Its dynamics is described by four coupled first-order differential equations that solve four state variables (u1, u2, q1, q2), wherein u1 and u2 are the normalized metallic channel radii of the memristors and q1 and q2 are the charges stored on the capacitors5. Since q1 and q2 are connected to the local membrane potentials VNa and VK by the linear relationships of q1 = C1VNa and q2 = C2VK, the four state variables can be rewritten as (u1, VNa, u2, VK) (See Supplementary Note 3). A benefit of this transformation is that VNa and VK are straightforward to measure experimentally. Some characters of spiking dynamics, e.g., limit cycle oscillation and bifurcation, can be revealed in the two-dimensional VNa–VK phase plane6. Several groups have used a single-stage Pearson-Anson relaxation oscillator as an LIF neuron27,28,29,30. Having only two state variables, such neurons may provide some simple spiking functionalities, but lack the heterogeneity and ergodicity of neuronal dynamics needed for more sophisticated neural networks.
The basic operational steps in experimental and simulated action potential (spike) generation are shown in Fig. 2b, with the analogous biological processes illustrated for pedagogical purpose. To be consistent with neuroscience convention, hyperpolarization means the membrane potential is driven toward negative direction, and depolarization is the opposite case. In the resting (quiescent) state, both the Na+ and K+ channels are closed (X1 and X2 are insulating). A resting potential (0.2–0.3 V) is produced by a small membrane leakage current flowing through the two oppositely-energized VO2 devices in insulating state. Hyperpolarization will be triggered by the activation of the Na+ channel if a suprathreshold input voltage or current stimulus (not shown) drives X1 into a metallic state. The Na+ channel membrane potential, VNa, is pulled down close to the negative d.c. bias –ENa, and its membrane capacitor C1 gets discharged. The neuron output, i.e., the K+ channel membrane potential VK, also gets pulled down through the coupling of RL2, but it remains above zero. The opening of Na+ channel is almost instantaneous due to the ultrafast Mott IMT process (seen in the simulated Na+ channel current), but the hyperpolarization of VNa is much slower as it is determined by the C1 discharge time constant. Depolarization is then triggered by the activation of the K+ channel. It occurs when the VNa hyperpolarization pulls VK down low enough to make the voltage across X2 larger than its switching threshold. After X2 switches to metallic state, VK gets pulled up close to the positive d.c. bias + EK, and its membrane capacitor C2 gets discharged. The time scale of depolarization is determined by the C2 discharge time constant. The spiking is finalized by a refractory (undershoot) period, during which the neuron is recovering and does not respond to the next input stimulus. The time scale for the action potential to fall, undershoot, then recover to resting is the longest, as C1 and C2 are slowly charged back to their resting states. In biological neurons, recovery is achieved by rebalancing the Na+ and K+ concentrations across the cell membrane by Na+-K+ pumps (conceptually shown by dashed lines) instead of voltage-gated Na+ and K+ protein channels (both are closed).
Action potential generation in a VO2 active memristor neuron. a Circuit diagram of a VO2 memristor neuron, consisting of two resistively coupled Pearson-Anson relaxation oscillators (RL1, C1, X1 and RL2, C2, X2, respectively). The negatively-biased memristor X1 acts as the voltage-gated Na+ channel, and the positively-biased memristor X2 acts as the voltage-gated K+ channel. Capacitors C1 and C2 are the corresponding membrane capacitances. b Basic steps in action potential (spike) generation of a VO2 neuron. (1) Resting state, in which both the Na+ and K+ channels are closed. A resting potential of 0.2–0.3 V is produced by a membrane leakage current flowing through the VO2 devices in their insulating state. (2) Hyperpolarization caused by the activation of the Na+ channel, which drives the membrane potential toward negative direction. (3) Depolarization caused by the activation of the K+ channel, which drives the membrane potential toward positive direction. (4) Refractory (undershoot), during which the neuron is recovering and does not respond to another stimulus. The central plots are experimental and simulated action potentials (top), the Na+ channel membrane potential VNa (middle), and simulated Na+ and K+ channel currents (bottom)
The neuron circuit shown in Fig. 1c continues to fire a train of evenly spaced spikes, or it fires periodic bursts of spikes when stimulated by a steady d.c. current input. These characteristics are known as part of the spiking behaviors for tonically active neurons (TANs). Phasically active neurons (PANs), on the contrary, may fire only a single spike at the onset of the steady d.c. current input due to transient dynamics, and remain quiescent afterwards as the system reaches the steady state. Phasic firing is known as Class 3 excitability31. Both TANs and PANs play important roles in the central nervous system. In a number of brain areas such as cortex, striatum, and midbrain, PANs act as differentiators or slope-detectors and are involved in a wide range of processes including motor control, coincidence detection in the auditory brainstem, cognition, and reward-related learning32,33. However, there is yet no demonstration of phasic spiking behaviors in active memristor neurons. We found that phasic spiking behaviors can be realized simply by replacing the load resistor RL1 with a capacitor Cin, or by inserting a capacitor Cin before RL1 in the tonic neuron circuit. In other words, the main difference between TANs and PANs is that TANs have resistively coupled dendritic inputs and PANs have capacitively-coupled dendritic inputs. Otherwise both types of neurons share the same circuit topology. If a capacitor Cin is placed in parallel with the load resistor RL1, the circuit turns into a mixed-mode neuron, and fires a phasic burst followed by a train of tonic spiking when stimulated by a steady d.c. current input. In biological neurons, Class 3 phasic behavior is attributed to a subthreshold K+ current, acting as a dynamic negative feedback to preclude spiking if the input rises too slowly, and the neuron shows no bifurcation to repetitive spiking no matter how strong the input is34.
Figure 3 shows the three VO2 active memristor prototype neuron circuits and the lists of their experimentally demonstrated biological neuron spiking behaviors. Experimental circuit parameters are listed in Supplementary Table 2. Four basic biological neuron spiking behaviors, including all-or-nothing firing (See Supplementary Fig. 10), refractory period (See Supplementary Figs. 11 and 12), spike frequency adaptation (See Supplementary Figs. 15 and 16), and spike latency (See Supplementary Fig. 17), are shared properties of both tonic and phasic neurons. Besides these shared spiking behaviors, In TANs, ten unique spiking behaviors are observed, including tonic spiking (See Supplementary Fig. 13), tonic bursting (See Supplementary Fig. 14), Class 1 excitability (See Fig. 4g), Class 2 excitability (See Fig. 4h), subthreshold oscillations (See Supplementary Fig. 18), integrator (See Supplementary Fig. 19), bistability (See Supplementary Fig. 20), inhibition-induced spiking (See Supplementary Fig. 21), inhibition-induced bursting (See Supplementary Fig. 22), and excitation block (See Supplementary Fig. 23). In PANs, eight unique spiking behaviors are observed, including phasic spiking, i.e., Class 3 excitability (See Supplementary Fig. 25), phasic bursting (See Supplementary Fig. 26), rebound spike (See Supplementary Figs. 27–29), rebound burst (See Supplementary Fig. 30), resonator (See Supplementary Fig. 24), threshold variability (See Supplementary Fig. 31), depolarizing after-potential (See Supplementary Fig. 32), and accommodation (See Supplementary Fig. 33). Together with the mixed-mode spiking behavior observed in mixed-mode neurons (See Supplementary Fig. 34), we have observed 23 types of known biological neuron spiking behaviors.
Three active memristor prototype neuron circuits and their experimentally demonstrated spiking behaviors. a Tonic excitatory neurons, with a resistive coupling to dendritic inputs, show tonic spiking (Supplementary Fig. 13), tonic bursting (Supplementary Fig. 14), Class 1 excitable (Fig. 4g), Class 2 excitable (Fig. 4h), subthreshold oscillations (Supplementary Fig. 18), integrator (Supplementary Fig. 19), bistability (Supplementary Fig. 20), inhibition-induced spiking (Supplementary Fig. 21), inhibition-induced bursting (Supplementary Fig. 22), and excitation block (Supplementary Fig. 23). b Phasic excitatory neurons, with a capacitive coupling to dendritic inputs, show phasic spiking, i.e., Class 3 excitable (Supplementary Fig. 25), phasic bursting (Supplementary Fig. 26), rebound spike (Supplementary Figs. 27–29), rebound burst (Supplementary Fig. 30), resonator (Supplementary Fig. 24), threshold variability (Supplementary Fig. 31), depolarizing after-potential (Supplementary Fig. 32), and accommodation (Supplementary Fig. 33). Other biological neuron spiking behaviors, including all-or-nothing firing (Supplementary Fig. 10), refractory period (Supplementary Figs. 11 and 12), spike frequency adaptation (Supplementary Figs. 15 and 16), and spike latency (Supplementary Fig. 17), are shared properties of both tonic and phasic neurons. c mixed-mode neurons, with both resistive and capacitive couplings (RL1, Cin in parallel) to dendritic inputs, show mixed-mode spiking (Supplementary Fig. 34) behavior
The 23 biological neuron spiking behaviors experimentally demonstrated in single VO2 active memristor neurons. a Tonic spiking. b Phasic spiking. c Tonic bursting. d Phasic bursting. e Mixed mode. f Spike frequency adaptation. g Class 1 excitable. h Class 2 excitable. i Spike latency. j Subthreshold oscillations. k Resonator. l Integrator. m Rebound spike. n Rebound burst. o Threshold variability. p Bistability. q Depolarizing after-potential. r Accommodation. s Inhibition-induced spiking. t Inhibition-induced bursting. u All-or-nothing firing. v Refractory period. w Excitation block. All the behaviors are measured from a single tonic, phasic, or mixed-mode neuron circuit that consist of only 2 VO2 active memristors and 4 or 5 passive R, C elements. For more details, see Supplementary Figs. 10–34
Figure 4 summarizes the 23 experimentally demonstrated spiking behaviors in VO2 neurons. All the behaviors are measured from a single tonic, phasic, or mixed-mode neuron circuit that consist of only 2 VO2 active memristors and 4 or 5 passive R, C elements. The VO2 memristors are homogeneous in the sense that they have the same size (100 × 100 nm2) and are fabricated on the same wafer, with small spreading in switching characteristics. The heterogeneity in spiking dynamics is achieved by controllable circuit parameters, i.e., values of R, C elements or input-stage impedance. One can also control the area ratio of the two VO2 devices to achieve asymmetry in the emulated Na+ and K+ ion channels. In comparison, a CMOS artificial neuron constructed with nearly 1300 logic gates (each gate uses a minimum of two transistors) replicated 11 biological neuron behaviors using single neurons, and another 9 behaviors using 2 or 3 neurons35. The stark contrast in active device counts between memristor neurons and CMOS neurons to achieve similar level of biological fidelity is a manifestation of the importance of native biomimeticity. Controllability of neuron spiking characteristics is important for network design and neural coding. Spike-timing properties, e.g., tonic spike frequency (See Fig. 5c), tonic burst frequency and number of spikes per burst (See Supplementary Figs. 14k and l), and spike latency (See Supplementary Fig. 17c), can be directly controlled by the capacitor values or the strength of input stimuli.
Capacitance-dependent operating regimes in a tonic VO2 active memristor neuron. a Diagram of operating regimes determined by the values of C1 and C2 membrane capacitors. When C2 > C1, the neuron exhibits Class 2 excitable spiking and subthreshold oscillations (see (b)). When C2 < C1, the neuron exhibits Class 1 excitable spiking (see (c)). When C2 < 0.35C1, the neuron exhibits Class 1 excitable bursting (see (d)). Various combinations of C1 and C2 are sampled (colored dots) by measuring time dependence of neuron output with a linearly ramped input current. (b–d) Typical neuron input and output vs. time (top panels), and the current-dependence of instantaneous spike frequency (bottom panels) sampled from Class 2 excitable spiking, Class 1 excitable spiking, and Class 1 excitable bursting regimes, respectively
In Hodgkin’s classification, there are three basic classes of neuron excitability that can be discerned by spiking patterns: Class 1, Class 2, and Class 331. The nonlinear dynamical mechanism responsible for each class of excitability is reasonably well understood. Class 3 excitability, or phasic spiking, has been discussed above. A closer look at tonic neurons found that they can be converted between being Class 1 and Class 2 excitable, simply by adjusting the Na+ and K+ membrane time constants. In Figure 5, spike patterns of a tonic VO2 neuron subject to a linearly ramped input current are recorded at different values of C1 and C2 membrane capacitors. Other circuit parameters are left unchanged and the same value is used for the two load resistors RL1 and RL2. Therefore the membrane time constants are determined by C1 and C2. For the cases of C2 < C1 (fast K+, slow Na+), the neuron exhibits Class 1 excitability, and shows tonic spiking (if 0.35C1 < C2 < C1) or tonic bursting (if C2 < 0.35C1). In Class 1 regime, the observed spike onset threshold and initial frequency are relatively low. Theoretically, the initial frequency can be arbitrarily low. The spike frequency increases with the strength of input current with a pronounced slope. For the cases of C2 > C1 (slow K+, fast Na+), the neuron exhibits Class 2 excitability with much larger spike onset thresholds. The spike frequency is relatively constant and insensitive to changes in the input strength. In Class 2 regime, spiking is oftentimes preluded by subthreshold oscillations with sawtooth-shaped waveforms, indicating that it is the relaxation oscillation of the K+ channel. In canonical models, Class 1 and Class 2 excitabilities belong to different bifurcations from stable steady state to periodic (spiking) behavior as the stimulus parameter is varied36. There are 4 to 6 possible types of bifurcations for each class37. To find out the specific bifurcations responsible for the observed classes of excitabilities, a nullcline analysis mapping the four-dimensional nonlinear system into the VNa–VK phase plane without losing part of the dynamics is needed, in a way similar to FitzHugh-Nagumo dimensionality reduction of the HH model25,38. Since we experimentally observed excitation block in a Class 2 tonic VO2 neuron (See Supplementary Fig. 23), it is possible that a supercritical Andronov-Hopf bifurcation drives the observed Class 2 excitability37.
Stochasticity of VO2 neurons
Finally, we applied the classic stochastic spike train analysis, i.e., the joint interspike interval (JISI) analysis, to study stochasticity and correlation in spike patterns. The results show that VO2 memristor neurons exhibit input-noise sensitive stochastically phase-locked firing, aka skipping, in a manner similar to biological neurons39,40. In a first-order JISI analysis, the relationship between consecutive spike firings is inspected by analyzing a 3-spike pattern, which includes two interspike intervals (ISIs). An ISI is defined as the time difference between consecutive spikes \(\tau _n = t_n - t_{n - 1}\), where tn is the time of occurrence for the nth spike. The scatter plot of (τn, τn+1) pairs, which is referred to as a return map (Poincaré map), is used to reveal the correlation between consecutive first-order ISIs. White noise signals with different amplitudes are superimposed on a steady current clamp (82.5 µA) input for a tonic VO2 neuron, and the excited spike trains within a 35 ms time duration are recorded. Figure 6 shows the measured spike patterns (only the initial sections of ~ 3 ms are shown for clarity) and JISI return maps at peak-to-peak white noise amplitudes in the range of 5 µApp to 50 µApp. When the input noise is low (Fig. 6a), the neuron exhibits regular tonic spiking with ISIs tightly clustered around a predominant fundamental value (ISI median = 29.3 µs). As the input noise increases (Fig. 6b), sporadic drop-outs in firing start to emerge, while most of the firing is still clustered around the fundamental ISI. At even higher noise levels (Fig. 6c, d), the neuron exhibits irregular spiking with many drop-outs, resulting in widely scattered JISI pairs in return maps. The JISI pairs cluster around regular grids roughly at multiples of the fundamental ISI, which is also evident in the ISI histograms. Similar arrhythmic firings, or skipping, have been observed in biological neurons such as thermosensitive mammalian cold receptors41. These receptors show irregular spikes that are phase-locked to an underlying periodic oscillation, with a random integer number of oscillation cycles skipped between spikes. The firing irregularity increases with temperatures, consistent with our case of elevated input noise. The fundamental ISI, however, is robust against noise and does not shift or vanish. When the firing is missed, the neuron still exhibits subthreshold oscillations with sawtooth waveforms. Scatter recurrence plots of adjacent spike amplitudes (See Supplementary Figs. 35a–f) show that spike amplitude also develops irregularity and skewness as the input noise rises. The mean spike amplitude first decreases quickly with the input noise, then partially recovers at input noise higher than ~20 µApp. A similar trend is seen in the skewness of spike amplitude distribution (See Supplementary Fig. 35g).
Stochastically phase-locked firing (skipping) in a tonic VO2 active memristor neuron. a–d Tonic spike trains excited by an input d.c. current of 82.5 µA amplitude and 35 ms duration. For clarity, only the initial sections of ~3 ms duration are displayed. White noise signals with 5 µApp, 15 µApp, 25 µApp, and 50 µApp peak-to-peak values, respectively, are added to the current input to study its impact on the firing pattern and the correlation between consecutive interspike intervals (ISIs). e–h Joint interspike interval (JISI) scatter plots (aka return maps) of the spike trains shown in (a–d). Also shown are the histograms of the ISI distributions. The numbers of spikes used to generate the JISI plots are 1149, 1113, 620, and 754, respectively
Discussion
For memristor neurons to be biologically competitive, their EE needs to be > 1013 spikes/J (energy use < 0.1 pJ/spike), and their area needs to be < 100 µm2 (See Supplementary Fig. 2). We use SPICE simulations to analyze the dynamic and static power scaling of tonic VO2 neurons (See Supplementary Figs. 2, 36, 37, and Note 4). Our simulations show that at 1 fF μm−2 specific membrane capacitance (a value easily attainable by using common dielectrics), VO2 neurons show superior EE–area scaling than the best-case simulated HH cells at neuron sizes smaller than 70 μm2, and can surpass the estimated human brain EE of 1.8 × 1014 spikes/J (or 5.6 fJ/spike energy use) at neuron sizes smaller than 3 μm2. The results show that it is feasible for VO2 neurons to achieve biologically competitive EE and area.
In our case, a variety of neuronal dynamics is achieved by customizing the passive R, C elements (and circuit topology) without the need of varying VO2 device parameters. This scheme simplifies the IC design and fabrication, and memristor neurons with fixed R, C elements can exhibit spike frequency adaptation. To achieve more adaptivities in neuronal dynamics, such as an evolution from Class 1 excitability to Class 2 excitability, one may introduce passive memristors or memcapacitors42 in lieu of fixed R, C elements, if integration of memristor and memcapacitor technologies on the same substrate can be resolved.
Very recently, unsupervised all-memristor learning and pattern classification have been demonstrated using single-stage memristor neurons30. We have simulated a simple one-neuron one-synapse circuit using a VO2 model neuron and a TaOx passive memristor model3 (See Supplementary Fig. 38). Without needing to adjust the VO2 or TaOx model parameters, simulated TaOx synaptic weight (conductance) can be continuously increased or decreased by the spikes sent from the VO2 neuron. This shows the feasibility of analog potentiation and depression as the precursors for biologically plausible STDP learning. All-memristor neural networks with unsupervised causal STDP learning may provide compelling solutions to computationally hard problems such as Bayesian reasoning43 in highly parallel and energy-efficient fashion.
A potential issue for VO2 neurons is that the Mott transition at near 67 °C posts a stringent requirement for core-level and chip-level thermal management, especially if an on-chip CMOS co-processor is involved. This risk can be mitigated by introducing a dopant that may lift the IMT critical temperature (TC) higher. TC ~96 °C has been reached with 5.9 at % Ge doping in sputtered VO2 films44.
Finally, since both active memristor neurons and passive memristor synapses are fabricated from deposited thin-film structures, it is feasible in principle to vertically stack repeated pairs of memristive neurosynaptic cores to directly map to the brain cortical layers. A possible fabrication procedure for stackable integrated memristor neuron is shown in Supplementary Fig. 39. The proposed integrated neuron only requires up to three layers of interconnect metals. Passive memristor synapse array can be directly stacked on top. Such a pseudo-three-dimensional (two-and-a-half-dimensional) connectivity cannot be easily achieved using conventional CMOS technology.
Methods
VO2 device fabrication
The VO2 active memristor devices for the experimental demonstration were fabricated in house using electron-beam lithography, thin-film deposition and liftoff. Bottom electrodes of 50–600 nm width and 30 nm thickness (5 nm Ti/25 nm Pt) were patterned on silicon nitride covered silicon substrates with a liftoff process. This was followed by a blanket deposition of 100-nm-thick polycrystalline VO2 films deposited by reactive sputtering. Finally, top electrodes of 50–600 nm width and 75 nm thickness (5 nm Ti/70 nm Pt) were patterned with a liftoff process perpendicular to the bottom electrode to form the 50 × 50 nm2 to 600 × 600 nm2 metal/VO2/metal crossbar junction. The nearly-pure monoclinic VO2 phase in the sputtered oxide films is confirmed by comprehensive structural and compositional characterizations, including grazing incidence X-ray diffraction, X-ray photoemission spectroscopy, Rutherford backscattering spectroscopy, and secondary ion mass spectroscopy (See Supplementary Fig. 4). High-resolution transmission electron microscopy reveals a sharp interface between the columnar VO2 grains and the amorphous SiNx substrate without sign of interface roughening or interfacial layer. The monoclinic VO2 phase is further confirmed by selected area electron diffraction (See Supplementary Fig. 5). In contrast to ref. 5, the as-deposited VO2 films do not require electroforming, and all the tested devices showed upfront Mott-transition-induced resistive switching and negative differential resistance in their very first current-voltage sweep, as shown in Supplementary Fig. 7.
Electrical characterization
Electrical characterization of VO2 active memristor devices and VO2 neuron circuits was carried out using a probe station equipped with four source measure units, an oscilloscope, an arbitrary waveform generator, and a voltage-to-current converter (stimulus isolator). The oscilloscope voltage probes have 10 MΩ and < 4 pF input impedance. The discrete neuron circuits were constructed by connecting the two VO2 memristors on the same wafer to external resistors and capacitors through coaxial cables. Electrical characterizations of the completed VO2 devices, summarized in Supplementary Fig. 6, showed device metrics favorable for large-scale neuron ICs. Electroforming-free and volatile resistive switching are observed for almost all of the as-grown devices, as illustrated by highly uniform switching I–V traces from devices located across all the reticles (See Supplementary Fig. 7). The coefficient of variation in switching threshold voltage is 7–13% for device sizes from 50 nm to 600 nm (See Supplementary Fig. 8). The Mott-transition mechanism is supported by the temperature (T) dependence of the zero-bias conductance measured with the wafer mounted on a temperature-controlled heater stage (See Supplementary Fig. 6c). It shows a thermally activated transport in the insulating state at T < 60 °C, with a single activation energy of ~0.2 eV that is close to reported values45. At T > 60 °C, the conductance surges up as the material turns from an insulator to a metal. Typical device yield, reproducible across samples and deposition sessions, is in the range of 98–100% for the 576 devices (36 reticles and 16 devices/reticle) fabricated on a 3-inch SiNx/Si wafer, for crossbar devices having junction area from 50 × 50 nm2 to 600 × 600 nm2. The switching voltage threshold, ranging from 0.4 V to 1.3 V for all the devices tested so far, is size-dependent and tunable by the VO2 film process conditions. It also scales with the film thickness in theory, which is not yet studied experimentally. Threshold voltages of ~0.5 V or lower is competitive if compared to the supply voltage in advanced CMOS transistors. The robustness in resistive switching is demonstrated by a switching endurance of > 26.6 million pulsed-mode on/off switching cycles, without discernible change in the device I–V after the endurance test. The actual endurance number is unknown, but could be several decades higher than the instrumentation-limited measured number.
SPICE simulations
The SPICE model used to simulate the VO2 switching dynamics and neuron spiking behaviors is based on the same mathematical equations outlined in ref. 21. See Supplementary Table 3 for the values used for the VO2 material parameters. All the simulated neuron behaviors used the same VO2 device model with a cylindrical-shaped VO2 conduction channel of 56 nm in radius and 100 nm in length to match the actual VO2 crystal volume in 100 × 100 nm2 sized and 100 nm-thick nano-crossbar devices used in the experiments, and only varied the values of R, C elements. Series electrode resistance of 150–500 Ω, and parallel VO2 channel leakage resistance of 13 kΩ–17 kΩ were included in simulations to take into account their effects on the voltage drop across the memristors and the standby current in the insulating phase.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Xia, Q. et al. Memristor-CMOS hybrid integrated circuits for reconfigurable logic. Nano. Lett. 9, 3640–3645 (2009).
Khiat, A., Ayliffe, P. & Prodromakis, T. High density crossbar arrays with sub- 15 nm single cells via liftoff process only. Sci. Rep. 6, 32614 (2016).
Kim, S. et al. Experimental demonstration of a second-order memristor and its ability to biorealistically implement synaptic plasticity. Nano. Lett. 15, 2203–2211 (2015).
Wang, Z. et al. Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing. Nat. Mater. 16, 101–108 (2016).
Pickett, M. D., Medeiros-Ribeiro, G. & Williams, R. S. A scalable neuristor built with Mott memristors. Nat. Mater. 12, 114–117 (2013).
Lim, H. et al. Reliability of neuronal information conveyed by unreliable neuristor-based leaky integrate-and-fire neurons: a model study. Sci. Rep. 5, 09776 (2015).
Izhikevich, E. M. Which model to use for cortical spiking neurons? IEEE. Trans. Neural Netw. 15, 1063–1070 (2004).
Chua, L. O., Sbitnev, V. & Kim, H. Hodgkin–Huxley axon is made of memristors. Int. J. Bifur. Chaos 22, 1230011 (2012).
Burr, G. W. et al. Experimental demonstration and tolerancing of a large-scale neural network (165000 synapses) using phase-change memory as the synaptic weight element. IEEE Trans. Electron Dev. 62, 3498–3507 (2015).
Prezioso, M. et al. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 521, 61–64 (2015).
Eryilmaz, S. B. et al. Brain-like associative learning using a nanoscale non-volatile phase change synaptic device array. Front. Neurosci. 8, 205 (2014).
Choi, S., Shin, J. H., Lee, J., Sheridan, P. & Lu, W. D. Experimental demonstration of feature extraction and dimensionality reduction using memristor networks. Nano. Lett. 17, 3113–3118 (2017).
Tuma, T., Pantazi, A., Le Gallo, M., Sebastian, A. & Eleftheriou, E. Stochastic phase-change neurons. Nat. Nanotech. 11, 693–699 (2016).
Chua, L. O. & Kang, S. M. Memristive devices and systems. Proc. IEEE 64, 209–223 (1976).
Chua, L. O., Sbitnev, V. & Kim, H. Neurons are poised near the edge of chaos. Int. J. Bifurc. Chaos 22, 1250098 (2012).
Ascoli, A., Tetzla, R., Chua, L. O., Yi, W. & Williams, R. S. Memristor emulators: a note on modeling. in Advances in Memristors, Memristive Devices and Systems (Springer International Publishing AG, Switzerland, 2017).
Alexandrov, A. S., Bratkovsky, A. M., Bridle, B., Savel’ev, S. E. & Strukov, D. B. Current-controlled negative differential resistance due to Joule heating in TiO2. Appl. Phys. Lett. 99, 202104 (2011).
Ovshinsky, S. R. Reversible electrical switching phenomena in disordered structures. Phys. Rev. Lett. 21, 1450 (1968).
Czubatyj, W. & Hudgens, S. J. Thin-film ovonic threshold switch: its operation and application in modern integrated circuits. Electron. Mater. Lett. 8, 157–167 (2012).
Ielmini, D. Threshold switching mechanism by high-field energy gain in the hopping transport of chalcogenide glasses. Phys. Rev. B 78, 035308 (2008).
Pickett, M. D. & Williams, R. S. Sub-100 fJ and sub-nanosecond thermally driven threshold switching in niobium oxide crosspoint nanodevices. Nanotechnol 23, 215202 (2012).
Yi, W., Oh, T. C., Crowell, J. A., Flores, E. A. & King, P. A. Low-voltage threshold switch devices with current-controlled negative differential resistance based on electroformed vanadium oxide layer. US Pat. Appl. No. 15/417, 049 (2017).
Crane, H. D. The neuristor. IRE Trans. Elect. Comput. 9, 370–371 (1960).
Crane, H. D. Neuristor—a novel device and system concept. Proc. IRE 50, 2048–2060 (1962).
Nagumo, J., Arimoto, S. & Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. IRE 50, 2061–2070 (1962).
Wilamowski, B. M., Czarnul, Z. & Bialko, M. Novel inductorless neuristor line. Electron. Lett. 11, 355–356 (1975).
Moon, K. et al. High density neuromorphic system with Mo/Pr0.7Ca0.3MnO3 synapse and NbO2 IMT oscillator neuron. In IEEE International Electron Devices Meeting (IEDM) (IEEE, Washington, DC, USA, 2015) https://doi.org/10.1109/IEDM.2015.7409721.
Farhat, N. H. & Eldefrawy, M. H. Bifurcating neuron: characterization and dynamics. In Proc. Photonics for Computers, Neural Networks, and Memories . Vol 1773, 23–35 (SPIE, San Diego, CA, 1992).
Stoliar, P. et al. A leaky-integrate-and-fire neuron analog realized with a Mott insulator. Adv. Funct. Mater. 27, 1604740 (2017).
Wang, Z. et al. Fully memristive neural networks for pattern classification with unsupervised learning. Nat. Electron. 1, 137–145 (2018).
Hodgkin, A. L. The local electric changes associated with repetitive action in a non-medullated axon. J. Physiol. 15, 165–181 (1948).
Schultz, W. Predictive reward signal of dopamine neurons. J. Neurophysiol. 80, 1–27 (1998).
Meng, X., Huguet, G. & Rinzel, J. Type III excitability, slope sensitivity and coincidence detection. Discret. Contin. Dyn. Syst. A 32, 2729–2757 (2012).
Rothman, J. S. M. The roles potassium currents play in regulating the electrical activity of ventral cochlear nucleus neurons. J. Neurophysiol. 89, 3097–3113 (2003). P. B.
Cassidy, A. S et al. Cognitive computing building block: A versatile and efficient digital neuron model for neurosynaptic cores. In Proc. International Joint Conference on Neural Networks (IJCNN) (IEEE, Dallas, TX, USA, 2013).
Rinzel, J. E. B. Analysis of neural excitability and oscillations. in Methods in neuronal modeling (MIT Press, Cambridge, MA, 1989).
Izhikevich, E. M. Neural excitability, spiking and bursting. Int. J. Bifur. Chaos 10, 1171–1266 (2000).
FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1, 445–466 (1961).
Segundo, J. P., Altshuler, E., Stiber, M. & Garfinkel, A. Periodic inhibition of living pacemaker neurons. I. Locked, intermittent, messy and hopping behaviors. Int. J. Bifur. Chaos 1, 549–581 (1991).
Fitzurka, M. A. & Tam, D. C. A joint interspike interval difference stochastic spike train analysis: detecting local trends in the temporal firing patterns of single neurons. Biol. Cybern. 80, 309–326 (1999).
Longtin, A. H. K. Encoding with bursting, subthreshold oscillations, and noise in mammalian cold receptors. Neural Comput. 8, 215–255 (1996).
Di Ventra, M., Pershin, Y. V. & Chua, L. O. Circuit elements with memory: memristors, memcapacitors, and meminductors. Proc. IEEE 97, 1717–1724 (2009).
Dagum, P. & Luby, M. Approximating probabilistic inference in Bayesian belief networks is NP-hard. Artif. Intell. 60, 141–153 (1993).
Krammer, A. et al. Elevated transition temperature in Ge doped VO2 thin films. J. Appl. Phys. 122, 045304 (2017).
Beaumont, A., Leroy, J., Orlianges, J.-C. & Crunteanu, A. Current-induced electrical self-oscillations across out-of-plane threshold switches based on VO2 layers integrated in crossbars geometry. J. Appl. Phys. 115, 154502 (2014).
Acknowledgements
This work was supported by HRL Laboratories, LLC. We acknowledge P. A. King and S. J. Kim for fabrication and electrical test support, and T. C. Oh for electrical tests at the early stage of this project.
Author information
Authors and Affiliations
Contributions
W.Y. conceived and simulated the devices and circuits, designed the experiments, and supervised the project. W.Y., S.K.L., X.B., J.A.C. and E.A.F. fabricated the devices. W.Y. and K.K.T. designed the electrical test setups and carried tests. W.Y. wrote the manuscript. K.K.T. contributed to analysis of the results. All authors commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yi, W., Tsang, K.K., Lam, S.K. et al. Biological plausibility and stochasticity in scalable VO2 active memristor neurons. Nat Commun 9, 4661 (2018). https://doi.org/10.1038/s41467-018-07052-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-07052-w
This article is cited by
-
Memristors on ‘edge of chaos’
Nature Reviews Electrical Engineering (2024)
-
Collective dynamics and long-range order in thermal neuristor networks
Nature Communications (2024)
-
Computational elements based on coupled VO2 oscillators via tunable thermal triggering
Nature Communications (2024)
-
Mott neurons with dual thermal dynamics for spatiotemporal computing
Nature Materials (2024)
-
Crossmodal sensory neurons based on high-performance flexible memristors for human-machine in-sensor computing system
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.