Abstract
Due to their strong dependence on local atonic environments, NMR chemical shifts are among the most powerful tools for strucutre elucidation of powdered solids or amorphous materials. Unfortunately, using them for structure determination depends on the ability to calculate them, which comes at the cost of high accuracy first-principles calculations. Machine learning has recently emerged as a way to overcome the need for quantum chemical calculations, but for chemical shifts in solids it is hindered by the chemical and combinatorial space spanned by molecular solids, the strong dependency of chemical shifts on their environment, and the lack of an experimental database of shifts. We propose a machine learning method based on local environments to accurately predict chemical shifts of molecular solids and their polymorphs to within DFT accuracy. We also demonstrate that the trained model is able to determine, based on the match between experimentally measured and ML-predicted shifts, the structures of cocaine and the drug 4-[4-(2-adamantylcarbamoyl)-5-tert-butylpyrazol-1-yl]benzoic acid.
Similar content being viewed by others
Introduction
Solid-state nuclear magnetic resonance (NMR) spectroscopy is among the most powerful methods for determining the atomic-level structure and dynamics of powdered and amorphous solids. Notably, solid-state NMR directly probes the local atomic environments and thus allows for characterization without the need for long-range order. This has led to its broad use today in many fields including for instance materials and pharmaceutical chemistry. In the latter the determination of structure and packing is essential to elaborate structure–property relations for formulations in the drug development process.
A revolution in solid-state NMR has occurred with the introduction of accurate methods to calculate chemical shifts1,2,3, in particular using plane wave density functional theory (DFT) methods developed for periodic systems based on the projected augmented wave (PAW)/gauge including PAW (GIPAW) approach4,5,6. This has enabled very rapid development of chemical shift-based NMR crystallography, which is now widely used to validate structures of molecular solids and identify known polymorphs7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26, or more recently in combination with crystal structure prediction (CSP) protocols, to determine de novo crystal structures from powders27,28,29,30,31,32. Recent studies also suggest that the structural accuracy of chemical shift-based solid-state NMR crystallography is at least comparable with more traditional methods, such as single crystal X-ray diffraction33.
The power of the method arises from the fact that plane wave DFT with the GIPAW method is accurate enough to reproduce the exquisite sensitivity of chemical shifts to changes in local atomic environments. However, this approach also has severe limitations. The cubic scaling of the computational cost with system size prevents the application to larger and more complex crystals, or nonequilibrium structures. If one wanted to use more accurate ab initio calculations, the expense is prohibitive.
Machine learning (ML) is emerging as a new tool in many areas of chemical and physical science, and potentially provides a method to bridge the gap between the need for high accuracy calculations and limited computational power34,35,36,37,38. Notably, prediction of chemical shifts for the specific case of proteins in solution using methods based on large experimental databases, using traditional39,40,41,42,43,44,45,46 or machine learning approaches47,48,49, have been considerably successful in predicting shifts based on local sequence and structural motifs, and are widely used today. While there are some examples of machine learned experimental and ab-initio chemical shifts of liquid and gas phase molecules50,51,52,53,54, to date there is only one example of machine learning being applied to calculations of chemical shifts in solids, which deals with the specific case of silicas55. Molecular solids are characterized by the combinatorial complexity and diversity of organic chemistry, the subtle dependence on conformations, and the long- and short-range effects of crystal packing, which leads to a considerably broader range of chemical environments and possible chemical shieldings than found, e.g., in proteins. All of these aspects, compounded by the fact that there is no extensive database of experimental chemical shifts for molecular solids, make this class of systems particularly challenging for machine learning.
Here, we develop a machine learning framework to predict chemical shifts in solids which is based on capturing the local environments of individual atoms, and which makes it well suited for the prediction of such local properties. The protocol is schematically illustrated in Fig. 1. In the absence of a database of experimental shifts, and given that experiments alone do not provide a 1:1 mapping between chemical shifts and a single atomic configuration, we train the model on DFT calculated chemical shifts for structures taken from the Cambridge Structural Database (CSD)56 chosen to be as diverse as possible, and then show that the method can predict chemical shifts in a test set with R2 coefficients between the chemical shifts calculated with DFT and with ML of 0.97 for 1H, 0.99 for 13C, 0.99 for 15N, and 0.99 for 17O, corresponding to root-mean-square-errors (RMSEs) of 0.49 ppm for 1H, 4.3 ppm for 13C, 13.3 ppm for 15N, and 17.7 ppm for 17O. Predicting the chemical shifts for a polymorph of cocaine, with 86 atoms in the unit cell, using the ML method takes less than a minute of central processing unit (CPU) time, thus reducing the computational time by a factor of between 5 to 10 thousand, without any significant loss in accuracy as compared to DFT.
Most significantly, even though no experimental shifts were used in training, we show that the model has sufficient accuracy to be used in a chemical shift-driven NMR crystallography protocol to correctly determine, based on the match between experimentally measured and ML-predicted shifts, the correct structure of cocaine, and the drug 4-[4-(2-adamantylcarbamoyl)-5-tert-butylpyrazol-1-yl]benzoic acid (AZD8329). We also show that it is possible to calculate the NMR spectra of very large molecular crystals. For this we calculate the chemical shifts of six structures from the CSD with between 768 and 1584 atoms in the unit cells.
Results
Training and validation using DFT calculated shifts of known crystal structures
Machine learning models should by definition be trained on the property that is to be predicted. Here, that corresponds to experimental chemical shifts. However, for molecular solids there are currently only around 100 compounds with reliable crystal structures and for which assigned 1H or 13C shifts have been published, despite the rapidly increasing activity of NMR in crystal structure determination. This is at least an order of magnitude too few structures to hope to determine a reliable prediction model. In this light, we note that today GIPAW chemical shift calculations can accurately reproduce experimental shifts13,57. Thus we propose to develop a machine learning model to predict chemical shifts by training the model on a database made up of GIPAW calculated shifts from a large and diverse set of reference crystal structures. If the model can then accurately predict GIPAW chemical shifts, we hypothesize that it should also be in good agreement with experimental shifts. We also note in this context that even if there was a database of experimental shifts, there would be a challenge to machine learning related to the fact that the experiment reports on structures that include dynamics or distributions, making the connection between shifts and environments ambiguous. Learning using GIPAW calculated shifts does not suffer from this problem.
The approach we take to predicting chemical shifts in molecular solids is illustrated in Fig. 1. We use the Gaussian process regression (GPR) framework58 to predict the chemical shift of a new atomic configuration based on a statistical model that identifies the correlations between structure and shift for a reference set of training configurations, for which the chemical shifts have been determined by a GIPAW DFT calculation. The predicted chemical shielding for a given atom is given by
where X and \({X}_i\) correspond, respectively to a description of the chemical environment of the atom for which we are making a prediction, and that of one of the training configurations. The weights \(\alpha _i\) are obtained by requiring that Eq. (1) is consistent with the values computed by DFT for the reference structures. The essential ingredient that differentiates one GPR-based framework from another is the kernel function \(k\left( {{X},{X}_i} \right)\), which describes and assesses the similarity between atomic environments, and provides basis functions to approximate the target properties.
Here, our model relies on the smooth overlap of atomic positions (SOAP) kernel59,60, in which any atomic environment is represented as a three-dimensional neighborhood density given by a superposition of Gaussians, one centered at each of the atom positions in a spherical neighborhood within a cut-off radius rc from the core atom. This framework, combined with GPR, has been used to model the stability and properties of a number of different systems35,59,60, and has been extended to the prediction of tensorial properties61. We can see that this choice of kernel should be particularly well adapted to predicting chemical shifts, since it describes the local environments around each atom without any simplification, and this is indeed what the chemical shift also probes, as it is determined by the screening of the nucleus from the main magnetic field by the electron density at the nucleus. Note that it should be possible to tune and train other ML methods to accurately predict chemical shifts of molecular crystals. While these possibilities will be explored in future work, the model we present here is already accurate enough to substitute for DFT calculations in chemical shift-based NMR crystallography.
As shown in Fig. 1, in the absence of an experimental database of shifts the model is developed by using a reference training set of structures for which chemical shifts are calculated with GIPAW DFT. To obtain a model which is robust and general, the training set should be as large, as reliable, and as diverse as possible. We first extract from the CSD a large set of about 61,000 structures, corresponding to all the structures in the CSD with fewer than 200 atoms, in order to make DFT chemical shift calculation affordable, and containing C and H and allowing for N and/or O, to reduce the space to organic molecular crystals (we call this set CSD-61k, see Supplementary Methods for details on the structures selection). Given that performing a GIPAW calculation for all of these structures would be prohibitively demanding, we then select a random subset of 500 structures (CSD-500, see Supplementary Note 1 and Supplementary Dataset 2) that are representative of the chemical diversity in the CSD, and we use it to test the accuracy of our model. For cross-validation and training, instead, we select 2000 structures (corresponding to about 185,000 atomic environments) out of the CSD-61k using a farthest point sampling algorithm62,63 (CSD-2k, see Supplementary Note 2 and Supplementary Dataset 1). This step ensures near-uniform sampling of the conformational space, improving the quality of the model when using a relatively small number of reference calculations.
To avoid including spurious environments in the model, e.g., environments which might not be well described by DFT, we also automatically detect and discard from the training set atomic environments with values of the DFT calculated shifts that are anomalous based on a cross-validation procedure described in the Supplementary Methods. Note that using this unbiased statistical analysis we detected only a small fraction of environments as outliers (e.g., 211 out of 76,214 for 1H, or 0.3%). This is discussed in detail in the Supplementary Methods. We observe that the performance of the model degrades noticeably if one does not use this procedure. This pruning as well as the parameter optimization procedure, described below, were done exclusively using cross-validation on the CSD-2k set. (Notably the test sets were not subject to any curation.)
In order to reduce the computational cost of the training and testing procedures we then finally remove from the training set all the symmetrically equivalent environments. In case of 1H, this reduced the size of the training set from 70,000 to about 35,000 different atomic environments. (Details of the selection method and the members of the different sets used are given in the Supplementary Methods and Supplementary Note 3.)
All the atomic positions of the structures in the training and testing sets were relaxed with DFT, using the Quantum Espresso suite64,65,66, prior to calculation of the chemical shieldings using the GIPAW DFT method4,5. Note that the DFT relaxation ensures “reasonable” geometries will be used even for crystal structures containing errors (e.g., improbable 1H positions). Parameters for the DFT calculations are given in the Supplementary Methods. The calculated chemical shieldings σ are converted to the corresponding chemical shifts δ through the relationship δ = σref − σ. Here, we used a σref of 30.8 ppm (for 1H) and 169.5 ppm (for 13C), found through linear regression between the calculated and experimental chemical shifts for cocaine.
Figure 2 shows the chemical shift error between the DFT calculations and the ML predictions for the CSD-500 set, which is representative of the expected accuracy for the entire CSD-61k. The figure shows the overall prediction accuracy for 1H chemical shifts as RMSE in ppm between the shifts calculated with DFT and with the protocol described above, which we refer to in the following as ShiftML, as a function of the cut-off radius (rc) and as a function of the number of training structures included from CSD-2k. The effect of the different cut-off radii is clearly visible. For example, for rc = 2 Å the prediction error for a small training set (<10 structures or <100 atomic environments) can be smaller than for the larger radii, but does not improve significantly with increasing size of the training set. On the contrary, for rc = 7 Å we observe a relatively large prediction error for a small training set, but even with 2000 structures (35,000 environments), the prediction error is still decreasing. A similar behavior is observed for the prediction errors of the 13C, 15N, and 17O chemical shifts (see Supplementary Figures 5–8).
1H chemical shift prediction error of the trained model for the CSD-500 set. The RMSE prediction error between chemical shifts calculated with ShiftML and GIPAW DFT is shown for different local environment cut-off radii, and for the multi-kernel (labeled as msk), as a function of the training set size
The observed differences in the behavior of the prediction error with respect to rc clearly indicates the influence of the different extents of the local environment on the chemical shift. Short-range interactions are sufficient to explain the rough order of magnitude of the shift, but long-range interactions are required to learn about the higher order influences of next-nearest neighbors on shifts. However, for long-range interactions, a much larger number of environments is needed in order to determine the correlation between environment and shift.
We exploit these differences to generate a combined SOAP kernel consisting of a linear combination of the single local environment kernels35, with weightings of 256 (rc = 2 Å), 128 (rc = 3 Å), 32(rc = 4 Å), 8 (rc = 5 Å and rc = 6 Å), and 1 (rc = 7 Å). This weighting was determined by rough optimization around values inspired by previous experience35, and by cross-validation on the CSD-2k training set (as described in the Supplementary Methods). It is clear that learning with the combined kernel leads consistently to lower prediction errors than any of the single kernels, although the improvement in performance varies between nuclei (see Supplementary Figures 5–8).
Figure 3a–d shows correlation plots between 1H, 13C, 15N, and 17O chemical shifts calculated by DFT and by ShiftML for the CSD-500 set trained on the whole CSD-2k combined kernel. Using the combined kernel, we reach an error between ShiftML and DFT calculated chemical shifts of 0.49 ppm for 1H (4.3 ppm for 13C, 13.3 ppm for 15N, and 17.7 ppm for 17O). This is very comparable with reported DFT chemical shift accuracy for 1H of 0.33–0.43 ppm13,57, while requiring a fraction of the computational time and cost: less than 1 CPU minute compared to ~62–150 CPU hours for DFT chemical shift calculation on structures containing 86 atoms (around 350 valence electrons) (see Supplementary Figure 4). For the other nuclei, the ML accuracy is slightly lower than reported values (1.9–2.2 ppm for 13C, 5.4 ppm for 15N, and 7.2 ppm for 17O)13,57, which is not surprising as there are (currently) significantly fewer training environments for the heteronuclei than for 1H.
The R2 coefficients between the chemical shifts calculated with DFT and with ShiftML are 0.97 for 1H, 0.99 for 13C, 0.99 for 15N, and 0.99 for 17O.
Note that the CSD-500 set used for testing is selected randomly from CSD-61k and not curated. Indeed, we find that many of the atomic environments in the CSD-500 set with a relatively high prediction RMSE possess either unusual cavities inside their crystal structure, possibly indicating an organic cage surrounding noncrystalline solvent or other atoms, or exhibit strongly delocalized π-bonding networks. While there is no theoretical reason preventing the machine learning model from correctly describing such environments, they are rare and not well represented within the training set. CSD-500 thus constitutes a fairly demanding test set.
Predicting shifts for polymorphs
Having evaluated the power of the trained model to predict the diverse CSD-500 set, we now look at the capacity to predict potentially subtler differences by looking at a set of polymorphs of a given structure. Figure 4 shows the correlation between the 1H shifts calculated by GIPAW DFT and by ShiftML for 30 polymorphs of cocaine and 14 polymorphs of AZD8329, all of which were previously generated with a CSP procedure16,27. The figure clearly shows that ShiftML is able to accurately predict the differences in 1H chemical shift for different polymorphs.
Comparison of predictions from ShiftML and GIPAW DFT for polymorphs of cocaine and AZD8329. a Histogram showing the distribution of the differences between 1H chemical shifts calculated with GIPAW and with ShiftML for the polymorphs of cocaine (blue), and the polymorphs of AZD8329 (orange). b Scatterplot showing the correlation between 1H chemical shifts calculated with GIPAW and ShiftML for cocaine (blue) and AZD8329 (orange). The black line indicates a perfect correlation
We find a chemical shift prediction error (RMSE) between GIPAW DFT and ShiftML for 1H for the cocaine polymorphs of 0.37 ppm and for AZD8329 of 0.46 ppm. Note that these values are slightly less than for the CSD-500 set, which might be expected when looking at these two fairly typical organic structures, and suggesting that the randomly selected CSD-500 indeed provides a good overall benchmark.
Note that for these cases the DFT structure optimization and GIPAW chemical shift calculation were done with a different DFT program (CASTEP)67, which suggests that ShiftML is robust with respect to small deviations from the fully optimized structures. (As shown in the Supplementary Figure 2, performing the prediction using Quantum Espresso consistently leads to a comparable prediction accuracy.)
For the heteronuclei we obtain an RMSE between GIPAW DFT and ShiftML for cocaine of 3.8 ppm for 13C, 12.1 ppm for 15N, and 15.7 ppm for 17O. For AZD8329 the 15N and 17O RMSEs are proportionally larger (17.7 and 54.7 ppm), and we attribute this to the fact that the molecule contains a rather unusual C–O…H–N /C–O…H–O H-bonded dimer structure, for which the learning is thus even sparser than for the heteronuclei in general. To illustrate the unusual nature of this motif, we note that the calculated 17O shifts using DFT also change by up to 50 ppm for structures relaxed either by the CASTEP protocol used in ref. 30, or the Quantum Espresso protocol used here (the RMSE between ML and DFT for the Quantum Espresso relaxed structures is reduced to 10.9 and 11.5 ppm for 15N and 17O, respectively). The RMSE of 4.0 ppm for 13C for AZD8329 is in line with the other systems.
Predicting experimental shifts and structure determination
Further, the significance of the method is illustrated by comparison to experimentally measured shifts. This comparison is particularly important since the training protocol did not involve any experimentally measured chemical shifts. We find that the predicted shifts are accurate enough to allow crystal structure determination for both cocaine and AZD8329 from powder samples in a chemical shift-driven NMR crystallography approach.
Figure 5a, b shows the correlation between experimentally measured 1H chemical shifts and the 1H chemical shifts calculated by ShiftML for crystal structures of the six molecules shown in Fig. 6 (numerical values of the experimental chemical shifts, the crystal structures, and the shifts calculated with ShiftML are given in the Supplementary Methods and Supplementary Dataset 8). The comparison between experimental and calculated 1H chemical shifts for all crystal structures (for a total of 68 shifts) gives an error (RMSE) of 0.39 ppm and a R2 coefficient of 0.99. This compares very favorably to the equivalent agreement found between GIPAW DFT and experiment which for this set of structures is a RMSE of 0.38 ppm.
Comparison of ShiftML to experimentally measured shifts. a Histogram showing the distribution of differences between experimentally measured 1H chemical shifts and 1H chemical shifts calculated with ShiftML for six different crystal structures (see Supplementary Methods for the structures and numerical values of the shifts). b Scatterplot showing the correlation between these experimentally measured 1H chemical shifts and shifts calculated with ShiftML. c, d Comparison between calculated and experimental 1H chemical shifts for the most stable structures obtained with CSP for cocaine (c) and AZD8329 (d). For each candidate structure an aggregate RMSE is shown between experimentally measured shifts and shifts calculated using either GIPAW (blue) or ShiftML (red). The gray zones represent the confidence intervals of the GIPAW DFT 1H chemical shift RMSD, as described in the text13, and candidates (in c and d) that have RMSEs within this range would be determined as correct crystal structures using a chemical shift-driven solid-state NMR crystallography protocol
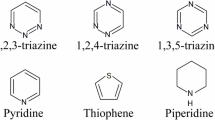
Chemical structures of the six molecules used to evaluate the correlation between experimentally measured 1H chemical shifts and the shifts calculated by ShiftML. The structures are given as AZD8329 (a), theophylline (b), cocaine (c), uracil (d), 3,5-dimethylimidazole and 4,5-dimethylimidazole (e) and naproxen (f)
Figure 5c, d shows in blue the RMSE between DFT calculated and experimental 1H chemical shifts for the 30 polymorphs predicted by CSP to have the lowest energy for cocaine and the 14 cis polymorphs of AZD8329. For both molecules the only structure in agreement with the GIPAW DFT calculations, to below a 1H DFT chemical shift confidence interval of 0.49 ppm13, is the correct crystal structure. In the same plots we overlay the result where the experimental shifts are now compared to shifts predicted with ShiftML. Note that the RMSE between experiment and the predicted chemical shifts follows the same trends as for the DFT calculated shifts, and that here again the only structures below the confidence interval of 0.49 ppm are the two correct crystal structures. Note, that the cut-off of 0.49 ppm with respect to experiment has been evaluated for GIPAW DFT chemical shifts13,57 and to rigorously repeat the CSP procedure for the ML method, the accuracy should be re-evaluated using more extensive benchmarking of ShiftML to experiment, which will be the subject of further work.
Predicting shifts for large structures
Finally, we note that the accuracy of the method does not depend on the size of the structure, and that the prediction time is linear in the number of atoms. For the structures we calculate here the prediction time actually appears nearly constant, because it is dominated by the loading time of the reference SOAP vector (see Fig. 7a). We have used this method to calculate the NMR spectra (shown in Fig. 7b–g) for six structures from the CSD having among the largest numbers of atoms per unit cell (containing only H, C, N, and O), with between 768 and 1584 atoms per unit cell. (See Supplementary Figure 10 for the chemical formula). The values of the predicted chemical shifts are given as CSD-6 in the Supplementary Note 4. Figure 7a shows the comparison between the GIPAW calculation time and the required ML prediction time. We estimate that the whole calculation would require around 16 CPU years by GIPAW. ShiftML requires less than 6 CPU minutes to calculate the shifts for all the compounds.
Chemical shift calculation times and large structures. a DFT GIPAW calculation time (blue) and ShiftML prediction time (turquoise) for different system sizes. The GIPAW DFT calculation time for the six large structures (orange) is estimated from a cubic dependence on the number of valence electrons in the structure (see Supplementary Methods). b-g 3D-shemes and 1H NMR spectra predicted with ShiftML, of the six large molecular crystals with CSD refcodes: b CAJVUH69, Natoms = 828, c RUKTOI70, Natoms = 768, d EMEMUE71, Natoms = 860, e GOKXOV72, Natoms = 945, f HEJBUW73, Natoms = 816, and g RAYFEF74, Natoms = 1584
Discussion
We have presented a ML model based on local environments to predict chemical shifts of molecular solids containing HCNO to within current DFT accuracy. The R2 coefficients between the chemical shifts calculated with DFT and with ShiftML are 0.97 for 1H, 0.99 for 13C, 0.99 for 15N, and 0.99 for 17O. The approach allows the calculation of chemical shifts for structures with ~100 atoms in less than 1 min, reducing the computational cost of chemical shift predictions in solids by a factor of between five to ten thousand compared to current DFT chemical shift calculations, and thereby relieves a major bottleneck in the use of calculated chemical shifts for structure determination in solids.
Far from being just a benchmark of a machine-learning scheme, the method is accurate enough to be used to determine structures by comparison to experimental shifts in chemical shift-based NMR crystallography approaches to structure determination, as shown here for cocaine and AZD8329. The ML model only scales linearly with the number of atoms and, for the prediction of individual structures, is dominated by a constant I/O overhead. Here it allows the calculation of chemical shifts for a set of six structures with between 768 and 1584 atoms in their unit cells in less than 6 min (an acceleration of a factor 106 for the largest structure).
The accuracy of the method is likely to increase further with the size of the training set, and subsequently with the future evolution of the accuracy of the method used to calculate the reference shifts used in training (here DFT), or by using experimental shifts if a large enough set were available. A web version based on the protocol described here is publicly available at http://shiftml.epfl.ch.
The model used here can easily be extended to organic solids including halides or other nuclei, and to network materials such as oxides, and these will be the subject of further work.
Methods
Computational details
For the SOAP kernels59,60, each atomic environment is represented as a three-dimensional neighborhood density given by a superposition of Gaussians, one centered at each of the atom positions in a spherical neighborhood within a cut-off radius rc from the core atom. The Gaussians have a variance \(\varsigma\)2, and a separate density is built for each atomic species. The kernel is then constructed as the symmetrized overlap between the amplitudes representing X and X′. This degree of overlap thus measures the similarity between the environments X and X′.
The SOAP and GPR parameters are given in the Supplementary Methods. SOAP-based structural kernels contain several adjustable hyper-parameters, which are discussed in ref. 60. However, we have not systematically explored the full parametric space here, instead we chose reasonable values of the parameters without extensive fine-tuning, based on previous experience35 and with some optimization by cross-validation on the CSD-2k training set (see Supplementary Methods for details). We also combine kernels computed for different cutoff radii to capture the contributions to shifts from different length scales35, as is described in detail above. The calculations of the local environment, the similarity kernel and the weighted correlations were done using the glosim2 package68.
In summary, the Supplementary Information contains details on the structure selection, the crystal structure prediction procedure, the DFT calculations, the GPR method, the SOAP kernels, the FPS algorithm, the detection procedure of unusual environments, the NMR crystallography approach, the DFT calculation time estimates, the prediction parameters optimization, the learning curves and the evaluation curves for 1H, 13C, 15N, and 17O. Additionally we also provide the ShifML predicted and GIPAW chemical shieldings for all cocaine and AZD8329 polymorphs as well as the geometries, the assigned experimental chemical shifts and the chemical shifts calculated with GIPAW DFT and ShiftML for the comparison to experimentally measured shifts. The Supplementary Information also contains the chemical formula and predicted chemical shieldings of the CSD-6 set predicted with ShiftML, the Refcodes for CSD-2k and CSD-500 and the relaxed geometries and GIPAW DFT calculated chemical shifts of all investigated crystal structures.
Code availability
The machine learning code to calculate the SOAP environments, the kernels, and the chemical shifts is called glosim2, and is publicly available at https://github.com/cosmo-epfl/glosim2. The DFT codes used to optimize geometry and calculate chemical shifts are available from the corresponding developers.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information. In particular, all crystallographic structures used are referenced in the Supplementary Information and are publicly available at the Cambridge Structural Database. The relaxed crystal structures with the chemical shieldings calculated by GIPAW DFT and ShiftML are included in the supplementary information files and in the Supplementary Datasets.
References
Dedios, A. C., Pearson, J. G. & Oldfield, E. Secondary and tertiary structural effects on protein nmr chemical-shifts—an abinitio approach. Science 260, 1491–1496 (1993).
Facelli, J. C. & Grant, D. M. Determination of molecular symmetry in crystalline naphthalene using solid-state NMR. Nature 365, 325–327 (1993).
Sebastiani, D. & Parrinello, M. A new ab-initio approach for NMR chemical shifts in periodic systems. J. Phys. Chem. A 105, 1951–1958 (2001).
Pickard, C. J. & Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 63, 245101 (2001).
Yates, J. R., Pickard, C. J. & Mauri, F. Calculation of NMR chemical shifts for extended systems using ultrasoft pseudopotentials. Phys. Rev. B 76, 024401 (2007).
Blochl, P. E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 50, 17953–17979 (1994).
Ochsenfeld, C., Brown, S. P., Schnell, I., Gauss, J. & Spiess, H. W. Structure assignment in the solid state by the coupling of quantum chemical calculations with NMR experiments: a columnar hexabenzocoronene derivative. J. Am. Chem. Soc. 123, 2597–2606 (2001).
Harris, R. K. NMR crystallography: the use of chemical shifts. Solid State Sci. 6, 1025–1037 (2004).
Harper, J. K. & Grant, D. M. Enhancing crystal-structure prediction with NMR tensor data. Cryst. Growth Des. 6, 2315–2321 (2006).
Harris, R. K. Applications of solid-state NMR to pharmaceutical polymorphism and related matters. J. Pharm. Pharmacol. 59, 225–239 (2007).
Othman, A., Evans, J. S., Evans, I. R., Harris, R. K. & Hodgkinson, P. Structural study of polymorphs and solvates of finasteride. J. Pharm. Sci. 96, 1380–1397 (2007).
Salager, E., Stein, R. S., Pickard, C. J., Elena, B. & Emsley, L. Powder NMR crystallography of thymol. Phys. Chem. Chem. Phys. 11, 2610–2621 (2009).
Salager, E. et al. Powder crystallography by combined crystal structure prediction and high-resolution 1H solid-state NMR spectroscopy. J. Am. Chem. Soc. 132, 2564–2566 (2010).
Webber, A. L., Emsley, L., Claramunt, R. M. & Brown, S. P. NMR crystallography of campho[2,3-c]pyrazole (Z’ = 6): combining high-resolution 1H-13C solid-state MAS NMR spectroscopy and GIPAW chemical-shift calculations. J. Phys. Chem. A 114, 10435–10442 (2010).
Dudenko, D. et al. A strategy for revealing the packing in semicrystalline pi-conjugated polymers: crystal structure of bulk poly-3-hexyl-thiophene (P3HT). Angew. Chem. Int. Ed. Engl. 51, 11068–11072 (2012).
Baias, M. et al. Powder crystallography of pharmaceutical materials by combined crystal structure prediction and solid-state 1H NMR spectroscopy. Phys. Chem. Chem. Phys. 15, 8069–8080 (2013).
Pawlak, T., Jaworska, M. & Potrzebowski, M. J. NMR crystallography of alpha-poly(l-lactide). Phys. Chem. Chem. Phys. 15, 3137–3145 (2013).
Santos, S. M., Rocha, J. & Mafra, L. NMR crystallography: toward chemical shift-driven crystal structure determination of the beta-lactam antibiotic amoxicillin trihydrate. Cryst. Growth Des. 13, 2390–2395 (2013).
Ludeker, D. & Brunklaus, G. NMR crystallography of ezetimibe co-crystals. Solid. State Nucl. Magn. Reson. 65, 29–40 (2015).
Paluch, P., Pawlak, T., Oszajca, M., Lasocha, W. & Potrzebowski, M. J. Fine refinement of solid state structure of racemic form of phospho-tyrosine employing NMR crystallography approach. Solid. State Nucl. Magn. Reson. 65, 2–11 (2015).
Watts, A. E., Maruyoshi, K., Hughes, C. E., Brown, S. P. & Harris, K. D. M. Combining the advantages of powder X-ray diffraction and NMR crystallography in structure determination of the pharmaceutical material cimetidine hydrochloride. Cryst. Growth Des. 16, 1798–1804 (2016).
Widdifield, C. M., Robson, H. & Hodgkinson, P. Furosemide’s one little hydrogen atom: NMR crystallography structure verification of powdered molecular organics. Chem. Commun. 52, 6685–6688 (2016).
Mali, G. Ab initio crystal structure prediction of magnesium (poly)sulfides and calculation of their NMR parameters. Acta Crystallogr. Sect. C Struct. Chem. 73, 229–233 (2017).
Harris, R. K., Joyce, S. A., Pickard, C. J., Cadars, S. & Emsley, L. Assigning carbon-13 NMR spectra to crystal structures by the INADEQUATE pulse sequence and first principles computation: a case study of two forms of testosterone. Phys. Chem. Chem. Phys. 8, 137–143 (2006).
Mifsud, N., Elena, B., Pickard, C. J., Lesage, A. & Emsley, L. Assigning powders to crystal structures by high-resolution (1)H-(1)H double quantum and (1)H-(13)C J-INEPT solid-state NMR spectroscopy and first principles computation. A case study of penicillin G. Phys. Chem. Chem. Phys. 8, 3418–3422 (2006).
Heider, E. M., Harper, J. K. & Grant, D. M. Structural characterization of an anhydrous polymorph of paclitaxel by solid-state NMR. Phys. Chem. Chem. Phys. 9, 6083–6097 (2007).
Baias, M. et al. De novo determination of the crystal structure of a large drug molecule by crystal structure prediction-based powder NMR crystallography. J. Am. Chem. Soc. 135, 17501–17507 (2013).
Fernandes, J. A., Sardo, M., Mafra, L., Choquesillo-Lazarte, D. & Masciocchi, N. X-ray and NMR crystallography studies of novel theophylline cocrystals prepared by liquid assisted grinding. Cryst. Growth Des. 15, 3674–3683 (2015).
Leclaire, J. et al. Structure elucidation of a complex CO2-based organic framework material by NMR crystallography. Chem. Sci. 7, 4379–4390 (2016).
Selent, M. et al. Clathrate structure determination by combining crystal structure prediction with computational and experimental (129) Xe NMR spectroscopy. Chemistry 23, 5258–5269 (2017).
Widdifield, C. M. et al. Does Z’ equal 1 or 2? Enhanced powder NMR crystallography verification of a disordered room temperature crystal structure of a p38 inhibitor for chronic obstructive pulmonary disease. Phys. Chem. Chem. Phys. 19, 16650–16661 (2017).
Nilsson Lill, S. O. et al. Elucidating an amorphous form stabilization mechanism for tenapanor hydrochloride: crystal structure analysis using X-ray diffraction, NMR crystallography, and molecular modeling. Mol. Pharm. 15, 1476–1487 (2018).
Hofstetter, A. & Emsley, L. Positional variance in NMR crystallography. J. Am. Chem. Soc. 139, 2573–2576 (2017).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Bartok, A. P. et al. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 3, e1701816 (2017).
Xue, D. et al. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 7, 11241 (2016).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 16028 (2016).
Rupp, M., Tkatchenko, A., Muller, K. R. & von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Shen, Y. & Bax, A. Protein backbone chemical shifts predicted from searching a database for torsion angle and sequence homology. J. Biomol. NMR 38, 289–302 (2007).
Neal, S., Nip, A. M., Zhang, H. Y. & Wishart, D. S. Rapid and accurate calculation of protein H-1, C-13 and N-15 chemical shifts. J. Biomol. NMR 26, 215–240 (2003).
Wishart, D. S., Watson, M. S., Boyko, R. F. & Sykes, B. D. Automated H-1 and C-13 chemical shift prediction using the BioMagResBank. J. Biomol. NMR 10, 329–336 (1997).
Iwadate, M., Asakura, T. & Williamson, M. P. C alpha and C beta carbon-13 chemical shifts in proteins from an empirical database. J. Biomol. NMR 13, 199–211 (1999).
Xu, X. P. & Case, D. A. Automated prediction of (15)N, (13)C(alpha), (13)C(beta) and (13)C‘ chemical shifts in proteins using a density functional database. J. Biomol. NMR 21, 321–333 (2001).
Moon, S. & Case, D. A. A new model for chemical shifts of amide hydrogens in proteins. J. Biomol. NMR 38, 139–150 (2007).
Vila, J. A., Arnautova, Y. A., Martin, O. A. & Scheraga, H. A. Quantum-mechanics-derived 13Calpha chemical shift server (CheShift) for protein structure validation. Proc. Natl Acad. Sci. USA 106, 16972–16977 (2009).
Kohlhoff, K. J., Robustelli, P., Cavalli, A., Salvatella, X. & Vendruscolo, M. Fast and accurate predictions of protein NMR chemical shifts from interatomic distances. J. Am. Chem. Soc. 131, 13894–13895 (2009).
Meiler, J. PROSHIFT: protein chemical shift prediction using artificial neural networks. J. Biomol. NMR 26, 25–37 (2003).
Han, B., Liu, Y., Ginzinger, S. W. & Wishart, D. S. SHIFTX2: significantly improved protein chemical shift prediction. J. Biomol. NMR 50, 43–57 (2011).
Shen, Y. & Bax, A. SPARTA+: a modest improvement in empirical NMR chemical shift prediction by means of an artificial neural network. J. Biomol. NMR 48, 13–22 (2010).
Rupp, M., Ramakrishnan, R. & von Lilienfeld, O. A. Machine learning for quantum mechanical properties of atoms in molecules. J. Phys. Chem. Lett. 6, 3309–3313 (2015).
Blinov, K. et al. Performance validation of neural network based 13C NMR prediction using a publicly available data source. J. Chem. Inf. Model. 48, 550–555 (2008).
Smurnyy, Y. D., Blinov, K. A., Churanova, T. S., Elyashberg, M. E. & Williams, A. J. Toward more reliable 13C and 1H chemical shift prediction: a systematic comparison of neural-network and least-squares regression based approaches. J. Chem. Inf. Model. 48, 128–134 (2008).
Aires-de-Sousa, J., Hemmer, M. C. & Gasteiger, J. Prediction of 1H NMR chemical shifts using neural networks. Anal. Chem. 74, 80–90 (2002).
Kuhn, S., Egert, B., Neumann, S. & Steinbeck, C. Building blocks for automated elucidation of metabolites: machine learning methods for NMR prediction. BMC Bioinforma. 9, 400 (2008).
Cuny, J., Xie, Y., Pickard, C. J. & Hassanali, A. A. Ab initio quality NMR parameters in solid-state materials using a high-dimensional neural-network representation. J. Chem. Theory Comput. 12, 765–773 (2016).
Groom, C. R., Bruno, I. J., Lightfoot, M. P. & Ward, S. C. The Cambridge Structural Database. Acta Crystallogr. B 72, 171–179 (2016).
Hartman, J. D., Kudla, R. A., Day, G. M., Mueller, L. J. & Beran, G. J. Benchmark fragment-based (1)H, (13)C, (15)N and (17)O chemical shift predictions in molecular crystals. Phys. Chem. Chem. Phys. 18, 21686–21709 (2016).
Rasmussen, C. E. & Williams, C. K. Gaussian Processes for Machine Learning. Vol. 1 (MIT Press, Cambridge, 2006).
Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 1–16 (2013).
De, S., Bartok, A. P., Csanyi, G. & Ceriotti, M. Comparing molecules and solids across structural and alchemical space. Phys. Chem. Chem. Phys. 18, 13754–13769 (2016).
Grisafi, A., Wilkins, D. M., Csanyi, G. & Ceriotti, M. Symmetry-adapted machine learning for tensorial properties of atomistic systems. Phys. Rev. Lett. 120, 036002 (2018).
Ceriotti, M., Tribello, G. A. & Parrinello, M. Demonstrating the transferability and the descriptive power of sketch-map. J. Chem. Theory Comput. 9, 1521–1532 (2013).
Campello, R. J. G. B., Moulavi, D., Zimek, A. & Sander, J. Hierarchical density estimates for data clustering, visualization, and outlier detection. ACM Trans. Knowl. Discov. Data 10, 5 (2015).
Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Varini, N., Ceresoli, D., Martin-Samos, L., Girotto, I. & Cavazzoni, C. Enhancement of DFT-calculations at petascale: nuclear magnetic resonance, hybrid density functional theory and Car–Parrinello calculations. Comput. Phys. Commun. 184, 1827–1833 (2013).
Clark, S. J. et al. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 220, 567–570 (2005).
F. Musil, S. De & M. Cerrioti. Glosim2 package, https://github.com/cosmo-epfl/glosim2 (2017).
Arico-Muendel, C. C. et al. Orally active fumagillin analogues: transformations of a reactive warhead in the gastric environment. ACS Med. Chem. Lett. 4, 381–386 (2013).
Dao, H. T., Li, C., Michaudel, Q., Maxwell, B. D. & Baran, P. S. Hydromethylation of unactivated olefins. J. Am. Chem. Soc. 137, 8046–8049 (2015).
Garozzo, D. et al. Inclusion networks of a calix[5]arene-based exoditopic receptor and long-chain alkyldiammonium ions. Org. Lett. 5, 4025–4028 (2003).
Bats, J. W. CSD Commun. (2010).
Huang, G. B. et al. Selective recognition of aromatic hydrocarbons by endo-functionalized molecular tubes via C/N-H center dot center dot center dot pi interactions. Chin. Chem. Lett. 29, 91–94 (2018).
Plater, M. J., Harrison, W. A., Machado de los Toyos, L. & Hendry, L. The consistent hexameric paddle-wheel crystallisation motif of a family of 2,4-bis(n-alkylamino)nitrobenzenes: alkyl=pentyl, hexyl, heptyl and octyl. J. Chem. Res 41, 235–238 (2017).
Acknowledgments
We are grateful for financial support from Swiss National Science Foundation Grant no. 200021_160112. F.M. and S.D. were supported by the NCCR MARVEL, funded by the Swiss National Science Foundation. M.C. acknowledges funding by the European Research Council under the European Union’s Horizon 2020 research and innovation program (Grant agreement no. 677013-HBMAP). This work was also supported by EPFL through the use of the facilities of its Scientific IT and Application Support Center.
Author information
Authors and Affiliations
Contributions
F.M.P. conceived the project, performed experiments, analyzed the data, and wrote the paper. A.H. conceived the project, performed experiments, analyzed the data, and wrote the paper. F.M. performed experiments, analyzed the data, and wrote the paper. S.D. performed experiments and analyzed the data. M.C. conceived the project, supervised the experiments, analyzed the data, and wrote the paper. L. E. conceived the project, supervised the experiments, analyzed the data, and wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Paruzzo, F.M., Hofstetter, A., Musil, F. et al. Chemical shifts in molecular solids by machine learning. Nat Commun 9, 4501 (2018). https://doi.org/10.1038/s41467-018-06972-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-06972-x
This article is cited by
-
Advances of machine learning in materials science: Ideas and techniques
Frontiers of Physics (2024)
-
QM assisted ML for 19F NMR chemical shift prediction
Journal of Computer-Aided Molecular Design (2024)
-
Atomic-level structure determination of amorphous molecular solids by NMR
Nature Communications (2023)
-
Machine-learning-based predictions of imprinting quality using ensemble and non-linear regression algorithms
Scientific Reports (2023)
-
A duplication-free quantum neural network for universal approximation
Science China Physics, Mechanics & Astronomy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.