Abstract
Meso-porous electrodes (pore width « 1 µm) are a central component in electrochemical energy storage devices and related technologies, based on the capacitive nature of electric double-layers at their surfaces. This requires that such charging, limited by ion transport within the pores, is attained over the device operation time. Here we measure directly electric double layer charging within individual nano-slits, formed between gold and mica surfaces in a surface force balance, by monitoring transient surface forces in response to an applied electric potential. We find that the nano-slit charging time is of order 1 s (far slower than the time of order 3 × 10−2 s characteristic of charging an unconfined surface in our configuration), increasing at smaller slit thickness, and decreasing with solution ion concentration. The results enable us to examine critically the nanopore charging dynamics, and indicate how to probe such charging in different conditions and aqueous environments.
Similar content being viewed by others
Introduction
Conducting materials with a large surface-to-volume ratio, such as meso-porous electrodes (pore widths « 1 μm), are important in a range of technologies1,2,3,4,5,6. Prominent among these are supercapacitors4,5, but also batteries7,8, fuel cells9,10 and electrocatalysts11,12, while emerging applications include capacitive deionization13,14, and the extraction of renewable energy through capacitive mixing of aqueous solutions of different salt concentrations15,16. Charge is stored in supercapacitors when electrolyte ions form (capacitive) electrical double layers (EDLs) at the surface of oppositely charged electrodes under an externally applied voltage17. Since the amount of charge stored is proportional to the available electrode surface area, materials with a high specific area (such as porous electrodes) are clearly at a premium; but they are only fully useful if ion transport enables equilibrium EDL formation over the entire pore within the relevant charging/discharging time. It is crucial therefore to be able to characterize and understand the dynamics of EDL formation within nano-pores.
In equilibrium, the EDL at a charged surface screens the associated electric field, with an exponential decay length (the Debye length) \(\lambda _{\mathrm{D}} = \sqrt {\frac{{\varepsilon \varepsilon _0k_{\mathrm{B}}T}}{{2c_oe^2}}}\) (for 1:1 electrolyte), where c0 is the concentration of salt in the bulk solution, ε0 is the permittivity of free space, ε is the dielectric constant, kBT the thermal energy, and e the electronic charge18. Changes in the surface potential rearrange the ionic atmosphere comprising the EDL to a new equilibrium configuration19, a dynamic process known as EDL charging. This is well understood for planar electrodes in bulk solution, where the characteristic charging time is defined by τc = λDH / Ɗ (where H is the distance between electrodes and Ɗ is the ion diffusion coefficient)19,20,21,22, but for the case of EDL charging in nano-confined geometries (as in porous electrodes) the dynamics may be much slower. This is because, in small diameter pores, changes to the EDL are constrained by the limited supply of ions within the pore23,24,25,26,27 and the time for ions to access the entire pore from the reservoir with which it is in contact.
A widely used description of ion transport in pores is the classic “Transmission-Line” (TL) model, by de Levie6,24,28, where the pore – a closed cylinder of length Lp and diameter hp (Lp » hp » λD) in contact with an ion reservoir - is treated as an equivalent TL circuit composed of a set of resistors and capacitors, yielding a time for EDL charging within the pore τTL = (Lp2 / Ɗ)(λD /hp). This characteristic time scales as the diffusion time (Lp2/Ɗ) for ions to traverse the pore length Lp, modulated by the ratio (λD/ hp). The latter is the extent of the near-surface EDL region (~λD), within which ion redistribution must occur due to the potential change, relative to the pore diameter hp, within which little overall change occurs. The charging dynamics of an EDL confined in a single nano-pore have been investigated primarily theoretically, e.g. refs. 6,29,30,31,32,33,34,35, while several treatments have extended the TL treatment, and different charging dynamics have recently been predicted for EDLs confined in dimensions comparable with its Debye length6,28,36. Experimentally, charging dynamics have been probed within (macroscopic) porous electrodes25,37,38,39, but, to our knowledge, no measurements of EDL charging dynamics within a single nano-pore – the basic element of such electrodes—have been reported to date.
Here we use a surface force balance (SFB) to probe experimentally the charging dynamics of an EDL confined to a nano-slit between two surfaces, in response to a step-change in the surface potential (or charge) of one of them (arising from a step ∆Ψapp in the potential applied to it). We find that the response to such a step is governed by two successive processes: Immediate formation of a strong electric field across the pore due to elimination of the screening, arising from the instantaneous charge imbalance in the EDL, followed by a slower process in which the ionic atmosphere of the EDL rebuilds to screen the generated electric field while charging the nano-pore interior (the gold acquires its new surface potential value over a time δt much faster than EDL charging time as it is associated with drift motion of electrons which is orders of magnitude faster than for ions in solution11,40). Our results show that full EDL charging within the nano-slit occurs over times of order 0.5–1 s, far longer than τc ≈ 3 × 10−2 s in our configuration (where τc = λDH / Ɗ, and the values of λD, H and Ɗ are given below). They reveal that the charging time increases at smaller slit thickness, and decreases with increasing ion concentration in the electrolyte solution, suggesting that the process of EDL charging within the nano-slit is largely limited by diffusion of ions from the bulk reservoir to which the nano-slit is coupled24,28,36. These findings demonstrate the ability of the SFB to access and probe the EDL charging dynamics within a single nanoscale gap (« 1 μm), the basic element of porous electrodes, providing a method for probing EDL charging in nano-confined slits with different surfaces and under different conditions.
Results
Probing EDL charging in a nano-slit with the SFB
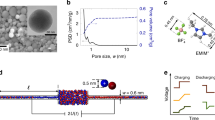
Figure 1a shows a schematic of the experimental SFB configuration used in this study, where a single-crystal mica surface faces a smooth gold surface (r.m.s. roughness ca. 3 Å) at a controlled potential41,42,43. The absolute separation D between the surfaces is determined (to ± 3 Å) by multiple beam interference and monitored via video-recording of the wavelengths of the interference fringes44,45.
a Schematic of the Surface Force Balance (SFB) and three-electrode configuration, with the principle components labeled, as described in detail in the experimental section. During measurements, the electrodes are immersed in an electrolyte solution inside a quartz bath, custom-designed to prevent leakage of current to the ground. Potentials applied to the gold surface were in the so-called double-layer range (i.e., where the electrode is ideally polarized), to ensure, crucially, the absence of any electrochemical reactions44,45 (Supplementary note 5). b A section through the intersurface gap at closest separation D, showing its pore-like structure, where λD is the Debye length, L is the radius of the circular pore, δD is the change in pore width at a distance L from the pore center due to curvature of the surfaces (δD ≅ L2/2R). The schematic is not to scale: L is typically 100 μm, while D is of order 100 nm, giving a (diameter/thickness) ratio of ca. 1000 for the pore/slit. c D(t) traces taken in 5 mM NaNO3 at D = 50 nm based on video recording of the motion of the interference fringes in the SFB, in response to positive and negative potential steps as indicated by the upper potential trace. The obtained peaks reflect the movement of the lower surface (mica) in response to application of a positive (‒ 0.2 V → 0.2 V) or negative (0.2 V → ‒ 0.2 V) step potentials. Scale bars: horizontal – 2 s; vertical – 10 nm. d A magnified view of the peak circled in red in the D(t) plot in (c), demonstrating its asymmetric shape, where ∆ts and ∆tr signify the initial motion and relaxation time, as shown, and ∆D is the distance shift from initial surface separation Di = 50 nm to extremal separation Df = 27.8 nm (prior to its relaxation back to Di). Scale bars: horizontal – 0.2 s; vertical – 5 nm
We probe the perturbation and the charging of the EDL through its transient effect on the force between the gold and mica surfaces. A typical dynamic measurement, conducted in 5 mM NaNO3 (λD = 4.3 nm), is shown in Fig. 1c. Initially, the surfaces are brought to a given initial separation Di (» λD). Then, either a positive (–0.2 V → + 0.2 V) or negative ( + 0.2 V → −0.2 V) potential step ∆Ψapp is applied to the gold while monitoring the gold-mica separation D (Fig. 1c). After ∆Ψapp is applied at time t = 0 (Fig. 1d), the gold electrode – both outside and within the confined nano-slit – accumulates a new surface charge density over a very short time δt (typically < 10–9 s due to drift motion of electrons11,40) as it attains its new surface potential value Ψgold. This generates (at δt) an unscreened electric field19 which exerts an electrostatic force Fe(t = δt ≈ 0) on the negatively charged mica, bending the spring Kn on which it is mounted by ∆D to an extremal separation Df relative to the gold, over a time ∆ts. As ions transport to reconstruct the EDL (EDL charging) within the nanopore, Fe is progressively screened and the surfaces relax to their initial separation Di over a further time ∆tr (Fig. 1d), since, in all cases in our study, Di » λD. This transient motion manifests as a peak, with a characteristic asymmetric shape, in the D vs. t trace (Fig. 1d) and a period of (∆ts + ∆tr) which characterizes the charging time of the EDL within the nano-slit. Away from the nano-slit – at the unconfined gold surface - the EDL equilibrates over a time τc19 ( = λDH/Ɗ ≈ 3 × 10−2s), which is much shorter than the EDL charging time (0.5–2 s) within the nanopore measured in our experiments. For example, for the configuration of Fig. 1d, a characteristic time (∆ts + ∆tr) ≈ 0.85 s was obtained in response to a potential step of -0.2 V → + 0.2 V. Overall, this indicates three different time scales following the potential step: (∆ts + ∆tr) ≫ τc ≫ δt. Thus, the times (∆ts + ∆tr) we measure in our experiments, corresponding to the EDL equilibration within the nano-pore, are well separated from τc, the time for EDL equilibration at the unconfined gold away from the nanopore.
The initial (t = 0) instantaneous electric field across the gap depends on the effective surface potentials Ψgold at the gold surface at different applied potentials Ψapp; these may be extracted from normal force vs. surface-separation D profiles, as shown in Fig. 2a. In Fig. 2b are shown D(t) traces in response to Ψapp = –0.2 V → + 0.2 V and back again, at selected Di values covering the range of pore widths Di examined. Importantly, this also demonstrates the repeatability and reproducibility of our dynamic measurements, indicating that no chemical reaction occurs at the gold (this is shown directly by cyclic voltammetry, ref. 45 and in the Supplementary Figure 4). In Fig. 2c are magnified peaks at different Di values. Such transient peaks reflect the EDL perturbation by ∆Ψapp (at t = 0) and its subsequent charging, and are analyzed below (for clarity we focus on the –0.2 V → + 0.2 V transition though identical considerations apply to the reverse transition).
a Interaction profiles Fn(D)/R between gold and bare mica surfaces across 2 mM NaNO3, at a given contact point, under different applied potentials Ψapp. Gold surface potential Ψgold values in legend are extracted from respective fits (black curves) to the PB equation with constant charge (mica) vs. constant potential (gold) boundary conditions, augmented by vdW attraction44,45. b An example for dynamic measurements (D(t) plots) taken at different surface separations, in response to positive and negative step potential between – 0.2 V and + 0.2 V. The peaks indicate the transient movement of the lower surface (mica) in response to application of the step potential changes. Measurements both of the interaction profiles (a) and the response to potential changes were performed between the same surfaces and salt solution (2 mM NaNO3). c A magnified view of transient peaks (circled in the D(t) plots in b) obtained at different gold-mica separations, where Di and Df are the initial and extremal surface separation values, respectively. Scale bars: horizontal – 0.2 s; vertical – 5 nm
Transient forces during EDL charging
The force Fe(t) attracts the charged mica surface due to the induced positive charge on the gold surface, changing the surface separation Di by ∆D(t) = (Di – D(t)). This motion is opposed by the bending of the spring (of constant Kn) on which the mica surface is mounted, which exerts an opposing force Fk = Kn∆D, and by a hydrodynamic damping force FH (arising from extrusion of the liquid as the surfaces approach or separate). Van der Waals (vdW) attraction between the surfaces is negligible since D is always > 20 nm, and we may set the normal surface force as equal to Fe. The equation of motion is thus Fe(t) = Fk + FH + m(d2D/dt2), where the last term is inertial and m is the mass of the mica surface and its mount. We note that the magnitude of m(d2D/dt2) (where m ≈ 3 × 10–3 kg), as determined from the D vs. t plots (Fig. 1d or Fig. 2b), is ca. 10–9N, which is negligible compared with the hydrodynamic (FH = O(10−6 N)) and spring (Fk = O(10–6 N)) force terms, and may be ignored. The hydrodynamic force, between a sphere approaching a flat a closest distance D away across a liquid of viscosity η, is46 FH = 6πR2η[(dD / dt) / D], and the equation of motion becomes:
Before solving equation 1, we address an important qualitative point concerning the EDL charging. Following the potential change on the gold surface at t = 0, Fe is a maximum but immediately begins to decay as the EDL recharges. During the initial motion (t < ∆ts) Fe exceeds Fk, but at t = ∆ts, where D = Df (Fig. 1d), it has decayed so that Fe(∆ts) = Fk = Kn(Di – Df). At longer times t > ∆ts, Fe becomes smaller than the spring force Fk, and the mica surface is pushed back towards its equilibrium position D = Di over the period ∆tr. The crucial point is whether the period ∆tr is due to hydrodynamic damping alone, or to a slower process due to Fe decay arising from increased screening associated with EDL charging limited by ion transport within the gap. To resolve this we solve for the motion of the surfaces from D = Df at the peak to D = Di, on the assumption of hydrodynamic damping alone. The relevant equation is simply equation (1) with Fe set to zero, and boundary condition D = Df at t = 0. The resulting D(t) variation is given in Fig. 3 and shown as the red curves in Fig. 3a. We see that for traces at Di ≳ 80 nm, D approaches Di significantly slower than can be accounted for by hydrodynamic damping alone. This shows that D(t) is dominated by the slow decay in Fe rather than by hydrodynamic damping, so that (∆ts + ∆tr) = τEDL provides a measure of the time τEDL for the EDL charging (we note that for both hydrodynamic damping and EDL charging, the characteristic times vary as (1/D); however, at small Di the mean value of D across the pore is significantly larger than Di, which reduces the EDL charging time but leaves the hydrodynamic damping time unchanged, so that it becomes more dominant at the smallest Di values such as Di < ca. 80 nm. This is also manifested in the ∆D vs. Di plot (Supplementary Figure 1) as a decrease in ∆D at D < ca. 80 nm). To solve equation (1), we require an explicit form for Fe(t). We approximate the instantaneous initial force (just after application of the potential change on the gold surface) as Fe(0) = πRεε0(∆Ψeff)2 / D(t = 0), which is the force between a conducting sphere (radius R) and a conducting plane a closest distance D apart47 (D « R) differing in potentials by ∆Ψeff. In our configuration ∆Ψeff = Ψgold,eff – Ψmica (at t = 0), the effective potential difference at t = 0 between the opposing gold and mica surfaces, where Ψgold,eff is the instantaneous effective gold surface potential (t = 0) arising from the abrupt variation of the gold surface charge (Supplementary Note 1). This may be evaluated from the potentials extracted from the force vs. distance profile at the relevant applied potentials44, Fig. 2a. The decay with time of Fe(t) is complex, depending on flux of ions between the bulk and the nano-slit which in turn modifies the initial gold surface charge (i.e. at t = δt) within the confined area until the EDL is fully relaxed. To proceed, we may assume that Fe decays exponentially with a characteristic time τ due to the progressive screening of the electrostatic force with time, as the near-surface ion concentration rearranges following the potential change. Equation (1) then becomes:
We seek an approximate solution by recognizing that D does not change too greatly from Di during the transient response (particularly for the larger Di values), and replace D by Di in the denominators of the terms for Fe and FH. This gives:
which for boundary condition D = Di at t = 0, solves as:
where Fe(0) = πRεε0∆Ψ0(∆Ψeff)2 / Di and fH = 6πR2η / Di.
A magnified view of peaks measured at different surface separations (Di) in 2 mM NaNO3. a The red solid lines describe the motion of the lower surface from Di to Df in the presence of hydrodynamic damping alone as obtained by the analytical solution \(D\left( t \right) = D_{\mathrm{i}}D_{\mathrm{f}}/\left\lceil {\exp \left( { - tk_{\mathrm{n}}D_{\mathrm{i}}/6{\mathrm{\pi }}R^2\eta} \right)\left( {D_{\mathrm{i}} - D_{\mathrm{f}}} \right) + D_{\mathrm{f}}} \right\rceil\) to the equation of motion \(k\Delta D\left( t \right) = 6{\mathrm{\pi }}R^2\eta[({\mathrm{d}}D/{\mathrm{d}}t)/D(t)]\) with a boundary condition D(t = 0) = Df. They show that for the larger Di values (Di > ca. 80 nm, see Fig. 4a) the relaxation of the surfaces from Df back to Di is significantly slower than can be accounted for by hydrodynamic damping. Scale bars: horizontal – 0.4 sec; vertical – 5 nm. b The black solid lines are the solution to equation (3) which describes the transient motion in surface separation D(t) in response to a positive step potential (‒ 0.2 V → + 0.2 V), where for all traces the parameters are fully determined (no adjustable parameters) (Supplementary note 6). Scale bars: horizontal – 0.4 sec; vertical – 5 nm
Equation (3) describes the transient change in D in response to ∆Ψapp. We note that at the peak in D(t), at t = ∆ts, (dD/dt) = 0 so that for this value of t ( = ∆ts), equation (2’) yields the value of τ directly. This may then be used in the expression for D (equation (3)). In Fig. 3b, this is done for the D vs. t traces at different Di values, showing a close quantitative fit with no adjustable parameters (all parameters are determined, Fig. 3). We confirmed the validity of our approximate solution by numerically solving equation (2) (Supplementary note 4). The numerical solution shows the behavior of D(t) to be close to that predicted by equation (3) over the range of D values in our experiments, and as expected, closest at higher D values where the approximation leading to equation (3) is best (Supplementary Figure 3).
Effect of confinement on EDL charging time
In Fig. 4 we gather together results for the EDL charging times for different Di values, that is, different thicknesses of the nano-slit, showing the variation with Di of ∆ts, ∆tr and (∆ts + ∆tr) (inset to Fig. 4a). While the values shown are for ∆Ψapp = −0.2 V → + 0.2 V and + 0.2 V →−0.2 V in 2 mM salt, similar behavior is seen at different salt concentrations (Fig. 4b), and for different salts (Fig. 4c), as well as for other potential variations (Supplementary note 3). In Fig. 4a the broken and solid black curves are the calculated values of ∆ts and ∆tr, respectively, from equation (3). The red curve in Fig. 4a is the calculated hydrodynamic damping time from the peak maximum (corresponding to the red curves shown in Fig. 3a), in the absence of any electrostatic force Fe, and shows that such damping alone cannot account for the significantly longer decay times ∆tr at Di ≳ 80 nm.
EDL charging at different nano-slit thickness Di. a Variation of ∆ts (diamonds) and ∆tr (circles), obtained from transient peaks in D as indicated in the inset. Measurements were taken in 2 mM NaNO3 solution and in response to positive – 0.2 V → + 0.2 V (green) and negative + 0.2 V → ‒ 0.2 V (red) step potentials. The black dashed line and the black solid line are, respectively, the calculated values of ∆ts and ∆tr at different Di values based on equation (3). The solid red line describes the relaxation time ∆tr in the presence of hydrodynamic damping alone as derived from calculated curves (Fig. 3a) at different Di values using equation (2’), as shown in Fig. 3a for selected peaks. b EDL charging time τEDL (∆ts + ∆tr), at different surface separations Di in response to positive −0.2 V → + 0.2 V (green squares) and negative + 0.2 V → −0.2 V (red squares) step potentials in 2 mM NaNO3 (taken from data in (a)); and in 5 mM NaNO3 (black triangles). The upper and lower black solid lines are the calculated values of (∆ts + ∆tr) at different Di values based on equation (3), for the 2 mM and 5 mM cases, respectively, where all parameters are fully determined (no adjustable parameters) (Supplementary note 6). The solid blue curve is the best fit of the characteristic time according to the transmission line model, τTL = (L2λD/Ɗhp), using a Debye length of λD = 6.8 nm, diffusion coefficient of a nitrate ion Ɗ = 1.6 × 10−9 m2 s‒1 and hp = Di. The fit to the data shown corresponds to L = 150 μm. c. The EDL charging time (∆ts + ∆tr), at different surface separations Di in response to positive – 0.1 V → + 0.2 V (green squares) and negative + 0.2 V → ‒0.1 V (red squares) step potentials in 2 mM LiClO4
Figure 4b shows the variation of the overall charging time ((∆ts(Di) + ∆tr(Di)) with Di for two different salt concentrations, 2 mM (squares) and 5 mM (triangles), where the solid black curves are the calculated fits from equation (3) for the two cases. These curves show good agreement with the respective measured charging times (∆ts(Di) + ∆tr(Di)), indicating that our equations, which provide a description of the dynamics, though they do not clarify the mechanism of the nano-slit charging, can provide a good description of the data. The blue curve is the variation of the characteristic charging time τTL according to the transmission line model for nano-pore charging, described earlier and discussed in the following section.
Figure 4c shows the variation of the overall charging time when the NaNO3 salt in Fig. 4a, b is replaced by a different salt, LiClO4, which moreover has much larger differences between its ionic diffusion coefficients (Li+ and ClO4−), as considered in the following section.
Mechanism of nano-slit charging
It is of interest to consider the EDL charging dynamics in the context of the classic transmission line (TL) approach noted earlier24,28,36. In our configuration (Fig. 1b), the nano-pore or nano-slit is the gold-mica gap about the region of closest approach, D = Di, strictly the region between two crossed cylinders of mean radius R. Its effective geometry – as in the Derjaguin approximation18, which is valid for Di « R in the present case – is that of a circular slit bounded by a spherical surface and a flat, with a slit radius r = L, in contact with an ion reservoir (because the slit is formed by two orthogonal cylindrical surfaces, it is symmetric about its midplane). L is the distance required by ions from the reservoir (at r = L) to fully permeate the pore to its center (r = 0), where its thickness is hp = Di, to compensate for the charge induced on the gold by the potential step ∆Ψapp. Within the TL model, the characteristic charging time of the EDL within such a circular slit is then expected to scale as τTL = (L2 / Ɗ)(λD/hp)6,24. The surface separation at r = L, D = Di + (L2/2 R) (Fig. 1b), must be sufficiently large to provide for the required excess of ions. This corresponds to a value L ≈ (2 R∆σ / c0e)1/2 (Supplementary note 2), where ∆σ is the change in the gold surface charge density σ arising from ∆Ψapp. In Fig. 4b, it is shown as a solid blue curve, the characteristic time τTL = (L2 / Ɗ)(λD / hp) expected for a pore of length L, and width hp = Di. The fit to the experimental data corresponds to L = 150 μm. This is within a factor 2 of the value L = (2 R∆σ / c0e)1/2 ≈ 87 μm evaluated for the corresponding potential step (∆Ψapp = + 0.2 V → –0.2 V in 2 mM salt) (Supplementary Note 2), which is believed to arise from the different geometries considered in the two cases.
The characteristic time τTL = (L2 / Ɗ)(λD / hp) also predicts that EDL charging is faster for higher salt concentrations, since (in our configuration) a larger c0 is associated both with a smaller L (~c0–1/2), as well as a smaller λD (~c0–1/2), suggesting τTL ~ c0–3/2. This is indeed observed for EDL charging from higher salt concentrations as shown in Fig. 4b, where the experimental charging time is roughly 3.5-fold larger in the 2 mM NaNO3 salt compared with the 5 mM salt, similar to the expected ratio (c0, 2 mM/c0, 5 mM)–3/2 ≈ 4.
In addition, we would expect from the expression for τTL that ions with different diffusion coefficients Ɗ would result in different charging times. Additional cations need to permeate the slit from the reservoir when the applied potential change renders the surface charge more negative (e.g. ∆Ψapp = + 0.2 V → –0.2 V), and additional anions need to permeate for the opposite case. For the NaNO3 salt, Fig. 4a, b, where the Ɗ values for Na+ (Ɗ = 1.3 × 10–9 m2 s–1) and NO3–(Ɗ = 1.9 × 10–9 m2 s–1) differ by some 40%, there is a slight indication that EDL charging is slower when ∆Ψapp = + 0.2 V → – 0.2 V (red squares in Fig. 4a, when it is controlled by transport of slower Na+ ions) relative to ∆Ψapp = – 0.2 V → + 0.2 V (green squares, when charging occurs by transport of NO3– ions). However, when NaNO3 is replaced by LiClO4, where the Ɗ values for the latter (1 × 10–9 m2 s–1 and 1.8 × 10–9 m2 s–1 for the Li+ and ClO4– ions respectively) differ by twice as much as for the former, there is a more marked effect of the mobility of the ion type permeating the slit on the charging time. This is seen by the differences between the red (charging by Li+ transport) and green (charging by ClO4− transport) data in Fig. 4c. This is especially the case in Fig. 4c for Di > ca. 80 nm, where ion transport rather than hydrodynamic effects dominates the dynamics (see Figs. 3a and red curve in 4a); indeed, the difference between the charging times for anionic vs. cationic transport demonstrates clearly that the decay of the transient forces that we measure is dictated by diffusive-transport of ions from the reservoir. Finally, we would expect that different potential steps would result in a different charging times through their effect on the surface charge density change ∆σ and hence on the effective slit radius L (~ (∆σ)1/2), as indeed is seen (Supplementary Figure 2). Thus, this broad agreement of the absolute magnitude as well as the variation of the predicted charging times τTL = (L2 / Ɗ)(λD / hp) with our measured EDL charging for different slit widths, salt concentrations, ionic mobility and surface potential changes, indicates the validity of the TL concept and its scaled behavior for our system.
Discussion
In summary, we report the first measurements of EDL charging dynamics within a single nano-confined circular pore (or slit) following a step change in the surface potential (and charge) of one of the confining surfaces. This is done, using an SFB, by monitoring the transient change in surface forces due to an instantaneous electric field arising from the EDL perturbation, which decays as the EDL charges. Our results are in line with the characteristic times expected from the transmission line model applied to our nano-slit geometry, and indicate that such an approach could be used for probing EDL charging dynamics within single nano-slits in different conditions and aqueous environments.
Methods
Materials
Gold pellets, 99.999% pure, were purchased from Kurt J. Lesker and evaporated from a graphite crucible. Sodium nitrate, NaNO3, 99.99% pure was purchased from Merck Millipore and used as received. Lithium perchlorate, LiClO4, 99.99% pure was purchased from Sigma-Aldrich and used as received.
Preparation of salt solutions
NaNO3 and LiClO4 were dissolved in purified water with a total organic content of less than 1 ppb (TOC < 1), a resistivity of 18.2 MΩ cm and pH = 5.8.
Surface force balance experiment
An atomically smooth back silvered mica and molecularly smooth gold surface are glued to cylindrical fused-silica lenses (curvature radius R ≈ 1 cm) in a crossed-cylinder configuration, equivalent to the geometry of a sphere on a flat, with the lower lens (mica) mounted on a horizontal leaf spring (spring constant K = 81.5 ± 2.7 Nm−1) and the top lens (gold) mounted on a sectored piezoelectric tube (PZT). The gold surface, serving as a working electrode (W), is connected to a potentiostat together with two platinum wires, acting as reference (R) and counter (C) electrodes, as described in detail elsewhere44,45. During all measurements, the electrodes are immersed in an electrolyte solution inside a quartz bath, custom-designed to prevent leakage of current to the ground, and the distance H between them is of order a few mm. The distance between the surfaces is measured with a resolution of 1.0 ± 0.3 nm using multiple beam optical interferometry, and the normal forces between the surfaces are monitored through the bending of the horizontal spring and measured via a dynamic approach with a force sensitivity of ~50–100 nN, as previously described in detail48,49.
Video capture and analysis
The absolute surface separation between the surfaces during EDL charging and dynamic force measurements was continuously monitored, by capturing the fringes of equal chromatic order (FECO) position, using a fast video recording camera (SONY XC-HR70) with a frame rate of 60 frames per s. In our gold/medium/mica/silver two-layer interferometer system each pixel is equivalent to an absolute distance of ca. 0.2–0.3 nm. The separation between the surfaces was determined using the multilayer matrix method, as previously described in detail50,51.
Data availability:
The data sets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Change history
02 May 2019
The original version of this Article contained an error throughout in which an incorrect symbol was used for the diffusion coefficient: it should be cambria math, italicized, and not bold. These have been corrected in both the PDF and HTML versions of the Article.
References
Li, W., Liu, J. & Zhao, D. Mesoporous materials for energy conversion and storage devices. Nat. Rev. Mater. 1, 16023 (2016).
Chabi, S., Peng, C., Hu, D. & Zhu, Y. Ideal three-dimensional electrode structures for electrochemical energy storage. Adv. Mater. 26, 2440–2445 (2014).
Vlad, A. & Balducci, A. Supercapacitors: Porous materials get energized. Nat. Mater. 16, 161–162 (2017).
Salanne, M. et al. Efficient storage mechanisms for building better supercapacitors. Nat. Energy 1, 16070 (2016).
Simon, P. & Gogotsi, Y. Materials for electrochemical capacitors. Nat. Mater. 7, 845–854 (2008).
Mirzadeh, M., Gibou, F. & Squires, T. M. Enhanced charging kinetics of porous electrodes: surface conduction as a short-circuit mechanism. Phys. Rev. Lett. 113, 097701 (2014).
Bruce, P. G., Freunberger, S. A., Hardwick, L. J. & Tarascon, J.-M. Li-O2 and Li-S batteries with high energy storage. Nat. Mater. 11, 19–29 (2012).
Peng, Z., Freunberger, S. A., Chen, Y. & Bruce, P. G. A reversible and higher-rate Li-O2 battery. Science 337, 563–566 (2012).
Irvine, J. T. S. et al. Evolution of the electrochemical interface in high-temperature fuel cells and electrolysers. Nat. Energy 1, 15014 (2016).
O’hayre, R., Cha, S.-W., Prinz, F. B. & Colella, W. Fuel Cell Fundamentals. (John Wiley & Sons, Hoboken, New Jersey, USA, 2016).
Bard, A. J. & Faulkner, L. R. Electrochemical Methods: Fundamentals and Applications Vol. 2 (Wiley: New York, 2001). .
Lu, Q. et al. Highly porous non-precious bimetallic electrocatalysts for efficient hydrogen evolution. Nat. Commun. 6, 6567 (2015).
Porada, S., Zhao, R., Van Der Wal, A., Presser, V. & Biesheuvel, P. Review on the science and technology of water desalination by capacitive deionization. Prog. Mater. Sci. 58, 1388–1442 (2013).
Suss, M. et al. Water desalination via capacitive deionization: what is it and what can we expect from it? Energy Environ. Sci. 8, 2296–2319 (2015).
Brogioli, D. Extracting renewable energy from a salinity difference using a capacitor. Phys. Rev. Lett. 103, 058501 (2009).
Rica, R., Ziano, R., Salerno, D., Mantegazza, F. & Brogioli, D. Thermodynamic relation between voltage-concentration dependence and salt adsorption in electrochemical cells. Phys. Rev. Lett. 109, 156103 (2012).
Forse, A. C., Merlet, C., Griffin, J. M. & Grey, C. P. New perspectives on the charging mechanisms of supercapacitors. J. Am. Chem. Soc. 138, 5731–5744 (2016).
Evans, D. F. & Wennerstrom, H. The Colloidal Domain: Where Physics, Chemistry, and Technology Meet 2nd edn, (Wiley-VCH, New York, New York, USA, 1999).
Bazant, M. Z., Thornton, K. & Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 70, 021506 (2004).
Anson, F. C., Martin, R. F. & Yarnitzky, C. Creation of nonequilibrium diffuse double layers and studies of their relaxation. J. Phys. Chem. 73, 1835–1842 (1969).
Morrow, R., McKenzie, D. & Bilek, M. The time-dependent development of electric double-layers in saline solutions. J. Phys. D: Appl. Phys. 39, 937 (2006).
Lim, J., Whitcomb, J., Boyd, J. & Varghese, J. Transient finite element analysis of electric double layer using Nernst-Planck-Poisson equations with a modified Stern layer. J. Colloid Interface Sci. 305, 159–174 (2007).
Lee, G. J. & Pyun, S.-I. Experimental study on ion penetration into pores with pore fractality at carbon electrode for EDLC. J. Electrochem. Soc. 154, B593–B600 (2007).
De Levie, R. On porous electrodes in electrolyte solutions: I. capacitance effects. Electrochim. Acta 8, 751–780 (1963).
Chmiola, J. et al. Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer. Science 313, 1760–1763 (2006).
Chmiola, J., Yushin, G., Dash, R. & Gogotsi, Y. Effect of pore size and surface area of carbide derived carbons on specific capacitance. J. Power Sources 158, 765–772 (2006).
Lee, G. J. & Pyun, S.-I. Theoretical approach to ion penetration into pores with pore fractal characteristics during double-layer charging/discharging on a porous carbon electrode. Langmuir 22, 10659–10665 (2006).
Biesheuvel, P. & Bazant, M. Nonlinear dynamics of capacitive charging and desalination by porous electrodes. Phys. Rev. E 81, 031502 (2010).
Bazant, M. Z. & Squires, T. M. Induced-charge electrokinetic phenomena: theory and microfluidic applications. Phys. Rev. Lett. 92, 066101 (2004).
Squires, T. M. & Bazant, M. Z. Induced-charge electro-osmosis. J. Fluid. Mech. 509, 217–252 (2004).
Pean, C. et al. On the dynamics of charging in nanoporous carbon-based supercapacitors. ACS Nano 8, 1576–1583 (2014).
Kondrat, S. & Kornyshev, A. Charging dynamics and optimization of nanoporous supercapacitors. J. Phys. Chem. C. 117, 12399–12406 (2013).
Zhao, R., Biesheuvel, P., Miedema, H. & Bruning, H., . & Van der Waal, A. Charge efficiency: a functional tool to probe the double-layer structure inside of porous electrodes and application in the modeling of capacitive deionization. J. Phys. Chem. Lett. 1, 205–210 (2009).
Hemmatifar, A., Stadermann, M. & Santiago, J. G. Two-dimensional porous electrode model for capacitive deionization. J. Phys. Chem. C. 119, 24681–24694 (2015).
Kondrat, S., Wu, P., Qiao, R. & Kornyshev, A. A. Accelerating charging dynamics in subnanometre pores. Nat. Mater. 13, 387–393 (2014).
Sakaguchi, H. & Baba, R. Charging dynamics of the electric double layer in porous media. Phys. Rev. E 76, 011501 (2007).
Korenblit, Y. et al. High-rate electrochemical capacitors based on ordered mesoporous silicon carbide-derived carbon. ACS Nano 4, 1337–1344 (2010).
Redondo, E., Carretero-González, J., Goikolea, E., Ségalini, J. & Mysyk, R. Effect of pore texture on performance of activated carbon supercapacitor electrodes derived from olive pits. Electrochim. Acta 160, 178–184 (2015).
Forse, A. C. et al. Direct observation of ion dynamics in supercapacitor electrodes using in situ diffusion NMR spectroscopy. Nat. Energy 2, 16216 (2017).
Bockris, J., Reddy, A. & Gamboa-Aldeco, M. in Fundamentals of Electrodics Vol. 2 (Springer US, Kluwer Academic Publishers, New York, USA, 2000).
Chai, L. & Klein, J. Large area, molecularly smooth (0.2 nm rms) gold films for surface forces and other studies. Langmuir 23, 7777–7783 (2007).
Tivony, R. & Klein, J. Modifying surface forces through control of surface potentials. Faraday Discuss. 199, 261–277 (2017).
Shrestha, B. R., Baimpos, T., Raman, S. & Valtiner, M. Angstrom-resolved real-time dissection of electrochemically active noble metal interfaces. ACS Nano 8, 5979–5987 (2014).
Tivony, R., Dan, B. Y., Silbert, G. & Klein, J. Direct observation of confinement-induced charge inversion at a metal surface. Langmuir 31, 12845–12849 (2015).
Tivony, R., Iuster, N. & Klein, J. Probing the surface properties of gold at low electrolyte concentration. Langmuir 32, 7346–7355 (2016).
Chan, D. Y. & Horn, R. The drainage of thin liquid films between solid surfaces. J. Chem. Phys. 83, 5311–5324 (1985).
Hudlet, S., Saint Jean, M., Guthmann, C. & Berger, J. Evaluation of the capacitive force between an atomic force microscopy tip and a metallic surface. Eur. Phys. J. B 2, 5–10 (1998).
Kampf, N., Ben-Yaakov, D., Andelman, D., Safran, S. A. & Klein, J. Direct measurement of sub-debye-length attraction between oppositely charged surfaces. Phys. Rev. Lett. 103, 118301–118304 (2009).
Klein, J. & Kumacheva, E. Simple liquids confined to molecularly thin layers. I. Confinement-induced liquid to solid phase transitions. J. Chem. Phys. 108, 6996–7009 (1998).
Clarkson, M. T. Multiple-beam interferometry with thin metal-films and unsymmetrical systems. J. Phys. D: Appl. Phys. 22, 475–482 (1989).
Born, M. & Wolf, E. Principles Of Optics - Electromagnetic Theory Of Propagation, Interference And Diffraction Of Light. (Cambridge Univ. Press, Cambridge U.K, 1999).
Acknowledgements
We thank Ohad Cohen for his help with the numerical solutions, Alexander Vaskevich for helpful discussions and Maarten Biesheuvel for useful comments. We thank the European Research Council (Advanced grant CartiLube), the Israel Science Foundation and the Minerva Foundation for financial support. This research was made possible in part by the historic generosity of the Harold Perlman family.
Author information
Authors and Affiliations
Contributions
J.K., R.T. and G.S. conceived the idea and designed the experiments. R.T. conducted the experiments and analyzed the data. S.S. and P.P. assisted with theoretical aspects of EDL charging dynamics. R.T. and J.K. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tivony, R., Safran, S., Pincus, P. et al. Charging dynamics of an individual nanopore. Nat Commun 9, 4203 (2018). https://doi.org/10.1038/s41467-018-06364-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-06364-1
This article is cited by
-
Electrotunable friction with ionic liquid lubricants
Nature Materials (2022)
-
On the origins of conductive pulse sensing inside a nanopore
Nature Communications (2022)
-
The effects of slit-pore geometry on capacitive properties: a molecular dynamics study
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.