Abstract
Strong Coulomb interactions in single-layer transition metal dichalcogenides (TMDs) result in the emergence of strongly bound excitons, trions, and biexcitons. These excitonic complexes possess the valley degree of freedom, which can be exploited for quantum optoelectronics. However, in contrast to the good understanding of the exciton and trion properties, the binding energy of the biexciton remains elusive, with theoretical calculations and experimental studies reporting discrepant results. In this work, we resolve the conflict by employing low-temperature photoluminescence spectroscopy to identify the biexciton state in BN-encapsulated single-layer WSe2. The biexciton state only exists in charge-neutral WSe2, which is realized through the control of efficient electrostatic gating. In the lightly electron-doped WSe2, one free electron binds to a biexciton and forms the trion–exciton complex. Improved understanding of the biexciton and trion–exciton complexes paves the way for exploiting the many-body physics in TMDs for novel optoelectronics applications.
Similar content being viewed by others
Introduction
Single-layer transition metal dichalcogenides (TMDs) represent a new class of atomically thin semiconductors with superior optical and optoelectronic properties1,2. The two-dimensional nature of single-layer TMDs results in reduced screening and enhanced Coulomb interaction, giving rise to excitonic complexes such as exciton, trion, and biexciton with binding energy orders of magnitude larger than that of conventional semiconductors such as GaAs3. Large spin–orbit coupling4,5,6,7 leads to the splitting of the valence bands in TMDs, and the resulting valence band minimum with different spin configurations breaks the symmetry at the corners of TMDs’ Brillouin zone, i.e., K and K′ valleys. The different valleys can be accessed selectively through circularly polarized light8,9,10, providing a valley degree of freedom that can be exploited for valleytronics11,12,13,14. Besides the exciton, the higher order charge-complexes such as trions15,16 and biexcitons also possess a valley degree of freedom, and they can be further used as entangled photon sources17. Fundamental understanding of the charge-complexes in TMDs is thus critical for fully utilizing the potential of TMDs for novel optoelectronics applications.
Despite recent developments in the understanding of excitons and trions in TMDs18,19, an unambiguous measure of the biexciton-binding energy remains elusive. Many experimental studies based on linear photoluminescence (PL) spectroscopy reported a biexciton-binding energy larger than theoretical predictions20,21,22,23,24,25,26,27, while recent coherent pump-probe spectroscopy measurements reported a value close to the theoretical prediction28,29.
Here we demonstrate that, by fabricating a clean single-layer WSe2 sandwiched by two h-BN flakes, we can detect unambiguous evidence of biexciton PL emission in charge-neutral WSe2 at low temperature, and the observed binding energy is in excellent agreement with the theoretical calculations30,31,32,33,34. We also perform PL spectroscopy as a function of the carrier density and reveal the formation of the electron-bound biexciton exists in the lightly n-doping regime only.
Results
Excitation power-dependent PL spectra of monolayer WSe2
To preserve the WSe2 monolayer crystal quality and probe the intrinsic optical behavior, we constructed the BN/WSe2/BN structure with the pickup method35, during which the WSe2 was never exposed to any polymer (Note 1 of SI). A piece of few-layer graphene (labeled as graphite) was used as the contact electrode of the single-layer WSe2, while another piece was used as the transparent top-gate electrode on the top layer BN, as shown in Fig. 1a, b. The high quality of the WSe2 sample is illustrated in Fig. 1c, which displays low-temperature PL spectra measured under the 633 nm continuous-wave (CW) laser excitation. Indeed, the linewidth of the exciton (located at 1.740 eV) can be as narrow as ~4 meV, significantly less than that from the typical single-layer exfoliated WSe2 on SiO236,37, which results in a clear fine structure of well separated PL features. The emission from the exciton (X0) is observed at 1.740 eV. The two peaks at 1.712 eV and 1.705 eV correspond to intervalley and intravalley trions38,39, which we label as \({\mathrm{X}}_1^ -\) and \({\mathrm{X}}_2^ -\), respectively. The PL peak at 1.697 eV is attributed to the emission from the spin-forbidden dark exciton transition40,41,42, which is observed here because our high numerical aperture (NA) objective collects the out-of-plane p-polarized dark exciton emission43.
PL spectra of BN-encapsulated single-layer WSe2 device at 4.2 K. a Schematic of the BN-encapsulated single-layer WSe2. One piece of few-layer graphene (graphite) is used as the contact electrode and another piece is used as the transparent top-gate electrode. b The microscope image of the device. Scale bar: 10 µm. c PL spectra of the single-layer WSe2 for different excitation powers. The CW laser of wavelength 633 nm was used as the excitation source. d Integrated PL intensity of WSe2 as a function of the excitation power, and the XX and XX− peaks clearly exhibit a nonlinear power dependence with the power law close to 2
The most salient feature of the PL spectra in Fig. 1c is that, as the excitation power increases, additional PL peaks at 1.723 and 1.691 eV emerge. The integrated PL intensity of these two peaks, along with the exciton PL intensity, is plotted as a function of the excitation power in Fig. 1d. The power law dependence of the integrated PL intensity, expressed as I ∝ Pα, where I stands for the integrated PL intensity and P for the excitation power, is evidently different for the two new emergent peaks compared with that of the exciton. From the fitting to the experimental data in Fig. 1c, we obtained α = 1.94 for the peak at 1.723 eV and α = 1.82 for the peak at 1.691 eV, significantly larger than that of the exciton (α = 1.29) and close to what is expected for biexciton (α = 2).
The binding energy of the biexciton, ΔXX, is defined as the energy difference between the two excitons in the free state and the biexciton in the bound state. If we assume that the radiative recombination of the biexciton emits one photon, ΔXX is equal to the emitted photon energy of the free exciton (ħωX) minus the emitted photon energy of the biexciton (ħωXX), i.e., \(\Delta _{{\mathrm{XX}}} = \hbar \omega _{\mathrm{X}} - \hbar \omega _{{\mathrm{XX}}}\). Theoretical calculations have predicted the biexciton-binding energy to be ~20 meV33,34,44,45. The emerging PL peak at 1.723 eV lies 17 meV below the exciton peak, in excellent agreement with the predictions for the biexciton-binding energy. Considering the nearly quadratic (α = 1.94) power dependence of the PL intensity, we assign the peak at 1.723 eV to the true biexciton peak which we label as XX. The other emerging PL peak at 1.691 eV, 49 meV below the exciton peak, was recently reported as the biexciton peak20. Considering that the power law exponent α = 1.82, being close to the expected value of 2 for a biexciton, we interpret this peak as a negative charge bound biexciton XX−, based on the following PL spectra study as a function of the gate voltage. We note that the XX and XX− PL peaks are detected at as low excitation power as 40 µW, which corresponds to a power density of 1274 W/cm2 and an exciton density of 6×109/cm2 for a CW laser excitation centered at 633 nm (assuming that the absorption coefficient of WSe2 is 10% and the lifetime of bright exciton is around 15 ps2,46,47), significantly lower than what has been used to observe the previous “biexciton” peak, which either involves pulse laser excitation20 or CW laser excitation with large power25.
Gate-voltage-dependent PL spectra of WSe2
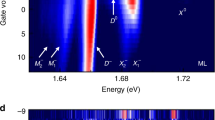
To investigate further the origin of the emerging PL peaks, we measured the PL spectra as a function of the carrier density using another device with an efficient top-gate enabling accurate tuning between the p-type and n-type doping regimes. The gate voltage-dependent PL spectra are shown as a color plot in Fig. 2a, in which the color represents the PL intensity. The PL spectra at specific gate voltages, corresponding to the line cuts in Fig. 2a, are shown in Fig. 2b. At the top gate voltage of −0.5 V (black line in Fig. 2b), the WSe2 is close to charge-neutral, and only two PL peaks are observed. The exciton (X0) peak is the most pronounced one centered at 1.724 eV, and the biexciton (XX) peak is located at 1.708 eV, thus indicating the 16 meV biexciton-binding energy for the second device. At the gate voltage of −2.5 V (magenta line in Fig. 2b), the WSe2 is strongly p-doped and the positive trion peak X+ occurs at 1.701 eV, while the exciton peak disappears. At the top gate voltage of 0.2 V (blue line in Fig. 2b), the WSe2 is n-doped, and the exciton peak is quenched. However, the two negative trion peaks emerge at 1.689 and 1.696 eV, which corresponds to the intravalley and intervalley trions, respectively39. Interestingly, the biexciton (XX) peak disappears, but the XX− peak at 1.676 eV appears.
PL spectra of WSe2 as a function of the top gate voltage. a Color plot of the PL spectra as a function of the top gate voltage. The color represents the PL intensity. Inset: enhanced color plot of the biexciton region. b PL spectra at the top gate voltage of −2.5, −0.5, and 0.2 V, corresponding to p-doped (magenta), intrinsic (black), and n-doped (blue) region. c Integrated PL intensity for X0, XX, X+, and \({\mathrm{X}}_1^ -\) as a function of the top gate voltage. It is evident that the XX only exists in the charge-neutral region while XX− exits in the lightly n-doped region
The sensitive gate dependence of the XX and XX− peaks closely correlates to the PL intensity of the exciton and trions. We plot the integrated PL intensity as a function of the gate voltage for different peaks in Fig. 2c. It is evident that the PL intensity of the exciton peak (black line in Fig. 2c) quickly vanishes in the strongly p-doped (VTG < −2.0 V) and n-doped (VTG > 0.5 V) regimes. The PL for the trions, both the positive and the negative ones, is sensitive to the gate voltage. The PL for the positive trion (X+, blue line) occurs when the gate voltage is less than −1.0 V, and the PL for the negative trions emerges when the gate voltage is greater than −0.5 V. This observation enables us to determine the charge-neutral region to be between −1.0 and −0.5 V, where the biexciton PL is peaked (red line in Fig. 2c). In contrast, the PL of XX− (purple line in Fig. 2c) does not show up in the charge-neutral region, and only emerges at higher gate voltage from −0.5 to 0.5 V (corresponding to the slightly n-doped region). Considering the doping dependence of XX− PL and its characteristic intensity power law, we assign XX− to an electron-bound biexciton.
Valley-polarized PL spectra
The detailed valley configuration of XX and XX− can be probed using the circularly polarized PL spectroscopy, where we selectively excite and probe a particular valley of WSe2. The band structure at the K and K′ valleys for WSe2 is shown in Fig. 3b. It is worth noting that the spin–orbit coupling not only gives rise to the large spin splitting in the valence band but also generates a splitting on the order of tens of meV in the conduction band4,5,6,7,48,49. For WS2 and WSe2, this splitting leads to an opposite spin configuration between the conduction band minimum (CBM) and the valence band maximum (VBM) in the same valley, hosting a ground state exciton which is optically dark40,42. We excited the device with circularly polarized light, such as right circularly polarized light (σ+), and detected the PL emission with the same or opposite helicity. The valley polarization, defined as the ratio of right circular and left circular components of the emitted PL, i.e.,\(\it P = \frac{{I_{{\mathit \sigma} ^ {\mathrm +} } - I_{{\mathit \sigma} ^ - }}}{{I_{{\mathit \sigma} ^ {\mathrm +} } {\mathrm +} I_{{\mathit \sigma} ^ - }}}\), measures the capability of the TMD to maintain the valley information. Interestingly, XX and XX−exhibit higher valley polarization of 0.19 and 0.20, respectively, both higher than the valley polarization of the exciton (0.12), as shown in Fig. 3a. This valley polarization suggests that both XX and XX− involve a bright exciton in the K valley, which we excited with σ+ light. Since XX− is a five-particle complex, the lowest energy configuration that maintains the valley polarization can only be the one shown in Fig. 3b. This configuration can be viewed as a biexciton bound to a free electron, or equivalently, a trion bound to one dark exciton. The negative charge bound biexciton is thus effectively a trion–exciton complex (negative trion). The biexciton state of XX is composed of four particles, and one possible configuration is shown in Fig. 3c, with one bright exciton in K valley and one dark exciton in K’ valley. One alternative configuration is shown in the SI (Supplementary Figure 3e). Our following magneto-PL spectroscopy study confirms that the configuration shown in Fig. 3c is the right configuration for XX.
Valley-polarized PL spectra and biexciton configurations. a PL spectra with circularly polarized (σ+) excitation and the same (σ+) or opposite (σ−) helicity detection. Valley polarization, defined as \(\frac{{I_{\sigma ^ + } - I_{\sigma ^ - }}}{{I_{\sigma ^ + } + I_{\sigma ^ - }}}\), where I is the integrated PL intensity, is calculated for exciton (0.12), biexciton (0.19), and electron-bound biexciton (0.20). b, c Trion–exciton and biexciton configurations with the solid dots being the electron and the empty one being the hole. Blue color stands for spin up and orange for spin down
Magneto-PL spectra of WSe2
In the presence of an out-of-plane magnetic field, the degeneracy of the K and K′ valleys is lifted, and the spectra of K (K′) valley can be selectively accessed through σ+(σ−) excitation with σ+(σ−) detection configuration as shown in Fig. 4d. The PL spectra as a function of the magnetic field for different valleys are shown in Fig. 4a (σ−σ−) and in Fig. 4b (σ+σ+) as a color plot. It is evident that the PL peak positions (dashed lines) in Fig. 4a, b exhibit a linear shift as a function of the B field due to the Zeeman shift, and the slope is opposite in sign for the (σ+σ+) and (σ−σ−) configurations. The opposite Zeeman shifts for the different valleys result in a Zeeman splitting of the PL peaks in the spectra, as shown in Fig. 4d. The Zeeman splitting between the two valleys can be expressed as \(\Delta = \Delta _{\sigma ^ + \sigma ^ + } - \Delta _{\sigma ^ - \sigma ^ - } = g\mu _{\mathrm{B}}B\), where the \(\mu _{\mathrm{B}}\) is the Bohr magneton, which is about 58 µeV/T, and \(\Delta _{\sigma ^ + \sigma ^ + }(\Delta _{\sigma ^ - \sigma ^ - })\) is the Zeeman shift in the σ+σ+(σ−σ−) configuration. Linear fitting of the experimentally obtained Zeeman splitting Δ as a function of the B field (Fig. 4c) determines that the g-factor for the exciton (black dots in Fig. 4c) is −3.64 ± 0.08. Our experimentally extracted value is in good agreement with the theoretical calculation gX = −4.0 (Supplementary Table 1), and it is also consistent with previous reports7,50,51. The PL emission of XX and XX− involves the recombination of one bright exciton, and the expected g factor should be the same as that for the exciton. We obtained a XX g-factor (Fig. 4c) of −4.03 ± 0.07 and a XX− g-factor of −5.33 ± 0.18 in Fig. 4c, also in good agreement with the theoretical expectation. The deviation from the theoretical expectations is potentially due to the increased Coulomb interaction in the many-particle complex, which is not taken into account in the theoretical calculations30,31.
Magneto-PL spectra of WSe2. a, b Color plot of the PL spectra of WSe2 as a function of B field at 4.2 K for the σ−σ− and σ+σ+ configuration. The dashed lines are the eye guide to the shift of different PL peaks. c g-factors for different peaks calculated from the Zeeman splitting between the σ−σ− and σ+σ+ states as a function of B field, extracted from the magneto-PL spectra in a and b. d PL spectra for (σ−) excitation and σ+(σ−) detection of exciton, biexciton and trion–exciton complexes, respectively (B = 17 T)
The PL intensity ratio of the two Zeeman splitted states (σ+σ+ and σ−σ−) in the B field provides insight into the detailed configuration of the biexciton. The Zeeman splitting lifts the energy degeneracy at the K and K′ valleys and creates two states with the energy difference of \(\Delta = g\mu _{\mathrm{B}}B\), which leads to unequal complex population of the two states, and hence, different PL emission intensities. We use the quasi-thermal equilibrium picture for a qualitative understanding of the PL difference for the σ+σ+ and σ−σ− configurations. The exciton PL intensity in the B field, shown in Fig. 4d, is higher in the state that emits photon with the lower energy (σ−σ−), consistent with the quasi-thermal equilibrium picture. We emphasize, however, a quantitative understanding is not easily accessible because of the short exciton lifetime and the finite intervalley scattering complicates the exact thermal equilibrium of the two states. In contrast to the behavior of the exciton, the spectrally higher energy state for biexciton (XX) at ~1.726 eV exhibits much higher PL intensity than that of the lower energy state in the spectra, as shown in Fig. 4d. The apparent contradiction arises from the fact that the real energy difference between the two Zeeman splitted states for the biexciton (or other high-order excitonic complex) is determined by the total g-factor, gt, which should include the contributions from all the constituent particles. On the contrary, the emission photon energy in PL is only determined by the bright exciton which radiatively recombines to emit a photon, and hence the PL peak position difference between the two states is determined by the spectral g-factor, gs. The difference between the total g factor (gt) and the spectral g-factor (gs) indicates that the spectrally lower energy state is not necessarily lower in total energy.
We can calculate the total g-factor for the biexciton to be \(g_{{\mathrm{XX}}}^{\mathrm{t}} = 4.0\) for the configuration in Fig. 3c (Supplementary Table 1), which has the opposite sign of the spectral g-factor of gs = −4.03 ± 0.07 (experiment) or −4.0 (theory). The positive total g-factor means that the spectrally higher energy state (PL peak emits higher energy photon) actually has overall lower energy and should have higher PL intensity. This idea is consistent with our observation in Fig. 4d (XX panel). The alternative configuration involving the intervalley dark exciton has a total g-factor of zero (Supplementary Table 1), and it cannot explain the drastic biexciton PL intensity difference between the σ+σ+ and σ−σ− configurations. The total g-factor for the XX− state is calculated to be 6.0 (Supplementary Table 1), which is also opposite in sign to the spectral g-factor of –5.33 ± 0.18 (experiment). Therefore, for the XX− state, σ−σ− configuration is also lower in total energy and should have higher PL intensity, which is consistent with our observation (Fig. 4d).
It is interesting to note that the magneto-PL spectra of the dark exciton state at 1.691 eV are intrinsically different from other PL peaks. While all other states exhibit a single peak in the circularly polarized detection scheme, the emission from the dark exciton splits into two peaks in the B field (magenta lines in Fig. 4a, b). This is because that the optical selection rule in TMDs originates from the conservation of the out-of-plane quasi angular momentum with respect to the three-fold rotational symmetry. However, the optically dark exciton can only couple to an out-of-plane optical field, which has zero out-of-plane angular momentum. Therefore, responses from both valleys can be excited and detected simultaneously, which were detected by an objective with large NA and showed up as the two separate peaks in the spectra. The spectra g-factor of the dark exciton is experimentally determined to be −9.75 ± 0.18 (Fig. 4c), in good agreement with the expected value of −8.0 (Supplementary Table 1) and the experimental result with the g-factor of −9.4 ± 0.152. The unique behavior of the dark exciton confirms that the emission from the excitonic complexes of biexciton and trion–exciton both originate from a bright exciton.
Discussion
In summary, we have fabricated a high-quality single-layer WSe2 device by employing BN encapsulation, and revealed both the biexciton and (negative) trion–exciton complexes through low-temperature PL spectroscopy. The binding energy of the biexciton in the BN-encapsulated single-layer WSe2 is determined to be about 16–17 meV, in agreement with the theoretical calculations30,31 and previous coherent pump-probe measurements28,29. The biexciton state only exists in charge-neutral WSe2, and the trion–exciton complex only emerges in lightly n-doped WSe2. Improved understanding of the high-order excitonic complexes in high-quality WSe2 devices will enable further investigation of many-body physics and furnish new opportunities for novel quantum optoelectronics based on TMDs. During finalization of the manuscript, we became aware of a related recent work53.
Data availability
The data that support the findings of this study are available from the authors on reasonable request, see author contributions for specific data sets.
References
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 8, 634–638 (2013).
Li, Y. et al. Valley splitting and polarization by the zeeman effect in monolayer MoSe2. Phys. Rev. Lett. 113, 1–5 (2014).
Macneill, D. et al. Breaking of valley degeneracy by magnetic field in monolayer MoSe2. Phys. Rev. Lett. 114, 1–5 (2015).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2. Nat. Phys. 11, 148–152 (2015).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nat. Phys. 11, 141–147 (2015).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 494–498 (2012).
Gong, Z. et al. Magnetoelectric effects and valley-controlled spin quantum gates in transition metal dichalcogenide bilayers. Nat. Commun. 4, 1–6 (2013).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat. Commun. 3, 885–887 (2012).
Ye, Z., Sun, D. & Heinz, T. F. Optical manipulation of valley pseudospin. Nat. Phys. 13, 26–29 (2017).
Plechinger, G. et al. Trion fine structure and coupled spin-valley dynamics in monolayer tungsten disulfid. Nat. Commun. 7, 1–9 (2016).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2. Nat. Mater. 12, 207–211 (2012).
Ross, J. S. et al. Electrical control of neutral and charged excitons in a monolayer semiconductor. Nat. Commun. 4, 1–8 (2013).
Courtade, E. et al. Charged excitons in monolayer WSe2: experiment and theory. Phys. Rev. B 96, 1–12 (2017).
Qiu, D. Y., Da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: Many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 1–5 (2013).
Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014).
You, Y. et al. Observation of biexcitons in monolayer WSe2. Nat. Phys. 11, 477–481 (2015).
Okada, M. et al. Observation of biexcitonic emission at extremely low power density in tungsten disulfide atomic layers grown on hexagonal boron nitride. Sci. Rep. 7, 1–7 (2017).
Plechinger, G. et al. Identification of excitons, trions and biexcitons in single-layer WS2. Phys. Status Solidi Rapid Res. Lett. 9, 457–461 (2015).
Qin, Q. et al. Excited state biexcitons in atomically thin MoSe2. ACS Nano 11, 7468–7475 (2017).
Shang, J. et al. Observation of excitonic fine structure in a 2D transition-metal dichalcogenide semiconductor. ACS Nano 9, 647–655 (2015).
Nagler, P. et al. Zeeman splitting and inverted polarization of biexciton emission in monolayer WS2. Phys. Rev. Lett. 121, 057402 (2018).
Lee, Y. H. & Kim, J. Biexciton emission from edges and grain boundaries of triangular WS2 monolayers. ACS Nano 10, 2399–2405 (2016).
Paradisanos, I. et al. Room temperature observation of biexcitons in exfoliated WS2 monolayers. Appl. Phys. Lett. 110, 193102 (2017).
Steinhoff, A. et al. Biexciton fine structure in monolayer transition metal dichalcogenides. Preprint at https//arxiv.org/abs/1801.04225 (2018).
Hao, K. et al. Neutral and charged inter-valley biexcitons in monolayer MoSe2. Nat. Commun. 8, 1–7 (2017).
Fang, S. et al. Ab initio tight-binding Hamiltonian for transition metal dichalcogenides. Phys. Rev. B. 92, 1–15 (2015).
Rybkovskiy, D. V., Gerber, I. C. & Durnev, M. V. Atomically inspired k·p approach and valley Zeeman effect in transition metal dichalcogenide monolayers. Phys. Rev. B. 155406, 1–9 (2016).
Kidd, D. W., Zhang, D. K. & Varga, K. Binding energies and structures of two-dimensional excitonic complexes in transition metal dichalcogenides. Phys. Rev. B. 93, 1–10 (2016).
Kylänpää, I. & Komsa, H. P. Binding energies of exciton complexes in transition metal dichalcogenide monolayers and effect of dielectric environment. Phys. Rev. B. 92, 1–6 (2015).
Mayers, M. Z., Berkelbach, T. C., Hybertsen, M. S. & Reichman, D. R. Binding energies and spatial structures of small carrier complexes in monolayer transition-metal dichalcogenides via diffusion Monte Carlo. Phys. Rev. B. 92, 1–5 (2015).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Zhang, Z. et al. Robust epitaxial growth of two-dimensional heterostructures, multiheterostructures, and superlattices. Science 6814, 1–9 (2017).
Cadiz, F. et al. Excitonic linewidth approaching the homogeneous limit in MoS2-based van der Waals heterostructures. Phys. Rev. X. 7, 1–12 (2017).
Yu, H., Liu, G., Gong, P., Xu, X. & Yao, W. Dirac cones and Dirac saddle points of bright excitons in monolayer transition metal dichalcogenides. Nat. Commun. 5, 1–7 (2014).
Jones, A. M. et al. Excitonic luminescence upconversion in a two-dimensional semiconductor. Nat. Phys. 12, 1–11 (2016).
Zhang, X. X. et al. Magnetic brightening and control of dark excitons in monolayer WSe2. Nat. Nanotechnol. 12, 883–888 (2017).
Zhou, Y. et al. Probing dark excitons in atomically thin semiconductors via near-field coupling to surface plasmon polaritons. Nat. Nanotechnol. 12, 856–860 (2017).
Zhang, X. X., You, Y., Zhao, S. Y. F. & Heinz, T. F. Experimental evidence for dark excitons in monolayer WSe2. Phys. Rev. Lett. 115, 1–6 (2015).
Wang, G. et al. In-plane propagation of light in transition metal dichalcogenide monolayers: optical selection rules. Phys. Rev. Lett. 047401, 1–7 (2017).
Zhang, D. K., Kidd, D. W. & Varga, K. Excited biexcitons in transition metal dichalcogenides. Nano Lett. 15, 7002–7005 (2015).
Szyniszewski, M., Mostaani, E., Drummond, N. D. & Fal’Ko, V. I. Binding energies of trions and biexcitons in two-dimensional semiconductors from diffusion quantum Monte Carlo calculations. Phys. Rev. B. 95, 1–5 (2017).
Cui, Q., Ceballos, F., Kumar, N. & Zhao, H. Transient absorption microscopy of monolayer and bulk WSe2. ACS Nano 8, 2970–2976 (2014).
Bernardi, M., Palummo, M., Grossman, C. & Scienti, R. Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 13, 3664–3670 (2013).
Kormányos, A., Zólyomi, V., Drummond, N. D. & Burkard, G. Spin-orbit coupling, quantum dots, and qubits in monolayer transition metal dichalcogenides. Phys. Rev. X. 4, 1–16 (2014).
Wang, G. et al. Spin-orbit engineering in transition metal dichalcogenide alloy monolayers. Nat. Commun. 6, 1–7 (2015).
Mitioglu, A. A. et al. Optical investigation of monolayer and bulk tungsten diselenide (WSe2) in high magnetic fields. Nano Lett. 15, 4387–4392 (2015).
Wang, G. et al. Magneto-optics in transition metal diselenide monolayers. 2D Mater. 2, 034002 (2015).
Robert, C. et al. Fine structure and lifetime of dark excitons in transition metal dichalcogenide monolayers. Phys. Rev. B. 155423, 1–8 (2017).
Chen, S.Y., Goldstein, T., Taniguchi, T., Watanabe, K. & Yan, J. Coulomb-bound four- and five-particle valleytronic states in an atomically-thin semiconductor. Preprint at https://arxiv.org/abs/1802.10247 (2018).
Acknowledgements
The device fabrication was supported by Micro and Nanofabrication Clean Room (MNCR), operated by the Center for Materials, Devices, and Integrated Systems (cMDIS) at Rensselaer Polytechnic Institute (RPI). S.-F.S. acknowledges support from the Air Force Office of Scientific Research through Grant FA9550-18-1-0312. Z.Lu. and D.S. acknowledge support from the US Department of Energy (DE-FG02-07ER46451) for magneto-photoluminescence measurements performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation through NSF/DMR- 1157490, NSF/DMR-1644779, and the State of Florida. S.B.Z. was supported by the US Department of Energy under Grant No. DE-SC0002623. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and the CREST (JPMJCR15F3), JST. We thank Prof. Feng Wang, Prof. Ronald Hedden, Prof. Jun Yan, Dr. Long Ju, Ting Cao, and Debjit Ghoshal for helpful discussions.
Author information
Authors and Affiliations
Contributions
S.-F.S. conceived the experiment. Z.L., Y.M., Y.C., and Z.L. fabricated the devices. K.W. and T.T. grew the h-BN crystal. Z.L., T.W. and Z.L. performed the measurements. S.-F.S., Z.L., T.W., C.J. and Y.C. analyzed the data. S.-F.S. supervised the project. S.-F.S. wrote the manuscript with the input from all the other co-authors. All authors discussed the results and contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Z., Wang, T., Lu, Z. et al. Revealing the biexciton and trion-exciton complexes in BN encapsulated WSe2. Nat Commun 9, 3719 (2018). https://doi.org/10.1038/s41467-018-05863-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05863-5
This article is cited by
-
Raman scattering excitation in monolayers of semiconducting transition metal dichalcogenides
npj 2D Materials and Applications (2024)
-
Dipolar many-body complexes and their interactions in stacked 2D heterobilayers
Nature Reviews Physics (2024)
-
Atomic-scale visualization of the interlayer Rydberg exciton complex in moiré heterostructures
Nature Communications (2024)
-
Excitonic Complexes in Two-Dimensional Transition Metal Dichalcogenides
Nature Communications (2023)
-
Essential role of momentum-forbidden dark excitons in the energy transfer responses of monolayer transition-metal dichalcogenides
npj 2D Materials and Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.