Abstract
The fracture toughness of glassy materials remains poorly understood. In large part, this is due to the disordered, intrinsically non-equilibrium nature of the glass structure, which challenges its theoretical description and experimental determination. We show that the notch fracture toughness of metallic glasses exhibits an abrupt toughening transition as a function of a well-controlled fictive temperature (Tf), which characterizes the average glass structure. The ordinary temperature, which has been previously associated with a ductile-to-brittle transition, is shown to play a secondary role. The observed transition is interpreted to result from a competition between the Tf-dependent plastic relaxation rate and an applied strain rate. Consequently, a similar toughening transition as a function of strain rate is predicted and demonstrated experimentally. The observed mechanical toughening transition bears strong similarities to the ordinary glass transition and explains the previously reported large scatter in fracture toughness data and ductile-to-brittle transitions.
Similar content being viewed by others
Introduction
The fracture toughness quantifies a material’s ability to resist catastrophic failure in the presence of a crack. It is of enormous practical importance, as it is a major limiting factor in the structural integrity of a broad range of natural and engineering systems, and of great fundamental importance, as it challenges our understanding of the strongly non-linear and dissipative response of materials under the extreme conditions prevailing near defects1. Understanding the fracture toughness of glassy materials, which lack long-range crystalline order and are characterized by intrinsically disordered non-equilibrium structures, is a pressing problem in general and particularly for metallic glasses (MGs)2.
MGs constitute a relatively new and broad class of amorphous materials with a combination of plastic-like processability and exceptional strength and elasticity—superior to their crystalline counterparts—holding great promise for wide-ranging structural and functional applications3,4,5,6. A major impediment, however, for their widespread usage as structural materials is not their strength, but rather their often low and highly variable fracture toughness3.
Progress in understanding, predicting, and controlling the fracture toughness of MGs has been, on the whole, limited by the lack of: first, a theoretical understanding of the intrinsically disordered, non-equilibrium glassy states of matter; second, techniques to generate well-reproduced, well-defined glassy states; and third, accurate and reproducible fracture toughness samples and measurements. Glasses are non-equilibrium materials featuring disordered atomic structures whose properties are processing and history dependent6,7. From a theoretical perspective, currently there exists no general framework to quantify the disordered atomic structures of glasses and no complete understanding of the relation between these structures and glassy dynamics, most notably, irreversible plastic deformation that occurs in response to external driving forces. From an experimental perspective, carefully and reproducibly controlling the state of a glass and realizing these states in mechanical test samples has been very challenging, and has hampered accurate and reproducible fracture toughness measurements2.
Here, we show that the notch fracture toughness of MGs exhibits an abrupt toughening transition as a function of the fictive temperature (Tf), whereas the ordinary temperature plays a secondary role. This observed mechanical toughening transition, which we theoritically explain, bears strong similarities to the ordinary glass transition and explains the previously reported large scatter in fracture toughness data and ductile-to-brittle transitions. The presented results open the way for a broader usage of tougher and well-reproducible MGs as structural materials.
Results
Fracture toughness sample synthesis of well-controlled T f
We use a thermoplastic forming (TPF) method that allows precise and reproducible measurements of the notch fracture toughness. Specifically, we thermoplastically mold MGs into single edge notch tension (SENT) fracture toughness samples. The selected geometry and particular notch radius of the samples were kept constant for all of the experiments reported in this work (see Methods). The glass was then heated to a temperature Tf, in the vicinity of the calorimetric glass transition temperature (Tg), and annealed at this temperature for a time that exceeds the structural relaxation time (τSR) at Tf, ensuring full equilibration (see Methods). Subsequently, the glass was rapidly quenched to room temperature at a rate exceeding (Tf−Tg)/τSR in order to minimize structural relaxation during the quench. The fictive temperature is also calculated through heat capacity measurements to verify that it identifies with the annealing temperature for the considered protocol8,9 (see Supplementary Fig. 6).
This protocol yields glasses whose metastable structural state is well characterized by Tf—a temperature characterizing the structural degrees of freedom of the glass where it has fallen out-of-equilibrium (often referred to as the fictive temperature10,11 or glass-transition-upon-cooling)—which is different from the calorimetric glass transition temperature, Tg. Tf is set by the annealing time and is maintained through fast cooling to avoid relaxation to a lower Tf upon cooling to the test temperature T. Tg, as typically used for MGs, is determined upon heating with rates of typically 20 K/min (0.3 K/s). The magnitude of thermal fluctuations, on the other hand, is determined by the ordinary temperature (T). Whereas the ordinary temperature T characterizes the vibrational degrees of freedom of the glass that quickly equilibrate with the heat reservoir, Tf encapsulates the glass structure which is affected by its annealing and fabrication history. Our preparation protocol results in highly precise and reproducible glassy states, and consequently toughness measurements, with insignificant sample-to-sample variations. Measurements of the notch fracture toughness (KQ) were carried out for glasses with Tf varied by ~100 K around Tg, which corresponds to more than six orders of magnitude in relaxation times, and T was varied over ~500 K, from 77 K to 573 K, and at a given applied strain rate (\(\dot\varepsilon\)) as a function of Tf. These measurements allow us to disentangle the dependence of KQ on a well-defined and controlled non-equilibrium structural state of a glass encoded in Tf and on thermal vibrations quantified by T, probing the unique properties of glasses. Three MGs—Zr44Ti11Ni10Cu10Be25 (Tg = 623 K), Pd43Cu27Ni10P20 (Tg = 578 K), and Pt57.5Cu14.7Ni5.3P22.5 (Tg = 503 K)—were studied. These MGs were selected since they include representatives of the two primary classes of MGs, metal–metal and metal–metalloid alloys6, which exhibit a wide range of toughness and fragility levels12, and varying degrees of β relaxation13.
Abrupt transition of the fracture toughness as a function of T f
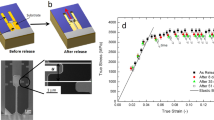
We first determined the fracture toughness as a function of the fictive temperature by fixing T = 300 K (room temperature), well below Tg for all three MGs, and varied Tf. KQ(T = 300 K, Tf) for a fixed strain rate of 10-4/s for all three glasses is shown in Fig. 1a. KQ exhibits an abrupt toughening transition between a brittle-like regime below a threshold value of Tf (\(T_{\mathrm{f}}^{\mathrm{DB}}\)) and a ductile-like regime above it. The degree of toughening across the transition is dramatic for all three MGs and can be as high as ~260% (for Zr44Ti11Ni10Cu10Be25). Such transition as a function of the fictive temperature, which is our main finding, has not been previously reported and is significantly more pronounced than the ductile-to-brittle transition observed for different ordinary temperatures (Fig. 1b)14,15,16. Note, though, that earlier work did indicate that structural relaxation affects the ductility of MGs17. The MG-specific threshold for which KQ(Tf) starts to increase rapidly is surprisingly close to Tg for all three MGs, which may already suggest some relation to the ordinary glass transition. The transition is accompanied by a significant increase in the plastic zone size prior to catastrophic failure, as shown in Fig. 1c for Zr44Ti11Ni10Cu10Be25. We hypothesize that the brittle-like and ductile-like behaviors observed in Fig. 1a are associated with different microscopic failure mechanisms, which should have distinct fractographic signatures below vs. above the transition. To test this hypothesis, we performed scanning electron microscope scans of the post-mortem fracture surfaces. The resulting images for Zr44Ti11Ni10Cu10Be25 are shown in Fig. 1d for the same Tf values considered in Fig. 1c. The revealed fracture surface morphology exhibits a marked transition from dimple structures, previously reported to be associated with brittle fracture18, below \(T_{\mathrm{f}}^{\mathrm{DB}}\), to river-like patterns above \(T_{\mathrm{f}}^{\mathrm{DB}}\), which have been associated with ductile fracture19. This change in fracture surface morphology coincides with the transition in KQ observed in Fig. 1a. In fact, quite remarkably, at the transition, dimple structures and river-like patterns appear to coexist (sub-panel for Tf/Tg = 1 in Fig. 1d). A similar fractographic behavior of the fractured surface of Pd43Cu27Ni10P20 and Pt57.5Cu14.7Ni5.3P22.5 was also observed (Supplementary Fig. 1).
The notch fracture toughness of metallic glasses exhibits a dramatic transition as a function of fictive temperature, Tf. a The notch fracture toughness KQ, normalized by its minimal value KQ,min, as a function of Tf, normalized by the glass temperature Tg, for Zr44Ti11Ni10Cu10Be25 (black squares), Pd43Cu27Ni10P20 (red circles), and Pt57.5Cu14.7Ni5.3P22.5 (blue triangles). The error bars represent 1 standard deviation of five samples per data point. The dashed lines serve as a guide to the eye. b KQ for Zr44Ti11Ni10Cu10Be25 as a function of Tf (measured at room temperature, black symbols—bottom axis) and T (red symbols—top axis, measured at T) with Tf = 683 K >\(T_{\mathrm{f}}^{\mathrm{DB}}\) (red circles) and Tf = 583 K <\(T_{\mathrm{f}}^{\mathrm{DB}}\) (red triangles). The dashed lines represent polynomial fits of the data. c The plastic zone ahead of the notch root just prior to failure of Zr44Ti11Ni10Cu10Be25 for several Tf. Dimension lines indicate the plastic zone size. For Tf < \(T_{\mathrm{f}}^{\mathrm{DB}}\), the plastic zone is small, while for Tf > \(T_{\mathrm{f}}^{\mathrm{DB}}\) it is significantly larger. The plastic zone is symmetric with respect to the main axis of the notch (darker areas are optical effects). The scale bars are 100 μm. d The fracture morphology of Zr44Ti11Ni10Cu10Be25 for various Tf. As the threshold \(T_{\mathrm{f}}^{\mathrm{DB}}\) is surpassed (top right), the fracture morphology changes from fractal-like structures (characteristic of brittle-like fracture) to river-like patterns (characteristic of ductile-like fracture). The scale bars are 50 μm
Comparison of the T f and T dependence of the fracture toughness
One may ask whether the observed toughening (ductile-to-brittle) transition that occurs as a function of Tf (Fig. 1a) is related to the previously reported ductile-to-brittle transition in MGs that occurs as a function of the ordinary temperature T13,17,20. We directly compare the dependence of KQ on T in Fig. 1b to the dependence of KQ on Tf in Fig. 1a by also measuring KQ as a function of T for Zr44Ti11Ni10Cu10Be25, spanning a temperature region from 77 to 573 K. Similar experiments were also conducted for Pd43Cu27Ni10P20 (Supplementary Fig. 2). We find that the variation of KQ with Tf is significantly larger than the negligible variation of KQ with T over the same temperature range (Fig. 1b), highlighting the structural nature of the transition. These results lead us to conclude that the fracture toughness of MGs is qualitatively and dramatically more sensitive to the non-equilibrium structural state of the glass quantified by Tf than to the (ordinary) temperature T (at least down to very low ordinary temperatures compared to \(T_{\mathrm{f}}^{\mathrm{DB}}\), where another transition might take place, see the red data points at the liquid nitrogen temperature in Fig. 1b).
Variation of structural and response quantities with T f
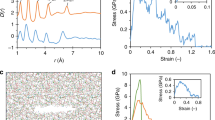
To understand the origin of the abrupt and dramatic transition as a function of Tf, we studied other structural and response quantities of glasses as a function of Tf. Specifically, we quantified the enthalpy recovery, the shear modulus (G), and the atomic pair distribution function (G(r)), and its response to applied stress21,22 for Zr44Ti11Ni10Cu10Be25 as a function of Tf. Enthalpy recovery, which has been associated with free volume23 and the ductile-to-brittle transition17, varies significantly, by more than an order of magnitude over the Tf range we considered (Fig. 2a). However, this variation occurs smoothly, without abrupt changes, particularly near Tf/Tg = 0.98, where KQ exhibits a strong variation with Tf (cf. Fig. 1a). G, which has been widely associated with ductility and fracture toughness of MGs24, decreases gradually as Tf increases (Fig. 2b). The inset shows the variation of G with T at a fixed Tf = 593 K, which is one order of magnitude smaller than the reduction in G as a function of Tf. High-energy X-ray diffraction measurements were used to extract the radial distribution function G(r) as a function of Tf (inset of Fig. 2c). More information on the structure function and pair distribution function of different fictive temperatures glasses is shown in Supplementary Figs. 3–4. The amplitude of the first peak of G(r), shown in Fig. 2c, exhibits a mild and gradual variation with Tf. The elastic heterogeneity of Zr44Ti11Ni10Cu10Be25 under uniaxial stress was measured through the anisotropy of the pair distribution function (∣Y∣)25 (see Methods for a precise definition of ∣Y∣). ∣Y∣, shown in Fig. 2d, also exhibits a rather mild and gradual variation with Tf. Therefore, we conclude that these structural and response quantities do not reveal any signature of the abrupt increase as a function of Tf that is exhibited by KQ.
Structural and response quantities of the Zr44Ti11Ni10Cu10Be25 metallic glass exhibit gradual changes as a function of Tf. a Enthalpy recovery as a function of Tf obtained from differential scanning calorimetry of SENT fracture toughness samples. The error bars are quantified by 1 standard deviation from three samples. b The shear modulus G as a function of Tf, obtained from dynamic mechanical analysis at room temperature. (inset) G as a function of T at fixed Tf = 593 K. c The amplitude of the first peak of the pair distribution function G(rp) as a function of Tf. (inset) The pair distribution function G(r) for the two extreme cases: Tf = 573 and 683 K. d The anisotropy ∣Y∣of the pair distribution function under a compressive stress of 1 GPa as a function of Tf (see Methods for the precise definition of ∣Y∣)
Mechanical glass transition
What is then the physical origin of the Tf-dependent toughening transition observed in Fig. 1a? On the one hand, the transition is clearly sensitive to the initial non-equilibrium structural state of the glass, as quantified by Tf (Fig. 1a). On the other hand, several structural and response quantities (Fig. 2), which are often associated with the toughness of glasses, do not change significantly around a MG-specific value of \(T_{\mathrm{f}}^{\mathrm{DB}}\). Taken together, these results suggest that the initial non-equilibrium structural state of the glass plays a crucial, but not exclusive, role in the observed toughening transition. Following the theoretical work of refs. 26,27, we propose that the origin of this toughening transition is a competition between two time scales. The time scales involved are the plastic deformation time scale (τplastic), which controls the plastic dissipation in the vicinity of the notch where stresses are close to the yield strength, and the loading time scale (\(\tau_{\dot\varepsilon}\)), which is inversely proportional to the applied strain rate. τplastic is inversely proportional to the density of plasticity carriers (i.e., shear transformation zones, sometimes also related to concepts such as soft spots28,29, flexibility volume30, core-shells31, and flow units32,33,34), which is a strongly increasing function of Tf and a much weaker increasing function of T27. It has been proposed that τplastic also depends on the local stress, as it provides the activation energy for plastic rearrangements27,35.
Indeed, we found that glasses which are tested at significantly different temperatures T fail under the same macroscopic conditions, indicating that the aforementioned dependence of τplastic on the local stresses and Tf is much stronger than on T. Specifically for Zr44Ti11Cu10Ni10Be25 with Tf = 593 K and T = 593 K, we measured KQ = 45.2 ± 3 MPa m1/2, which is, within experimental error, identical to KQ = 43.2 ± 3 MPa m1/2 measured for Zr44Ti11Cu10Ni10Be25 at Tf = 593 K and T = 300 K (see empty circle symbols in Fig. 1b). As the local stresses (set by the sample’s geometry and the external loading) and T are identical in both cases these results reveal a significantly higher sensitivity of τplastic, and hence of KQ, to the intense stresses near the notch and Tf compared to T, which has been also observed for Pd43Cu27Ni10P20 MG.
The time scale that competes with τplastic is the inverse of the strain rate, \(\dot\varepsilon\), in the plastic zone, \(\tau_{\dot\varepsilon}, \tau_{\dot\varepsilon} \propto {\dot\varepsilon}^{-1}\). In the brittle-like regime, we expect the glass response to be predominantly elastic, with limited plastic relaxation of stresses, corresponding to τplastic >> \(\tau_{\dot\varepsilon}\). In the ductile-like regime, we expect more extensive plastic deformation, corresponding to τplastic << \(\tau_{\dot\varepsilon}\). As \(\tau_{\dot\varepsilon}\) is independent of Tf and τplastic is a strongly decreasing function of Tf, an abrupt toughening transition, qualitatively similar to the one observed experimentally (Fig. 1a), is expected to occur when τplastic ≈ \(\tau_{\dot\varepsilon}\). Furthermore, as τplastic is also a function of T, yet a much weaker function compared to Tf27, we expect a rather mild decrease of the toughness with T, consistent with previously reported ductile-to-brittle transitions, as well as with our KQ(T) data (Fig. 1b and Supplementary Fig. 2).
This theoretical picture suggests that the fracture toughness of glasses is not an entirely intrinsic material property, as it predicts a dependence on the externally applied strain rate \(\dot\varepsilon\). The proposed crossover of time scales suggests that for fixed Tf (and T), KQ exhibits an abrupt toughening transition when \(\dot\varepsilon\) drops below a MG-specific threshold value. To test this important prediction, we performed measurements of KQ for the Zr44Ti11Ni10Cu10Be25 MG over a wide range of strain rates \(\dot\varepsilon\) for two values of Tf (both below and above the transition in Fig. 1a). The results, presented in Fig. 3, reveal a Tf-dependent toughening transition with decreasing \(\dot\varepsilon\), as suggested by the proposed crossover of time scales.
The fracture toughness of metallic glasses also exhibits a toughening transition with decreasing strain rate. KQ as a function of strain rate \(\dot\varepsilon\) for Zr44Ti11Ni10Cu10Be25 with Tf/Tg = 1.06 (Tf > \(T_{\mathrm{f}}^{\mathrm{DB}}\), black squares) and Tf/Tg = 0.95 (Tf < \(T_{\mathrm{f}}^{\mathrm{DB}}\), red circles). The error bars represent 1 standard deviation calculated from three samples
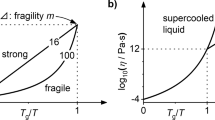
These results suggest that the toughening transition observed in Figs. 1a and 3 may be viewed as a mechanical glass transition in analogy with the conventional glass transition (Fig. 4). With this interpretation, the role of the structural relaxation time, τSR, in the conventional glass transition is played by τplastic and the role of the cooling rate, \(\dot R\), in the conventional glass transition is played by \(\dot\varepsilon\). The corresponding role of the thermodynamic quantity that is used to probe the conventional glass transition as a function of T, e.g., the enthalpy H, is KQ(Tf) in the mechanical glass transition.
Analogy between the conventional glass transition and the mechanical glass transition based on a crossover of time scales. a The conventional glass transition, probed by the dependence of the enthalpy on T, originates from a competition between the internal structural relaxation time, τSR, and the external time scale set by the cooling rate, \(\tau_{\dot R} \). The glass transition occurs approximately at τSR ≈ \(\tau_{\dot R} \). b In analogy to the conventional glass transition, the mechanical glass transition (probed by the dependence of the fracture toughness on Tf) originates from the competition between the plastic relaxation time scale, τplastic, and the (near notch) deformation time scale, \(\tau_{\dot\varepsilon}\), which is proportional to the applied strain rate. c A ductile-to-brittle transition can also be observed as a function of temperature, as τplastic is also a weak function of T, but it is significantly less pronounced than the toughening transition as a function of Tf
Discussion
Our results, in addition to their fundamental importance for glass physics, have significant practical implications as they offer a well-defined procedure to realize the practically maximal fracture toughness of MGs defined by their composition and by the strain rate in a specific application. Such realization can be achieved by carefully controlling Tf through the annealing protocols described above. As a consequence, the observed KQ(Tf) defines a critical cooling rate (setting τplastic) to achieve ductile behavior, distinct from the critical cooling rate for glass formation. Previously, it has been proposed to control the toughness of glasses by the cooling rate through the glass transition36. This procedure and other relaxation procedures, however, reported a gradual variations of the toughness or other properties like hardness37, similar to those observed here for structure and response quantities (Fig. 2), in sharp contrast to dramatic toughening transition reported here (Fig. 1). Moreover, the abrupt toughening transition and the existence of \(T_{\mathrm{f}}^{\mathrm{DB}}\) might be at the heart of the large scatter in the reported fracture toughness values for chemically identical MGs2, which most likely were measured for different—and uncontrolled—values of Tf. Since \(T_{\mathrm{f}}^{\mathrm{DB}}\) is also strain rate dependent, and shifts to higher Tf with increasing strain rate, MGs may behave significantly different in high and low strain rate applications. Taken together, our findings reveal and explain a mechanical glass transition, which should be integrated into glass theories and be technologically considered for a much broader usage of MGs as tough, highly reproducible structural materials.
Methods
Notch fracture toughness sample preparation
Three bulk MG formers were utilized to study the effect of chemistry and fictive temperature on the notch fracture toughness, Zr44Ti11Ni10Cu10Be25, Pd43Cu27Ni10P20, and Pt57.5Cu14.7Ni5.3P22.5. Amorphous Zr44Ti11Ni10Cu10Be25 was obtained from Materion. Pd43Cu27Ni10P20 and Pt57.5Cu14.7Ni5.3P22.5 were prepared by induction melting the constituents in quartz tubes and subsequently fluxed in B2O3 at 1350 K. The flux materials were then removed and the alloys were re-melted and cast into the amorphous state by rapid water quenching. MGs were formed into SENT samples, which were fabricated by a TPF process into silicon molds. SENT samples were designed in Layout Editor software and were transferred onto the photomask. A layer of positive photoresist was spun on a silicon wafer of thickness ~10 µm. The wafer was etched as defined by the design using a deep reactive ion etching process to a final depth of 350 µm. TPF of SENT samples was accomplished by heating the silicon mold and MG into the supercooled liquid region under applied pressure. Excess material was removed by sanding. All samples were polished to a 1 µm finish after annealing to maintain the same roughness prior to mechanical testing.
Fictive temperature manipulation
Liquids from above Tm are cooled to glassy states at Tf,1. To ensure same thermal history of the glass phase, all samples were heated to Tg + 10 K. SENT samples were brought to a given fictive temperatures by annealing the glass at various temperatures with 1.5 times the relaxation time defined by the Vogel–Fulcher–Tammann (VFT) relation to ensure the new equilibrium at Tf has been reached38. The VFT parameters can be obtained by differential scanning calorimetry (DSC) experiments in combination with fitting the VFT equation \(\tau = \tau _0\exp ( {\frac{{D^{\ast} T_{0}}} {{T - T_{0}}}} )\), where τ is the relaxation time at T and τ0 is the infinite temperature relaxation time. DSC experiments were employed to determine D* and T0 as described by Launey and Kruzic et al39,40,41. Detailed of the thermal history of samples is shown in Supplementary Fig. 5. Determination of fictive temperature through specific heat measurements8,9 is also explained in Supplementary Method.
Fracture toughness measurements
Mechanical testing of as-fabricated SENT samples with different Tf was tested using uniaxial tensile testing with quasi-static displacement control with an initial strain rate of 10−4 s−1. Here, we measure conditional (notch) fracture toughness, KQ, and not Kc for two reasons. First, since MG’s metastable nature limits their casting dimension, it is generally difficult to obey the standard KIC procedure. Second, the objective of this study is to understand the dependence of Tf on the relative change of toughness, which required decoupling this effect from other scattering effects. However, absolute values of fracture toughness reported here may have similar limitations as previous measurements of the fracture toughness of MGs. KQ was obtained using the relation \(K_{\mathrm{Q}} = \sigma \sqrt {{\mathrm{\pi }}a} {\mathrm{F}}\left( {\frac{a}{W}} \right),\) where σ is the applied far-field stress, a is the notch length of 2.5 mm, notch root radius of 10 µm, w is the sample width of 5 mm, and the geometry factor \({\mathrm{F}}\left( {\frac{a}{W}} \right) = \sqrt {\frac{{2W}}{{{\mathrm{\pi }}a}}{\mathrm{tan}}\frac{{{\mathrm{\pi }}a}}{{2W}}} \cdot \frac{{0.752 + 2.02\left( {\frac{a}{W}} \right) + 0.37(1 - {\mathrm{sin}}\frac{{\pi a}}{{2W}})^3}}{{{\mathrm{cos}}\frac{{\pi a}}{{2W}}}}\). According to the guidelines provided by ASTM E399 for a plain-strain KIC, the thickness t, the notch length a, and the length of the uncracked ligament (W−a) need to satisfy the following condition, a, t, W−a ≥ 2.5\( \left( {\frac{{K_c}}{{\sigma _y}}} \right)^2\), where σy is the yield strength of the MG. For example, the MG Zr44Ti11Ni10Cu10Be25 has yield strength σy = 1.9 GPa. Hence, the suggested geometric requirement is a, t, W−a ≥ 8 mm, which is difficult to realize for most MGs. Therefore, we measure KQ instead. In addition, we have shown in ref. 42 that KIC can be extracted from our KQ measurements.
Atomic structure, elastic constant, and thermal characterization
As-cast material and all test samples were confirmed to be in an amorphous state by Rigaku Smartlab X-ray diffraction. Standard thermal analysis and enthalpy recovery experiments were performed by Perkin Elmer diamond DSC with a heating rate of 20 K/min. The heat capacity (Cp) was measured as a function of temperature to estimate the Tf values. The samples were heated from 313 K after equilibration for 300 s to 663 K at a heating rate of 10 K/min, then let equilibrated for 2 min. Samples were then cooled to 573 K with a cooling rate of 10 K/min and then cooled to 313 K at 20 K/min. Samples were subjected to a second run with the repeating procedure. Based line measurements were carried out, and a sapphire sample was used as a reference for the Cp measurement. All the measurements were done under an argon atmosphere.
Shear moduli were obtained from dynamic mechanical testing using a TA Instruments Ares G2 performed using the torsion clamps. The gauge lengths of the samples varied from 8 to 12 mm. The samples were tested at 0.01% strain at 1 Hz frequency from 320 to 770 K at a heating rate of 5 K per min. An auto tension of 0.1 N (≈10 g) was used to ensure proper measurements.
High-energy X-ray diffraction for characterization of atomic structure was carried out at the Advanced Photon Source (Argonne National Laboratory) beamline 1-ID and 6-ID. The incident energy was tuned to 100 keV and a 2D area detector was placed ~34 cm behind the sample. Calibration was performed using the CeO2 NIST powder standard. High-energy X-ray diffraction data were processed by FIT2D software43. The MTS loading frame was used for the in situ structural study under uniaxial compression (see Supplementary Method for details on in situ structural study).
Data availability
All data generated or analyzed during this study are included in this published article (and its Supplementary Information).
Change history
05 September 2018
This Article was originally published without the accompanying Peer Review File. This file is now available in the HTML version of the Article; the PDF was correct from the time of publication.
References
Broek, D. Elementary Engineering Fracture Mechanics. 1 edn (Springer, The Netherlands, 2012).
Xu, J., Ramamurty, U. & Ma, E. The fracture toughness of bulk metallic glasses. JOM 62, 10–18 (2010).
Ashby, M. F. & Greer, A. L. Metallic glasses as structural materials. Scr. Mater. 54, 321–326 (2006).
Das, J. et al. “Work-hardenable” ductile bulk metallic glass. Phys. Rev. Lett. 94, 205501 (2005).
Zhong, L., Wang, J. W., Sheng, H. W., Zhang, Z. & Mao, S. X. Formation of monatomic metallic glasses through ultrafast liquid quenching. Nature 512, 177–180 (2014).
Greer, A. L. Metallic glasses. Science 267, 1947–1953 (1995).
Sastry, S., Debenedetti, P. G. & Stillinger, F. H. Signatures of distinct dynamical regimes in the energy landscape of a glass-forming liquid. Nature 393, 554–557 (1998).
Yue, Y.-Z. Characteristic temperatures of enthalpy relaxation in glass. J. Non-Cryst. Solids 354, 1112–1118 (2008).
Yue, Y. Z., Christiansen, Jd & Jensen, S. L. Determination of the fictive temperature for a hyperquenched glass. Chem. Phys. Lett. 357, 20–24 (2002).
Tool, A. Q. Relation between inelastic deformability and thermal expansion of glass in its annealing range. J. Am. Ceram. Soc. 29, 240–253 (1946).
Narayanaswamy, O. S. A model of structural relaxation in glass. J. Am. Ceram. Soc. 54, 491–498 (1971).
Gallino, I., Schroers, J. & Busch, R. Kinetic and thermodynamic studies of the fragility of bulk metallic glass forming liquids. J. Appl. Phys. 108, 063501 (2010).
Yu, H. B. et al. Tensile plasticity in metallic glasses with pronounced beta relaxations. Phys. Rev. Lett. 108, 015504 (2012).
Raghavan, R., Murali, P. & Ramamurty, U. Ductile to brittle transition in the Zr41.2Ti13.75Cu12.5Ni10Be22.5 bulk metallic glass. Intermetallics 14, 1051–1054 (2006).
Gu, X. J., Poon, S. J., Shiflet, G. J. & Lewandowski, J. J. Ductile-to-brittle transition in a Ti-based bulk metallic glass. Scr. Mater. 60, 1027–1030 (2009).
Bian, Z., Chen, G. L., He, G. & Hui, X. D. Microstructure and ductile-brittle transition of as-cast Zr-based bulk glass alloys under compressive testing. Mat. Sci. Eng. 316, 135–144 (2001).
Wu, T. W. & Spaepen, F. The relation between embrittlement and structural relaxation of an amorphous metal. Philos. Mag. B-Phys. Condens. Matter Stat. Mech. Electron. Opt. Magn. Prop. 61, 739–750 (1990).
Xi, X. K. et al. Fracture of brittle metallic glasses: brittleness or plasticity. Phys. Rev. Lett. 94, 125510 (2005).
Spaepen, F. On the fracture morphology of metallic glasses. Acta Metall. 23, 615–620 (1975).
Raghavan, R., Murali, P. & Ramamurty, U. On factors influencing the ductile-to-brittle transition in a bulk metallic glass. Acta Mater. 57, 3332–3340 (2009).
Egami, T. Structural relaxation in amorphous Fe40Ni40P14 B6 studied by energy dispersive X-ray diffraction. J. Mater. Sci. 13, 2587–2599 (1978).
Srolovitz, D., Egami, T. & Vitek, V. Radial distribution function and structural relaxation in amorphous solids. Phys. Rev. B 24, 6936–6944 (1981).
Evenson, Z. & Busch, R. Enthalpy recovery and free volume relaxation in a Zr44Ti11Ni10Cu10Be25 bulk metallic glass. J. Alloy. Compd. 509, S38–S41 (2011).
Lewandowski, J. J., Wang, W. H. & Greer, A. L. Intrinsic plasticity or brittleness of metallic glasses. Philos. Mag. Lett. 85, 77–87 (2005).
Dmowski, W., Iwashita, T., Chuang, C. P., Almer, J. & Egami, T. Elastic heterogeneity in metallic glasses. Phys. Rev. Lett. 105, 205502 (2010).
Rycroft, C. H. & Bouchbinder, E. Fracture toughness of metallic glasses: annealing-induced embrittlement. Phys. Rev. Lett. 109, 194301 (2012).
Vasoya, M., Rycroft, C. H. & Bouchbinder, E. Notch fracture toughness of glasses: dependence on rate, age, and geometry. Phys. Rev. Appl. 6, 024008 (2016).
Ding, J., Patinet, S., Falk, M. L., Cheng, Y. & Ma, E. Soft spots and their structural signature in a metallic glass. Proc. Natl Acad. Sci. USA 111, 14052–14056 (2014).
Li, W., Bei, H., Tong, Y., Dmowski, W. & Gao, Y. F. Structural heterogeneity induced plasticity in bulk metallic glasses: from well-relaxed fragile glass to metal-like behavior. Appl. Phys. Lett. 103, 171910 (2013).
Ding, J. et al. Universal structural parameter to quantitatively predict metallic glass properties. Nat. Commun. 7, 13733 (2016).
Ye, J. C., Lu, J., Liu, C. T., Wang, Q. & Yang, Y. Atomistic free-volume zones and inelastic deformation of metallic glasses. Nat. Mater. 9, 619–623 (2010).
Argon, A. S. Plastic deformation in metallic glasses. Acta Metall. 27, 47–58 (1979).
Ju, J. D., Jang, D., Nwankpa, A. & Atzmon, M. An atomically quantized hierarchy of shear transformation zones in a metallic glass. J. Appl. Phys. 109, 053522 (2011).
Falk, M. L. & Langer, J. S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 57, 7192–7205 (1998).
Guan, P. F., Chen, M. W. & Egami, T. Stress-temperature scaling for steady-state flow in metallic glasses. Phys. Rev. Lett. 104, 205701 (2010).
Kumar, G., Neibecker, P., Yanhui, L. & Schroers, J. Critical fictive temperature for ductility in metallic glasses. Nat. Commun. 4, 1536 (2013).
Smedskjaer, M. M., Jensen, M. & Yue, Y. Effect of thermal history and chemical composition on hardness of silicate glasses. J. Non-Cryst. Solids 356, 893–897 (2010).
Moynihan, C. T., Easteal, A. J., Bolt, M. A. & Tucker, J. Dependence of the fictive temperature of glass on cooling rate. J. Am. Ceram. Soc. 59, 12–16 (1976).
Launey, M. E., Busch, R. & Kruzic, J. J. Effects of free volume changes and residual stresses on the fatigue and fracture behavior of a Zr–Ti–Ni–Cu–Be bulk metallic glass. Acta Mater. 56, 500–510 (2008).
Kuno, M. A., Shadowspeaker, L., Schroers, J. & Busch, R. Thermodynamics of the Pd43Ni10Cu27P20 Bulk Metallic Glass Forming Alloy. MRS Online Proc. 806 (2003).
Legg, B. A., Schroers, J. & Busch, R. Thermodynamics, kinetics, and crystallization of Pt57.3Cu14.6Ni5.3P22.8 bulk metallic glass. Acta Mater. 55, 1109–1116 (2007).
Chen W., et al. Test sample geometry for fracture toughness measurements of bulk metallic glasses. Acta Mater. 145, 477–487 (2018).
Hammersley, A. P., Svensson, S. O. & Thompson, A. Calibration and correction of spatial distortions in 2D detector systems. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 346, 312–321 (1994).
Acknowledgements
We warmly thank Prof. Frans Spaepen for fruitful discussions. This work was supported by the U.S. Department of Energy through the Office of Science, Basic Energy Sciences, Materials Science and Engineering Division (No. DE SC0004889). Structural characterization was carried out at the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility, operated for the DOE Office of Science by Argonne National Laboratory under Contract DE-AC02-06CH11357. E.B. acknowledges support from the Richard F. Goodman Yale/Weizmann Exchange Program. A.D. acknowledges support by the Department of Energy through grant No. DE-SC0016179.
Author information
Authors and Affiliations
Contributions
J.S., T.E., E.B., J.K., Z.L., and W.C. designed and developed the study. J.K., R.Y., G.P. conducted the main experiments (sample preparation, TPF, fracture toughness, and DSC). H.W. and W.D. conducted the X-ray diffraction experiment and analyzed the results. A.D. and U.D.S. conducted DMA experiment and analyzed the data. E.B., M.F., M.D.S., and C.S.O. developed the theoretical model. J.K., J.S., E.B., T.E. analyzed the data and wrote the manuscript. All authors contributed to the discussion of the results and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ketkaew, J., Chen, W., Wang, H. et al. Mechanical glass transition revealed by the fracture toughness of metallic glasses. Nat Commun 9, 3271 (2018). https://doi.org/10.1038/s41467-018-05682-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05682-8
This article is cited by
-
Structure, mechanical, and chemical performance evolution of aluminosilicate glass modified by Nd2O3
Journal of the Australian Ceramic Society (2024)
-
Size-dependent vitrification in metallic glasses
Nature Communications (2023)
-
Aging and rejuvenation during high-temperature deformation in a metallic glass
Science China Physics, Mechanics & Astronomy (2022)
-
Enhancing ductility in bulk metallic glasses by straining during cooling
Communications Materials (2021)
-
Atomic-scale homogeneous plastic flow beyond near-theoretical yield stress in a metallic glass
Communications Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.