Abstract
Transition metal dichalcogenide materials are unique in the wide variety of structural and electronic phases they exhibit in the two-dimensional limit. Here we show how such polymorphic flexibility can be used to achieve topological states at highly ordered phase boundaries in a new quantum spin Hall insulator (QSHI), 1T′-WSe2. We observe edge states at the crystallographically aligned interface between a quantum spin Hall insulating domain of 1T′-WSe2 and a semiconducting domain of 1H-WSe2 in contiguous single layers. The QSHI nature of single-layer 1T′-WSe2 is verified using angle-resolved photoemission spectroscopy to determine band inversion around a 120 meV energy gap, as well as scanning tunneling spectroscopy to directly image edge-state formation. Using this edge-state geometry we confirm the predicted penetration depth of one-dimensional interface states into the two-dimensional bulk of a QSHI for a well-specified crystallographic direction. These interfaces create opportunities for testing predictions of the microscopic behavior of topologically protected boundary states.
Similar content being viewed by others
Introduction
Materials exhibiting the quantum spin Hall effect (QSHE) create new opportunities for directly imaging the spatial extent of topologically protected one-dimensional (1D) edge states and for determining how they interact with bulk states and defects. Such systems, however, can be difficult to isolate and to access via microscopy. HgTe and InAs/GaAs quantum wells, for example, are well-known QSHIs1,2, but are not easily accessible to high-resolution scanned probe microscopy because they are buried interface systems. Bi-based surface systems (predicted to be QSHIs3,4) have shown evidence for QSHI behavior and are more accessible to scanned probe microscopy, but exhibit strong substrate interactions5,6,7. Monolayer transition metal dichalcogenide (TMD) materials (MX2 where M = Mo, W, and X = S, Se, and Te) in the distorted octahedral 1T′ phase, on the other hand, are a new class of QSHIs8 that retain their topological properties on different substrates and are completely accessible to high-resolution scanned probe microscopy9,10,11. Monolayer 1T′-WTe2 films have recently been shown to exhibit all of the hallmarks of the QSH effect (e.g., band inversion, helical edge states, and edge-state quantum conduction) via angle-resolved photoemission spectroscopy (ARPES)9, scanning tunneling microscopy/spectroscopy (STM/STS)9,10,11, and transport measurements12,13. Monolayer 1T′-WTe2, however, poses challenges for quantitative microscopy of topological edge states due to the high degree of structural disorder in the edges of 2D 1T′-WTe2 islands produced by molecular beam epitaxy (MBE). Although the existence of topological edge states is protected against disorder, quantitative characterization of their decay lengths, dispersion features, and defect interactions requires crystallographically well-ordered edges since these properties strongly depend on edge orientation14,15,16, strain, and chemical environment17.
In order to achieve structurally well-defined boundaries in a fully accessible QSHI, we grew mixed-phase WSe2 monolayers on SiC(0001) using MBE growth techniques. Single-layer WSe2 is bimorphic with two stable crystalline phases (1H and 1T′ (Fig. 1a)) that are close in energy8, thus enabling the growth of mixed topological/trivial phases with crystallographically defined phase boundary interfaces. The 1H phase (which is the structural ground state of WSe2) has a much larger electronic bandgap18,19 than the 1T′ phase, thus allowing the two phases to be easily distinguished. The onset of the QSHE in mixed-phase WSe2 thus results in topologically protected states at crystallographically well-defined 1T′–1H phase boundary interfaces. We have verified the QSHI ground state of 1T′-WSe2 using ARPES, STM/STS, and first-principles calculations. ARPES reveals the existence of inverted bands at the Fermi energy (EF) and the presence of a bulk bandgap. STS measurements confirm the bulk bandgap seen by ARPES and further demonstrate the existence of topological interface states within this bandgap that are spatially localized at 1T′-WSe2 boundaries. These boundary states are easily observable at crystallographically well-ordered 1T′–1H interfaces, but can also be seen at the irregular 1T′ edges. The structural perfection of the 1T′–1H boundary allows us to measure an interface state decay length of 2 nm into bulk 1T′-WSe2, agreeing with the results of ab initio numerical simulations.
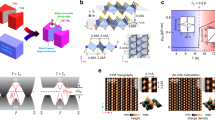
Atomic structure of mixed-phase single-layer WSe2. a Calculated unit cells and side-view sketches of the 1T′ and 1H phases of single-layer WSe2. Se (W) atoms are depicted in blue (orange). b RHEED pattern of single-layer 1T′/1H-mixed-phase WSe2. Red and white arrows indicate diffraction stripes from 1T′ and 1H phases, respectively. c Core-level XPS spectrum of single-layer 1T′/1H mixed-phase WSe2. Insets show zoom-in of the Se (blue) and W (orange) peaks for the 1T′ (dT’, fT’) and 1H (dH, fH) phases. d Atomically resolved STM image of single-layer 1T′-WSe2. The unit cell is indicated in blue (Vs = +500 mV, It = 1 nA). e Side and top view close-up of the 1T′-WSe2 STM image with a sketch of calculated 1T′-WSe2 (only upper-layer Se atoms are depicted in top view)
Results
Structural characterization of single-layer 1T′-WSe2
Our experiments were carried out on high-quality single layers of WSe2 grown on epitaxial bilayer graphene (BLG) on 6H-SiC(0001) by MBE. In order to obtain the metastable 1T′-WSe2 phase, the temperature of the BLG/SiC(0001) substrate was held at 500 K during growth, a significantly lower temperature than required to grow the more stable 1H phase (675 K). Under these growth conditions the RHEED pattern of single-layer WSe2 (Fig. 1b) shows the formation of an additional large lattice periodicity (5.8 Å) consistent with the 1T′ phase that coexists with the shorter 1H phase periodicity (3.3 Å). XPS measurements of the WSe2 layers (Fig. 1c) reveal the emergence of two new pairs of peaks (dT′ and fT′) near the characteristic Se (dH) and W (fH) peaks for the 1H phase19, suggesting the presence of an additional lattice symmetry for W and Se20. STM imaging confirms that our WSe2 layers are composed of coexisting domains of 1H and 1T′ phase (Supplementary Fig. 1). Figure 1d shows an atomically resolved STM image of the 1T′ phase of WSe2, which is characterized by straight atomic rows of two non-equivalent zigzag atomic chains. The 1T′ phase of Fig. 1d exhibits a period enlargement to 5.73 ± 0.09 Å along the x direction compared to the 1H phase, in good agreement with the RHEED spectra. Adjacent atomic rows in 1T′-WSe2 exhibit a slight translational shift along the y-direction due to a shear angle that varies between 2° and 6° depending on the domain, similar to that observed previously for other TMD materials21,22. We identify the atomic rows in the STM images of Fig. 1d, e as originating from W-Se zigzag chains (see sketch in Fig. 1e), in good agreement with the expected structural distortion of the 1T′ phase8. The ball-and-stick model shown in Figs. 1a, e corresponds to our calculated relaxed atomic structure of 1T′-WSe2.
Electronic characterization of single-layer 1T′-WSe2
We experimentally characterized the electronic structure of coexisting 1H and 1T′ phases of single-layer WSe2 via ARPES and STS. Figure 2c shows the Fermi surface (FS) intensity map for a 0.8 monolayer (ML) coverage of mixed-phase WSe2 measured via ARPES. The observed FS structure is entirely due to the 1T′ phase since the valence band (VB) maximum of 1H-WSe2 has a much higher binding energy at E = −1.1 eV19. The FS is composed of two small elliptical electron pockets at the Λ points located along ΓY (Fig. 2a). The three equivalent rotational domains of the 1T′ phase on BLG leads to the emergence of three pairs of these features rotated by 120° (Fig. 2b), thus forming a ring-like FS around the Γ point. Figure 2d shows the measured band dispersion along the ΓY direction of the Brillouin zone (BZ). Due to the rotational domains, contributions from both the ΓY and ΓP directions can be resolved. The VB maximum is approximately 170 ± 20 meV below the EF and exhibits a flattened, non-parabolic onset shape along ΓY. Naturally occurring n-type doping in our samples shifts the conduction band (CB) below EF, which is why the electron pockets at Λ are visible in the ARPES spectrum. This reveals the existence of an indirect bandgap (Eg) that can be quantified by taking the difference of the energy positions of the CB minimum (at the Λ point) and the VB maximum (at the Γ point) from two energy distribution curves (EDCs) of the ARPES spectrum (taken along the dashed lines in Fig. 2d). As shown in Fig. 2f, we extract a bandgap value of Eg = 120 ± 20 meV centered at E = −110 meV ± 20 meV. The observed band dispersion and gap value is characteristic of band inversions predicted for 1T′-TMD materials8.
ARPES characterization of single-layer 1T′-WSe2. a Sketch of the first Brillouin zone of 1T′-WSe2. Relevant high-symmetry points are indicated. b Three surface Brillouin zones corresponding to the three rotational 1T′-WSe2 domains on the BLG surface represented by three different colors. The Fermi surface pockets from each rotational domain are indicated by ellipses of corresponding colors. Black dashed line represents the experimental ARPES line cut shown in d. c Experimental 1T′-WSe2 Fermi surface measured by ARPES. d High-resolution ARPES band dispersion along the Y-Γ-Y direction. Due to the presence of rotational domains, contributions from both Γ-Y and Γ-P directions are observed in a single ARPES measurement (T = 60 K and photon energy E = 75 eV). e Calculated bands for the 1T′ phase of single-layer WSe2 along Γ-Y (brown) and Γ-P (green) directions. A downward rigid shift of 130 meV has been added to account for n-doping seen in the experiment. f EDCs from the momentum positions marked with dashed blue and red lines in d
The local density of states (LDOS) of mixed-phase, single-layer WSe2 was measured via STS point spectroscopy, as seen in Fig. 3a. The 1H phase of monolayer WSe2 shows a bandgap of 1.94 eV, in good agreement with previous measurements19, but the 1T′ phase reveals a finite, asymmetric LDOS that extends across both the occupied state and unoccupied state regions. The most pronounced feature in the unoccupied state region of the 1T′ phase is a broad, asymmetric peak centered around + 0.24 V. The finite LDOS seen in the occupied state region of the 1T′ phase (−1 V < Vs < 0 V) confirms that the bands observed in ARPES at low binding energy (Fig. 2d) belong to the 1T′ phase since this energy range is clearly gapped out for the 1H phase. Also prominent in the electronic structure of the 1T′ phase is a gap-like feature located at Vs = −130 ± 5 mV. Figure 3c shows a close-up of this feature (the boxed region of Fig. 3a). The width of this 1T′ gap feature can vary depending on surface position, but it has an average FWHM = 85 mV ± 21 meV (see Supplementary Note 3 for gap statistics). A second dip feature located at EF can be seen in the dI/dV curves taken for 1T′-WSe2. A similar zero-bias feature has also been seen in 1T′-WTe2 and has been attributed to the opening of a Coulomb gap23. These characteristic features are seen throughout the 1T′ bulk region for islands with the narrowest widths larger than ~8 nm. For 1T′ islands of smaller widths the zero-bias feature is replaced by a larger size-dependent energy gap that opens at EF and dominates the electronic structure, ostensibly due to size quantization effects24. The bulk gap feature observed by STM spectroscopy at VS = −130 mV is consistent with the ARPES bulk bandgap for 1T′-WSe2 when lifetime broadening effects are taken into account (Supplementary Note 3). Such broadening likely arises from a combination of electronic, vibrational, and defect-based scattering, as well as coupling to the graphene substrate25.
STS characterization of single-layer mixed-phase WSe2. a STS spectra obtained in the 1T′ (orange) and 1H (blue) regions of single-layer WSe2 (f = 614 Hz, It = 0.3 nA, Vrms = 4 meV). The inset shows an STM image of coexisting 1T′ and 1H regions with a well-ordered interface between them (Vs = +500 mV, It = 0.1 nA). b Calculated LDOS(E) of bulk single-layer 1T′-WSe2 (black curve) compared to experimental STS spectrum (orange curve). c Close-up view of the boxed region in a shows low-energy experimental STS spectrum taken for 1T′-WSe2 phase. d Calculated LDOS(E) for 1T′-WSe2 over the same energy range as in c
In order to further understand the electronic structure of single-layer 1T′-WSe2, we also characterized its quasiparticle interference (QPI) patterns near EF via Fourier transform (FFT) analysis of dI/dV images. Figure 4b–d show constant-bias dI/dV maps taken in the same pristine region of 1T′-WSe2 for energies within the CB (b and c) as well as in the VB (d). The QPI patterns observed in the dI/dV maps exhibit long-range oscillations with wave fronts parallel to the x-direction and closely spaced rows aligned parallel to the y-direction (i.e., the atomic rows). The corresponding FFT images of the conductance maps (Fig. 4e–g) show distinct features that reflect the band structure contours at these different energies.
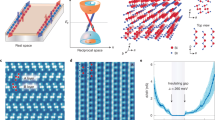
Quasiparticle interference patterns in single-layer 1T′-WSe2. a Calculated band structure of single-layer 1T′-WSe2 along Γ-Y (brown) and Γ-P (green) directions in the ± 1 eV range. b–d Experimental dI/dV conductance maps taken at b Vs = +100 mV, It = 0.15 nA, c Vs = − 40 mV, It = 0.15 nA, and d Vs = − 300 mV, It = 0.15 nA (14 nm × 26.4 nm, f = 614 Hz, Vrms = 4 meV). e–g FFTs of the conductance maps in b–d. h–j Calculated QPI patterns for h E =+100 meV, i E = − 40 meV, and j E = − 300 meV
The electronic features we have described up to now for bulk single-layer 1T′-WSe2 are consistent with an inverted bandgap and the occurrence of the QSHI phase. A key feature of QSHIs, however, is the existence of helical states at the boundaries. WSe2 is particularly well-suited to explore the existence of such states due to the coexistence of the 1T′ and 1H phases, which leads to straight, defect-free interfaces as shown in Figs. 3a, 5a. Figure 5b shows a color-coded series of dI/dV spectra measured along the 5.3 nm-long black arrow in Fig. 5a oriented perpendicular to the 1T′–1H interface (the interface is marked by a dashed white line). The 1T′–1H interface is defined as the point where the STM topograph height reaches 50% of the height difference from the 1H average terrace height to the 1T′ average terrace height for Vs = − 0.52 V, I = 0.2 nA. This definition is also valid for other biases within the range −0.6 V < Vs < −0.1 V and It ≤ 0.5 nA (the 1T′ terrace is 2.9 ± 0.2 Å higher than the 1H terrace under these standard tunneling conditions). Figure 5b shows that the STS feature identified as the bulk bandgap at −130 meV is present in the bulk 1T′ material only for distances greater than 2 nm from the 1T′–1H interface.
Spatial extent of atomically well-ordered 1D interface state in single-layer 1T′-WSe2. a STM topograph of the 1T′–1H interface (Vs = − 525 mV, It = 0.2 nA). Dashed line shows interface location (see text). b Color-coded dI/dV spectra taken along the path marked by the arrow in a (f = 614 Hz, It = 0.6 nA, Vrms = 4 meV). c dI/dV curves extracted from b. d Experimental dI/dV map taken in the same region as a for Vs = − 130 meV. Dashed line shows same interface location as in a. e Average dI/dV linescan oriented along the X direction in d for Vs = −130 mV
The 1T′-WSe2 bulk gap disappears at distances closer than 2 nm from the 1T′–1H interface and a prominent peak emerges in the LDOS at the same energy that previously showed a gap. This is illustrated in Fig. 5c which shows dI/dV curves taken in the bulk region (orange curve) and in the edge region (blue curve) as indicated by the dashed lines in Fig. 5b. The emergence of this peak is consistent with the existence of a 1D topologically protected edge state as expected for a QSHI. In order to resolve the spatial extent of the interface state, we mapped the dI/dV conductance near the 1T′–1H interface with sub-nm resolution. Figure 5d shows a dI/dV map of the same region shown in Fig. 5a at the bias voltage at the center of the interface-state peak (Vs = −130 meV). This map shows bright intensity in the 1H phase region above the 1T′–1H interface. This is due to electronic states from the 1T′ phase leaking into the gapped 1H phase, similar to the phenomenon of metal-induced-gap-states (MIGS)26. Below the 1T′–1H interface in the 1T′ phase region a very uniform band of increased dI/dV intensity can be seen that penetrates 2 nm into the 1T′ bulk (marked interface state). This reveals the spatial extent of the topological interface state that resides in the bulk energy gap of single-layer 1T′-WSe2 (see Fig. 5e for average linescan profile). The penetration depth of 2 nm that we extract from this linescan is in reasonable agreement with previous predictions for topological edge states8. (STM spectroscopy performed at the disordered edges of 1T′-WSe2 islands also show the spectral signature of topologically protected edge states, but in this case disorder prevent any quantitative determination of edge-state width (see Supplementary Note 4).)
Density functional theory calculations and comparison with the experiments
In order to better understand the topological behavior of this mixed-phase system, we performed ab initio calculations using density functional theory (DFT) (see Methods). The resulting relaxed structure (Fig. 1a) is consistent with previous calculations for this phase8 and agrees well with our STM topographic images (Fig. 1e). Figures 2e, 4a show the band structure along Y-Γ-Y (red) and P-Γ-P (green) directions over a wide energy range calculated using a hybrid functional. The results of our band structure calculations agree well with the ARPES results shown in Fig. 2 after performing a rigid shift of -130 meV to account for the n-type doping observed in our samples. The non-parabolic flattened shape of the VB near the Γ-point closely follows the expected band structure arising from the inversion of bands having opposite parity27, a prerequisite for topologically non-trivial electronic structure. The calculated band structure also shows an energy gap of 123 meV with band edges along the ΓY direction, in reasonable agreement with both our ARPES and STS results.
Comparison of the calculated bulk 1T′-WSe2 LDOS(E) with experimental STM dI/dV spectra shows qualitative agreement over a broad energy range as seen in Fig. 3b. The gap structure, the rise in VB LDOS as energy is decreased, and the CB peak feature near 0.2 eV are all observed. However, a quantitative comparison here would require calculating lifetime broadening effects (Supplementary Note 3) as well as energy-dependent tunneling transmission probabilities. The dip feature observed in the STS at EF is also not captured by our calculations, likely due to its origin from, either phonon-assisted inelastic tunneling28 or electron-electron interactions due to the Efros-Shklovskii mechanism23,29. We have also simulated 1T′-WSe2 QPI patterns that take into account the band inversion and gap opening seen in Fig. 4a. Figure 4h–j show the calculated QPI patterns for energies at + 100 meV, −40 meV, and −300 meV in comparison to the experimental QPI patterns of Fig. 4e–g. Here the agreement is reasonable for features such as the multi-lobe structure along ky and the elongation along kx, which are clearly seen for energies in the CB (Figs. 4e, h and 4f, i). In the VB (Fig. 4g, j), however, several high-intensity features in the calculated FFT are absent in the experimental data. The origin for this discrepancy may be due to either a lack of experimental resolution (due to limitations in the size of the 1T′ phase domains that were imaged to obtain the experimental FFTs) or to differences between the theoretical and experimental Fermi contours.
The calculated electronic structure for a single-layer WSe2 1T′–1H interface model structure is shown in Fig. 6. The proposed interface model (Fig. 6a) was chosen because its electronic structure best matches our experimental data. Although the experimental interface has a well-defined crystallographic orientation, it is not possible to verify its atomic structure due to limitations in experimentally resolving the chemical bonds. Our calculation of the interface electronic structure was performed using a standard DFT approach due to the large model size (see Methods). This results in a reduced band gap (29 meV) compared to the more realistic bandgap (123 meV) of the more accurate hybrid functional calculations shown in Figs. 2–4. Despite this bandgap discrepancy, it is still useful to examine the wavefunction behavior resulting from this interface structure. Figure 6b shows the calculated dispersion of topologically protected interface states running parallel to the 1T′–1H interface shown in Fig. 6a. A total of three bands span the bulk band gap. The odd number of bands is consistent with a topological origin and spin-momentum locking is clearly manifested. The pair of bands at higher energy can be attributed to Rashba-split states derived from the bulk conduction band, but the band at lower energy is topological in origin since it connects bulk valence and conduction bands. Figure 6c demonstrates how extrema in the dispersion of these interface-state bands give rise to a large LDOS intensity within the bulk bandgap (marked by the black arrow), consistent with the experimental dI/dV curve in Fig. 5c. The decay of LDOS(E) with distance from the 1T′–1H interface (Fig. 6d, black curve) shows that these states are localized within approximately 2 nm of the interface in the 1T′ domain, consistent with the experimental interface-state decay length shown in Fig. 5d, e.
WSe2 1T′–1H interface electronic structure. a Sketch of the structural model used to theoretically investigate the 1T′–1H interface in single-layer WSe2. The interface position x = 0 is indicated. b Momentum- and spin-resolved LDOS(E) at the 1T′–1H interface shows the dispersion and spin-momentum locking of the interface states (blue/red curves show different spin polarizations). c Energy-resolved LDOS at the 1T′–1H interface (blue curve) in single-layer WSe2 compared to the LDOS at a point well within the 1T′ bulk region (red curve). d Dependence of LDOS at the band gap energy on distance from the 1T–1H interface compared to experimental dI/dV linecut at Vs = −130 mV (from Fig. 5e)
In conclusion, our measurements support the results of first-principles calculations and provide evidence for the presence of the QSHI phase in single-layer 1T′-WSe2. The ability to observe 1D interface-states at atomically well-ordered boundaries between trivial and nontrivial phases allows us to extract new quantitative information on these novel states, such as their penetration depth into the 1T′-WSe2 bulk, a previously inaccessible parameter due to edge disorder. This creates new opportunities for investigating topologically non-trivial electronic phases in 2D TMDs and takes us a step closer to the integration of 2D QSH layers into more complex heterostructures that exploit topologically protected charge and spin transport.
Methods
Experimental details
Monolayer WSe2 was grown by MBE on epitaxial BLG on 6H-SiC(0001) (resistivity of ρ ~ 0.1 Ω cm) at the HERS endstation of Beamline 10.0.1 (Advanced Light Source, Lawrence Berkeley National Laboratory) with a base pressure of ~3 × 10−10 Torr. Bilayer graphene on SiC(0001) was first prepared by following the procedure detailed in ref.18. To grow the TMD monolayer, pure W and Se were evaporated from an electron-beam evaporator and a standard Knudsen cell, respectively, while keeping the flux ratio of W to Se at 1:15. In order to protect the film from contamination and oxidation during transport through air to the ultrahigh vacuum (UHV) STM chamber, a Se capping layer (thickness ~10 nm) was deposited on the sample surface after growth. The Se capping layer was removed for STM experiments by annealing the sample to ~500 K in UHV for 30 min. STM and STS experiments were performed in an Omicron LTSTM operated at T = 4 K. The STM tip was calibrated by measuring reference spectra on the graphene substrate in order to avoid tip artifacts. STM/STS analysis and rendering was done using WSxM software30.
Theoretical details
First-principles calculations were performed using DFT within the generalized gradient approximation (GGA)31 as implemented in the Quantum-ESPRESSO package32 and within the HSE0333 hybrid functional using the VASP package34. The single-particle Hamiltonian for valence and conduction states included relativistic corrections through ultrasoft pseudopotentials35 adapted from ref.36. The plane-wave basis set cutoff for wavefunctions was set to 80 Ry. Reciprocal space sampling was performed on an 11 × 18 k-point mesh in the rectangular Brillouin zone. The WSe2 monolayers were decoupled along the out-of-plane direction by 1.5 nm of vacuum. Prior to calculating electronic properties, the atomic coordinates and in-plane lattice constants were fully relaxed. QPI patterns were calculated via the autocorrelation function of electronic bands as implemented in WannierTools:37
where \(E_n\left( k \right)\) is the energy dispersion of the nth Bloch band. The autocorrelation functions presented in Fig. 4h–j were calculated on a fine 1200 × 2400 k-point mesh. We find that explicitly including the matrix elements does not qualitatively change the calculated QPI patterns. The electronic structure of a 1T′–1H interface presented in Fig. 6 was calculated using the non-equilibrium Green’s function technique38. The Hamiltonian matrix elements were obtained in the numerical localized orbital basis set implementation39,40 within GGA. The atomic basis set (W7.0-s2p2d2f1 for Tungsten and Se7.0-s3p3d1 for Selenium) as well as other parameters were converged to a perfect agreement with reference GGA results of our Quantum-ESPRESSO calculations and ref. 8. The Hamiltonian matrix elements were obtained using models with periodic boundary conditions imposed both along and across the interface. These models contain two interfaces per supercell and measure ca. 11 nm in the direction perpendicular to the interface. Only half of the supercell containing one interface was retained for non-equilibrium Green’s function calculations, and the size of the scattering region measures approximately 6 nm.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request.
References
König, M. et al. Quantum spin hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Knez, I., Du, R. R. & Sullivan, G. Evidence for helical edge modes in inverted InAs/GaSb quantum wells. Phys. Rev. Lett. 107, 136603 (2011).
Murakami, S. Quantum spin hall effect and enhanced magnetic response by spin-orbit coupling. Phys. Rev. Lett. 97, 236805 (2006).
Liu, Z. et al. Stable nontrivial Z2 topology in ultrathin Bi(111) films: A first-principles study. Phys. Rev. Lett. 107, 136805 (2011).
Yang, F. et al. Spatial and energy distribution of topological edge states in single Bi(111) bilayer. Phys. Rev. Lett. 109, 016801 (2012).
Drozdov, I. K. et al. One-dimensional Topological Edge States of Bismuth Bilayers. Nat. Phys. 10, 664–669 (2014).
Reis, F. et al. Bismuthene on a SiC substrate: A candidate for a high-temperature quantum spin Hall material. Science 357, 287 (2017).
Qian, X., Liu, J., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347 (2014).
Tang, S. et al. Quantum spin Hall state in monolayer 1T′-WTe2. Nat. Phys. 13, 683–687 (2017).
Chen, J. et al. Quantum effects and phase tuning in epitaxial hexagonal and monoclinic MoTe2 monolayers. ACS Nano 11, 3282–3288 (2017).
Jia, Z. Y. et al. Direct visualization of a two-dimensional topological insulator in the single-layer 1T′-WTe2. Phys. Rev. B 96, 041108 (R) (2017).
Fei, Z. et al. Edge conduction in monolayer WTe2. Nat. Phys. 13, 677–682 (2017).
Wu, S. et al. Observation of the quantum spin Hall effect up to 100 kelvin in a monolayer crystal. Science 359, 76–79 (2018).
Wang, Z. F. et al. Topological edge states in a high-temperature superconductor FeSe/SrTiO3(001) film. Nat. Mater. 15, 968–973 (2016).
Pauly, C. et al. Subnanometre-wide electron channels protected by topology. Nat. Phys. 11, 338–343 (2015).
Sessi, P. et al. Robust spin-polarized midgap states at step edges of topological crystalline insulators. Science 354, 1269–1273 (2016).
Wang, Z. F., Chen, L. & Liu, F. Tuning topological edge states of Bi(111) bilayer film by edge adsorption. Nano. Lett. 14, 2879–2883 (2014).
Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014).
Zhang, Y. et al. Electronic structure, surface doping, and optical response in epitaxial WSe2 thin films. Nano. Lett. 16, 2485–2491 (2016).
Cho, S. et al. Phase patterning for ohmic homojunction contact in MoTe2. Science 349, 625–628 (2015).
Qin, X. R., Yang, D., Frindt, R. F. & Irwin, J. C. Real-space imaging of single-layer MoS2 by scanning tunneling microscopy. Phys. Rev. B 44, 3490–3493 (1991).
Das, P. K. et al. Layer-dependent quantum cooperation of electron and hole states in the anomalous semimetal WTe2. Nat. Commun. 7, 10847 (2016).
Song, Y. -H. et al. Observation of Coulomb gap in the quantum spin Hall candidate single-layer 1T′-WTe2. Preprint at https://arxiv.org/abs/1711.07286 (2017).
Han, M. Y., Özyilmaz, B., Zhang, Y. & Kim, P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 98, 206805 (2007).
Brar, V. W. et al. Observation of carrier-density-dependent many-body effects in graphene via tunneling spectroscopy. Phys. Rev. Lett. 104, 036805 (2010).
Tersoff, J., Laboratories, a T. T. B. & Hill, M. Schottky barrier heights and the continuum of gap states. Phys. Rev. Lett. 52, 465–468 (1984).
Choe, D.-H., Sung, H.-J. & Chang, K. J. Understanding topological phase transition in monolayer transition metal dichalcogenides. Phys. Rev. B 93, 125109 (2016).
Zhang, Y. et al. Giant phonon-induced conductance in scanning tunnelling spectroscopy of gate-tunable graphene. Nat. Phys. 4, 627–630 (2008).
Efros, A. L. & Shklovskii, B. I. Coulomb gap and low temperature conductivity of disordered systems. J. Phys. C. Solid State Phys. 8, L49 (1975).
Horcas, I. et al. WSXM: A software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 78, 013705 (2007).
Perdew, J. P., Ernzerhof, M. & Burke, K. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B—Condens. Matter Mater. Phys. 54, 11169–11186 (1996).
Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895 (1990).
Lejaeghere, K. et al. Reproducibility in density-functional theory calculations of solids. Science 351, aad3000 (2016). 1-11.
Wu, Q. S., Zhang, S. N., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: an open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Datta, S. Quantum transport: Atom to transistor. Quantum Transport: Atom to Transistor (2005).
Ozaki, T. & Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B—Condens. Matter Mater. Phys. 69, 195113 (2004).
Orbital basis sets of W and Se. OpenMX Project. http://www.jaist.ac.jp/~t-ozaki/vps_pao2013/ (2013).
Acknowledgements
We thank Reyes Calvo for fruitful discussions. This research was supported by the VdW Heterostructure program (KCWF16) (STM spectroscopy and QPI mapping) funded by the Director, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, of the US Department of Energy under Contract No. DE-AC02-05CH11231. Support was also provided by National Science Foundation award EFMA-1542741 (surface treatment and topographic characterization). The work at the ALS (sample growth and ARPES measurements) is supported by the Office of Basic Energy Sciences, US DOE under Contract No. DE-AC02-05CH11231. The work at the Stanford Institute for Materials and Energy Sciences and Stanford University (ARPES measurements) was supported by the Office of Basic Energy Sciences, US DOE under contract No. DE-AC02-76SF00515. S. T. acknowledges the support by CPSF-CAS Joint Foundation for Excellent Postdoctoral Fellows. H. R. acknowledges fellowship support from NRF, Korea through Max Planck Korea/POSTECH Research Initiatives No. 2016K1A4A4A01922028 and No. 2011-0031558. A.P. and O.V.Y. acknowledge support by the ERC Starting grant “TopoMat” (Grant No. 306504) (theoretical formalism development). Q.W. acknowledges support from NCCR Marvel (hybrid functional calculations). First-principles calculations were performed at the Swiss National Supercomputing Centre (CSCS) under project s832 and the facilities of Scientific IT and Application Support Center of EPFL. The work at Nanjing University (Y.Z.) is supported by the Fundamental Research Funds for the Central Universities N°. 020414380037 (surface structure analysis). The SIMES work is supported by DOE BES, Division of Materials Sciences. M.M.U. acknowledges support by Spanish MINECO under grant no. MAT2017-88377-C2-1-R (data analysis).
Author information
Authors and Affiliations
Contributions
M.M.U., Y.Z. and S.K.M. conceived the work and designed the research strategy. M.M.U., A.M.R., Y.C., D.W. and Z.P. measured and analyzed the STM/STS data. Y.Z., H.Y. and S.T. performed the MBE growth and ARPES and XPS characterization of the samples. A.P. and Q. W. performed the theoretical calculations. F.W. participated in the interpretation of the experimental data. S.K.M. and Z.X.S. supervised the MBE growth and ARPES and XPS characterization. O.V.Y. supervised the calculations. M.F.C. supervised the STM/STS experiments. M.M.U. wrote the paper with help from O.V.Y. and M.F.C. M.M.U. and M.F.C. coordinated the collaboration. All authors contributed to the scientific discussion and manuscript revisions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisherʼs note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ugeda, M.M., Pulkin, A., Tang, S. et al. Observation of topologically protected states at crystalline phase boundaries in single-layer WSe2. Nat Commun 9, 3401 (2018). https://doi.org/10.1038/s41467-018-05672-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05672-w
This article is cited by
-
Controlling structure and interfacial interaction of monolayer TaSe2 on bilayer graphene
Nano Convergence (2024)
-
A hybrid topological quantum state in an elemental solid
Nature (2024)
-
Quantum transport response of topological hinge modes
Nature Physics (2024)
-
Boundary modes of a charge density wave state in a topological material
Nature Physics (2024)
-
A substitutional quantum defect in WS2 discovered by high-throughput computational screening and fabricated by site-selective STM manipulation
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.