Abstract
In order to model realistic quantum devices it is necessary to simulate quantum systems strongly coupled to their environment. To date, most understanding of open quantum systems is restricted either to weak system–bath couplings or to special cases where specific numerical techniques become effective. Here we present a general and yet exact numerical approach that efficiently describes the time evolution of a quantum system coupled to a non-Markovian harmonic environment. Our method relies on expressing the system state and its propagator as a matrix product state and operator, respectively, and using a singular value decomposition to compress the description of the state as time evolves. We demonstrate the power and flexibility of our approach by numerically identifying the localisation transition of the Ohmic spin-boson model, and considering a model with widely separated environmental timescales arising for a pair of spins embedded in a common environment.
Similar content being viewed by others
Introduction
The theory of open quantum systems describes the influence of an environment on the dynamics of a quantum system1. It was first developed for quantum optical systems2, where the coupling between system and environment is weak and unstructured. In such situations, one can almost always assume that the environment is memoryless and uncorrelated with the system—that is, the Markov and Born approximations hold—allowing a time-local equation of motion to be derived for the open system. The resulting Born–Markov master equation works because the environment-induced changes to the system dynamics are slow relative to the typical correlation time of the environment.
There are now a growing number of quantum systems where a structureless environment description is not justified, and memory effects3 play a significant role. These include micromechanical resonators4, quantum dots5,6 and superconducting qubits7, and can underpin emerging quantum technologies such as the single-photon sources needed for quantum communication8. In addition, structured environments are ubiquitous in problems involving the strong interplay of vibrational and electronic states. For example, those involving the photophysics of natural photosynthetic systems9,10, complex organic molecules used for light emission or solar cells11, or semiconductor quantum dots12,13,14,15. Similar problems arise when considering non-equilibrium energy transport in molecular systems16 or non-adiabatic processes in physical chemistry17. Non-Markovian effects can even be a resource for quantum information18,19.
Various approaches exist for dealing with non-Markovian dynamics1,3. Some particular problems have exact solutions20. For others, unitary transformations can uncover effective weak coupling theories, and perturbative expansions beyond the Born–Markov approximations12,21; these techniques typically yield time-local equations and are limited to certain parameter regimes. Diagrammatic formulations of such perturbative expansions can also form the basis for numerically exact approaches, for example, the real-time diagrammatic Monte Carlo as implemented in the Inchworm algorithm22,23. Finally, there are non-perturbative methods that enlarge the state space of the system. This can be through hierarchical equations of motion24, through capturing part of the environment within the system Hilbert space25,26,27 or by using augmented density tensors (ADTs) to capture the system’s history28,29. These can be very powerful but require either specific assumptions about the environments24,27 or resources that scale poorly with bath memory time.
In this Article, we describe a computationally efficient, general and yet numerically exact approach to modelling non-Markovian dynamics for an open quantum system coupled to an harmonic bath. Our method, which we call the time-evolving matrix product operator (TEMPO), exploits the ADT28,29 to represent a system’s history over a finite bath memory time τc. If the bath is well behaved, then using a singular value decomposition (SVD) to compress the ADT on the fly is expected to enable accurate calculations with computational resources scaling only polynomially with τc. We demonstrate the power of TEMPO by exploring two contrasting problems: the localisation transition in the spin-boson model (SBM)30 and spin dynamics with an environment that has both fast and slow correlation timescales—a problem for which other methods are not available. For both these problems we observe polynomial scaling with memory time.
Results
Time-evolving matrix product operators
In this section, we outline how the TEMPO algorithm works; further details are provided in the Methods section. We start by introducing the ADT. To define the notation and our graphical representation of it, we first consider the evolution of a Markovian system, which can be described by a density operator that contains d2 numbers for a d-dimensional Hilbert space. Usually, the density operator is written as a d × d matrix, but we instead use a length d2 vector with elements ρi(t). To evolve by a timestep Δ, we write
where \({\cal L}\) is the Liouvillian1. The graphical representation of this is shown in Fig. 1a. The red circle represents the density operator, with the protruding ‘leg’ indicating this is a tensor of rank one, that is, a vector. This leg is indexed by an integer i = 1,…,d2. The blue square with two legs represents the propagator \({\mathrm{e}}^{{\mathrm{\Delta }}{\cal L}}\), written as a d2 × d2 superoperator1. The matrix–vector multiplication in Eq. (1) is shown by joining a leg of the propagator to the density operator, indicating tensor contraction. This contraction generates the density operator at time t + Δ.
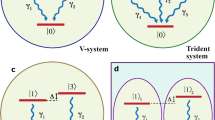
Schematic description of the TEMPO algorithm. a Pictorial representation of matrix–vector multiplication. In b we show how the ADT can be decomposed into an MPS. c The full tensor network starting from an initial standard density operator which is grown to an ADT with K legs, as shown in d, where we have contracted the contents of the green box. To propagate forward one step, we contract the ADT with the next row of the propagator, as in e. A schematic representation of the spin-boson model is shown in f
In order to capture non-Markovian dynamics, we extend our representation of the state at time t from a vector to an ADT, representing the history of the system. This is motivated by the path integral of a system interacting linearly with a bosonic environment. After integrating out the environment, the influence of the environment on the system can be captured by an ‘influence functional’ of the system paths alone1. The influence functional couples the current evolution to the history, and captures the non-Markovian dynamics. Makri and Makarov28,29 showed that by considering discrete timesteps, and writing the sum over system states in a discrete basis, the path integral could be reformulated as a propagator for the ADT, written as a discrete sum over paths. The influence functional becomes a series of influence functions Ik(j, j′) that connect the evolution of the amplitude of state j to the amplitudes of states j′ an integer number, k, of timesteps ago. This approach is known as the quasi-adiabatic path integral (QUAPI).
As described so far, the ADT grows at each timestep, to record the lengthening system history. However, the influence functions have no effect once kΔ exceeds the bath correlation time τc. One can therefore propagate an ADT containing only the previous K = τc/Δ steps: this is the finite memory approximation. This means we consider an ADT of rank K, written as \(A^{i_1,i_2, \ldots \! ,i_K}(t)\), where each index runs over ik = 1,…,d2. The explicit construction of this tensor is described in the Methods section. In general \(A^{i_1,i_2, \ldots \! ,i_K}(t)\) contains d2K numbers, which scales exponentially with the correlation time τc. If the full tensor is kept, one quickly encounters memory problems, and typical simulations are restricted to K < 2031,32 . Improved QUAPI algorithms33,34 show that (for some models) typical evolution does not explore this entire space, leading us to seek a minimal representation of the ADT.
Matrix product states (MPS)35,36 are natural tools to represent high-rank tensors efficiently where correlations are constrained in some way. Examples include the ground state of one-dimensional (1D) quantum systems with local interactions37, steady state transport in 1D classical systems38 or time-evolving 1D quantum states39. Inspired by these results, we show how an ADT can be efficiently represented and propagated using standard MPS methods. One may decompose high-rank tensors into products of low-rank tensors using SVDs and truncation. By combining indices, the tensor A can be written as36:
Here, U, V are unitary matrices, and λα denotes a singular value of the matrix A. Truncation corresponds to throwing away singular values λα smaller than some cutoff λc, consequently reducing the size of the matrices U, V. This procedure can be iterated by sweeping k across the whole tensor. The result of this is shown graphically in Fig. 1b, and can be written as:
This provides an efficient representation of the state, with a precision controlled by λc.
\(A^{i_1,i_2, \ldots ,i_K}(t)\) can be time locally propagated using a tensor \(B_{i_1, \ldots ,i_K}^{j_i, \ldots ,j_K}\). Crucially, this propagation can be performed directly on the matrix product representation of A. Moreover, the tensor product description of \(B_{i_1, \ldots ,i_K}^{j_i, \ldots ,j_K}\), shown as the connected blue squares in Fig. 1c, has a small dimension, d2, for the internal legs. Similarly to the time evolution shown in Fig. 1a, the state A(t + Δ) is generated by contracting the legs of A(t) with the input legs of B. Contracting a tensor network with a MPS, and truncating the resulting object by SVDs is a standard operation36. In all the applications we discuss below, we find that as time propagates we are able to maintain an efficient representation of \(A^{i_1,i_2, \ldots ,i_K}(t)\) with precision determined by λc.
The structure of the propagator depends on the influence functions Ik(j, j′) as shown in Fig. 1c (see also Methods section). We use darker colours to represent influence functions corresponding to more recent time points, which are expected to generate stronger correlations in the ADT. The input and output legs of the propagator are offset in the figure, so time can be viewed as propagating from left to right. In effect, at each step the register is shifted so that the right-most output index corresponds to the new state: events that occurred more than τc ago are dropped, as illustrated by the white semicircles in Fig. 1, since they do not influence the future evolution. Evolution over a series of timesteps is depicted in Fig. 1c–e. In Fig. 1c we show the full tensor network. Assuming the initial state of the system is uncorrelated with its environment means it can be drawn as a regular density operator. In the ‘grow’ phase, a series of asymmetric B propagators are applied, which allow the relevant system correlations to extend in time. Once the system has grown to an object with K legs, we enter the regular propagation phase, shown in Fig. 1d, e.
Spin-boson phase transition
To demonstrate the utility of the TEMPO algorithm, we apply it to two problems of a quantum system coupled to a non-Markovian environment. We first consider the unbiased SBM30, which has long served as the proving ground for open system methods. The generic Hamiltonian of this model is
where the Si are the usual spin operators, \(a_i^\dagger\)(ai) and ωi are, respectively, the creation (annihilation) operators and frequencies of the ith bath mode, which couples to the system with strength gi. The behaviour of the bath is characterised by the spectral density function
This model is known to show a rich variety of physics depending on the particular form of spectral density and system parameters chosen. When the spectral density is Ohmic, \(J(\omega ) = 2\alpha \omega \,{\mathrm{exp}}( - \omega /\omega _{\mathrm{c}})\), the model is known to exhibit a quantum phase transition in the BKT universality class40, at a critical value of the system–environment coupling α = αc30,41. The transition takes the system from a delocalised phase below αc, where any spin excitation decays (〈Sz〉 = 0 in the steady state), to a localised phase above αc (〈Sz〉 ≠ 0 in the steady state). Most analytic results are restricted to the regime where the cutoff frequency \(\omega _{\mathrm{c}} \gg \Omega\). For example, when S describes a spin-1/2 particle, the phase transition occurs at \(\alpha _{\mathrm{c}} = 1 + {\cal O}(\Omega /\omega _{\mathrm{c}})\)30,40,42.
We are able to explore the dynamics around this phase transition using TEMPO. In Fig. 2a we show the polarisation dynamics of the spin-1/2 SBM for a range of α at K = 200. This memory length is an order of magnitude larger than standard ADT implementations30 and is required to reach the asymptotic limit of the dynamics in the vicinity of the phase transition. We achieve convergence by varying the timestep Δ and SVD cutoff λc. We take an initial condition 〈Sz〉 = + 1/2 with no excitations in the environment, and find 〈Sz(t)〉.
Behaviour of the spin-1/2 system through the localisation phase transition. a The dynamics captured at K = 200 for the values of α indicated. The dotted lines show the exponential fits to the data above α = 0.5. The vertical black line shows the location of the memory cutoff used. b The dependence of the decay rate of the exponential fit on 1/K. This allows us to analyse the behaviour as K → ∞. c The change in the decay rate as we go through the transition by varying α for the values of K indicated. In d, we give 68% (blue) and 95% (red) confidence intervals for the extrapolated decay rate which crosses zero at around \(\alpha _{\mathrm{c}} \simeq 1.25\). The bath cutoff frequency is ωc = 5 and everything is measured in units of the Hamiltonian driving term Ω
Before reaching the localisation transition at α = αc, one first reaches a crossover at \(\alpha \simeq 0.5\) from coherent decaying oscillations to incoherent decay29. For α > 0.5, we find 〈Sz〉 always decays to zero asymptotically as \(\langle S_z(t)\rangle \propto {\mathrm{exp}}( - \gamma t)\) to a very good approximation; fits to this function are shown as dashed lines in Fig. 2a. Decay to zero for all α > 0.5 conflicts with the existence of a localised phase at large α, where 〈Sz〉 should asymptotically approach a non-zero value. The origin of this discrepancy is the finite memory approximation, which produced a time-local equation in the enlarged space of K timesteps. Time-local dynamics of a finite system typically generates a gapped spectrum of the effective Liouvillian43. In the localised phase, α > αc, the spectral gap should vanish asymptotically as we increase the memory cutoff τc → KΔ. We should thus examine how the extracted decay rate, γ, depends on the memory cutoff. For α < αc, γ should remain finite as τc → ∞, while for α > αc it should vanish. In Fig. 2b we plot γ as a function of 1/K =Δ/τc for different values of α around the phase transition. At small α, γ does appear to remain finite as K → ∞, while at large α the behaviour appears consistent with localisation.
We may estimate the location of the phase transition by extrapolating 1/K → 0 for each α, and finding the smallest value of α consistent with γ → 0. To do this, we use cubic fits in Fig. 2b (solid lines), and extract the constant part, with the restriction that the extracted γ cannot be negative. In order to find the phase transition as accurately as possible, we must perform simulations up to very large values of K: we here perform simulations up to K = 200, something that would be simply impossible without the tensor compression we exploit. Errors in our fits are assessed by monitoring the sensitivity of the best-fit result to truncation precision λc. These errors are all <10−4 and so are smaller than the points in Fig. 2. This allows us to find an error in the extracted K → ∞ limit. The extracted values for γ are displayed in Fig. 2d where we show our estimate for its 68 and 95% confidence intervals. These suggest that \(\alpha _{\mathrm{c}} \simeq 1.25\), consistent with the known analytic results30,40,42 . We note that identifying αc precisely from the time dependence of 〈Sz〉 is particularly challenging: since the localisation transition is in the BKT class40, the order parameter approaches zero continuously.
The efficiency of TEMPO enables consideration of models with a larger local Hilbert space. To demonstrate this, we examine the localisation transition in the spin-1 SBM. Physically this could either arise from a spin-1 impurity or from a pair of spin-1/2 particles interacting with a common environment44. On switching to this problem, the local dimension of each leg of our state tensor increases from d2 = 4 to d2 = 9, reducing the values of K we can reach. However, we also find convergence occurs for larger timesteps, allowing access to similar values of τc.
In Fig. 3a we show the dynamics of this model, after initialising to 〈Sz〉 = 1. In this case, on both sides of the localisation transition, the dynamics shows complex oscillatory behaviour before settling down to an exponential decay. This introduces more uncertainty to our exponential fits. However, as shown in Fig. 3b the extracted decay rate vanishes at \(\alpha _{\mathrm{c}} \simeq 0.28\), indicative of the phase transition and agreeing with numerical renormalisation group results44,45, but in contrast to the results found using a variational ansatz46.
Behaviour of the spin-1 system through the localisation phase transition. a The dynamics captured at K = 80 for the values of α indicated. The dotted lines show the exponential fits to the data. b The change in the decay rate as we go through the transition by varying α for the values of K indicated. The system parameters are the same as Fig. 2
Two spins in a common environment
We next demonstrate the flexibility of TEMPO by applying it to a dynamical problem for which other methods are not available. We consider a pair of identical spins-1/2, at positions ra and rb, which couple directly to each other through an isotropic Heisenberg coupling Ω, and which both couple to a common environment, see Fig. 4a. The Hamiltonian reads:
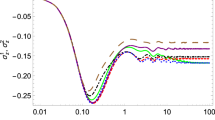
Dynamics of two coupled spins-1/2, separated by a distance R, interacting with the same environment. a A schematic of this system. b, c Dynamics of the system in 1D and 3D, respectively, at different values of the spin separation R. Insets to these plots are the corresponding spectral densities and bath correlation functions (see Methods section for details). The dimensionless couplings α used for 1D and 3D are α = 2 and α = 1, respectively. We set the speed of sound c = 1, so that all parameters are in units of Ω and we choose T = 0.5, ωc = 0.5. In all cases we have used 180 timesteps, but not used the memory cutoff meaning K = 180
The system–bath coupling constants have a position-dependent phase, \(g_{i,\nu } = g_i{\mathrm{e}}^{ - {\mathrm{i}}{\mathbf{k}}_i \cdot {\mathbf{r}}_\nu }\), where ki is the wavevector of the ith bosonic mode. We assume linear dispersion ωi = c|ki| and c = 1.
This model exhibits complex dissipative dynamics on two different timescales. The faster timescale describes dissipative dynamics of the spins due to interactions with their nearby environment, typically set by the ωc defined earlier. The other timescale is set by the spin separation R = |ra − rb| over which there is an environment-mediated spin–spin interaction. By changing R we can control the ratio of these timescales. The dimension, D, of the bath also has an effect: the intensity of environmental excitations propagating from one spin to the other will be stronger for lower D.
When the spins are close together, \(R < \omega _{\mathrm{c}}^{ - 1}\), it is difficult to distinguish local dissipative effects from the environment-mediated interaction and both master equation techniques13 and the standard ADT method47 generate accurate dynamics. Instead, we consider large separation \(R > \omega _{\mathrm{c}}^{ - 1}\), about which little is known. The ADT then requires both a small timestep \(\Delta \ll \omega _{\mathrm{c}}^{ - 1}\) to capture the fast local dissipative dynamics and a large cutoff time τc = KΔ > R to capture environment-induced interactions; hence, a very large K is needed. Using TEMPO we are able to investigate these dynamics without even having to go beyond the tensor growth stage shown in Fig. 1c, and thus avoid any error caused by a finite memory cutoff K.
We project onto the Sz,a + Sz,b = 0 subspace of the system, consisting of the two anti-aligned spin states, since this is the only sector with non-trivial dynamics. The effective Hamiltonian for this 2d subspace can then be mapped onto the spin-1/2 SBM, Eq. (4), albeit with a modified spectral density that depends on R. Details of this procedure are given in the Methods section.
In Fig. 4b, c we show dynamics for different R for environments with D = 1 and D = 3. Insets show the effective spectral densities, J(ω), and real part of the bath autocorrelation functions, C(t), which we define in the Methods section. We initialise the spins in a product state with 〈Sz,a〉 = 1/2, 〈Sz,b〉 = −1/2 and calculate the probability, P(t), of finding the system in this state at time t. The bath is initialised in thermal equilibrium at temperature T. For D = 1, after initial oscillations decay away over a timescale \(\sim \omega _{\mathrm{c}}^{ - 1}\), there are revivals at t = R. This is due to the strongly oscillating spectral density which results in a large peak at C(t = R). As expected for a one-dimensional environment, the profile of these secondary oscillations is independent of R when \(R \gg \omega _{\mathrm{c}}^{ - 1}\). Additionally for R = 20 more small amplitude oscillations appear at t ≈ 40, due to the effective interaction of the spins at t ≈ 20 sending more propagating excitations into the environment. For D = 3 the spectral density still has an oscillatory component, though it is much less prominent. The resulting peaks at C(t = R) are thus much smaller than the t = 0 peak and have only a small effect on the dynamics. Small amplitude oscillations can be seen at t ≈ R when R = 8, but with R = 16 it is difficult to see any significant features in the dynamics.
Discussion
We have presented a highly efficient method for modelling the non-Markovian dynamics of open quantum systems. Our method is applicable to a wide variety of situations. In well-established ADT methods, non-Markovianity is accounted for by encoding the system’s history in a high-rank tensor; we have overcome the restrictive memory requirements of storing this tensor by representing it as an MPS. We can then efficiently calculate open system dynamics by propagating this MPS via iterative application of an MPO. To test our technique we used it to find the localisation transition in the SBM, for both spin-1/2 and spin-1, and found estimates for the critical couplings, consistent with other techniques. We then applied our method to a pair of interacting spins embedded within a common environment, in a regime where a large separation of timescales prevents the use of other methods.
Precisely locating the phase transition is a rigorous test of any numerical method: as we found, very large memory times, up to K = 200 were required to precisely locate this point. Other improved numerical methods22,23,33 have demonstrated a degree of enhanced efficiency when considering conditions away from the critical coupling. As yet, other such general methods have not been used to precisely locate the transition.
The key to our technique is that tensor networks provide an efficient representation of high-dimensional tensors encoding restricted correlations. As well as the widespread application of such methods in low-dimensional quantum systems35,36,37,38,39, they have also been applied to sampling problems in classical statistical physics48, and analogous techniques (under the name ‘Tensor trains’) have been developed in computer science49. Moreover, there has been a recent synthesis showing how techniques developed in one context can be extended to others, such as machine learning50, or Monte Carlo sampling of quantum states51. Our work defines a further application for these methods, and future work may yet yield even more efficient approaches.
The methods described in this article are already very powerful in their ability to model general non-Markovian environments. They also enable easy extension to study larger quantum systems, by adapting other methods from tensor networks such as the optimal boson basis52—these will be the subject of future work. They may also be combined with approaches such as the tensor transfer method described in Ref. 53. This method allows efficient long time propagation of dynamics, so long as an exact map is known up to the bath memory time: TEMPO enables efficient calculation of the required exact map. With such tools available, the study of the dynamics of quantum systems in non-Markovian environments3 can now move from studying isolated examples to elucidating general physical principles, and modelling real systems.
Methods
TEMPO algorithm
In this section, we will present the details of the TEMPO algorithm, paying particular attention to how the ADT and propagator are constructed in a matrix product form.
The generic Hamiltonian of the models we consider is
where H0 is the (arbitrary) free system Hamiltonian and HE contains both the bath Hamiltonian and the system–bath interaction. Here \(a_i^\dagger\) (ai) and ωi are the creation (annihilation) operators and frequencies of the ith environment mode. The system operator O couples to bath mode i with coupling constant gi. As outlined in the main text, we work in a representation where d × d density operators are given instead by vectors with d2 elements. These vectors are then propagated using a Liouvillian as in Eq. (1) of the main text, \({\cal L} = {\cal L}_0 + {\cal L}_{\mathrm{E}}\), where \({\cal L}_0\) and \({\cal L}_{\mathrm{E}}\) generate coherent evolution caused by H0 and HE, respectively. It has been shown recently that it is straightforward to include additional Markovian dynamics in the reduced system Liouvillian54 in the ADT description.
If the total propagation over time tN is composed of N short time propagators \({\mathrm{e}}^{t_N{\cal L}} = ({\mathrm{e}}^{\Delta {\cal L}})^N\), we can use a Trotter splitting55
We note that the following arguments can be easily adapted to use the higher-order, symmetrized, Trotter splitting28,29,56 that reduces the error to Δ3. All the numerical results presented use this symmetrized splitting, but for ease of exposition we use the form of Eq. (9) here. We assume the initial density operator factorises into system and environment terms, with the environment initially in thermal equilibrium at temperature T. Time evolution can then be written as a path sum over system states, by inserting resolutions of identity between each \({\mathrm{e}}^{{\mathrm{\Delta }}{\cal L}_{\mathrm{E}}}{\mathrm{e}}^{{\mathrm{\Delta }}{\cal L}_0}\) and then tracing over environmental degrees of freedom. The result is the discretized Feynman–Vernon influence functional28,29, which yields the following form for the time evolved density matrix:
The indexing here is in a basis where O is diagonal. Each j index runs from 1 to d2, and due to the order of the splitting in Eq. (9), the initial state of the system has been propagated forward a single timestep, \(\rho _{j_1}({\mathrm{\Delta }}) = \left[ {{\mathrm{e}}^{{\mathrm{\Delta }}{\cal L}_0}} \right]_{j_1j_0}\rho _{j_0}(0)\). We have defined the influence functions
with
Here \(O_j^ -\) are the d2 possible differences that can be taken between two eigenvalues of O and \(O_j^ +\) the corresponding sums. The coefficients, ηk, quantify the non-Markovian correlations in the reduced system across k timesteps of evolution and are given by the integrals
where C(t) is the bath autocorrelation function
with temperature measured in units of frequency and with the spectral density \(J(\omega ) = \mathop {\sum}\nolimits_i |g_i|^2\delta (\omega _i - \omega )\).
The summand of the discretised path integral in Eq. (10) can be interpreted as the components of an N-index tensor \(A^{j_N,j_{N - 1}, \ldots ,j_1}\). This tensor is an ADT of the type originally proposed by Makri and Makarov28,29. We will show below that this N-index tensor can also be written as tensor network consisting of N(N + 1)/2 tensors with, at most, four legs each and that this network can be contracted using standard MPS-MPO contraction algorithms35,36, First we gather terms in the inner piece of the double product in Eq. (10) into a single object, which we write as components of an n-index tensor
Next, we define the (2n − 1)-index tensors
for n > 1, and the 1-index initial ADT:
We may now evolve this ADT in time iteratively by successive contraction of tensors. This process is shown graphically in Fig. 1c. The first contraction produces a 2-index ADT which describes the full state and history at the second time point:
We next contract with \(B_{i_2,i_1}^{j_3,j_2,j_1}\) to produce a 3-index ADT and so on. The nth step of this process then looks like
and the density operator for the open system at time tn = nΔ is recovered by summing over all but the jn leg,
from which observables can be calculated. At each iteration the size of the ADT grows by one index, since up to now we have made no cutoff for the bath memory time: we are in the ‘grow’ phase depicted in Fig. 1c. To compress the state after each application of this B tensor, we sweep along the resulting ADT performing SVD’s and truncating at each bond, throwing away the components corresponding to singular values smaller than our cutoff λc. This gives an MPS representation of the ADT, as given in Eq. (3). As discussed in Ref.57, we must in fact sweep both left to right and then right to left to ensure the most efficient MPS representation is found. If no bath memory cutoff is made, this whole process is repeated until the final time point is reached at n = N.
The (2n − 1)-index propagation tensor, B, can be represented as an MPO such that the above process of iteratively contracting tensors becomes amenable to standard MPS compression algorithms35,36. The form required is
where we define the rank-4 tensor
and the rank-2 and rank-3 tensors appearing at the ends of the product are
and
Upon substituting these forms, Eqs. (22)–(24), into Eq. (21) it is straightforward to verify that we recover the expression Eq. (16). The rank-(2n − 1) MPO, \(B_{i_{n - 1}, \ldots ,i_1}^{j_n,j_{n - 1}, \ldots ,j_1}\), is represented by the tensor network diagram in Fig. 5.
Tensor network diagram depicting the MPO decomposition of the rank-(2n + 1) tensor, B. The squares show the bk tensors in Eqs. (22)–(24), with k increasing right to left. The in and jn tensor indices correspond to the vertical legs with n increasing from left to right. When n = K the j1 leg is summed over to give the rank-2K propagation phase MPO, represented in the figure by contraction with a rank-1 object; the d2-dimensional vector whose elements are all equal to one
We note it has recently been shown that if the spectrum of O has degeneracies, then part of the sum in Eq. (10) can be performed analytically, vastly reducing computational cost of the ADT method for systems where the environment only couples to a small subsystem58. Here we can further exploit the fact that, even when there is no degeneracy in the d eigenvalues of O, there is always degeneracy in the d2 differences between its eigenvalues, \(O_j^ -\), that is, d of these differences are always zero. Using the same partial summing technique described in Ref. 57 we can thus reduce the dimension of the internal indices of the rank-(2n − 1) MPO, Eq. (21), from d2 to d2 − d + 1. Furthermore, if the eigenvalues of O are non-degenerate but evenly spaced, as is the case for spin operators, then there are only 2d − 1 unique values of \(O_j^ -\), allowing us to reduce the size of the bk tensors, Eq. (22), from \({\cal O}(d^8)\) to \({\cal O}(d^6)\).
The finite memory approximation can now be introduced by throwing away information in the ADT for times longer than τc = KΔ into the system’s history. To do this we write
Thus, when propagating \(A^{j_n, \ldots ,j_1}\) beyond the Kth timestep only indices jnto jn−K+1 have any relevance and we can sum over the rest. The way we do this in practice is to define the 2K-leg tensor MPO
such that contraction with a rank-K MPS is equivalent to first growing the MPS by one leg and then summing over (i.e. removing) the leg which is earliest in time. Repeating this contraction propagates an A-tensor MPS forward in time, but maintains its rank of K for all timesteps n > K. This is what we show in the ‘propagate’ phase of Fig. 1c. For some spectral densities, it is possible to improve the convergence with τc by making a softer cutoff59,60, but since TEMPO can go to very large values of K this is not necessary here.
For time-independent problems (as we study here), the ‘propagate’ phase involves repeated contraction with the same MPO, Eq. (26), which is independent of the timestep. To make this clear, it is convenient to change our index labelling (which, so far has referred to the absolute number of timesteps from t = 0). We will instead relabel the indices on the MPO and MPS as follows: \(B_{i_K, \ldots ,i_1}^{j_{K + 1}, \ldots ,j_2} \to B_{i_1, \ldots ,i_K}^{j_1, \ldots ,j_K}\) and \(A^{j_n, \ldots ,j_{n - K + 1}} \to A^{j_1, \ldots ,j_K}(t_n)\). The indices now refer to the distance back in time from the current time point. To summarise, with the new labelling we first grow the initial state into a K-index MPS, \(A^{j_1, \ldots ,j_K}(\tau _{\mathrm{c}})\), and then propagate as:
and the physical density operator is found via
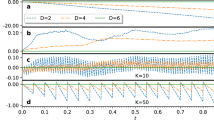
Having described the TEMPO algorithm we now briefly analyse the computational cost of applying it to the SBM of Eq. (4). In Fig. 6a we plot the total size, Ntot, of the MPS and maximum bond dimension, λmax, used to obtain converged results in Fig. 2 against coupling strength with K = 200. We find the most computationally demanding regime to be around α = 0.5, the point of crossover from underdamped to overdamped oscillations of Sz. We find the CPU time required is linear in the total memory requirement. For the largest memory required (at α = 0.5), the time to obtain 500 data points using TEMPO on the HPC Cirrus cluster was ≈20.5 h. In Fig. 2b we show how Ntot grows with K for different values of α. For α = 0.1,0.5 we see quadratic growth with K, while for couplings near and above the phase transition, α = 1,1.5, the growth is only linear. Both cases thus represent polynomial scaling, a substantial improvement on the exponential scaling of the standard ADT method for which one has Ntot = 4K
.
Mapping two spins in a common environment to a single spin model
We show here how to map Eq. (6) describing a pair of spin-1/2 particles in a common environment onto Eq. (4), a single spin-1/2 SBM. The Hamiltonian Eq. (6) has the property that the total z-component of the two-spin system is conserved, [Sz,a + Sz,b, H] = 0. Thus, the problem can be separated into three distinct subspaces: the two states with the spins anti-aligned (Sz,a + Sz,b = 0) form one subspace and the two aligned spin states (Sz,a + Sz,b = ±1) are the other two. The one-dimensional subspaces with aligned spins cannot evolve in time; hence, all non-trivial dynamics in this model happen in the Sz,a + Sz,b = 0 subspace. We therefore focus on this subspace. By doing so, we may subtract a term proportional to Sz,a + Sz,b from the system–bath coupling in Eq. (6). The remaining system–bath interaction is given by
The effective coupling here is \(\left| {\tilde g_i} \right| = \left| {g_{i,a} - g_{i,b}} \right| = 2g_i\,{\mathrm{sin}}\left[ {{\mathbf{k}}_i \cdot ({\mathbf{r}}_a - {\mathbf{r}}_b)/2} \right]\). These couplings lead to a modified effective spectral density13,61,
where Jp(ω) is the actual density of states of the bath. The function FD(ωR) arises from angular averaging in D-dimensional space, and so crucially depends on the dimensionality of the environment. Specifically we have:
where J0(x) is a Bessel function. We note that FD(ωR) → 0 as R → ∞ for D > 1, due to the diminishing effect of the environment-induced coupling in higher dimensions. (When considering R → ∞, we should note that in the original Hamiltonian we neglected any retardation in the Heisenberg interaction.) At small separations, R → 0, FD(ωR) → 1 and so J(ω) → 0 for all D due to the loss of relative phase shift between the couplings of the anti-aligned states to the environment.
For the bare density of states Jp(ω), we consider a simple model of e.g. a quantum dot in a phonon environment, for which the coupling constants appearing in the Hamiltonian, Eq. (6), have \(g_i \sim \sqrt {\omega _i}\)19. This means that in the continuum limit the spectral density for a D-dimensional environment is
where ωc describes a high-frequency cutoff and α is the strength of the interaction with the environment.
Data and code availability
The datasets generated during and/or analysed during the current study are available at: https://doi.org/10.17630/44616048-eaac-4971-bbff-1d36e2cef256. The TEMPO code is available at https://doi.org/10.5281/zenodo.1322407.
Change history
05 September 2018
This Article was originally published without the accompanying Peer Review File. This file is now available in the HTML version of the Article; the PDF was correct from the time of publication.
References
Breuer, H. -P. & Petruccione, F. The Theory of Open Quantum Systems (Oxford University Press, Oxford, 2002).
Walls, D. F. & Milburn, G. J. Quantum Optics 2nd edn (Springer, Berlin, 2007).
de Vega, I. & Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 89, 015001 (2017).
Gröblacher, S. et al. Observation of non-Markovian micromechanical brownian motion. Nat. Commun. 6, 7606 (2015).
Madsen, K. H. et al. Observation of non-Markovian dynamics of a single quantum dot in a micropillar cavity. Phys. Rev. Lett. 106, 233601 (2011).
Mi, X., Cady, J. V., Zajac, D. M., Deelman, P. W. & Petta, J. R. Strong coupling of a single electron in silicon to a microwave photon. Science 355, 156–158 (2017).
Potočnik, A. et al. Studying light-harvesting models with superconducting circuits. Nat. Commun. 9, 904 (2018).
Aharonovich, I., Englund, D. & Toth, M. Solid-state single-photon emitters. Nat. Photon. 10, 631–641 (2016).
Chin, A. W. et al. The role of non-equilibrium vibrational structures in electronic coherence and recoherence in pigment–protein complexes. Nat. Phys. 9, 113–118 (2013).
Lee, M. K., Huo, P. & Coker, D. F. Semiclassical path integral dynamics: photosynthetic energy transfer with realistic environment interactions. Annu. Rev. Phys. Chem. 67, 639–668 (2016).
Barford, W. Electronic and Optical Properties of Conjugated Polymers (Oxford University Press, Oxford, 2013).
McCutcheon, D. P. S., Dattani, N. S., Gauger, E. M., Lovett, B. W. & Nazir, A. A general approach to quantum dynamics using a variational master equation: application to phonon-damped rabi rotations in quantum dots. Phys. Rev. B 84, 081305 (2011).
McCutcheon, D. P. S. & Nazir, A. Coherent and incoherent dynamics in excitonic energy transfer: correlated fluctuations and off-resonance effects. Phys. Rev. B 83, 165101 (2011).
Kaer, P., Nielsen, T. R., Lodahl, P., Jauho, A.-P. & Mørk, J. Non-Markovian model of photon-assisted dephasing by electron–phonon interactions in a coupled quantum-dot–cavity system. Phys. Rev. Lett. 104, 157401 (2010).
Roy, C. & Hughes, S. Influence of electron–acoustic-phonon scattering on intensity power broadening in a coherently driven quantum-dot–cavity system. Phys. Rev. X 1, 021009 (2011).
Segal, D. & Agarwalla, B. K. Vibrational heat transport in molecular junctions. Annu. Rev. Phys. Chem. 67, 185–209 (2016).
Subotnik, J. E. et al. Understanding the surface hopping view of electronic transitions and decoherence. Annu. Rev. Phys. Chem. 67, 387–417 (2016).
Bylicka, B., Chruściński, D. & Maniscalco, S. Non-Markovianity and reservoir memory of quantum channels: a quantum information theory perspective. Sci. Rep. 4, 5720 (2014).
Xiang, G.-Y. et al. Entanglement distribution in optical fibers assisted by nonlocal memory effects. Phys. Lett. 107, 54006 (2014).
Mahan, G. D. Many Particle Physics 3rd edn (Springer, Berlin, 2000).
Jang, S. Theory of coherent resonance energy transfer for coherent initial condition. J. Chem. Phys. 131, 164101 (2009).
Cohen, G., Gull, E., Reichman, D. R. & Millis, A. J. Taming the dynamical sign problem in real-time evolution of quantum many-body problems. Phys. Rev. Lett. 115, 266802 (2015).
Chen, H.-T., Cohen, G. & Reichman, D. R. Inchworm Monte Carlo for exact non-adiabatic dynamics. ii. Benchmarks and comparison with established methods. J. Chem. Phys. 146, 054106 (2017).
Yoshitaka, T. & Kubo, R. Time evolution of a quantum system in contact with a nearly Gaussian-Markoffian noise bath. J. Phys. Soc. Jpn. 58, 101–114 (1989).
Garraway, B. M. Non-perturbative decay of an atomic system in a cavity. Phys. Rev. A 55, 2290–2303 (1997).
Iles-Smith, J., Lambert, N. & Nazir, A. Environmental dynamics, correlations, and the emergence of noncanonical equilibrium states in open quantum systems. Phys. Rev. A 90, 032114 (2014).
Schröder, F. A. Y. N. et al. Multi-dimensional tensor network simulation of open quantum dynamics in singlet fission. Preprint at https://arxiv.org/abs/1710.01362 (2017).
Makri, N. & Makarov, D. E. Tensor propagator for iterative quantum time evolution of reduced density matrices. I. Theory. J. Chem. Phys. 102, 4600 (1995).
Makri, N. & Makarov, D.E. Tensor propagator for iterative quantum time evolution of reduced density matrices. II. Numerical methodology. J. Chem. Phys. 102, 4611 (1995).
Leggett, A. J. et al. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 59, 1–85 (1987).
Nalbach, P., Ishizaki, A., Fleming, G. R. & Thorwart, M. Iterative path-integral algorithm versus cumulant time-nonlocal master equation approach for dissipative biomolecular exciton transport. N. J. Phys. 13, 063040 (2011).
Thorwart, M., Eckel, J. & Mucciolo, E. R. Non-Markovian dynamics of double quantum dot charge qubits due to acoustic phonons. Phys. Rev. B 72, 235320 (2005).
Sim, E. Quantum dynamics for a system coupled to slow baths: on-the-fly filtered propagator method. J. Chem. Phys. 115, 4450–4456 (2001).
Lambert, R. & Makri, N. Memory propagator matrix for long-time dissipative charge transfer dynamics. Mol. Phys. 110, 1967–1975 (2012).
Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. (NY) 326, 96–192 (2011).
Orús, R. A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann. Phys. (NY) 349, 117–158 (2014).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
Derrida, B., Evans, M. R., Hakim, V. & Pasquier, V. Exact solution of a 1d asymmetric exclusion model using a matrix formulation. J. Phys. A 26, 1493 (1993).
Vidal, G. Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 91, 147902 (2003).
Florens, S., Venturelli, D. & Narayanan, R. in Quantum Quenching, Annealing and Computation (eds Chandra, A. K., et al.) 145–162 (Springer, Berlin, Heidelberg, 2010).
Le Hur, K. in Understanding Quantum Phase Transitions (ed. Carr, L.) (CRC Press, New York, 2010)
Bulla, R., Tong, N.-H. & Vojta, M. Numerical renormalization group for bosonic systems and application to the sub-ohmic spin-boson model. Phys. Rev. Lett. 91, 170601 (2003).
Kessler, E. M. et al. Dissipative phase transition in a central spin system. Phys. Rev. A 86, 012116 (2012).
Orth, P. P., Roosen, D., Hofstetter, W. & Le Hur, K. Dynamics, synchronization, and quantum phase transitions of two dissipative spins. Phys. Rev. B 82, 144423 (2010).
Winter, A. & Rieger, H. Quantum phase transition and correlations in the multi-spin-boson model. Phys. Rev. B 90, 224401 (2014).
McCutcheon, D. P. S., Nazir, A., Bose, S. & Fisher, A.J. Separation-dependent localization in a two-impurity spin-boson model. Phys. Rev. B 81, 235321 (2010).
Nalbach, P., Eckel, J. & Thorwart, M. Quantum coherent biomolecular energy transfer with spatially correlated fluctuations. N. J. Phys. 12, 065043 (2010).
Johnson, T. H., Elliott, T. J., Clark, S. R. & Jaksch, D. Capturing exponential variance using polynomial resources: applying tensor networks to non-equilibrium stochastic processes. Phys. Rev. Lett. 114, 090602 (2015).
Oseledets, I. V. Tensor-train decomposition. J. Sci. Comput. 33, 2295–2317 (2011).
Stoudenmire, E. & Schwab, D. J. in Advances in Neural Information Processing Systems 29 (eds. Lee, D. D. et al.) 4799–4807 (Curran Associates, Red Hook, 2016).
Ferris, A. J. & Vidal, G. Perfect sampling with unitary tensor networks. Phys. Rev. B 85, 165146 (2012).
Guo, C., Weichselbaum, A., von Delft, J. & Vojta, M. Critical and strong-coupling phases in one- and two-bath spin-boson models. Phys. Rev. Lett. 108, 160401 (2012).
Cerrillo, J. & Cao, J. Non-Markovian dynamical maps: numerical processing of open quantum trajectories. Phys. Rev. Lett. 112, 110401 (2014).
Barth, A. M., Vagov, A. & Axt, V. M. Path-integral description of combined Hamiltonian and non-Hamiltonian dynamics in quantum dissipative systems. Phys. Rev. B 94, 125439 (2016).
Trotter, H. F. On the product of semi-groups of operators. Proc. Am. Math. Soc. 10, 545–551 (1959).
Suzuki, M. Generalized Trotter’s formula and systematic approximants of exponential operators and inner derivations with applications to many-body problems. Comm. Math. Phys. 51, 183–190 (1976).
Stoudenmire, E. M. & White, S. R. Minimally entangled typical thermal state algorithms. N. J. Phys. 12, 055026 (2010).
Cygorek, M., Barth, A. M., Ungar, F., Vagov, A. & Axt, V. M. Nonlinear cavity feeding and unconventional photon statistics in solid-state cavity QED revealed by many-level real-time path-integral calculations. Phys. Rev. B 96, 201201 (2017).
Vagov, A., Croitoru, M. D., Glässl, M., Axt, V. M. & Kuhn, T. Real-time path integrals for quantum dots: quantum dissipative dynamics with superohmic environment coupling. Phys. Rev. B 83, 094303 (2011).
Strathearn, A., Lovett, B. W. & Kirton, P. Efficient real-time path integrals for non-Markovian spin-boson models. N. J. Phys. 19, 093009 (2017).
Stace, T. M., Doherty, A. C. & Barrett, S. D. Population inversion of a driven two-level system in a structureless bath. Phys. Rev. Lett. 95, 106801 (2005).
Acknowledgements
We thank T.M. Stace for useful discussions and J. Iles-Smith for comments on an earlier version of this paper. A.S. acknowledges a studentship from EPSRC (EP/L505079/1). P.K. acknowledges support from EPSRC (EP/M010910/1). D.K. acknowledges support from the EPSRC CM-CDT (EP/L015110/1). J.K. acknowledges support from EPSRC programs 'TOPNES' (EP/I031014/1) and 'Hybrid Polaritonics' (EP/M025330/1). B.W.L. acknowledges support from EPSRC (EP/K025562/1). This work used EPCC's Cirrus HPC Service (https://www.epcc.ed.ac.uk/cirrus).
Author information
Authors and Affiliations
Contributions
The TEMPO code was developed by A.S., P.K. and D.K., following the identification of the MPS representation by J.K. Analysis of the two applications was performed by A.S., P.K. and B.W.L.. The project was directed by J.K. and B.W.L. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Strathearn, A., Kirton, P., Kilda, D. et al. Efficient non-Markovian quantum dynamics using time-evolving matrix product operators. Nat Commun 9, 3322 (2018). https://doi.org/10.1038/s41467-018-05617-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05617-3
This article is cited by
-
Unified framework for open quantum dynamics with memory
Nature Communications (2024)
-
Seeking a quantum advantage with trapped-ion quantum simulations of condensed-phase chemical dynamics
Nature Reviews Chemistry (2024)
-
Phase transitions in the classical simulability of open quantum systems
Scientific Reports (2023)
-
Succinct Description and Efficient Simulation of Non-Markovian Open Quantum Systems
Communications in Mathematical Physics (2023)
-
Simulation of open quantum systems by automated compression of arbitrary environments
Nature Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.