Abstract
Glasses are among the most widely used of everyday materials, yet the process by which a liquid’s viscosity increases by 14 decades to become a glass remains unclear, as often contradictory theories provide equally good descriptions of the available data. Knowledge of emergent lengthscales and higher-order structure could help resolve this, but this requires time-resolved measurements of dense particle coordinates—previously only obtained over a limited time interval. Here we present an experimental study of a model colloidal system over a dynamic window significantly larger than previous measurements, revealing structural ordering more strongly linked to dynamics than previously found. Furthermore we find that immobile regions and domains of local structure grow concurrently with density, and that these regions have low configurational entropy. We thus show that local structure plays an important role at deep supercooling, consistent with a thermodynamic interpretation of the glass transition rather than a principally dynamic description.
Similar content being viewed by others
Introduction
Whether the immense increase in viscosity that occurs in glass-forming liquids when they are cooled is related to a true thermodynamic transition at a non-zero (Kauzmann) temperature, or whether it is a kinetic phenomenon associated with structural relaxation times diverging only at zero temperature, remains controversial1. A distinctive feature of the glass transition is dynamic heterogeneity, whereby supercooled liquids do not relax uniformly but exhibit fast and slow regions. This may be due to the formation of ‘cooperatively re-arranging regions’ which undergo entropic melting2; the hierarchical interactions of mobility excitations3; the presence of geometric motifs such as icosahedra4 or a transition to a slow-moving phase with high overlap between particle positions5. Experimental evidence discriminating between these theoretical approaches would constitute a major step forward in our understanding of the glass transition.
By analogy with conventional phase transitions, one important route to distinguishing these theoretical perspectives lies in identifying relevant lengthscales and their behaviour. The heterogenous nature of viscous liquids allows us to distinguish two main types of lengthscales: dynamical lengthscales, which concern the typical spatial extent of regions with low (or high) mobility (e.g. ξ46,7, ξb8 or ξRG9), and static or structural lengthscales, which quantify the range of (non-crystalline) order (e.g. the point-to-set correlation length ξPTS10,11 or the extent of domains of particular locally favoured structures (LFS) ξLFS9,12). Some theories1,2,4 anticipate an increasing dynamic lengthscale that is accompanied by a growing structural lengthscale as the temperature is reduced. Detection of this coupled growth would therefore provide significant support for theories that propose a thermodynamic underpinning of the glass transition1,2,4, while its absence would favour theories which emphasise the dynamics3. Several attempts have been made to find coupled growth between dynamic and structural lengthscales13,14, but with mixed results: some find identical scaling between a dynamic correlation length ξ4 and structural lengthscales in experiment15 and computer simulation16,17. However, others find that in three dimensions (3D) while ξ4 increases strongly, structural correlation lengths grow weakly if at all9,10,13,14,18,19,20. Indeed, the lengthscales reported in ref. 16 for 3D systems are rather modest, perhaps relating to recent discoveries of significant differences between two and three dimensions for glass-forming systems21. Furthermore correlation between LFS and dynamically slow regions has to date been rather limited22,23.
Detection of non-crystalline order24 such as LFS4 requires coordinate data, thus it is generally only possible to directly probe the correlation between structure and dynamics in simulations and particle-resolved experiments. Both these methods provide data over a limited dynamical regime, where the relaxation time of the supercooled liquid is around four orders of magnitude larger than that of the high-temperature liquid14,25,26,27. This corresponds to a regime well described by mode-coupling theory28,29,30, yet at deeper supercooling there is expected to be a crossover from a caged to an ‘activated’ type of dynamics. Therefore between this mode-coupling crossover and the experimental glass transition Tg, we expect new physics not observed at weaker supercooling. In particular, at deep supercooling, relaxation events are expected to be ‘nucleated’ and the nature of the cooperatively relaxing regions is thought to change, in that they are expected to become more compact. Tantalising hints of this behaviour have been gleaned from experiments11 and simulation10. Pushing past the mode-coupling regime to Tg in molecular experiments, indirect measurements detect growth of dynamic lengthscales of up to five molecular diameters13,14,20. Recent inferences of structural lengthscales suggest a similar (i.e. quite small) value of a few molecular diameters at Tg20. In light scattering experiments on colloids, it has also been shown that the temporal evolution of the amounts of locally ordered and slow particles are intimately linked31. Yet in order to make progress in directly determining lengthscales and the relationship between local structure and dynamics, we require particle-resolved data closer to Tg than the mode-coupling regime studied thus far.
Colloidal particles are epitomised by the hard sphere model, for which the phase behaviour as a function of volume fraction (or reduced pressure) is similar to the case of simple molecules as a function of inverse temperature14,25. Thus supercooling is analogous to increasing density for colloidal hard spheres and we use the terms interchangeably throughout. To date, particle-resolved studies with colloids of diameter 1.5–3.5 μm15,25,32,33 rarely exceed 4 decades of supercooling. Crucially, the mode-coupling crossover is thought to occur after at least 5 decades of supercooling34. Since the Brownian time (τB = σ3πη/(8kBT) where η is the solvent viscosity and kBT is the thermal energy) taken by dilute colloids of diameter σ to diffuse their own radius is typically several seconds, the mode-coupling regime is normally reached on experimental timescales of several days or weeks—beyond the practical limit of most measurements. However, by changing the particle diameter the characteristic timescale of the system can be rescaled. Even decreasing the particle size by little more than a factor of two can increase the dynamic range available by an order of magnitude, sufficient to extend particle-resolved measurements up to and beyond the mode-coupling crossover. Previously, this regime has been accessed with such small colloids using dynamic light scattering34 and real-space fluorescent recovery35, but in both cases averaged dynamic properties were measured.
Here, we use super-resolution stimulated emission depletion microscopy (STED36) to access the detailed structure of a system of small colloids directly in real space with particle resolution. By tracking the particles in space and time, we extend real-space imaging to previously inaccessible timescales. The new dynamical regime we access reveals that the correlation between locally favoured structures and dynamically slow regions is significantly enhanced at deep supercooling. Furthermore, we identify growing static and dynamic lengthscales ξstatic and ξslow, associated with these locally favoured structures and slow-moving regions, respectively. Finally, by measuring the overlap of coordinates in different regions, we obtain evidence consistent with a decrease in the configurational entropy of the system. These results indicate the importance of local structure and its relation to a putative thermodynamic phase transition2 in dynamical arrest.
Results
Global dynamics
Figure 1a shows that we are able to resolve particles much smaller than those typically used for particle-resolved studies, and successfully track particle coordinates in 3D to enable structural analysis of the system (Fig. 1b, c). Supplementary Movies 1–4 also show that we may follow the particles over time for a wide range of volume fractions and relaxation times. Moreover, at volume fraction ϕ = 0.600, the system is very deeply supercooled—almost seven orders of magnitude slower than the low density liquid. The dynamics at this state point are two orders of magnitude slower than those at the value typically taken for the mode-coupling crossover ϕMCT ≈ 0.5837, accessing directly the regime beyond the mode-coupling transition where the mechanism of relaxation is predicted to change2.
It has been demonstrated1,38 for molecular systems that supercooled liquids continue to relax beyond the mode-coupling crossover, thus we expect to see the equivalent behaviour for this colloidal system. In order to do this we determine the structural relaxation time τα from the intermediate scattering function (Methods section) for a range of particle concentrations. We then construct an ‘Angell’ plot of relaxation time, but, rather than ϕ, we replot using the Carnahan–Starling equation of state Zcs = (1 + ϕ + ϕ2 − ϕ3)/(1 − ϕ)3 as a control parameter, following the arguments of Berthier and Witten39. This produces similar scaling of the relaxation time compared to thermal systems (where (inverse) temperature is the control parameter)40, and gives good agreement with simulations over the range of volume fractions described here41.
The resulting Angell plot is shown in Fig. 2a (For convenience we also show the conventional τα(ϕ) form in Supplementary Fig. 4) and two fits are used to describe the increasing structural relaxation time. First, we use a Vogel–Fulcher–Tammann (VFT) form:
where τ∞ is the relaxation time in a dilute system, ϕ0 is the point at which the relaxation time would diverge, A is a measure of the fragility and δ is an exponent typically set to one to recover the conventional VFT form. We see that the VFT fit gives a good agreement with the experimental data throughout the supercooled range. For δ = 1, the fit predicts a dynamical divergence at a volume fraction ϕ0 = 0.616 ± 0.002 (Z0 = 31.1). Second, we apply a fit of the mode-coupling prediction1,42 (Fig. 2a, green line): τα(ϕ) ~ (ϕMCT − ϕ)−γ where γ is ≈2.6 for hard spheres34 and ϕMCT is the predicted location of the colloidal glass transition within MCT. Unlike the VFT fit, which produces good agreement at all state points, the mode-coupling theory overestimates the structural relaxation time at high-volume fraction and predicts a dynamical divergence at ϕMCT = 0.590 ± 0.003. Similarly, an extrapolation of the relaxation time for a fixed γ of 2.6 at different wavevectors yields ϕMCT = 0.588 ± 0.00343 (Supplementary Fig. 5). However, the experiments clearly show a finite relaxation time for ϕ > ϕMCT. We thus obtain results from direct imaging consistent with those measured using reciprocal space techniques34, and demonstrate that our new measurements enable particle-resolved data to be obtained at timescales beyond the mode-coupling crossover.
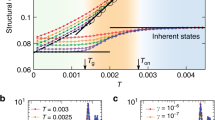
Structure and dynamics at deep supercooling. a Structural relaxation time in terms of Brownian time as a function of the reduced pressure Z and volume fraction ϕ for STED, confocal44 and simulations40. Key volume fractions are indicated on the top axis. Solid black line is a Vogel–Fulcher–Tammann fit to STED data (see text for details). Dashed green line is a power law fit from mode-coupling theory1. Crosses indicate state points equilibrated beyond the avoided mode-coupling transition. b Locally favoured structure populations from hard sphere experiments and simulations. Data and structures shown are 10-membered defective icosahedra (green) and 13-membered icosahedra (purple). Solid and dashed lines are a guide to the eye. Error bars correspond to standard deviation. c Static and dynamic lengthscales ξstatic and ξslow obtained for defective icosahedra and slow-moving particles respectively. Solid lines are fitted using Eq. (2). Error bars correspond to standard deviation. d Radial distribution function g(r) for sample state points at weak supercooling, close to the mode-coupling crossover and at deeper supercooling. Curves are offset for clarity. e gLFS(r), the spatial correlation of locally favoured structure and f gslow(r), the spatial correlation of immobility (Methods section) divided by g(r) for the same state points as d. Dotted lines are fits of the Ornstein–Zernike envelope function Eq. (5)
Local structure
We now exploit our methodology and investigate local structure at unprecedented degrees of supercooling. In Fig. 1b, c, coordinates are rendered in 3D. Previous work9,40 identified a 10-membered structure termed a defective icosahedron as the locally favoured structure for hard spheres. Particles in defective icosahedra are shown in green and particles in regular icosahedra of 13 particles are shown in purple in Fig. 1b, c. At deep supercooling, we see a dramatic increase in the number of particles detected in defective icosahedra, saturating at NLFS/N ~ 0.7 where N is the total number of particles detected and NLFS is the number of particles found in a LFS. We also see the emergence of a population of particles in full icosahedra, an order of magnitude greater than previously detected in hard sphere experiments44. The populations of local structures upon supercooling are shown in Fig. 2b for experiments and simulations. The populations of LFS are slightly lower in experiments than those measured in simulations. We attribute this to small tracking errors (missed particles or positional errors27) rather than an uncertainty in ϕ between experiments and simulations, due to their close agreement in the Angell plot (Fig. 2a).
That there are more particles in LFS, and that the number of particles in full icosahedra increases by an order of magnitude beyond previous measurements, suggests that some of the less conclusive studies involving LFS at weaker supercooling may not have been able to capture the full link between LFS and the dynamics, due to the limited timescales accessible16,19,45.
Static and dynamic lengthscales
A key means of discriminating between theoretical approaches to the glass transition would be the identification of structural and dynamic lengthscales. To this end, we determine structural and dynamic lengthscales based on 4-point correlation functions following ref. 6. We obtain a static lengthscale ξstatic corresponding to the size of regions rich in locally favoured structures9,12,46 and a dynamic lengthscale ξslow corresponding to the immobile or slow-moving regions6,47 (Methods section). As expected, the two-point pair distribution function shows little structural change over a range of volume fractions that correspond to nearly seven orders of magnitude of dynamic slowdown (Fig. 2d). However, by plotting the spatial correlation of particles in locally favoured structures (Fig. 2e) and of immobile particles (Fig. 2f) we see a clear separation with increasing density, corresponding to increased spatial correlation between the selected particles. Lengthscales corresponding to the sizes of these correlated regions were then obtained by fitting an Ornstein–Zernike envelope function Eq. (5) to the peaks of these spatial correlations16. In Fig. 2c we plot these static and dynamic lengthscales for experiments and simulations and fit them using the following expression, inspired by random first order transition theory40,48:
Here Z0 corresponds to the reduced pressure at which dynamical divergence is predicted from the VFT fit above. We emphasise that, although we reach exceptionally deep levels of supercooling for particle-resolved studies, the state points we equilibrate are still quite far from any true transition, so the lengthscales we identify are modest. Therefore the particular functional form used is a matter of choice, other forms would also fit our data (for example, the power law form taken in ref. 16 could also be used). We obtain ξ0 = 44.7 and θ = 2.17 ± 0.12 for the dynamic length and ξ0 = 22.4 and θ = 2.04 ± 0.13 for the static length. The exponent in both cases is the same within errors, so at the level of our analysis the two lengthscales are distinguished only by the prefactor. We see that the structural lengthscale increases significantly, more than doubling in the range we access. Previous efforts to extract a structural lengthscale from defective icosahedra at weaker supercooling only reported a small increase of a factor of ≈1.259. Here the dynamic lengthscale triples, and (within the accuracy of our measurements) grows at a similar rate to ξRG, the size of dynamically correlated regions based on a mutual information approach9. No evidence of non-monotonicity in either lengthscale10 is found.
Coupling between structure and dynamics
Studies to date have reported some correlation between structure and dynamics9,16,22. However, if one expects a causal link between the two, then structural properties should predict dynamical behaviour. Attempts to quantify such predictability have met with only limited success22,23. Here we show that a stronger relationship between local structure and dynamics is found at deeper supercooling. In Fig. 3 we quantify the relationship between structure and dynamics by plotting the mobility μi(t) = \(\left| {{\bf{r}}_i(t) - {\bf{r}}_i(0)} \right|\) of particles which spend relatively long periods in LFS (>75% of the trajectory) compared to those which spend little time in LFS (<25% of the trajectory), over a time interval ~ 0.5τα (Fig. 3a). We express this single-particle trajectory quantity as nLFS. In this sense, we track the persistence of particles in LFS and correlate it with mobility. (See Supplementary Fig. 6 for LFS persistence over different time intervals). At weak supercooling (ϕ = 0.523 (Zcs = 15.2), Fig. 3b), there is little distinction between the displacements of particles that persist in local structure and those that do not. This reflects the behaviour observed in Supplementary Movie 1, for which particle motion appears essentially liquid-like and homogeneous. Increasing the volume fraction close to the mode-coupling point (ϕ = 0.583 (Zcs = 23.8) Fig. 3c), we see a long tail of highly mobile particles which spend little time in defective icosahedra. In other words, fast particles tend not to be found in LFS9,16,49. Inspection of Supplementary Movie 2 supports this, where there are spatially distinct fast and slow regions. At ϕ = 0.598 (Zcs = 26.8), (Fig. 3d), the connection between structure and dynamics strengthens in the mobility distribution, as particles that persist in local structure appear more tightly caged by neighbouring particles than for trajectories at weaker supercooling. For particles with weak persistence in LFS the distribution of displacements is much broader, and the long tail observed for ϕ = 0.583 has developed into a secondary peak. This motion is shown in Supplementary Movie 3, where we see significant dynamic heterogeneity. Indeed there are some regions of the sample that undergo relatively persistent cooperative relaxation, while other regions are essentially immobile for the duration of the movie (32 h).
Local structure and dynamic correlations. a Schematic of particle displacements for a trajectory that persists in an icosahedral structure and a more mobile, structurally poor trajectory. b–e Distribution of particle mobility at δt ~ 0.5τα for defective icosahedra rich (nLFS > 0.75, green) and defective icosahedra poor (nLFS < 0.25, blue) trajectories, for volume fractions b 0.523, c 0.583 and d 0.598. e the same displacements as d but for icosahedra rich (purple) and poor (blue) trajectories at volume fraction 0.598
Given the predominance of particles in defective icosahedra for ϕ = 0.598 (Zcs = 26.8) (NLFS/N ~ 0.6, Fig. 2b), it is likely that some of these particles are relatively less mobile than the others, but detection of defective icosahedra alone does not fully capture this behaviour. Making the comparison of LFS-rich and LFS-poor trajectories for full icosahedra (Fig. 3e) shows a stronger link between structure and dynamics. Certainly, particles in full icosahedra move less than those in defective icosahedra, but the strongest difference compared to weaker supercooling is the distinct second peak at one particle diameter in the tail of fast-moving particles which spend little time in icosahedra, while no particles that persist in icosahedra move so far. This significant population of particles moving around σ rather than 2σ/3 is consistent with the idea that relaxation may occur through more discrete displacements at these deeper supercoolings, requiring cooperative motion of several particles in a relaxation event. Hints of this can be seen over long timescales (~107τB) in Supplementary Movie 3, but this is shown more clearly over intermediate timescales (~2 × 104 τB) in Supplementary Movie 4. This shows a relaxation event consisting of cooperative, discrete movements (of around 1 particle diameter) of several particles in an otherwise arrested sample.
Configurational entropy and local structure
In the previous sections, we have used the notion of LFS as a measure for the increase of structural ordering at high-volume fractions. This assumes that static correlations are captured in LFS domains and that no other mechanisms emerge at high-volume fractions. In order to test this hypothesis we now extend our analysis and consider alternative forms of structural measurement which are order agnostic, that is to say we do not consider any particular local structure.
The first such method is based on the degree of similarity or overlap between different regions of the system50,51. High overlap corresponds to very similar configurations (and vice versa). High overlap and thus a low configurational entropy is then expected by thermodynamic-based theories of the glass transition1,2,5. We choose to determine the overlap as it has recently been associated with the transition predicted by random first order transition theory51. Like the locally favoured structures, overlap is a many-body quantity, and such higher-order measures have been shown to be important in understanding structural quantities in glass-forming systems14,52,53. We determine the overlap through subsampling our particle-resolved data into distinct spherical regions which we term test spheres of a fixed number of particles No; these are then rotated and translated in order to bring the largest number of centres together, through singular value decomposition; finally the fraction of overlapping particles (i.e. closer than a pre-defined threshold λ(ϕ)) is measured (Fig. 4a, see Methods for more details). For simulated random configurations, the distribution of overlap values is (trivially) unchanged for all volume fractions. In the experimental system, in the range 0.523 ≤ ϕ ≤ 0.583 (15.2 ≤ Zcs ≤ 23.8), we see similar overlap distributions as for random configurations at all volume fractions, albeit for higher overlap (Fig. 4b). However, for ϕ = 0.598 (Zcs = 26.8), the experiments show a clear increase in the occurrence of regions with high overlap. This is an order agnostic indication of a higher degree of structural similarity at deeper supercooling, and a reduction in the number of the sampled possible arrangements, i.e. a lower configurational entropy. We now reverse the argument and ask: is high overlap (amorphous order) related to the LFS considered above? Our answer is positive from the following procedure: we enquire whether particles in the test spheres used in the overlap analysis are in LFS. The overlap distribution was then determined for the most LFS-rich/poor subsets of the overlap population (defined in the Methods). At ϕ = 0.523 (Fig. 4c) there is little difference between the total overlap, or the overlaps of structurally rich and poor test spheres. However, at ϕ = 0.598 (Fig. 4d) the LFS-poor test spheres clearly do not contribute to the characteristic long tail of overlaps, while the overlap distribution of the LFS-rich test spheres closely tracks the long tail of high overlaps observed for all test spheres. Therefore regions that are rich in icosahedral order are also those with high overlap (and so, low configurational entropy). This demonstrates the compatibility between locally favoured structures and amorphous order.
Static overlap fluctuations. a Schematic representation of the overlap calculation: isolated clusters of No particles are subsampled from a large configuration; for every pair of clusters, an optimal singular value decomposition (SVD) is found determining the rotation matrix R(α, γ, β) and the translation vector \(\vec u\) that maximise the overlap. For ease of representation, here No = 10 and Q = 0.7. b Probability distribution of overlap fluctuations for volume fractions 0.523, 0.562, 0.583 and 0.598. c, d Overlap fluctuations for all test spheres, and for the most LFS-poor (white) and rich (blue) 25% test spheres, at volume fractions 0.523 (c green) and 0.598 (d purple). c, d Samples of LFS-poor (left) and rich (right) test spheres, where green particles are in defective icosahedra and grey particles are not
So far we have described local structure and configurational entropy using higher-order properties. However, it is also possible to quantify local entropy from two-point correlations. While there are many different definitions of configurational entropy (in part due to the difficulty in identifying the vibrational contributions), a useful approximation which accounts for about 90% of the configurational entropy can be used for simple liquids, which requires only the pair correlation function as input53,54. This forms the basis of the two-body excess entropy contribution to the configurational entropy, or s2. To more clearly distinguish between different structures the locally averaged form \(\overline s _2\), that is to say, the average over nearest neighbours, is preferred16,54,55. To assess this, we calculate s2 and the locally averaged form \(\overline s _2\) for a range of state points (see Methods for more information). The distribution of \(\overline s _2\) for a deeply supercooled sample is shown in Fig. 5a. This shows correlated regions with high and low local excess entropy distributed throughout the sample. Furthermore, by considering the distribution of \(\overline s _2\) at different state points, we see increasing local order (i.e. lower values of \(\overline s _2\)) with supercooling (Fig. 5b). We now extend our analysis to consider the relationship between \(\overline s _2\) and locally favoured structures. By determining the probability distribution function of \(\overline s _2\) for particles identified and not identified in LFS, we see that occupancy of LFS consistently predicts particles of lower local excess entropy and vice versa (Fig. 5c). Intriguingly, we also see that for the state point ϕ = 0.583 (close to the mode-coupling crossover), the distribution of \(\overline s _2\) is relatively broad. A possible explanation for this emerges by considering the role of LFS. The distribution of \(\overline s _2\) for the particles in LFS is close to that of the more dense sample and vice versa, indicating that at this state point there are some regions that appear more supercooled and other regions that are more liquid-like, respectively, and selecting for LFS differentiates between the two. We also perform the same analysis for the non-locally averaged s2 which has much weaker spatial correlations (Supplementary Fig. 7a) and broader distributions (Supplementary Fig. 7b, c) than for \(\overline s _2\). This acts to obscure the clear trends shown for \(\overline s _2\), consistent with previous observations54.
Two-body excess entropy. a Spatial distribution of locally averaged two-body excess entropy \(\overline s _2\) for volume fraction 0.598. b Probability distributions of \(\overline s _2\) for a range of volume fractions. c Probability distributions of \(\overline s _2\) for a range of volume fractions for the whole particle population (solid line), particles identified in defective icosahedra (dashed line) and particles not identified in defective icosahedra (dotted line)
Discussion
We have used STED microscopy to study the particle-resolved dynamics and structure of glass-forming liquids at unprecedented degrees of supercooling. By obtaining the coordinates of particles much smaller than those imaged previously, our data has effective relaxation times up to three orders of magnitude longer than previous work. Significantly, this deeply supercooled regime passes the mode-coupling crossover, accessing a regime in which new physics is expected1,2. We obtained four main results which are explained below.
First, the emergence of a new kind of local structure, the icosahedron, at deep supercooling. This is distinct from, and we believe, more stable than the defective icosahedra identified previously for hard spheres9.
Second, at deeper supercooling there is a stronger correlation between dynamics and locally favoured structures. This indicates that earlier work where rather weak correlation was found9,14,18,19 may have been influenced by the limited degree of supercooling accessed.
Third, we find a significant increase in the static lengthscale ξstatic by more than a factor of two and in the dynamic lengthscale ξslow by a factor of three. While this may seem modest, we note that many studies have found it hard even to identify any increase in the structural lengthscale9,14,18,19, and that indirect measures of static and dynamic lengthscales at the operational molecular glass transition (seven decades in relaxation time beyond our particle-resolved results) are themselves not much larger than our measurements20. We suggest that the results presented here indicate a heightened emphasis of the role of LFS in dynamic arrest at deep supercooling when compared to other structural order parameters.
Finally we present an experimental investigation of the overlap order parameter, related to replica theory5. We find evidence of an increase in overlap at deep supercooling. Moreover, we find that regions of high overlap correspond to those rich in LFS, i.e. configurations with low mobility and low configurational entropy. This, combined with the growing amorphous LFS domains, is compatible with the fifth-order dielectric susceptibility measurements on molecular systems reported recently20. We also compare this with the local structural entropy and observe similar behaviour as the overlap. That is to say, we see that the distribution of \(\overline s _2\) captures the increased local order with volume fraction (Fig. 5). As for the overlap we also see that calculating the same distributions for particles detected in LFS further selects for regions of low configurational entropy.
We now consider the interpretation of our findings in the context of some theoretical approaches. The concurrent growth of the structural and dynamic lengthscales at deeper supercooling points towards the increasing role played by structural correlations in the dynamic slowdown, supporting theoretical approaches which imagine a phase transition related to thermodynamics1,2,4. This is also supported by the measurement of the increasing overlap between local regions of the supercooled liquid. However we emphasise that the relatively small lengthscales we obtain mean that our results should be regarded as consistent with some theoretical interpretations rather than anything conclusive. Concerning the connection to theories related to local structure4, our data are compatible with geometric frustration, where a frustrated transition to a state of icosahedra is predicted to be suppressed to deep supercooling12. We have now accessed such deeper supercooling and find heightened icosahedral ordering. The link between icosahedral ordering and high overlap consolidates the influence of geometric frustration with approaches which emphasise low configurational entropy. Our work thus provides support for thermodynamic (i.e. structural) theories of the glass transition over approaches which prioritise kinetic aspects.
More generally the use of STED microscopy presents several advantages over confocal microscopy for the study of colloidal systems. While the positions of sub-micron systems can be studied using other microscopy methods when confined to a 2D layer56 or at lower densities57, the key advantage of this approach is that it yields full 3D coordinates at very high densities. This technique provides an enhancement in spatial resolution beyond conventional confocal microscopy, enabling the use of smaller (but otherwise chemically identical) particles. Similar sized particles have previously been studied at comparable densities34,35 but crucially those measurements were performed using techniques that do not yield particle positions. Therefore this approach is compatible with the different methods previously applied to the study of dense colloidal hard spheres, but accesses new state points or new information that could not be obtained previously. One difficulty of measurements of this type is that exceptional mechanical and thermal stability is necessary: mechanical drift of the sample of just a few microns (very common during a conventional confocal microscope measurement but negligible compared to the size of the image) can result in the region of interest leaving the imaged volume, prematurely ending the measurement, while thermal fluctuations can result in the laser excitation and depletion spots misaligning, reducing the effectiveness of the STED mechanism. Nevertheless, this new technique holds great promise in the field of colloid and interface science, allowing for systems to be studied in real space that were previously only accessible using scattering or spectroscopic methods.
Methods
Sample preparation
Fluorescent dyed-poly methylmethacrylate (PMMA) colloids with a polyhydroxystearic acid comb stabiliser were synthesised using established one-pot dispersion polymerisation methods58. To enhance spatial resolution between particles, a non-fluorescent PMMA shell was grown on the fluorescent cores and cross-linked with ethylene glycol dimethacrylate (EGDM) to yield a total radius of 270 nm (polydispersity ~8%, τB = 34 ms). Particle sizes and polydispersity were determined via scanning electron microscopy (SEM) using a JEOL JSM 6330F (Tokyo, Japan). Particles were density and refractive index matched in a solvent mixture of cis-decalin and a saturated solution of tetrabutylammonium bromide salt in cyclohexylbromide (CXB).
Due to the small particle sizes and high-volume fractions used here, re-suspension of dried colloids produced poorly mixed samples. Therefore, to obtain fully dispersed suspensions, PMMA particles were swapped from dodecane to a (non-density matched) mixture of cis-decalin and CXB via repeated centrifugation and replacement of the supernatant with fresh cis-decalin and CXB. Density matching conditions were verified by centrifugation (Eppendorf 5415R temperature controlled centrifuge) for at least 20 min at 13,000 rpm. If the PMMA began to sediment or cream then further cis-decalin or CXB was added until it remained fully suspended after centrifugation. To obtain samples of specific volume fractions, density matched (at room temperature) samples were centrifuged at elevated temperature (to decrease the solvent density relative to the colloids), producing a close packed pellet \((\phi \simeq 0.64)\). The supernatant was removed and the pellet weight was determined. The pellet was then diluted by adding an amount of the supernatant to give a known volume fraction. Samples were then resuspended via vortex and roller mixing. Samples were loaded into cells constructed of three coverslips on a microscope slide, where two of the coverslips acted as a spacer, and sealed using epoxy. Samples were equilibrated while slowly rotating (~1 rpm) in a temperature controlled chamber. The structural relaxation time was monitored for waiting times of up to 100 days until it reached a steady state (Supplementary Fig. 2), at which point the sample was considered to be equilibrated59. For example, the state point ϕ = 0.598 reached equilibrium after 16 days, corresponding to more than 10τα. No noticeable crystallisation or sedimentation was detected during this time. Samples were imaged using a Leica SP8 inverted stimulated emission depletion microscope with a ×100 oil immersion lens in STED-3D mode, mounted on an optical table. The optical table was mounted on an acoustically damped five tonne concrete block in a low noise laboratory, to minimise vibrations and instrument drift during measurement. The fluorescent dye was excited using a supercontinuum light source. Depletion was induced using a 660 nm laser. Typically stacks, of volume (10–15 μm)3, were recorded with a sampling time between 10 s and 30 min depending on the volume fraction. Measurements were taken at least 20 particle diameters from the cell wall to minimise any structural or dynamic influence of surface layering, which typically persisted for around 5 particle diameters (Supplementary Fig. 3). Images were deconvolved with Huygens Professional version 15.05 prior to analysis (Scientific Volume Imaging, The Netherlands, http://svi.nl).
For samples at low density (ϕ ~ 0.50) it was not possible to obtain any dynamic information in the density matching solvent mixture due to the short relaxation times at these state points (τα < 500 ms). Therefore in order to obtain data at these volume fractions samples were also prepared in immersion oil (Sigma, η = 150 cP), which provided a good refractive index match and slowed down the particles sufficiently to successfully track particle trajectories, at the expense of density matching these suspensions. To minimise the influence of sedimentation during equilibration, these samples were stored slowly rotating prior to measurement. Furthermore, measurements in immersion oil were restricted to shorter times than the self-sedimentation time (~1 h). No noticeable vertical drift or sedimentation was detected during measurement for these samples.
Particle tracking
Particle tracking algorithms60 were used to determine particle coordinates from deconvolved STED microscopy data. The structural relaxation time τα was estimated from the intermediate scattering function (ISF), F(k, t) = \(\left\langle {\mathop {\sum}\nolimits_{j = 1}^N {\kern 1pt} {\mathrm{exp}}\left[ {i{\bf{k}} \cdot ({\bf{r}}(t + t\prime ) - {\bf{r}}(t\prime ))} \right]} \right\rangle\). This was determine from coordinate data in the case of both experiments and simulations. The lengthscale over which mobility is probed is set by the wavevector q, which here was taken to correspond to a particle diameter (q ~ 2πσ−1), close to the main peak in the static structure factor. The long-time tail of the ISF was fitted with a stretched exponential with time constant τα and stretching exponent b, where typically 0.9 < b ≤ 1. Fits to ISFs with a stretched exponential are shown in Supplementary Fig. 1. For some of the samples photobleaching (accelerated beyond conventional confocal microscopy measurements due to the additional contribution of the depletion laser) or sample drift became too significant to accurately track particle positions before the ISF fully decayed. Data for these samples is only reported for the interval where this effect is negligible, as shown in Supplementary Movies 1–4.
In order to verify volume fractions (initially determined by weight), the experimental hard sphere radius was determined by comparison with simulated polydisperse (8%) radial distribution functions of hard spheres. By multiplying the experimental hard sphere volume by the measured number density, a lower bound for the volume fraction of each sample (and their scaling) could be determined. These volume fractions and the scaling of τα with number density were referenced against a weakly supercooled fluid state in the regime accessible to computer simulation, with good agreement between their respective τα (Supplementary Fig. 4). Rendered images of particle coordinates were produced using Ovito61.
We identify local structure from particle coordinate data using the topological cluster classification (TCC)9,62. This method defines a bond network to identify arrangements of particles in LFS62.
Lengthscales
Lengthscales were determined from the real space g(r), subsampled for a particular parameter9. For the static lengthscale ξstatic the density–density correlation was found for particles in LFS:
which is the ratio of the ensemble average of particles in LFS at distance r (over bin width Δr) to the average number density ρ, where wi,LFS is a binary variable indicating whether particle i is in a LFS. A similar approach was used for slow-moving particles to determine the dynamic lengthscale ξslow, following47:
where μi,slow(t) is the particle immobility μmax(t) − μi(t) and \(\langle {\mu _{i,{\mathrm{slow}}}\left( {{\mathrm{\Delta }}t} \right)} \rangle\) is the average immobility.
The decay of ga(r) was then fitted using an Ornstein–Zernike envelope function6,9,16 as follows:
for a = LFS or slow, obtaining the structural length ξstatic and the dynamic length ξslow respectively. We note that these serve as lower bounds for the structural and dynamic lengths due to the size limits of the area that can be imaged by the microscope. For the structural length, this is also due to particles not found or mislocated in the particle tracking analysis, which result in fewer defective icosahedra compared to simulations (Fig. 2b), and thus do not contribute to the lengthscale measurement. For the dynamic length, making the comparison to χ4, we expect the lengthscale to be maximised at ~τα14. However, this time was not accessible in our most deeply supercooled sample, primarily due to photobleaching at long measurement times, therefore Δt ~ 0.5τα was used throughout.
Simulations
Event-driven molecular dynamics (MD) simulations were carried out with the DynamO package63. An equimolar five component mixture of hard spheres of polydispersity 8% (diameters 0.888σ, 0.95733σ, σ, 1.04267σ and 1.112σ) was used, with a system size of N = 1372. At least 3000 configurations were analysed for each state point. Configurations were equilibrated for at least 30τα and sampled for at least a further 30τα, where τα was determined by fitting a stretched exponential to the ISF at the main peak of the static structure factor, as for the particle tracking experiments.
Overlap fluctuations
In order to measure the overlap between distinct regions of the sampled configurations we proceed via subsampling. We select Ncentres equally spaced centres and identify the No = 64 closest particles to the centre in order to obtain Ncentres approximately spherical distinct regions. For every pair of test spheres S1, S2 we determine the degree of similarity between them performing singular value decomposition. This provides the rotation and translation matrices that maximise the following definition of the overlap:
where Θ is the Heaviside function, ∨ indicates the logical OR operation and λ is a cutoff length set to a value that scales as \(\lambda = \frac{1}{3}\root {3} \of {{1{\mathrm{/}}\rho }}\), with ρ being the number density. This threshold was chosen to be tolerant towards β relaxation within otherwise unchanged configurations and corresponded to ~0.4σ for all samples analysed. All the possible combinations between the Ncentres spheres are considered in order to obtain a sample of typically NQ ≈ 105 values for the overlap from which the histograms of Fig. 4 are computed. To determine the overlap distribution of the icosahedrally rich and poor subsets, the product of the fraction of LFS in the test spheres used to calculate the overlap was determined for each overlap value. The overlap distribution was then determined for the overlap values within the highest and lowest 10% of LFS products. This methodology is related to the notion of repeated patches, as previously explored in 2-dimensions64. For the overlap measurement of random configurations, the volume fraction controls the number density of particles and the cutoff length λ.
Two-body excess entropy
The two-body excess entropy16,55 is given by:
This can be also be calculated for each particle i in the system:
where \(g_{\rm{m}}^i(r)\) is the radial distribution function for particle i. To obtain a continous differentiable order parameter for each particle, we follow54, by calculating a ‘mollified’ pair distribution function:
where s is a broadening parameter, j are the neighbours of particle i and rij is their separation. The locally averaged parameter \(\overline s _2\) is then determined by averaging the contributions of particle i and its nearest neighbours.
Data availability
The raw data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Berthier, L. & Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 83, 587–645 (2011).
Lubchenko, V. & Wolynes, P. Theory of structural glasses and supercooled liquids. Ann. Rev. Phys. Chem. 58, 235–266 (2007).
Chandler, D. & Garrahan, J. P. Dynamics on the way to forming glass: bubbles in space-time. Ann. Rev. Phys. Chem. 61, 191–217 (2010).
Tarjus, G., Kivelson, S. A., Nussinov, Z. & Viot, P. The frustration-based approach of supercooled liquids and the glass transition: a review and critical assessment. J. Phys. Condens. Matter 17, R1143–R1182 (2005).
Parisi, G. & Zamponi, F. Mean-field theory of hard sphere glasses and jamming. Rev. Mod. Phys. 82, 789–845 (2010).
Lačević, N., Starr, F. W., Schrøder, T. B., Novikov, V. N. & Glotzer, S. C. Growing correlation length on cooling below the onset of caging in a simulated glass-forming liquid. Phys. Rev. E. 66, 030101 (2002).
Lačević, N., Starr, F. W., Schroder, T. B. & Glotzer, S. C. Spatially heterogeneous dynamics investigated via a time-dependent four-point density correlation function. J. Chem. Phys. 119, 7372–7387 (2003).
Shiba, H., Kawasaki, T. & Onuki, A. Relationship between bond-breakage correlations and four-point correlations in heterogeneous glassy dynamics: Configuration changes and vibration modes. Phys. Rev. E. 86, 041504 (2014).
Dunleavy, A. J., Wiesner, K., Yamamoto, R. & Royall, C. P. Mutual information reveals multiple structural relaxation mechanisms in a model glassformer. Nat. Commun. 6, 6089 (2015).
Kob, W., Roldán-Vargas, S. & Berthier, L. Non-monotonic temperature evolution of dynamic correlations in glass-forming liquids. Nat. Phys. 8, 164–167 (2012).
Nagamanasa, S., Nagamanasa, K. H., Sood, A. K. & Ganapathy, R. Direct measurements of growing amorphous order and non-monotonic dynamic correlations in a colloidal glass-former. Nat. Phys. 11, 403–408 (2015).
Turci, F., Tarjus, G. & Royall, C. P. From glass formation to icosahedral ordering by curving three-dimensional space. Phys. Rev. Lett. 118, 215501 (2017).
Karmakar, S., Dasgupta, C. & Sastry, S. Growing lengthscales and their relation to timescales in glass-forming liquids. Annu. Rev. Cond. Matt. Phys. 5, 255–284 (2014).
Royall, C. P. & Williams, S. R. The role of local structure in dynamical arrest. Phys. Rep. 560, 1–75 (2015).
Leocmach, M. & Tanaka, H. Roles of icosahedral and crystal-like order in the hard spheres glass transition. Nat. Commun. 3, 974 (2012).
Tanaka, H., Kawasaki, T., Shintani, H. & Watanabe, K. Critical-like behaviour of glass-forming liquids. Nat. Mater. 9, 324–331 (2010).
Mosayebi, M., Del Gado, E., Ilg, P. & Öttinger, H. C. Probing a critical lengthscale at the glass transition. Phys. Rev. Lett. 104, 205704 (2010).
Hocky, G. M., Markland, T. E. & Reichman, D. R. Growing point-to-set lengthscale correlates with growing relaxation times in model supercooled liquids. Phys. Rev. Lett. 108, 225506 (2012).
Charbonneau, B., Charbonneau, P. & Tarjus, G. Geometrical frustration and static correlations in a simple glass former. Phy. Rev. Lett. 108, 035701 (2012).
Albert, S. et al. Fifth-order susceptibility unveils growth of thermodynamic amorphous order in glass-formers. Science 352, 1308–1311 (2016).
Flenner, E. & Szamel, G. Fundamental differences between glassy dynamics in two and three dimensions. Nat. Commun. 6, 7392 (2015).
Hocky, G. M., Coslovich, D., Ikeda, A. & Reichman, D. Correlation of local order with particle mobility in supercooled liquids is highly system dependent. Phys. Rev. Lett. 113, 157801 (2014).
Jack, R. L., Dunleavy, A. J. & Royall, C. P. Information-theoretic measurements of coupling between structure and dynamics in glass-formers. Phys. Rev. Lett. 113, 095703 (2014).
Cubuk, E. D. et al. Identifying structural flow defects in disordered solids using machine-learning methods. Phys. Rev. Lett. 114, 108001 (2015).
Hunter, G. L. & Weeks, E. R. The physics of the colloidal glass transition. Rep. Prog. Phys. 75, 066501 (2012).
Gokhale, S., Sood, A. K. & Ganapathy, R. Deconstructing the glass transition through critical experiments on colloids. Adv. Phys. 65, 363–452 (2016).
Pinchaipat, R. et al. Experimental evidence for a structural-dynamical transition in trajectory space. Phys. Rev. Lett. 119, 028004 (2017).
Goetze, W. Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory. International Series of Monographs on Physics (Oxford University Press, Oxford, 2009).
Bengtzelius, U., Gotze, W. & Sjolander, A. Dynamics of supercooled liquids and the glass transition. J. Phys. C. 17, 5915–5934 (1984).
Leutheusser, E. Dynamical model of the liquid-glass transition. Phys. Rev. A. 29, 2765–2773 (1984).
Golde, S., Palberg, T. & Schöpe, H. J. Correlation between dynamical and structural heterogeneities in colloidal hard-sphere suspensions. Nat. Phys. 12, 712–717 (2016).
Higler, R., Krausser, J., van der Gucht, J., Zaccone, A. & Sprakel, J. Linking slow dynamics and microscopic connectivity in dense suspensions of charged colloids. Soft Matter 14, 780–788 (2017).
Zhang, B. & Cheng, X. Structures and dynamics of glass-forming colloidal liquids under spherical confinement. Phys. Rev. Lett. 116, 098302 (2016).
Brambilla, G. et al. Probing the equilibrium dynamics of colloidal hard spheres above the mode-coupling glass transition. Phys. Rev. Lett. 102, 085703 (2009).
Simeonova, N. B. & Kegel, W. K. Gravity-induced aging in glasses of colloidal hard spheres. Phys. Rev. Lett. 93, 035701 (2004).
Hell, S. W. Far-field optical nanoscopy. Science 353, 1163–1168 (2007).
van Megen, W., Mortensen, T. C. & Williams, S. R. Measurement of the self-intermediate scattering function of suspensions of hard spherical particles near the glass transition. Phys. Rev. E. 58, 6073–6085 (1998).
Richert, R. Scaling vs. vogel–fulcher-type structural relaxation in deeply supercooled materials. Phys. A. 287, 26–36 (2000).
Berthier, L. & Witten, T. A. Glass transition of dense fluids of hard and compressible spheres. Phys. Rev. E. 80, 021502 (2009).
Royall, C. P. & Kob, W. Locally favoured structures and dynamic lengthscales in a simple glass-former. J. Stat. Mech. Theory Exp. 2017, 024001 (2017).
Berthier, L., Coslovich, D., Ninarello, A. & Ozawa, M. Equilibrium sampling of hard spheres up to the jamming density and beyond. Phys. Rev. Lett. 116, 238002 (2016).
Götze, W. Recent tests of the mode-coupling theory for glassy dynamics. J. Phys. Condens. Matter 11, A1–A45 (1999).
Schweizer, K. S. & Saltzman, E. J. Entropic barriers, activated hopping, and the glass transition in colloidal suspensions. J. Chem. Phys. 119, 1181–1196 (2003).
Royall, C. P., Williams, S. R. & Tanaka, H. Vitrification and gelation in sticky spheres. J. Chem. Phys. 148, 044501 (2018).
Royall, C. P., Malins, A., Dunleavy, A. J. & Pinney, R. Strong geometric frustration in model glassformers. J. Non-Cryst. Solids 407, 34–43 (2015).
Malins, A., Eggers, J., Royall, C. P., Williams, S. R. & Tanaka, H. Identification of long-lived clusters and their link to slow dynamics in a model glass former. J. Chem. Phys. 138, 12A535 (2013).
Poole, P. H., Donati, C. & Glotzer, S. C. Spatial correlations of particle displacements in a glass-forming liquid. Phys. A. 261, 51–59 (1998).
Cammarota, C., Cavagna, A., Gradenigo, G., Grigera, T. S. & Verrochio, P. Numerical determination of the exponents controlling the relationship between time, length, and temperature in glass-forming liquids. J. Chem. Phys. 131, 194901 (2009).
Sausset, F. & Tarjus, G. Growing static and dynamic lengthscales in a glass-forming liquid. Phys. Rev. Lett. 104, 065701 (2010).
Berthier, L. & Kob, W. Probing a liquid to glass transition in equilibrium. Phys. Rev. Lett. 110, 245702 (2013).
Berthier, L. Probing a liquid to glass transition in equilibrium. Phys. Rev. E. 88, 022313 (2013).
Coslovich, D. Static triplet correlations in glass-forming liquids: a molecular dynamics study. J. Chem. Phys. 138, 12A539 (2013).
Banerjee, A., Sengupta, S., Sastry, S. & Bhattacharyya, S. M. Role of structure and entropy in determining differences in dynamics for glass formers with different interaction potentials. Phys. Rev. Lett. 113, 225701 (2014).
Piaggi, P. M. & Parrinello, M. Entropy based fingerprint for local crystalline order. J. Chem. Phys. 147, 114112 (2017).
Leocmach, M., Russo, J. & Tanaka, H. Importance of many-body correlations in glass transition: an example from polydisperse hard spheres. J. Chem. Phys. 138, 12A536 (2013).
Dreyfus, R. et al. Diagnosing hyperuniformity in two-dimensional, disordered, jammed packings of soft spheres. Phys. Rev. E. 91, 012302 (2015).
Kanai, T. et al. Crystallization and reentrant melting of charged colloids in nonpolar solvents. Phys. Rev. E. 91, 030301 (2015).
Elsesser, M. T., Hollingsworth, A. D., Edmond, K. V. & Pine, D. J. Large core- shell poly (methyl methacrylate) colloidal clusters: Synthesis, characterization, and tracking. Langmuir 27, 917–927 (2010).
El Masri, D. et al. Dynamic light scattering measurements in the activated regime of dense colloidal hard spheres. J. Stat. Mech. 2009, P07015 (2009).
Leocmach, M. & Tanaka, H. A novel particle tracking method with individual particle size measurement and its application to ordering in glassy hard sphere colloids. Soft Matter 9, 1447–1457 (2013).
Stukowski, A. Visualization and analysis of atomistic simulation data with ovito–the open visualization tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2009).
Malins, A., Williams, S. R., Eggers, J. & Royall, C. P. Identification of structure in condensed matter with the topological cluster classification. J. Chem. Phys. 139, 234506 (2013).
Bannerman, M. N., Sargant, R. & Lue, L. Dynamo: a free o(n) general event-driven simulator. J. Comp. Chem. 32, 3329–3338 (2011).
Sausset, F. & Levine, D. Characterizing order in amorphous systems. Phys. Rev. Lett. 107, 045501 (2011).
Acknowledgements
We thank Chiara Cammarota, Bob Evans, Elijah Flenner, Silvio Franz, Rob Jack, David Reichman, and Grzegorz Szamel for insightful suggestions. C.P.R. acknowledges the Royal Society, and the Kyoto University SPIRITS fund. J.E.H., F.T. and C.P.R. acknowledge the European Research Council (ERC consolidator grant NANOPRS, project 617266) and the Engineering and Physical Sciences Research Council (EP/H022333/1) for financial support.
Author information
Authors and Affiliations
Contributions
J.E.H. planned and performed the experiments. C.P.R. conceived and supervised the project. J.E.H and F.T. analysed the data. All authors contributed to the interpretation of the data and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hallett, J.E., Turci, F. & Royall, C.P. Local structure in deeply supercooled liquids exhibits growing lengthscales and dynamical correlations. Nat Commun 9, 3272 (2018). https://doi.org/10.1038/s41467-018-05371-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05371-6
This article is cited by
-
Probing excitations and cooperatively rearranging regions in deeply supercooled liquids
Nature Communications (2023)
-
Relationships between structure, memory and flow in sheared disordered materials
Nature Physics (2022)
-
Structure determines where crystallization occurs in a soft colloidal glass
Nature Physics (2021)
-
Revealing key structural features hidden in liquids and glasses
Nature Reviews Physics (2019)
-
Concentrated suspensions of Brownian beads in water: dynamic heterogeneities through a simple experimental technique
Science China Physics, Mechanics & Astronomy (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.