Abstract
Many superionic mixed ionic–electronic conductors with a liquid-like sublattice have been identified as high efficiency thermoelectric materials, but their applications are limited due to the possibility of decomposition when subjected to high electronic currents and large temperature gradients. Here, through systematically investigating electromigration in copper sulfide/selenide thermoelectric materials, we reveal the mechanism for atom migration and deposition based on a critical chemical potential difference. Then, a strategy for stable use is proposed: constructing a series of electronically conducting, but ion-blocking barriers to reset the chemical potential of such conductors to keep it below the threshold for decomposition, even if it is used with high electric currents and/or large temperature differences. This strategy not only opens the possibility of using such conductors in thermoelectric applications, but may also provide approaches to engineer perovskite photovoltaic materials and the experimental methods may be applicable to understanding dendrite growth in lithium ion batteries.
Similar content being viewed by others
Introduction
Superionic conductors are solids in which at least one type of atom forms a rigid sublattice framework and another type of atom forms a “melted” liquid-like sublattice composed of highly mobile charged atoms, i.e., ions1. The description of the ensemble of highly mobile ions in terms of a “liquid” sublattice derives from the fact that the entropy change during transition into the superionic phase is comparable to the entropy change during a solid/liquid phase transition1. This unique liquid-like ion migration is the basis for many phenomena and applications in the fields of solid-state ionics, e.g., of solid electrolytes, batteries, fuel cells, and various types of sensors2. Ion migration also occurs in materials with much lower ion mobility, and is often the origin of electric field-driven degradation in hybrid organic–inorganic perovskite solar cell materials (e.g., CH3NH3PbI3) and Cu-based photovoltaic materials3,4. Ion migration and the redox-based formation of conducting paths in dielectrics is the basis for future information storage technologies (atomic switching and memristive devices)5.
Recently, the application of superionic mixed ionic–electronic conductors (MIECs) with a liquid-like sublattice has been extended to the field of thermoelectrics (TEs). A concept named as “phonon-liquid electron-crystal” (PLEC) has been proposed to design and develop high-performance TE materials that conduct phonons like a liquid and electrons like a crystal6. A large family of novel Cu-, Ag- and Zn-based superionic MIECs have been identified satisfying this concept—with typical examples being Cu2-δX (X = S, Se, Te), Ag2Se, CuAgSe, Zn4Sb3, Cu5FeS4, Cu7PSe6, and Cu12Sb4S13, etc6,7,8,9,10,11,12. In a MIEC, both the ions and electrons (or holes) are mobile such that atom (rather than ion) migration is possible, which may lead to composition changes within the MIECs13. Many new and unusual electrical and thermal transport properties, such as the reduced specific heat, ultralow and temperature independent lattice thermal conductivity, and extremely high TE figure of merit zT > 2.0 have been observed and reported in these MIECs14. The high TE performance and the fact that Cu is relatively non-toxic and earth-abundant has attracted much attention to these MIECs for both fundamental studies and industrial applications.
Despite the high performance, the stability and reliability of MIECs are key concerns for long-term service in real applications for batteries, photovoltaics, and TEs. In Li-ion batteries, for instance, Li dendrite growth can result in catastrophic failure leading to combustion or explosion15. In CdTe–CuxTe solar cells, Cu atoms can migrate into the CdTe absorber and CdS window layers to form carrier traps that reduce device performance4. In TEs, the added potential risk using MIECs contributed to the discontinuation of Cu2–δSe development for aeronautics and space applications16,17. The mobile Cu species in Cu-based MIECs are prone to deposit on the surface at the cathode to form Cu metal when an external electric field or temperature gradient is applied (Fig. 1a). If Cu is not supplied at the anode, the Cu metal deposition at the cathode will change the initial material’s composition and degrade TE performance as the metal deficiency in MIECs is optimized for a high zT. In TE devices with MIECs, Cu metal deposition on the sample surface may also damage the contact between the TE material and the electrode by forming cracks to increase electrical/thermal resistance and degrade the power output and conversion efficiency18. In addition, the plating of Cu at the cathode may lead to the evaporation of chalcogenides at the anode, resulting in the breakage of the thermolegs19. This is partly why NASA stopped the program of Cu1.97Ag0.03Se1+y-based radioisotope thermal generators in 1981 after more than 10 years of research activity18. Therefore, metal deposition caused by ion flux must be restricted to improve the stability and reliability of TE devices consisting of MIECs before the use in any industrial application.
Atom migration and deposition in ion conductors. a Metallic Cu deposition on the surface of a Cu2S sample induced by a current. b–e Schematic of (b) the energy landscape for ions; c random ion motion without net flux; and d net ion flux under directional force or field. Due to a directional force or field and depending on the electrode constraints, MIECs may either reach a (e) steady state without net ion transport (and without metal deposition) or (f) continuous metal deposition (or other decomposition), if the local Cu concentration reaches a critical level determined by the stability range of the MIECs
In this study, through systematically investigating the behavior of various MIECs with a liquid-like ionic sublattice in an electric field with or without a temperature gradient, we reveal the relations of ion migration, metal deposition, and materials degradation in MIECs for TE application. A general model is proposed to reveal the thermodynamic threshold for decomposition of MIECs. With this understanding, we develop a strategy to improve the MIECs’ stability and reliability by adding electronically conducting, but ion-blocking interfaces in the material.
Results
Mechanism of ion transport in mixed conductors
The physical and chemical processes of atom migration and metal deposition in MIECs are presented in Fig. 1b–f. The mobile ions (Cu+ in Cu2S and Cu2Se) possess high diffusivities, as they have relatively low activation energies for migration, Ea (e.g., 0.19 eV in Cu2S and 0.14 eV in Cu2Se)20,21. Simply, neighboring sites are energetically close and jumps are frequent (Fig. 1b). If there is no directional force or field applied to the uniform material, the random motion of ions is equal in all directions and there will be no net mass transport in a specific direction (Fig. 1c). In response to an external driving force (an electric field or temperature gradient) the charge carriers (ions and electronic species) flow (Fig. 1d). If the electrodes do not allow for ion transfer, there can be no net ionic current in the stationary state, and a concentration gradient of ions will form within the material. For reasons of electroneutrality, this concentration gradient will lead to an equal concentration gradient of electrons, and in essence, a chemical composition gradient is formed. If the concentration variation remains within the stability limits of the material, i.e., within the homogeneous phase field defined by the phase diagram of the MIEC, the concentration gradient of the mobile component acts as diffusion force opposing the external applied force on the mobile component, and a steady-state condition is achieved, i.e., there is no driving force for further migration of the neutral component (Fig. 1e). In the following, we describe transport of the neutral metal component as transport of atoms for the sake of simplicity. In the steady-state condition with ion-blocking electrodes, the material can still transport a net flux of electric charge (via electrons or holes in the presence of an electric field) and heat (via electrons or holes and phonons in the presence of a temperature gradient), but the net flux of atoms is zero. This steady-state condition of vanishing atom transport, also called the Soret steady state22, is similar to the condition in a conventional TE material (e.g., Bi2Te3, PbTe, and SiGe)23,24,25.
However, the change in the chemical potential of the migrating atom may lead to decomposition of the MIEC and prevent the formation of a steady-state condition. At the electrode interface, a critical chemical potential may be reached where a decomposition (product) phase is favored. For instance, in Cu2-δ(Se,S), when the chemical potential of Cu at the cathode is equal to or higher than the chemical potential of Cu metal, the reduction of Cu+ to Cu metal at the cathode or the oxidation of selenium/sulfur anions to Se/S (solid and/or gaseous) at the anode can occur16,17,18,19. The chemical potential beyond which decomposition occurs also corresponds to a “solubility limit” of Cu in the MIEC. The maximum solubility of Cu precedes Cu metal deposition and the minimum solubility of Cu precedes Se/S oxidation. When the Cu concentration increases beyond this “solubility limit”, Cu metal will deposit at the cathode if the kinetics of metal crystallization allows (Fig. 1f). Once this happens, the material and the interface in the device can be permanently altered. We note that the deposition of Cu metal is hindered by a nucleation barrier. Then, for Cu deposition to occur, the chemical potential of Cu needs to be slightly higher than its standard potential, µ°(Cu), but all the general conclusions above remain the same.
The thermodynamic threshold for the maximum or minimum solubility in Cu-based MIECs can be reached if there is a sufficient change in the chemical potential of Cu atoms due to applied forces (electric field and temperature difference). In steady state, the net change in chemical potential of Cu atoms can be determined from the sum of the change in electrochemical potentials of the constituent ions and electronic carriers. Because copper atoms are in equilibrium with copper ions and electrons, the electrochemical potentials \(\left( {\tilde \mu } \right)\) are related by \(\mu _{\mathrm{Cu}} = \tilde \mu _{\mathrm{Cu}^ + } + \tilde \mu _{\mathrm{e}}\). Thus the change in chemical potential across the material (defined by the electrodes each end is in contact with),
Consequently, our goal is to relate experimental parameters to μCu in order to explain the critical condition of Cu metal deposition in Cu-based MIECs.
From the flux equation of linear nonequilibrium thermodynamics (see Supplementary Note 1)26,27, the electronic current density, J, is driven by the gradient of the electrochemical potential of the electronic species and the temperature gradient through the relation
where ze defines the charge (−1 for electrons or +1 for holes), F is Faraday’s constant, and σ is the specific electrical conductivity. Se which has the sign and units of the electronic Seebeck coefficient, captures the effect of thermodiffusion due to the temperature gradient ∇T. Using the analogous flux equation for ions, considering the case when ion-blocking electrodes are used (i.e., there is no ion flux, \(J_{{\mathrm{Cu}}^ + } = 0\)), then the electrochemical potential driving force exactly cancels the thermal driving force for ion migration. Explicitly,
and \(S_{{\mathrm{Cu}}^ + }\) similarly relates to the thermodiffusion of Cu ions. When the gradients in Eqs. (2) and (3) only apply in the x direction they can be integrated, which for linearly varying systems (such as MIECs28) is equivalent to being multiplied through by Δx = L (L is the effective length between electrodes), and used in the relation defined by Eq. (1). Upon rearranging, we arrive at
where S* accounts for the net effect of thermodiffusion and V is the experimental parameter (in units of voltage, calculated from J) of this study.
Because there are bounds to the chemical potential range over which the material can exist, there must be some critical chemical potential difference \(\left( {{\mathrm{\Delta }}\mu _{{\mathrm{Cu}}}^{{\mathrm{crit}}}} \right)\) at which Cu metal deposition occurs. From Eq. (4), it is straightforward to find the voltage corresponding to this critical chemical potential difference:
-
i.
in the isothermal case,
$$V_{\mathrm{c}} = - \frac{1}{{z_{\mathrm{e}}F}}{\mathrm{\Delta }}\mu _{{\mathrm{Cu}}}^{{\mathrm{crit}}}$$(5)where Vc is a critical voltage that results from a critical applied current density Jc, and,
-
ii.
in a temperature difference,
where it is important to note that the sign of ΔT(=Tanode–Tcathode) is important, as will be discussed.
From this analysis it is expected that a voltage difference, not current density, is the critical parameter for Cu deposition. We also note that in open circuit conditions (no electronic or ionic current) the thermodynamics predicts a critical ΔT resulting in Cu deposition at the cathode (when Vc = 0 in Eq. 6).
Further consideration of the isothermal condition (Eq. 5) reveals that Vc only depends on the composition of the compound relative to the “solubility limit”. This allows for the use of a microscopic defect model to relate off-stoichiometry, δ, (in Cu2-δX, X = S, Se) to the critical chemical potential in Cu-based MIECs. A parameter named as the critical off-stoichiometry (δc) is introduced here, corresponding to the “solubility limit” of Cu concentration at the cathode of the MIEC. Based on the theory proposed by Yokota and Korte et al.28,29,
where Ke is the equilibrium constant for electrons and holes that is independent of stoichiometry, R is the gas constant, and T is the temperature. The thermodynamic theory developed herein predicts that a given off-stoichiometry and temperature difference will result in limitations on the electrical potential difference that is stable across the material. Using this knowledge, the latter part of this paper will address possible ways to engineer stability in these materials for TE applications.
Isothermal ion transport in mixed conductors
Taking the family of Cu-based TE MIECs as an example, the determination of Vc is introduced for the isothermal case. When an externally applied electric field does not raise V between the two ends of the sample to the critical Vc value, the Cu atoms simply redistribute inside the sample to form a steady-state concentration gradient of Cu without metal deposition at the cathode (Fig. 1e). After removing the electric field, the Cu concentration gradient gradually returns to the initial homogeneous state (Supplementary Fig. 1). Thus, for V < Vc, the Cu redistribution under the external electric field is temporary, with no lasting effect on the MIEC. However, when the external electric field reaches Vc (Fig. 1f), Cu metal can deposit. Although metallic Cu is not thermodynamically stable after the electric field is removed, many of the metallic deposits cannot immediately diffuse back into the sample (kinetically limited). In this case, the average Cu concentration inside the MIEC is reduced (Supplementary Fig. 1), which causes measureable changes of the resistivity (Fig. 2a).
Critical electric potential difference (Vc) in the isothermal case. a Current density dependence of relative electrical resistance variation (R/R0) for several Cu-based mixed ionic/electronic conductors with L = 10 mm. b Experimentally determined Vc (L = 10 mm). c Material length L dependences of Vc and the critical current density Jc for Cu1.97S. The dashed line is a guide to the eyes. d Vc as a function of Cu off-stoichiometry δ in the Cu2-δS (δ = 0, 0.01, 0.03, 0.04, 0.06, and 0.1) samples with L = 10 mm. The dashed line represents the Vc curve based on Eq. 7. All measurements were carried out at 750 K
The Vc values for several Cu-based TE MIECs, including Cu2–δS (δ = 0, 0.01, 0.03, 0.04, 0.06, and 0.1), Cu2Se, and Cu2S0.5Se0.5, are experimentally determined at a constant temperature of 750 K (Supplementary Table 1) by using the apparatus and method shown in Supplementary Figs. 2, 3. The details can be found in the Supplementary Methods. The maximum Vc value for all samples is only 0.11 V (Fig. 2b). Such small values are consistent with the ease of observing Cu-metal deposition in these TE MIECs16,17. Notice that Vc is constant for a series of Cu1.97S samples with various material lengths, L, whereas Jc decreases with increasing L (Fig. 2c). This agrees well with Eqs. (4–7) in which Vc is not dependent on length but Jc is. Thus, although it may seem natural to be concerned about metal deposition due to high current density in a TE generator device, it is the voltage and not the current density that defines the critical quantity, which is in agreement with the insight of Eq. 4.
Furthermore, we found experimentally (Fig. 2d) that Vc gradually increases with increasing Cu off-stoichiometry (δ in Cu2-δS). Intuitively, this coincides with a reduction in the chemical potential of Cu as the off-stoichiometric material is more willing to accept Cu atoms. This trend can be well explained by Eq. (7). According to the Cu–S binary equilibrium phase diagram30, Cu2-δS has a wide composition range (0 < δ < 0.27) at 750 K. Thus, for these Cu2-δS (δ = 0, 0.01, 0.03, 0.04, 0.06, and 0.1) samples, constant values for δc (=−0.03) and Ke (=2.24 × 10−3) fit the experimental data well using Eq. (7) (Fig. 2d). In theory, δc should correspond to the Cu-rich phase boundary composition found on the phase diagram, but here it is used as a phenomenological constant. Since Ke = xnxp = exp(−ΔGe/RT), where xn and xp are the molar fractions of intrinsic electrons and holes, respectively29, the electron–hole pair free energy of formation, ΔGe, is estimated to be 0.4 eV; consistent with the band gap of cubic Cu2S reported by Lukashev et al.31 In addition, it was found experimentally that the Vc values for both Cu2S and Cu2Se increase with increasing temperature (Supplementary Fig. 4), which corresponds to an increase in \({\mathrm{\Delta }}\mu _{{\mathrm{Cu}}}^{{\mathrm{crit}}}\) associated with the increase in phase width of these MIECs with temperature30,32.
Ion transport of mixed conductors in temperature difference
In the non-isothermal case, the relative directions of the electric current and the heat flux are expected to have dramatic effects on Vc (Eq. 6). If the current direction is the same as the heat flux direction (i.e., Tanode > Tcathode), the electrical potential and temperature difference work together to drive atom migration to the cathode. Conversely, when the direction of the electric current is opposite to the heat flux (i.e., Tcathode > Tanode), the current and temperature difference have opposed driving forces for atom migration. Although the necessary condition for metallic Cu to plate out is that the chemical potentials of Cu in the MIEC are that of Cu metal at the cathode, this is a necessary but not sufficient condition because some degree of overpotential may be required to initiate and drive the electrodeposition reaction. The rate of deposition is not addressed in the thermodynamics analysis here.
Nevertheless, irrespective of overpotential effects, \({\mathrm{\Delta }}\mu _{{\mathrm{Cu}}}^{{\mathrm{crit}}}\) is expected to be constant for a given temperature difference, regardless of the relative flux directions. This is because the range of chemical potentials corresponds to the range in compositional phase space, which is negligibly impacted by the electric field. For engineering applications, this allows us to contrast the critical current densities that can be applied relative to the temperature difference. For a constant magnitude of |∆T| and \({\mathrm{\Delta }}\mu _{{\mathrm{Cu}}}^{{\mathrm{crit}}}\) in Eq. (6), we can write
when the current is applied in the same direction as the temperature gradient (Jc,same), or
when the current is applied in the opposite direction as the temperature gradient (Jc,opposite). Here, L and σavg are the effective length and average electrical conductivity across the superionic phase on the sample, respectively. Put another way, Vc,same and Vc,opposite are different from the isothermal case due to the additional potential that results from the thermodiffusion of charged species (generalized Seebeck effect).
Taking Cu1.97S as an example, the critical current density in the non-isothermal case is measured by using the apparatus and method shown in Supplementary Fig. 5. The details can be found in the Supplementary Methods. At a constant |ΔT|(= 673–300 K), a significant difference in critical current density is required depending on the relative flux directions (Fig. 3a). If the current direction is the same as the heat flux direction, Jc,same ≈ 0.3 A cm−2 is large enough to obtain metallic Cu deposition near the cold side. However, if the current direction is reversed, Jc,opposite ≈ 20 A cm−2 is required to obtain metallic Cu deposition at the hot side. This observation is in agreement with the thermodynamic expectations, although overpotential effects may contribute. To further demonstrate the trend predicted by Eqs. 8 and 9 , Vc,same and Vc,opposite were evaluated as a function of increasing |∆T| by using the σavg data shown in Supplementary Table 2 (Fig. 3b). As expected, Vc,opposite is found to increase with |∆T| and Vc,same is found to decrease with |∆T| (Fig. 3b).
Critical electric potential difference (Vc) under a temperature gradient. a The relative Seebeck coefficient variation (S/S0) as a function of the current density for Cu1.97S at Tcathode = 300 K and Tanode = 673 K. The positive J means that the current direction is the same as the heat flux direction. The negative J means that the current direction is opposite to the heat flux direction. b Experimentally determined Vc,same and Vc,opposite as a function of |∆T|, showing qualitative agreement with Eqs. 8 and 9. The temperatures at the anode and cathode for each flux direction can be found in text. The length of all measured samples is 6 mm. The dashed lines are guides to the eye
Strategy to improve stability in mixed conductors
In real TE generators the direction of the current flowing through the p-type legs is always the same as the direction of the heat flux (Supplementary Fig. 6). Consequently, the thermodynamic understanding validated through the temperature difference experiments is very helpful to design stable TE devices based on these high performance MIECs. Eq. 4 and Fig. 2c clearly show that Vc is length independent; thus, Vc,same in Eq. 8 is length independent as well. Changing the geometry cannot change the critical chemical potential—it is fixed for a given temperature, temperature gradient, and off-stoichiometry. However, the total voltage across a TE leg can be increased by using a series connection of several segments of MIEC material, in which electrically conducting, but ion-blocking interfaces are used between the individual segments. The reason for this is simple: the total voltage across the series-segmented leg, Vleg, is the sum of voltages across each segment, Vseg. When n segments are approximately the same length, and each segment has the same critical voltage, Vseg,c, the critical voltage for the entire leg is Vleg,c = n Vseg,c.
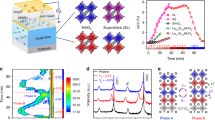
The schematic of this strategy is shown in Fig. 4a. These interfaces limit the ion movement but allow the free movement of the electrons or holes. Schematically, the ion concentration distribution rises linearly (as in Fig. 1e) in each segment, but because the chemical potential is reset by the ion-blocking interfaces a saw-tooth like pattern can be obtained. Engineering the number of segments n can allow for high voltages (and corresponding current densities) without reaching the critical chemical potential that results in the degradation of the material.
Ion-blocking strategy to improve stability in thermoelectric ion conductors. a Schematic for limiting the ion movement by including thin electron-conducting and ion-blocking interfaces; either grain boundaries (red areas) or a secondary phase (yellow areas). b Schematic of ion-blocking electrically conducting interfaces that allow the concentration profile to be reset at each interface so that the ion concentration does not ever reach the upper limit. c Relative resistance variation (R/R0) as a function of current density for different Cu1.97S samples at a constant temperature of 750 K without a temperature difference. d Relative Seebeck coefficient variation (S/S0) as a function of current density for different Cu1.97S samples under the condition of temperature difference (Tanode = 673 K and Tcathode = 300 K). The insets in (c) and (d) show the optical images of the measured Cu1.97S samples. The critical current density was measured across the segment in the middle
Initially, we test this strategy at a constant temperature of 750 K. The unsegmented Cu1.97S leg exhibits a critical applied current density of ≈11 A cm−2. However, for a three-segment Cu1.97S leg, the critical applied current density is ≈30 A cm−2 (Fig. 4c). This is in excellent agreement with the thermodynamic theory. The critical chemical potential for Cu at 750 K is then equivalent to Vseg,c = 0.09 V, as determined from the unsegmented leg. Because Vc is geometry independent, each segment has this same critical voltage. When the three segments are connected in series the critical voltage across the leg rises to Vleg,c = 0.27 V, exactly as expected.
Series segmentation is also effective in the non-isothermal case. As before, the critical voltage for the leg is the sum of critical voltages for each segment. However, the temperature dependencies of \({\mathrm{\Delta }}\mu _{{\mathrm{Cu}}}^{{\mathrm{crit}}}\) and S* may lead to different critical voltages for each segment. Nevertheless, the unsegmented leg can only substantiate a small current density of Jc,same = 0.3 Acm−2 (Fig. 4d). A three-segment leg, was found to sustain a significantly larger current density, Jc,same ≈ 3.0 A cm−2, about one order of magnitude higher than the unsegmented Cu1.97S leg (Fig. 4d). Correspondingly, the critical voltage across the leg is increased from Vc,same = 0.002 V to about 0.018 V. If more Cu-atom blocking layers are added, the critical total voltage across the leg can be expected to continue to increase. Therefore, the present data strongly suggests that MIECs can indeed sustain large current densities and achieve high stability whenever the local chemical potential is engineered to be lower than the corresponding critical chemical potential.
Discussion
By understanding the thermodynamic principles behind ion and atom migration and metal deposition in TE MIECs, we derive a thermodynamic model to understand the critical electrical potential difference for decomposition of non-stoichiometric MIECs at constant temperature, and demonstrate that it is a critical voltage, not current, that is the limiting factor. In the more complicated case of concurrent electrical and thermal fluxes, the experimental observations are in excellent qualitative agreement with the thermodynamic predictions. Furthermore, we propose the use of ion-blocking but electrically conducting interfaces to enhance the critical electric potential difference in engineering applications. This is most efficiently done with a grain-boundary engineered microstructure. This study clearly shows that ion migration and metal deposition can be effectively suppressed in MIECs, which has been an overwhelming concern, but not solved before. Consequently, the technique demonstrated herein to increase the critical potential opens a new possibility of using these TE MIECs in real applications. We expect that the mechanism and strategies proposed in this study for TE materials should also be valid for other ionic conductors, and thus can be used in the research areas of, photovoltaics, solid electrolytes, and various sensors. Although the strategy of blocking ion transport is not applicable for batteries, the experimental and theoretical methods for characterizing and understanding atom deposition in MIECs should be applicable to Li batteries.
Methods
Materials synthesis
The detailed preparation process of the Cu-based TE MIECs used in the present study can be found elsewhere14.
Critical voltage determination
The experimental parameter, Vc, was ascertained by monitoring the electronic properties (e.g., electrical resistance R and Seebeck coefficient S) of the material after applying different electric currents or temperature gradients. Because the TE properties of the MIEC, especially the electrical resistance R and (electronic) Seebeck coefficient S, are very sensitive to the chemical composition, by monitoring the variation of the relative electrical resistance (R/R0, where R0 is the initial electrical resistance) or relative Seebeck coefficient (S/S0, where S0 is the initial Seebeck coefficient) under different current densities, the critical Vc can be determined. The critical current density, Jc, corresponds to the point when R/R0 (or S/S0) begins to decrease is shown in Fig. 2a.
In the isothermal case, the chemical potential of Cu atoms is determined by the voltage on the sample generated by the electric current (see Eq. 4), which is determined experimentally as \(V = \frac{{JL}}{\sigma }\), where J is the applied electric current density, and σ and L are the electrical conductivity and effective length of the MIEC, respectively. In the evaluation of Vc, the temperature is set 750 K. The length of the measured sample is 10 mm. The typical 4-point electrical conductivity at the experimental temperature is used for resistance measurement. More measurement details can be found in Supplementary Methods.
In the non-isothermal case and Tanode > Tcathode (Eq. 6), the electrical potential and temperature difference work together to drive atom migration to the cathode. In this case, the Cu metal deposition will occur at the superionic-phase/normal-phase interface if Tcathode is lower than the superionic phase transition temperature of the MIEC; or, at the cathode if Tcathode is above the superionic phase transition temperature. When the relative fluxes are opposed (Tcathode is the hot side), Cu metal deposits at the cathode so long as Tcathode is above the superionic phase transition temperature. This was accounted for in the effective length, L, used to calculate Vc. In the evaluation of Vc,same, the cathode temperature Tcathode was fixed at 300 K, but |∆T| was calculated relative to the superionic phase transition temperature of Cu1.97S (≈ 350 K). The anode temperatures, Tanode, were 473, 523, 573, 623, and 673 K. To determine Vc,opposite, Tanode was fixed at 300 K and Tcathode was set to 473, 523, 573, 623, and 673 K. The length of the measured sample is 6 mm.
Segmented leg construction
The Jc and Vleg,c values for a n = 3 segmented Cu1.97S leg (total length is Lleg = 10 mm) are experimentally obtained. The leg is made by bonding three Lseg ≈ 3.3 mm pieces together by using conductive carbon paste as the Cu-atom blocking layer. The data of this three-segment Cu1.97S leg are compared with those of the unsegmented Cu1.97S leg (Lleg = L = 10 mm). Figure 4d shows the relative Seebeck coefficient variation S/S0 values for a three-segment Cu1.97S leg with Lseg = 2 mm, Tanode = 673 K, and Tcathode = 300 K. The leg was fabricated in the same manner previously described. The data for the unsegmented Cu1.97S leg (Lleg = L = 6 mm) is included for comparison.
Data availability
All data are available from the authors upon reasonable request.
The raw data contained in Figs. 2, 3, 4 and Supplementary fig. 4 are available upon request from X.S.
References
Boyce, J. B. & Huberman, B. A. Superionic conductors: transitions, structures, dynamics. Phys. Rep. 51, 189–265 (1979).
Knauth, P. & Tuller, H. L. Solid-state ionics: roots, status, and future prospects. J. Am. Ceram. Soc. 85, 1654–1680 (2002).
Eames, C. et al. Ionic transport in hybrid lead iodide perovskite solar cells. Nat. Commun. 6, 7497 (2015).
Rohatgi, A. et al. An improved understanding of efficiency limiting defects in polycrystalline CdTe/CdS solar cells. In Conf. Record of the 22nd IEEE Photovoltaic Specialists Conference, 962–966 (IEEE, New York, 1991).
Waser, R. & Aono, M. Nanoionics-based resistive switching memories. Nat. Mater. 6, 833–840 (2007).
Liu, H. et al. Copper ion liquid-like thermoelectrics. Nat. Mater. 11, 422–425 (2012).
Xiao, C. et al. Superionic phase transition in silver chalcogenide nanocrystals realizing optimized thermoelectric performance. J. Am. Chem. Soc. 134, 4287–4293 (2012).
Ishiwata, S. et al. Extremely high electron mobility in a phonon-glass semimetal. Nat. Mater. 12, 512–517 (2013).
Qiu, P. F. et al. Sulfide bornite thermoelectric material: a natural mineral with ultralow thermal conductivity. Energy Environ. Sci. 7, 4000–4006 (2014).
Weldert, K. S. et al. Thermoelectric transport in Cu7PSe6 with high copper ionic mobility. J. Am. Chem. Soc. 136, 12035–12040 (2014).
Snyder, G. J. et al. Disordered zinc in Zn4Sb3 with phonon-glass and electron-crystal thermoelectric properties. Nat. Mater. 3, 458–463 (2004).
Lu, X. et al. High performance thermoelectricity in earth-abundant compounds based on natural mineral tetrahedrites. Adv. Energy Mater. 3, 342–348 (2013).
Riess, I. Mixed ionic–electronic conductors-material properties and applications. Solid State Ion. 157, 1–17 (2003).
Shi, X., Chen, L. & Uher, C. Recent advances in high-performance bulk thermoelectric materials. Int. Mater. Rev. 61, 379–415 (2016).
Chen, N. et al. Biomimetic ant-nest ionogel electrolyte boosts the performance of dendrite-free lithium batteries. Energy & Environ. Sci. 10, 1660–1667 (2017).
Brown, D. R., Day, T., Caillat, T. & Snyder, G. J. Chemical stability of (Ag, Cu)2Se: a historical overview. J. Electron. Mater. 42, 2014–2019 (2013).
Dennler, G. et al. Are binary copper sulfides/selenides really new and promising thermoelectric materials? Adv. Energy Mater. 4, 1301581 (2014).
Hinderman, J. D. Thermoelectric Materials Evaluation Program Annual Technical Report for Fiscal Years 1980/1981. Report No. MMM-2331-0691 (U.S. Department of Energy, United States, 1981).
Stapfer, G. & Garvey, L. Progress Report No. 29 for a Program of Thermoelectric Generator Testing and RTG Degradation Mechanisms Evaluation. Report No. DOE/ET/33003--T2 (U.S. Department of Energy, United States, 1979).
Balapanov, M. Kh et al. Ionic conductivity and chemical diffusion in superionic LixCu2–xS (0 ≤x ≤ 0.25). Phys. Status Solidi b 1, 114–119 (2004).
Yakshibaev, R. A. et al. Ionic conductivity and diffusion in superionic conductor α-Cu2− δSe. Fiz. Tverd. Tela 26, 3641–3645 (1984).
Allnatt, A. R. & Lidiard, A. B. Atomic Transport in Solids. (Cambridge University Press, Cambridge, 1993).
Kim, S. I. et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 348, 109–114 (2015).
Biswas, K. et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 489, 414–418 (2012).
Joshi, G. et al. Enhanced thermoelectric figure-of-merit in nanostructured p-type silicon germanium bulk alloys. Nano. Lett. 8, 4670–4674 (2008).
Wagner, C. The thermoelectric power of cells with ionic compounds involving ionic and electronic conduction. Prog. Solid State Chem. 7, 1–37 (1972).
Werner, K. & Wiegand, S. Thermal Nonequilibrium Phenomena in Fluid Mixtures. (Springer, Berlin, 2002); 146–183.
Yokota, I. On the electrical conductivity of cuprous sulfide: a diffusion theory. J. Phys. Soc. Jpn. 8, 595–602 (1953).
Korte, C. & Janek, J. Nonosothermal transport properties of α-Ag2+δS: partial thermopowers of electrons and ions, the soret effect and heats of transport. J. Phys. Chem. Solids 58, 623–637 (1997).
Chakrabarti, D. J. & Laughlin, D. E. The Cu–S (copper–sulfur) system. J. Phase Equilibria 4, 254–271 (1983).
Lukashev, P. & Lambrecht, W. R. L. Electronic and crystal structure of Cu2−xS: full-potential electronic structure calculations. Phys. Rev. B 76, 195202 (2007).
Massalski, T. B., Okamoto, H., Subramanian, P. R., & Kacprzak, L. Binary Alloy Phase Diagrams 2nd edn (ASM International, Materials Park, OH,1990).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (NSFC) under the No. 51625205, the Key Research Program of Chinese Academy of Sciences (Grant No. KFZD-SW-421),and the Program of Shanghai Subject Chief Scientist (16XD1403900). P.Q. acknowledges the support by the Youth Innovation Promotion Association of CAS under Grant No. 2016232. GJS and MTA acknowledge funding from the Solid-State Solar-Thermal Energy Conversion Center (S3TEC), an Energy Frontier Research Center, funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences (DE-SC0001299) as well as support from the NASA Science Mission Directorate’s Radioisotope Power Systems Thermoelectric Technology Development program.
Author information
Authors and Affiliations
Contributions
P.Q., X.S, and G.J.S. conceived the idea. P.Q., Y.L., Y.Z., and T.M. performed the experiment study. M.T.A., H.C., G.J.S., and J.J. performed the equation derivation and model calculation. P.Q, S.M.H, W.Q.Z., W.G.Z., J.Y., C.U., X.S., G.J.S., and L.C. discussed and analyzed the data. P.Q., M.T.A., X.S, G.J.S., and L.C. wrote and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qiu, P., Agne, M.T., Liu, Y. et al. Suppression of atom motion and metal deposition in mixed ionic electronic conductors. Nat Commun 9, 2910 (2018). https://doi.org/10.1038/s41467-018-05248-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05248-8
This article is cited by
-
Mobile ion confinement for better thermoelectrics
Nature Materials (2024)
-
Highly stabilized and efficient thermoelectric copper selenide
Nature Materials (2024)
-
Synergistically optimized electron and phonon transport in high-performance copper sulfides thermoelectric materials via one-pot modulation
Nature Communications (2024)
-
Enhanced service stability and thermoelectric performance in Cu2−δSe-based composites
Science China Materials (2024)
-
Quinoxaline derivatives as cathode for aqueous zinc battery
Journal of Solid State Electrochemistry (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.