Abstract
Hydrogen bond symmetrisations in H-bonded systems triggered by pressure-induced nuclear quantum effects (NQEs) is a long-known concept but experimental evidence in high-pressure ices has remained elusive with conventional methods. Theoretical works predicted quantum-mechanical tunneling of protons within water ices to occur at pressures above 30 GPa, and the H-bond symmetrisation transition to occur above 60 GPa. Here we used 1H-NMR on high-pressure ice up to 97 GPa, and demonstrate that NQEs govern the behavior of the hydrogen bonded protons in ice VII already at significantly lower pressures than previously expected. A pronounced tunneling mode was found to be present up to the highest pressures of 97 GPa, well into the stability field of ice X, where NQEs are not anticipated in a fully symmetrised H-bond network. We found two distinct transitions in the NMR shift data at about 20 GPa and 75 GPa attributed to the step-wise symmetrisation of the H-bond.
Similar content being viewed by others
Introduction
Water in its liquid and solid forms is ubiquitous in nature, being one of the most abundant molecule in the universe, and it is thought to be a prerequisite to sustain life in our solar system and beyond. Water is one the main constituent of ocean exoplanets and icy moons like Ganymede, Europa, Enceladus, and Titan with possible existence of deep high-pressure ice layers in their internal structure. The hydrosphere of these bodies could be up to 900 km thick in icy satellites and up to several thousand kilometers in Ocean exoplanets1,2. Understanding their internal structure and evolution is crucial to determine their potential habitability and for interpreting upcoming NASA Europa Clipper and ESA Juice space missions3,4.
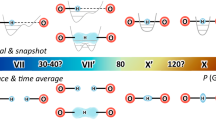
Water molecules have been known for a long time to form a very specific type of chemical bonding—hydrogen bonds5. Under high pressure, the phase diagram of H2O exhibit an exotic behavior with more than 15 stable crystalline phases at variable temperature and pressure conditions6. The high-pressure region, above 3 GPa, is mostly dominated by the three ice phases VII, VIII, and X (Fig. 1). Both ice VII and VIII are molecular solids consisting of distinct H2O units linked to each other by hydrogen bonds. Ice X, on the other hand, exhibits a fully symmetrised hydrogen bond network, thus rendering a dissociation of the H2O molecules, forming an atomic solid at pressures of about 50–70 GPa at room temperature7. One of the most enigmatic phenomena in the high-pressure phase diagram of water is the transition from the hydrogen disordered phase ice VII into the hydrogen ordered phase of ice X8. It is widely believed that this transition is preceded by nuclear quantum effects (NQEs)7,9, or specifically, pronounced proton delocalization due to tunneling motion within the symmetric double-well potential of the hydrogen bonds in ice VII.
Phase diagram of H2O and schematic representation of hydrogen bond symmetrisation. a Phase diagram of H2O. The insets show the schematic symmetries of the high-pressure phases of ice VII, VIII, and X. Round symbols denote NMR measurements within this study, different colors relate different separate high pressure NMR experiments. b Sequence of hydrogen bond symmetrisation with pressure
Evidence of hydrogen-bond symmetrisation and potential room-temperature proton tunneling in ice VII are sparse and often contradictory. This obviously relates to experimental difficulties. Hydrogen atoms remain effectively invisible to X-ray diffraction or emission spectroscopy10,11, leaving for observations only the heavier oxygen sublattice, which does not show significant transitions in the pressure range of interest12,13. While Raman-spectroscopy and neutron diffraction are more sensitive to H-bonds, they also yield ambiguous and often contradictory results,14,15.
Given these experimental difficulties, a direct observation of H-bond symmetrisation or NQEs remain mostly elusive in high-pressure experiments with the techniques discussed above.
One of the most promising spectroscopic methods to deal with these problems is nuclear magnetic resonance (NMR) spectroscopy, where proton NMR is best known for providing one of the highest possible NMR signal strengths, and allows direct observation of the electronic and structural environment of the nuclei. However, an application of NMR spectroscopy at high pressures, particularly in diamond anvil cells (DACs), was unfeasible, with set-ups unable to surpass 8 GPa on average, with rare exceptions reaching pressures above 10 GPa16,17.
Recently, a novel technique to detect the faint NMR signals by application of electro-magnetic Lenz lenses in Diamond indenter cells was introduced allowing for NMR experiments at pressures of up to 70 GPa18. In this study, we used a refined NMR resonator using a so called double stage Lenz lens (DSLL) structure19 at pressures approaching the megabar regime to investigate compression-induced nuclear quantum effects in ices. With this novel approach, we were able to follow the hydrogen bond symmetrisation in ice VII and its transition to the proton ordered phase X, one of the most sought after elusive effects in high-pressure sciences proposed 46 years ago.
Results and Discussion
High pressure NMR resonator
Recently, Spengler et al.20 demonstrated that the NMR sensitivity, in particular the limit of detection in the time domain, can be locally amplified with the use of so called Lenz lenses (LL). The LL-resonators form, in a general sense, a flux transformer picking up the high frequency B1 field generated by an excitation coil which is part of a standard LC tank circuit. The stored magnetic field energy will be deposited within a geometrically predefined area, leading to a locally enhanced B1 field. Recently, the significant advantage of these LLs for high pressure NMR was realized, and 1H-NMR spectra at pressures up to 70 GPa could be acquired in a toroidal diamond indenter cell18.
Here, a refined resonator structure has been employed which can be used within a standard DAC.
The basic idea is to accommodate a stable resonator structure for a pair of identical diamonds which can be driven by a high-inductance excitation coil. Figure 2a shows a schematic picture of such a setup. Numerical field simulations, right side of Fig. 2a, demonstrate that a DSLL arrangement is indeed able to significantly amplify the B1 field within the 100 pl sample chamber.
Summary of the experimental setup. a High-pressure NMR resonator setup. The inset shows the zoomed-in region around the anvil's culet. Both Lenz lenses are formed on the anvil's pavilion by copper deposition and subsequent shaping, using a focused ion beam. Simulations of the RF magnetic field generated by the resonator setup demonstrate the magnification in B1 at the sample cavity necessary for detecting NMR signals from the 100 pl sample cavity (80 µm diameter, 20 µm height prior to compression). b SEM images for the double stage Lenz lens (DSLL) resonator structure on one diamond. c Raman spectra accumulated at the diamond edge at the center of the sample cavity at pressures of 75 GPa and 97 GPa. Red arrows indicate the spectral position used for pressure determination. d Proton NMR spectra at different pressures as well as from empty cells, evidencing the origin of the acquired signals from the H2O samples from within the sample chamber
High magnetic field data
1H-NMR spectra on ice from 8 to 90 GPa are shown in Fig. 3a. We performed several experiments using four independently loaded cells, with overlapping and reproducible results (Fig. 3b).
NQEs of protons have several observable effects on 1H-NMR spectra. First, random rapid tunneling from one to another minimum in a symmetric double-well energy potential will result in motional averaging of the NMR signals21. Second, 1H-NMR spectra in low barrier hydrogen bonds (LBHBs) exhibit significant de-shielding, with high proton shifts of about 20–40 ppm22.
Furthermore, it was shown that proton tunneling leads to a zero field splitting and detectable tunneling side bands. This effect was widely investigated for the tunnel rotation of methyl groups at low temperatures23,24,25. The simpler case of tunneling effects on NMR spectra when tunneling occurs solely along a linear axis, i.e., within a symmetric double-well potential, were predicted by Johnson26 and Johnston27. In general, rapid proton tunneling introduces an exchange between the allowed, magnetic transitions with Δm = 1, and forbidden, or combination transitions. The position of the tunnel side bands (t.s.b.) greatly depends on the magnitude of the tunnel frequency with spectral positions at υ = υ0 ± υt/2 where υ0 is the center frequency of the Δm = 1 transition and υt is the tunnel frequency. Clough et al.28 showed that at low magnetic fields, the t.s.b. intensity is significantly improved, leading to a possible observation of higher order tunneling modes of up to 1 MHz.
The 1H-NMR spectra shown in Fig. 3a) were de-convoluted, see Fig. 4, into Gaussian and Lorentzian contributions and attributed to localized immobile protons and randomly tunneling protons delocalized over the energy hypersurface of the hydrogen bond. At pressures above 20 GPa, a pronounced tunnel splitting could be observed with tunnel frequencies between 70 and 80 kHz (Fig. 3d).
The proton signals of ice VII below 17 GPa could be best described with a superposition of two contributions of a Gaussian line of roughly 100 ppm in line width, and an almost purely Lorentzian signal of about 30 ppm width, see Fig. 3. While a hetero- and homonuclear dipole–dipole broadening can explain the Gaussian contribution, the sharp Lorentzian contribution is related to atomic or molecular motion of either single protons or whole-water molecules. However, it has been shown through molecular dynamic (MD) simulations29 and Raman spectroscopy30 that molecular diffusion in ice VII is negligible, leaving only single-protonic motion as a possible reason for such sharp proton signals in ice VII. Considering the geometry of the symmetric double-well potential of the HBHB regime, two possible mechanisms could originate protonic motion: thermally excited site hopping from one potential minimum to the other, or quantum-mechanical tunneling of the protons through the energy barrier. Theoretical analysis31 has shown that proton site hopping in ice VII at room temperature would be energetically unfavorable, leaving quantum-mechanical tunneling as the only possible effect responsible for the observed sharp signals.
Comparing the signal intensities of both Gaussian and Lorentzian contributions at 8 GPa, a ratio of 4:1 of protons localized in one of the two minima of the double-well potential, i.e., Iimmob, and rapidly tunneling protons, i.e., Imob, could be extracted. Using the same deconvolution procedure, the relative signal intensities of both contributions were analysed as a function of pressure and shown in the mid panel of Fig. 4b. For pressures up to 17 GPa, the relative intensity of the Gaussian contribution was found to continuously decrease; whereas, the Lorentzian contribution increased with pressure. At 17 GPa, the 1H-NMR signals exhibit a small splitting of about 18 kHz. This second signal was also de-convoluted using Gaussian and Lorentzian signal contributions. At about 18–22 GPa, a cross-over between Iimmob and Imob could be observed for both signals. At pressures of about 60 GPa, we found a maximum and minimum intensity of the Lorentzian and Gaussian contributions, respectively. At higher pressures, this trend reversed again with a second cross-over expected in a pressure of pressures of 100–120 GPa. This will occur when the majority of protons become localized in the fully symmetrised H-bonds of ice X.
The second proton signal observed at pressures above 17 GPa can be interpreted as result of tunnel splitting, and thus quantum-mechanical tunneling of protons within the hydrogen bond network. Another possible explanation would be due to the observed existence of multi-site disorder in ice VII32, but this can be ruled out considering that known proton chemical shift ranges of hydronium or hydroxyl ions are in the order of 10 ppm33, well within the observed linewidths of the spectra shown in Fig. 3a). Also, small variations in the O–H bond lengths, as inferred by neutron diffraction studies would lead to marginal increases in the Gaussian linewidths as the dipole–dipole interaction is slightly modified. Therefore, the presence of multi-site disorder would not be detected with this method as effects would most likely be below the spectral resolution limit or very small in magnitude.
Another important aspect is the impact of non-hydrostatic pressure conditions on NMR spectra. In general, one might expect the most pronounced effects for quadrupolar nuclei (i.e., I > 1/2), such as the aluminium nucleus 27Al (I = 5/2). It could be shown16, that for these nuclei non-hydrostatic pressure conditions result in a significant line broadening originating from a non-isotropic deformation of the local charge distribution surrounding each quadrupole nucleus. However, I = 1/2 nuclei, such as hydrogen, do not possess a nuclear quadrupole moment which could interact with a potential electric field gradient influenced by non-hydrostatic pressure conditions, thus quadrupolar line broadening effects can be excluded34. Also, an another possible effect mediated through non-hydrostaticity would be a distribution of the diamagnetic shielding of the protons along a pressure gradient. In that case, the proton chemical shifts would vary depending on the respective pressure conditions. In principle, such an effect would lead to line broadenings which are in the order of the known chemical shift ranges of each nucleus. In the case of proton NMR, this would account to line broadening effects of about 10–20 ppm, which is much smaller compared to the observed linewidths of the spectra shown in Figs. 3–5. However, as the effects of non-hydrostaticity on NMR spectra and shifts have not yet been fully characterized in a series of similar compounds, these effects are unlikely to be the cause of the observed signals and shifts of the protons within the hydrogen bonds in ice VII or X.
Low field NMR spectra of Ice X at 97 GPa. a Full 1H-NMR spectrum at a magnetic field of 405 mT, centered around the magnetic (Δm = 1) signal. b High-field side of the 1H-NMR spectra between 125 and 1225 mT. Colored regions indicate the positions of the Δm = 1 signals, as well as tunneling side bands (t.s.b.)
Clough et al.28 argue that in the case of intermediate tunnel frequencies υT of 50–100 kHz, tunnel side bands, can be observed in high-field NMR. The intensity of these side bands fall off as υT−2, thus only relatively small values of υT can be observed. Extractable tunnel splittings Δt from spectra shown in Fig. 3a) begin to appear at 17 GPa, and have been found to increase up to 75 kHz (Fig. 3d). Clearly, the resolution of this method is limited by the FWHM line width of the main NMR signal, as a splitting of ΔT < 15 kHz would strongly overlap with the allowed magnetic (Δm = 1) signal. Remarkably, υT does not change significantly between 20 and 90 GPa, in a pressure region where quantum-mechanical tunneling is believed to be absent due to the unimodal probability distribution of the protons localized in symmetric hydrogen bonds31. A possible reason for the constancy of υT over such a broad pressure range could be that several tunneling modes are present at significantly higher frequencies, remaining undetectable with high-field NMR. In this case, the observed ΔT = 75 kHz (at pressures above 20 GPa) could be due to the lowest observable tunneling mode which corresponds to very small energy barriers.
Low magnetic field data
In order to elucidate this issue, additional measurements at low magnetic fields have been conducted. Figure 5 shows several 1H-NMR spectra of ice X at 97 GPa at magnetic fields ranging from 125 to 1225 mT. As can be seen, in contrast to the high field spectra shown in Fig. 3a), the magnetic Δm = 1 signal is flanked on both sides by tunnel side bands with tunnel splittings of about 40 kHz. The reason for the non-detectability of the down-field side band at 9 T is most likely due to significant broadenings and distortions of the forbidden transitions at these fields. Obviously, the general spectral positions of these inner tunnel side bands do not change relative to the magnetic signals, even after sweeping over a whole order of magnitude in B0. This zero field splitting can be considered a further evidence for pronounced proton tunneling. Strikingly, higher order tunneling side bands at about 200 and 560 kHz could also be observed, which indicates that the observed tunnel splitting at high field is indeed due to a lower lying tunneling mode.
Discussion
The observed evolution of both Iimmob and Imob is consistent with the predicted evolution31 of the energy barrier of the double-well potential of the H-bond (Fig. 1b), i.e., increasing pressure reduces height and width of the barrier, increasing the probability of the protons to tunnel between the energy minima of the double-well potential. Thus, the relative intensity of signal due to localized protons declines; whereas, the intensity of signal originating from quantum-mechanical tunneling increases with decreasing oxygen–oxygen distances. At about 60 GPa, the majority of the protons participate in collective tunneling motion as Imob reaches its maximum. At pressures above 60–70 GPa, the tunnel probability declines as height and width of the energy barrier approach zero, thus localizing the protons with pressure, leading to an increase in Iimmob.
The upper panel of Fig. 4b shows chemical shift values δ as a function of pressure. Two distinct transitions are evident at pressures of 20 and 75 GPa, respectively. While the pressure of the second transition is in very good agreement with the proposed transition for a symmetric hydrogen bond network in ice X, the first transition has not been observed with other methods and can be associated with a transition from the HBHB regime to the LBHB regime35. Thus, our NMR shift data indicates that a Low-Barrier Hydrogen Bond exists in ice VII not only at significantly lower pressures, but also in a pressure range where NQEs should be absent.
Our study indicates a much more complex scenario of the interplay between pressure-induced NQEs and the hydrogen bond symmetrisation in high-pressure ices than what could be anticipated from other experimental work in this field. In fact, up to this point no clear experimental distinction between the HBHB and LBHB regimes could be defined, whereas theoretical estimates vary often by tens of GPa between 30 and 60 GPa. Moreover, it could be shown that the LBHB–>SHB transition is indeed not a continuous one but exhibits a clear transition pressure of about 75 GPa.
Methods
Double stage Lenz lenz (DSLL) resonator preparation
The resonators were built in the following way. After pre-indenting a 200 µm rhenium gasket to about 15–20 µm, a thin layer of copper (1–2 µm) was deposited on the diamonds. The shape of the LLs was cut out from the copper layer using a focused ion beam (Scios Dual beam from FEI), Fig. 2b. As a result, the first stage LL typically runs from the outer rim of the diamonds pavilion toward close to the rim of the diamonds culet, with a thin 15 µm slit running all along the 1 mm pavilion (Fig. 2b). The second stage LL, is typically placed on the culet face having about 230 µm outer diameter and 80 µm inner diameter which closely follows the geometry of the gasket hole.
To ensure electrical insulation between both LLs and the metallic gasket, a 1 µm layer of Al2O3 was deposited on the gaskets.
Preparation of the excitation coil
The excitation coil was made from 100 µm thick, PTFE insulated copper wire, consisting of 4 turns per coil, having a diameter of about 4 mm. After loading and closing of the cells, both coils were connected accordingly to form a Helmholtz coil pair yielding ~300 nH inductance. The overall resistance at 400 MHz was found to be about 1.5 Ω, thus the resonators quality should be 500. Using a spectrum analyzer, we found a quality factor of 530 in good agreement with the estimate.
Test measurements at ambient pressure
First test measurements at ambient conditions, see 1H-NMR spectrum at 1 bar in Fig. 2d, demonstrates the excellent sensitivity of the DSLL setup. In order to prove that the recorded signals stem from the sample and not from spurious signals, additional measurements on an empty cell as well as on a recovered, opened and cleaned cell have been conducted, Fig. 2d. No significant proton NMR signals could be acquired in these cases.
Pressure calibration
Pressure was measured using the first derivative of the pressure dependent shift of the first order Raman spectra of the diamond collected at the diamond edge in the center of the culet36,37, Fig. 2c shows two typical Raman spectra from two different DACs at pressures of 75 GPa and 97 GPa.
High field NMR
High field NMR measurements have been conducted at a magnetic field of 9.03 T corresponding to a resonance frequency of about 400 MHz. Proton signals were collected using a π/2–π/2 solid echo pulse sequence with pulse separations of 50 µs in order to acquire the full spin echo. Typical r.f. pulses of 2 µs at 10 W average pulse power were used. Pressure dependent NMR shift measurements were calibrated against water at ambient conditions placed in a similar setup in a DAC, Fig. 2d, to account for intrinsic frequency shifts originating from the pressure cell assembly. The shift measurements were repeated with four different DACs at overlapping pressure ranges to ensure high reproducibility of the found effects.
Low field NMR
Low field NMR measurements have been conducted in a DAC pressurized to 97 GPa, using a tunable electro-magnet of maximum 1.4 T field strength. The preparation procedure of this cell closely followed the above mentioned description. Proton signals have been accumulated between 125 and 1225 mT, using a single r.f. pulse of 1 µs length at an average pulse power of 35 W.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Sotin, C., Grasset, O. & Mocquet, A. Mass–radius curve for extrasolar Earth-like planets and ocean planets. ICARUS 191, 337–351 (2007).
Journaux, B. et al. Salt partitioning between water and high-pressure ices. Implication for the dynamics and habitability of icy moons and water-rich planetary bodies. Earth Planet. Sci. Lett. 463, 36–47 (2017).
Grasset, O. et al. JUpiter ICy moons Explorer (JUICE): an ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 78, 1–21 (2013).
Phillips, C. B. & Pappalardo, R. T. Europa clipper mission concept: exploring Jupiter’s Ocean Moon. Eos, Trans. Am. Geophys. Union 95, 165–167 (2014).
Kollman, P. A. & Allen, L. C. The theory of the hydrogen bond. Chem. Rev. 72, 283–303 (1972).
Petrenko, V. F. & Whitworth, R. W. Physics of Ice. 259–292 https://doi.org/10.1093/acprof:oso/9780198518945.001.0001 (Oxford University Press, Oxford, 2002).
Benoit, M., Marx, D. & Parrinello, M. Tunnelling and zero-point motion in high-pressure ice. Nature 392, 258–261 (1998).
Holzapfel, W. B. On the symmetry of the hydrogen bonds in ice VII. J. Chem. Phys. 56, 712–715 (1972).
Marx, D. Proton transfer 200 years after Von Grotthuss: Insights from ab initio simulations. Chemphyschem 7, 1849–1870 (2006).
Loubeyre, P., LeToullec, R., Wolanin, E., Hanfland, M. & Hausermann, D. Modulated phases and proton centring in ice observed by X-ray diffraction up to 170 GPa. Nature 397, 503–506 (1999).
Stojilovic, N. Why can’t we see hydrogen in X-ray photoelectron spectroscopy? J. Chem. Educ. 89, 1331–1332 (2012).
Somayazulu, M. et al. In situ high-pressure x-ray diffraction study of H2O ice VII. J. Chem. Phys. 128, 64510 (2008).
Wolanin, E. et al. Equation of state of ice VII up to 106 GPa. Phys. Rev. B - Condens. Matter Mater. Phys. 56, 5781–5785 (1997).
Zha, C.-S., Tse, J. S. & Bassett, W. A. New Raman measurements for H2O ice VII in the range of 300 cm−1 to 4000 cm−1 at pressures up to 120 GPa. J. Chem. Phys. 145, 124315 (2016).
Guthrie, M. et al. Neutron diffraction observations of interstitial protons in dense ice. Proc. Natl Acad. Sci. USA 110, 10552–10556 (2013).
Meier, T. At its extremes: NMR at Giga -pascal pressures. Annu. Rep. NMR Spectrosc. 94, 1–74 (2017).
Meier, T. Journey to the Centre of the Earth: Jule Vernes’ dream in the laboratory from an NMR perspective. Prog. Nucl. Magn. Reson. Spectrosc. 106-107, 26–36 (2018).
Meier, T. et al. Magnetic flux tailoring through Lenz lenses for ultrasmall samples: a new pathway to high-pressure nuclear magnetic resonance. Sci. Adv. 3, eaao5242 (2017).
Meier, T. et al. NMR at pressures up to 90 GPa. J. Magn. Reson. 292, 44–47 (2018).
Spengler, N., While, P. T., Meissner, M. V., Wallrabe, U. & Korvink, J. G. Magnetic Lenz lenses improve the limit-of-detection in nuclear magnetic resonance. PLoS ONE 12, e0182779 (2017).
Pintar, M. M. in Introductory Essays. NMR 13 Basic Principles and Progress 13, https://doi.org/10.1007/978-3-642-66395-6_10, 125–136 (Springer, Berlin, Heidelberg, 1976).
Frey, P. A., Whitt, S. A. & Tobin, J. B. A low-barrier hydrogen bond in the catalytic triad of serine proteases. Science 264, 1927–1930 (1994).
Clough, S., Heidemann, A., Horsewill, A. J., Lewis, J. D. & Paley, M. N. J. The correlation of methyl tunnelling and thermally activated reorientation. J. Phys. C. Solid State Phys. 14, L525–L529 (1981).
Apaydin, F. & Clough, S. Nuclear magnetic resonance line shapes of methyl groups undergoing tunnelling rotation. J. Phys. C. Solid State Phys. 1, 313 (1968).
Clough, S., Hill, J. & Poldy, F. Tunnelling sidebands of methyl group hyperfine structure. J. Phys. C. Solid State Phys. 5, 1739–1744 (1972).
Johnson, C. S. Tunneling effects in the NMR spectrum of a spin in a symmetrical double-well potential. J. Magn. Reson. 73, 545–547 (1987).
Johnston, E. R. Fictitious spin description of tunneling effects in NMR. J. Magn. Reson. 79, 143–147 (1988).
Clough, S., Horsewill, A. J., McDonald, P. J. & Zelaya, F. O. Molecular tunneling measured by dipole-dipole – driven nuclear magnetic resonance. Phys. Rev. Lett. 55, 1794–1796 (1985).
Ghesquière, P. et al. Diffusion of molecules in the bulk of a low density amorphous ice from molecular dynamics simulations. Phys. Chem. Chem. Phys. 17, 11455–11468 (2015).
Noguchi, N. & Okuchi, T. Self-diffusion of protons in H2O ice VII at high pressures: Anomaly around 10 GPa. J. Chem. Phys. 144, 234503 (2016).
Lin, L., Morrone, J. A. & Car, R. Correlated tunneling in hydrogen bonds. J. Stat. Phys. 145, 365–384 (2011).
Nelmes, R. J. et al. Multisite disordered structure of ice VII to 20 GPa. Phys. Rev. Lett. 81, 2719–2722 (1998).
Kresge, A. J. Proton NMR chemical shifts of hydronium and hydroxyl ions. J. Chem. Phys. 39, 1360–1361 (1963).
Levitt, M. H. Spin Dynamics: Basics of Nuclear Magnetic Resonance 2nd Edn (John Wiley & Sons, Chichester, 2000).
Garcia-Viloca, M., Gelabert, R., González-Lafont, A., Moreno, M. & Lluch, J. M. Is an extremely low-field proton signal in the NMR spectrum conclusive evidence for a low-barrier hydrogen bond? J. Phys. Chem. A 101, 8727–8733 (1997).
Akahama, Y. & Kawamura, H. High-pressure Raman spectroscopy of diamond anvils to 250 GPa: method for pressure determination in the multimegabar pressure range. J. Appl. Phys. 96, 3748 (2004).
Akahama, Y. & Kawamura, H. Pressure calibration of diamond anvil Raman gauge to 310GPa. J. Appl. Phys. 100, 043516 (2006).
Acknowledgements
We would like to thank Professor Ernst Rössler and Thomas Körber for provision of the 9.3 T NMR system. Furthermore, we thank Nobuyoshi Miyajima and Katharina Marquardt for provision of the FIB, and help with the ion milling (grant number: INST 90/315-1 FUGG). The authors T.M. and L.D., were funded by the Bavarian Geoinstitute through the Free State of Bavaria. S.P. and S.K. were financed by the german research society (PE 2334/1-1 and DU-393/13-1). We also acknowledge the help of Prof. Natalia Dubrovinskaia for provision of the low-field NMR equipment.
Author information
Authors and Affiliations
Contributions
T.M. designed and built the NMR resonator, prepared DACs and conducted experiments. S.P. and S.K. performed the FIB based shaping of the Lenz lenses. T.M., S.P. and L.D. analysed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meier, T., Petitgirard, S., Khandarkhaeva, S. et al. Observation of nuclear quantum effects and hydrogen bond symmetrisation in high pressure ice. Nat Commun 9, 2766 (2018). https://doi.org/10.1038/s41467-018-05164-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05164-x
This article is cited by
-
Hydrogen bond symmetrisation in D2O ice observed by neutron diffraction
Nature Communications (2024)
-
Trace element detection in anhydrous minerals by micro-scale quantitative nuclear magnetic resonance spectroscopy
Nature Communications (2024)
-
Rich proton dynamics and phase behaviours of nanoconfined ices
Nature Physics (2024)
-
The role of hydrogen bonds in hydrous minerals stable at lower mantle pressure conditions
Progress in Earth and Planetary Science (2022)
-
Structural independence of hydrogen-bond symmetrisation dynamics at extreme pressure conditions
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.