Abstract
Two-dimensional electron systems have attracted attention as thermoelectric materials, which can directly convert waste heat into electricity. It has been theoretically predicted that thermoelectric power factor can be largely enhanced when the two-dimensional electron layer is far narrower than the de Broglie wavelength. Although many studies have been made, the effectiveness has not been experimentally clarified thus far. Here we experimentally clarify that an enhanced two-dimensionality is efficient to enhance thermoelectric power factor. We fabricated superlattices of [N unit cell SrTi1−xNb x O3|11 unit cell SrTiO3]10—there are two different de Broglie wavelength in the SrTi1−xNb x O3 system. The maximum power factor of the superlattice composed of the longer de Broglie wavelength SrTi1−xNb x O3 exceeded ∼5 mW m−1 K−2, which doubles the value of optimized bulk SrTi1−xNb x O3. The present approach—use of longer de Broglie wavelength—is epoch-making and is fruitful to design good thermoelectric materials showing high power factor.
Similar content being viewed by others
Introduction
Currently, more than 60% of the energy produced from fossil fuels is lost as waste heat. Thermoelectric energy conversion, which is the process where waste heat is transformed into electricity by the Seebeck effect, is attracting attention as a potential energy harvesting technology1,2,3,4. The performance of thermoelectric materials is generally evaluated in terms of a dimensionless figure of merit,
where Z is the figure of merit, T is the absolute temperature, S is the thermopower (Seebeck coefficient), σ is the electrical conductivity, and κ is the sum of the electronic (κele) and lattice thermal conductivities (κlat) of a thermoelectric material.
There are two strategies to improve ZT of a thermoelectric material. One is to reduce κlat. Recently, state-of-the-art nanostructuring techniques have reduced κlat significantly through phonon scattering by nanosized structural defects5,6,7,8. Such techniques have realized high-performance thermoelectric materials with a large ZT of 1.5−2. The other strategy is an enhancement of the product S2∙σ, which is called power factor (PF). However, it is extremely difficult to enhance PF due to the trade-off relationship between S and the carrier concentration (n). Therefore, PF has a local maximum value in three-dimensional (3D) bulk systems.
In a two-dimensional electron system (2DES) such as metal/insulator superlattices, electron carriers are confined within a thin layer (thickness thinner than the de Broglie wavelength, λD). 2DES is an efficient strategy to achieve an enhanced PF. The effectiveness of 2DES was theoretically predicted by Hicks and Dresselhaus9; 2DES in extremely narrow layers exhibits an enhanced S without reducing σ because the density of states (DOS) near the bottom of the conduction band increases as the 2DES layer thickness decreases. These layers are narrower than the λD,
where h, m*, and kB are Planck’s constant, effective mass of conductive electron or hole, and Boltzmann constant, respectively9,10,11,12,13.
Many experimental studies have been made to clarify the effectiveness of 2DES to enhance PF using PbTe/Pb1−xEu x Te multiple-quantum-well10, electron-doped SrTiO3-based superlattices14,15, SiGe-based superlattices16,17, and Bi2Te3-based superlattices18. These 2DES layers showed enhanced S. However, total enhancement of PF was very small because of the insulator layer thickness. Thus, the effectiveness of 2DES has not been experimentally clarified thus far.
Here we experimentally clarify that an enhanced two-dimensionality is efficient to improve thermoelectric PF. We fabricated superlattices of [N unit cell SrTi1−xNb x O3|11 unit cell SrTiO3]10—there are two different de Broglie wavelength in the SrTi1−xNb x O3 system. The maximum PF of the superlattice composed of the longer de Broglie wavelength SrTi1−xNb x O3 exceeded ~5 mW m−1 K−2, which doubles the value of optimized bulk SrTi1−xNb x O3. The present approach—use of longer de Broglie wavelength—is epoch-making and is fruitful to design good thermoelectric materials showing high PF.
Results
Hypothesis
In order to enhance total PF of 2DES, two-dimensionality should be enhanced. Use of longer λD should be effective if the electron carriers are confined within a defined thickness layer (Fig. 1). Very recently, we observed a steep decrease in m*/me at x ~ 0.3 in SrTiO3–SrNbO3 solid solution system, SrTi1−xNb x O3 (x is ranging from 0.05 to 0.9; Fig. 2)19. The ratio x of SrTi1−xNb x O3 can be divided into two regions, region A (x is <0.3) and region B (x is >0.3). The origin of the two regions is most likely due to the difference in the overlap population between the Ti 3d and Nb 4d orbitals (rTi3d is 48.9 pm and rNb4d is 74.7 pm)20. We calculated λD values of SrTi1−xNb x O3 using the Eq. (2). The λD value in region B is ~5.3 nm, which is 27% longer than that in region A (~4.1 nm). One can expect that S-enhancement factor in region B is much higher than that in region A because of higher two-dimensionality. Therefore, we hypothesized that SrTi1−xNb x O3-based 2DES can be used to clarify the effectiveness of 2DES to enhance PF experimentally.
Thermoelectric effect of a 2D electron system. a Schematic illustration of thermoelectric Seebeck effect in a 2DES. A thermoelectric power output (S·ΔT·I) can be obtained when ΔT is introduced. b The hypothesis that a 2DES with longer de Broglie wavelength (λD) shows a larger enhanced factor of thermopower
SrTiO3–SrNbO3 solid solution: a model system having two different λD. x-dependent effective mass (m*/me, white symbols) and λD (gray symbols) for SrTi1 − xNb x O3 solid solutions. m*/me exerts a decreasing tendency with x, resulting in an increased λD. Sharp changes in both m*/me and λD are detected around x = 0.3 due to the conduction band transition from Ti 3d to Nb 4d. The properties of SrTi1 − xNb x O3 solid solutions can be divided into two regions based on the conduction bands (Ti 3d → region A and Nb 4d → region B). Inset: schematic illustrations of conduction electrons at regions A and B. At region B, λD is ∼5.3 nm, while it is ∼4.1 nm at region A
We fabricated [N uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices (N is ranging from 1 to 12, x is ranging from 0.2 to 0.9) by a pulsed laser deposition (PLD) technique on insulating (001) LaAlO3 (pseudo-cubic perovskite, the lattice parameter, a is 3.79 Å) single-crystal substrates using dense ceramic disks of a SrTiO3–SrNbO3 mixture and SrTiO3 single crystal as the targets. The thicknesses of different layers were monitored in situ using the intensity oscillation of the reflection high-energy electron diffraction (RHEED) spots. (See Experimental Section.) High-resolution X-ray diffraction (XRD) measurements revealed that the resultant superlattices were heteroepitaxially grown on (001) LaAlO3 with cube-on-cube epitaxial relationship with superlattice structure. Atomically smooth surfaces with stepped and terraced structure were observed by an atomic force microscopy (AFM).
Microstructure and electronic structure
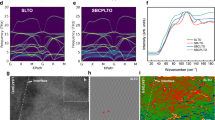
Figure 3a summarizes the atomic arrangements of the [1 uc SrTi0.4Nb0.6O3|11 uc SrTiO3]10 superlattice. Rather bright bands are observed near each SrTi0.4Nb0.6O3 layer in the Cs-corrected high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image. In the magnified image, the #4 atom in the B-site column is brighter than the nearby atoms. However, there is no obvious difference in the A-site column, indicating Nb substitution occurs for the #4 atom in the B-site column. The electron energy loss spectroscopy signal of #4 is broader than that of the nearby atoms, implying the coexistence of Ti4+/Ti3+ in the SrTi0.4Nb0.6O3 layers21. Therefore, in our superlattice fabrication, Nb ions are successfully confined into 1 uc of SrTi0.4Nb0.6O3 layers22.
Experimental and theoretical analyses of the 2DES. a Cross-sectional HAADF-STEM image of the [1 uc SrTi0.4Nb0.6O3|11 uc SrTiO3]10 superlattice. Layer stacking sequence is also shown. Rather bright bands are seen near each SrTi0.4Nb0.6O3 layer. In the magnified image, the #4 atom in the B-site column is brighter than the nearby atoms, whereas no obvious difference is observed in the A-site column. EELS spectrum of #4 is broader than that of nearby atoms, indicating the coexistence of Ti4+/Ti3+ in the SrTi0.4Nb0.6O3 layers. b The calculated partial DOS of Nb 4d or Ti 3d in the [1 uc SrNbO3|10 uc SrTiO3] superlattice. The Fermi energy (EF) is located on the higher-energy side of the conduction band minimum for the first and second nearest neighbor (Ti first NN and Ti second NN). SrTiO3 layers together with 1 uc SrNbO3 layer (Nb) suggest that the electron carriers can seep from the SrTi1 − xNb x O3 layers into the SrTiO3 layers
In order to clarify the 2DES formation, the electronic band structures of the [1 uc SrNbO3|10 uc SrTiO3] superlattices were calculated based on the projector-augmented wave (PAW) method (Fig. 3b). The EF is located on the higher-energy side of the conduction band minimum for the first and second nearest-neighbor SrTiO3 layers (Ti first NN and Ti second NN) together with the 1 uc SrNbO3 layer (Nb). The electron carriers can seep from the SrNbO3 layers into the SrTiO3 layer. Delugas et al.23 have also predicted theoretically that for lower Nb substituted samples, it is much easier for the electrons, especially in the d xz and d yz bands, to spread out to the neighboring SrTiO3 layers, reducing the two-dimensionality. However, as the Nb content increases, the minimum thickness of the barrier layer may be reduced to 5 uc in the SrNbO3 case. There is no doubt that the electron diffusion cannot be removed thoroughly in superlattice structure, but diffusion effects can be effectively suppressed by the high Nb substitution. From the band calculation, 2DES in our work is mainly confined to the 1 uc SrTi1−xNb x O3 layers and should contribute to the S enhancement.
In order to further confirm the superlattice structure, we measured the κ of the [1 uc SrTi0.4Nb0.6O3|11 uc SrTiO3]10 superlattice along the cross-plane direction by time-domain thermal reflectance (TDTR) method. The total κ could be suppressed to ~3.3 W m−1 K−1, similar to the minimum value of CaTiO3/SrTiO3-based superlattices (κ ~ 3.2 W m−1 K−1) reported by Ravichandran et al.24. From these results, we judged that our [N uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices (N is ranging from 1 to 12, x is ranging from 0.2 to 0.9) are appropriate for us to clarify the effectiveness of 2DES to enhance PF.
Thermoelectric properties
The electrical conductivity (σ), carrier concentration (n), and Hall mobility (μHall) of the superlattices were measured at room temperature by a conventional d.c. four-probe method with a van der Pauw geometry. S was measured at room temperature by creating a temperature difference (ΔT) of ~4 K across the film using two Peltier devices. Figure 4a summarizes the n-dependent S of [N uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices (N is ranging from 1 to 12, x = 0.2, 0.3, and 0.8) along with bulk (~100-nm-thick SrTi1−xNb x O3 films, x = 0.2, 0.3, and 0.8, respectively) values for comparison. The bulk S for x = 0.2 was −143 μV K−1, x = 0.3 was −73 μV K−1, and x = 0.8 was −19 μV K−1. The n value was measured based on the total thickness of the 2DES, which includes the insulating SrTiO3 layers. All the 2DES samples show enhanced thermopower (−S) with a reduced N. Compared to the bulk samples at a similar n, a much higher −S is observed in superlattices as N is reduced below 3 uc.
Two-dimensionality of 2DES: a key to enhance thermopower. a Plots of thermopower of the 2DESs, [N uc SrTi1 − xNb x O3|11 uc SrTiO3]10 superlattices (x = 0.2, 0.3, and 0.8), versus the carrier concentration (n). Compared to bulk values (gray squares), all the 2DESs show an enhanced −S as N is reduced under 3 uc. b Enhancement factors in –S (S2DES/SBulk) for three sets of 2DESs. For x = 0.2 and 0.3 2DESs, the highest S2DES/SBulk values are obtained at N = 1, which are 4 and 5, respectively, while that of x = 0.8 can reach 10
To confirm the increasing two-dimensionality with x, the S-enhancement factors (S2DES/SBulk) were plotted versus the N values (Fig. 4b). For 2DES with x = 0.2 and 0.3, the highest S2DES/SBulk values are around 4 and 5, respectively, whereas that for the x = 0.8 counterpart is ~10. As hypothesized, the enhanced S2DES/SBulk should stem from the increasing λD with x. In our experiment, S2DES/SBulk for the x = 0.2 and 0.3 2DESs are saturated around 11 uc, which is consistent with λD in region A (~4.2 nm indicated by dashed line λDA). As λD increases in region B, the saturation position for the x = 0.8 2DES has a thickness larger than the λD (~5.2 nm indicated by dashed line λDB). As a result, a significantly enhanced two-dimensionality is achieved in the x > 0.3 region B, which fits well with our hypothesis and suggests that region B has the potential to further enhance the thermoelectric PF.
Based on the conclusions above, we have enhanced the thermoelectric PF in [1 uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices by adjusting x between 0.2 and 0.9. Figure 5 summarizes the n dependences of the thermoelectric properties of [1 uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices at room temperature along with the reported bulk values for comparison19. Following the bulk values, σ increases almost linearly with n (Fig. 5a), indicating that n dominates σ. In the SrTi1−xNb x O3 system, carriers are mostly due to Nb substitution. The high n also induces a highly Nb substituted region with a superiority in σ. However, σ for the superlattices remains lower than the bulk value due to the coexistence of 11 uc SrTiO3 insulating layers.
Double enhancement of the thermoelectric power factor in a 2DES. Carrier concentration dependences of a electrical conductivity (σ), b Hall mobility (μHall), c thermopower (−S), and d power factor [PF (S2·σ)] of [1 uc SrTi1 − xNb x O3 | 11 uc SrTiO3]10 2DESs (x is ranging from 0.2 to 0.9) at room temperature. Similar to the trends in the bulk values, σ increases almost linearly with n. μHall for lower x samples (x ≤ 0.5) fluctuates around 3–5 cm2 V−1 s−1, while that for higher x ones (x ≥ 0.6) is ~6 cm2 V−1 s−1. Slope of –S versus log n for bulk SrTi1 − xNb x O3 is –198 μV K−1, which is ∼1.5 times lower than –300 μV K−1 for the 2DESs. Double enhancement of PF is seen in x = 0.6 (5.1 mW m−1 K−2 at n ∼ 8 × 1020 cm−3). Since the PF values are scattered due to the rather large distribution of μHall (3–6 cm2 V−1 s−1), we calculated PFs using the relationship between S and n (c) at constant μHall (6 cm2 V−1 s−1). The optimized PF of the 2DES should be ~5 mW m−1 K−2 at n ∼ 8 × 1020 cm−3, which doubles that of bulk SrTi1 − xNb x O3 (PF ∼ 2.5 mW m−1 K−2 at n ∼ 2 × 1021 cm−3)
μHall for lower x of 2DESs (x ≤ 0.5) fluctuates around 3–5 cm2 V−1 s−1, while for higher x 2DESs (x ≥ 0.6) values are ~6 cm2 V−1 s−1 (Fig. 5b). Usually, μHall is controlled by the conduction band of materials along with the effects of crystal defects such as impurities and grain boundaries. In the bulk samples, μHall sharply increases due to the transition of the conduction band from Ti 3d to Nb 4d as x increases into the highly Nb substituted region19. This pattern is also observed in the superlattice counterparts. A higher μHall (≥6 cm2 V−1 s−1) is observed in samples with x ≥ 0.6 than that for x ≤ 0.5 (3–5 cm2 V−1 s−1). Compared to the bulk samples, all the superlattices exert a much lower μHall, which may result from an insufficient crystal quality or electron diffusion into the pure SrTiO3 barrier layers. Regardless, a conduction band transition from Ti 3d to Nb 4d is recognized in our superlattice systems. Due to the high overlapping population of the Nb 4d orbital, a superior electron transport property is realized in higher x of 2DES.
Figure 5c plots the S values for all the superlattices versus n along with the reported bulk values19. The solid line depicts the overall tendency. In the diagram, the superlattices have a significantly enhanced –S compared to bulk samples at similar n values. As indicated by the solid lines, the experimental points for 2DES and bulk show different slopes of –300 and –200 μV K−1 per decade, respectively. The relationship between –S and neff can be expressed by Eq. (3)
where kB is the Boltzmann constant and e is an electron charge. A and B are the parameters that depend on the type of materials and their electronic band structures. Bulk shows a 3D electronic band structure with a parabolic shaped DOS near EF, where the A value = 1 and the slope reflects a constant value of −kB/e·ln10 (−198 μV K−1). On the other hand, the slope of the 2DESs may reach −300 μV K−1 per decade, indicating that the A value = 1.5. Therefore, the 2DESs work well to enhance the S even for the whole superlattice, including SrTiO3 insulating layers.
Finally, we calculated PF of the [1 uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices (x is ranging from 0.2 to 0.9) using the observed S and σ values (Fig. 5d). PF is doubly enhanced for x = 0.6 (5.1 mW m−1 K−2 at n ~ 8 × 1020 cm−3). Since the PF values are scattered due to the rather large distribution of μHall (3–6 cm2 V−1 s−1), we calculated PFs using the relationship between S and n (c) at constant μHall (6 cm2 V−1 s−1). The optimized PF of the 2DES should be ~5 mW m−1 K−2 at n ~ 8 × 1020 cm−3, which doubles that of bulk SrTi1−xNb x O3 (PF ~ 2.5 mW m−1 K−2 at n ~ 2 × 1021 cm−3).
Discussion
The present 2DES, [1 uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices (x is ranging from 0.2 to 0.9), has several merits to enhance PF as compared with other 2DESs such as PbTe/Pb1−xEu x Te multiple-quantum-well10, SiGe-based superlattices16,17, and Bi2Te3-based superlattices18, which are already commercialized thermoelectric materials. This is because SrTi1−xNb x O3 can be deposited with 1 uc layer accuracy by PLD. Therefore, we can easily reduce the 2DEG thickness to ~0.4 nm (1 uc layer). Further, there are two different λD in SrTi1−xNb x O3; ~4.1 nm in the low conducting region and ~5.3 nm in the high conducting region. For enhancing PF, both S and σ play important roles. The present research implies that high conducting region is effective to enhance the thermoelectric PF in the 2DES. Herein highly Nb substitution are revealed to have the coexistence of both a high electron transport (high n and μHall) and a high two-dimensionality (large λD).
In summary, we have experimentally clarified that an enhanced two-dimensionality of 2DES is efficient to improve thermoelectric PF. We measured the thermoelectric properties of 2DESs [N uc SrTi1−xNb x O3|11 uc SrTiO3]10 superlattices (N is ranging from 1 to 12, x is ranging from 0.2 to 0.9) because there are two different λD in this 2DES (x > 0.3: λD~5.3 nm; x < 0.3: λD~4.1 nm). The S-enhancement factor S2DES/SBulk of the 2DES (N = 1) for x > 0.3 were ~10, whereas those for x < 0.3 were 4–5. Maximum PF of the 2DES (N = 1, x = 0.6) exceeded ~5 mW m−1 K−2, which doubles the value of optimized bulk SrTi1−xNb x O3 (PF ~ 2.5 mW m−1 K−2). The present 2DES approach—use of longer λD—is epoch-making and is fruitful to design good thermoelectric materials showing high PF.
Methods
Fabrication and analyses of the 2DESs
A series of superlattices with the chemical formula of [N uc SrTi1−xNb x O3 | 11 uc SrTiO3]10 (N is ranging from 1 to 12, x is ranging from 0.2 to 0.9) were fabricated by a PLD technique using dense ceramic disks of a SrTiO3–SrNbO3 mixture and a SrTiO3 single crystal as the targets. The substrate was insulating (001) LaAlO3 (pseudo-cubic perovskite, lattice parameter, a is 3.79 Å, the surface area: 1 cm × 1 cm). The growth conditions were precisely controlled; the substrate temperature was 900 °C, the oxygen pressure was ~10−4 Pa, and the laser fluence was ~1.2 J cm−2 per pulse. The thicknesses of different layers were monitored in situ using the intensity oscillation of the RHEED spots. Details of our PLD growth process of the superlattices are reported elsewhere14,25.
Crystallographic analyses of the resultant superlattices were performed by XRD (Cu Kα1, ATX-G, Rigaku Co.), AFM (Nanocute, Hitachi Hi-Tech), and STEM (200 keV, JEM-ARM 200CF, JEOL Co. Ltd). TEM samples were fabricated using a cryo ion slicer (IB-09060CIS, JEOL Co. Ltd). HAADF images were taken with the detection angle of 68–280 mrad. Electron energy loss spectra were acquired in STEM mode with the energy resolution of 0.8 eV.
Measurements of the thermoelectric properties of the 2DESs
Electrical conductivity (σ), carrier concentration (n), and Hall mobility (μHall) were measured at room temperature by a conventional d.c. four-probe method with a van der Pauw geometry. S was measured at room temperature by creating a temperature difference (ΔT) of ~4 K across the film using two Peltier devices. (Two small thermocouples were used to monitor the actual temperatures of each end of a superlattice.) The thermo-electromotive force (ΔV) and ΔT were measured simultaneously, and the S values were obtained from the slope of the ΔV–ΔT plots (the correlation coefficient: >0.9999).
Cross-plane thermal conductivity (κ) was measured by TDTR (Picotherm Co.) method. Mode-locked fiber pulse lasers with 1550 and 775 nm wavelengths were used for heating and measuring, respectively. Both lasers are with the repetition frequency of 20 MHz and pulse duration of 0.4 ps. Before measurement, Mo film with a thickness of 100 nm was first deposited on the surface of the sample as the transducer. During measurement, time-dependent transient thermoreflectance phase signal of Mo transducer was measured, from which κ was further simulated. Time-domain thermoreflectance was measured based on amplified laser systems (5 kHz and ~200 fs centered at 1030 nm). Degenerate pump and probe photons were separated by the cross polarization, and a polarizing filter was employed before the lock-in detection. A mechanical delay stage was used for time scan up to 1.5 ns. Pump to probe intensity ratio was >15, and the size ratio was around 6.
Energy band calculation of the 2DES
Band structure for the [1 uc SrNbO3|10 uc SrTiO3] superlattice was calculated based on the PAW method26, as implemented in the VASP code27,28. We adopted the Heyd–Scuseria–Ernzerhof hybrid functionals29,30,31 and a plane-wave cutoff energy of 550 eV. 6 × 6 × 6 and 6 × 6 × 2 k-point meshes were employed in the total-energy evaluations and geometry optimization for the perovskite unit cells of SrTiO3 and the superlattice cell, respectively. The in-plane lattice constant of the superlattice cell was fixed at the optimized value of SrTiO3 while the out-of-plane lattice constant and the atomic coordinates were fully relaxed.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
DiSalvo, F. J. Thermoelectric cooling and power generation. Science 285, 703–706 (1999).
Snyder, G. J. & Toberer, E. S. Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008).
Vining, C. B. An inconvenient truth about thermoelectrics. Nat. Mater. 8, 83–85 (2009).
Zhang, Q. H. et al. Thermoelectric devices for power generation: recent progress and future challenges. Adv. Eng. Mater. 18, 194–213 (2016).
Hsu, K. F. et al. Cubic AgPb m SbTe2+m: bulk thermoelectric materials with high figure of merit. Science 303, 818–821 (2004).
Poudel, B. et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 320, 634–638 (2008).
Il Kim, S. et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 348, 109–114 (2015).
Biswas, K. et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 489, 414–418 (2012).
Hicks, L. D. & Dresselhaus, M. S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 47, 12727–12731 (1993).
Hicks, L. D., Harman, T. C., Sun, X. & Dresselhaus, M. S. Experimental study of the effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 53, 10493–10496 (1996).
Hung, N. T., Hasdeo, E. H., Nugraha, A. R. T., Dresselhaus, M. S. & Saito, R. Quantum effects in the thermoelectric power factor of low-dimensional semiconductors. Phys. Rev. Lett. 117, 036602 (2016).
Mao, J., Liu, Z. H. & Ren, Z. F. Size effect in thermoelectric materials. npj Quantum Mater. 1, 16028 (2016).
Hung, N. T., Nugraha, A. R. T. & Saito, R. Two-dimensional InSe as a potential thermoelectric material. Appl. Phys. Lett. 111, 092107 (2017).
Ohta, H. et al. Giant thermoelectric Seebeck coefficient of two-dimensional electron gas in SrTiO3. Nat. Mater. 6, 129–134 (2007).
Choi, W. S., Ohta, H. & Lee, H. N. Thermopower enhancement by fractional layer control in 2D oxide superlattices. Adv. Mater. 26, 6701–6705 (2014).
Koga, T., Cronin, S. B., Dresselhaus, M. S., Liu, J. L. & Wang, K. L. Experimental proof-of-principle investigation of enhanced Z(3D)T in (001) oriented Si/Ge superlattices. Appl. Phys. Lett. 77, 1490–1492 (2000).
Samarelli, A. et al. The thermoelectric properties of Ge/SiGe modulation doped superlattices. J. Appl. Phys. 113, 233704 (2013).
Peranio, N., Eibl, O. & Nurnus, J. Structural and thermoelectric properties of epitaxially grown Bi2Te3 thin films and superlattices. J. Appl. Phys. 100, 114306 (2006).
Zhang, Y. et al. Thermoelectric phase diagram of the SrTiO3-SrNbO3 solid solution system. J. Appl. Phys. 121, 185102 (2017).
Shannon, R. D. Revised effective ionic-radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 32, 751–767 (1976).
Ohtomo, A., Muller, D. A., Grazul, J. L. & Hwang, H. Y. Artificial charge-modulation in atomic-scale perovskite titanate superlattices. Nature 419, 378–380 (2002).
Mizoguchi, T., Ohta, H., Lee, H. S., Takahashi, N. & Ikuhara, Y. Controlling interface intermixing and properties of SrTiO3-based superlattices. Adv. Funct. Mater. 21, 2258–2263 (2011).
Delugas, P. et al. Doping-induced dimensional crossover and thermopower burst in Nb-doped SrTiO3 superlattices. Phys. Rev. B 88, 045310 (2013).
Ravichandran, J. et al. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 13, 168–172 (2014).
Mune, Y., Ohta, H., Koumoto, K., Mizoguchi, T. & Ikuhara, Y. Enhanced Seebeck coefficient of quantum-confined electrons in SrTiO3/SrTi0.8Nb0.2O3 superlattices. Appl. Phys. Lett. 91, 192105 (2007).
Blochl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 124, 219906 (2006).
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F. & Scuseria, G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106 (2006).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Acknowledgements
This research was supported by Grants-in-Aid for Scientific Research on Innovative Areas “Nano Informatics” (25106003, 25106005, and 25106007) from the Japan Society for the Promotion of Science (JSPS). H.O. was supported by Grants-in-Aid for Scientific Research A (17H01314) and B (26287064) from the JSPS. Y.Z. thanks to the China Scholarship Council (CSC) for a scholarship to study in Japan. Y.M.S. acknowledge the grant from Taiwan Ministry of Science and Technology (MOST 104-2112-M-009-023-MY3 and MOST 104-2738-M-009-006), and the Center for Emergent Functional Matter Science of National Chiao Tung University from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan. A part of this work was supported in part by the Network Joint Research Center for Materials and Devices and by Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials.
Author information
Authors and Affiliations
Contributions
Y.Z. performed the sample preparation and measurements. B.F. and Y.I. performed the STEM analyses. H.H. and I.T. performed the energy band calculations. C.P.C. and Y.M.S. provided measurements on the time-domain thermoreflectance. H.O. planned and supervised the project. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Y., Feng, B., Hayashi, H. et al. Double thermoelectric power factor of a 2D electron system. Nat Commun 9, 2224 (2018). https://doi.org/10.1038/s41467-018-04660-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-04660-4
This article is cited by
-
Anomalous enhancement of thermoelectric power factor in multiple two-dimensional electron gas system
Nature Communications (2024)
-
Giant thermoelectric power factor in charged ferroelectric domain walls of GeTe with Van Hove singularities
npj Computational Materials (2020)
-
Giant thermoelectric power factor in ultrathin FeSe superconductor
Nature Communications (2019)
-
Tuning the Electrical and Thermoelectric Properties of N Ion Implanted SrTiO3 Thin Films and Their Conduction Mechanisms
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.