Abstract
Nanoscale systems that coherently couple to light and possess spins offer key capabilities for quantum technologies. However, an outstanding challenge is to preserve properties, and especially optical and spin coherence lifetimes, at the nanoscale. Here, we report optically controlled nuclear spins with long coherence lifetimes (T2) in rare-earth-doped nanoparticles. We detect spins echoes and measure a spin coherence lifetime of 2.9 ± 0.3 ms at 5 K under an external magnetic field of 9 mT, a T2 value comparable to those obtained in bulk rare-earth crystals. Moreover, we achieve spin T2 extension using all-optical spin dynamical decoupling and observe high fidelity between excitation and echo phases. Rare-earth-doped nanoparticles are thus the only nano-material in which optically controlled spins with millisecond coherence lifetimes have been reported. These results open the way to providing quantum light-atom-spin interfaces with long storage time within hybrid architectures.
Similar content being viewed by others
Introduction
Quantum systems with spin qubits that can be optically controlled allow efficient qubit initialization and readout, and quantum gate operations1. Moreover, photonic quantum states can be mapped to and/or entangled with spin qubits for storage and processing2,3,4. Such schemes are investigated in solid-state systems like colour centres in diamond, quantum dots in semi-conductors, and rare-earth-doped crystals. Targeted applications include quantum memories for light2,5,6 or microwave photons7, and quantum processors1. In this respect, crucial advances are expected at the nanoscale that include single qubit control and readout8, multiple qubit gate operation1,9, and extremely sensitive and localized sensing and imaging10. Strongly enhancing light–matter interactions using nano- or micro-cavities11,12, or coupling different quantum systems to build hybrid devices with an optical interface13,14 are other attractive possibilities. Optical control of spins can also be useful in nanoscale systems. Optical excitations are faster than direct radio-frequency (RF) excitations because they take advantage of strong optical transitions15, while ensuring spatial selectivity because of light’s much shorter wavelength. It may also lead to simpler fabrication of devices by avoiding incorporating antennas in proximity to the spins.
However, coherence lifetimes are often significantly shortened in nano-materials16,17, impairing their use for quantum technologies. Indeed, surface effects, and/or high concentration of defects or impurities due to the synthesis process can cause strong dephasing mechanisms16. The latter can be partially cancelled in nanostructures embedded in bulk crystals11,18. For rare earths, this approach has led to promising demonstrations, including single spin coherent control19 and quantum storage20. However, freestanding nanoparticles have a higher flexibility for integration with other systems. For example, nanodiamonds containing NV centers and rare-earth-doped nanoparticles have been integrated in high-finesse, fibre-based micro-cavities21,22, to increase fluorescence rates through the Purcell effect. This enables fast single qubit state readout or efficient single photon emission. Other hybrid structures for quantum technologies have been proposed like nanodiamonds deposited on an active substrate23 or interacting with plasmons in metallic particles24. Furthermore, nanoparticles could also enable photon and phonon density of states engineering to create bandgaps and achieve longer optical and spin population and coherence lifetimes25,26,27.
In the following, we investigate the nuclear spin coherence of rare-earth dopants in nanoparticles at low temperatures. These materials have unique properties for nanoscale systems, showing narrow optical linewidths, down to 45 kHz at 1.3 K, and limited spectral diffusion28. This is favourable to coupling to high-finesse optical cavities and using electric dipole–dipole interactions for quantum gate implementation. In these nanoparticles, we now demonstrate nuclear spin coherence lifetimes from 1.3 ± 0.2 ms up to 8.1 ± 0.6 ms in Eu3+-doped Y2O3 nanoparticles using a fully-optical protocol, which includes spin echo and spin dynamical decoupling (DD). High fidelity between excitation and echo phases is moreover observed, as required for quantum storage. These results suggest that rare-earth-doped nanoparticles, presenting both narrow optical and spin linewidths, could find multiple applications in optical quantum technologies.
Results
Spin coherence in rare-earth-doped nanoparticles
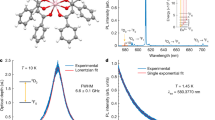
Experiments were carried out on 0.5 % Eu3+:Y2O3 nanoparticles of 400 ± 80 nm composed of 130 ± 10 nm crystallites obtained by homogeneous precipitation and high temperature annealing27. The particles were placed in a cryostat in the form of a powder and excited by laser pulses (see Methods). With a nuclear spin I = 5/2, the 151Eu isotope presents three doubly degenerated ground-state nuclear spin levels at zero magnetic field (Fig. 1a). To probe the \(\pm \left| {1/2}\rangle \right. \leftrightarrow \pm \left| {3/2}\rangle \right.\) hyperfine transition, the thermally distributed ground-state population was first initialized by optical pumping to the \(\pm \left| {1/2}\rangle \right.\) level for a subset of ions within the inhomogeneously broadened optical absorption line (Fig. 1b). Spin coherent states were subsequently created and rephased following an all-optical spin-echo sequence29,30, using two-color pulses at frequencies ω1 and ω2 (Fig. 1c). A weak single-frequency pulse was applied at time 2τ with frequency ω2 to convert the spin coherence into an optical coherence at ω1. This resulted in a beating at ω2–ω1 on the photodiode signal that was revealed with a signal to noise ratio (SNR) of about 10 by a fast Fourier transform (FFT) as displayed in Fig. 1d.
All-optical nuclear spin coherence investigation in 151Eu3+-doped Y2O3 nanoparticles. a 151Eu3+ ground-state hyperfine structure in Y2O3. Two-color laser pulses (at ω1 and ω2 frequencies) resonant with the 7F0→5D0 transition at 580.883 nm create coherent states between the \(\pm \left| {1{\mathrm{/}}2}\rangle \right.\) and \(\pm \left| {3{\mathrm{/}}2}\rangle \right.\) nuclear spin levels. \(\pm \left| {{\mathrm{exc}}}\rangle \right.\) represents the excited state hyperfine levels. b Optical transmission spectrum after optical pumping. Ground-state population initialization to \(\pm \left| {1{\mathrm{/}}2}\rangle \right.\) corresponds to a lower transmission at ω1. High transmission (~95%) at 0 (ω2) and 33.99 MHz (ω3) evidences efficient population depletion in the \(\pm \left| {3{\mathrm{/}}2}\rangle \right.\) and \(\pm \left| {5{\mathrm{/}}2}\rangle \right.\) levels. ωopt = 516.098 THz (580.883 nm). c All-optical spin-echo sequence with heterodyne detection. Each sequence is preceded by optical pumping and followed by chirped pulses to reset the spin population to equilibrium. d Fast Fourier transform of the heterodyne signal revealing the spin echo at 29.34 MHz
The spin-echo sequence was first used to determine the inhomogeneous broadening of the \(\pm \left| {1{\mathrm{/}}2}\rangle \right. \leftrightarrow \pm \left| {3{\mathrm{/}}2}\rangle \right.\) transition, which was found equal to 107 ± 8 kHz (Fig. 2a). This value, identical to that reported on Y2O3:Eu3+ bulk crystals31 and ceramics32, reflects the high crystalline quality of the particles. The decay of the spin-echo amplitude as a function of the increasing pulse separation reveals a coherence lifetime of 1.3 ± 0.2 ms (Fig. 2b), corresponding to a homogeneous linewidth Γh = (π T2)−1 of 250 Hz. This spin coherence lifetime is one order of magnitude lower compared to Eu3+:Y2O3 bulk transparent ceramics (T2 = 12 ms32) and Eu3+:Y2SiO5 bulk single crystals (T2 = 19 ms33). In contrast, the nanoparticles’ optical coherence lifetime is two orders of magnitude lower than the bulk values: T2opt = 7 µs28 versus T2opt = 1.1 ms (C. W. Thiel, personal communication). Thus, the spin coherence is much more preserved when scaling down in size than the optical coherence. This is consistent with a previous analysis in which we proposed that optical dephasing is mainly due to perturbations related to surface electric charges28. These charges have,however, little influence on nuclear spin transitions as the ratio between optical and nuclear Stark coefficients is expected to be about 5 orders of magnitude34. This suggests that magnetic perturbations are responsible for the dephasing of the spin transition. Indeed, under a weak magnetic field, the homogeneous linewidth decreases and reaches 110 Hz at 9 mT (Fig. 2c). This variation can be modelled by magnetic dipole–dipole interactions between Eu3+ spins and defects carrying electron spins (Fig. 2c and Supplementary Discussion). A small magnetic field reduces the dipole–dipole interaction Hamiltonian to secular terms, which in turn reduces Eu3+ spin frequency shifts due to defect spin flips and, therefore, dephasing. Quantitative analysis was performed assuming that Eu3+ spin dephasing is due to frequency shifts following a Gaussian distribution. The inferred defect concentration, 6.4 × 1017 cm−3 or 25 ppm relative to Y, also indicates that spin T2 could be increased in higher quality samples35.
151Eu3+ spin inhomogeneous and homogeneous linewidths. a Inhomogeneous linewidth of the \(\pm \left| {1{\mathrm{/}}2}\rangle \right. \leftrightarrow \pm \left| {3{\mathrm{/}}2}\rangle \right.\) spin transition obtained by monitoring the spin-echo amplitude as a function of the frequency detuning ω2–ω1 for a fixed time delay 2τ of 400 µs (circles). Solid line: Lorentzian fit corresponding to a full width at half maximum of 107 ± 8 kHz. b Spin-echo decay at zero magnetic field. A single-exponential fit yields a coherence lifetime T2 of 1.3 ± 0.2 ms, corresponding to a Γh = 250 Hz homogeneous linewidth. c Homogeneous linewidth evolution under an applied external magnetic field. A fast decrease in Γh is observed for weak fields, corresponding to a coherence lifetime increasing from 1.3 ms to 2.9 ms (Supplementary Fig. 6). Solid line: modelling by interactions with defects carrying electron spins at a concentration of 6.4 ×1017 cm−3 (see Supplementary Discussion). Error bars and uncertainties correspond to ±1 standard error
All-optical spin dynamical decoupling
A well-known approach to control dephasing is DD36. Here, a train of π pulses is applied to refocus frequency shifts due to fluctuations that are slow compared to the pulse separation. This principle was applied but with π pulses corresponding to two-color laser pulses instead of the usual RF ones33. To the best of our knowledge this the first demonstration of an all-optical spin DD. A crucial point for DD, is the phase coherence of the π pulses. We achieved it by generating the two frequency shifted laser beams using a single acousto-optic modulator (AOM) and having them spatially overlap (see Methods). This ensured a highly stable relative phase between the two lasers beams and therefore phase coherent excitation, rephasing, and detection of the spins coherence.
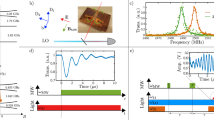
The CPMG (Carl-Purcell-Meiboom-Gill)37 DD sequence used in our experiments is shown in Fig. 3a. Coherence lifetimes extended by DD, T2DD, were determined by recording the spin-echo amplitude vs. the total evolution time (n×τDD). This is efficient in preserving coherences along the x-axis of the Bloch sphere, but not those along the y-axis. This effect is due to the accumulation of errors in the π pulse areas that have a larger effect for Y coherences than for X ones. In our powder, such pulse area errors are expected to be particularly high because of the random light scattering and orientation of the particles, which further increases the spread in spin Rabi frequencies. Indeed, significant increase in coherence lifetime over the two-pulse echo value of 1.3 ms were achieved only for Y excitations (Fig. 3b). The π pulse delay τDD was then varied, resulting in T2DD = 8.1 ± 0.6 ms for the optimal value τDD = 300 µs, a 6-fold increase compared to the two-pulse echo T2 (Fig. 3c). T2DD variation with τDD, shown in Fig. 3d, can be explained by a balance between short τDD delays implying a higher number of pulses during a given evolution time and, therefore, accumulating pulse areas errors, and long delays that are less efficient in refocusing fluctuations33 (see Supplementary Discussion). We also noted that applying a field of 0.7 mT decreased T2DD, in opposition to T2 (Fig. 3e). This could be explained by an increase in pulse errors when the transition broadens under magnetic field (Supplementary Fig. 2).
All-optical dynamical decoupling. a CPMG sequence with optical 2-color excitation and rephasing π pulses. The initial excitation pulse has a Y phase and the π pulses an X phase. This is obtained by varying the relative phase between the two frequency components of the optical pulses. b Echo decays (circles) for different initial phases and exponential fits (lines). A much lower T2DD is observed for an X initial phase (~1.0 ms) than for an Y one (~3.0 ms). This is due to the accumulation of pulse errors and confirms that our DD sequence behaves as a CPMG one. c Spin-echo decays (circles) obtained for τDD = 150, 200 and 300 µs with n ≤ 60, and exponential fits (lines). d Experimental (circles) and modelled (line) T2DD evolution as a function of τDD. (see Supplementary Fig. 5). The data point represented by the black circle was discarded for the fit. e Spin-echo decays (circles) with and without a weak magnetic field. Solid line: exponential fits. Error bars and uncertainties correspond to ±1 standard error
We finally investigated the variation of spin-echo phase as a function of the initial excitation phase in the 2 pulse and DD all-optical sequences (see Methods). They were found to be highly correlated, even for the DD case, in which a lower SNR was achieved (Fig. 4, Supplementary Fig. 7 and Supplementary Fig. 8). This confirmed the fully coherent character of the spins driving and detection. These experiments can also be considered as an optical memory with spin storage, with the initial and final light fields at ω1 being input and output signals (Figs. 1c and 3a). The high correlations of Fig. 4 then correspond to a high phase fidelity, an essential requirement towards an optical memory operating at the quantum level. In this respect, further investigations on the noise level introduced by all-optical DD will be necessary to assert the possibility of long time high-fidelity storage with spins. It will also be important to achieve faithful all-optical operations on spin states for quantum memories and processors. Suitable schemes using resonant two-color excitations have been proposed for rare-earth-doped crystals38,39, reaching experimental π pulse fidelity of 96%40. Similar results could be achieved in a single Eu3+-doped nanoparticle, where interactions between light and ions are well defined, as long as optical pulses much shorter than the optical T2 (7 µs28), but still longer than the inverse of the hyperfine splitting ((29 × 106)−1 = 34 ns) are used. The corresponding high Rabi frequencies could be obtained by placing the particle in an optical micro-cavity21.
Echo phase correlation. a, c Real and imaginary parts of the spin-echo signal FFT (circles) as a function of the excitation pulse phase for a two-pulse echo and a DD sequence (τ = 300 µs, τDD = 150 µs, n = 10). Solid lines: fit with a sine function. Error bars were estimated from the signal to noise ratio in Supplementary Fig. 7 and Supplementary Fig. 8. b, d Echo pulse phase derived from FFT signals (a, c) as a function of the excitation pulse phase (see Methods). Lines: linear fit; R correlation coefficient. Echo phase error bars were calculated by error propagation from the FFT signal to noise ratio
While the spin coherence lifetimes reported here are within a factor of ten from bulk values, they could still be increased in samples with lower content of magnetic defects or by polarising them at lower temperatures and higher magnetic fields. Moreover, at the single particle level, T2 could be further improved by several orders of magnitude by taking advantage of reduced pulses area errors in DD and using clock transitions that appear in europium and other rare-earth ions under suitable magnetic fields41. This could open the way to nanoscale quantum light–matter-spin interfaces, useful for quantum memories with processing capabilities, hybrid opto-mechanical systems, or coupling to optical micro-cavities. Nanoparticles doped with essentially any rare-earth ion can also be synthesized in different size, shape and layered structures, as shown by their huge development as luminescent probes42. Although quantum grade materials are very demanding, our results suggest that rare-earth ion-doped nanoparticles could be an extremely versatile platform for nanoscale quantum technologies.
Methods
Nanoparticles synthesis and structural characterization
0.5% Eu3+:Y2O3 nanoparticles with 400 ± 80 nm average diameter and 130 ± 10 nm crystallite size were grown by homogeneous precipitation27. An aqueous solution of Y(NO3)3•6H2O (99.9% pure, Alfa Aesar), Eu(NO3)3•6H2O (99.99% pure, Reacton), and urea (CO(NH2)2 > 99% pure, Sigma) was first heated at 85 °C for 24 h in a Teflon reactor, yielding Eu3+:Y(OH)CO3.nH2O particles in suspension. The metal and urea concentrations were 7.5 mmol L−1 and 0.5 mol L−1. After cooling to room temperature, the carbonate particles were collected via centrifugation, washed with distilled water once and absolute ethanol twice to remove the byproducts, and finally dried at 80 °C for 24 h. They were calcined at 1200 °C during 6 h (heating rate: 3 °C min−1) to obtain Eu3+:Y2O3 particles. The body-centered cubic Y2O3 structure (Ia-3 space group) of the particles and their average crystallite size were determined by X-ray diffraction. No evidence of other parasitic phases was found. The morphology, size, and dispersion of the particles were obtained by scanning electron microscopy (Supplementary Fig. 1).
Experimental setup
The sample, consisting of an ensemble (≈1011–1012) of particles in form of loose powder, was placed between two glass plates with a copper spacer (~500 µm thickness) inside a He bath cryostat (Janis SVT-200). The excitation was provided by a Sirah Matisse DS laser, with a linewidth of ~150 kHz and operating at 516.098 THz (580.883 nm vac.) The laser beam was first sent through a double pass AOM with central frequency of 200 MHz (AA Optoelectronic MT200-B100A0, 5-VIS) followed by a single pass AOM (AA Optoelectronic MT110-B50A1-VIS) with a center frequency of 110 MHz. Both AOMs were driven by an arbitrary waveform generator (AWG) (Agilent N8242A) with 625 MS s−1 sampling rate. The two-color pulses, generated by the single pass AOM, were coupled to a single-mode fiber in order to ensure spatial overlapping. The overlapped beams were then focused onto the sample, within the cryostat, with a 75 mm focal length lens and the scattered light collected with a 5 mm focal length lens mounted directly behind the sample holder. An avalanche photo diode (APD) (Thorlabs 110 A/M) was used as detector. A scheme of the experimental setup is displayed in Supplementary Fig. 3. The sample temperature was monitored with a temperature sensor (Lakeshore DT-670) attached to the sample holder with thermally conducting grease and tuned by controlling the helium gas flow and the pressure inside the cryostat. The cryostat was operated in gas mode to maintain a constant temperature of 5 K. Magnetic fields perpendicular to the laser beam propagation axis were applied by means of Helmholtz coils sitting outside the cryostat.
Two-pulse spin-echo measurements
Pulse areas in the two-pulse echo sequence were optimized to maximize the spin-echo signal. Data presented in this work were obtained with 100 µs-long pulses and total optical powers, P1 + P2, of the order of 120 mW, where P1 and P2 correspond to the optical powers applied to the ω1 and ω2 transitions, respectively. Although this input power is large compared to single crystal measurements, the scattering in the nanoparticles significantly reduces the input power incident in the sample. The power ratio between the two laser fields P1 and P2 was also optimized to maximize the spin-echo signal. Lower excitation power was used for the heterodyne pulse (~14 mW). Possible heating of the nanoparticles by the laser was checked by varying laser power and was found negligible in the measurements. The inhomogeneous linewidth of the 29 MHz spin transition was measured by monitoring the spin-echo signal as a function of the frequency difference (ω2–ω1) in the two-color pulses for a fixed delay time τ. The transition linewidth was estimated by a Lorentzian lineshape fit within an incertitude interval which was derived from the experimental SNR and the fit accuracy. The decay of the spin-echo signal with increasing τ was used to determine the nuclear spin coherence lifetime. The value was derived by single-exponential fit within an uncertainty also given by the experimental SNR and the fit accuracy.
Dynamical decoupling and phase correlations measurements
DD experiments were carried out with 20-µs-long π pulses in order to access a large excitation bandwidth (about 50 kHz, half of the spin inhomogeneous linewidth) and short π-pulse separation times (τDD). The preservation of the excitation phase coherence along the DD sequence was confirmed by the observation of stable beating patterns from a photodiode at the output of the fiber for times exceeding 30 s. The spin-echo phase was directly derived from the real (Re) and imaginary (Im) parts of the spin-echo signal FFT as
The error \({\mathrm{\Delta }}\theta _{{\mathrm{echo}}}\) was calculated by classical error propagation from the uncertainty associated to the real and imaginary FFT parts, ΔRe and ΔIm. Those were estimated from the SNR in Supplementary Fig. 7 and Supplementary Fig. 8. As observed, the SNR is clearly larger in Supplementary Fig. 8 due to the weaker spin-echo signal obtained after 10 π-pulses, corresponding to a total evolution time of 1.5 ms compared to the total evolution time of 600 µs in the two-pulse echo case.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014).
Yang, S. et al. High-fidelity transfer and storage of photon states in a single nuclear spin. Nat. Photonics 10, 507–511 (2016).
Gündoğan, M., Ledingham, P. M., Almasi, A., Cristiani, M. & de Riedmatten, H. Quantum storage of a photonic polarization qubit in a solid. Phys. Rev. Lett. 108, 190504 (2012).
Hensen, B. et al. Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Bussières, F. et al. Quantum teleportation from a telecom-wavelength photon to a solid-state quantum memory. Nat. Photonics 8, 775–778 (2014).
Press, D. et al. Ultrafast optical spin echo in a single quantum dot. Nat. Photonics 4, 367–370 (2010).
Grezes, C. et al. Multimode storage and retrieval of microwave fields in a spin ensemble. Phys. Rev. X 4, 021049–021049 (2014).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 9, 666–670 (2014).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).
Schmitt, S. et al. Submillihertz magnetic spectroscopy performed with a nanoscale quantum sensor. Science 356, 832–837 (2017).
Zhong, T., Kindem, J. M., Miyazono, E. & Faraon, A. Nanophotonic coherent light-matter interfaces based on rare-earth-doped crystals. Nat. Commun. 6, 8206 (2015).
Kaupp, H. et al. Scaling laws of the cavity enhancement for nitrogen-vacancy centers in diamond. Phys. Rev. A. 88, 053812 (2013).
Yeo, I. et al. Strain-mediated coupling in a quantum dot-mechanical oscillator hybrid system. Nat. Nanotechnol. 9, 106–110 (2014).
Kurizki, G. et al. Quantum technologies with hybrid systems. PNAS 112, 3866–3873 (2015).
Becker, J. N., Görlitz, J., Arend, C., Markham, M. & Becher, C. Ultrafast all-optical coherent control of single silicon vacancy colour centres in diamond. Nat. Commun. 7, 13512 (2016).
Knowles, H. S., Kara, D. M. & Atatüre, M. Observing bulk diamond spin coherence in high-purity nanodiamonds. Nat. Mater. 13, 21–25 (2014).
Perrot, A. et al. Narrow optical homogeneous linewidths in rare earth doped nanocrystals. Phys. Rev. Lett. 111, 203601 (2013).
Bhaskar, M. K. et al. Quantum nonlinear optics with a germanium-vacancy color center in a nanoscale diamond waveguide. Phys. Rev. Lett. 118, 223603 (2017).
Siyushev, P. et al. Coherent properties of single rare-earth spin qubits. Nat. Commun. 5, 3895 (2014).
Zhong, T. et al. Nanophotonic rare-earth quantum memory with optically controlled retrieval. Science 357, 1392–1399 (2017).
Casabone, B. et al. Cavity-enhanced spectroscopy of a few-ion ensemble in Eu3+:Y2O3. Preprint at https://arxiv.org/abs/1802.06709 (2018).
Johnson, S. et al. Tunable cavity coupling of the zero phonon line of a nitrogen-vacancy defect in diamond. New J. Phys. 17, 122003 (2015).
Andrich, P. et al. Long-range spin wave mediated control of defect qubits in nanodiamonds. npj Quantum Inf. 3, 28 (2017).
Gong, J., Steinsultz, N. & Ouyang, M. Nanodiamond-based nanostructures for coupling nitrogen-vacancy centres to metal nanoparticles and semiconductor quantum dots. Nat. Commun. 7, 11820 (2016).
Lutz, T. et al. Modification of phonon processes in nanostructured rare-earth-ion-doped crystals. Phys. Rev. A. 94, 013801 (2016).
Jahnke, K. D. et al. Electron–phonon processes of the silicon-vacancy centre in diamond. New J. Phys. 17, 043011 (2015).
de Oliveira Lima, K., Rocha Gonçalves, R., Giaume, D., Ferrier, A. & Goldner, P. Influence of defects on sub-Å optical linewidths in Eu3+: Y2O3 particles. J. Lumin. 168, 276–282 (2015).
Bartholomew, J. G., de Oliveira Lima, K., Ferrier, A. & Goldner, P. Optical Line Width Broadening Mechanisms at the 10 kHz Level in Eu3+:Y2O3 Nanoparticles. Nano. Lett. 17, 778–787 (2017).
Ham, B. S., Shahriar, M. S., Kim, M. K. & Hemmer, P. R. Spin coherence excitation and rephasing with optically shelved atoms. Phys. Rev. B 58, 11825–11828 (1998).
Guillot-Noël, O. et al. Hyperfine structure and hyperfine coherent properties of praseodymium in single-crystalline La2(WO4)3 by hole-burning and photon-echo techniques. Phys. Rev. B 79, 155119 (2009).
Babbitt, W., Lezama, A. & Mossberg, T. Optical dephasing, hyperfine structure, and hyperfine relaxation associated with the 580.8-nm F07-5D0 transition of europium in Eu3+:Y2O3. Phys. Rev. B 39, 1987–1992 (1989).
Karlsson, J., Kunkel, N., Ikesue, A., Ferrier, A. & Goldner, P. Nuclear spin coherence properties of 151Eu3 + and 153Eu3 + in a Y2O3 transparent ceramic. J. Phys. Condens. Matter 29, 125501 (2017).
Arcangeli, A., Lovrić, M., Tumino, B., Ferrier, A. & Goldner, P. Spectroscopy and coherence lifetime extension of hyperfine transitions in 151Eu3+:Y2SiO5. Phys. Rev. B 89, 184305 (2014).
Macfarlane, R. M., Arcangeli, A., Ferrier, A. & Goldner, P. Optical measurement of the effect of electric fields on the nuclear spin coherence of rare-earth ions in solids. Phys. Rev. Lett. 113, 157603 (2014).
Kunkel, N., Bartholomew, J., Binet, L., Ikesue, A. & Goldner, P. High-resolution optical line width measurements as a material characterization tool. J. Phys. Chem. C. 120, 13725–13731 (2016).
Viola, L. & Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A. 58, 2733–2744 (1998).
Meiboom, S. & Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 29, 688 (1958).
Roos, I. & Mølmer, K. Quantum computing with an inhomogeneously broadened ensemble of ions: suppression of errors from detuning variations by specially adapted pulses and coherent population trapping. Phys. Rev. A. 69, 022321 (2004).
Walther, A. et al. High-fidelity readout scheme for rare-earth solid-state quantum computing. Phys. Rev. A. 92, 022319 (2015).
Rippe, L., Julsgaard, B., Walther, A., Ying, Y. & Kröll, S. Experimental quantum-state tomography of a solid-state qubit. Phys. Rev. A. 77, 022307 (2008).
Zhong, M. et al. Optically addressable nuclear spins in a solid with a six-hour coherence time. Nature 517, 177–180 (2015).
Gai, S., Li, C., Yang, P. & Lin, J. Recent progress in rare earth micro/nanocrystals: soft chemical synthesis, luminescent properties, and biomedical applications. Chem. Rev. 114, 2343–2389 (2014).
Acknowledgements
This research work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 712721 (NanOQTech). We thank John Bartholomew, Hugues de Riedmatten, and Thierry Chanelière for useful comments and discussions on the manuscript.
Author information
Authors and Affiliations
Contributions
J.K. developed the optical setup; D.S., J.K., A.Fo., and P.G. performed the experiments; D.S., J.K., A.Fe., and P.G. discussed, modelled, and analyzed the results; and D.S. and P.G. wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Serrano, D., Karlsson, J., Fossati, A. et al. All-optical control of long-lived nuclear spins in rare-earth doped nanoparticles. Nat Commun 9, 2127 (2018). https://doi.org/10.1038/s41467-018-04509-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-04509-w
This article is cited by
-
Controlling single rare earth ion emission in an electro-optical nanocavity
Nature Communications (2023)
-
Ultra-narrow optical linewidths in rare-earth molecular crystals
Nature (2022)
-
Optical spin-state polarization in a binuclear europium complex towards molecule-based coherent light-spin interfaces
Nature Communications (2021)
-
Dynamic control of Purcell enhanced emission of erbium ions in nanoparticles
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.