Abstract
Electronic properties and lattice vibrations are expected to be strongly correlated in metal-halide perovskites, due to the soft fluctuating nature of their crystal lattice. Thus, unveiling electron–phonon coupling dynamics upon ultrafast photoexcitation is necessary for understanding the optoelectronic behavior of the semiconductor. Here, we use impulsive vibrational spectroscopy to reveal vibrational modes of methylammonium lead-bromide perovskite under electronically resonant and non-resonant conditions. We identify two excited state coherent phonons at 89 and 106 cm−1, whose phases reveal a shift of the potential energy minimum upon ultrafast photocarrier generation. This indicates the transition to a new geometry, reached after approximately 90 fs, and fully equilibrated within the phonons lifetime of about 1 ps. Our results unambiguously prove that these modes drive the crystalline distortion occurring upon photo-excitation, demonstrating the presence of polaronic effects.
Similar content being viewed by others
Introduction
Solution processed hybrid lead-halide perovskites are an emergent class of materials for efficient optoelectronic devices1. Despite the technological appeal, a comprehensive understanding of their photo-excitation dynamics is still lacking. A crucial, missing information is the nature of carriers, a key issue for the description of transport and recombination processes, two unique characteristics of these materials also in focus of a lively debate2,3,4,5,6. In fact, the reported carrier recombination rates7 are remarkably low, i.e., comparable to the best ones reported for single crystalline semiconductors2 and orders of magnitude lower than those predicted by the Langevin model4. On the other hand, modest charge mobilities have been reported, i.e., much lower than those of crystalline semiconductors albeit higher than those found in organic (disordered) semiconductors8. Given the polar nature of the perovskite lattice, it has been suggested8, in order to justify the low mobilities, that carriers localize as large polarons in contrast to a pure band-like picture where carriers act as delocalized Bloch waves. This picture would be consistent with carrier transport and temperature dependence of the homogenous linewidths of electronic transitions9, pointing to the presence of strong electron–phonon scattering mechanism. The importance of this interaction mechanism has also been indicated by light-enhanced local disorder observed through electron diffraction10. Recently, it has been suggested11 that photogenerated electrons relax into a distinct dark electronic state which extends the charge carrier lifetime. Although the proposed mechanism is compatible with both the band-like and large polaron pictures, an experimental method able to disentangle these effects is still missing. Therefore, both the nature of such state and the reaction pathway which would lead to its population remain unclear12.
Here, we use impulsive vibrational spectroscopy (IVS), a time domain Raman technique, to unveil the phonon spectra of the ground and excited electronic states in methylammonium lead-bromide perovskite (MAPbBr3) polycrystalline thin films. Raman spectroscopy is an ideal tool to investigate electron–phonon coupling in materials13,14. While ground state vibrational features in lead halide perovskites have been thoroughly addressed15,18,19,20,21,20, identifying the correlation between the phonon modes and electronic excitations is one of the major challenges in the field. To address this issue, it would be imperative to perform the measurements with a resonant excitation. Detecting spontaneous Raman signals from excited electronic states using a single resonant excitation is not trivial. Moreover, the presence of a large background signal from photoluminescence (PL) may obscure the low frequency region that contains the most relevant modes of the inorganic moiety. Within this context, IVS21,24,23 represents a powerful technique to circumvent these limitations and resolve both ground and excited state Raman bands with high spectral resolution. In fact, since the measurement is performed in the time domain, there are no spectral limitations neither artefacts arising from elastic pump-scattering and PL.
IVS exploits two femtosecond laser pulses to obtain the Raman vibrations of the system under investigation (Fig. 1a). First, Raman interactions convert an incoming optical pump pulse into an impulsive force acting on the solid-state lattice. This results in collective lattice displacements, namely coherent phonons, provided that the duration of the pump pulse is shorter than the Raman active mode vibrational period. Then, the interaction with a delayed probe pulse leads to the generation of a third order electronic polarization in the material, which modulates the transmission of the probe. The overall result is the appearance of a time oscillating transmissivity change at the frequencies of the stimulated coherent phonon modes, detected by the time-delayed probe pulse. This oscillating response is always superimposed on a transient absorption (TA) signal, which arises when carriers are photo-generated. The underlying exponential electronic kinetics responsible for such TA background is subtracted from the detected signal to extract the oscillating temporal dynamics22,24. These time domain signals are then Fourier transformed to obtain the vibrational Raman spectra. This allows us to determine the phonons coupled to the electronic transition that rule the structural rearrangement in MAPbBr3 upon photo-carrier generation.
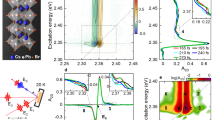
Concept of the Impulsive vibrational spectroscopy experiment on MAPbBr3. a IVS pulse scheme and MAPbBr3 crystal structure. After a tunable delay from the interaction with a femtosecond pump pulse, an ultrashort broadband probe pulse interrogates the system and reveals the stimulated lattice vibrations. b Visible absorption spectrum of a polycrystalline thin film of MAPbBr3: the red and green arrows indicate respectively the 1.86 eV off-resonant and the resonant 2.46 eV pump photon energies used in our experiments. The colored box represents the analyzed probe spectral regions. c The experimentally detected differential signal shows the photo-induced modifications of the transmission profile as a function of the time delay between the two pulses. d The signal consists in oscillating components, which carry the phonon frequencies, superimposed to the TA exponential dynamics. e The vibrational information is directly obtained by Fourier Transforming the experimental data after the subtraction of the TA decay
Results
Figure 1b shows the absorption spectrum of the polycrystalline thin film of MAPbBr3 (see Methods section for details on sample preparation), where the red and green arrows indicate the 1.86 eV (665 nm) off-resonant and 2.46 eV (503 nm) resonant excitation pulses used in our experiments. To avoid photo-degradation, the sample was encapsulated by a thick PMMA layer and measured in air, preventing the formation of intra-gap defect states25. The basics of the performed IVS experiment are provided in Fig. 1c–e and detailed in Supplementary Note 1. For both the actinic excitation energies, we observe an underlying transient absorption signal, in agreement with previous reports26. The pump pulse duration is 30 (50) fs for the 1.86 (2.46) eV, which is much shorter than the periods of the vibrational modes of interest. Figure 2a–c reports the IVS spectra under such excitations. Since the detection of the probe is spectrally dispersed, it provides us with a probe-wavelength resolved vibrational coherence map27,30,29. The exact procedure used for the data analysis is detailed in Supplementary Note 1. Briefly, for both the off-resonance and resonant excitations, we consider probe wavelengths around the TA maximum (from 510 to 540 nm, photon energies from 2.43 to 2.30 eV), where the IVS cross section is enhanced. Multiple TA traces acquired during the experiment are reported in Supplementary Figure 4. To factor out cross phase modulation artefacts, due to pump and probe temporal overlap, time traces have only been considered from 250 fs onwards in the data analysis. After removing the superimposed dynamics from the TA signal (Supplementary Figure 2), we apply Fourier transformation at each probe wavelength. Zero padding algorithm and Kaiser–Bessel windowing are exploited to enhance the spectral definition. The resulting 2D vibrational maps are shown in Fig. 2a and 2c. The average of these maps over all the detected probe wavelengths is reported in Fig. 2b (while slices at selected wavelengths are shown in Supplementary Figure 3), where the green and red shaded spectra correspond to resonant and off-resonant excitations, respectively. The obtained Raman spectra are fitted with Gaussian functions to extract the peak positions of the various modes, which are plotted as a function of probe wavelength in Fig. 2d, for both the pumps. The 2D vibrational map recorded at red-shifted probe wavelengths are reported in Supplementary Figure 5.
Impulsive vibrational spectroscopy on MAPbBr3 under different resonance regimes. Probe-wavelength resolved IVS maps, upon resonant (EPump = 2.46 eV) and non-resonant (EPump = 1.86 eV) excitations (a, c, respectively). The maps have been obtained by Fourier transforming the oscillating component of the TA data (see Fig. 1), to retrieve the vibrational spectra. b Average of the IVS maps over different probe wavelengths. Green and red shaded Raman spectra refer to resonant and non-resonant conditions, respectively. d Fitted peaks positions of the measured Raman modes (with the corresponding 95% confidence boundaries) as a function of the probed wavelength. Red and green symbols refer to Raman modes obtained by pumping at 1.86 and 2.46 eV, respectively. Vertical dashed lines indicate the position of MAPbBr3 ground state vibrational modes reported in literature25. e, f Representations of the ISRS and DECP processes, respectively. The red arrows indicate the double interactions with the pump pulse, which generates a vibrational coherence in the ground and excited state27. In ISRS, immediately after photoexcitation, the vibrational wavepacket is peaked at the equilibrium position and then starts oscillating along the normal mode coordinate. In DECP, the ground state wavepacket is projected onto the excited state, where it begins oscillating from a starting position far from the equilibrium. We stress that for other class of materials, as III–V semiconductors, additional generation mechanisms are possible42
In the off-resonant case, we observe peaks at 64, 78, 98, 121, 134 cm−1. These frequencies are in good agreement with theoretical calculations and continuous wave (CW) Raman spectra18,30,31 (for which the peak positions of the modes are reported in Fig. 2d as dashed vertical lines31), and represent the vibrational degrees of freedom exhibited by the lead-halide octahedra, pointing to the inherent softness of the inorganic cage15. The modes at 98 and 134 cm−1 have been assigned to the symmetric stretch modes of the Br–Pb–Br bond, the mode at 121 cm−1 to the asymmetric stretch. The 64 and 78 cm−1 are the corresponding symmetric and asymmetric scissoring modes. The measured full widths at half maximum of the modes are in agreement with phonon dephasing times Γ−1 ~1 ps. Under such non-resonant excitation regime, coherent phonons are generated exclusively by a Stimulated Raman Scattering process, Impulsively activated by a pump pulse shorter than the phonon period (ISRS)21. Within such a scenario, coherent lattice motions are induced in the electronic ground state and the obtained spectrum is analogous to the CW Raman.
Using green resonant pump, we observe four modes of which 64 and 121 cm−1 were also present in the non-resonant case. The strong presence of these modes in the current case can be attributed to the selective enhancement of the ISRS for the ground state vibrational modes which are strongly coupled to the electronic transition32,33 via electron–phonon interactions (Fig. 2e). Such coupling has also been observed via temperature dependent photoluminescence spectroscopy9 and via mid infrared spectroscopy34. Remarkably, we observe additional phonon modes at 89 and 106 cm−1 that are not present in the CW Raman. In fact, in the presence of an excited state potential energy surface shifted with respect to the ground state, coherent vibrational modes can also be stimulated via a displacive excitation process (DECP). This is illustrated in Fig. 2f for the case of molecular systems, where a geometrical rearrangement of the atoms is driven by the dynamics of the vibrational wavepacket in the electronically excited state. In close analogy, in crystalline materials DECP allows for the generation of coherent phonons at frequencies distinct from the ground state vibrational modes35. Hence, we suggest the 89 and 106 cm−1 lines, appearing only in resonant-IVS, to be DECP generated. Analysis of the fluence dependence and phase lag between the measured phonons (presented in Supplementary Note 2) further substantiate this assignment. Specifically: (i) ISRS and DECP modes scale differently with pump fluences (Supplementary Figure 7). (ii) The relative phase difference between those modes observed in the non-resonant case is approximately null (see Supplementary Note 2 and Supplementary Figure 6), due to a wavepacket generation occurring in the energy minimum of the stimulated vibrational coordinate (Fig. 2e). On the other hand, there is a non-zero phase difference between the ISRS modes (64 and 121 cm−1) and the DECP (89 and 106 cm−1) observed in the resonant-IVS (Supplementary Figure 6), as these latter originate from the vertical projection of the initial ground state wavepacket onto an out-of-equilibrium position of the new lattice geometry (Fig. 2f). Accordingly, these are the modes driving the crystalline distortion through transient lattice oscillations, leading to a new configuration—along a specific reaction coordinate—reached after a quarter of the period of the corresponding phonon (T/4 = 80 and T/4 = 95 fs), and completely relaxed within the phonon lifetime (Γ−1 ~1 ps).
Discussion
Although in crystalline materials the lattice coordinates of the excited states are usually expected to remain similar to that of the ground state36, our observations indicate a geometrical reorganization upon electronic excitation in the case of methylammonium lead-bromide perovskite, which may be due to their strongly polar nature37. This is consistent with some recent observations on hybrid perovskites performed by means of optical Kerr effect [7]. Notably, shifts in the equilibrium positions and vibrational energies of the crystal in the presence of photo-generated carriers presented here are highly suggestive of strong electron–phonon coupling and thus of the polaronic nature of the carriers38. Within the Fröhlich model39 (see Supplementary Note 3), an estimate of the electron–phonon coupling strength is expressed through the dimensionless coupling constant α38, which can be directly extracted from the DECP phonon frequencies obtained by the IVS measurements as
ω eff represents the weighted sum of the DECP frequencies and is calculated through the relation \(\omega _{eff} = \sqrt {\mathop {\sum}\nolimits_i {A_i^2/\mathop {\sum }\limits_i \frac{{A_i^2}}{{\omega _i^2}}} }\), being A i the spectral amplitudes of the modes, ε is the dielectric constant of vacuum, while we consider ε0 = 25 and ε∞ = 6.7 for the static and high frequency dielectric constants40. We estimate αe = 1.84, αh = 1.28, for electron and hole, respectively. We note that these values are in agreement with those obtained for other hybrid perovskites by previous studies9, in which the estimations were based on combined first-principles calculations and indirect PL measurements.
These results allow estimating a lower bound for the polaron binding energy (Eb), which can be evaluated from the DECP frequencies and a perturbative expansion in terms of the coupling constant α within the Fröhlich formalism, obtaining an effective value \(\frac{{E_{\mathrm b}}}{{K_{\mathrm B}}} \approx {{538}}\) K. This suggests a possible rationale for the extended carrier lifetime. Indeed an energy barrier equal to Eb, significantly above the thermal energy kBT, should be crossed by the carriers to relax back into the groundstate and restore the original lattice geometry.
It should be stressed that our estimates are based on electron–phonon interactions within a Fröhlich-like mechanism, whilst the observation of lattice reorganization upon photo-excitation suggests presence of additional strong coupling contributions. The unambiguous ultrafast dynamics presented here can offer experimental benchmarks in order to further develop polaron models in these materials.
Interestingly, on the timescale of the observed lattice rearrangement, the transient absorption spectrum presents a photo-bleaching band arising from the state-filling convolved with a derivative like line-shape (see Supplementary Figure 1), which is generally the signature of Coulomb effects on the electronic/excitonic transition41. Although photo-bleaching follows the charge carrier dynamics, living for hundreds of picoseconds26, the derivative feature decays within the first picosecond, i.e., during the time interval taken by the new lattice geometry to equilibrate, supporting the presence of ionic displacements which could potentially screen any Coulomb correlations.
In conclusion, by contrasting the response obtained upon resonant and non-resonant pumping, we demonstrated how IVS can be employed to isolate those phonons coupled to a specific electronic transition in hybrid perovskites. Most importantly, we revealed the key phonon modes, generated via displacive excitation mechanism, which provide the pathway to the photo-induced lattice modification occurring upon carrier generation. Since electronic band states, as well as Wannier excitons would not show an associated pattern of displaced atomic equilibrium positions, our results provide evidence for the polaronic nature of photo-excitation in methylammonium lead-bromide perovskite. We anticipate our approach to be applicable to different lead halide perovskites to reveal general aspects and system-specific peculiarities of the photocarriers nature.
Methods
Sample preparation
Lead(II) bromide (PbBr2, ≥98%) and N,N-dimethylformamide (DMF, anhydrous, 99.8%) were purchased from Sigma-Aldrich; methylammonium bromide (MABr) was purchased from Dyesol. All chemicals were used without any further purification. Glass substrates were cleaned in acetone and isopropyl alcohol for 10 min by sonication. The cleaned glass substrates were treated with Oxygen plasma for 10 min before the perovskite deposition. An equimolar solution of PbBr2 and MABr was prepared in DMF (20 wt%) and spin coated on the substrate at 3000 rpm for 60 s, and immediately annealed at 100 °C for 15 min, under inert atmosphere. In order to avoid photo-degradation, the sample was encapsulated by a thick polymethyl methacrylate (PMMA) layer and measured in air, which hampers the formation of intra-gap defect states. The details of the experimental setup are reported in Supplementary Note 1.
Data availability
All relevant data are available from the authors.
References
Stoumpos, C. C. & Kanatzidis, M. G. The renaissance of halide perovskites and their evolution as emerging semiconductors. Acc. Chem. Res. 48, 2791–2802 (2015).
Zhu, X. Y. & Podzorov, V. Charge carriers in hybrid organic-inorganic lead halide perovskites might be protected as large polarons. J. Phys. Chem. Lett. 6, 4758–4761 (2015).
Stranks, S. & Snaith, H. J. Metal-halide perovskites for photovoltaic and light-emitting devices. Nat. Nanotechnol. 10, 391–402 (2015).
Herz, L. M. Charge-carrier dynamics in organic-inorganic metal halide perovskites. Annu. Rev. Phys. Chem. 67, 65–89 (2016).
Miyata, K. et al. Large polarons in lead halide perovskites. Sci. Adv. 3, e1701217 (2017).
Ghosh, T., Aharon, S., Etgar, L. & Ruhman, S. Free carrier emergence and onset of electron−phonon coupling in methylammonium lead halide perovskite films. J. Am. Chem. Soc. 139, 18262–18270 (2017).
Srimath Kandada, A. R. & Petrozza, A. Research Update: luminescence in lead halide perovskites. APL Mater. 4, 91506 (2016).
Zhu, H. et al. Screening in crystalline liquids protects energetic carriers in hybrid perovskites. Science 353, 1409–1413 (2016).
Wright, A. D. et al. Electron–phonon coupling in hybrid lead halide perovskites. Nat. Commun. 7, 11755 (2016).
Wu, X. et al. Light-induced picosecond rotational disordering of the inorganic sublattice in hybrid perovskites. Sci. Adv. 3, e1602388 (2017).
Hutter, E. M. et al. Direct–indirect character of the bandgap in methylammonium lead iodide perovskite. Nat. Mater. 16, 115–120 (2017).
Moser, J.-E. Perovskite photovoltaics: slow recombination unveiled. Nat. Mater. 16, 4–6 (2017).
Castro Neto, A. H. & Guinea, F. Electron–phonon coupling and Raman spectroscopy in graphene. Phys. Rev. B 75, 45404 (2007).
Ferrante, C. et al. Raman spectroscopy of graphene under ultrafast laser excitation. Nat. Commun. 9, 308 (2018).
Quarti, C., Grancini, G. & Mosconi, E. The Raman Spectrum of the CH3NH3PbI3 hybrid perovskite: interplay of theory and experiment. J. Phys. Chem. Lett. 5, 279–284 (2014).
Park, B. et al. Resonance Raman and excitation energy dependent charge transfer mechanism in halide substituted hybrid perovskite solar cells. ACS Nano 9, 2088–2101 (2015).
Brivio, F. et al. Lattice dynamics and vibrational spectra of the orthorhombic, tetragonal, and cubic phases of methylammonium lead iodide. Phys. Rev. B 92, 144308 (2015).
Leguy, A. M. A. et al. Dynamic disorder, phonon lifetimes, and the assignment of modes to the vibrational spectra of methylammonium lead halide perovskites. Phys. Chem. Chem. Phys. 18, 27051–27066 (2016).
Selig, O. et al. Organic cation rotation and immobilization in pure and mixed methylammonium lead-halide perovskites. J. Am. Chem. Soc. 139, 4068–4074 (2017).
Monahan, D. M. et al. Room-temperature coherent optical phonon in 2D electronic spectra of CH3NH3PbI3 perovskite as a possible cooling bottleneck. J. Phys. Chem. Lett. 8, 3211–3215 (2017).
Dhar, L., Rogers, J. A. & Nelson, K. A. Time-resolved vibrational spectroscopy in the impulsive limit. Chem. Rev. 94, 157–193 (1994).
Liebel, M., Schnedermann, C., Wende, T. & Kukura, P. Principles and applications of broadband impulsive vibrational spectroscopy. J. Phys. Chem. A 119, 9506–9517 (2015).
Kahan, A., Nahmias, O., Friedman, N., Sheves, M. & Ruhman, S. Following photoinduced dynamics in bacteriorhodopsin with 7-fs impulsive vibrational spectroscopy. J. Am. Chem. Soc. 129, 537–546 (2007).
Schnedermann, C. et al. Vibronic dynamics of the ultrafast all-trans to 13-cis photoisomerization of retinal in channelrhodopsin-1. J. Am. Chem. Soc. 138, 4757–4762 (2016).
Motti, S. G. et al. Photo-induced emissive trap states in lead halide perovskite semiconductors. ACS Energy Lett. 1, 726–730 (2016).
Grancini, G. et al. Role of microstructure in the electron–hole interaction of hybrid lead halide perovskites. Nat. Photonics 9, 695–701 (2015).
Liebel, M. & Kukura, P. Broad-band impulsive vibrational spectroscopy of excited electronic states in the time domain. J. Phys. Chem. Lett. 4, 1358–1364 (2013).
Monacelli, L. et al. Manipulating impulsive stimulated raman spectroscopy with a chirped probe pulse. J. Phys. Chem. Lett. 8, 966–974 (2017).
Gdor, I., Ghosh, T., Lioubashevski, O. & Ruhman, S. Nonresonant raman effects on femtosecond pump–probe with chirped white light: challenges and opportunities. J. Phys. Chem. Lett. 8, 1920–1924 (2017).
Yaffe, O. et al. Local polar fluctuations in lead halide perovskite crystals. Phys. Rev. Lett. 118, 136001 (2017).
Niemann, R. G. et al. Halogen effects on ordering and bonding of CH3NH3 + in CH3NH3PbX3 (X = Cl, Br, I) Hybrid perovskites: a vibrational spectroscopic study. J. Phys. Chem. C 120, 2509–2519 (2016).
Trommer, R. & Cardona, M. Resonant Raman scattering in GaAs. Phys. Rev. B 17, 1865–1876 (1978).
Stevens, T., Kuhl, J. & Merlin, R. Coherent phonon generation and the two stimulated Raman tensors. Phys. Rev. B 65, 144304 (2002).
Sendner, M. et al. Optical phonons in methylammonium lead halide perovskites and implications for charge transport. Mater. Horiz. 3, 613–620 (2016).
Zeiger, H. J. et al. Theory for displacive excitation of coherent phonons. Phys. Rev. B 45, 768 (1992).
Pinczuk, A. & Burstein, E. in Light Scattering in Solids I (ed. Cardona, M.) 23–78 (Springer, 1983).
Shiang, J. J., Goldstein, A. N. & Alivisatos, A. P. Lattice reorganization in electronically excited semiconductor clusters. J. Chem. Phys. 92, 3232–3233 (1990).
Emin, D. Polarons (Cambridge University Press, 2013).
Fröhlich, H. Electrons in lattice fields. Adv. Phys. 3, 325–361 (1954).
Chang, Y. H., Park, C. H. & Matsuishi, K. First-principles study of the structural and the electronic properties of the lead-halide-based inorganic-organic perovskites (CH3NH3) PbX3 and CsPbX3 (X = Cl, Br, I). J. Korean Phys. Soc. 44, 889–893 (2004).
Schmitt-Rink, S., Chemla, D. & Miller, D. Theory of transient excitonic optical nonlinearities in semiconductor quantum-well structures. Phys. Rev. B 32, 6601–6609 (1985).
Pfeifer, T., Dekorsy, T., Kütt, W. & Kurz, H. Generation mechanism for coherent LO phonons in surface-space-charge fields of III-V-compounds. Appl. Phys. A Solids Surf. 55, 482–488 (1992).
Author information
Authors and Affiliations
Contributions
A.P. and A.R.S.K. pointed out the scientific case. G.B., G.F., C.F., and T.S. designed the experiment. G.B. and G.F. performed the measurements and analyzed the data, with contribution from A.R.S.K. M.G. prepared the samples. G.B., G.F., A.R.S.K., C.F., A.P., and T.S. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Batignani, G., Fumero, G., Srimath Kandada, A.R. et al. Probing femtosecond lattice displacement upon photo-carrier generation in lead halide perovskite. Nat Commun 9, 1971 (2018). https://doi.org/10.1038/s41467-018-04367-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-04367-6
This article is cited by
-
Anisotropic carrier dynamics and laser-fabricated luminescent patterns on oriented single-crystal perovskite wafers
Nature Communications (2024)
-
Exciton dissociation in 2D layered metal-halide perovskites
Nature Communications (2023)
-
Phonon-driven intra-exciton Rabi oscillations in CsPbBr3 halide perovskites
Nature Communications (2023)
-
Optical control of exciton spin dynamics in layered metal halide perovskites via polaronic state formation
Nature Communications (2022)
-
Light-intensity-dependent photoresponse time of organic photodetectors and its molecular origin
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.