Abstract
Anthropogenic impacts are perturbing the global nitrogen cycle via warming effects and pollutant sources such as chemical fertilizers and burning of fossil fuels. Understanding controls on past nitrogen inventories might improve predictions for future global biogeochemical cycling. Here we show the quantitative reconstruction of deglacial bottom water nitrate concentrations from intermediate depths of the Peruvian upwelling region, using foraminiferal pore density. Deglacial nitrate concentrations correlate strongly with downcore δ13C, consistent with modern water column observations in the intermediate Pacific, facilitating the use of δ13C records as a paleo-nitrate-proxy at intermediate depths and suggesting that the carbon and nitrogen cycles were closely coupled throughout the last deglaciation in the Peruvian upwelling region. Combining the pore density and intermediate Pacific δ13C records shows an elevated nitrate inventory of >10% during the Last Glacial Maximum relative to the Holocene, consistent with a δ13C-based and δ15N-based 3D ocean biogeochemical model and previous box modeling studies.
Similar content being viewed by others
Introduction
Nitrogen (N) is a fundamental component of amino acids and thus, essential for all living organisms1. The increasing use of chemical fertilizers to provide food for a growing global population and the burning of fossil fuels lead to a severe rise of fixed nitrogen in the biosphere2. Nitrate (NO3−) is one of the main limiting nutrients in the modern ocean3 and nitrate fertilization is considered to contribute to the ongoing ocean deoxygenation4,5. A strong climate sensitivity has been predicted for the global NO3− inventory and feedbacks on climate by the coupling of the biogeochemical carbon (C) and nitrogen (N) cycles through the biological pump1. A quantitative reconstruction of past reactive N inventories and feedbacks on other biogeochemical cycles throughout time might help us to predict scenarios for the future. Nevertheless, despite different estimates from numerical models, quantitative paleo-records for past reactive N budgets in the oceans are not yet available.
The main source for bioavailable N in the modern ocean is N2-fixation, performed by cyanobacteria6,7, while the main loss of mineralized N results from denitrification and anaerobic ammonium oxidation (Anammox) in oxygen deficient zones (ODZs) in the sediments as well as in the water column7,8,9. Estimates of past inventories of reactive N species are mainly based on geological records of the fractionation between the N isotopes 15N and 14N (given as δ15N in ‰) in bulk sedimentary organic matter (δ15Nbulk). The complexity of various Ncycle processes influencing δ15N (e.g. N2 fixation, sedimentary or water column denitrification, NO3− utilization, remineralization and nitrification) complicates a quantitative reconstruction of the N budget based on δ15N alone.
Models have used global δ15Nbulk records for estimating changes in the past N budget. Box modeling studies10,11 agree that the inventory of reactive N was likely elevated during cold phases mainly due to a reduction of denitrification in the water column and seafloor sediments, related to enhanced O2 solubility in colder seawater and decreased area of shelf sediments from lower sea level, respectively. Additionally, enhanced N2 fixation from atmospheric iron deposition has been proposed8,12. Estimated changes from box models based on δ15Nbulk range from 5 to 100%7,10,11 increase of reactive N during glacials as compared to interglacials. Another box model study, which is not based on δ15Nbulk13, predicts changes in the global oceanic nutrient budgets due to changes in sea-level, dust deposition, and ocean circulation. This study estimates an increase in dissolved N (DN) of ~16% during the late Holocene compared to the Last Glacial Maximum. This is generally consistent with a study representing glacial nitrogen cycling constrained by isotopes in a 3D global ocean biogeochemical model considering LGM boundary conditions that predicts a glacial Nbio increase between 6.5 and 22%7.
A main focus of our study is the reconstruction of past NO3− concentrations ([NO3−]) using the pore density of benthic foraminifera. Foraminifera are one of the rare examples of eukaryotes which are able to use NO3− as an electron acceptor when oxygen is depleted within their habitats and play an important role in the oceanic benthic nitrogen cycle14,15,16. The pore density in the shells of Bolivina spissa is significantly correlated to the [NO3−] in their habitats because the pores facilitate the uptake of electron acceptors for respiration17. A comprehensive review about the functionality of pores in benthic foraminifera can be found in ref. 18. The functionality of pores in Foraminifera ranges from gas exchange for the uptake of electron acceptors and the release of metabolic waste products like CO219 to the uptake of dissolved organic material20. Foraminifera from oxygen depleted environments typically show an increased porosity21 and often a clustering of mitochondria under the pores19,22. Several recent studies describe the influence of oxygen availability on foraminiferal pore characteristics23−25. While some species adapt their porosity by changing the size of their pores25, other species are adapting the numbers of pores (pore density) in their tests17,23,24.
Benthic Foraminifera from oxygen depleted environments have recently been shown to use NO3− as electron acceptor14,15. At least one species, B. spissa, from the Peruvian ODZ, adapts its pore density to the availability of NO3− in its habitat17. A comparison of 232 measurements of the pore density in B. spissa to the bottom water nitrate concentrations ([NO3−]BW] from 8 different sampling locations at the Peruvian continental margin revealed a significant linear relationship between both parameters. Another species from the Peruvian ODZ, Bolivina seminuda, has been shown to have a high affinity to NO3− availability26. The tests of B. seminuda are highly porous17. Every species of the genus Bolivina which has been analyzed so far, including B. seminuda, has the ability to denitrify15,27, which implies that denitrification is a common strategy of Bolivinidae for survival under oxygen depleted conditions. This makes species from this genus in particular candidates for paleo NO3− reconstruction by analyses of pore characteristics as an empirical proxy.
We determined the pore density of the benthic foraminiferal species B. spissa as a quantitative paleoproxy for [NO3−] in intermediate waters (1250 m) at the Peruvian continental margin over the last deglaciation. The foraminiferal pore density is providing a tool to reconstruct past [NO3−] in a high lateral and temporal resolution allowing to test model predictions. A comparison of the reconstructed [NO3−] to the stable carbon isotope ratio (δ13C) in our sedimentary record shows the same correlation as in intermediate depths of the modern Pacific, enabling us to reconstruct regional differences in deglacial [NO3−]. A first analysis of deglacial δ13C records reveals the same trend in deglacial [NO3−] change as reconstructed by the pore density and predicted by the different model studies.
Results
Deglacial changes in the oceanic reactive N inventory
We reconstructed bottom water NO3− concentrations ([NO3−]BW) using sediment core M77/2 52-2 (5°29′S; 81°27′W; 1250 m) from the Peruvian continental margin over the last deglaciation. Past [NO3−]BW was reconstructed using the pore density of the benthic foraminiferal species B. spissa (Fig. 1a, b; Supplementary Table 1) following the method published in ref. 18. The pore densities of 819 specimens were analyzed for this record to provide a statistically robust dataset in a sufficient temporal resolution (Fig. 1a). We distinguished between five different time intervals including the Last Glacial Maximum (LGM; 22–17 kyr BP), Heinrich Stadial 1 (H1; 17–15 kyr BP), Antarctic Cold Reversal (ACR; 15–12 kyr BP), Early Holocene (EH; 11.7–8.2 kyr BP) and Middle to Late Holocene (MLH; 8–0 kyr BP). The lowest pore densities (highest [NO3−]BW) occurred during the LGM. This difference is highly significant compared to all other individual time intervals (P < 0.001; N = 136; two-sided heteroscedastic Student´s T-test). The highest pore densities, and thus lowest [NO3−]BW, have been found for the MLH. This difference is also highly significant compared to all other time intervals (P < 0.001; N = 353).
Quantitative NO3− reconstruction and additional proxy records for sediment core M77/2 52-2 and comparison to different modeled NO3− budgets. a Pore density of Bolivina spissa and δ18OFORAM measured on Uvigerina peregrina (core M77/2 52-2). Error bars represent the standard error of the mean (1 SEM). Single data points represent mean pore density of 7–22 specimens (see Supplementary Table 1). b [NO3−]BW calculated from the pore density of B. spissa after equation 4 and inverse δ13CFORAM measured on U. peregrina (core M77/2 52-2). Error bars represent 1 SEM including a complete error propagation (see equations 5 and 6). Magenta symbols: Model predictions from our 3D global biogeochemical model based on δ15Nbulk for the location of M77/2 52-2. Gray line: Modern [NO3−]M in the same water depth taken from the closest station available in the GLODAPv2 database34 (Station see Methods). c Black: Relative changes of [NO3−]BW calculated from the pore density of B. spissa (core M77/2 52-2) compared to modern [NO3−] (indicated in b). Error bars represent 1 SEM. Turquoise line: Modeled relative changes of global [NO3−] based on global δ15Nbulk records (modified after ref. 10; model run for strong water column denitrification feedback)10. Magenta line: Relative changes of global dissolved inorganic nitrogen (DIN) predicted by the boxed earth system model from ref. 13. Gray crosses: Record of relative [NO3−]BW change based on the δ13CFORAM measured on U. peregrina (core M77/2 52-2) using equation 2. Blue triangle: Relative change of [NO3−] at the intermediate Pacific between LGM (19–23 kyrs BP) and Late Holocene (0–6 kyrs BP). Relative [NO3−] change was also calculated after equation 2 using the offset of mean δ13CFORAM measured on Cibicidoides spp. between the two time intervals in 14 sediment records from the Pacific. Error bars represent 1 SEM. Data has been taken from Petersen et al.37 and two additional references75,76. See Methods section for location details and local variability. Magenta square: Model predictions from our 3D global biogeochemical model based on δ15Nbulk for the location of M77/2 52-2 (ΔLGM-Pre-Ind.: Offset between both time intervals from b). d Record of δ15Nbulk and accumulation rates of organic matter52 in M77/2 52-2. The error bar is representing the standard deviation (2σ) of δ15N measurements on the reference standard (Acetanilide)
A comparison with continuous transient global box model simulations covering the last deglaciation10,11,13 provided evidence that the NO3− inventory at this location is driven by fluctuations of the global reactive N-inventory. A plot which compares relative changes in the global reactive N budget over the last deglaciation from the different modeling approaches with our quantitative [NO3−]BW record is shown in Fig. 1c. The pore density derived NO3− inventory during the LGM was elevated compared to the Holocene which corroborates estimations from previous biogeochemical model studies7,10,11,13 although it also reveals fluctuations in [NO3−]BW in a much higher temporal resolution. A 50-100% higher reactive N inventory is suggested for the LGM by another box model study by Eugster et al.11 and thus probably overestimates this change by one order of magnitude according to our reconstruction.
The δ15Nbulk record of our sediment core (Fig. 1d) showed trends similar to other records from the Eastern Tropical South Pacific (ETSP) and the Eastern Tropical North Pacific (ETNP)10,28. It depicted the typical maximum of δ15Nbulk in these regions during the last deglaciation, which was caused by an acceleration in water column denitrification relative to the LGM10,28. The increase in benthic denitrification at the shallow shelf due to sea level rise and increased shelf area was slower than the increase of denitrification in the water column. The balancing between enhanced denitrification in the water column and sedimentary denitrification by N2 fixation, which introduces low δ15N into the ocean, at the onset of the Holocene leads to a subsequent reduction in δ15Nsed.org29.
Deglacial coupling of δ13C and NO3 − in intermediate depths
A comparison between the reconstructed [NO3−]BW and δ13C measured on Uvigerina peregrina in the same sediment core (δ13CFORAM, Fig. 1b) showed a strong coupling starting from the LGM and persisting over deglaciation until the Late Holocene. The mean δ13C signature of dissolved inorganic carbon (δ13CDIC) in seawater is controlled by the balance between terrestrial and marine carbon sources and sinks13,30,31,32, while the spatial distribution of δ13CDIC is mainly controlled by photosynthesis, respiration, and the ventilation and mixing between different water masses30,31,32,33. Autotrophic organisms preferably take up the lighter isotope 12C during photosynthesis. Thus, surface water masses have more positive δ13CDIC and are depleted in DIC, since 12C-carbon is preferably exported as organic matter. In intermediate to deep water masses organic matter is readily remineralized by respiration, which leads to an increase in DIC and a decrease of δ13CDIC within these water masses. An increase in photosynthesis leads to a higher export productivity and thus a stronger gradient in δ13CDIC between surface and deep water masses established through the biological carbon pump.
Since photosynthesis and respiration both influence the distribution of major nutrients in the ocean, there is an inverse relationship between δ13CDIC and [NO3−] and [PO43−] in the modern ocean, with a stronger correlation to [NO3−] than [PO43−]33. The distributions of [NO3−] and δ13CDIC in water masses of the modern Pacific, taken from the GLODAPv2 database34, are shown in Fig. 2a, b. Both distributions are similar since the main processes affecting δ13C also affect the NO3− distribution. Surface water masses show high δ13CDIC and low [NO3−] through primary productivity, while the intermediate to deep water masses show low δ13CDIC and higher [NO3−] through remineralization of exported organic matter. All these processes define the endmembers of δ13CDIC and [NO3−] in different water masses and thus the mixing processes between different water masses follow the same trend.
Distribution of NO3- and δ13CDIC in the modern Pacific and [NO3−]-δ13CDIC-coupling in the intermediate Pacific - modern and downcore. All data for the modern Pacific have been taken from the GLODAPv2 database34. a Distribution of [NO3−] in the modern Pacific34. b Distribution of δ13C of dissolved inorganic carbon (DIC; δ13CDIC) in the modern Pacific34. The Ocean Data View software has been used to compile these plots62. c Correlation between [NO3−] and δ13CDIC in intermediate water depths (700–2000 m) of the modern Pacific (red, N = 4779) and between [NO3−]BW and δ13CFORAM in the sediment record of M77/2 52-2 (black, N = 44). Both linear regressions neither differ significantly in slope (P = 0.15) nor in intercept (P = 0.13). Due to graphical reasons all δ13C below −1‰ have been cut in this plot, although they were included into the fit. For a complete plot of all data points see Supplementary Figure 4B
A comparison of the correlation of downcore [NO3−]BW and δ13CFORAM, and the correlation of dissolved NO3− and δ13CDIC in intermediate water depths (700–2000 m) of the recent Pacific34, is shown in Fig. 2c. Both linear regressions were highly significant (P < 0.001) and neither slopes nor intercepts significantly differed from each other (Slope: P = 0.15; Intercept: P = 0.13). Thus, [NO3−]BW and δ13C in our downcore record showed basically the same correlation over the last 22 kyrs as [NO3−] and δ13C of DIC in intermediate water depths of the modern Pacific. We propose that the linear regression between [NO3−] and δ13CDIC (eq. 1 and eq. 2) can be used to quantitatively reconstruct past [NO3−].
Alternatively solved for [NO3−]:
3D Biogeochemical model on deglacial δ13CDIC-[NO3 −] coupling
The distribution of δ13C and [NO3−] has been modeled for the modern ocean, the pre-industrial Holocene and the LGM (Fig. 3) using a coupled 3D ocean circulation-biogeochemical isotope model. The model system used here is an improved version of Somes et al.7 by including the carbon isotope cycling following Schmittner and Somes35,36 and optimizing LGM iron deposition patterns to better reproduce δ15Nbulk observations (see Supplementary Figure 1). The modeling results indicated no significant difference in the relationship of the δ13CDIC-[NO3−] correlation in the deep intermediate Pacific at our core location (i.e. [NO3−]BW µM; Supplementary Figure 2) during the different climatic time intervals. This supported our comparison of the M77/2-52-2 sediment record to the modern δ13CDIC-[NO3−] distribution. The [NO3−]BW reconstruction using our pore density proxy during the LGM and MLH at our sampling location corresponded well to our independent global biogeochemical model based on sedimentary δ15Nbulk records. The predictions of our global 3D biogeochemical model for the sampling location of M77/2 52-2 are shown in Fig. 1b for the LGM and the pre-industrial Holocene. The best prediction from this model of 7.4% (uncertainty range 2.7–11%; Supplementary Table 2), was generally consistent with the relative offset in the nitrate inventory between the LGM and MLH of ~10% from our pore density record. It has to be noted that the model predicted that the increase to the global [NO3−] inventory was 1.5 µM larger than at our core location.
Model simulations of [NO3−]-δ13CDIC coupling in the intermediate Pacific for different time intervals. Correlation between [NO3−] and δ13CDIC in intermediate water depths (700–2000 m) of the Pacific for the for the modern (red crosses; 1990–2010 average after accounting for decreased atmospheric δ13CCO2), pre-industrial (blue x’s) and LGM (black squares) from the 3D ocean biogeochemical isotope model
Intermediate Pacific [NO3 −] records by the use of δ13CForam
The reconstructed relative [NO3−]BW changes from the pore density of B. spissa and another [NO3−]BW reconstruction based on the δ13CFORAM record on U. peregrina and equation 2 are showing the same trends and magnitude (Fig. 1c). The δ13CFORAM based reconstruction is more noisy. This is probably due to the sample size and numbers of measurements for each data point. The pore density record averages individual measurements on a higher number of specimens (N ~ 20), while the δ13CFORAM record consists only of a single measurement on a bulk sample of a few specimens (N ~ 5). Another reason might be an influence of microhabitat preferences of U. peregrina on δ13CFORAM (Supplementary Note 1).
Globally, more than 400 records of δ13CFORAM measured on epifaunal Cibicidoides spp. are available37. From the compilation of downcore records we extracted all available δ13CFORAM records from Pacific intermediate water depths (700–2000 m, Supplementary Table 3). This provides the possibility to test if the δ13CDIC-[NO3−]-correlation might be also used at different sampling locations. Using the offset between mean δ13C from the LGM (19–23 kyrs BP) to the late Holocene (0–6 kyrs BP), we calculated the average relative change of [NO3−] between both time intervals. Once again, this result indicates that [NO3−] was 3.0 (±0.5 1 SEM; N = 14) µmol/kg higher during the LGM (Fig. 1c). These first tests indicate that δ13CFORAM from Pacific intermediate water depths might indeed be used to reconstruct deglacial [NO3−] changes. An attempt to use these records to reconstruct regional differences in the intermediate Pacifific is shown in Supplementary Figure 3 (see Methods section for details).
Discussion
In this study, we show the application of a new quantitative NO3− paleoproxy using pore density of the benthic foraminiferal species B. spissa. Furthermore, we propose that δ13CFORAM in benthic foraminifera from Pacific intermediate water depths is directly coupled to [NO3−] (Fig. 1). A first comparison of different available δ13CFORAM records measured on tests of the epibenthic Cibicidoides from the Pacific at intermediate water depths show similar trends as the pore density record and global biogeochemical model predictions (Fig. 1c).
We found a distinct offset of [NO3−]BW between the LGM and the MLH (Fig. 1b, c). The depletion of reactive N during warm periods compared to glacial periods can be explained by lower denitrification activity during the glacials1,7,10,11,12. N2 fixation may have also been stimulated by enhanced iron deposition11,12,13, although δ15Nsed.org records from the tropical North Pacific and Atlantic indicate reduced N2 fixation during glacials38,39 in response to reduced N loss, consistent with our 3D biogeochemical isotope model. Iron fertilization also led to additional export production and transport of remineralized NO3− into the deep Southern Ocean waters. This resulted in a reduction of preformed [NO3−] in Subantarctic Mode Waters (SAMW), which supply the tropical regions with preformed nutrients, affecting NO3− limitation at lower latitudes7.
A stronger stratification of Antarctic water masses due to decreased meridional overturning during the LGM probably supported the storage of remineralized nutrients in sluggish Antarctic Bottom Water and thus supported the decrease of preformed NO3− during the LGM40. This led to a decreased transport of preformed NO3− to the tropics limiting productivity, which reduces the volume of ODZs and thus denitrification7. Furthermore, the low sea level during the LGM led to a reduction of shelf seafloor area from 0 to 100 m water depths by 73%13. Shelf and hemipelagic sediments are the main contributors to sedimentary N loss processes29,41 today. Both processes, water column denitrification in ODZs and sedimentary denitrification, the main sinks for reactive N, were dampened during the LGM compared to the MLH28. The most distinctive offset to the global model predictions appears during H1, when [NO3−]BW was depleted for ~4 kyrs (Fig. 1b). This offset most probably represents local dynamics not accounted for in the coarse resolution of box model studies which are discussed in the Supplementary Note 2 together with local O2 fluctuations and their possible influence on local [NO3−]BW.
A comparison between the reconstructed [NO3−]BW and δ15Nbulk. (Fig. 1b, d) in our sediment core shows a phase shift at the beginning of the last deglaciation (~18 kyr BP): High [NO3−]BW during the LGM corresponds to more isotopic light δ15Nbulk while [NO3−]BW and δ15N were in phase during the deglaciation and the Holocene. At first glance, this might appear contradicting since heavier δ15Nbulk indicates higher water column denitrification, which would result in NO3− depletion. However, sediment core M77/2 52-2 is located in intermediate water depths well below the most oxygen (O2) depleted center of the ODZ near the thermocline. Deglacial water column denitrification mainly occurred in ODZs, and was probably stimulated by an enhanced supply of preformed nutrients that led to an increase in export production. As such, more organic N was transferred to intermediate water depths by the biological pump where it was decomposed to NO3− and increased ambient [NO3−]BW despite the N loss at shallower water depths.
Our comparison of δ13CFORAM to the reconstructed [NO3−]BW using the pore density proxy show how closely the oceanic carbon and nitrogen cycle were coupled over the last glacial/interglacial cycle in the Pacific. δ13CFORAM has extensively been used as a proxy of paleoproductivity before but also as proxy for ventilation and oxygenation42,43. Nevertheless, our study shows that the ratio between [NO3−]BW and δ13CFORAM over the last 22 kyrs at our sampling location remained unchanged and implies the possibility that δ13CFORAM might also be used as a quantitative NO3− proxy at intermediate water depths. Several locations of the modern Pacific show relatively low δ13CDIC values (Supplementary Figure 4). The positions of these locations mainly follow the distribution of anthropogenic CO2 in the Pacific (Scupplementary Note 3 and Supplementary Figure 5). Since the deglacial correlation between δ13CFORAM and reconstructed [NO3−]BW is not influenced by anthropogenic CO2, deviations from this correlation could even be used to trace anthropogenic CO2 in the modern ocean.
A factor controlling the mean δ13CDIC in seawater is the exchange of atmospheric CO2 with the ocean surface. A change in atmospheric pCO2 would also mediate disequilibrium in the surface ocean. However, a recent study showed that this pCO2 effect would cause a maximum δ13CDIC offset in subsurface waters of the Southern Ocean of ~0.2‰44. This deglacial offset is even smaller in other parts of the oceans and close to zero at our sampling location and thus cannot explain the changes of δ13CForam in our downcore record. Despite this low deglacial offset in δ13CDIC by the pCO2 effect the authors of named study caution to interpret δ13CForam as a nutrient proxy. The pCO2 effect might mask the influence of the biological pump on δ13CDIC if the pCO2 gradient is very strong at times of high atmospheric pCO2 such as during the early Cenozoic.
The fact that the correlation between δ13CDIC and NO3− in intermediate water depths of the Pacific was stable over the last deglaciation is unexpected at a first glance. Indeed, the main processes which control the distribution of δ13CDIC and NO3− in the oceans all influence both parameters as discussed above. However, the main factors controlling the oceanic NO3− budget (e.g., denitrification and N2 fixation) do not individually influence δ13CDIC in the same direction. It is possible that the main background driver controlling both processes is the deglacial change in sea level. The decreased area of continental shelves during the LGM in comparison to interglacial conditions led to a lower benthic denitrification and thus higher [NO3−], and a lower burial rate of organic carbon and thus a lower mean oceanic δ13C. Strong nitrogen cycle feedbacks are required to realistically model deglacial δ15N10. In this case, the main factor controlling the oceanic NO3− budget would indeed be the change in benthic denitrification due to the extension of shelf seafloor. The mean oceanic δ15N is controlled by the ratio of pelagic to benthic denitrification28 and the balance from N2 fixation. The decrease of δ15Nbulk in the Eastern Tropical North and South Pacific starting ~12 kyr BP can indeed be modeled by increasing the ratio of benthic to pelagic denitrification28 since benthic denitrification fractionates δ15N much less than pelagic denitrification.
Another factor, controlling both δ13CDIC and [NO3−] in different water masses is the ventilation and thus their reservoir age. Consistent evidence from different studies indicate a poorly ventilated deep Pacific during the LGM45,46,47. Data from the Eastern Equatorial Pacific (EEP) is very scarce, though, and shows some strong contrasts between different sampling locations and approaches45,47,48,49. Nevertheless, it is likely that deep water masses at the EEP were also poorly ventilated during the LGM. This older water mass would increase [NO3−] and reduce δ13CDIC by remineralization, as well as reduce oxygen concentration ([O2]) at these depths.
Contrarily, redox proxy records from the EEP indicate higher [O2] during the LGM at depths similar to our sampling location50. This is consistent with other redox proxy records from shallower depths in the Peruvian upwelling region, which indicated a less pronounced ODZ and lower primary productivity during the LGM51. Indeed, the accumulation rates of organic carbon (Acc. Rate. Corg) at our sampling site were lower during the LGM52 which also indicates a lower primary productivity above this sampling site (Fig. 1d). The elevated [O2] during the LGM are in disagreement with poorly ventilated water masses and thus cannot directly explain the tendencies within our record due to local changes in water mass ventilation. This suggests that local changes to overlying productivity have a strong impact on [O2]BW, whereas [NO3−]BW is more influenced by the global NO3− inventory that is determined by the large-scale balance between N2 fixation and denitrification. It might well be, though, that total changes in the nutrient budget of the Pacific are partly related to an increased reservoir age of the deep water masses, related to decreased meridional overturning.
The comparison of our record to the other deglacial δ13CFORAM records is considered as evidence, that coupling of [NO3−] and δ13CDIC was mainly controlled by the biological carbon pump at our sampling location in the intermediate Eastern Equatorial Pacific, and possibly at other regions of the intermediate Pacific. The situation might be different in the Atlantic Ocean, at greater depths or further back in Earth’s history. Independent calibrations are thus substantial to extend the application of δ13CForam as a quantitative [NO3−] proxy. Furthermore, it is unlikely that this proxy would work at shallow depths where the pCO2 effect might predominate the effect of the biological carbon pump.
Our 3D biogeochemical modeling results support that [NO3−] at our sampling location records changes in the global budget (predicted at our location: ∆NO3− = 3.0 µM), but also is affected by iron fertilization at high latitudes. Iron fertizliation decreases preformed nutrients in SAMW and shallow Antarctic Intermediate Water (AAIW), where our core location exists, of the Pacific due to the transfer of more remineralized nutrients to the deep Pacific. This process is observationally constrained in the 3D model by direct comparison to δ15Nbulk across the Southern Ocean (Supplementary Figure 1), which records changes to surface [NO3−] utilization in response to dust deposition7. Sensitivity simulations associated with Southern Ocean iron fertilization uncertainties cause [NO3−] changes at our location of ±0.7 µM on top of the direct impact on global [NO3−] (Supplementary Table 2). The increase to global [NO3−] in the model was 1.5 µM larger than bottom water [NO3−] change at our core location, which suggests that our sampling location underestimates changes to the global [NO3−] inventory.
Nevertheless, in order to prove coupling between δ13CDIC and [NO3−] in intermediate water depths at different locations on glacial/interglacial timescales, a systematic downcore comparison of benthic δ13CFORAM and the pore density of B. spissa needs to be extended. Although the presence of B. spissa is limited to the Pacific, it occurs both on the Eastern and Western Pacific continental margin17,53−55. The biogeochemical model results of our study revealed no significant difference of the δ13CDIC–[NO3−] correlation between the LGM and the pre-industrial Holocene at intermediate water depths of the Pacific. Whereas all evidence is pinpointing that the δ13CDIC–[NO3−] correlation remained stable at Pacific intermediate depths on Glacial-Interglacial timescales, the validity of this correlation in other basins, on different timescales or greater water depths is not yet constrained. We therefore caution to use this correlation on a global scale before additional work has been done on testing this proxy approach in different ocean basins.
Methods
Stratigraphy of sediment core M77-2 52-2
Core M77/2-52-2 was recovered during R/V Meteor cruise M77/2 in 200856. The age model and δ18O and δ13C data of sediment core M77/2-52-2 has already been published57 and added to the appendix. Volume defined samples were taken using cutoff syringes at 10 cm intervals. The samples were wet sieved on a 63−µm screen. The remaining >63 µm fraction of the samples was dried at 50 °C, weighed and stored for further analysis. Stable oxygen isotope (δ18OFORAM) measurements of the cores were done with three to six individuals of benthic foraminiferal species Uvigerina peregrina. The tests of single species were crushed. Isotopic measurements were done with a Thermo Scientific MAT253 mass spectrometer equipped with an automated CARBO Kiel IV carbonate preparation device at GEOMAR, Kiel. Isotope values were reported in per mil (‰) relative to the VPDB (Vienna Pee Dee Belemnite) scale and calibrated vs. NBS 19 (National Bureau of Standards) as well as to an in-house standard (Solnhofen limestone). Long-term analytical accuracy (1-sigma) for δ18OFORAM and δ13CFORAM was better than 0.06‰ and 0.03‰ on the VPDB scale. The data for δ18O and δ13C is listed in the Supplementary Table 1.
For the stable nitrogen isotope (δ15N) measurements, 10–15 mg of freeze dried bulk sediments were analyzed using a Thermo Scientific Flash 2000 Elemental Analyzer coupled to a Thermo Scientific Delta V Advantage isotope ratio mass spectrometer (IRMS) at NIOZ, Texel. Results were expressed in standard δ-notation relative to atmospheric N2 and the precision as determined using laboratory standards calibrated to certified international reference standards were <0.3‰. The data for δ18O, δ13C, and δ15N are listed in the Supplementary Table 1.
The already published age model is based on five 14C AMS dating measurements performed at Beta Analytic, Inc., Florida, USA, on the planktonic foraminifera species Neogloboquadrina dutertrei57. Conventional radiocarbon datings were calibrated applying the marine calibration set Marine 1358 and using the software Calib 7.059. Reservoir age of 102 yrs was taken into account according to the marine database (http://calib.qub.ac.uk/marine/). Ages are expressed in thousands of years (kyr) before 1950 AD (abbreviated as cal kyr BP). The radiocarbon based chronology of the core was supplemented and tuned using Analyseries software with δ18O record from a nearby core M77/2-059-160 and the Antarctic EPICA δ18O reference stack61.
Quantitative [NO3 −] record using foraminiferal pore density
Depending on the availability 7–22 Bolivina spissa specimens were picked of the >63 µm fraction from each sample of sediment core M77/2-52-2. All of the 819 specimens were mounted on aluminum stubs by the use of adhesive carbon pads. They were not sputter coated to preserve them for future geochemical analyses. Scanning electron micrographs were produced for every single individual using a Hitachi table top scanning electron microscope (TM3000 accelerating voltage of 5–15 kV and using back-scattered electrons (BSE) detector. Following the method published in ref. 17 to minimize ontogenetic effects we determined the pore density of the first (youngest) ten chambers only, relating to an area of about 50,000–60,000 µm2. For the calculation of [NO3−]BW we used the data shown in Fig. 7d of ref. 17. We plotted the data inversely to achieve a function in the form of Eq. 2:
where [NO3−]BW is the reconstructed bottom water nitrate concentration and PD is the pore density of B. spissa. The corresponding linear fit is shown in the Supplementary Figure 6. The resulting function (Eq. 4) has been used to quantitatively reconstruct [NO3−]BW.
For the calculation of the errors for the reconstructed [NO3−]BW a complete error propagation has been done including both the uncertainty of the mean PD within the samples and the uncertainties of the calibration function. The error propagation has been applied to Eq. 3 in the form of equation Eq. 5:
where \(\sigma _x\) is the uncertainty (1sd) of the corresponding parameter x (in this case [NO3−]BW, a, b and PD). Considering Eq. 4 this results in Eq. 6 for the calculation of \(\sigma _{\left[ {\mathrm {NO}_3^ - } \right]_{\mathrm {BW}}}\).
The standard error of the mean (SEM) for one sample was then calculated according to Eq. 7:
where n is the number of specimens analyzed in each sample. The results for each sample are summarized in Supplementary Table 1.
Recent δ13C on DIC and [NO3 −] in the intermediate Pacific
All data for recent δ13CDIC and [NO3−] are taken from the GLODAPv2 database34. The Ocean Data View (ODV) software has been used to compile the plots for Fig. 2a, b62. The dataset, which is shown in Fig. 2 and has been used to calculate equation 1 of the main manuscript, includes all data from 700–2000 m the recent Pacific, including parts of the Southern Ocean. Longitudinal boundaries were set to 118°E and 73°S, while latitudinal boundaries were set to 63°N and 79°S (Supplementary Figure 4A). This dataset includes 4956 measurements of both δ13C on DIC and [NO3−]. Due to graphical reasons, all δ13C below −1‰ have been cut Fig. 2c of the main manuscript. Nevertheless, all data were included into the linear fit shown in Fig. 2c and eq. 1. A complete plot of all data points can be found in Supplementary Figure 4B. Stations with low δ13C mainly follow the distribution of anthropogenic CO2 in the Pacific (Supplementary Note 3). The recent [NO3−] shown in Fig. 1b has been taken from the station within the GLODAPv2 database34 which was located closest to the location and within the same water depth of M77/2-52-2 (Station ID: 33205; Cruise: 316N19930222; Station: 356(B); 5°31’S; 85°50’W; 1278 m; [NO3−] = 41.1 µmol/l). This concentration was also used to calculate the Δ[NO3−] for the downcore data from the pore density shown in Fig. 1c.
Biogeochemical modeling results on δ13CDIC-[NO3 −] coupling
We use an improved model version of Somes et al.7, which is based on the UVic Earth System Climate Model63 with a version of Kiel biogeochemistry64. The physical ocean-atmosphere-sea ice model includes a three-dimensional (1.8 × 3.6°, 19 vertical levels) general circulation model of the ocean (Modular Ocean Model 2) with parameterizations such as diffusive mixing along and across isopycnals, eddy-induced tracer advection65, computation of tidally-induced diapycnal mixing over rough topography including sub-grid scale66, as well as anisotropic viscosity67 and enhanced zonal isopycnal mixing schemes in the tropics to mimic the effect of zonal equatorial undercurrents68. A two-dimensional, single level energy-moisture balance atmosphere and a dynamic-thermodynamic sea ice model are used, forced with prescribed monthly climatological winds69 and ice sheets70.
The LGM simulations were forced with boundary conditions from 21 kyr BP following the Paleo Model Intercomparison Project71 protocols as closely as possible with our model setup. This includes lower atmospheric concentrations of the greenhouse gases carbon dioxide, nitrous oxide, and methane, changes of Earth’s orbit, and the increased area and height of ice sheets70. The ocean grid bathymetry and total ocean volume remains unchanged relative to the pre-industrial simulation. However, effects of reduced sea level on sedimentary N loss are accounted for by calculating a new sub-grid scale bathymetry scheme assuming a constant 120 meters sea level reduction. An improved atmospheric Fe mask based on Somes et al., 20177 was applied by optimizing the model with δ15N observations (Supplementary Figure 1). These simulations assume global PO43− and phytoplankton N:P ratios were 10% higher during the LGM.
The marine ecosystem-biogeochemical model coupled within the ocean circulation includes 2 nutrients in the inorganic (NO3− and PO43−) and organic (DON and DOP) phases, 2 phytoplankton (ordinary and N2-fixing diazotrophs), zooplankton, sinking detritus, as well as dissolved O2, dissolved inorganic carbon, alkalinity, and Δ14C64. Iron limitation is calculated using monthly surface dissolved iron fields prescribed from the BLING model72.
The δ13C model is based on Schmittner and Somes35. The oceanic carbon cycle is governed by air-sea gas exchange of CO2, which fractionates isotopes such that surface ocean DIC is ~2‰, ~8.5‰ enriched compared to the atmosphere δ13CCO2 = −6.5‰. However, fractionation during air-sea gas exchange is temperature dependent such that colder waters have higher δ13CDIC. Uptake of DIC by phytoplankton fractionates by about −20‰ and depends on the pCO2 of surface waters. Remineralization of the isotopically light organic carbon in the subsurface increases DIC and decreases δ13CDIC there. Biological production of CaCO3 at the surface and dissolution at depths affects DIC and alkalinity in the model but its effect on carbon isotopes is negligible. Transient anthropogenic changes to atmospheric δ13CCO2 are accounted in the modern model simulation following Schmittner et al.36.
Nitrogen isotopes are fractionated by inventory-altering (N2 fixation and N loss) and internal-cycling (NO3− uptake, excretion, DON remineralization) processes in the model73. N2 fixation introduces isotopically light atmospheric nitrogen into the ocean (δ15NNfix = −1 ‰), whereas N loss fractionates strongly in the water column (ɛWCNl = 20‰) and lightly in the sediments (ɛSedNl = 3.75‰). NO3− uptake by phytoplankton fractionates NO3− at 6‰ in the model. Zooplankton excretion fractionates at 4‰ enriching its biomass in 15N relative to phytoplankton. DON remineralizes with a fractionation factor of 1.5‰ to reproduce upper ocean δ15N-DON observations mainly occurring within the range of 3–6‰74. For a detailed discussion about offsets between measurements and modeling of the modern δ13CDIC-[NO3−]-coupling see Supplementary Note 4 and Supplementary Figure 7.
Regional offsets between Holocene and LGM NO3 − inventories
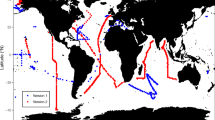
A compilation of deglacial δ13CFORAM change measured downcore on tests of Cibicidoides spp. has been published in ref. 37. We extracted all records from this compilation available from 700–2000 m using the same latitude/longitude window mentioned above (see also Supplementary Figure 4A). Relative [NO3−] changes were calculated after equation 1 using the offset of mean δ13CFORAM measured on Cibicidoides spp. between LGM (19–23 kyrs BP) and Late Holocene (0–6 kyrs BP). Four downcore datasets from two additional references75,76 were added which were not included in ref. 37. The results are compiled in Supplementary Table 3. For the comparison of mean deglacial changes in the Pacific NO3− inventories which is shown in Fig. 1c of the main manuscript, only the 14 stations located in the Pacific and measured on Cibicidoides spp. were used. These stations are clearly marked in Supplementary Table 3. The mean Pacific [NO3−] was 3.0 ( ± 0.5 1 SEM; N = 14) µmol/kg higher during the LGM. The mean offset between LGM and Holocene is slightly lower (2.3 ± 0.5 µmol/kg (1 SEM); N = 23) if also the sampling locations outside the Pacific are included. For a regional comparison of deglacial NO3− changes, including all stations see Supplementary Figure 3. The general trend of all stations again indicates a higher NO3− inventory during the LGM. Only individual stations in the Sea of Japan, the East China Sea and on the Southern Australian Continental Margin indicate no changes between LGM and Late Holocene. One station at the Southern Australian Continental Margin even indicated a depletion of NO3− during the LGM compared to the late Holocene. The highest deglacial [NO3−] changes are located a station south of New Zealand and in the Sea of Okhotsk, which is probably related to the high latitudes of these sediment cores. The Sea of Okhotsk was still covered by ice during the LGM.
Data availability
All data which support the findings of this study are either available online or within the Supplementary material. The foraminiferal pore density, reconstructed [NO3−]BW, δ18O, δ13C and δ15N for sediment record M77/2-52-2 is available in Supplementary Table 1. The data for δ13CFORAM and the reconstructed deglacial [NO3−] offsets for all records from the intermediate Pacific is available in Supplementary Table 3. The model code and output for the 3D Biogeochemical modeling on deglacial δ13CDIC-[NO3−] coupling are available on the GEOMAR Thredds Server (https://thredds.geomar.de).
References
Gruber, N. & Galloway, J. N. An Earth-system perspective of the global nitrogen cycle. Nature 451, 293–2296 (2008).
Hanke, A. & Strous, M. Climate, fertilization, and the nitrogen cycle. J. Cosmol. 8, 1838–1845 (2010).
Moore, C. M. et al. Processes and patterns of oceanic nutrient limitation. Nat. Geosci. 6, 701–710 (2013).
Stramma, L. et al. Expanding oxygen-minimum zones in the tropical oceans. Science 320, 655–658 (2008).
Schmidtko, S., Stramma, L. & Visbeck, M. Decline in global oceanic oxygen content during the past five decades. Nature 542, 335–339 (2017).
Karl, D. et al. Dinitrogen fixation in the world’s oceans. Biogeochemistry 57-58, 47–98 (2002).
Somes, C. et al. A three-dimensional model of the marine nitrogen cycle during the last glacial maximum constrained by sedimentary isotopes. Front. Mar. Sci. 4, 108 (2017).
Eugster, O. & Gruber, N. A probabilistic estimate of global marine N-fixation and denitrification. Glob. Biogeochem. Cycles 26, GB4013 (2012).
Devries, T. et al. Marine denitrification rates determined from a global 3-D inverse model. Biogeosciences 10, 2481–2496 (2013).
Deutsch, C. et al. Isotopic constraints on glacial/interglacial changes in the oceanic nitrogen budget. Glob. Biogeochem. Cycles 18, n/a–n/a (2004).
Eugster, O. et al. The dynamics of the marine nitrogen cycle across the last deglaciation. Paleoceanography 28, 116–129 (2013).
Falkowski, P. G. Evolution of the nitrogen cycle and its influence on the biological sequestration of CO2 in the ocean. Nature 387, 272–275 (1997).
Wallmann, K., Schneider, B. & Sarntheim, M. Effects of eustatic sea-level change, ocean dynamics, and nutrient utilization on atmospheric pCO2 and seawater composition over the last 130 000 years: a model study. Clim. Past. 12, 339–375 (2016).
Risgaard-Petersen, N. et al. Evidence for complete denitrification in a benthic foraminifer. Nature 443, 93–96 (2006).
Pina-Ochoa, E. et al. Widespread occurence of nitrate storage and denitrification among Foraminifera and Gromiida. Proc. Natl Acad. Sci. USA 107, 1148–1153 (2010).
Glock, N. et al. The role of benthic foraminifera in the benthic nitrogen cycle of the Peruvian oxygen minimum zone. Biogeosciences 10, 4767–4783 (2013).
Glock, N. et al. Environmental influences on the pore-density in tests of Bolivina spissa. J. Foramin. Res. 41, 22–32 (2011).
Glock, N., Schönfeld, J. & Mallon, J. in ANOXIA: Evidence for Eukaryote Survival and Paleontological Strategies, Cellular Origin, Life in Extreme Habitats and Astrobiology Vol. 21 (eds Altenbach, A. V., Bernhard, J. M. & Seckbach, J.) 540–556 (Springer Science+Business Media, 2012).
Leutenegger, S. & Hansen, H. J. Ultrastructural and radiotracer studies of pore function in foraminifera. Mar. Biol. 54, 11–16 (1979).
Berthold, W. U. Ultrastructure and function of wall perforations in Patellina corrugata Williamson, Foraminiferida. J. Foramin. Res. 6, 22–29 (1976).
Kaiho, K. Benthic foraminiferal dissolved-oxygen index and dissolved-oxygen levels in the modern ocean. Geology 22, 719–722 (1994).
Bernhard, J. M., Bowser, S. S. & Goldstein, S. An ectobiont-bearing foraminiferan, Bolivina pacifica, that inhabits microxic pore waters: Cell-biological and paleoceanographic insights. Environ. Microbiol. 12, 2107–2119 (2010).
Kuhnt, T. et al. Relationship between pore density in benthic foraminifera and bottom-water oxygen content. Deep Sea Res. 76, 85–95 (2013).
Kuhnt, T. et al. Automated and manual analyses of the pore density-to-oxygen-relationship in Globobulimina turgida (Bailey). J. Foramin. Res. 44, 5–16 (2014).
Petersen, J. et al. Improved methodology for measuring pore patterns in the benthic foraminiferal genus Ammonia. Mar. Micropalentol. 128, 1–13 (2016).
Cardich, J. et al. Calcareous benthic foraminifera from the upper central Peruvian margin: control of the assemblage by pore water redox and sedimentary organic matter. Mar. Ecol. Prog. Ser. 535, 63–87 (2015).
Bernhard, J. et al. Potential importance of physiologically diverse benthic foraminifera in sedimentary nitrate storage and respiration. J. Geophys. Res. 117, doi: 10.1029/2012jg001949 (2012).
Galbraith, E. D. et al. The acceleration of oceanic denitrification during deglacial warming. Nat. Geosci. 6, 579–584 (2013).
Devol, A. Direct measurements of nitrogen gas fluxes from continental shelf sediments. Nature 349, 319–321 (1991).
Emerson, S. & Hedges, J. I. Processes controlling the organic carbon content of open ocean sediments. Paleoceanography 3, 621–634 (1988).
Broecker, W. S. & Maier-Reimer, E. The influence of air and sea exchange on the carbon isotope distribution in the sea. Glob. Biogeochem. Cycles 6, 315–320 (1992).
Lynch-Stieglitz, J. et al. The influence of air-sea exchanges on the isotopic composition of oceanic carbon: Observations and modeling. Glob. Biogeochem. Cycles 9, 653–6666 (1995).
Ortiz, J. D. et al. Anthropogenic CO2 invasion into the northeast Pacific based on concurrent 13CDIC and nutrient profiles from the California Current. Glob. Biogeochem. Cycles 14, 917–929 (2000).
Olsen, A. et al. The Global Ocean Data Analysis Project version 2 (GLODAPv2)-an internally consistent data product for the world ocean. Earth Syst. Sci. Data 8, 297–323 (2016).
Schmittner, A. & Somes, C. J. Complementary constraints from carbon (13C) and nitrogen (15N) isotopes on the glacial ocean’s soft-tissue biological pump. Paleoceanography 31, 669–693 (2016).
Schmittner, A. et al. Biology and air-sea gas exchange controls on the distribution of carbon isotope ratios (δ13C) in the ocean. Biogeosciences 10, 5793–55816 (2013).
Petersen, C. D., Lisiecki, L. E. & Stern, J. V. Deglacial whole-ocean δ13C change estimated from 480 benthic foraminiferal records. Paleoceanography 29, 549–563 (2014).
Ren, H. et al. Foraminiferal isotope evidence of reduced nitrogen fixation in the ice age Atlantic Ocean. Science 323, 244–248 (2009).
Ren, H. et al. Impact of glacial/interglacial sea level change on the ocean nitrogen cycle. Proc. Natl Acad. Sci. USA 114, 6759–6766 (2017).
Skinner, L. C. et al. Ventilation of the deep Southern Ocean and deglacial CO2 rise. Science 328, 1147–1151 (2010).
Christensen, J. P. et al. Denitrification in continental shelf sediments has major impact on the oceanic nitrogen budget. Glob. Biogeochem. Cycles 1, 96–116 (1987).
Zahn, R., Winn, K. & Sarnthein, M. Benthic foraminiferal 13C and accumulation rates of organic carbon: Uvigerina peregrina group and Cibicidoides wuellerstorfi. Paleoceanography 1, 27–42 (1986).
Sarnthein, M. K. et al. Global variations of surface ocean productivity in low and mid-latitudes: Influence on CO2. Paleoceanography 3, 361–399 (1988).
Galbraith, E. D. et al. The impact of atmospheric pCO2 on carbon isotope ratios of the atmosphere and ocean. Glob. Biogeochem. Cycles 29, 307–324 (2015).
Shackleton, N. et al. Radiocarbon age of last glacial Pacific deep water. Nature 335, 708–711 (1988).
Sikes, E. L. et al. Old radiocarbon ages in the southwest Pacific Ocean during the last glacial period and deglaciation. Nature 303, 555–559 (2000).
De la Fuente, M. et al. Increased reservoir ages and poorly ventilated deep waters inferred in the glacial Eastern Equatorial Pacific. Nat. Commun. 6, 7420 (2015).
Broecker, W. S. et al. Ventilation of the glacial deep Pacific ocean. Science 306, 1169–1172 (2004).
Stott, L. et al Radiocarbon age anomaly at intermediate water depth in the Pacific Ocean during the last deglaciation. Paleoceanography 24, PA2223 (2009).
Moffitt, S. E. et al. Paleoceanographic insights on recent oxygen minimum zone expansion: lessons for modern oceanography. PLoS ONE 10, e0115246 (2015).
Salvatteci, R. et al. Centennial to millennial-scale changes in oxygenation and productivity in the Eastern Tropical South Pacific during the last 25,000 years. Quat. Sci. Rev. 131, 102–117 (2016).
Doering, K. et al. Changes in diatom productivity and upwelling intensity off Peru since the last glacial maximum: response to basin-scale atmospheric and oceanic forcing. Paleoceanography 31, 1453–11473 (2016).
Zheng, S. & Fu, Z. in Checklist of Marine Biota of China Seas (ed. Liu, J. Y.) 108-174 (China Science Press, Academia Sinica, Beijing, 2008).
Glud, R. N. et al. Nitrogen cycling in a deep ocean margin sediment (Sagami Bay, Japan). Limnol. Ocean. 54, 723–734 (2009).
Kim, S. et al. Modern benthic foraminiferal diversity of Jeju Island and initial insights into the total foraminiferal diversity of Korea. Mar. Biodivers. 46, 337–354 (2016).
Pfannkuche, O. et al. Climate-Biogeochemistry Interactions in the Tropical Ocean of the SE-American Oxygen Minimum Zone - Cruise No. M77 - October 22, 2008 - February 18, 2009 - Talcahuano (Chile) - Colon (Panama) (Meteor Ber University, Hamburg, 2011).
Erdem, Z. et al. Peruvian sediments as recorders of an evolving hiatus for the last 22 thousand years. Quat. Sci. Rev. 137, 1–14 (2016).
Reimer, J. et al. INTCAL13 and marine radiocarbon age calibration curves 0-50,000 years cal BP. Radiocarbon 55, 1869–1887 (2013).
Stuiver, M. & Reimer, P. J. Extended 14C data base and revised Calib 3.0 14C age calibration program. Radiocarbon 35, 215–230 (1993).
Mollier-Vogel, E. et al. Rainfall response to orbital and millenial forcing in northern Peru over the last 18 ka. Quat. Sci. Rev. 76, 29–38 (2013).
EPICA Community Members. One-to-one coupling of glacial climate variability in Greenland and Antarctica. Nature 444, 195–198 (2006).
Schlitzer, R. Ocean Data View (Alfred Wegener Institute Helmholtz Center for Polar and Marine Research, 2015).
Weaver, A. J. et al. The UVic earth system climate model: model description, climatology, and applications to past, present and future climates. Atmos. Ocean 39, 361–428 (2001).
Somes, C. J. & Oschlies, A. On the influence of “non-Redfield” dissolved organic nutrient dynamics on the spatial distribution of N2 fixation and the size of the marine fixed nitrogen inventory. Glob. Biogeochem. Cycles 29, 973–993 (2015).
Gent, P. R. & McWilliams, J. C. Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 20, 150–155 (1990).
Schmittner, A. & Egbert, G. D. An improved parameterization of tidal mixing for ocean models. Geosci. Model Dev. 7, 211–224 (2014).
Large, W. G. et al. Equatorial circulation of a Global Ocean climate model with anisotropic horizontal viscosity. J. Phys. Oceanogr. 31, 518–536 (2001).
Getzlaff, J. & Dietze, H. Effects of increased isopycnal diffusivity mimicking the unresolved equatorial intermediate current system in an earth system climate model. Geophys. Res. Lett. 40, 2166–2170 (2013).
Kalnay, E. et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–471 (1996).
Peltier, W. R. Global glacial isostacy and the surface of the ice-age Earth: the ICE-5G (VM2) model and GRACE. Annu. Rev. Earth. Planet. Sci. 32, 111–149 (2004).
Braconnot, P. et al. Evaluation of climate models using palaeoclimatic data. Nat. Clim. Change 2, 417–424 (2012).
Galbraith, E. D. et al. Regional impacts of iron-light colimitation in a global biogeochemical model. Biogeosciences 7, 1043–1064 (2010).
Somes, C. J. et al Simulating the global distribution of nitrogen isotopes in the ocean. Glob. Biogeochem. Cycles 24, GB4019 (2010).
Knapp, A. N., et. al. Interbasin isotopic correspondence between upper-ocean bulk DON and subsurface nitrate and its implications for marine nitrogen cycling, Glob. Biogeochem. Cycles 25, GB4004 (2010).
van der Kaars, S. et al. Humans rather than climate the primary cause of Pleistocene megafaunal extinction in Australia. Nat. Commun. 8, 14142 (2017).
Herguera, J. Intermediate and deep water mass distribution in the Pacific during the Last Glacial Maximum inferred from oxygen and carbon stable isotopes. Quat. Sci. Rev. 29, 1228–1245 (2010).
Acknowledgements
The scientific party on R/V Meteor cruise M77 is acknowledged for their general support and help with the coring operation and sampling. Tal Dagan supported this manuscript with feedback about the statistical evaluation of this study. We thank Ralph Schneider for the provision of the sediment core material used for this study and Ralf Schiebel for constructive feedback on an early draft of this manuscript. Additionally, we would like to thank Joachim Oesert for support at the electron microscope and Andreas Schmittner for developing and sharing the 13C model code. Funding was provided by the Deutsche Forschungsgemeinschaft (DFG) through the SFB 754 “Climate–Biogeochemistry Interactions in the Tropical Ocean” and the European Research Council (ERC) under the European Union’s Seventh Framework Program (FP7/2007-2013) ERC grant agreement [339206]. C.J.S. received support for his contribution from the PalMod project.
Author information
Authors and Affiliations
Contributions
N.G. analyzed and interpreted the foraminiferal pore density data, did the database investigation, main interpretation of δ13C records and core-writing of the manuscript. Z.E. provided the age model and stratigraphy and performed the δ15N analyses for core M77/2-55-2. K.W. provided the continuously modeled, global reactive N-inventory and contributed to the interpretation of the δ13C records. C.J.S. did the 3D Biogeochemical modeling on deglacial δ13CDIC-[NO3−] coupling. V.L. contributed to the initial interpretation of the nitrate record. J.S. provided additional information about available δ13C records. S.G. provided access to the electron microscope for the determination of foraminiferal pore densities. A.E. contributed to the discussion of data and interpretation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Glock, N., Erdem, Z., Wallmann, K. et al. Coupling of oceanic carbon and nitrogen facilitates spatially resolved quantitative reconstruction of nitrate inventories. Nat Commun 9, 1217 (2018). https://doi.org/10.1038/s41467-018-03647-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-03647-5
This article is cited by
-
A deep-learning automated image recognition method for measuring pore patterns in closely related bolivinids and calibration for quantitative nitrate paleo-reconstructions
Scientific Reports (2023)
-
The Peruvian oxygen minimum zone was similar in extent but weaker during the Last Glacial Maximum than Late Holocene
Communications Earth & Environment (2022)
-
Scaling laws explain foraminiferal pore patterns
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.