Abstract
Ultrafast spectroscopy with attosecond resolution has enabled the real time observation of ultrafast electron dynamics in atoms, molecules and solids. These experiments employ attosecond pulses or pulse trains and explore dynamical processes in a pump–probe scheme that is selectively sensitive to electronic state of matter via photoelectron or XUV absorption spectroscopy or that includes changes of the ionic state detected via photo-ion mass spectrometry. Here, we demonstrate how the implementation of combined photo-ion and absorption spectroscopy with attosecond resolution enables tracking the complex multidimensional excitation and decay cascade of an Auger auto-ionization process of a few femtoseconds in highly excited krypton. In tandem with theory, our study reveals the role of intermediate electronic states in the formation of multiply charged ions. Amplitude tuning of a dressing laser field addresses different groups of decay channels and allows exerting temporal and quantitative control over the ionization dynamics in rare gas atoms.
Similar content being viewed by others
Introduction
In the last decade, time-resolved spectroscopy with attosecond resolution1,2,3,4,5,6,7,8,9,10,11,12,13 has revolutionized our understanding of electron dynamics by capturing ultrafast processes in atoms, molecules and solids in real time. While the first photoelectron studies with attosecond resolution could, for example, track a few-femtosecond Auger process14, meanwhile ultrafast metrology became so advanced that unexpected delays in photoemission from atoms were discovered4,15, most recently down to sub-attosecond precision5. Attosecond time-resolved mass spectroscopy16,17 provided the first time-domain observation of field-induced tunnel ionization manifesting itself in a step-like rise in the ion yield. More recently, attosecond transient absorption detection could launch and detect valence electron wavepackets in atoms11, examine their interference with continuum states13 and enabled studying tunnel ionization in solids18.
Photoelectron detection techniques generally suffer from electron backgrounds produced by strong laser fields or secondary electrons that do not carry any information about the dynamics under inspection. The detection of the correspondingly produced ions, however, is background-free. Nevertheless, both methods require the release of photoelectrons and thus are suitable only for the study of ionizing events. Transient absorption spectroscopy (TAS) in contrast is not limited to phenomena liberating electrons and is the method of choice for investigating bound–bound transitions19,20. Instead of measuring the yield of generated charge carriers, TAS measures the spectrally resolved absorption of an attosecond extreme ultraviolet (XUV) pulse in a medium that has been coherently excited by an XUV pulse or dressed by an intense, time-delayed near-infrared (NIR) few-cycle laser pulse. This method typically provides a higher resolution in energy (ΔE/E ~ 10−3) than ion or electron detection (ΔE/E ~ 10−2 at best). However, it generally lacks the dynamic range to simultaneously detect the characteristic absorption signals of different co-existing ionic charge states due to insufficient spectral bandwidth or due to the absorption cross-sections and abundances of the different ionization states that typically vary by several orders of magnitude. TAS experiments have been successful in recording auto-ionizing state lifetimes in xenon12 and other species21. However, even a detailed theoretical investigation could not explain whether the interrogating ultrashort and intense NIR laser pulse couples the auto-ionizing states to neighboring resonances or to which extent excited electrons are promoted into the ionization continuum by the laser field22. In contrast, the ion detection that enabled the first observation of tunneling electrons in neon and xenon could track the change in ion yield of different charge states. However, mass spectroscopic studies to this date cannot resolve individual shake up satellites16.
To overcome the limitations of single observable experiments and in order to draw a complete picture of the co-evolving excitation/ionization dynamics, in this article we demonstrate the benefit of combining ion spectroscopy and transient absorption with attosecond temporal resolution. Merging these detection methods provides complementary insight into the excitation/decay mechanism as the transient absorption maps the initiating resonant excitation and the ion detection sensitively records the subsequent branching into intermediate and final states. The combination of transient absorption with ion spectroscopy compensates the limits in the simultaneous detection of several ionic states that absorption spectroscopy typically brings along. The prerequisite is that the pump–probe experiment can be performed twice under identical experimental conditions except for differing target densities optimized for the two detection methods. Adjusting the laser electric field amplitude allows selectively addressing different intermediate states of the auto-ionization cascades that follow the XUV excitation resulting in different apparent lifetimes. With that, the experimentalist obtains control of the temporal evolution and the absolute yield of the ionization dynamics by accessing different level groups in the cascade with different NIR intensities. The accompanying absorption measurement enables the determination of the instrument response function, the lifetimes of resonantly excited states involved in the process and proves that the overall conditions of the experiment (resonant excitation and ionization) remain unchanged for a large range of NIR intensities.
Results
Experiment
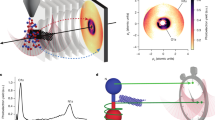
To explore the decay dynamics of highly excited krypton (see Fig. 1a), a phase-stabilized Ti:Sapphire few-cycle laser14,16,17 is used to produce isolated attosecond pulses (cp. Supplementary Fig. 1) via high harmonic generation in a pump–probe scheme united with a reflectron-type ion spectrometer and an XUV grating spectrometer (see Fig. 1b and Supplementary Note 1 for details). Figure 1c shows the transmission spectrum without (violet) and with (green) krypton gas sample with the NIR pulse preceding the XUV pulse by 150 fs. For the same time delay, Fig. 1d depicts the corresponding ion spectrum with singly, doubly and triply charged krypton ions. For the time-resolved studies, we measured the krypton transmission and ion spectrum scanning the arrival time difference between XUV and laser pulse.
Overview of the experiment. a Krypton excitation and decay scheme. The XUV pulse excites the 3d−15/2 np/3d−13/2 np states (violet arrow) that can decay via different Auger cascades (green arrows). Depending on the NIR laser intensity, the different intermediate Kr+ states can be further ionized to Kr3+: at low NIR intensities, the intermediate 4s−2np states can be ionized to Kr3+ (thin red arrow, INIR = (8.6 ± 1) × 1013 W cm−2), at higher NIR intensities, the 4p−34dnp/4s−14p−1np states can be ionized to Kr3+ (thick red arrow, (2.9 ± 0.5) × 1014 W cm−2). The direct XUV ionization and the corresponding decay channels are not shown for the sake of clarity, but are considered in the data analysis. For a more detailed figure see refs.17,31 for example. b Experimental setup with a double mirror configuration introducing a time delay between the XUV pulse and the NIR few-cycle pulse (the XUV pulse arriving first for positive time delays). XUV and NIR beams are focused into a krypton gas cloud. The remaining XUV radiation transmitted by the Kr gas is measured by an XUV spectrometer, while the Kr ions are detected by a reflectron-type ion spectrometer. c Incident XUV spectrum centered at 90 eV (violet) and a typical krypton transmission spectrum (green) showing the 3d−15/2 5p transition at 91.23 eV and the 3d−15/2 6p/3d−13/2 5p transitions at 92.45 eV, respectively. d Measured ion spectrum yielding singly, doubly and triply charged krypton ions. For the absorption and ion spectra of c and d, the NIR pulse was set to advance the XUV pulse by 150 fs (Δt = − 150 fs)
Merging ultrafast absorption and ion mass spectroscopy
Figure 2a shows the spectrally resolved change in absorbance (optical density OD = −log10(I t (Δt)/I0), with I0 as incident XUV spectrum) as function of the XUV/NIR time delay, while Fig. 2b depicts the isotope-resolved Kr3+ ion yield change. The absorbance starts to transiently decrease at XUV/NIR pulse synchrony while the Kr3+ ion yield shortly rises, however, with a slightly retarded response with respect to the absorption change.
Absorption and ionization spectroscopy measurements. a Spectrally resolved optical density OD with respect to the time delay between the XUV and the NIR pulse, revealing the 3d−15/25p and 3d−15/26p/3d−13/25p resonances at 91.23 eV and 92.45 eV, respectively. The XUV pulse is preceding the NIR pulse for positive times on the delay axis. The absorbance at the resonances transiently decreases at XUV/NIR pulse overlap and subsequently recovers almost to its original value, with an exponential time constant corresponding to the state lifetimes. b Time-dependent and isotope-resolved Kr3+ ion yield. For all isotopes similarly, the Kr3+ ion yield rises shortly before XUV/NIR pulse overlap and decays with a slower time constant when compared to the transient absorption in the left panel to a persistent elevated count rate. In both cases, the NIR intensity was (8.6 ± 1) × 1013 W cm−2
Ionization dynamics in krypton
To reveal further details of the ionization dynamics, Fig. 3 presents the absorbance ΔOD at 91.23 eV (corresponding to the 3d5/25p resonance23) relative to the OD measured at Δt = −30 fs and the Kr3+ ion yield added up over the four most abundant krypton isotopes for two different NIR intensities: Fig. 3a for low NIR intensity of (8.6 ± 1) × 1013 W cm−2 and Fig. 3b for high NIR intensity of (2.9 ± 0.5) × 1014 W cm−2. For both cases, the absorbance decreases on a quick (<10 fs) time scale before it recovers almost to its original value. The time constant of the fast ΔOD decrease reflects the instrument response and the NIR pulse duration. A least squares fit gives an instrument response function24 of 1.8 ± 0.4 fs and hence a duration of 4.5 ± 1 fs for the Gaussian-shaped NIR pulse while the exponential recovery of the absorbance after pulse overlap yields a 6.8 ± 1.5 fs and a 7.7 ± 2.2 fs auto-ionization state lifetime of the 3d−1np levels for low and high NIR intensity, respectively. These lifetime results agree well with the previously reported value of 7.9 ± 0.2 fs25. Potential NIR intensity-dependent effects like the ac Stark shift or resonant coupling to neighboring states resulting in a broadening or even splitting of the resonances could be excluded by careful investigation of the resonance center positions and line shapes for all recorded time delays. This and the comparison to the literature values confirm that the initial Auger decay is virtually unaffected by different NIR laser field intensities. Recovery of the Kr3+ yield shows a strong dependence on the intensity of the applied NIR laser field: the number of Kr3+ ions increases when the XUV and the NIR pulses start to overlap, but not as quickly as the absorption changes at the 3d−1np resonances. This is because at pulse overlap, a significant part of the Kr3+ ions result from a cascaded Auger decay following the resonant 3d−1np excitation. Hence, the Kr3+ ion yield rise time does not only depend on the NIR pulse duration but also on the lifetimes of the resonantly excited 3d−1np states. Taking into account the instrument response function and the 3d−1np lifetime for the increase of the Kr3+ ion yield curve, a least squares fit yields a time constant of 9.3 ± 3.7 fs for the tail of the Kr3+ ion count rate that corresponds to the effective lifetime of the intermediate state of the Auger cascade (here: INIR = (8.6 ± 1) × 1013 W cm−2). This value differs from the previously reported value of 20 ± 4 fs17: our presented study is to our knowledge the first one that systematically investigates the ionization dynamics in krypton for different NIR intensities. As the lowest NIR intensity is twice as high as previously17, different auto-ionization paths in the de-excitation of the Kr+ ions become visible and may lead to a different apparent/effective decay time. In practice, we here observe an effective lifetime for the 3d−1np→4s–2np→4s−14p−1/4p−34d cascades that arise from a large number of individual but not resolved fine-structure transitions. This is confirmed by our multiconfiguration Dirac–Fock calculations using the GRASP26 and RATIP27 codes and by taking the average of all the individual lifetimes, weighted by their relative decay probabilities. This theoretical approach is for the first time applied to reveal effective lifetimes of different potential group cascades (see Supplementary Note 5 for details).
Absorbance change ΔOD and Kr3+ ion yield vs. time delay. The change in absorbance or optical density ΔOD states the difference of the optical density OD = −log10(I t (Δt)/I0) at a given time delay Δt (I t (Δt) is the transmitted signal at time delay Δt, I0 is the reference intensity measured at a time delay t R = −30 fs). a At lower NIR intensities of (8.6 ± 1) × 1013 W cm−2, the absorbance (light green, left scale) transiently drops around pulse overlap, while the Kr3+ ion yield (blue, right scale) shortly rises before it settles to an elevated ion yield of almost 160 counts in 20 s integration time. b At a NIR intensity three times as high, (2.9 ± 0.5) × 1014 W cm−2, the absorbance (dark green, left scale) transiently drops around pulse overlap similar to a, while the Kr3+ ion yield (orange, right scale) shortly rises before it settles to an elevated ion yield of about 860 counts in 20 s integration time with a slower decay constant when compared to a. Please see Supplementary Note 2 for longer scans
Control of krypton ionization dynamics
Figure 4 shows for three different NIR intensities that the observed decay time increases for higher NIR intensities due to a second set of decay channels (3d−1np → 4s−14p–1np/4p−34dnp → 4p−2). This second set (indicated by B in Fig. 1a) has a much longer effective lifetime as it was already speculated17: A double exponential decay fit gives rise to a second decay time of 60 ± 28 fs, if we apply 9.3 fs as the first decay time that has been found for the lowest intensity. At higher NIR intensity, channel B results in an increase of the amplitude ratio B/A. Amplitude A corresponds to the Auger cascade emerging at low NIR intensities. The results of our theoretical calculations of the effective lifetimes with 6 fs for the 4s−2np levels and 49 fs for the 4s−14p−1np/4p−34dnp levels agree very well with the measurements.
Control of Kr ionization dynamics. Time-dependent Kr3+ ion yield for three different NIR intensities: a INIR = (8.6 ± 1) × 1013 W cm−2, b INIR = (1.7 ± 0.5) × 1014 W cm−2 and c INIR = (2.9 ± 0.5) × 1014 W cm−2. While for all three intensities, the rise in the Kr3+ ion yield obeys the 7.9 fs 3d−1np lifetime, the subsequent decrease of the ion counts is strongly affected by the NIR intensity: a double exponential least squares fit yields the decay constants of τ A = 9.3 ± 3.7 fs and τ B = 60 ± 26 fs with varying contributions in their amplitudes for the three intensities: a A = 207 ± 53, B = 0 ± 7, b A = 149 ± 35, B = 38 ± 13 and c A = 40 ± 31, B = 272 ± 140. This change of the amplitude ratio B/A describes well the expected case that a second channel is starting to be addressed for elevated NIR intensities (see the levels marked with the green capital letters A and B in Fig. 1a and the text for details). For the highest intensity, an accompanying pulse of the ultrashort NIR laser pulse increases the ion yield at around 70–120 fs time delay (see Supplementary Note 3 for more details). Please note that the scaling, the initial and final values of the ion yields differ significantly for the three NIR intensities. The violet numbers on the right side of each panel indicate the difference between the maximum of the fitting function and the value the fitting function relaxes to for large time delays (see Supplementary Note 4 for a detailed explanation for the different ion yield values). The error bars show the standard error of the average of six measurements
There occurs a transient drop in the Kr3+ ion production shortly before pulse overlap (approximately at −5 fs) that depends on the NIR intensity but appears independent of the carrier envelope phase (strongest dip at high NIR intensities, best visible in Fig. 3b). This dip has been observed previously17, and its origin is not yet understood. It could result from a transient population transfer28 but may arise also as a Fano-type resonance29 that is embedded into the Kr2+ continuum.
Discussion
While a control of the end configuration in the dissociative ionization process of deuterium by tuning the carrier envelope phase has been already demonstrated30, we have shown here that combined attosecond transient absorption and mass spectrometry allows the observation and control of the XUV-induced ionization dynamics in rare gas atoms. The study reveals the role of intermediate electronic and ionic states and highlights how laser-induced state coupling can be used to control the post-excitation decay dynamics. The experiment simultaneously determines the instrument response function, the effective lifetimes of the resonantly excited states and confirms that the initiating resonant excitation is not affected by the dressing laser field amplitude while the evolution of the post-excitation decay can be dynamically and quantitatively manipulated.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Itatani, J. et al. Attosecond streak camera. Phys. Rev. Lett. 88, 173903 (2002).
Yakovlev, V. S., Gagnon, J., Karpowicz, N. & Krausz, F. Attosecond streaking enables the measurement of quantum phase. Phys. Rev. Lett. 105, 73001 (2010).
Guggenmos, A. et al. Attosecond photoelectron streaking with enhanced energy resolution for small-bandgap materials. Opt. Lett. 41, 3714–3717 (2016).
Schultze, M. et al. Delay in photoemission. Science 328, 1658–1662 (2010).
Ossiander, M. et al. Attosecond correlation dynamics. Nat. Phys. 13, 280–285 (2016).
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Klünder, K. et al. Probing single-photon ionization on the attosecond time scale. Phys. Rev. Lett. 106, 143002 (2011).
Tao, Z. et al. Direct time-domain observation of attosecond final-state lifetimes in photoemission from solids. Science 353, 62–67 (2016).
Pazourek, R. et al. Time-resolved photoemission on the attosecond scale: opportunities and challenges. Faraday Discuss. 163, 353–376 (2013).
Pazourek, R., Nagele, S. & Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 87, 765–802 (2015).
Goulielmakis, E. et al. Real-time observation of valence electron motion. Nature 466, 739–743 (2010).
Bernhardt, B. et al. High-spectral-resolution attosecond absorption spectroscopy of autoionization in xenon. Phys. Rev. A 89, 23408 (2014).
Kaldun, A. et al. Observing the ultrafast buildup of a Fano resonance in the time domain. Science 354, 738–741 (2016).
Drescher, M. et al. Time-resolved atomic inner-shell spectroscopy. Nature 419, 803–807 (2002).
Siek, F. et al. Angular momentum-induced delays in solid-state photoemission enhanced by intra-atomic interactions. Science 357, 1274–1277 (2017).
Uiberacker, M. et al. Attosecond real-time observation of electron tunnelling in atoms. Nature 446, 627–632 (2007).
Uphues, T. et al. Ion-charge-state chronoscopy of cascaded atomic Auger decay. New J. Phys. 10, 25009 (2008).
Schultze, M. et al. Attosecond band-gap dynamics in silicon. Science 346, 1348–1352 (2014).
Liu, Z. et al. Phase reconstruction of strong-field excited systems by transient-absorption spectroscopy. Phys. Rev. Lett. 115, 33003 (2015).
Ott, C. et al. Reconstruction and control of a time-dependent two-electron wave packet. Nature 516, 374–378 (2014).
Wang, H. et al. Attosecond time-resolved autoionization of argon. Phys. Rev. Lett. 105, 143002 (2010).
Li, X. et al. Investigation of coupling mechanisms in attosecond transient absorption of auto-ionizing states: comparison of theory and experiment in xenon. J. Phys. B: At. Mol. Opt. Phys. 48, 125601 (2015).
Haensel, R., Keitel, G., Schreiber, P. & Kunz, C. Optical absorption of solid krypton and xenon in the far ultraviolet. Phys. Rev. 188, 1375–1380 (1969).
Pedersen, S. & Zeweil, A. H. Femtosecond real time probing of reactions XXII Kinetic description of probe absorption fluorescence depletion and mass spectrometry. Mol. Phys. 89, 1455–1502 (1996).
Sairanen, O.-P., Kivimäki, A., Nõmmiste, E., Aksela, H. & Aksela, S. High-resolution pre-edge structure in the inner-shell ionization threshold region of rare gases Xe, Kr, and Ar. Phys. Rev. A 54, 2834–2839 (1996).
Jönsson, P., He, X., Froese Fischer, C. & Grant, I. P. The grasp2K relativistic atomic structure package. Comput. Phys. Commun. 177, 597 (2007).
Fritzsche, S. The RATIP program for relativistic calculations of atomic transition, ionization and recombination properties. Comput. Phys. Commun. 183, 1525 (2012).
Gibson, G. N., Freeman, R. R., McIlrath, T. J. & Muller, H. G. Excitation and ionization dynamics in short-pulse multiphoton ionization. Phys. Rev. A 49, 3870–3874 (1994).
Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 124, 1866–1878 (1961).
Kling, M. F. et al. Control of electron localization in molecular dissociation. Science 312, 246–248 (2006).
Verhoef, A. J. et al. Time-and-energy-resolved measurement of Auger cascades following Kr 3d excitation by attosecond pulses. New J. Phys. 13, 113003 (2011).
Acknowledgements
The authors warmly acknowledge Hartmut Schröder and Martin Schultze for instrumental support and discussions, as well as Marinus Mayerbacher’s and Alexander Späh’s contributions to the vacuum setup. B.B. wants to thank the Alexander von Humboldt foundation and the Carl Zeiss foundation for financial support. N.M.K. acknowledges hospitality and financial support from DIPC (San Sebastian/Donostia) and from the theory group in cooperation with the SQS work package of European XFEL (Hamburg). R.K. acknowledges a Consolidator Grant from the European Research Council (ERC-2014-CoG AEDMOS). S.O.S. gratefully acknowledges funding by the German Federal Ministry of Education and Research (BMBF) under Contract No. 05K16SJA. This work was supported by the Max Planck Society, the Deutsche Forschungsgemeinschaft Cluster of Excellence: Munich Centre for Advanced Photonics (http://www.munich-photonics.de).
Author information
Authors and Affiliations
Contributions
Experimental studies and analysis of experimental and theoretical signatures were carried out by K.H., M.M., V.S. and B.B. Theory and modeling were performed by S.O.S. and R.B., supervised by S.F. Customized XUV optics were provided by A.G. J.R., A.D., R.H., M.S.W. and R.K. contributed to the experimental setup and measurement. The manuscript was written by N.M.K. and B.B. All authors discussed the results and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hütten, K., Mittermair, M., Stock, S. et al. Ultrafast quantum control of ionization dynamics in krypton. Nat Commun 9, 719 (2018). https://doi.org/10.1038/s41467-018-03122-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-03122-1
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.