Abstract
Mendelian-like inheritance of germline DNA methylation in cancer susceptibility genes has been previously reported. We aimed to scan the genome for heritable methylation marks associated with breast cancer susceptibility by studying 25 Australian multiple-case breast cancer families. Here we report genome-wide DNA methylation measured in 210 peripheral blood DNA samples provided by family members using the Infinium HumanMethylation450. We develop and apply a new statistical method to identify heritable methylation marks based on complex segregation analysis. We estimate carrier probabilities for the 1000 most heritable methylation marks based on family structure, and we use Cox proportional hazards survival analysis to identify 24 methylation marks with corresponding carrier probabilities significantly associated with breast cancer. We replicate an association with breast cancer risk for four of the 24 marks using an independent nested case–control study. Here, we report a novel approach for identifying heritable DNA methylation marks associated with breast cancer risk.
Similar content being viewed by others
Introduction
DNA methylation is a breast cancer risk factor. Several genome-wide studies of DNA methylation have found evidence that global methylation levels measured in blood-derived DNA is associated with breast cancer risk for women in the general population, and for women from families at high genetic risk1,2,3. While increased global methylation is associated with a reduced risk, increased methylation levels within functional promoters have been associated with an increased risk of breast cancer2,3.
Candidate gene approaches have been used to assess whether methylation at CpG islands of breast cancer susceptibility genes is associated with breast cancer risk. Women carrying germline mutations in BRCA1 have a substantially elevated risk of breast cancer and their tumours typically have distinctive histological features4,5,6. We found that peripheral blood DNA methylation at the BRCA1 promoter was associated with an estimated 3.5-fold (95% CI, 1.4–10.5) increased risk of breast cancer diagnosed before the age of 40 years7. Hansmann et al.8 reported that 1.4% of 600 women from the German Consortium for Hereditary Breast and Ovarian Cancer had constitutive BRCA1 hypermethylation confined to one of the two alleles8.
Women carrying specific rare germline mutations in ATM are also at substantially elevated risk of breast cancer9,10,11. Flanagan et al.12 performed methylation microarray analyses of peripheral blood DNA across several genes including BRCA1, BRCA2, CHEK2, ATM, TP53, CDH1, and MLH1, and demonstrated that gene body hypermethylation of ATM was associated with an estimated threefold increased risk of breast cancer12. Brennan et al.13 combined two nested case–control studies of women at high risk of breast cancer and found evidence that methylation at an intragenic locus in ATM (ATMmvp2a) was associated with increased risk of breast cancer13.
Potapova et al.14 described promoter region methylation of PALB2 was evident in ~7% of breast and ovarian cancers, including those with germline mutations in BRCA2, using methylation-specific PCR and bisulfite sequencing14. In contrast, Mikeska et al.15 found little evidence of PALB2 methylation in high-grade serous ovarian cancers using a methylation-sensitive high-resolution melting assay15.
The terminology being used to describe these observations is variable and vulnerable to misuse and misinterpretation. The term ‘epimutation’ is strictly defined as a heritable change in gene activity that is not associated with a DNA mutation but rather with gain or loss of DNA methylation or other heritable modification of chromatin16. Changes in gene expression through altered DNA methylation or histone modifications induced from cis- or trans-acting genetic factors known as methylation Quantitative Trait Loci, (mQTL) are therefore not epimutations in this strict sense.
Epimutations and mQTLs can mimic germline mutations in their effect on cancer predisposition and it is likely that their contribution has been largely underestimated due to limited research beyond the candidate gene approaches described above8. These phenomena could therefore account for some of the familial risk of breast cancer that is not yet identified.
Intergenerational transmission of epimutations (as described by the authors in the initial reports) has been observed in MLH1 and MSH2 in the context of Lynch Syndrome (LS), a hereditary condition in which genetic mutations in key mismatch repair genes predispose individuals to colorectal, endometrial, and other cancers17. While two thirds of LS cases carry germline genetic mutations at the DNA mismatch genes18, a small proportion of LS has been associated with epimutations19,20. It has since been demonstrated that some methylation marks at MLH1 and MSH2 that are transmitted transgenerationally are in fact linked to nearby cis-acting genetic variants and consequently follow Mendelian inheritance patterns21,22, and are thus not strictly epimutations. Other MLH1 epimutations occur sporadically and have not been linked to underlying genetic variations23; while these epimutations are often observed in a familial context, they do not follow complete Mendelian inheritance patterns23.
We hypothesised that breast cancers in multiple-case breast cancer families with no known genetic susceptibility mutations are in part due to the contribution of heritable DNA methylation marks (including true epimutations and mQTLs). To test this, we assessed genome-wide DNA methylation for 25 multiple-case breast cancer families using the Infinium HumanMethylation450 K BeadArray. One or more women with breast cancer in these families had been previously screened for, and found not to carry germline mutations in known breast cancer susceptibility genes. In this study, we report a new analytic approach to identify CpG sites with Mendelian-like inheritance patterns and a set of 24 heritable methylation sites associated with breast cancer risk.
Results
DNA methylation within families
After removing 3949 poorly performing CpG probes (detection p-value < 0.05), β-values and M-values were obtained from a total of 481,563 analysable CpG probes across DNA samples from 210 individuals in 25 families (20 families participating in kConFab and 5 families participating in the ABCFR). β-values denote % methylation levels obtained from the HM450K platform, where 0 indicates 0% methylation and 1 indicates 100% methylation. Due to the heteroscedastic nature of β-values, the log2 ratio of methylation intensity, known as M-values, are also calculated and used for all statistical analyses24.
DNA samples were collected from 87 breast cancer cases (one third of the cases had blood collected prior to diagnosis) and 123 unaffected controls. In order to examine the overall genome-wide methylation similarities between samples and families, a hierarchical clustering analysis was performed according to M-values across 481,563 probes. No distinct clustering by case–control status was observed but some families shared similar overall methylation patterns (Supplementary Fig. 1).
Heritable methylation sites
The proportion of probes within 10 bp of known single-nucleotide polymorphisms (SNPs) increased significantly with ∆l (p < 0.0001, and see Fig. 1). We then removed all probes within 10 bp of known SNPs and those located on sex chromosomes (see Methods). We screened the remaining 365,169 sites for those most consistent with having a Mendelian pattern of inheritance using the statistic Δl (Supplementary Fig. 2A). The 1000 most Mendelian methylation marks (those with the highest values of Δl) are listed in Supplementary Data 1. These marks all have values of ∆l above 77, which suggests that they are highly heritable. We estimated carrier probabilities for the 1000 most heritable methylation marks using family structure alone.
Heritable methylation sites associated with breast cancer
Of the 1000 most Mendelian methylation marks, 24 of them had carrier probabilities that were associated with breast cancer at the Bonferroni-adjusted p-value threshold of 5 × 10−5 (all p-values between 2 × 10−5 and 7.4 × 10−10, see Table 1 and Supplementary Fig. 2B). Notably, five of the heritable methylation marks were clustered together at VTRNA2-1. For all 24 marks, the methylation (β) differences were substantial (Δβ > 0.30) between individuals, with most of these marks showing methylation patterns distinctly falling into hypermethylated (β > 0.80), hypomethylated (β < 0.20), or hemimethylated (β ~ 0.50) groups, indicating potential allele-specific methylation pattern at these sites (Supplementary Fig. 3 and Supplementary Table 1). While unbiased hazard ratios could not be calculated (see Statistical Methods), the risk of breast cancer increased with carrier probabilities for all 24 sites (Supplementary Table 2, where the low carrier probabilities for some CpGs reflect the very low prior carrier probability), and the estimated effect of the hypothetical genetic variant on the M-values of each site can be seen from Supplementary Fig. 3 and Supplementary Table 2. For example, for cg06536614, ‘carriers’ are hemimethylated and ‘non-carriers’ are hypomethylated. In contrast, for cg18584561, ‘carriers’ are hypomethylated and ‘non-carriers’ have generally higher methylation levels but these are spread over a range of methylation.
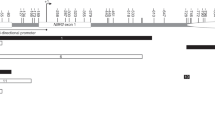
The five probes associated with the VTRNA2-1 locus (previously known as miR886) encompass a ~50 bp region 150 bp upstream from the transcription start site and overlapping a CpG island. Although these probes target 5 independent proximally located CpG sites, the 50mer probes largely overlapped with each other (Fig. 2). In addition to these 5 CpG sites, DNA methylation at other proximal CpG probes showed similar patterns, although not meeting statistical significance. Within each individual, the methylation patterns at all CpGs across this VTRNA2-1 promoter region were consistent, suggesting allelic methylation at this locus (Fig. 2b). Two recent studies have suggested that this region might be maternally imprinted25,26. We have tested this in eight trios (father, mother, and child) and included additional siblings when possible by performing clonal bisulfite sequencing. We observed strong hypermethylation of the maternally inherited allele, confirming the maternal imprinting of this locus. We found complete loss of methylation in one child whose three other siblings retained the methylation in the maternal allele (Supplementary Fig. 4).
DNA methylation at the VTRNA2-1 promoter. a Genomic locations of 6 HM450K probes associated with VTRNA2-1 promoter region. b DNA methylation levels (β-values) of these 6 probes labelled by breast cancer status. β-values for each individual are shown on y axis for 6 VTRNA2-1 probes. c Average DNA methylation levels across all six probes shown separately for individual families and labelled by breast cancer status. β-values are shown on y axis for members from each family (y axis)
One of the heritable methylation marks associated with breast cancer risk was located close to the 5′ end of the gene Growth Regulation by Estrogen Breast Cancer 1 (GREB1). The methylation patterns of all samples at this methylation site grouped clearly into hypomethylated, hemimethylated, or hypermethylated. Only 13 of our 210 samples were hypermethylated at this methylation site. We found three of the other methylation marks overlapping promoter regions of DUSP22, TMC3, and PPP2R5C. Nine other heritable methylation marks were located in gene body regions of MMP27, ANO10, CLGN, ZZEF1, PNKD, XYLT1, c7orf50, RASA3, and IL10RB, while six heritable methylation marks were not known to be associated with any gene (Table 1). The ZZEF1, PNKD, c7orf50, RASA3, and IL10RB probes overlapped CpG island shores or shelves. The MMP27, ANO10, XYLT1, and GREB1 probes encompassed enhancer regions.
Breast cancer risk association in the general population
Altogether, 433 invasive breast cancer cases and their matched controls were included in the analysis2. The median follow-up time was 9.5 years, interquartile range (IQR): 5.0 to 13.1 years. Supplementary Fig. 5 shows β-methylation value distribution for MCCS cases and controls for the 24 methylation sites showing heritable methylation patterns and associated with breast cancer in the family-based analyses. Of the 24 sites, four showed linear association with risk of breast cancer in the MCCS at the nominal significance threshold p < 0.05 (Table 2). The significant CpG probes were cg18584561 (GREB1; OR per standard deviation (s.d.): 1.18, 95% CI: 1.03–1.36), cg01741999 (PNKD; OR per 1 s.d.: 1.26, 95% CI: 1.03–1.54), cg03916490 (C7orf50; OR per 1 s.d.: 0.83, 95% CI: 0.72–0.96) and cg27639199 (TMC3; OR per 1 s.d.: 1.19, 95% CI: 1.03–1.36).
When comparing values belonging to the smaller vs. larger ‘peak’ of the methylation variable distribution, the results were consistent and more significant (Table 3). At cg18584561 (GREB1), which was trimodal, both the hypomethylated and hypermethylated peaks were associated with decreased breast cancer risk (OR = 0.60 (95% CI: 0.45–0.80), and OR = 0.56, (95% CI: 0.34–0.95), respectively). The methylation pattern at cg27639199 (TMC3) was also trimodal where the hypermethylated peak was strongly associated with breast cancer risk (OR = 2.16 (95% CI: 1.26–3.72)). At cg03916490 (C7orf50), reduced methylation was associated with the breast cancer risk (OR = 1.61 (95% CI: 1.16–2.24)). An annotated CpG probe (cg18514595) was associated with breast cancer risk when categorised into three methylation peaks.
These associations were robust to further adjustment for Houseman’s white blood cell composition, and to further adjustment for additional breast cancer risk factors (parity, hormonal replacement therapy use, age at menarche and menopausal status). Similar results were also found when restricting the analyses to DNA that was extracted from dried blood spots (Supplementary Table 3) and when repeating the analyses with carrier probabilities in place of M-values (Supplementary Table 4).
Associations between genetic variants and DNA methylation
Genotyped and imputed variants from the iCOGS ( ± 1 kb of cg18584561, GREB1) representing 251 MCCS participates was included in the analysis. This region had eight common variants (in linkage disequilibrium) nominally associated with breast cancer risk. We found a very strong linear association between methylation at cg18584561 and the genotypes at this region (p = 1 × 10−65–1 × 10−71). The association between these genetic variants and the corresponding methylation β-value is presented graphically in Supplementary Fig. 6.
Association with breast cancer estrogen receptor status
We tested whether methylation levels at any of these 24 CpG sites were influenced by ER status in our nested case–control study and found evidence for three methylation marks cg06536614 (ER-; OR = 1.02 (95% CI: 0.86–1.21) vs. ER + : OR = 0.71 (95% CI: 0.53–0.96), p-value (heterogeneity) = 0.03), cg01074083 (ER-; OR = 1.08 (0.90–1.29) vs. ER + : OR = 0.72 (0.53–0.98), p-value = 0.02) and cg23947138 (ER-: OR = 0.80 (0.68–0.94) vs. ER + : OR = 1.24 (0.93–1.65), p-value = 0.01). This result is shown in Supplementary Table 3.
Discussion
Genome-wide studies of heritable DNA methylation studies in the context of familial breast cancer have not been conducted previously, although ~50% of familial breast cancer cases cannot be explained by what we currently know about genetic risk27. In this study, we tested whether heritable DNA methylation marks are associated with breast cancer risk in multiple-case breast cancer families that do not carry pathogenic mutations in known breast cancer susceptibility genes.
The hierarchical clustering analysis of all detected probes demonstrated that genome-wide methylation patterns were similar within some families, indicating that shared genetics might have an influence on DNA methylation, as shown in previous studies28. However, overall genome-wide methylation did not appear to segregate with affected status in any families (Supplementary Fig. 1).
We developed a new statistical methodology, based on an expectation–maximisation algorithm and genetic segregation analysis, to identify heritable DNA methylation marks using the HM450 K platform (see Methods). We validated this analytic approach by showing that it identifies probes that are known to overlap SNPs (the methylation measurements at these probes are likely to be influenced by the underlying SNPs). We then removed all SNP-overlapping probes from the analysis, screened the remaining probes for those with the most Mendelian-like inheritance patterns and tested some of the most heritable methylation marks for association with breast cancer. Note that our screening for probes with Mendelian-like inheritance patterns removed many probes that cannot be associated with familial breast cancer, so this screening step greatly increased our statistical power for detecting probes associated with familial breast cancer.
We found 24 probes associated with breast cancer risk after adjusting for multiple testing (Table 1). Five of these 24 CpG probes were adjacently located at the promoter region of a vault RNA, VTRNA2-1 (previously known as nc886 or miR886; Fig. 2). This vault RNA has been shown to be involved in the inhibition of protein kinase R (PKR) activity29 and acts as a tumour suppressor in several cancer types29,30,31,32. It is located at chromosome 5q13, which is often associated with cancer-associated LOH including basal-like breast cancers33,34. Hypomethylation at this promoter, suggestive of loss of imprinting, occurs systematically in specific individuals in diverse populations, at least partially due to periconceptional environment and is stable for at least 10 years35. Silver et al. (2015) also noted that VTRNA2-1 exhibits all the hallmarks of ‘metabolic imprinting’ and is likely to be a determinant of cancer risk35. Here we have shown that methylation at the VTRNA2-1 promoter is also associated with heritable breast cancer risk that is measurable in DNA extracted from blood.
All 210 DNAs included in this study had hemi- or hypomethylation across all CpG probes at the VTRNA2-1 locus (Fig. 2) indicating potential allele-specific DNA methylation (ASM). ASM at this locus has been reported previously by studies utilising clonal bisulfite sequencing of multiple tissue types25,26. However, these studies did not explore nearby genetic variation that could be superimposed on imprinting to influence the allelic methylation pattern. Hemimethylation patterns generally associated with genomic imprinting were only observed in 170 of the 210 DNAs (~80%) included in our study (Fig. 2). Genomic imprinting is usually highly effective and loss-of-imprinting is often associated with growth retardation syndromes or tumour development36. In reference to other typically imprinted region (e.g., H19/IGF2), the methylation at VTRNA2-1 seemed exceptionally variable in the families included in our study. Romanelli et al. also report an atypical imprinting pattern at this locus and concluded this region was a polymorphically imprinted differentially methylated region26. By performing clonal bisulfite sequencing within families, we confirmed the polymorphic imprinting of this locus as reported by above studies (Supplementary Fig. 4).
We hypothesised that breast cancer arising in multiple-case breast cancer families with no known genetic mutation might be in part due to the contribution of heritable DNA methylation marks (including epimutations and mQTLs). As discussed above, methylation at the VTRNA2-1 promoter is a strong epimutation candidate but many of the other identified heritable methylation marks are likely to be mQTLs. More work is required to characterise these marks further. It is not likely that common genetic variation currently recognised to be associated with breast cancer risk (already identified via genome-wide-association-studies) underlies these methylation marks. The currently published risk-associated SNP closest to any of the identified heritable methylation marks is located ~1.5b MB from cg18584561 (GREB1). We found a strong linear association between the DNA methylation pattern at cg18584561 (GREB1) and 8 proximal common genetic variants (Supplementary Fig. 6). The genotypes of all 8 SNPs strongly correlated with the methylation pattern (e.g., DNAs hypermethylated at cg18584561 were homozygous across this region). This suggests a potential mQTL at this locus.
The other 19 CpG probes were all located in different genomic regions. We showed that a single CpG overlapping the transcription start region of the GREB1 gene is associated with heritable breast cancer risk. This gene codes for the protein ‘growth regulation by oestrogen in breast cancer 1’ and has been shown to play a critical role in hormone dependent breast cancer37,38. There is currently no direct evidence of epigenetic regulation of this gene.
Four of the 24 methylation marks were associated with breast cancer risk in an independent nested case–control study of methylation and breast cancer risk (Table 2). This outcome provides information with which one could use to hypothesise further about the relative frequency of the 24 methylation marks. For some marks, such as the one at GREB1, approximately half of the families appear to be methylated which is consistent with replication being possible in a population-based sample, another fraction (~10%) of the population are hypermethylated at this CpG. Interestingly, both the hypomethylated and hypermethylated profiles were associated with a decreased breast cancer risk, with similar estimated risk reduction of 40–45%. At cg03916490 (C7orf50), about 30% of the nested case–control participants were not strongly hypermethylated, which was associated with a 60% increase in risk. It is possible that the marks that did not validate in the nest case–control sample were either not present or at a very low frequency. Fig 3 graphically illustrates our analytical approach using 2 CpGs with different ‘carrier’ probabilities as examples (cg06536614 and cg18584561).
Analytical study approach. An overview of the analytical approach for each of the 1000 most-Mendelian probes in the multiple-case family-based analyses (a) and for the replication study of 24 probes in the population-based, case–control analyses (b). A measure of Mendelian heritability was calculated for all probes not on a sex chromosome or within 10 base pairs of a SNP (not depicted). For each of the 1000 most-Mendelian probes, a Mendelian model was fitted to the probe’s M-values and this was used to calculate carrier probabilities (e.g., for a hypothetical genetic variant that causes aberrant DNA methylation at the probe), then these carrier probabilities were tested for association with breast cancer (note that unbiased p-values could be calculated but unbiased risks could not because we could not adjust for ascertainment). This gave 24 highly heritable methylation marks that were associated with breast cancer, and a nested case–control study was used to test the M-values of each of these probes for association with breast cancer and to estimate the corresponding odds ratios (ORs)
Two thirds of the bloods collected from affected members of the multiple-case breast cancer families were collected after breast cancer diagnosis. Reverse causation is therefore a potential reason for non-replication of some of the methylation marks in the nested case–control study where blood samples were collected several years before breast cancer diagnosis.
Our study has two advantages over previous genome-wide studies. First, our approach utilises DNA methylation levels, which are important intermediate biomarkers that have not been incorporated into previous studies. Second, screening methylation marks for heritability is an effective way of greatly reducing the set of marks to test for association with breast cancer risk, but because all germline genetic variants are heritable by definition, this screening step could not be applied to previous studies.
Heritable methylation sites are interesting, regardless of whether or not they are associated with breast cancer susceptibility. We have devised a method for identifying heritable methylation sites and we have used this as a screening step to increase our power for detecting heritable methylation marks that are associated with breast cancer. This work could found a new area of exploration in the context of disease susceptibility. Specifically for breast cancer, this work provides new opportunities for increasing the precision of current risk prediction models, new strategies for cancer control (including screening) and new opportunities for the development of (or repurposing of) epigenetic therapeutics targeting these risk factors including chemo-prevention.
Methods
Study subjects
Multiple-case breast cancer families. Subjects were members of 25 multi-generational families with multiple cases of breast cancer. The families were participants in the Kathleen Cunningham Foundation Consortium for Research into Familial Breast Cancer (kConFab) and the Australian Breast Cancer Family Registry (ABCFR)39,40. The present study was based on samples and phenotypic data from a total of 210 family members (87 affected and 123 unaffected) from 25 families and phenotypic data on their relatives.
One or more members of these families had undergone previous genetic testing and were not found to carry a mutation in a known breast cancer susceptibility gene. Genomic DNA was isolated from blood samples or (if no blood specimen was available) from Epstein-Barr virus transformed cell lines (Supplementary Data 2). All participants provided signed informed consent to participate in the relevant research resources. This study was approved by the Human Research Ethics Committee of The University of Melbourne (1441955) and meets the principles of the Declaration of Helsinki.
Melbourne Collaborative Cohort Study (MCCS)
Data from an independent nested case–control study of methylation as a risk factor for breast cancer within the Melbourne Collaborative Cohort Study (MCCS) were used to test the findings from the family analysis41. This included breast cancer cases with a first diagnosis of invasive adenocarcinoma of the breast (International Classification of Diseases for Oncology, C50) occurring between blood collection and 31 December 2007 and ascertained by record linkage to the population-based Victorian Cancer Registry (VCR), and to the Australian Cancer Database. Controls were selected through incidence density sampling and matched with cases on year of birth, year of baseline attendance, country of origin and, when possible, type of baseline blood specimen (dried blood spot, buffy coat, or lymphocyte). The HM450K array was used to measure genome-wide methylation in DNA prepared from peripheral blood sample collected prior to cancer diagnosis of the cases as described by Severi et al. (2014)2. All participants provided signed informed consent to participate in the relevant research resources.
Bisulfite conversion and the HM450K array
A total of 500 ng of genomic DNA per sample was bisulfite converted using Zymo Gold EZ-DNA kit (Irvine, CA). Prior to processing the bisulfite converted samples on the Infinium HM450 K BeadArray, the conversion was confirmed using bisulfite-specific PCR designed in-house42. The Infinium HM450 K (San Diego, CA) was performed using the TECAN automated liquid handler (Männedorf, Switzerland) according to the manufacturer’s instruction.
HM450K data processing
All bioinformatic processing was performed with R version 3.2.043. Raw intensity signals were imported and processed using the minfi package44. All samples had an average detection p-value < 0.001, indicating good quality data. Therefore, no sample was removed from the analysis. Wherever possible, individuals from the same families were run on the same chips. Individual CpG probes with detection p-value greater than 0.05 (3949 CpG probes) were deemed unreliable and excluded from further analyses. All samples were Illumina and SWAN normalised to reduce technical bias between Type 1 and Type 2 probes45. β-values and M-values were calculated in minfi24,44. β-values denote relative methylation percentage calculated from the ratio of the methylated probe intensity and the overall intensity, where 0 indicates 0% methylation and 1 indicates 100% methylation24. Due to the heteroscedastic nature of β-values and unsuitable for many statistical tests, M-values, which are the log2 of β-values, are also calculated24. Methylation measures from twelve technical duplicates were used for testing the reproducibility of methylation measures and removed from subsequent analysis. No further batch correction method was performed.
Clonal bisulfite sequencing
Clonal bisulfite sequencing was performed to test for the parent-of-origin allelic methylation patterns of the VTRNA2-1 locus as previously described25. Germline DNA provided by 8 families, including 16 children were included in this analysis. All DNAs were first genotyped for rs2346019, (located at the downstream region of VTRNA2-1) using High-Resolution Melt curve analysis run on a RotorGene thermocycler (Qiagen, Hilden, Germany). Families where the allelic-specific methylation could be discriminated using this genotype information were selected for the bisulfite sequencing analysis (i.e., parents with disparate genotypes whose children were heterozygote at rs2346019). A set of previously published bisulfite-specific primers were used for amplifying the VTRNA2-1 locus25. Cloning was performed using a TOPO-TA kit and at least 10 colonies per individual? were selected for Sanger Sequencing.
Statistical methods
Our method for identifying heritable methylation marks is based on a generalisation of the standard expectation–maximisation (EM) algorithm for Gaussian mixtures to allow for non-independent group memberships. These calculations were performed using custom code implemented in R version 3.1.143 because existing general segregation analysis software was too slow to make the calculations feasible for almost half a million probes.
For each methylation site (CpG probe), two statistical models were fitted to the site’s M-values: a mixture model, in which the M-values were modelled as a mixture of two normal distributions (with means and variances to be estimated); and a Mendelian model, which is the same as the mixture model except that group membership was modelled as the carrier status (e.g., for a rare variant) at an autosomal genetic locus. Therefore, group memberships are independent under the mixture model but not under the Mendelian model. The maximised log-likelihoods, lmix and lMendel, for these models were calculated using the EM algorithm, with lmix obtained from the standard EM algorithm for Gaussian mixtures46 and lMendel calculated using the modification of this algorithm described in The EM algorithm for the Mendelian model, below. For each model, setting the means and variances for the two groups to be equal corresponds to a Gaussian model in which the M-values follow a normal distribution, so this Gaussian model is nested inside both the mixture and Mendelian models. Using the likelihood ratio test to compare these models to the Gaussian model is uninformative because many probes appear to have a bimodal distribution, so instead we compared lmix to lMendel. A maxim from the field of statistical model selection is that the maximised log-likelihood quantifies how well a model fits the observed data47. Therefore, Δl = lMendel − lmix is a measure of how Mendelian the probe’s M-values are, over and above how bimodal they are. Note also that since the mixture and Mendelian models have the same number of model parameters, Δl is the difference between the AICs for these two models, so the AIC model-selection approach would select the Mendelian model in preference to the mixture model whenever Δl > 0 (and similarly for the BIC)47.
To validate the ability of the Δl statistic to identify methylation sites with Mendelian-like inheritance patterns, we calculated Δl for all 481,563 methylation sites and used logistic regression and the likelihood ratio test to test whether or not the proportion of probes within 10 bp of a known SNP increases with Δl. This is a test on the efficacy of our statistic Δl, because the observed M-values of methylation probes with nearby SNPs are likely to have Mendelian-like inheritance patterns, just as an artefact of how the HM450 K array measures methylation48. The HM450K probes are 50mer oligonucleotides in design with the interrogated target CpGs at the last base. A technical limitation of the platform is that a large proportion of probes overlap one or more known SNPs48. As the accuracy of methylation measurements relies on the efficient hybridising of probes to target complementary DNA fragment, SNPs within probes potentially interfere with this binding and interrupt the actual methylation measurements48. The observed methylation values are therefore biased by nearby SNPs and will tend to follow Mendelian patterns of inheritance. We could therefore assess if Δl identified heritable sites by testing whether probes with higher values of Δl were more likely to have nearby SNPs. In addition to the formal test above, we also binned probes by their values of Δl and graphed the proportion of probes within 10 bp of a known SNP for each bin. Known SNPs were defined by Illumina’s HM450 K Manifest v1.2 (see Web resources).
To identify heritable methylation marks associated with breast cancer, we first excluded all methylation probes on sex chromosomes or within 10 bp of known SNPs. Then we screened the remaining 365,169 probes for those most consistent with a Mendelian pattern of inheritance, using the statistic Δl. Note that this screening was based on the structure of the 25 families and did not use any data on breast cancer-affected status or age. For each of the 1000 most Mendelian sites (those with the highest values of Δl), we calculated carrier probabilities for the hypothetical genetic variant that determines group membership in the Mendelian model. These calculations used standard techniques from segregation analysis49, in which the observed M-values played the role of the ‘phenotypes’ and the Gaussian densities (with the model parameters equal to their maximum likelihood estimates from the Mendelian model) played the role of the ‘penetrance’ function. The calculation of these carrier probabilities also only used pedigree structure and M-values, not age or breast cancer data.
Cox proportional hazards survival analysis was then used to test for associations between breast cancer and the carrier probabilities for the 1000 most Mendelian methylation marks. These analyses were conducted in R version 3.1.143 using the coxph function of the survival package50. To adjust for multiple testing, a Bonferroni-corrected p-value threshold of 0.05/1000 was used to determine statistical significance. Note that the effects of multiple testing were greatly reduced in our study because we screened the methylation sites for those with Mendelian inheritance patterns before testing for association with breast cancer.
The families in this study were ascertained because they each contained multiple breast cancer cases, and no adjustment for this ascertainment criterion was made. This means that our hazard ratio estimates are biased, so we do not report these here, but since the ascertainment criterion has no effect on the test statistic under the null hypothesis, our p-values for association with breast cancer are valid. These p-values were based on the likelihood ratio test, not the Wald test, so variances for the hazard ratios were not needed and hence were not estimated using either standard maximum likelihood or robust variance estimators.
The EM algorithm for the Mendelian model
This section gives a detailed, mathematical description of our generalization of the standard EM algorithm for Gaussian mixtures to allow for non-independent group memberships, as well as a precise description of the above statistic \(\Delta\ell\) and its two related statistical models.
The statistic Δl for measuring how Mendelian the inheritance pattern of a given site is: for each of the methylation sites, we fitted two statistical models to the sites’ M-values x1,…,x n , where n is the number of people with epigenome-wide data and x i is the site’s M-value for person i. The first model is a mixture of two Gaussians, so under this model there are binary random variables y1,…,y n so that: the n bivariate random variables (x1,y1),…,(x n ,y n ) are independent; and for each j = 0 or 1, P(y i = j) = α j and (x i |y i = j) ~N(μ j σ j 2), where θ = (α0,α1,μ0,μ1,σ0,σ1) is a vector of parameters to be estimated while satisfying the constraint α0 + α1 = 1. In this paper, we will also impose the additional constraint that α1 = 0.01, so α0 and α1 are fixed constants. The second model is the same as the first, except that the group membership variables y1,…,y n are modelled as the carrier status for a rare, autosomal genetic variant, with y i = 1 if individual i is a carrier and y i = 0 if he or she is a non-carrier. Note that y i and y j will generally be dependent random variables if individuals i and j belong to the same pedigree, though we still assume that x1,…,x n are conditionally independent given y1,…,y n .
We will refer to these models as the mixture and Mendelian models, respectively. Setting μ0 = μ1 and σ0 = σ1in either of these models gives a third model for the M-values, in which x1,…,x n are independent and follow a univariate normal distribution, that we call the Gaussian model. The maximised log-likelihoods \(\ell _{\rm mix}\), \(\ell _{\rm Mendel}\), and \(\ell _{\rm Gauss}\) of these three models measure the goodness-of-fit of each model to the site’s M-values47. Since the Gaussian model is nested inside the other two models, \(\ell _{\rm mix}\) and \(\ell _{\rm Mendel}\) can both be formally compared to \(\ell _{\rm Gauss}\) using a likelihood ratio test in order to determine if either of these models gives a more parsimonious fit to the data than the Gaussian model. However, the M-values of a very large number of the sites are bimodal, so these tests very often prefer both of the other models to the Gaussian model. To discover sites whose methylation patterns are Mendelian, we therefore compare \(\ell _{\rm Mendel}\) to \(\ell _{\rm mix}\), even though the mixture and Mendelian models are not nested. Since these models have the same number of parameters, \({\mathrm{\Delta}}\ell = \ell _{\rm Mendel} - \ell _{\rm mix}\) is the difference in both the AIC and BIC of the two models, so if \({\Delta}\ell > 0\) then the AIC and BIC would both favour the Mendelian model over the mixture model as the more parsimonious description of the data47. Also, since \(\ell _{\rm mix}\) and \(\ell _{\rm Mendel}\) measure the goodness-of-fit of these models to the site’s M-values47, the better the Mendelian model fits the data compared to the mixture model, the larger \({\Delta}\ell\) should be. We therefore interpret \({\Delta}\ell\) as a statistic which measures how ‘Mendelian’ the site is, i.e. how consistent the observed M-values at the site are with a Mendelian pattern of inheritance within families.
Note that we have assumed that all familial aggregation of aberrant DNA methylation is due to a major gene, so \(\ell _{\rm Mendel}\) and hence \({\Delta}\ell\) will be upwardly biased if part of this familial aggregation is caused by multiple genes of small effect (i.e., a polygenic effect), or if our model is misspecified in other ways. However, note that we only use \({\Delta}\ell\) to rank the methylation sites, and this ranking is completely insensitive to a wide range of biases. Also, while there are good theoretical and empirical reasons for using \({\Delta}\ell\) to screen the methylation sites, this screening is not a formal statistical procedure, so even if \({\Delta}\ell\) were biased then this would have no effect on the validity of our tests for association with breast cancer (the only formal part of our analysis). Finally, we note that replacing the Mendelian model with a mixed model (a model that incorporates a polygene in addition to a major gene) would possibly identify sites with polygenic but not Mendelian patterns of inheritance, which we are not interested in here.
A detailed description of the EM algorithm for the Mendelian model: since our analysis included approximately 480,000 sites, efficient algorithms were needed to maximise the likelihoods. For the mixture model this was straight-forward, because the EM algorithm for a mixture of Gaussians results in analytical update formulae46, which can be iterated to rapidly converge (in most cases) to the maximum likelihood estimates. For the Mendelian model, we used a modification of this algorithm that we now describe in detail.
In the EM algorithm for the Mendelian model, we took the M-values x1,…,x n of a given site as the observed data and the binary carrier statuses y1,…,y n as the hidden data. For now, the reader can simply think of y1,…,y n as variables defining group memberships, as in the standard EM algorithm for Gaussian mixtures46, though with the caveat that y1,…,y n are not independent. With model parameters θ = (α0,α1,μ0,μ1,σ0,σ1) as above, if θ t is the estimate of these parameters at iteration t then the EM algorithm chooses the estimate θ t + 1 at the next iteration to be the argument which maximises the function of θ given by
where x = (x1,…,x n ), y = (y1,…,y n ), \({\Bbb E}[ \cdot ]\) is the expectation functional and P(x,y|θ) is the likelihood of the full data at parameter value θ. More precisely, if \({\cal Y}\) = {0,1}n is the set of all binary vectors of length n, then
since the M-values x1,…,x n are assumed to be conditionally independent given the carrier statuses y, with the distribution of x i only a function of y i . The first sum in (1) is a function only of the parameters μ0, μ1, σ0, and σ1, while the second sum only depends on α0 and α1. So, to find θ that maximises Q(θ,θ t ), we can maximise these two functions separately. In the analysis presented in this paper, however, α0 and α1 were fixed to the values 0.99 and 0.01, respectively, so we focus on maximising the first term of (1) here.
Let δ ij denote the Kronecker delta, and for each j = 0 or 1, let φ(x i |μ j ,σ j ) be the probability density function for the normal distribution N(μj,σ2) evaluated at x i , so that P(x i |y i ,θ) = ϕ(x i |μyi,σyi). Then the first sum in (1) is
where
so that \(q_{il}^t\) is the carrier probability for person i corresponding to x and the parameter values θ t when l = 1 (note that the t in \(q_{il}^t\) is a general superscript, not a power). Therefore, (2) is a weighted log-likelihood of normal distributions, so it can be maximised in exactly the same way as for the standard EM algorithm for Gaussian mixtures46. This gives the following parameter values at iteration t + 1, for each l = 0,1:
where \(w_{il}^t = q_{il}^t/\mathop {\sum }\limits_{j = 1}^n q_{jl}^t\) and, as before, the superscripts t and t + 1 are not exponents.
To calculate these estimates, we used the definition (3) of \(q_{il}^t\) and the following expression for P(y|x,θ t ). Let F be the partition of {1,…,n} into families, so that F is a set of sets of indices, with each f∈F of the form f = {i1,…,i k }, where i1,…,i k are all of the people in a given family with epigenome-wide methylation data. For any such f∈F, let xf = (xi1,…,xik) and yf = (yi1,…,y ik ) be the observed and hidden data for the family, respectively. Then since the carrier statuses and M-values of people from different families are independent,
To calculate P(y|x,θ t ) from the right-hand side of (5), we note that, as before,
Also, P(yf|θ t ) can be calculated using standard techniques from segregation analysis49, as described in more detail in Statistical methods, above. Finally, the denominator P(xf|θ t ) in the right-hand side of (5), which is just a normalising constant, can be obtained by summing the numerator overall values of yf. Therefore, P(y|x,θ t ) can be calculated from (5), so substituting this into (3) gives \(q_{il}^t\) which, by (4), gives the updated parameters for the EM algorithm.
Improving calculation speeds: our analyses of ~480,000 sites would not be feasible without a number of techniques to improve the speed of the EM algorithm for the Mendelian model, so we briefly describe two of these techniques now.
The Mendelian model is a segregation analysis model49, and for such models the most time-consuming part of the calculation is summing overall possible genotype combinations for all family members in each family. However, this part of the calculation is essentially common to all methylation sites, so we obtain considerable improvements in speed by performing this calculation once and storing the results for later use.
More precisely, the update equations (4) for the EM algorithm depend on the carrier probabilities P(yf|θ t ) via (3) and (5), where we recall that yf is a set of carrier statuses for all of the members of family f with epigenome-wide data. Using standard techniques from segregation analysis49, P(yf|θ t ) can be expressed as a sum over all genotype combinations for the family which are consistent with the genotypes yf. Evaluating these sums is usually very time-consuming, however P(yf|θ t ) depends on \(\alpha _0^t\) and \(\alpha _1^t\) but not on \(\mu _0^t\), \(\mu _1^t\), \(\sigma _0^t\) or \(\sigma _1^t\), and \(\alpha _0^t\) and \(\alpha _1^t\) are held fixed for all t, so P(yf|θ t ) does not depend on t or the M-values xf. Therefore, we calculated P(yf|θ t ) once for every possible combination yf of genotypes, and stored these values of P(yf|θ t ) for later use in the update equations (4) (via (3) and (5)) for each methylation site.
We also used a simplifying assumption. To reduce the number of genotype combinations yf for which we had to store values of P(yf|θ t ), we assumed that no more than 1 of the founders in each family is a carrier and that no founder is a homozygote carrier (as usually holds if the variant is rare). This assumption is not essential, however, and it can be weakened (e.g., to allow 2 variants or less among the alleles of the founders) or entirely dispensed with (if the families are not too large and not too many family members have epigenome-wide data).
Testing 24 methylation marks in the MCCS
For each of the 24 CpG sites of interest, we first estimated odds ratios (OR) for breast cancer risk using conditional logistic regression models, for a one standard deviation increase in the methylation M-values in blood HM450K data set of 433 cases and their matched controls from the MCCS. The models were adjusted for body mass index, tobacco smoking, alcohol drinking, time between blood collection, and cancer diagnosis, and sample type (DNA extracted from dried blood spots, peripheral blood mononuclear cells, and buffy coats, although the vast majority (97%) of case–control pairs were successfully matched on sample type). For methylation marks exhibiting a bimodal or trimodal distribution, we categorised the methylation variables into groups corresponding to the observed ‘peaks’ of hypo, hemimethylated or hypermethylated, based on visual inspection of the M-value distribution (Supplementary Fig. 4). We used the same models as for the continuous variable analyses. The larger peak was chosen as the reference category. Sensitivity analyses were conducted: (1) further adjusting the models for blood cell composition as estimated by the algorithm by Houseman et al.51; (2) further adjusting the models for age at menarche, menopausal status, number of live births, and use of hormonal replacement therapy; (3) restricting the analyses to DNA prepared from dried blood spots.
Associations between genetic variants and DNA methylation
Data for all variants with 1 kb of the GREB1 probe that were genotyped or imputed using the iCOGS array were retrieved for MCCS participants included in the Breast Cancer Association Consortium52. A total of 251 participants (231 cases and 20 controls) had iCOGS and HM450K data available. Association between genotype and methylation was assessed using linear regression, with beta-value as the outcome variable and allele count as the explanatory variable. The allele count was estimated by rounding the allele dose to an integer value.
Web resources
Illumina Infinium HumanMethylation450K manifest was downloaded from http://support.illumina.com/array/array_kits/infinium_humanmethylation450_beadchip_kit/downloads.html
Data availability
All DNA methylation data (HM450K array) has been deposited to GEO (Accession No. GSE104942) and all bisulfite sequencing data has been deposited into BankIt2071934 (MG686237-MG686418) and is freely available.
References
Delgado-Cruzata, L., Wu, H. C., Liao, Y., Santella, R. M. & Terry, M. B. Differences in DNA methylation by extent of breast cancer family history in unaffected women. Epigenetics. 9, 243–248 (2014).
Severi, G. et al. Epigenome-wide methylation in DNA from peripheral blood as a marker of risk for breast cancer. Breast Cancer Res. Treat. 148, 665–673 (2014).
van Veldhoven, K. et al. Epigenome-wide association study reveals decreased average methylation levels years before breast cancer diagnosis. Clin. Epigenet. 7, 67 (2015).
Armes, J. E. et al. The histologic phenotypes of breast carcinoma occurring before age 40 years in women with and without BRCA1 or BRCA2 germline mutations: a population-based study. Cancer 83, 2335–2345 (1998).
Lakhani, S. R. et al. Multifactorial analysis of differences between sporadic breast cancers and cancers involving BRCA1 and BRCA2 mutations. J. Natl. Cancer Inst. 90, 1138–1145 (1998).
Southey, M. C. et al. Morphological predictors of BRCA1 germline mutations in young women with breast cancer. Br. J. Cancer 104, 903–909 (2011).
Wong, E. M. et al. Constitutional methylation of the BRCA1 promoter is specifically associated with BRCA1 mutation-associated pathology in early-onset breast cancer. Cancer Prev. Res (Phila.) 4, 23–33 (2011).
Hansmann, T. et al. Constitutive promoter methylation of BRCA1 and RAD51C in patients with familial ovarian cancer and early-onset sporadic breast cancer. Hum. Mol. Genet. 21, 4669–4679 (2012).
Bernstein, J. L. et al. Population-based estimates of breast cancer risks associated with ATM gene variants c.7271T>G and c.1066-6T>G (IVS10-6T>G) from the Breast Cancer Family Registry. Hum. Mutat. 27, 1122–1128 (2006).
Goldgar, D. E. et al. Rare variants in the ATM gene and risk of breast cancer. Breast Cancer Res. 13, R73 (2011).
Tavtigian, S. V. et al. Rare, evolutionarily unlikely missense substitutions in ATM confer increased risk of breast cancer. Am. J. Hum. Genet. 85, 427–446 (2009).
Flanagan, J. M. et al. DNA methylome of familial breast cancer identifies distinct profiles defined by mutation status. Am. J. Hum. Genet. 86, 420–433 (2010).
Brennan, K. et al. Intragenic ATM methylation in peripheral blood DNA as a biomarker of breast cancer risk. Cancer Res. 72, 2304–2313 (2012).
Potapova, A., Hoffman, A. M., Godwin, A. K., Al-Saleem, T. & Cairns, P. Promoter hypermethylation of the PALB2 susceptibility gene in inherited and sporadic breast and ovarian cancer. Cancer Res. 68, 998–1002 (2008).
Mikeska, T., Alsop, K., Australian Ovarian Cancer Study Group, Mitchell, G., Bowtell, D. D. & Dobrovic, A. No evidence for PALB2 methylation in high-grade serous ovarian cancer. J. Ovarian Res. 6, 26 (2013).
Oey, H. & Whitelaw, E. On the meaning of the word ‘epimutation’. Trends Genet. 30, 519–520 (2014).
Lynch, H. T. Hereditary nonpolyposis colorectal cancer (HNPCC). Cytogenet. Cell. Genet. 86, 130–135 (1999).
Peltomaki, P. & de la Chapelle, A. Mutations predisposing to hereditary nonpolyposis colorectal cancer. Adv. Cancer Res. 71, 93–119 (1997).
Hitchins, M. P. et al. Inheritance of a cancer-associated MLH1 germ-line epimutation. N. Engl. J. Med. 356, 697–705 (2007).
Suter, C. M., Martin, D. I. & Ward, R. L. Germline epimutation of MLH1 in individuals with multiple cancers. Nat. Genet. 36, 497–501 (2004).
Hitchins, M. P. et al. Dominantly inherited constitutional epigenetic silencing of MLH1 in a cancer-affected family is linked to a single nucleotide variant within the 5’UTR. Cancer Cell. 20, 200–213 (2011).
Ligtenberg, M. J. et al. Heritable somatic methylation and inactivation of MSH2 in families with Lynch syndrome due to deletion of the 3’ exons of TACSTD1. Nat. Genet. 41, 112–117 (2009).
Hitchins, M. P. The role of epigenetics in Lynch syndrome. Fam. Cancer 12, 189–205 (2013).
Du, P. et al. Comparison of Beta-value and M-value methods for quantifying methylation levels by microarray analysis. BMC Bioinformatics 11, 587 (2010).
Paliwal, A. et al. Comparative anatomy of chromosomal domains with imprinted and non-imprinted allele-specific DNA methylation. PLoS Genet. 9, e1003622 (2013).
Romanelli, V. et al. Variable maternal methylation overlapping the nc886/vtRNA2-1 locus is locked between hypermethylated repeats and is frequently altered in cancer. Epigenetics 9, 783–790 (2014).
Turnbull, C. & Rahman, N. Genetic predisposition to breast cancer: past, present, and future. Annu. Rev. Genom. Hum. Genet. 9, 321–345 (2008).
McRae, A. F. et al. Contribution of genetic variation to transgenerational inheritance of DNA methylation. Genome Biol. 15, R73 (2014).
Lee, K. et al. Precursor miR-886, a novel noncoding RNA repressed in cancer, associates with PKR and modulates its activity. RNA 17, 1076–1089 (2011).
Kunkeaw, N. et al. Cell death/proliferation roles fornc886, a non-coding RNA, in the protein kinase R pathway in cholangiocarcinoma. Oncogene 32, 3722–3731 (2013).
Lee, H. S. et al. Epigenetic silencing of the non-coding RNA nc886 provokes oncogenes during human esophageal tumorigenesis. Oncotarget 5, 3472–3481 (2014).
Lee, K. S. et al. nc886, a non-coding RNA of anti-proliferative role, is suppressed by CpG DNA methylation in human gastric cancer. Oncotarget 5, 3944–3955 (2014).
Johannsdottir, H. K. et al. Chromosome 5 imbalance mapping in breast tumors from BRCA1 and BRCA2 mutation carriers and sporadic breast tumors. Int. J. Cancer 119, 1052–1060 (2006).
Wang, Z. C. et al. Loss of heterozygosity and its correlation with expression profiles in subclasses of invasive breast cancers. Cancer Res. 64, 64–71 (2004).
Silver, M. J. et al. Independent genomewide screens identify the tumor suppressor VTRNA2-1 as a human epiallele responsive to periconceptional environment. Genome Biol. 16, 118 (2015).
Reik, W. & Murrell, A. Genomic imprinting. Silence across the border. Nature 405, 408–409 (2000).
Ghosh, M. G., Thompson, D. A. & WeigelR. J. PDZK1 and GREB1 are estrogen-regulated genes expressed in hormone-responsive breast cancer. Cancer Res. 60, 6367–6375 (2000).
Rae, J. M. et al. GREB 1 is a critical regulator of hormone dependent breast cancer growth. Breast Cancer Res. Treat. 92, 141–149 (2005).
John, E. M. et al. The Breast Cancer Family Registry: an infrastructure for cooperative multinational, interdisciplinary and translational studies of the genetic epidemiology of breast cancer. Breast Cancer Res.: BCR 6, R375–R389 (2004).
Osborne, R. H. et al. kConFab: a research resource of Australasian breast cancer families. Kathleen Cuningham Foundation Consortium for Research into Familial Breast Cancer. Med. J. Aust. 172, 463–464 (2000).
Giles, G. G. & English, D. R. The Melbourne Collaborative Cohort Study. Iarc. Sci. Publ. 156, 69–70 (2002).
Wong, E. M. et al. Tools for translational epigenetic studies involving formalin-fixed paraffin-embedded human tissue: Applying the Infinium HumanMethyation450 Beadchip assay to large population-based studies. BMC Res. Notes 8, 543 (2015).
Core, T. R. R: A language and environment for statistical computing, R Foundataion for Statistical Computing. (R programming software, Vienna, Austria, 2015).
Aryee, M. J. et al. Minfi: a flexible and comprehensive Bioconductor package for the analysis of Infinium DNA methylation microarrays. Bioinformatics 30, 1363–1369 (2014).
Maksimovic J., Gordon L., Oshlack A. SWAN: Subset quantile within-array normalization for Illumina Infinium Human Methylation450 BeadChips. Genome Biol. 13, R44 (2012).
Bilmes J. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and Hidden Markov Models. Technical Report ICSC-TR-97-02 (The University of Berkeley 1998).
Wit, E., van den Heuvel, E. & Romeijn, J. W. All models are wrong…’: an introduction to model uncertainty. Stat. Neerl. 66, 217–236 (2012).
Naeem, H. et al. Reducing the risk of false discovery enabling identification of biologically significant genome-wide methylation status using the HumanMethylation450 array. BMC Genomics 15, 51 (2014).
Lange K. Mathematical and Statistical Methods for Genetic Analysis (Springer, 2002).
Therneau T. M. A Package for Survival Analysis in S. R package version 238 (2015).
Houseman, E. A. et al. DNA methylation arrays as surrogate measures of cell mixture distribution. BMC Bioinformatics 13, 86 (2012).
Michailidou, K. et al. Genome-wide association analysis of more than 120,000 individuals identifies 15 new susceptibility loci for breast cancer. Nat. Genet. 47, 373–380 (2015).
Acknowledgements
The Australian site of Breast Cancer Family Registry was supported by grant UM1 CA164920 from the USA National Cancer Institute. The content of this manuscript does not necessarily reflect the views or policies of the National Cancer Institute or any of the collaborating centres in the Breast Cancer Family Registry (BCFR), nor does mention of trade names, commercial products, or organisations imply endorsement by the USA Government or the BCFR. We thank Heather Thorne, Eveline Niedermayr, all the kConFab research nurses and staff, the heads and staff of the Family Cancer Clinics, and the Clinical Follow-Up Study (which has received funding from the NHMRC, the National Breast Cancer Foundation, Cancer Australia, and the National Institute of Health (USA)) for their contributions to this resource, and the many families who contribute to kConFab. kConFab is supported by a grant from the National Breast Cancer Foundation, and previously by the National Health and Medical Research Council (NHMRC), the Queensland Cancer Fund, the Cancer Councils of New South Wales, Victoria, Tasmania and South Australia, and the Cancer Foundation of Western Australia. We would like to express our gratitude to the many thousands of Melbourne residents who continue to participate in the Melbourne Collaborative Cohort Study, the original investigators, programme managers and the diligent team who recruited the participants and who continue working on follow-up. The MCCS methylation work was supported by the National Health and Medical Research Council (Grant number 1011618); and the Victorian Breast Cancer Research Consortium. M.C.S. is a Senior Research Fellow and J.L.H. is a Senior Principal Research Fellow of the National Health and Medical Research Council of Australia. This work was supported by an Early Career Research Award to JEJ from The University of Melbourne.
Author information
Authors and Affiliations
Consortia
Contributions
This study was first conceived and designed by J.E.J., E.M.W. and M.C.S. J.E.J. performed all laboratory experiments. J.E.J., J.G.D., R.L.M. and P.A.D. performed bioinformatics and statistical analyses. R.L.M. and G.G.G. facilitated the inclusion and interpretation of the data from the MCCS. Study materials were provided by kConFab, ABCFR, and MCCS. The manuscript was first structured by J.E.J., J.G.D., and M.C.S. D.E., J.L.H. and D.E.G. provided significant intellectual contributions. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Joo, J.E., Dowty, J.G., Milne, R.L. et al. Heritable DNA methylation marks associated with susceptibility to breast cancer. Nat Commun 9, 867 (2018). https://doi.org/10.1038/s41467-018-03058-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-03058-6
This article is cited by
-
Machine learning unveils an immune-related DNA methylation profile in germline DNA from breast cancer patients
Clinical Epigenetics (2024)
-
The impact of circulating protein levels identified by affinity proteomics on short-term, overall breast cancer risk
British Journal of Cancer (2024)
-
Methylation marks in blood DNA reveal breast cancer risk in patients fulfilling hereditary disease criteria
npj Precision Oncology (2024)
-
Heritable methylation marks associated with prostate cancer risk
Familial Cancer (2023)
-
Relationship Between Breast Cancer Risk and Polymorphisms in CLOCK Gene: A Systematic Review and Meta-Analysis
Biochemical Genetics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.