Abstract
Electron correlation and multielectron effects are fundamental interactions that govern many physical and chemical processes in atomic, molecular and solid state systems. The process of autoionization, induced by resonant excitation of electrons into discrete states present in the spectral continuum of atomic and molecular targets, is mediated by electron correlation. Here we investigate the attosecond photoemission dynamics in argon in the 20–40 eV spectral range, in the vicinity of the 3s−1np autoionizing resonances. We present measurements of the differential photoionization cross section and extract energy and angle-dependent atomic time delays with an attosecond interferometric method. With the support of a theoretical model, we are able to attribute a large part of the measured time delay anisotropy to the presence of autoionizing resonances, which not only distort the phase of the emitted photoelectron wave packet but also introduce an angular dependence.
Similar content being viewed by others
Introduction
The development of attosecond sources based on high-order harmonic generation (HHG) in gases has opened the possibility to investigate electron dynamics on its natural timescale1. Recently, pump-probe experiments with the pump in the extreme ultraviolet (XUV) range and the probe in the infrared (IR)2,3showed the feasibility to access and measure photoemission delays, which were introduced theoretically in the 50s4,5 and reviewed in6. Since then, it has become a very active field of research in attosecond science7,8. Attosecond photoemission dynamics was studied experimentally with the attosecond streak camera in atomic2,9 and solid state targets10, and addressed theoretically2,11,12. This was complemented by detailed interferometric measurements using the RABBIT (reconstruction of attosecond beatings by interference of two-photon transitions) technique3 in atoms13,14,15,16, molecules17 and solid targets18.
In the simplest case, when the electron is promoted into a flat (non-resonant) continuum by direct laser-assisted photoionization, the measured delay after absorbing a single XUV photon is related to the phase shifts of the departing electron induced by the ionic potential and laser field, respectively. One part of this so-called atomic time delay is the Wigner delay4,5, which can be expressed as the energy derivative of the scattering phase and is equivalent to the group delay of the departing electron wave packet. Thus the Wigner delay has a direct link to the classical trajectory with the center of the electron wave packet following the Ehrenfhest’s theorem19. In absence of resonances, this quantity can be accessed with attosecond techniques if other contributions are carefully subtracted11,20.
Compared to the direct ionization into the continuum, the situation becomes more complicated when ionization occurs in the vicinity of autoionizing states9,21,22. Autoionizing states are highly excited short-living states that ultimately decay into the continuum, thus opening an alternative ionization path. The interference between the direct and autoionizing pathways gives rise to the well-known Fano profiles in the photoionization cross sections23, which have been directly measured in atoms24 and molecules25 with high precision using for instance monochromatic synchrotron radiation. Despite their value, these studies are unable to access the correlated dynamics of the photoionized resonant electron wave packet. This information can be obtained by measuring atomic time delays with attosecond techniques17,26. As an example, the build-up of a Fano resonance in time domain has been observed using both RABBIT27 and attosecond transient absorption28. Yet, to date the angular behavior of resonant atomic time delays, from which we can gain more insight, remains unexplored.
Recently, techniques combining multicolor fields (e.g., XUV-IR) with electron momentum detection have been used to retrieve angular-resolved phase and amplitude of ionizing electron wave packets29,30. A benchmark study performed with helium31 in non-resonant conditions showed that photoionization time delays had almost no angular dependence, except at large angles relative to the laser polarization. For He, the absorption of a single XUV photon opens only one ionization channel (1s→εp), but a second IR probe photon is required in the attosecond RABBIT technique to measure time delays. Therefore, the observed time delay anisotropy was attributed to phase differences between final quantum states with different angular symmetry resulting from two-photon (XUV+IR) ionization.
In this work, we demonstrate how the angular dependence of the atomic time delays is affected by correlation effects associated to the mechanism of autoionization, thus giving access to angle-resolved multi-electron dynamics on the attosecond time scale. We present measurements of the differential photoionization cross section of argon in a spectral energy range where the 3s13p6np series of autoionizing resonances can be efficiently populated32,33. The measured photoelectron angular distributions (PADs) obtained by one-photon absorption are in excellent agreement with static measurements from studies performed with synchrotron radiation. In addition, we get access to the angle-resolved atomic time delays at photon energies spanning an autoionizing resonance. Our results show that the atomic time delay measured near these resonances depends strongly on the electron emission angle relative to the polarization of the ionizing XUV field. The ratio of the ionization channels 3p→εd and 3p→εs abruptly changes across the resonances, leading to a strong variation of the ionization delay with the electron emission angle and energy.
Results
Experimental results
Results from two experiments, performed at ETH Zurich and Lund University are presented. Figure 1 shows the HHG spectra used in these experiments. In both cases, the 17th harmonic is resonant with an autoionizing state, the 3s−15p (ETH) and the 3s−14p (Lund) states34. The two experiments are both based on the RABBIT technique, but using different detection setups presented in details in the Methods section (see also refs. 26 and 35).
Extreme ultraviolet spectra of the attosecond pulse trains used in the experiment. The XUV radiation is generated by focusing the IR beam into an argon target. The vertical lines show the energy position of the 3s−1np series of autoionizing states converging to the 3s threshold. In the ETH experiment (red line), the 5p state (at 27.99 eV, highlighted in green) is resonant with harmonic 17 (HH17), while in the Lund experiment (blue line) it is the 4p (26.6 eV, also highlighted in green). The black dashed line indicates the position of the 3s−14s autoionizing state
The atomic delays were measured with the XUV-IR interferometric RABBIT technique36,37. When an atom with ionization potential Ip is ionized by an XUV attosecond pulse train (APT), photoelectrons are released in the continuum at discrete kinetic energies equal to Ekin = EHH−Ip, where EHH = (2q+1)ħω defines the XUV photon energy comb of the APT (ω is the IR laser frequency). When an IR dressing field is added, we obtain two-color two-photon transitions with a photoelectron spectrum that exhibits additional sidebands (SBs) at energies in-between two consecutive APT comb peaks38. These energies correspond to the absorption of an XUV photon combined with the additional absorption or emission of an IR photon. Any SB energy can be reached by two different interfering ionization channels37. As explained in more details in the discussion below, the amplitude of the sideband signal oscillates as:
where Δϕatto is the phase difference between the consecutive frequency comb peaks of the APT and therefore corresponds to the so-called attochirp39, while Δϕatomic is the accumulated atomic phase difference between the two quantum paths (absorption and emission of an IR photon)36.
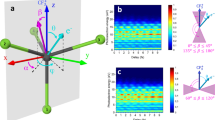
Our experimental setups allow us to record angle-resolved RABBIT spectrograms. Fig. 2 shows examples of the results obtained with the ETH setup. Similar data were measured in the Lund experiment. Fig. 2a presents an angle-integrated spectrogram, displaying clear sideband oscillations. Fig. 2b shows a delay-integrated photoelectron spectrum as a function of the emission angle θ, defined relative to the common XUV and IR polarization axis. We determine the photoelectron angular distributions for several discrete photon energy values, over all emission angles except in the region θ = 0, where the detection efficiency of the reaction microscope drops. Fig. 2c presents the angle- and delay-integrated spectrum.
RABBIT measurements obtained with the ETH experimental setup. a Angle-integrated photoelectron spectrum as a function of the XUV-IR delay. b Delay-integrated photoelectron spectrum as a function of the emission angle θ relative to the common axis of polarization of the XUV and IR pulses. c Integration of the spectrogram in angle and delay results in the 1D spectrum where sidebands appear between consecutive harmonics
A cosine fit of the (angular-resolved) sideband signal as a function of the delay between XUV and IR pulses returns the value of the total phase Δϕ = Δϕatto+Δϕatomic3. By subtracting Δϕatto, the energy- and angle-dependent atomic time delay, defined as τatomic ≈ Δϕatomic/2ω18,40, can be retrieved. The atomic time delay can in turn often be written as a sum of two contributions: τatomic ≈ τW+τcc11. The first term is related to one-photon ionization and, in the case of single-channel photoionization, is the Wigner delay \((\tau _W \approx {\mathrm{{\Delta} }}\eta _\ell /2\omega )\), where \(\eta _\ell\) is the scattering phase and \(\ell\) the angular momentum. The second term arises from laser-induced continuum-continuum transitions τcc ≈ Δφcc/2ω.
Delay-integrated asymmetry parameters
In spherical coordinates, the photoelectron angular distribution dσ/dΩ measured within a solid angle dΩ = sinθdθdφ and resulting from the (multiphoton) photoionization of atoms by linearly polarized photons is given by29:
where σ is the total photoionization cross section, θ is the angle between the emitted photoelectron and the polarization axis of the XUV light, Lmax is the maximum electron’s angular momentum to which the expansion in terms of the Legendre polynomials P j of order j is performed. The β j parameters are the coefficients of the Legendre polynomials. The photoelectron angular distributions are symmetric and we expect the odd (β1, β3 and so on) order parameters to be zero.
In a first analysis, we extract the energy-dependent values of the anisotropy parameters β from the PADs. It is well-known that autoionization leads to a change of the anisotropy parameter β32,41,42
Figure 3a, b shows the experimental photoelectron angular distributions in polar coordinates (panels a and b) for harmonic order 17 (HH17) and sideband 16 (SB16), using the harmonic spectrum shown in red in Fig. 1 (ETH). The PADs are constructed by filtering the counts of the delay-integrated spectrogram (Fig. 2b) with a 0.7 eV wide energy window centered at the harmonic (or sideband) peak. The green lines represent the fit of the distributions, which account for the detector geometry (Eq. (2) is multiplied by sin(θ) to account for the geometrical effect related to the solid angle]. In the case of single-photon absorption (harmonics), the sum in Eq. (2) includes only one term, j = 2, and the fit of the distributions returns the values of β2. For two-photon absorption (sidebands), we stopped the expansion of Eq. (2) at j = 4. The fit of the distributions returns vanishing β1 and β3, which is consistent with the fact that our PADs are left-right symmetric.
Photoelectron angular distributions and β parameters. a and b represent two photoelectron angular distributions (PAD) in polar coordinates for electron kinetic energies corresponding to HH17 and SB16, respectively, as measured in the ETH experiment with the reaction microscope detector. The green solid lines are the fit of Eq. 1, multiplied by sin(θ) to account for the detector geometry, to the data. c Values of β2 parameter as a function of photon energy sampled at the harmonic (solid line) obtained in the ETH (in red) and Lund (in blue) experiments. The black dots are taken from33 and the arrows at 26.6 eV and 28 eV indicate the positions of the 3s→4p and the 3s→5p autoionization resonances. d Values of β2 parameter (solid lines) and β4 parameter (dashed lines) as a function of photon energy sampled at sideband energy positions for the ETH (in red) and Lund (in blue) experiments. In panels c and d, the data represent the mean value extracted by independent datasets, while the error bars indicate the standard deviation
Figure 3c, d show the coefficients of the Legendre polynomials (Eq. 1) as a function of the absorbed photon energy for both the harmonic (c, β2 only) and sideband peaks (d, β2 and β4). Our data, indicated in red (ETH) and blue (Lund) compare well with synchrotron measurements (black dots)33, thus validating our experiments. The 3s−14p state clearly influences the β2 coefficient at the 17th harmonic and 16th sideband (SB16) energies in the Lund experiment, while the effect of the 3s−15p state is weakly observed on SB16 in the ETH results. The variation of the β2 coefficient for SB16, larger than that observed in HH17, (Lund experiment) might be influenced by the presence of the 3s−14s autoionizing state (25.2 eV, see Fig. 1), which can be populated by two-photon transitions with the 15th or 17th harmonics. Note that the large bandwidth of the XUV and IR radiation used in the present work significantly blurs the effect of the resonances compared to synchrotron radiation. The different widths of the two resonances, 80 meV for the 4p and 28.5 meV for the 5p32 explain the stronger effect observed in the Lund experiment.
Delay-dependent asymmetry parameters
In comparison to static data acquired at synchrotrons, our pump-probe measurements show worse energy resolution, however they provide access to complementary time-dependent information. Fig. 4a shows the behavior of β2 as a function of XUV-IR delay for harmonics and sidebands. Here, we present the data from the Lund experiment (obtained with the blue spectrum in Fig. 1). Similar behavior was observed in the ETH experiment. The first observation is that the β2 values for the harmonics and sidebands are oscillating with the same frequency 2ω, as expected in the RABBIT setting, but with opposite phases. For the sidebands, the variation of β2 decreases in amplitude as the photon energy increases, while that of the harmonics remains constant for the harmonics, as shown in Fig. 4b.
Time-dependent β2 parameters. Panel a shows the values of β2 parameter for SB14, SB16, SB18 (blue symbols), SB22 (black symbols) and HH17 (yellow symbols), extracted from a fit of the momentum distributions at different XUV-IR delays in the Lund experiment, for which HH17 is resonant with the 3s−14p autoionizing state. b Amplitude of β2 oscillations as a function of kinetic energy. For the harmonics, it is approximately constant, while it decreases for the sidebands
Angular dependence of the atomic delays
In Fig. 5 we compare the angular dependence of the atomic time delay for two different sidebands, SB14, which is not affected by the 3s−1np resonances (Fig. 5a) and SB16, such that H17 is resonant with the 3s−15p autoionizing state (Fig. 5b). As described in ref. 31, the angle-dependent atomic delay is retrieved by filtering the detected photoelectrons at different emission angles with respect to the common polarization axis of the XUV/IR pulses. For each angular sector, a RABBIT spectrogram is constructed and the SB signal is obtained by integrating the spectrogram in an energy window centered at the peak of the SB position. The atomic delays shown in Fig. 5 for each angular sector are referenced against the values retrieved for a sector between 0 to 30 degrees. We have chosen the reference angular range as large as 30 degrees in order to minimize the error in the reference phase. We also present results of a numerical calculation, where the angle-resolved atomic phase is extracted by computing the partial complex amplitudes of the two-photon transition matrix elements. The latter are calculated following two different approaches depending on whether the contribution from a resonant state is included or not. While in the non-resonant case, the matrix elements are evaluated by using second-order time dependent perturbation theory43, here without including resonant configurations, in the resonant case they include both resonant and non-resonant paths by using a generalization of the Fano configuration interaction formalism for two-photon transitions44,45. Further details on how the atomic phase and the matrix elements are calculated are presented in Supplementary Note 1.
Angular-resolved time delays. a, b show the atomic time delay (red symbols) as a function of electron emission angle for SB14 and SB16 (ETH experiment). Data obtained in Lund for SB14 are also indicated (blue open squares). The delays are referenced to the value retrieved for electrons departing within an opening angle of up to 30 degrees. The green lines show the calculated delays in resonant (solid) and nonresonant (dashed) conditions. The error bars indicate the standard deviation as extracted by a series of independent measurements
The general trend of the angle variation of the atomic time delays is the same as in the case of helium31, with the delay becoming more and more negative as the emission angle becomes larger (>50°). For SB14, the experimental data is reproduced by second-order time dependent perturbation theory43, as can be seen in Fig. 5a. There is no need to include any autoionizing state, because the harmonics involved (HH13 and HH15) are both placed at energies smaller than the first state of the np series (4p) and thus are not hitting any resonance (Fig. 1).
For SB16, however, the situation is very different. As seen in Fig. 5b, quantitative agreement between the data and the model is achieved only if the 3s−15p resonance is accounted for. This is accomplished with the theoretical model that was previously validated in helium by comparison with ab-initio calculations44,45 and extended here to obtain angular information in argon (see Supplementary Note 1). The parameters for the 3s−15p resonance, like the energy position, autoionization width and Fano’s q parameter are taken from ab initio calculations based on a multiconfigurational Hartree-Fock (MCHF) approach46. When the resonance is neglected, the estimated time delay anisotropy is too small, as indicated by the dashed line.
Angular-resolved energy dependence of the atomic delays
Figure 6 presents a spectrally and angularly resolved analysis of the time delays. We here concentrate on the Lund experiment, where we scanned the laser wavelength between 780 and 794 nm so that the 17th harmonic spanned the resonance. In this case, we did not use the normalization applied in Fig. 5, but normalized the delays, for each wavelength, with respect to a line between the angle-integrated delays obtained by analyzing SB14 and SB22, similarly to the procedure used in ref. 26. Fig. 6 shows striking differences between the spectral dependence of the delay within SB14 and SB16. For SB14 (Fig. 6a), the delay is relatively flat and decreases for large angles; it barely depends on energy. For SB16, when H17 is resonant with 3s−14p, (Fig. 6b), the energy variation of the delay shows the characteristic behavior of the phase change across a Fano resonance46. The angle-integrated variation of the delay (not shown here) is lower than that observed in ref. 26, due to the larger XUV and IR bandwidths used in the present work. One of the key conclusions of this work is that the energy variation of the delay also changes with angle. Interestingly, in contrast to the non-resonant case, across the resonance the delay first increases and then decreases with angle. The delay curves at different angles seem to cross at the same point at 25.2 eV. The general behavior of the delay as a function of angle and energy is discussed in the next section.
Energy and angle-resolved time delays measured in the Lund experiment. Relative atomic delay as a function of sideband photon energy (for two-photon transitions) for different emission angles for SB14 (a) and SB16 (b). The error bars represent the standard deviation as extracted by a series of independent measurements
Discussion
Here we provide a qualitative explanation of the different effects observed in the experiments, based upon simple arguments. The angle-dependent delay measured in two-photon experiments is theoretically obtained by averaging the angle-resolved RABBIT probability over the orientation of the parent ion (in the case of argon, m = −1,0,1). However, to understand how the angular dependence of the RABBIT phase arises, it is enough to consider only one orientation. We thus restrict our discussion to m = 0, and first describe resonant one-photon ionization, and subsequently anisotropy and delay measurements by the RABBIT technique.
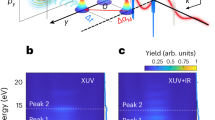
We concentrate here on the 3s−14p autoionizing state, whose effect on the amplitude and phase of the partial ionization channels 3p→εs and 3p→εd is presented in Fig. 7a, b. The shown data have been obtained from a multiconfiguration Hartree-Fock (MCHF) calculation46. Away from the resonant state, the 3p→εd channel dominates by a factor ~5 (in amplitude) over the 3p→εs channel. However, the amplitude of the 3p→εd channel decreases rapidly close to the Fano resonance, while that of the 3p→εs channel increases. This obviously affects the geometrical properties of the emitted electron wave packet. The probability amplitude for one-photon ionization from the ground state 3p, m = 0 can be written as:
where \(A_\ell ^{(1)}\) are the photoionization amplitudes for the \(3p \to \varepsilon \ell\) channel, \(\eta _\ell\) the scattering phases and \(Y_{\ell m}(\theta )\) (m = 0) the spherical harmonics. Using the amplitudes \(A_\ell ^{(1)}\) and phases \(\eta _\ell\) from ref. 46 (Fig. 7a, b), the variation of the phase of M(1) with energy and angle is shown in Fig. 7c. At small and large angles, the phase variation with energy resembles the phase variation of the 3p →εd channel. However, at 54.7° (also called the magic angle), when Y20 goes to zero (see inset in Fig. 7), the phase variation is that of the 3p→εs channel. In Fig. 7c, the curves cross at around the XUV photon energy of 26.6 eV, when the amplitude of the 3p→εd channel becomes small at the resonance. In this case, and in general when there is only one channel for ionization, the phase variation does not depend on emission angle.
Amplitude and phases for one and two-photon transitions. Amplitude (in atomic units) (a) and phase (b) of one-photon ionization for the 3p→εs (blue) and 3p→εd channels close to the 3s−14p autoionizing state46. Phase variation as a function of energy for one-photon (c) and two-photon (d) ionization, calculated according to Eq. (7). Note that the x axes in this figure refers to the photon energy of the 17th harmonic (single photon transition), whose position is spanned across the 4p resonance. The spherical harmonics involved are indicated as an inset
The RABBIT technique allows the determination of atomic delays via interferometry. However, as explained below, since it is based upon two-photon XUV-IR transitions, it also changes the angular momentum of the final states and consequently the photoelectron angular distributions.38,47. For any ionization channel leading to the same final state, our experimental measurement involves three two-photon pathways: 3p→λ→ℓ, with (λ, ℓ) = (0,1),(2,1),(2,3). Let us denote the amplitude of the respective pathways by \(E_{\ell \lambda }\), the phase by \(\varphi _{\ell \lambda }^{(E)}\) for the emission path, where an XUV photon is absorbed and an IR photon is emitted. The angular part is a spherical harmonic \(Y_{\ell 0}\). We assume that the XUV and IR fields are delayed by τ and omit any additional phase due to the fields (e.g. the attochirp). The two-photon transition amplitude (m = 0), can then be written as:
Denoting the amplitude and phase of the term within the curly brackets E(θ) and \(\varphi _{\mathrm{E}}\left( \theta \right) = {\mathrm{Arg}}\left[ {E\left( \theta \right)} \right]\) respectively, and the corresponding quantities for path A A(θ) and φA(θ) , where both photons are absorbed, the RABBIT amplitude can be expressed as
Thus, the sideband intensity simply reads as
As can be seen, in this general case, the phase of the oscillations depends on the emission angle48, and the angular distributions vary with the delay.
We now examine how Eq. (6) simplifies for particular cases. In the non-resonant case and at high kinetic energy, the two interfering paths become comparable, i.e., \(A\left( \theta \right) \approx E\left( \theta \right)\), \(\varphi _{\mathrm{A}}(\theta ) \approx \varphi _{\mathrm{E}}\left( \theta \right) + {\mathrm{{\Delta} }}\varphi\), where \({\mathrm{{\Delta} }}\varphi\) is assumed to be angle-independent, Eq. (6) reduces to
so that the angular distributions have the same form, and hence the same value of asymmetry parameters β, for all τ. As this approximation should improve with increasing kinetic energy, the PADs should become increasingly independent of the delay, in agreement with the experimental results shown in Fig. 4. Alternatively, as suggested in ref. 49, this behavior might also result from changes in the phases involved in the two-photon transitions as the photon energy increases.
Under the assumption that the resonance does not appreciably affect continuum-continuum transitions, the phase for the channel \(3p \to \lambda \to \ell\) (e.g. emission path) is approximately equal to \(\eta _\lambda ^E + \varphi _{_{cc}}^E + \lambda \pi /2\)11, where \(\eta _\lambda ^E\) is the scattering phase of the intermediate continuum state, and where \(\varphi _{cc}^E\) originates from the IR-induced continuum-continuum transition. At high kinetic energy, \(\varphi _{cc}^E\) can be calculated with an asymptotic approximation, and is then independent of the intermediate or final state angular momenta11. If in addition the 3p→s channel can be neglected, the phase terms in Eq. (6) factorize out of the curly bracket and, using \(\varphi _{cc}^E \approx - \varphi _{cc}^A\) as well as \(\mathrm{\Delta} \eta _2 = \eta _2^E - \eta _2^A\), Eq (6) becomes
In this case, the atomic delay is isotropic. As can be seen in Fig. 5a, this is indeed the case for emission angles θ < 45º. The angular dependence observed for large angles is therefore due to the non-negligible contribution of the 3p→s channel and/or the breakdown of the asymptotic approximation for the φ cc phase. When only one intermediate channel is accessible, as in helium at low photon energies31, the anisotropy of the atomic delay is solely due the breakdown of the asymptotic approximation. More details on this point are given in the Supplementary Note 2.
We now consider the resonant case. The measured angular dependence of the phase in our two-photon measurement is not a direct “copy” of that for one-photon ionization because the continuum-continuum transition, needed for the phase measurement, projects the resonant state onto different angular momentum states, and thus modifies the angular distribution. To qualitatively describe the effect of the IR-induced transitions on the one-photon phase, we focus on the 3s−14p resonance and assume that, for the non-resonant XUV + IR absorption path that involves HH15, the one-photon channel 3p→s is negligible in comparison with the 3p→d one. This is a reasonable approximation since the latter channel is dominant in this range of photon energies (Fig. 7a). We also neglect the angular momentum dependence of φ cc . In Eq. (6), \(\eta _A(\theta ) = \eta _2^A + \varphi _{cc}^A\), which does not depend on angle, thus providing a true reference phase. We also assume that the radial part of \(E_{\ell \lambda }\) is proportional to the corresponding one-photon amplitude. The angle-resolved determination of the phase of the RABBIT oscillations as a function of energy allows us to study the variation of the phase of \(\eta _E(\theta )\). The results of this simplified model are shown in Fig. 7d. The atomic delay varies with energy similarly to that of the one-photon amplitude at angles where the 3p→εd channel dominates. This behavior changes at the angle 40°, when the spherical harmonic \(Y_{30}\) goes to zero. For this angle, the energy dependence of the delay is not that of the 3p→εs channel, as in the one-photon ionization case, but results from the combination of the two channels appearing in the factor that goes with \(Y_{10}\) in Eq. (4). As in the one-photon case, the curves cross at the one-photon energy of 26.6 eV, i.e., there is no angular dependence, because the 3p→εd channel becomes negligible. Although this simple model does not allow us to explain all aspects of the experimental results, it does show that it is the delicate interplay between the different open channels that is actually responsible for the complex angular variation of the spectrally resolved phase observed in the experiment (Fig. 6b).
In conclusion, we have presented measurements of the two-color (i.e., XUV- IR) differential photoionization cross section of argon and extracted time-dependent anisotropy parameters as well as energy and angle-dependent atomic time delays. The spectrum of the employed XUV radiation lies in the energy region where several singly excited bound states decay via autoionization. The presence of autoionizing states clearly manifests in the measured time delays for both the narrow 3s−15p and the broad 3s−14p resonances. They are also very visible in the anisotropy parameters extracted from time-integrated photoelectron angular distributions generated by two-photon absorption. These results demonstrate not only that the phase of the photoelectron wave packet is significantly distorted in the presence of resonances, which prevents one from interpreting the Wigner delay as photoemission time delay9,50, but also that this distortion depends on the electron emission angle. The effect of the resonance on the angular dependence of the atomic delay is due to the existence of several open channels with different angular emission properties and with a varying amplitude across the resonance.
Methods
Experimental setup
In both ETH and Lund experiments, a Ti:Sapphire laser system generated IR pulses with a duration of ~30 fs and optimal center wavelength of 780 nm. The Lund experimental setup allows the tuning of the laser center wavelength from this value up to 794 nm. The pulses are split into two arms, with the most intense part of the beam focused into a gas target filled with argon, to generate an APT centered at a photon energy of about 35 eV and with a spectral envelope of about 12 eV FWHM (full-width-half-maximum). After the attosecond pulse generation, an aluminum filter is used to remove the IR radiation co-propagating with the XUV beam. The second branch of the IR beam is used as a weak probe for the RABBIT technique.
In both experiments, the intensity of the IR probe beam has been measured to be \(3 \cdot 10^{11}\mathrm{W}{\mathrm{cm}}^{ - 2}\), low enough to ensure the weak field conditions needed for RABBIT. Both arms of the interferometer are actively stabilized in order to minimize sources of systematic errors and ensure stability of the delay in the attosecond range. After recombination of the IR probe with the XUV APT, the two beams further propagate collinearly onto a toroidal mirror that focuses them onto the argon gas jet located inside an electron spectrometer.
In the ETH experiment, the spectrometer contains a reaction microscope detector51. This detection scheme allows for the retrieval of the full 3D momentum vector in coincidence for each individual charged particle over the full 4π solid angle. In all of the results presented, the data represent the mean value extracted by 15 independent datasets, while the error bars indicate the standard deviation.
In the Lund experiment uses a velocity-map imaging (VMI) detector52, which measures the projection of the electron distribution onto a position-sensitive detector. This detection technique is well adapted to the geometry of the interaction, with a common XUV and IR polarization axis, chosen to be perpendicular to the detector axis. The 3D-electron momentum distributions are obtained by inversion of the 2D-projections using the pBasex algorithm53. The Lund results include 10 datasets, at different fundamental wavelengths.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Schultze, M. et al. Delay in photoemission. Science 328, 1658–1662 (2010).
Klünder, K. et al. Probing Single-Photon ionization on the attosecond time scale. Phys. Rev. Lett. 106, 143002 (2011).
Wigner, E. P. Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 98, 145–147 (1955).
Smith, F. T. Lifetime matrix in collision Theory. Phys. Rev. 118, 349–356 (1960).
Carvalho, C. A. A. D. & Nussenzveig, H. M. Time delay. Phys. Rep. 364, 83–174 (2002).
Pazourek, R., Nagele, S. & Burgdörfer, J. Time-resolved photoemission on the attosecond scale: opportunities and challenges. Farad Discuss. 163, 353–376 (2013).
Maquet, A., Caillat, J. & Taïeb, R. Attosecond delays in photoionization: time and quantum mechanics. J. Phys. B: Mol. Opt. Phys. 47, 1–13 (2014).
Sabbar, M. et al. Resonance effects in photoemission time delays. Phys. Rev. Lett. 115, 133001 (2015).
Cavalieri, A. L. et al. Attosecond spectroscopy in condensed matter. Nature 449, 1029 (2007).
Dahlström, J. M., L’Huillier, A. & Maquet, A. Introduction to attosecond delays in photoionization. J. Phys. B 45, 183001 (2012).
Pazourek, R., Nagele, S. & Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 87, 765–802 (2015).
Guénot, D. et al. Measurements of relative photoemission time delays in noble gas atoms. J. Phys. B: Mol. Opt. Phys. 47, 245602 (2014).
Palatchi, C. et al. Atomic delay in helium, neon, argon and krypton. J. Phys. B: Mol. Opt. Phys. 47, 245003 (2014).
Cattaneo, L. et al. Comparison of attosecond streaking and RABBITT. Opt. Express 24, 29060–29076 (2016).
Swoboda, M. et al. Phase measurement of resonant Two-Photon ionization in helium. Phys. Rev. Lett. 104, 103003 (2010).
Haessler, S. et al. Phase-resolved attosecond near-threshold photoionization of molecular nitrogen. Phys. Rev. A. 80, 011404(R) (2009).
Locher, R. et al. Energy-dependent photoemission delays from noble metal surfaces by attosecond interferometry. Optica 2, 405–410 (2015).
Ehrenfest, P. Bemerkung über die angenäherte Gültigkeit der klassischen Mechanik innerhalb der Quantenmechanik. Z. Phys. 45, 455–457 (1927).
Nagele, S. et al. Time-resolved photoemission by attosecond streaking: extraction of time information. J. Phys. B 44, 081001 (2011).
Pratt, S. T. Excited-state molecular photoionization dynamics. Rep. Prog. Phys. 58, 821–883 (1995).
Seaton, M. J. Quantum defect theory. Rep. Prog. Phys. 46, 167–257 (1983).
Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 124, 1866–1878 (1961).
Schmidt, V. Photoionization of atoms using synchrotron radiation. Rep. Prog. Phys. 55, 1483–1659 (1992).
Lefebvre-Brion, H. & Field, R. W. In The Spectra and Dynamics of Diatomic Molecules. (Elsevier Academic Press 2004).
Kotur, M. et al. Spectral phase measurement of a fano resonance using tunable attosecond pulses. Nat. Comm. 7, 10566 (2015).
Gruson, V. et al. Attosecond dynamics through a Fano resonance: Monitoring the birth of a photoelectron. Science 354, 734–738 (2016).
Kaldun, A. et al. Observing the ultrafast buildup of a Fano resonance in the time domain. Science 354, 738–741 (2016).
Laurent, G. et al. Attosecond control of orbital parity mix interferences and the relative phase of even and odd harmonics in an attosecond pulse train. Phys. Rev. Lett. 109, 083001 (2012).
Villeneuve, D. M., Hockett, P., Vrakking, M. J. J. & Niikura, H. Coherent imaging of an attosecond electron wave packet. Science 356, 1150–1153 (2017).
Heuser, S. et al. Angular dependence of photoemission time delay in helium. Phys. Rev. A. 94, 063409 (2016).
Berrah, N. et al. Angular-distribution parameters and R-matrix calculations of Ar 3s−1 -> np resonances. J. Phys. B: Mol. Opt. Phys. 29, 5351–5365 (1996).
Southworth, S. H., Parr, A. C., Hardis, J. E., Dehmer, J. L. & Holland, D. M. P. Calibration of a monochromator / spectrometer system for the measurement of photoelectron angular distributions and branching ratios. Nucl. Instr. Meth Phys. ResA 246, 782–786 (1986).
Wu, S. L. et al. Electron-impact study in valence and autoionization resonance regions of argon. Phys. Rev. A. 51, 4494–4500 (1995).
Sabbar, M. et al. Combining attosecond XUV pulses with coincidence spectroscopy. Rev. Sci. Instrum. 85, 103113 (2014).
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Muller, H. G. Reconstruction of attosecond harmonic beating by interference of two-photon transitions. Appl. Phys. B. 74, S17–S21 (2002).
Picard, Y. J. et al. Attosecond evolution of energy- and angle-resolved photoemission spectra in two-color (XUV + IR) ionization of rare gases. Phys. Rev. A. 89, 031401 (2014).
Mairesse, Y. et al. Attosecond Synchronization of High-Harmonic Soft X-Rays. Science 302, 1540–1543 (2003).
Lucchini, M. et al. Light-Matter interaction at surfaces in the spatiotemporal limit of macroscopic models. Phys. Rev. Lett. 115, 137401 (2015).
Becker U., Shirley D. A. in: VUV and Soft X-ray Photoionization. Plenum Press, New York 1996).
Reid, K. L. Photoelectron angular distributions. Annu. Rev. Phys. Chem. 54, 397–424 (2003).
Dahlström, J. M. & Lindroth, E. Corrigendum: Study of attosecond delays using perturbation diagrams and exterior complex scaling. J. Phys. B: Mol. Opt. Phys. 49, 209501 (2016).
Jiménez-Galán, Á., Argenti, L. & Martín, F. Modulation of attosecond beating in resonant Two-Photon ionization. Phys. Rev. Lett. 113, 263001 (2014).
Jiménez-Galán, Á., Martín, F. & Argenti, L. Two-photon finite-pulse model for resonant transitions in attosecond experiments. Phys. Rev. A. 93, 023429 (2016).
Carette, T., Dahlström, J. M., Argenti, L. & Lindroth, E. Multiconfigurational Hartree-Fock close-coupling ansatz: Application to the argon photoionization cross section and delays. Phys. Rev. A. 87, 023420 (2013).
Ivanov, I. A. & Kheifets, A. S. Angle-dependent time delay in two-color XUV+IR photoemission of He and Ne. Phys. Rev. A. 96, 013408 (2017).
Dahlström, J. M. & Lindroth, E. Study of attosecond delays using perturbation diagrams and exterior complex scaling. J. Phys. B: Mol. Opt. Phys. 47, 124012 (2014).
Hockett, P. Angle-resolved RABBITT: theory and numerics. J. Phys. B: Mol. Opt. Phys. 50, 154002 (2017).
Argenti, L. et al. Control of photoemission delay in resonant two-photon transitions. Phys. Rev. A. 95, 043426 (2017).
Ullrich, J. et al. Recoil-ion and electron momentum spectroscopy: reaction-microscopes. Rep. Prog. Phys. 66, 1463–1545 (2003).
Eppink, A. T. J. B. & Parker, D. H. Velocity map imaging of ions and electrons using electrostatic lenses: Application in photoelectron and photofragment ion imaging of molecular oxygen. Rev. Sci. Instrum. 68, 3477–3484 (1997).
Garcia, G. A., Nahon, L. & Powis, I. Two-dimensional charged particle image inversion using a polar basis function expansion. Rev. Sci. Instrum. 75, 4989–4996 (2004).
Acknowledgements
C.C., S.H, M.L., L.G. and U.K acknowledge support by the ERC advanced Grant No. ERC-2012-ADG_20120216 within the seventh framework program of the European Union and by the NCCR MUST, funded by the Swiss National Science Foundation. A.J.-G. acknowledges support from the DFG QUTIF grant IV 152/6-1. L.A. acknowledges support from the TAMOP NSF Grant No. 1607588, as well as UCF fundings. The Lund group acknowledges support from the ERC advanced grant PALP (339253), the Knut and Alice Wallenberg Foundation, the Swedish Research Council and the Swedish Foundation for Strategic Research. E.L. acknowledges support from the Swedish Research Council, Grant No. 2016-03789. J.M.D. acknowledges support from the Swedish Research Council, Grant No. 2014-03724. C.M., C.L.M.P., A.J.-G., L.A. and F.M. acknowledge computer time from the CCC-UAM and Marenostrum Supercomputer Centers and financial support from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC advanced Grant 290853 XCHEM, the MINECO projects FIS2013-42002- R and FIS2016-77889-R, and the European COST Action XLIC CM1204.
Author information
Authors and Affiliations
Contributions
C.C., S.H., and M.L. performed the ETH experiment and analyzed the data. S.Z., D.B., M.I., S.N., S.M., M.G. performed the Lund experiment and analyzed the data. L.R., P.J. built the VMI spectrometer. All the authors were involved in the data interpretation. C.M., C. L. M. P., Á.J.G., L.A., J.M.D., E.L. and F.M. developed the theoretical model. C.C., F.M., A.L. and U.K. wrote the manuscript, which all the authors discussed.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cirelli, C., Marante, C., Heuser, S. et al. Anisotropic photoemission time delays close to a Fano resonance. Nat Commun 9, 955 (2018). https://doi.org/10.1038/s41467-018-03009-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-03009-1
This article is cited by
-
Berry curvature in the photoelectron emission delay
npj Computational Materials (2024)
-
Bright continuously tunable vacuum ultraviolet source for ultrafast spectroscopy
Communications Physics (2024)
-
Attosecond delays in X-ray molecular ionization
Nature (2024)
-
Attosecond dynamics of multi-channel single photon ionization
Nature Communications (2022)
-
The multi-photon induced Fano effect
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.