Abstract
Recent studies highlight that oceanic motions associated with horizontal scales smaller than 50 km, defined here as submesoscales, lead to anomalous vertical heat fluxes from colder to warmer waters. This unique transport property is not captured in climate models that have insufficient resolution to simulate these submesoscale dynamics. Here, we use an ocean model with an unprecedented resolution that, for the first time, globally resolves submesoscale heat transport. Upper-ocean submesoscale turbulence produces a systematically-upward heat transport that is five times larger than mesoscale heat transport, with winter-time averages up to 100 W/m2 for mid-latitudes. Compared to a lower-resolution model, submesoscale heat transport warms the sea surface up to 0.3 °C and produces an upward annual-mean air–sea heat flux anomaly of 4–10 W/m2 at mid-latitudes. These results indicate that submesoscale dynamics are critical to the transport of heat between the ocean interior and the atmosphere, and are thus a key component of the Earth’s climate.
Similar content being viewed by others
Introduction
Variations in the heat content of the ocean–atmosphere-coupled system influence Earth’s climate1,2. Turbulent motions in the upper ocean (down to ~300 m depths) occur across a broad range of spatial scales, from ~1000 km down to ~1 km and even smaller scales, and influence the partitioning of heat between the ocean and atmosphere as suggested by local studies3,4. Satellite images during the past four decades reveal broadly distributed submesoscale (~0.1–50 km) turbulence over the global ocean5, typically characterized by surface frontal structures in the form of eddies and elongated filaments (Fig. 1a, b). Only recently, regional numerical and observational studies4 have shown that submesoscales may explain more than 50% of the total vertical velocity variance in the ocean’s upper 300 m. This implies that submesoscale fluxes are a potentially efficient route for the vertical transport of heat, nutrients, oxygen, and climatically important dissolved gases. Submesoscale structures are produced by several classes of surface frontal instabilities3,4,5,6,7,8,9,10,11 that tend to be intensified in the winter when the mixed layer depth is large. Additionally, submesoscales may transport heat vertically from cold to warm waters (up-gradient)4,5,6,7,8,9,10,11,12, the opposite sense of traditional subgrid-scale parameterizations (down-gradient) in climate models. This unique property is not captured in climate models that have insufficient resolution to simulate these submesoscale dynamics. Useful parameterizations13 have been proposed and implemented for certain submesoscale processes, although these involve sometimes-unsettled coefficients while other submesoscale processes remain uncaptured, e.g., wind-front interactions and frontogenesis. The full impact of submesoscale turbulence on ocean vertical heat transport and air–sea heat exchange has not previously been directly quantified on a global scale, representing a potential gap in our understanding of the evolution of global oceanic and atmospheric heat content13. Accurately assessing the impact of submesoscale turbulence requires explicit resolution of motions at these scales, which remains computationally challenging for global ocean simulations.
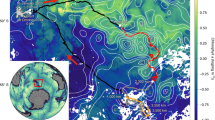
Overview of global submesoscale structures and distributions. a Satellite image of a large bloom of cyanobacteria in the Baltic Sea on August 11, 2015 showing submesoscale eddies, fronts, and filaments. Figure 1a sourced from NASA (images by Norman Kuring, NASA's Ocean Color Web). See https://landsat.visibleearth.nasa.gov/view.php?id=86449. b Observations11 of submesoscale structures from sunglitter in the Andikithiron Channel northwest of Crete on October 7, 1984. Ship tracks are labeled A, B. c, d Simulated global snapshot of ocean turbulence at ~2-km resolution, as well as expanded views for local regions, for c Northern and d Southern Hemisphere winters. The quantity shown is relative vorticity (s−1), a measure of the spin of fluid parcels, that emphasizes fast-rotating submesoscale turbulence especially in the winter hemisphere (see Supplementary Figure 1 for Rossby number). The same global maps but with a higher pixel resolution can be found at web.gps.caltech.edu/~zhan/nailed/Figure1a.png
In this study, we make a major advance toward realizing this challenge by using a novel global ocean simulation with an unprecedented ~2 km horizontal resolution that, for the first time, globally resolves the ocean submesoscale heat transport at the 10–50-km scale range. We find that submesoscale turbulence produces a large and systematically upward heat transport globally throughout the upper ocean: the winter-time averages are 20–100 W/m2 across most of the mid-latitudes, peaking at 500–1000 W/m2 over shorter intervals of days to weeks. These amplitudes, consistent with recent in situ observations11, are comparable to air–sea heat fluxes, and are more than five times larger than the mesoscale vertical heat transport in most regions of the ocean. Comparison with a lower resolution simulation shows that submesoscale vertical heat transport warms the sea surface by 0.06–0.3 °C and produces an upward annual mean air–sea heat flux anomaly of 4–10 W/m2 in most mid-latitude areas. The latter is comparable to climatological air–sea heat fluxes. These results suggest that submesoscale processes are critical to setting the magnitude of the vertical heat flux between the interior ocean, the surface ocean, and the atmosphere, as well as the geographic location and temporal variability of these fluxes over days to months, and are therefore a key component of the global heat budget.
Results
An ultrahigh-resolution global ocean simulation
Here, we use a global ocean model with unprecedented resolution (1/48°, 90 levels, see “Methods”). The horizontal resolution, ~2 km at mid-latitude, captures physical processes at wavelengths down to a scale of ~10 km14,15. This ocean simulation has been evaluated, locally, using in situ observations in terms of the kinetic energy levels at different wavelengths and frequencies14,15. The simulation is progressively spun up from coarser resolution (initially 1/6°), observationally constrained model solutions16, which results in a quasi-equilibrated and realistic upper ocean state above the first 500 m (see “Methods”). Throughout this manuscript, we use the term submesoscale to designate a spatial scale smaller than the mesoscale: a horizontal scale ≲0.5° in terms of longitude (~50 km at mid-latitudes), roughly below the first deformation radius in most of the global ocean9,17,18,19,20,21,22 (in terms of wavelengths). Our simulation can resolve the 10–50 km submesoscale range (see “Methods”); we discuss the potential impact of the still unresolved submesoscale range below.
Overview of global submesoscale structures and distributions
The simulation shows that submesoscale turbulence populates the global upper ocean with coherent structures (10–50 km) embedded in the larger-scale ocean circulation (Fig. 1c, d and Supplementary Figure 1). Relative vorticity ζ, the curl of the velocity field, is a useful diagnostic for visualizing the ocean submesoscales. The relative vorticity (Fig. 1) on March 1, 2012 (Northern Hemisphere winter) and September 1, 2012 (Southern Hemisphere winter) reveals the geographic variability of submesoscale turbulence. Submesoscales in our simulation are everywhere characterized by a myriad of eddies as small as ~10 km intertwining with elongated and wavy filaments, as seen in the expanded panels of Fig. 1. There is a pronounced global seasonal signal in the ζ-field, characterized by larger magnitudes and smaller scales during the winter. Relative vorticity values comparable to Earth’s rotation rate (Supplementary Figure 1) are found in almost all ocean basins. This suggests4,23 strong and wide-spread vertical velocities in the upper ocean: in the 20°–60° mid-latitude band during the winter, about 51% and 2% of ocean area at 40 m depth has magnitudes larger than 10 m/day and 40 m/day, respectively (Supplementary Figure 2a–b). The above characteristics dominate not only in the Gulf Stream and Kuroshio, as already reported18,20,24, but also in a large number of unexplored regions that are critical for ocean–atmosphere exchange, including the Southern Ocean, the high-latitude North Atlantic, the broad subtropical oceans, and the Mediterranean, Black, and Arabian Seas. Note that these regions generally have deep mixed layer depths, which is an important factor for producing intense submesoscale motions.
Temporal variabilities of submesoscale characteristics
The time series of submesoscale vorticity and vertical heat transport exhibit not only a strong winter-peaked seasonality, but also a significant intermittency at daily to weekly time scales (Fig. 2, see “Methods”). The latter is associated with the short timescales of submesoscale dynamics3,22. The time series of the root-mean-square values of ζ and vertical velocity confirm their strong correlation (Fig. 2) and therefore the frontal character of submesoscale turbulence. This relationship is due to the ageostrophic circulation described by the omega equation23. The energetic vertical motions cause significant vertical heat transport at submesoscales, up to 500–1000 W/m2 (Fig. 2). The seasonal variability of the vertical heat flux has an amplitude of up to 200 W/m2, and its variability over shorter intervals of days to weeks peaks at 500–1000 W/m2. Our results suggest that submesoscale turbulence dramatically enhances the upper-ocean heat exchange at diverse time scales ranging from days to seasons, which applies broadly across the global ocean.
Temporal variability of submesoscale characteristics. Local time series of submesoscale band (~10–50 km, see “Methods”) root mean square (rms) relative vorticity (black), rms vertical velocity (blue), and vertical heat transport (positive: upward) at 40 m and 200 m depths (magenta and red, respectively). Dashed curves are the sinusoidal seasonal cycle fit for relative vorticity. The locations are in the a high-latitude North Atlantic (57°N, 26°W), b Kuroshio Extension (38.1°N, 156°E), c eastern Indian Ocean (38.3°S, 118°E), d Agulhas Current (40°S, 18°E). The results here are averaged over a 1° × 1° square box in each location. The correlation between the time series suggests a strong dynamic connection between the different quantities. Submesoscale upward heat transport can reach a significant amplitude up to 500–1000 W/m2, consistent with values inferred from recent observations10, and is characterized by a strong intermittency (days to weeks) and a winter-peaked seasonality
Global patterns of submesoscale vertical heat transport
The enhancement of the near-surface vertical heat transport by submesoscales is ubiquitous over the global ocean (Fig. 3). This heat transport is systematically upward (upgradient): it acts to produce a surface warming and a deeper cooling, intensified in winter. In the wintertime Southern Hemisphere, large submesoscale heat fluxes at 40-m depth cover most of the region between 20°S and 60°S (Fig. 3b), where 66% and 5% of ocean area has amplitudes larger than 20 W/m2 and 100 W/m2, respectively. At 200-m depth, submesoscale fluxes retain their large amplitudes and mostly cover the 35°–60°S latitude band (Fig. 3d), where 48% and 10% of ocean area here has amplitudes larger than 20 W/m2 and 100 W/m2, respectively. Large submesoscale heat fluxes also occur in the wintertime Northern Hemisphere (Fig. 3a, c). These are strongest in the 20°–40°N band, where 65% and 11% of ocean area has amplitudes larger than 20 W/m2 and 100 W/m2, respectively, at 40 m depth. Similar amplitudes also occur in the Atlantic subpolar and polar gyres (40°–60°N), where 61% and 19% of ocean area has amplitudes larger than 20 W/m2 and 100 W/m2, respectively, at 200 m depth. During the summer, submesoscale fluxes are still positive but have a smaller amplitude and more limited spatial coverage. Only the region between 40°–60°S, as well as 40°–60°N in the Atlantic, still have significant submesoscale fluxes, where 32% and 46% of the area in these respective latitude bands have amplitudes larger than 10 W/m2 at 200 m depth (Fig. 3c, d).
Global patterns of submesoscale vertical heat transport. Values are spatially smoothed over 3° × 3° square boxes; positive values indicate upward. The heat flux is calculated at 40 m depth (a, b) and 200 m depth (c, d) during the winter or summer seasons: a, c Jan–March mean and b, d Jul–Sep mean. In most area of mid-latitudes, vertical heat transport at submesoscales is ~20–100 W/m2 and is systematically upwards
Importantly, in most regions the amplitudes of the submesoscale heat transport, 20–100 W/m2 over the winter hemisphere (Fig. 3, see above), are comparable to or larger than the climatological net air–sea heat fluxes25 (~10–200 W/m2) and mesoscale vertical fluxes (≲20 W/m2 over most of the ocean’s surface area; Supplementary Figure 3). Specifically, submesoscale vertical fluxes are more than five times larger than mesoscale vertical fluxes in 72% of ocean area in winter hemispheres (Fig. 3a, b vs Supplementary Figure 3a, b). The globally averaged submesoscale heat flux is 9 ± 3.5 W/m2, compared to a mesoscale heat flux of 1.5 ± 0.2 W/m2 (the global integrated values are ~3.0, 4.6, 2.0, and 2.9 PW for submesoscale flux in Fig. 3a–d, respectively, compared to only ~0.6, 0.6, 0.5, and 0.5 PW for mesoscale flux in Supplementary Figure 3a–d, respectively). These comparisons suggest a key role for submesoscale motions in controlling upper ocean vertical heat transport on a global scale. Mesoscale heat fluxes (Supplementary Figure 3) do not exhibit a seasonal cycle and are less systematically upward, which highlights a marked difference between mesoscale and submesoscale motions in modulating the near-surface heat budget. Moreover, this explicit quantification at submesoscales (Figs. 2–3) shows that the heat transport has a stronger temporal intermittency24, has larger amplitudes (~2–4 times larger), and exceeds 10 W/m2 over a greater proportion of the ocean (~3 times greater), as compared to studies that parameterize submesoscale motions26.
Global air–sea heat flux modulated by submesoscale dynamics
These characteristics of the directly resolved submesoscale heat flux, in particular the large amplitudes and broad coverage (Figs. 2–3), suggest that its misrepresentation in coupled climate models could produce significant biases in the magnitude, the temporal variability, and the geographical location of ocean–atmosphere heat exchange. To test this, we compare two simulations with identical configurations except for the horizontal resolution (1/48° vs 1/24°). The nonlinear nature of turbulence (e.g., meso- or smaller scale fluctuations) could cause chaotic differences between two models due to the position of individual coherent structures. Therefore, we apply statistical averaging (annual mean, and 3° × 3° spatial mean) to our following analyses to compare statistical properties, although differences in coherent structure at larger scales, e.g., standing eddies in western boundary currents or the Antarctic Circumpolar Current (ACC), could still lead to differences between the two model runs (e.g., both positive and negative difference in these regions such as in Fig. 4). The 1/48° model exhibits a greater conversion from potential energy to kinetic energy (Supplementary Figure 5a), consistent with resolving submesoscale instabilities over a greater range of wavelengths, ~10–50 km, as compared to ~20–50 km for the 1/24° model (see “Methods”). Consequently, the global submesoscale field is more active in the 1/48° model (Supplementary Figure 5b–c). This produces stronger submesoscale upward heat fluxes in the upper ocean: 62% and 5% of the ocean area at 20°–60° mid-latitudes have fluxes that are more than 4 W/m2 and 10 W/m2 stronger, respectively (Fig. 4a and Supplementary Figure 5d; annual-mean here and for below). This acts to warm the sea surface (Fig. 4b): 64% and 8% of ocean area at 20°–60° mid-latitudes becomes more than 0.06 °C and 0.3 °C warmer, respectively. Again, these effects (Fig. 4) are mainly caused by submesoscale motions in the 10–20 km range. This result is further explained as follows: the stronger submesoscale upward heat flux in the 1/48° model (Fig. 4a and Supplementary Figure 5d), i.e., the stronger restratification flux, causes a shallower mixed layer in the 1/48° model (dashed and dotted curves in Supplementary Figure 4b; Fig. 4d). This process is equivalent to a stronger slumping of isopycnals7,27 (approximately temperature contours) in the 1/48° model (solid curves in Supplementary Figure 4b). This submesoscale-driven slumping of temperature contours explains the ocean surface warming (roughly within the range of wintertime mixed layer; Supplementary Figure 4b, b) and the deeper cooling (roughly below the wintertime mixed layer; Supplementary Figure 4b). This sea surface warming (Fig. 4b) results in a larger release of heat from the ocean to the atmosphere via intensified upward air–sea heat flux anomalies (Fig. 4c): 60% and 8% of the ocean area between 20° and 60° in both hemispheres show an intensification of the annual-average air–sea flux by more than 4 W/m2 and 10 W/m2, respectively. This increase in air–sea flux ultimately balances the stronger submesoscale upward heat flux (Fig. 4c vs 4a, see also explanation in “Methods”). This 4–10 W/m2 air–sea flux response is a significant fraction of the climatological, as well as our model’s, net air–sea heat flux, which is ≲20 W/m2 over broad regions of the ocean basins25.
Sensitivity of the global heat budget to model resolution. Global maps of the annual-mean difference of a submesoscale vertical heat flux, b ocean surface temperature, c net air–sea heat flux, and d mixed layer depth between the 1/48° model and the 1/24° model (1/48° model minus 1/24° model). Values are spatially smoothed over 3° × 3° square boxes. The two models have identical setups except for the horizontal resolution. The model differences here are mainly caused by submesoscale at 10–20 km range. In most area of mid-latitudes, the 1/48° model exhibits upward heat transport at submesoscales larger than the 1/24° model, by ~4–10 W/m2 (a; about 14% larger, as in Supplementary Figure 5d). This results in a sea surface warming of ~0.06–0.3 °C (see b). This is ultimately compensated by a stronger upward ocean–atmosphere heat exchange (~4–10 W/m2, c vs a). The 1/48° model generally has a shallower mixed layer depth than the 1/24° model (see d). This is due to a stronger restratification in the 1/48° model (i.e., heat flux as in a) and is linked to most of the difference in sea surface temperature (see b). This is illustrated further in Supplementary Figure 4
Discussion
Our numerical simulation of the global ocean has permitted an estimate of the vertical heat fluxes caused by submesoscale motions at ~10–50 km range (in terms of wavelengths, see “Methods”). This global ocean simulation is state of the art in terms of resolution; at the time of writing this manuscript, it remains impractical to go beyond a ~2 km resolution in a global model. We acknowledge that the heat flux contributions from submesoscale motions not resolved by this model (~0.1–10 km) could be significant and could quantitatively alter the values presented in this study. However, recent studies provide strong evidence that the total heat flux, including the full range of submesoscale motions, should remain upward (positive) and, if anything, are likely to be even larger than the values reported here. Indeed, a process study12 showed that submesoscale dynamics at the 0.1–10 km range leads to a significant restratification of the upper ocean (in particular through filamentary intensification) and therefore produce an upward heat flux. Other process studies7,28,29,30,31 suggested similar behavior. A more recent study32, using a non-hydrostatic model in a 200-km square domain, found that physical scales from 10 km down to 250 m lead to upward buoyancy fluxes and therefore upward heat fluxes, with a magnitude comparable to our estimate. Extrapolation of these localized or process-based results to the global ocean still needs to be examined.
An acknowledged limitation of this study is that the atmosphere and ocean are not fully coupled. In our global ocean simulation, modifications to sea surface temperature (SST) by submesoscale heat fluxes necessarily impact air–sea fluxes since the latter are parameterized using bulk formulae involving SST33. However, atmospheric variables, such as surface wind, air temperature, and humidity that also impact air–sea fluxes, are prescribed in our model, rather than being influenced by SST as they are in a fully coupled system. Thus, there is an additional uncertainty related to our calculated submesoscale and surface heat fluxes due to air–sea coupling. Submesoscale fluxes may modulate atmospheric dynamics that in turn lead to feedback on ocean dynamics. Indeed, multiple studies have pointed out the impact of eddy-driven SST anomalies on the stability of the overlying atmosphere34 and surface pressure anomalies35. These interactions may significantly influence wind stress36,37,38 and the location and strength of the atmospheric jet streams39,40,41, as well as mid-latitude storms42. This raises the possibility that SST changes reported in our study—most significant at mid-latitudes—may impact atmospheric storm-tracks, and therefore produce a feedback on the large-scale ocean circulation as well as on ocean submesoscale motions. This feedback may also include wind-front interactions43, wind-driven changes in mixed layer depth44 and ocean stratification,45 the change of wind energy input to the ocean46, and changes in air–sea turbulent fluxes47.
These results indicate that the oceanic submesoscale heat fluxes may impact ocean dynamics at both larger and smaller scales through the interaction with atmospheric dynamics. This impact may only be assessed and quantified through a global ocean–atmosphere-coupled model with a spatial resolution similar to the one considered in the present study. This simulation does not yet exist due to its computational expense.
We emphasize that critical regions for ocean heat uptake from the atmosphere48, e.g., the Southern Ocean and high-latitude North Atlantic, as well as regions that influence the atmospheric storm tracks, e.g., the Kuroshio Extension and Gulf Stream, are particularly affected by the strong submesoscale heat transport (~20–100 W/m2 in winter, Fig. 3). These regions suffer from uncertainty in the quantification of the local air–sea heat fluxes49. This can be partially attributed to the commonly neglected26 submesoscale heat transport, which may impact the partitioning of heat between the ocean and atmosphere (Fig. 4). Furthermore, the modification of air–sea heat fluxes due to submesoscale processes may influence the formation of deep, intermediate, and mode waters, which controls the downwelling and upwelling branches of the meridional overturning circulation50. Finally, this study has implications for the exchange of carbon and oxygen between the atmosphere, ocean surface, and ocean interior, which will be sensitive to near-surface submesoscale vertical fluxes. In particular, the Southern Ocean, where submesoscale activity is particularly strong (Fig. 3), accounts for up to 40% of global anthropogenic carbon uptake51. An important and likely computationally affordable next step is to explore the potential impact of oceanic submesoscale motions on atmospheric circulation and the feedback on air–sea flux and ocean state, using a high-resolution ocean model that is coupled to at least the atmospheric boundary layer. The impact of even smaller-scale oceanic motions than can be resolved in our study on the large-scale heat transport also needs to be explored, likely using a basin-scale ocean model.
Methods
Model description
We use a set of global, full-depth ocean and sea ice numerical simulations carried out using the Massachusetts Institute of Technology general circulation model (MITgcm) on a Latitude-Longitude polar Cap (LLC) grid16. The computation is enabled by NASA Advanced Supercomputing. The model output analyzed in this study is from the so-called LLC4320 simulation, which has a nominal horizontal grid spacing of 1/48° (0.75 km near Antarctica, 2.3 km at the Equator, and 1 km in the Arctic Ocean). We also use the LLC2160 simulation for the results presented in Fig. 4, which has a nominal horizontal grid spacing of 1/24°. Horizontal wavenumber spectra suggest14 that the effective resolution of LLC4320 and LLC2160 is about 10 km and 20 km, respectively. The 1/48° simulation spans 14 months from September 10, 2011 to November 15, 2012. The spin-up of this simulation is described in Appendix D and Table D2 of ref. 16; it progresses from a 1/6° global ocean state estimate generated by the Estimating the Circulation and Climate of the Ocean, Phase II (ECCO2) project16, to 1/12° and then 1/24° simulations. The 1/12°, 1/24°, and 1/48° simulations are forced with six-hourly surface atmospheric fields (10-m wind velocity, 2-m air temperature and humidity, downwelling long and shortwave radiation, and atmospheric pressure load) from the 0.14° European Centre for Medium-Range Weather Forecasting (ECMWF) atmospheric operational model analysis, starting in 2011. These three simulations also include tidal forcing for the 16 most significant components, applied as additional atmospheric pressure forcing. Vertical mixing is parameterized based on the critical value of Richardson number and is implemented using the K-Profile Parameterization (KPP) scheme52 that has been extensively used and evaluated in ocean modeling studies53,54. The 1/48° simulation has been evaluated using in situ observations in terms of the kinetic energy level at different wavelengths and frequencies14,15. This simulation’s air–sea fluxes have similar magnitudes as climatological fluxes. This is because our model’s global SST distributions are in realistic range and the air–sea fluxes in our model depend on SST and the prescribed reanalysis of atmospheric state such as near-surface air temperature, humidity, and wind speed according to the bulk formulae of ref. 33. This study focuses on submesoscales and its seasonality. The current integration of this simulation is able to reach the equilibrium state for submesoscale dynamics because of their short timescales. We are aware that it would take longer integration to reach the equilibrium state for the larger-scale ocean dynamics in the global ocean, which is beyond the capacity of the most powerful computers at the current time50. Note that the 1/48° simulation is integrated using primitive equations (i.e., with hydrostatic assumption). The horizontal grid spacing and the hydrostatic assumption indicate that the 1/48° simulation cannot adequately resolve symmetric instability. But to a large extent, we expect the 1/48° simulation to resolve some other crucial sources for generating submesoscale turbulence, such as the mixed layer instability7,9,17,18,26, wind-front interactions43, and strain-induced frontogenesis3,28.
Relative vorticity ζ
Relative vorticity is defined as the rotational component of horizontal motions: v x − u y , with u and v the zonal and meridional velocities and x and y the zonal and meridional coordinates; subscripts here imply partial differentiation. Here, ζ is a measure of the spin of a fluid parcel. A useful non-dimensional number characterizing the surface frontal structure is ζ/f, where f is the Coriolis parameter due to the Earth rotation. When this non-dimensional number (also called Rossby number, Supplementary Figure 1) is larger than 0.1, the vertical velocity associated with these frontal structures may be large18,55,56. About 10% of ocean area in the winter hemisphere (20°–60° latitude band) has a surface |Ro| ~0.4 (Supplementary Figure 1c). Root-mean-square Rossby number can reach ~0.4 during winter in basin-scale domains (Supplementary Figure 1d), suggesting that individual amplitudes of Rossby number can reach O(1). Smaller-scale motions, if resolved, should increase the Rossby number amplitudes.
Definition and computation of submesoscale and mesoscale fields
We use the term submesoscale to designate a spatial scale just smaller than the mesoscale: a horizontal scale ≲0.5° in terms of longitude (~50 km at mid-latitudes), roughly below the first deformation radius in most of the global ocean9,17,18,19,20,21,22 (in terms of wavelengths, i.e., need to times a factor of π). The lower bound of submesoscales is often considered3 as O(0.1 km), but in our model is ~10 km, which is the effective resolution of our model14 since our numerical resolution is 1/48°, ~2 km at mid-latitudes (physical length scales really represented in the simulation are usually five times the numerical resolution). Therefore, submesoscale in this study refers to the range 1/10°–0.5° (~10–50 km). To focus on submesoscale processes, for all fields analyzed, we apply daily averaging to filter out most of the internal gravity waves14. The submesoscale component of ζ, denoted as ζ′, are the anomalies of the daily mean ζ from its 0.5° × 0.5° spatial mean (averaging over a 0.5° × 0.5° square box). Therefore, ζ′ is a spatial-temporal variable and approximately represents the component of ζ in the 1/48°–0.5° scale range (~2–50 km). Similarly, we can define the submesoscale component for other quantities such as temperature and vertical velocity. In our test, it yields essentially the same results when using 1° instead of 0.5° as the upper bound for defining submesoscales. The vertical heat flux (Figs. 2–4) is defined as Cpρw′T′, where Cp is the specific heat capacity, ρ is the density, w′ and T′ are the submesoscale components of vertical velocity and temperature, respectively. The spatial and temporal filters above have been similarly and widely used in other studies to deliver the submesoscale field22,57,58. The mesoscale component of a quantity is defined as the temporal anomalies of a given quantity from the annual average and has a spatial scale larger than 0.5° (averaging over a 0.5° × 0.5° square box)22.
Sensitivity analysis shown in Fig. 4
We perform a sensitivity analysis by comparing two simulations with identical setups except for the horizontal resolution (1/48° vs 1/24°). The 1/48° model resolves submesoscale instabilities over slightly broader wavelengths than the 1/24° model14 (~10–50 km vs ~20–50 km). This powers a stronger global submesoscale field in the 1/48° model (Supplementary Figure 5a–c) and produce a stronger submesoscale upward heat transport in most area of mid-latitude upper ocean (Supplementary Figure 5d). This causes a warmer sea surface in the 1/48° model (Fig. 4b) and is ultimately balanced by a stronger upward ocean–atmosphere heat exchange (Fig. 4c). This response, to leading order, may be explained by a classic thermodynamic equation59 that captures the evolution of upper-ocean temperature T:
Here C is the total heat capacity of the upper layer (the system we focus on), S is the heating source, and –λT is the negative feedback from air–sea heat flux, where λ can be approximated as a positive constant locally59. In the 1/48° model, S is larger due to a stronger incoming submesoscale heat flux from below (Fig. 4a). From Eq. (1), this causes a higher temperature T (Fig. 4b), and hence a larger upward air–sea heat exchange λT in the 1/48° model. The change in λT ultimately closely balance with the difference of S in the two model simulations (Fig. 4c vs 4a) such that the systems approach a quasi-steady state (dT/dt ~0 in an annual-mean sense). In this case for the upper 40 m ocean59, λ is ~15 Wm2/K and C is ~16 × 107 Jm2/K. Therefore, the timescale C/λ is about a few months, which means that the air–sea flux (−λT) can respond to the forcing S by a timescale of months. This is captured in our simulations (see Supplementary Figure 4 for a further illustration). See the main text for the discussion of caveats.
Code availability
The instructions and code for running the 1/24° and 1/48° simulations are available by the following websites:
http://wwwcvs.mitgcm.org/viewvc/MITgcm/MITgcm_contrib/llc_hires/llc_2160/
http://wwwcvs.mitgcm.org/viewvc/MITgcm/MITgcm_contrib/llc_hires/llc_4320/
Data availability
The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information Files, or from the corresponding authors on request.
References
Trenberth, K. E., Fasullo, J. T. & Balmaseda, M. A. Earth’s energy imbalance. J. Clim. 27, 3129–3144 (2014).
Roemmich, D. et al. Unabated planetary warming and its ocean structure since 2006. Nat. Clim. Change 5, 240–245 (2015).
McWilliams, J. C. Submesoscale currents in the ocean. Proc. R. Soc. A 472, 20160117 (2016).
Klein, P. & Lapeyre, G. The oceanic vertical pump induced by mesoscale and submesoscale turbulence. Annu. Rev. Mar. Sci. 1, 351–375 (2009).
Munk, W., Armi, L., Fischer, K. & Zachariasen, F. Spirals on the sea. Proc. R. Soc. Lond. A 456, 1217–1280 (2010).
Lapeyre, G., Klein, P. & Hua, B. L. Oceanic restratification forced by surface frontogenesis. J. Phys. Oceanogr. 36, 1577–1590 (2006).
Boccaletti, G., Ferrari, R. & Fox-Kemper, B. Mixed layer instabilities and restratification. J. Phys. Oceanogr. 37, 2228–2250 (2007).
Fox-Kemper, B., Ferrari, R. & Hallberg, R. Parameterization of mixed layer eddies. Part I: theory and diagnosis. J. Phys. Oceanogr. 38, 1145–1165 (2008a).
Callies, J., Flierl, G., Ferrari, R. & Fox-Kemper, B. The role of mixed-layer instabilities in submesoscale turbulence. J. Fluid Mech. 788, 5–41 (2016).
Buckingham, C. E. et al. Seasonality of submesoscale flows in the ocean surface boundary layer. Geophys. Res. Lett. 43, 2118–2126 (2016).
Thompson, A. F. et al. Open-ocean submesoscale motions: a full seasonal cycle of mixed layer instabilities from gliders. J. Phys. Oceanogr. 46, 1285–1307 (2016).
McWilliams, J., Colas, F. & Molemaker, M. Cold filamentary intensification and oceanic surface convergence lines. Geophys. Res. Lett. 36, L18602 (2009).
Fox-Kemper, B. et al. Parameterization of mixed layer eddies. III: implementation and impact in global ocean climate simulations. Ocean Model. 39, 61–78 (2011).
Rocha, C. B., Gille, S. T., Chereskin, T. K. & Menemenlis, D. Seasonality of submesoscale dynamics in the kuroshio extension. Geophys. Res. Lett. 43, 11304–11311 (2016).
Rocha, C. B., Chereskin, T. K., Gille, S. T. & Menemenlis, D. Mesoscale to submesoscale wavenumber spectra in Drake Passage. J. Phys. Oceanogr. 46, 601–620 (2016).
Menemenlis, D. et al. ECCO2: high resolution global ocean and sea ice data synthesis. Mercat. Ocean Q. Newsl. 31, 13–21 (2008).
Callies, J. & Ferrari, R. Interpreting energy and tracer spectra of upper-ocean turbulence in the submesoscale range (1–200 km). J. Phys. Oceanogr. 43, 2456–2474 (2013).
Sasaki, H., Klein, P., Qiu, B. & Sasai, Y. Impact of oceanic-scale interactions on the seasonal modulation of ocean dynamics by the atmosphere. Nat. Commun. 5, 5636 (2014).
Bühler, O., Callies, J. & Ferrari, R. Wave–vortex decomposition of one-dimensional ship-track data. J. Fluid Mech. 756, 1007–1026 (2014).
Callies, J., Ferrari, R., Klymak, J. M. & Gula, J. Seasonality in submesoscale turbulence. Nat. Commun. 6, 6862 (2015).
Klein, P., Lapeyre, G., Roullet, G., Le Gentil, S. & Sasaki, H. Ocean turbulence at meso and submesoscales: connection between surface and interior dynamics. Geophys. Astrophys. Fluid Dyn. 105, 421–437 (2011).
Capet, X., McWilliams, J. C., Molemaker, M. J. & Shchepetkin, A. Mesoscale to submesoscale transition in the california current system. Part I: flow structure, eddy flux, and observational tests. J. Phys. Oceanogr. 38, 29–43 (2008).
Hoskins, B., Draghici, I. & Davies, H. A new look at the ω‐equation. Q. J. R. Meteorol. Soc. 104, 31–38 (1978).
Qiu, B., Chen, S., Klein, P., Sasaki, H. & Sasai, Y. Seasonal mesoscale and submesoscale eddy variability along the north pacific subtropical countercurrent. J. Phys. Oceanogr. 44, 3079–3098 (2014).
Large, W. & Yeager, S. The global climatology of an interannually varying air–sea flux data set. Clim. Dyn. 33, 341–364 (2009).
Fox-Kemper, B. & Ferrari, R. Parameterization of mixed layer eddies. Part II: prognosis and impact. J. Phys. Oceanogr. 38, 1166–1179 (2008).
Su, Z. & Ingersoll, A. P. On the minimum potential energy state and the eddy size–constrained APE density. J. Phys. Oceanogr. 46, 2663–2674 (2016).
Capet, X., McWilliams, J. C., Molemaker, M. J. & Shchepetkin, A. Mesoscale to submesoscale transition in the california current system. Part II: frontal processes. J. Phys. Oceanogr. 38, 44–64 (2008).
Gula, J., Molemaker, M. J. & McWilliams, J. C. Submesoscale cold filaments in the Gulf Stream. J. Phys. Oceanogr. 44, 2617–2643 (2014).
Thomas, L. N., Taylor, J. R., Ferrari, R. & Joyce, T. M. Symmetric instability in the Gulf Stream. Deep Sea Res. II 91, 96–110 (2013).
Thomas, L. N. & Lee, C. M. Intensification of ocean fronts by down-front winds. J. Phys. Oceanogr. 35, 1086–1102 (2005).
Barkan, R., Winters, K. B. & McWilliams, J. C. Stimulated imbalance and the enhancement of eddy kinetic energy dissipation by internal waves. J. Phys. Oceanogr. 47, 181–198 (2017).
Large, W. G. & Yeager, S. G. Diurnal to Decadal Global Forcing For Ocean And Sea-ice Models: The Data Sets And Flux Climatologies (National Center for Atmospheric Research, Boulder, 2004).
Wallace, J. M., Mitchell, T. & Deser, C. The influence of sea-surface temperature on surface wind in the eastern equatorial Pacific: Seasonal and interannual variability. J. Clim. 2, 1492–1499 (1989).
Lindzen, R. S. & Nigam, S. On the role of sea surface temperature gradients in forcing low-level winds and convergence in the tropics. J. Atmos. Sci. 44, 2418–2436 (1987).
Xie, S.-P. Satellite observations of cool ocean–atmosphere interaction. Bull. Am. Meteorol. Soc. 85, 195–208 (2004).
Spall, M. A. Midlatitude wind stress–sea surface temperature coupling in the vicinity of oceanic fronts. J. Clim. 20, 3785–3801 (2007).
Lambaerts, J., Lapeyre, G., Plougonven, R. & Klein, P. Atmospheric response to sea surface temperature mesoscale structures. J. Geophys. Res. 118, 9611–9621 (2013).
Feliks, Y., Ghil, M. & Simonnet, E. Low-frequency variability in the midlatitude atmosphere induced by an oceanic thermal front. J. Atmos. Sci. 61, 961–981 (2004).
Minobe, S., Kuwano-Yoshida, A., Komori, N., Xie, S.-P. & Small, R. J. Influence of the Gulf Stream on the troposphere. Nature 452, 206 (2008).
Nakamura, H., Sampe, T., Goto, A., Ohfuchi, W. & Xie, S. P. On the importance of midlatitude oceanic frontal zones for the mean state and dominant variability in the tropospheric circulation. Geophys. Res. Lett. 35, L15709 (2008).
Booth, J. F., Thompson, L., Patoux, J. & Kelly, K. A. Sensitivity of midlatitude storm intensification to perturbations in the sea surface temperature near the Gulf Stream. Mon. Weather Rev. 140, 1241–1256 (2012).
Thomas, L. & Ferrari, R. Friction, frontogenesis, and the stratification of the surface mixed layer. J. Phys. Oceanogr. 38, 2501–2518 (2008).
Sallée, J., Speer, K. & Rintoul, S. Zonally asymmetric response of the southern ocean mixed-layer depth to the southern annular mode. Nat. Geosci. 3, 273 (2010).
Su, Z. et al. An idealized model of Weddell Gyre export variability. J. Phys. Oceanogr. 44, 1671–1688 (2014).
Byrne, D., Münnich, M., Frenger, I. & Gruber, N. Mesoscale atmosphere ocean coupling enhances the transfer of wind energy into the ocean. Nat. Commun. 7, 11867 (2016).
Yu, L. & Weller, R. A. Objectively analyzed air-sea heat fluxes for the global ice-free oceans (1981-2005). Bull. Am. Meteorol. Soc. 88, 527–539 (2007).
Chen, X. & Tung, K.-K. Varying planetary heat sink led to global-warming slowdown and acceleration. Science 345, 897–903 (2014).
Bourassa, M. A. et al. High-latitude ocean and sea ice surface fluxes: challenges for climate research. Bull. Am. Meteorol. Soc. 94, 403–423 (2013).
Lévy, M. et al. Modifications of gyre circulation by sub-mesoscale physics. Ocean Model. 34, 1–15 (2010).
Sallée, J.-B., Matear, R. J., Rintoul, S. R. & Lenton, A. Localized subduction of anthropogenic carbon dioxide in the Southern Hemisphere oceans. Nat. Geosci. 5, 579–584 (2012).
Large, W. G., McWilliams, J. C. & Doney, S. C. Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–404 (1994).
Large, W. G., Danabasoglu, G., Doney, S. C. & McWilliams, J. C. Sensitivity to surface forcing and boundary layer mixing in a global ocean model: annual-mean climatology. J. Phys. Oceanogr. 27, 2418–2447 (1997).
Fernández-Castro, B. et al. Microstructure turbulence and diffusivity parameterization in the tropical and subtropical Atlantic, Pacific and Indian Oceans during the Malaspina 2010expedition. Deep Sea Res. I 94, 15–30 (2014).
Klein, P. et al. Upper ocean turbulence from high-resolution 3D simulations. J. Phys. Oceanogr. 38, 1748–1763 (2008).
Mensa, J. A. et al. Seasonality of the submesoscale dynamics in the Gulf Stream region. Ocean Dyn. 63, 923–941 (2013).
Capet, X., Campos, E. & Paiva, A. Submesoscale activity over the Argentinian shelf. Geophys. Res. Lett. 35, L15605 (2008).
Uchida, T., Abernathey, R. & Smith, S. Seasonality of eddy kinetic energy in an eddy permitting global climate model. Ocean Model. 118, 41–58 (2017).
Vallis, G. K. Climate and the Oceans (Princeton University Press, Princeton, 2012).
Acknowledgements
This research was carried out, in part, at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (NASA). Support was provided by the Cryospheric Sciences, Physical Oceanography, and Modeling, Analysis, and Prediction (MAP) programs. Additionally, Z.S. received support from the NASA Postdoctoral Program (NPP) fellowship. P.K. received support from CNRS (France), LabexMer (ANR-10-LABX-19-01) as well as of the NASA-CNES SWOT mission. J.W. is supported by the NASA-CNES SWOT mission. A.F.T. is supported by the David and Lucille Packard Foundation and NASA grant NNX16AG42G. Computations were carried out at the NASA Advanced Supercomputing (NAS) facilities.
Author information
Authors and Affiliations
Contributions
Z.S. and P.K. planned the research and wrote the manuscript. Z.S. did the analyses. D.M. conducted the numerical simulation. J.W., A.F.T., and D.M. contributed to interpretation of the results and improving the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Su, Z., Wang, J., Klein, P. et al. Ocean submesoscales as a key component of the global heat budget. Nat Commun 9, 775 (2018). https://doi.org/10.1038/s41467-018-02983-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-02983-w
This article is cited by
-
Observations reveal vertical transport induced by submesoscale front
Scientific Reports (2024)
-
Simulated Sea Surface Salinity Data from a 1/48° Ocean Model
Scientific Data (2024)
-
Frontogenesis at Jovian high latitudes
Nature Physics (2024)
-
Dynamics of submesoscale processes and their influence on vertical heat transport in the southeastern tropical Indian Ocean
Ocean Dynamics (2024)
-
Processes responsible for mixed layer variations near mesoscale eddies in the Bay of Bengal
Ocean Dynamics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.