Abstract
Controllable metal–insulator transitions (MIT), Rashba–Dresselhaus (RD) spin splitting, and Weyl semimetals are promising schemes for realizing processing devices. Complex oxides are a desirable materials platform for such devices, as they host delicate and tunable charge, spin, orbital, and lattice degrees of freedoms. Here, using first-principles calculations and symmetry analysis, we identify an electric-field tunable MIT, RD effect, and Weyl semimetal in a known, charge-ordered, and polar relativistic oxide Ag2BiO3 at room temperature. Remarkably, a centrosymmetric BiO6 octahedral-breathing distortion induces a sizable spontaneous ferroelectric polarization through Bi3+/Bi5+ charge disproportionation, which stabilizes simultaneously the insulating phase. The continuous attenuation of the Bi3+/Bi5+ disproportionation obtained by applying an external electric field reduces the band gap and RD spin splitting and drives the phase transition from a ferroelectric RD insulator to a paraelectric Dirac semimetal, through a topological Weyl semimetal intermediate state. These findings suggest that Ag2BiO3 is a promising material for spin-orbitonic applications.
Similar content being viewed by others
Introduction
Cross-controlling of order parameters by external stimuli in a single-phase material is of great interest in both fundamental research and technological applications1,2. For instance, metal-to-insulator transitions (MIT) driven by the application of an electric field represent a viable way for designing energy-efficient logic devices3,4,5. Ferroelectric compounds, whose spontaneous electric polarization can be reversed by the application of an external electric field, are among the most promising materials to achieve this type of switch6, owing to the many different driving forces enabling ferroelectric behavior, including cooperative interactions of lattice distortions, charge, spin, and orbital ordering7,8,9,10. Among the different types of MIT observed in nature11 (Mott12, Peierls13, Slater14, Lifshitz15, Verwey16, to name a few), the Peierls MIT, associated with a crystal lattice distortion, frequently exhibits a higher transition temperature (e.g., VO2: TMIT ~ 340 K;17 YNiO3: TMIT ~ 580 K18). Although Peierls-like MITs are ubiquitous in oxides, the breathing mode involving cation-oxygen bond length disproportionation usually does not couple with ferroelectric displacements17,19,20,21.
Recent studies have shown that an external electric field could also be employed to switch the Rashba–Dresselhaus (RD) spin splitting in ferroelectric materials22,23,24. The RD spin splitting is a consequence of lifting the spin degeneracy, typically occurring in materials with strong spin–orbit coupling (SOC) lacking inversion symmetry25,26,27. The most interesting outcome of the RD effect is that an electron moving under an electric field (E) or a gradient of the crystal potential (E = −∇V) behaves as it experiences an effective magnetic field Beff ∞ E × p/mc2, where p, m, and c are momentum, mass, and speed of light, respectively, that couples to the spin of the electron28. Owing to its promising applications in spin-orbitronics devices such as the Datta–Das spin field-effect transistor29, the RD effect has gained growing research attention24,28,30,31,32. The tunability of the RD splitting by applying an external field is primary possible due to the dependence of Beff on the crystal potential gradient, which is strongly affected by crystal structure distortions24,30,32,33.
Additionally, Weyl semimetals are a topological phase whose low energy excitations are the massless chiral fermions34. Weyl semimetals are the realization of Weyl fermions in condensed matter systems and exhibit many exotic properties35. Since the Weyl semimetal typically only exists in crystals without either time-reversal or inversion symmetry, but not both, it is also possible to activate a Weyl semimetal phase in a topologically trivial material by applying an external field. Although the magnetic field induced Weyl semimetal has been discovered in GdPtBi recently36, the electric field promoted Weyl semimetal has not been reported yet.
Here, we explore the possibility of simultaneously controlling the MIT, RD spin splitting, and Weyl fermions in a single-phase ferroelectric oxide using an electric field by means of first-principles calculations and symmetry analysis. We demonstrate that this paradigm can be realized in the room temperature phase of the known Peierls-like semiconductor Ag2BiO3. We identify an atypical polar structural distortion that arises from the octahedral-breathing mode associated with Bi3+/Bi5+ charge disproportion. This mechanism enables an unexpected route for tuning the MIT, RD spin splitting, and Weyl semimetallic state simultaneously by applying an external electric field. The modulation of the charge disproportion guides the transition from a polar insulating phase exhibiting RD spin splitting to a nonpolar spin-degenerate Dirac semimetallic state. Remarkably, we find that across the MIT transition there exists an intermediate topological Weyl semimetallic state, manifested by a non-degenerate band crossing around the Fermi level and non-trivial surface states connecting Weyl nodes with opposite chirality.
Results
Ground state structural and electronic properties
At room temperature (and up to at least 380 K) Ag2BiO3 crystallizes in a polar structure with Pnn2 (No. 34) space group37 (Fig. 1a). At 220 K the polar Pnn2 phase is converted to another polar monoclinic structure Pn (No. 7). There is no further observed phase transition down to 2 K37. In the Pnn2 phase, each octahedra shares an edge (along [100]) and a corner (along [011] and [0\(\bar 1\)1] directions) with its adjacent octahedra, resulting in a checkerboard-like distribution of inequivalent Bi3+/Bi5+ sites (nominal oxidation state) characterized by different Bi3+/Bi5+–O bond lengths of 2.34 and 2.13 Å, respectively37. This charge-ordered pattern is responsible for opening a band gap (0.7 eV38), which has been observed in other Bi oxides39,40, and for the onset of ferroelectric behavior, which is observed for the first time. Our density functional theory (DFT) calculations find that the fully relaxed low-temperature Pn phase is nearly degenerate with the Pnn2 phase in energy, and correctly reproduce the bond length disproportionation, see Supplementary Tables 1 and 2 for a full structural characterization. We also find a direct band gap of 0.53 eV between the occupied Bi3+ and the unoccupied Bi5+ 6s orbitals hybridized with O-2p states at the R point k = (1/2,1/2,1/2) (Fig. 1c). The slight underestimation of the band gap is due to inaccuracies in the semilocal functional within DFT. The accuracy of DFT in reproducing the crystal structures (lattice constants, volume, and Bi–O bond lengths), energy difference between ferroelectric and paraelectric phases, and band gaps is assessed with various functionals commonly used for ferroelectric oxides41,42 (Supplementary Table 1).
Structural and electronic properties of Ag2BiO3. Crystal structure of a the ferroelectric Pnn2 and b the hypothetical paraelectric Pnna phase. Red, gray, green, blue, and purple spheres are O2−, Ag+, Bi4+, Bi3+, and Bi5+ ions, respectively. c and d are the band structures of the Pnn2 and Pnna phases, respectively. The Fermi level is shifted to 0 eV. High symmetry points in the first Brillouin zone are defined in Supplementary Figure 1. e and f are the spin textures of the inner and outer branches of conduction bands at the R point in the polar Pnn2 phase. The color code indicates the energy level with respect to the bottom of conduction band
Since the R point preserves time-reversal symmetry and the whole crystal lacks inversion symmetry, Kramers pairs (E↑ (k) = E↓ (−k)) are observed at the conduction band minimum and valence band maximum. Owing to the strong SOC of the Bi cation, both the lowest conduction band and the highest valence band split into two branches, forming inner and outer bands with opposite spin rotation patterns (Fig. 1e, f). The spin splitting (ΔE RD ) is larger at the lowest conduction band and exhibits strong anisotropy, manifested by a larger ΔE RD in the R–T k x direction (6.4 meV) compared to that in the R–U k y direction (0.7 meV). Therefore, a combined Rashba and Dresselhaus spin splitting is expected, similar to the case of the formamidinium tin iodide perovskite FASnI3 and consistent with a C2v symmetry, in which both Rashba and Dresselhaus spin splitting are symmetry allowed33. The dispersion relation of the resulting electronic states is given, to linear order, by the coupling Hamiltonian HRD = αR(k y σ x −k x σ y ) + αD(−k x σ x + k y σ y ), with \(\alpha _{\mathrm{R}} \sim 0.07\) eV Å and \(\alpha _{\mathrm{D}} \sim 0.17\) eV Å the fitted Rashba and Dresselhaus parameters. The predominant contribution of Dresselhaus character, i.e., αD > αR, is consistent with the calculated spin orientations showing also parallel components to the associated crystal momentum. The ground state band structure of the Pn phase is also insulating and exhibits very similar dispersion (Supplementary Figure 2), consistent with the structural similarity between the Pnn2 and Pn phases.
Symmetry analysis and lattice dynamics
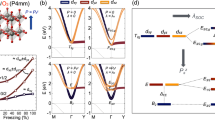
By means of symmetry analysis based on representation theory43,44, we find that Pnn2 is a subgroup of Pnna (Fig. 1b). Our DFT calculations show that the Pnna phase is only 5.3 meV per atom higher in energy than Pnn2, and can be considered as the parent phase of Pnn2. The super group of Pnna is Imma, which is 1,391 meV per f.u. higher in energy than Pnn2. The Imma polymorph is too high in energy to be achieved at elevated temperature. The main structure difference between the Pnna and Pnn2 phases is the splitting of the Bi Wyckoff positions in the lower symmetry phase Pnn2, which permits the Bi3+/Bi5+ charge disproportionation (Fig. 1; Supplementary Table 2). From the point view of representation theory, Pnna is connected with the room temperature phase Pnn2 by a one-dimensional order parameter \(\Gamma _{2^ {-}}\) and with the low-temperature phase Pn by a combination of the \(\Gamma _{2^ {-}}\) and another one-dimensional order parameter \(\Gamma _{3^ {-}}\), i.e., \(\Gamma _{2^ {-}} \oplus \Gamma _{3^ {-}}\). This assessment is validated by the phonons dispersions of the Pnna phase (Fig. 2a), which exhibit two unstable phonon modes at Γ with imaginary frequencies ν = 392i cm−1 (\(\Gamma _{2^ {-}}\)) and ν = 30i cm−1 (\(\Gamma _{3^ {-}}\)). The condensation of the force constant eigenvector of \(\Gamma _{2^ {-}}\) mode directly generates the room temperature phase Pnn2, whereas a simultaneous condensation of the \(\Gamma _{2^ {-}}\) and \(\Gamma _{3^ {-}}\) modes, i.e., \(\Gamma _{2^ {-}} \oplus \Gamma _{3^ {-}}\) establishes the Pn phase.
Phonon properties of Pnna-structured Ag2BiO3. a Phonon dispersions of the hypothetical paraelectric phase Pnna. Negative frequencies correspond to imaginary modes. b, c The atomic displacements (force constant eigenvectors, black arrows) of the \(\Gamma _{2^ {-}}\) mode in real space for BiO6 octahedra and Ag cations, respectively. Note that the amplitude of Ag and Bi cation are enlarged for clarity. The color coding for atoms matches that in Fig. 1
The main vibrational characteristic of the \(\Gamma _{2^ {-}}\) mode is a Bi–O breathing distortion that causes the Bi3+/Bi5+ disproportionation (Fig. 2b, c). Surprisingly, this mode is polar and is the primary order parameter for this paraelectric (Pnna) to ferroelectric (Pnn2) transition, which produces a spontaneous polarization (Pz) of 8.87 μC cm−2 (Fig. 3f). Considering that \(\Gamma _{2^ {-}}\) is a one-dimensional order parameter and the fact that the calculated polar displacement Q and ΔE/μ (where ΔE and μ are the energy differences between the paraelectric and ferroelectric states of the material and the dipole moment of ferroelectric phase, respectively) of Ag2BiO3 are comparable with known ferroelectric materials (Supplementary Figure 3), Ag2BiO3 should be electric-field tunable with moderate fields.
The evolution of crystal structure and electronic properties of Ag2BiO3 as a function of polar mode (\(\Gamma _2^ -\)) amplitude. a Projected density of states (the gray shading represents the total density of states), b Bi–O bond lengths, c Bader charges of Bi atoms (note that since the description of charge states in solid is ambiguous, the charge calculated using Bader’s method should not be used for quantitative comparison with the formal charge (Bi3+ and Bi5+)), d energy difference (ΔE) between paraelectric phase (Pnna) and ferroelectric phase (Pnn2), e Rashba–Dresselhaus parameters α along R–U and R–T directions, f spontaneous ferroelectric polarization (Pz), and g band structure along the U–R–T direction. The gray-white gradient background represent the transition from the metallic (gray) and insulating (white) phases. h Free energy of ferroelectric Ag2BiO3 (Pnn2) as a function of the external electric field (|E|) and polar distortion (\(Q_{\Gamma _2^ - }\)). The free energy density G in the Landau–Ginzburg polynomial expansion with the amplitude of polar distortion \(Q_{\Gamma _2^ - }\) is: \(G = F_0 + \frac{\alpha }{2}Q_{\Gamma _2^ - }^2 + \frac{\beta }{4}Q_{\Gamma _2^ - }^4 + \frac{\gamma }{6}Q_{\Gamma _2^ - }^6 - |{\mathbf{E}}|Q_{\Gamma _2^ - }\), where F0 is the free energy density of the paraelectric phase (Pnna). α, β, and γ are the coefficients
To the best of our knowledge, this is the first example of a polar octahedra-breathing mode. Typically, the breathing mode in perovskites with the corner-sharing octahedra does not lift inversion symmetry19. The reason for such an unusual behavior in Ag2BiO3 is the coexistence of both corner-sharing and edge-sharing octahedra, which leads to a distorted octahedral framework with inversion centers on occupied Bi cation sites. The bond-disproportionation in combination with the low-crystal symmetry enables an acentric octahedral-breathing mode. As a result, oxygen displacements along the c axis in the BiO6 octahedra are not completely compensated, as illustrated in Fig. 2c. Both Ag and Bi atoms have small polar distortions along the c axis as well. The polarity of the \(\Gamma _{2^ {-}}\) mode and its connection with the Bi3+/Bi5+ disproportionation is the crucial factor enabling the tunability of the electronic structure and spin properties of Ag2BiO3, as elaborated below.
Tunable MIT with RD and Weyl states
Unlike the ferroelectric Pnn2 phase, the nonpolar Pnna phase exhibits a semimetallic band structure without RD spin splitting (Fig. 1d). Nonetheless we find that the Pnna phase exhibits a Dirac point at the S point of the Brillouin zone, similar in nature to those defined in double Dirac semimetals45,46,47. This feature is also independent of DFT functional (Supplementary Figure 6). The \(\Gamma _{2^ {-}}\) mode breaks the mirror symmetry protecting the Dirac point and leads to the opening of a gap, as evidenced in Fig. 4a. This is due to the suppression of the charge disproportionation which produces half-filled Bi4+ 6s orbitals crossing the Fermi level (Fig. 1d). This means that the \(\Gamma _{2^ {-}}\) order parameter simultaneously drives a ferroelectric and a metal-to-insulator transition (Fig. 3). The \(\Gamma _{2^ {-}}\)-driven paraelectric-to-ferroelectric transition is associated with a continuous increase of the spontaneous polarization and of the overall ferroelectric energy gain ΔE (Fig. 3d, f). The progressive increase of the amplitude of \(\Gamma _{2^ {-}}\) is coupled with an enhanced charge disproportionation between the two inequivalent Bi sites, measured in terms of Bi–O bond length difference (Fig. 3b), valence Bader charges (Fig. 3c), and by a monotonous increase of the band gap (Fig. 3a). This type of MIT is common to other bismutathes19,48. The degree of the ferroelectric distortion influences the RD splitting as well, owing to the coupling between the polar distortion and the potential gradient surrounding the Bi3+ and Bi5+ cations. This can be quantified by the RD spin splitting coefficient αRD defined as \(2\Delta E_{{\mathrm{RD}}}{\mathrm{/}}\Delta k_{{\mathrm{RD}}}\). Figure 3e illustrates that αRD decreases linearly with the amplitude of \(\Gamma _{2^ {-}}\) until \(Q_{\Gamma _2^ - }\) ≈ 0.25 Å. For \(Q_{\Gamma _2^ - } < 0.25\) Å there is a band crossing between the valence and conduction RD bands (Fig. 3g), and then αRD is ill-defined.
Weyl semimetal phase of Ag2BiO3. a Electronic band structure. b The corresponding Fermi surface (0.08 eV above the Fermi level) on the (001) surface. The filled circles indicate the projected Weyl points on the surface for two pairs of Weyl points with opposite chirality (+ and −). c Two dimensional plot of the Berry curvature showing the opposite chirality of one pair of Weyl nodes. A 3D plot is given in Supplementary Figure 4
Interestingly, our calculations reveal that during the ferroelectric-to-paraelectric transition at \(Q_{\Gamma _2^ - } = 0.22\) Å, there exists an intermediate phase that shows the typical hallmark of a Weyl semimetal state, similar to the Weyl semimetal recently found in HgPbO349. Weyl semimetals are a class of quantum materials characterized by nonzero Fermi surface Chern numbers, which manifest as a linear band crossing around the Fermi level with non-degenerate spins in a system with either time-reversal or inversion symmetry broken50. In this intermediate phase of Ag2BiO3, the Weyl node is located near the R point with k = (0.4975,0.4725,0.4988), about 0.08 eV above the Fermi level (Fig. 4a, b). Symmetry considerations indicate that there are four pairs of Weyl nodes, whose coordinates are given in Supplementary Table 3. The four pairs of Weyl points are protected by a mirror operation, which is preserved through the entire transition from the insulating-ferroelectric phase to the metallic centrosymmetric phase, i.e., always coexisting with the \(\Gamma _{2^ {-}}\) mode. The Weyl nodes appear only at a specific interval of the \(\Gamma _{2^ {-}}\) distortions as a result of balancing two competing interactions: (a) going towards the insulating phase the chemical bonding become progressively stronger (bonding/antibonding interactions increase) and destroys the Weyl nodes; (b) on the other side, approaching the metallic phase the broken inversion symmetry gradually fades away, which again results in the a disappearance of the Weyl nodes.
The presence of a Weyl node in the bulk phase is typically associated with topological non-trivial surface states, which connect two Weyl nodes with opposite chirality, and appear as broken Fermi arcs states. To inspect this feature, we have derived the (001) surface electron structure by the Green’s function based tight-binding method based on the maximally localized Wannier functions51,52,53,54,55. The resulting Fermi arcs presented in Fig. 4b. Moreover, the calculation of the Berry curvature confirms the topological Weyl nature of this intermediate phase (Fig. 4c).
Discussion
We have established that two pairs of distinct properties, insulator/metal and RD/non-RD, through a Weyl semimetal state, are closely connected with the ferroelectric structure distortion in Ag2BiO2, indicating a potentially tunable MIT and spin splitting by applying an electric field. Since the energy difference between the semimetal paraelectric (Pnna) and insulating-ferroelectric (Pnn2) phases is only 5.3 meV per atom and the polarization is relatively large (8.87 μC cm−2), it is expected that the insulating phase could be suppressed (but not passed) by a relative small electric field (E) applied opposite to the direction of the spontaneous polarization (P) through the interaction P ⋅ E in the free energy. This is depicted in Fig. 3h based on a Landau–Ginzburg phenomenological model56. If the frequency of the electric field pulse is carefully chosen, there should be an oscillation between the Pnn2 and Pnna phases. By increasing the strength of the electric field, the insulating phase of Ag2BiO3 becomes more conducting, as shown by the density of states provided in Fig. 3a. Since the paraelectric phase is a poor metal, however, the free carriers will tend to screen the external electric field and therefore, the metallic phase is expected to survive only for a short time. This causes the so-called oscillating electroresistance effect (ER), which has potential applications in random access information storage57. If the applied pulse electric field is strong enough, however, the Bi3+/Bi5+ charge-order can be melted and converted into a metallic phase, a phenomena called colossal ER, which has been observed in charge-ordered insulators with strongly competing metallic phases, Pr0.7Ca0.3MnO3, R0.5Ca0.5MnO3 (R = Nd, Gd, and Y)1,2, and LuFe2O46.
We have demonstrated a controllable metal–insulator transition, Rashba–Dresselhaus spin splitting effect, and Weyl semimetallic state by applying an electric field in the experimentally available charge-ordered oxide Ag2BiO3 by means of first-principles calculations. The functionalized electric-field tunable MIT could make Ag2BiO3 a suitable material for lower power memory applications compared to magnetic field controlled MITs. Moreover, the semiconducting nature of Ag2BiO3 could allow for the injection of a reasonable number of carriers (if the Fermi level is properly tuned) without suppressing the ferroelectric instability, eventually resulting in electrically controllable spin polarized currents as a consequence of the Rashba–Dresselhaus effect58. The higher stability of oxides in atmospheric conditions and the higher ferroelectric Curie temperature of Ag2BiO3 over organic–inorganic metal halide perovskites and GeTe, the prototypical ferroelectric Rashba semiconductors22,33, make this bismuthate more practical for realistic applications59. Finally, the electric-field tunable Weyl semimetallic state proposed here will enable future studies on intertwined ferroelectric and topological phenomena.
Methods
Computational details
All the first-principles calculations were conducted by using the projector-augmented wave pseudopotential methed60,61 as implemented in the Vienna ab intio Simulation Package (VASP)62,63. PBEsol exchange-correlation functional64 and the plane-wave basis set with energy cutoff of 520 eV were used. The Monkhorst-Pack k-points grids of 10×10×6, was used to sample the Brillouin zones. All the crystal structures were fully relaxed until the Hellmann–Feynman foreces acting on each atom were less than 0.01 eV Å−1. The phonon dispersion was calculated by using finite displacement method as implemented in the Phonopy code65. Spin orbital coupling is included in all the electronic structures calculations. The symmetry analysis was conducted using the PSEUDO program provided by the Bilbao crystallographic server43,66. The spontaneous ferroelectric polarization was calculated by using Born effective charges (Z*) of the ferroelectric phase (Pnn2) and the structure distortion (u) of ferroelectric phase with respect to reference paraelectric phase (Pnna) as \(P_\alpha = \frac{e}{\Omega }\mathop {\sum}\nolimits_{k,\beta } Z_{k,\alpha \beta }^ \ast u_{k,\beta }\) where, Ω and e are the volume of unit cell and elementary charge, respectively. The spin texture of the lowest conduction band have been computed by plotting, for each momentum vector on the k x –k y plane, the expectation values of the Pauli σ-matrices onto the Kohn–Sham wavefunctions, i.e., the vectorial quantity S i (n,k) = \(\langle \Psi _{n,k}|\sigma _i|\Psi _{n,k}\rangle\), with i = x,y,z and n referring to either the inner or the outer branch of the conduction bands. Represented as a vector, the k-space distribution of the S i (n,k) resulted in a combined Rashba and Dresselhaus spin-pattern.
The surface state calculations have been performed using a Green’s function based tight-binding (TB) approach51. The TB model Hamiltonian was constructed by means of maximally localized Wannier functions (MLWFs52,53) obtained by the the Wannier90 code54 and constructed from Bi 5s and O 6p orbitals by employing VASP2WANNIER9055. The TB parameters were obtained from the MLWFs overlap matrix. Finally, the berry curvatures based on the first-principles Bloch functions provided by VASP following the recipe described in ref. 67. The topological charge of each Weyl point (WP) is defined by the integration of the Berry curvature over a closed surface enclosing that WP, and was computed by employing the Wilson-loop method68.
Data and code availabity
All data are available from the corresponding authors upon reasonable request. All codes used in this work are either publicly available or available from the authors upon reasonable request.
References
Asamitsu, A., Tomioka, Y., Kuwahara, H. & Tokura, Y. Current switching of resistive states in magnetoresistive manganites. Nature 388, 50–52 (1997).
Rao, C. N. R., Raju, A. R., Ponnambalam, V., Parashar, S. & Kumar, N. Electric-field-induced melting of the randomly pinned charge-ordered states of rare-earth manganates and associated effects. Phys. Rev. B 61, 594–598 (2000).
Aetukuri, N. B. et al. Control of the metal insulator transition in vanadium dioxide by modifying orbital occupancy. Nat. Phys. 9, 661 (2013).
Scherwitzl, R. et al. Electric-field control of the metal-insulator transition in ultrathin NdNiO3 films. Adv. Mater. 22, 5517–5520 (2010).
Yang, Z., Ko, C. & Ramanathan, S. Oxide electronics utilizing ultrafast metal-insulator transitions. Annu. Rev. Mater. Res. 41, 337–367 (2011).
Fujiwara, K., Hori, T. & Tanaka, H. Electric-field breakdown of the insulating charge-ordered state in LuFe2O4 thin films. J. Phys. D Appl. Phys. 46, 155108 (2013).
van den Brink, J. & Khomskii, D. I. Multiferroicity due to charge ordering. J. Phys. Condens. Matter 20, 434217 (2008).
Tokura, Y., Seki, S. & Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 77, 076501 (2014).
Young, J., Stroppa, A., Picozzi, S. & Rondinelli, J. M. Anharmonic lattice interactions in improper ferroelectrics for multiferroic design. J. Phys. Condens. Matter 27, 283202 (2015).
Picozzi, S. & Ederer, C. First principles studies of multiferroic materials. J. Phys. Condens. Matter 21, 303201 (2009).
Pickett, W. E., Quan, Y. & Pardo, V. Charge states of ions, and mechanisms of charge ordering transitions. J. Phys. Condens. Matter 26, 274203 (2014).
Mott, N. F. The basis of the electron theory of metals, with special reference to the transition metals. Proc. Phys. Soc. A 62, 416 (1949).
Peierls, R. E. Quantum Theory of Solids (Clarendon Press, Oxford, UK, 1955)
Slater, J. C. Magnetic effects and the Hartree-fock equation. Phys. Rev. 82, 538–541 (1951).
Lifshitz, I. M. Anomalies of electron characteristics of a metal in the high pressure region. Sov. Phys. JETP 11, 1130 (1960).
Verwey, E. J. W. Electronic conduction of magnetite (Fe3O4) and its transition point at low temperatures. Nature 144, 327–328 (1939).
Morin, F. J. Oxides which show a metal-to-insulator transition at the neel temperature. Phys. Rev. Lett. 3, 34–36 (1959).
Alonso, J. A. et al. Charge disproportionation in RNiO3 perovskites: simultaneous metal-insulator and structural transition in YNiO3. Phys. Rev. Lett. 82, 3871–3874 (1999).
Balachandran, P. V. & Rondinelli, J. M. Interplay of octahedral rotations and breathing distortions in charge-ordering perovskite oxides. Phys. Rev. B 88, 054101 (2013).
Zhou, J.-S., Goodenough, J. B. & Dabrowski, B. Exchange interaction in the insulating phase of RNiO3. Phys. Rev. Lett. 95, 127204 (2005).
Zhou, Q. & Kennedy, B. J. High temperature structure of BaBiO3—a synchrotron X-ray powder diffraction study. Solid State Commun. 132, 389 (2004).
Di Sante, D., Barone, P., Bertacco, R. & Picozzi, S. Electric control of the giant Rashba effect in bulk GeTe. Adv. Mater. 25, 509–513 (2013).
Di Sante, D. et al. Intertwined Rashba, Dirac, and Weyl fermions in hexagonal hyperferroelectrics. Phys. Rev. Lett. 117, 076401 (2016).
Kunihiko, Y., Barone, P., Shishidou, T., Oguchi, T. & Picozzi, S. Coupling ferroelectricity with spin-valley physics in oxide-based heterostructures. Phys. Rev. Lett. 115, 037602 (2015).
Zhang, X., Liu, Q., Luo, J.-W., Freemam, A. J. & Zunger, A. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 10, 387–393 (2014).
Rashba, E. I. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 2, 1109 (1960).
Dresselhaus, G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 100, 580–586 (1955).
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & Duine, R. A. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 14, 871–882 (2015).
Datta, S. & Das, B. Electronic analog of the electrooptic modulator. Appl. Phys. Lett. 56, 665 (1990).
Picozzi, S. Ferroelectric Rashba semiconductors as a novel class of multifunctional materials. Front. Phys. 2, 10 (2014).
Liu, Q. et al. Search and design of nonmagnetic centrosymmetric layered crystals with large local spin polarization. Phys. Rev. B 91, 235204 (2015).
Kim, M., Im, J., Freeman, A. J., Ihm, J. & Jin, H. Switchable s = 1/2 and j = 1/2 Rashba bands in ferroelectric halide perovskites. PNAS 111, 6900 (2014).
Stroppa, A. et al. Tunable ferroelectric polarization and its interplay with spin-orbit coupling in tin iodide perovskites. Nat. Commun. 5, 5900 (2015).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Shekhar, C. et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 11, 645–649 (2015).
Hirschberger, M. et al. The chiral anomaly and thermopower of Weyl fermions in the half-heusler GdPtBi. Nat. Mater. 15, 1161–1165 (2016).
Oberndorfera, C. P. M., Dinnebiera, R. E., Ibbersonb, R. M. & Jansen, M. Charge ordering in Ag2BiO3. Solid State Sci. 8, 267 (2006).
Deibele, S. & Jansen, M. Bismuth in Ag2BiO3: tetravalent or internally disproportionated? J. Solid State Chem. 147, 117–121 (1999).
Franchini, C., Sanna, A., Marsman, M. & Kresse, G. Structural, vibrational, and quasiparticle properties of the peierls semiconductor BaBiO3: a hybrid functional and self-consistent GW+vertex-corrections study. Phys. Rev. B 81, 085213 (2010).
He, J., Franchini, C. & Rondinelli, J. M. Ferroelectric oxides with strong visible-light absorption from charge ordering. Chem. Mater. 29, 2445–2451 (2016).
Wang, F., Young, S. M., Zheng, F., Grinberg, I. & Rappe, A. M. Substantial bulk photovoltaic effect enhancement via nanolayering. Nat. Commun. 7, 10419 (2016).
Zhang, Y., Sun, J., Perdew, J. P. & Wu, X. Comparative first-principles studies of prototypical ferroelectric materials by LDA, GGA, and scan meta-GGA. Phys. Rev. B 96, 035143 (2017).
Aroyo, M. I. et al. Crystallography online: Bilbao crystallographic server. Chem. Commun. 43, 183 (2011).
Hatch, D. M. & Stokes, H. T. Invariants: program for obtaining a list of invariant polynomials of the order-parameter components associated with irreducible representations of a space group. J. Appl. Crystallogr. 36, 951–952 (2003).
Wieder, B. J., Kim, Y., Rappe, A. M. & Kane, C. L. Double Dirac semimetals in three dimensions. Phys. Rev. Lett. 116, 186402 (2016).
Bradlyn, B. et al. Beyond Dirac and Weyl fermions: unconventional quasiparticles in conventional crystals. Science 353, aaf5037 (2016).
Di Sante, D. et al. Realizing double Dirac particles in the presence of electronic interactions. Phys. Rev. B 96, 121106 (2017).
Franchini, C., Kresse, G. & Podloucky, R. Polaronic hole trapping in doped BaBiO3. Phys. Rev. Lett. 102, 256402 (2009).
Li, R. et al. Weyl ferroelectric semimetal. Preprint at https://arXiv:1610.07142 (2016)
Zahid Hasan, M., Xu, S.-Y. & Bian, G. Topological insulators, topological superconductors and Weyl fermion semimetals: discoveries, perspectives and outlooks. Phys. Scripta 2015, 014001 (2015).
Lopez Sancho, M. P., Lopez Sancho, J. M., Lopez Sancho, J. M. & Rubio, J. Highly convergent schemes for the calculation of bulk and surface green functions. J. Phys. F 15, 851 (1985).
Marzari, N. & Vanderbilt, D. Maximally localized generalized wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Franchini, C. et al. Maximally localized wannier functions in LaMnO3 within Pbe + U, hybrid functionals and partially self-consistent GW: an efficient route to construct ab initio tight-binding parameters for eg perovskites. J. Phys. Condens. Matter 24, 235602 (2012).
Ginzburg, V. L. & Landau, L. D. Phenomenological theory. J. Exp. Theor. Phys. USSR 20, 1064 (1950).
Garcia, V. et al. Giant tunnel electroresistance for non-destructive readout of ferroelectric states. Nature 460, 81–84 (2009).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Axel Hoffmann & Bader, S. D. Opportunities at the frontiers of spintronics. Phys. Rev. Appl. 4, 047001 (2015).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Hafner, J. Ab initio. Phys. Rev. B 48, 13115–13118 (1993).
Kresse, G. & Furthmüler, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6, 15 (1996).
Perdew, J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Deibele, S. & Jansen, M. Methods for pseudosymmetry evaluation: a comparison between the atomic displacements and electron density approach. Z. Krist. 220, 691–699 (2005).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Soluyanov, A. A. & Vanderbilt, D. Computing topological invariants without inversion symmetry. Phys. Rev. B 83, 235401 (2011).
Acknowledgments
Work at the University of Vienna was sponsored by the FWF project INDOX (Grant No. I1490-N19). Work at the Shenyang National Laboratory for Materials Science was supported by the National Science Fund for Distinguished Young Scholars (No. 51725103), by the National Natural Science Foundation of China (Grant Nos. 51671193 and 51474202), and by the Science Challenging Project No. TZ2016004. D.D.S. was supported by the German Research Foundation (DFG- SFB 1170) and acknowledges the ERC-StG-336012-Thomale-TOPOLECTRICS. J.M.R. was supported by the Army Research Office (W911NF-15-1-0017). All calculations were performed on the Vienna Scientific Cluster (VSC) and partially at the high-performance computational cluster in the Shenyang National University Science and Technology Park, as well as the National Supercomputing Center in Guangzhou (TH-2 system).
Author information
Authors and Affiliations
Contributions
J.H. and C.F. conceived and coordinated the project. J.M.R. and J.H. performed symmetry analysis of the ferroelectric phase transition. J.H. conducted the DFT calculations. D.D.S. carried out Rashba/Dresselhaus analysis. R.L. and X.-Q.C. analyzed and computed the topological properties (Weyl features) and Berry curvatures. All the authors contributed to discussions and writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
He, J., Di Sante, D., Li, R. et al. Tunable metal-insulator transition, Rashba effect and Weyl Fermions in a relativistic charge-ordered ferroelectric oxide. Nat Commun 9, 492 (2018). https://doi.org/10.1038/s41467-017-02814-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-02814-4
This article is cited by
-
Switchable Rashba anisotropy in layered hybrid organic–inorganic perovskite by hybrid improper ferroelectricity
npj Computational Materials (2020)
-
Topological phases in pyrochlore thallium niobate Tl2Nb2O6+x
npj Computational Materials (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.