Abstract
Quantum beats, periodic oscillations arising from coherent superposition states, have enabled exploration of novel coherent phenomena. Originating from strong Coulomb interactions and reduced dielectric screening, two-dimensional transition metal dichalcogenides exhibit strongly bound excitons either in a single structure or hetero-counterpart; however, quantum coherence between excitons is barely known to date. Here we observe exciton quantum beats in atomically thin ReS2 and further modulate the intensity of the quantum beats signal. Surprisingly, linearly polarized excitons behave like a coherently coupled three-level system exhibiting quantum beats, even though they exhibit anisotropic exciton orientations and optical selection rules. Theoretical studies are also provided to clarify that the observed quantum beats originate from pure quantum coherence, not from classical interference. Furthermore, we modulate on/off quantum beats only by laser polarization. This work provides an ideal laboratory toward polarization-controlled exciton quantum beats in two-dimensional materials.
Similar content being viewed by others
Introduction
When resonantly excited quantum states have mutual coherence, their quantum superposition leads to periodically oscillating signals in optical domains (e.g., fluorescence1, photon echo2,3, and pump-probe spectroscopy2), where the oscillation frequency exactly matches the energy separation of the coupled states (Fig. 1a)1,4,5. This phenomenon, referred to as quantum beats, is of great importance for understanding the coherence of excited states in light–matter interaction because it reveals the mutual quantum coherence directly in the time domain1,4,5. Moreover, quantum beats play a crucial role in understanding many intriguing coherent phenomena such as lasing without population inversion6 and quantum entanglement7. This effect can also be utilized in ultrafast optoelectronic devices, including tunable terahertz emitters8 and optical switches9.
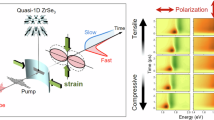
Quantum beats in ReS2. a Coherent superposition of resonantly excited two excitons (blue (X1) and red (X2) states) can lead to beating optical signals in the time domain (light blue oscillation). The oscillation period corresponds exactly to the energy different (ΔE) of the excited states. b Illustration of anisotropic excitons (dumbbell-shaped electron–hole pairs) in ReS2. The two lowest excitons, X1 and X2, are linearly polarized with different in-plane orientations. c Controlling quantum beats (light blue oscillations) of excitons by manipulating laser polarization (arrows). Blue (red) color represents X1 (X2). While the quantum beat is expected to be large when optical polarization is adjusted to excite both two excitons in a balanced way (upper schematics), it will weaken if only one of the two exciton states is excited by light asymmetrically (lower schematics). d, e Three-level system with a common state (d) and two independent two-level systems (e)
Recently, two-dimensional (2D) transition metal dichalcogenides (TMDs) have received considerable attentions due to their excellent excitonic properties, resulting from weak dielectric screening and strong quantum confinement10,11,12,13,14,15. To date, most of the related study has performed on MX2 (M = Mo, W; X = S, Se), where researchers have identified various types of excitonic coherent couplings16,17,18, such as exciton–trion19,20,21, exciton–ground22, and valley excitons23,24,25,26,27. For the quantum beats, however, only limited observations were reported19,20,21. The valley excitons do not exhibit quantum beats due to the energetic degeneracy. The so-called A–B excitons28, arising from the valence band splitting, have not shown any signature of coherence due to their rapid decoherence. Although only the exciton–trion has exhibited the quantum beats19,20,21, the presence of trions and their concentrations significantly depend on extrinsic conditions such as the doping level29,30. Because a trion state is a just charged version of a neutral exciton, they have same optical selection rules23, such that it is difficult to expect rich physics of exciton quantum beats arising from various combinations of light-polarization dependencies7,31,32.
Rhenium dichalcogenides are recently emerging 2D semiconductors containing a low in-plane crystal symmetry33,34,35,36. Interestingly, they exhibit strongly anisotropic excitons which have different orientations and optical selection rules for linearly polarized light37,38,39. Figure 1b illustrates the in-plane anisotropy of the lowest two excitons, labeled by X1 and X2, respectively, in a representative rhenium dichalcogenide ReS237. Recent studies have shown that these anisotropic excitons hold great potentials for various optoelectronic applications, such as light-polarization-controlled switches, modulators, and optical computations35,38,39,40,41,42,43. Also, unlike trions and valley excitons in MX2, the anisotropic excitons persist regardless of the doping level and the layer number37,38,44. Thus, one may expect that ReS2 may provide an ideal platform for studying coherent phenomena in 2D semiconductors. If ReS2 exhibits quantum beats, the non-identical orientations of the excitons may offer new polarization-dependent phenomena, as illustrated in Fig. 1c. However, the quantum coherence of ReS2 remains completely elusive.
Meanwhile, there has been one critical issue on observing the exciton quantum beats. It is known that only the coherent three-level system with a common state can generate quantum beats (e.g., Fig. 1d), but uncoupled oscillators cannot (Fig. 1e)4. The latter can cause quantum beats-like interference whose origin does not lie on the quantum superposition. Since it is very difficult to distinguish quantum beats from the classical interference, experimental verification of the pure quantum coherence has been significantly hindered4,45.
In this work, by using ultrafast two-pulse pump-probe spectroscopy, we observe quantum beats in a few-layer ReS2 and modulate the intensity of the quantum beats signal. Our observation identifies that the phenomenon arises from quantum coherence between X1 and X2 which behave exactly as a coherently coupled three-level system, even though they have completely different orientations and optical selection rules. Our theoretical investigations prove that our two-pulse pump-probe technique does not allow the interference hindering the observation of quantum beats, unlike the three-pulse four-wave mixing experiments. Further, we modulate on/off quantum beats only by laser polarization, highlighting the anisotropic nature of the ReS2 excitons.
Results
Sample and experiment
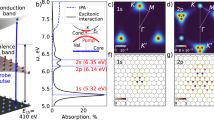
The few-layer ReS2 flake (8–9 layers; Fig. 2a) was exfoliated on a sapphire substrate from bulk single crystal, using polydimethylsiloxane-stamp-assisted mechanical exfoliation technique46. ReS2 has an anisotropic crystal structure with distorted 1T phase, forming Re chains along the b axis (thick white line in Fig. 2a)33,37,38. We identify the energies of the anisotropic excitons by using static spectroscopy. Figure 2b, c shows absorption resonances of the two lowest excitons (X1 at 1.531 eV and X2 at 1.566 eV), exhibiting characteristic dependencies on the light polarization (θ, which measures the polarization angle with respect to the b axis; see Fig. 2a). Corresponding θ-resolved spectral weights in Fig. 2d show their anisotropic nature more clearly (Supplementary Note 1)37,39.
Anisotropic excitons in ReS2. a Optical image of the few-layer ReS2. White line along the edge of the flake represents the b axis. θ is the angle optical polarization (arrow). Yellow graph shows the AFM profile along the dashed line. The scale bar is 20 μm. b–d Polarization-dependent absorption of the ReS2 (b) and several linecuts at four different θ (black lines in (c)). The blue (red) lines are Voigt fits of the X1 (X2). Corresponding Voigt spectral weights (dots) and fits (lines, Supplementary Note 1) are shown in d. Orange line in c is the pump profile
Our pump-probe experiments, based on a 250 kHz Ti:sapphire regenerative amplifier (Coherent 9050), were performed by using linearly polarized pulses centered at 800 nm (Supplementary Fig. 1). The pulse spectrum covers both X1 and X2 to excite them simultaneously (orange line in Fig. 2c). A weak portion of split beam serves as the probe pulse, which transmits the sample and reaches the detector after passing through a monochromator (Supplementary Fig. 2). The detection wavelength is set to the center of X1 and X2 (i.e., 800 nm) to maximize the beating amplitude47. We measure the differential transmittance (DT) as a function of pump-probe time delay (τ). The DT signal is defined by ΔT/T, where T is the probe intensity without pump, and ΔT is the pump-induced change in the probe intensity. Pump fluence was fixed at 15 μJ cm−2, and sample temperature was set at 79 K for all experiments.
Observation of quantum beats
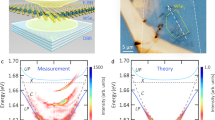
We first explore the θ-resolved quantum beats with co-polarized pump-probe configuration (i.e., θ = θpu = θpr, where θpu (θpr) is the pump (probe) polarization). Figure 3a shows measured DT traces; we observe periodically oscillating signals after τ ~ 0.15 ps (right side of the gray vertical line), exhibiting strong θ dependence. The oscillating DT can be described by a damped harmonic oscillator (\(B\exp ( { - \tau /\tau _{\mathrm{dephasing}}} )\cos \left( {\left( {2\pi /T_{\mathrm{p}}} \right)\tau + \varphi } \right)\), where B is the beating amplitude, \(\tau _{\mathrm{dephasing}}\) is the dephasing time constant, Tp is the oscillation period, and ϕ is the phase) superimposed on background (BG) dynamics. Figure 3b shows a fitting example, where a DT trace at θ = 150° (gray dots) is well reproduced by the model (solid line), and the BG-subtracted version (green dots) indeed exhibits the behavior of a simple damped harmonic oscillator. Importantly, the oscillation period of Tp = 116 fs agrees exactly with the energy splitting between X1 and X2 (ΔE ~ 35 meV) via the relation \(T_{\mathrm{p}} = 2\pi \hbar /\Delta E\)48. This oscillating behavior is one apparent hallmark of the quantum coherence arising from the exciton quantum beats (note that, although the laser pulse width (~50 fs) is not very short compare to the oscillation period, it does not prohibit the observation of quantum beats; see Supplementary Fig. 3). Other evidence corroborates this assignment. First, the beatings have almost the same Tp regardless of θ (Fig. 3c, d), which agrees with the fact that the X1–X2 splitting has no θ dependence37. Second, no pronounced phonon mode has been reported at this energy of 35 meV in ReS249, indicating that the oscillations do not come from the coherent phonon. In addition, no quantum beats were observed when the pump resonantly excites one of the two excitons, which further directly proves that the coherent oscillations do not originate from any single excitonic feature (Supplementary Fig. 4).
Polarization-dependent quantum beat of excitons with co-polarized pump-probe. a θ ( = θpr = θpu)-resolved DT (offset for clarity). Analyses of the quantum beat are performed on the right side of the vertical gray line. b Original DT trace (gray dots) and its BG-subtracted version (green dots) at θ = 150°. Solid lines are fits. c, d Polarization-dependent BG-subtracted DT signals (c) and fits (d). e Dashed lines are spectral weights of X1 (blue) and X2 (red), obtained from static absorption in Fig. 2d. The black line is their product. The gray and green areas, indicated by I and II, respectively, are the regions where the theoretical beating amplitude (proportional to the black line in e) is expected to have local maxima (see main text). f θ-dependent beating amplitude (dots, left axis) and dephasing time constants (triangles, right axis), extracted from the fits in d. The error bars represent 95% confidence intervals for the fitting parameters. g A schematic polar diagram illustrating the regions I and II and orientations of the excitons. The blue (red) line indicates the polarization angle at which the spectral weight of X1 (X2) is maximized
We obtained the dephasing time constant \(\tau _{{\mathrm{dephasing}}}\) = 100–200 fs, as indicated by triangles in Fig. 3f, where missing values are due to significantly large uncertainty. The population relaxation is unlikely to cause this rather fast dephasing because its time constant (10–40 ps)40 is much longer than \(\tau _{{\mathrm{dephasing}}}\). We assign the main dephasing mechanism to the inhomogeneity-induced dephasing, based on the fact that exciton absorption linewidths are dominated by the inhomogeneous broadening that originates from chalcogenide vacancy defects and other impurities (Supplementary Note 1). Thus, \(\tau _{{\mathrm{dephasing}}}\) sets the lower bound of the intrinsic X1–X2 decoherence time.
The observed \(\tau _{{\mathrm{dephasing}}}\) is comparable with the decoherence time of the valley excitons in monolayer MX2 (~100 fs at 10 K)27. This result is rather surprising, considering the following facts. First, unlike the energetically degenerate valley excitons, the X1–X2 dephasing dynamics should include the fast interexcitonic relaxation16 from the higher X2 to lower X1. Second, the experimental temperature of this work is relatively high (79 K). Therefore, our observation implies that the excitonic quantum coherence in ReS2 render significant robustness against relaxation dynamics and temperature variations. Further experiments, such as multidimensional16 and photon-echo27 spectroscopy, are required to accurately determine timescales of the interexcitonic relaxation and the decoherence mechanism.
We should comment on peak-like and oscillating DT signals near τ = 0 ps and at τ < 0 ps (left side of the gray vertical line in Fig. 3a). Such responses can arise from optical Stark effect38, coherent oscillations4, four-wave mixed signal in the probe direction50, and polariton propagation51. Because it is very elusive to distinguish the quantum beats from these processes near τ = 0 ps4, we performed analysis limiting τ longer than 0.15 ps, as mentioned above. This assumption will be justified as discussed later in Fig. 4.
Pump-polarization-dependent quantum beats. a, b θpu-resolved DT with offset (a) and its contour plot (b). θpr is set at 50°. Analyses are performed on the right side of the vertical gray line. c, d Comparison of beating amplitude obtained from theory (c) and experiments (d). In c, the square root of the product of the excitons’ spectral weights is shown, which is theoretically proportional to the beating amplitude (see Supplementary Note 3). Gray (green) area represents the region I (II). The error bars represent 95% confidence intervals for the fitting parameters
Quantum beats vs. polarization interference
In this section, we theoretically confirm that the observed quantum beats originate from the pure quantum coherence. As briefly discussed in the introduction, it is known that quantum beats can be generated only in a coupled three-level system with a common state (Fig. 1d). In contrast, the independent two-level oscillators (Fig. 1e) can cause quantum beats-like signal, the so-called polarization interference (PI), arising from electromagnetic interference at the detector4. Because PI has the same temporal shape as the quantum beats, many researchers have devoted much effort to distinguish these phenomena since the first discovery by Lambert et al.52. There exist somewhat complicated methods for the distinction of quantum beats form PI, which are based on time-resolved or spectrally resolved analyses in the three-pulse four-wave-mixing experiments45,53. However, for the two-pulse pump-probe technique, there has been no rigorous discussion on the PI issue although it has been widely utilized to study quantum beats over the past several decades2,48,50,54,55.
To resolve this issue, we perform theoretical analysis based on the semi-classical Liouville–von-Neumann equation (full calculations are provided in Supplementary Note 2). The key result is that the two-pulse pump-probe technique does not allow PI, meaning no additional check processes are required to confirm the occurrence of the real quantum beats, which is different from the case of the three-pulse four-wave-mixing experiments. Thus, the two-pulse pump-probe technique is a powerful and convenient tool to identify the quantum beats. Also, our theoretical analysis further confirms that the observed X1–X2 quantum beats originate from quantum coherence in a coupled three-level configuration.
Polarization-controlled quantum beats
We now discuss the θ dependence of the quantum beats. In Fig. 3c, d, the BG-subtracted DT traces show that the beating is clearly visible only at θ ~ 90–150°. This is corroborated by their Fourier transforms (see Supplementary Fig. 5), which show a peak near ΔE ~ 35 meV only at the same θ range. This clear θ dependence suggests that we can switch on/off the quantum beats simply by manipulating the laser optical polarization.
More in-depth understanding of the θ-dependent quantum beats can be obtained by considering a simple theoretical model. The beating amplitude B can be assumed to be proportional to the product of exciton spectral weight (SW), i.e., \(B \propto {\mathrm{SW}}_{\mathrm{1}} \times {\mathrm{SW}}_{\mathrm{2}}\) (refs 4,56), where subscripts 1 and 2 mean X1 and X2, respectively. In Fig. 3e, we plot the θ-dependent SW1 and SW2 (dashed lines) obtained from static absorption measurements, and their product (\({\mathrm{SW}}_{\mathrm{1}} \times {\mathrm{SW}}_{\mathrm{2}}\), solid black line). We see that B (\(\propto {\mathrm{SW}}_{\mathrm{1}} \times {\mathrm{SW}}_{\mathrm{2}}\)) shows peaks at θ ~ 50° and 140°, when SW1 and SW2 intersect. It indicates that quantum beats have relatively large intensity when the population of the two excitons is equally balanced56. Note that the magnitude of the two theoretical peaks is different because the polarization direction of each exciton (i.e., polarization directions at which each SW reaches its maximum, see blue and red lines in Fig. 3g) is not exactly orthogonal to each other. We refer these two peak areas to region I (gray shaded) and II (green shaded), respectively.
Let us now compare the prediction with the experimentally obtained B (black dots in Fig. 3f); while the measured B peak in the region II agrees well with the theory, a rather small value is observed in the region I. To explain the latter, we consider two possibilities. First, recent Raman spectroscopy of ReS2 showed that the most prominent phonon mode (mode III; ref. 49) has strong anisotropy, and the polarization angle at which the phonon response is maximized coincides with the region I. Thus, weak beats in this region may arise from the anisotropic exciton–phonon scattering which leads to extremely fast dephasing before the analyzed τ range. Second, as indicated by blue and red lines in Fig. 3g, the angle between X1 and X2 in the region I is smaller than that in the region II. Considering excitons’ anisotropic transitions follow similar polarization dependences in the momentum space57, electron and hole states of X2 can be located relatively close to those of X1 in the region I. This may lead to the fast dephasing through rapid relaxation from X2 to X1. More studies are needed to figure out this anomaly accurately.
So far we have discussed the polarization dependence of the quantum beats with co-polarized pump-probe configuration. Although this analysis offers meaningful physics of the anisotropic quantum coherence, further confirmation should be performed for more accurate understanding. For example, BG dynamics at τ > 0.15 ps in Fig. 3a show significant θ dependence, which may affect or mask the quantum beats signals in the DT transients. For this reason, we employed additional experiments under various pump-probe polarization configurations. Figure 4a shows DT traces measured by scanning θpu at a fixed θpr (=50°), and Fig. 4b displays its contour version (fits and Fourier spectra are provided in Supplementary Fig. 6). We can see that, unlike the case of co-polarization (Fig. 3a), BG dynamics in Fig. 4a has little dependence on θpu at τ > ~0.15 ps (right side of the vertical gray line). In contrast, the beating amplitude has similar polarization dependence as in the case of the co-polarization; the measured B (Fig. 4d) follows the theoretical prediction (Fig. 4c) only in the region II and show anomalously weak beating in the region I. This result suggests that the effect of BG dynamics on the quantum beat is trivial. Note that the square root of the theoretical curve (\(\sqrt {{\mathrm{SW}}_{\mathrm{1}} \times {\mathrm{SW}}_{\mathrm{2}}}\)) in Fig. 4c is due to the invariance of θpr (see Supplementary Note 3 and Supplementary Fig. 7 for the detailed discussion). Moreover, as shown in Fig. 4b, DT dips near τ = 0 ps exhibits the largest signal near θpu = 80°, which is completely different from the θpu dependence of B (Fig. 4d). This result implies that B does not have a significant correlation with the DT signals near τ = 0 ps, justifying our analysis performed at τ > 0.15 ps.
Finally, we examine how the exciton quantum beats change with θpr. Here θpu was fixed at 160° to obtain large beating, based on the results in Fig. 3. Overall shapes of DT traces (Fig. 5a; fits and Fourier spectra are provided in Supplementary Fig. 8) closely resemble those measured in the co-polarization experiment (Fig. 3a), meaning that the polarization dependence of the BG dynamics is determined by the probe. For the beating amplitude, however, its polarization dependence is different from the case of the co-polarization experiment in Fig. 3f; the measured B (dots in Fig. 5c) agrees well with the theory (line in Fig. 5b) both for regions I and II, i.e., shows no anomalous quenching of the quantum beats even in the region I. This can be understood by the following way. As discussed above, the anomalously weak beating possibly originates from the fast dephasing of excitons generated in the region I. Thus, excitons generated in the region II by excitation at θpu = 160° are not expected to suffer such fast dephasing, agreeing with the observation in Fig. 5c. This result supports the self-consistency of our analysis.
Probe-polarization-dependent quantum beats. a θpr-resolved DT with offset. θpu is fixed at 160°. Analyses are performed on the right side of the vertical gray line. b, c Comparison of beating amplitude obtained from theory (b) and experiments (c). Solid line in b is same as that in Fig. 4c. Gray (green) area represents the region I (II). The error bars represent 95% confidence intervals for the fitting parameters
Discussion
In summary, we have observed quantum beats of anisotropic excitons in 2D ReS2. Considering that researchers have observed only beatings between excitons and trions in 2D TMDs so far, our observation is rather surprising because the anisotropic excitons show completely different optical selection rules and orientations. Despite the presence of interexcitonic relaxation and the relatively high experimental temperature, the observed dephasing time of 100–200 fs is comparable to that of valley excitons in MX2 at 10 K, implying strong robustness of exciton coherence in ReS2. Moreover, we provide theoretical analysis which proves that the two-pulse pump-probe spectroscopy measure only pure quantum beats without being hindered by the unwanted interference (PI), unlike three-pulse four-wave-mixing experiments. This analysis is expected to be a theoretical basis justifying the use of the pump-probe in future quantum beats studies. We also study polarization-resolved quantum beats, including on/off control and anomalous polarization dependence. This result highlights the characteristic anisotropy of ReS2 excitons. Besides, because X1 and X2 are closely located near 800 nm in the spectral domain, it is possible to generate exciton quantum beats simply by injecting the output of commercial Ti:sapphire lasers without any wavelength conversion. Therefore, we expect that our work will stimulate theoretical and experimental discovery on the exciton quantum beats in two-dimensional materials.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Change history
22 March 2018
In the originally published HTML and PDF versions of this article, Figs. 3g and 4d contained typesetting errors affecting the way the data points were displayed. This has now been corrected in the HTML and PDF versions.
References
Dodd, J. N., Kaul, R. D. & Warrington, D. M. The modulation of resonance fluorescence excited by pulsed light. Proc. Phys. Soc. 84, 176–178 (1964).
Leo, K. et al. Coherent oscillations of a wave packet in a semiconductor double-quantum-well structure. Phys. Rev. Lett. 66, 201–204 (1991).
Leo, K., Damen, T. C., Shah, J., Gobel, E. O. & Kohler, K. Quantum beats of light hole and heavy hole excitons in quantum wells. Appl. Phys. Lett. 57, 19 (1990).
Shah, J. Ultrafast Spectroscopy of Semiconductors and Semiconductor Nanostructures (Springer, Berlin, Heidelberg, 1974).
Mukamel, S. Principles of Nonlinear Optical Spectroscopy (Oxford University Press, Oxford, 1995).
Scully, M. O., Zhu, S. Y. & Gavrielides, A. Degenerate quantum-beat laser: lasing without inversion and inversion without lasing. Phys. Rev. Lett. 62, 2813 (1989).
Lenihan, aS., Gurudev Dutt, M. V., Steel, D. G., Ghosh, S. & Bhattacharya, P. K. Raman coherence beats from entangled polarization eigenstates in InAs quantum dots. Phys. Rev. Lett. 88, 223601 (2002).
Planken, P. C. M. et al. Terahertz emission in single quantum wells after coherent optical excitation of light hole and heavy hole excitons. Phys. Rev. Lett. 69, 3800 (1992).
Kojima, O. et al. Ultrafast response induced by interference effects between weakly confined exciton states. J. Phys. Soc. Jpn. 77, 044701 (2008).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343 (2014).
Liu, G.-B., Xiao, D., Yao, Y., Xu, X. & Yao, W. Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem. Soc. Rev. 44, 2643–2663 (2015).
Castellanos-Gomez, A. Why all the fuss about 2D semiconductors? Nat. Photonics 10, 202–204 (2016).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Czech, K. J. et al. Measurement of ultrafast excitonic dynamics of few-layer MoS2 using state-selective coherent multidimensional spectroscopy. ACS Nano 9, 12146–12157 (2015).
Dey, P. et al. Biexciton formation and exciton coherent coupling in layered GaSe. J. Chem. Phys. 142, 212422 (2015).
Dey, P. et al. Optical coherence in atomic-monolayer transition-metal dichalcogenides limited by electron-phonon interactions. Phys. Rev. Lett. 116, 127402 (2016).
Hao, K. et al. Coherent and incoherent coupling dynamics between neutral and charged excitons in monolayer MoSe2. Nano Lett. 16, 5109–5113 (2016).
Jakubczyk, T. et al. Radiatively limited dephasing and exciton dynamics in MoSe2 monolayers revealed with four-wave mixing microscopy. Nano Lett. 16, 5333–5339 (2016).
Shepard, G. D. et al. Trion-species-resolved quantum beats in MoSe2. ACS Nano 11, 11550 (2017).
Moody, G. et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nat. Commun. 6, 8315 (2015).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 8, 634 (2013).
Ye, Z., Sun, D. & Heinz, T. F. Optical manipulation of valley pseudospin. Nat. Phys. 13, 26 (2017).
Wang, G. et al. Control of exciton valley coherence in transition metal dichalcogenide monolayers. Phys. Rev. Lett. 117, 187401 (2016).
Sie, E. J., Lui, C. H., Lee, Y. H., Kong, J. & Gedik, N. Observation of intervalley biexcitonic optical Stark effect in monolayer WS2. Nano Lett. 16, 7421–7426 (2016).
Hao, K. et al. Direct measurement of exciton valley coherence in monolayer WSe2. Nat. Phys. 12, 677–682 (2016).
Sim, S. et al. Exciton dynamics in atomically thin MoS2: interexcitonic interaction and broadening kinetics. Phys. Rev. B 88, 075434 (2013).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2. Nat. Mater. 11, 207 (2012).
Kozawa, D. et al. Evidence for fast interlayer energy transfer in MoSe2/WS2 heterostructures. Nano Lett. 16, 4087–4093 (2016).
Schmittrink, S. et al. Polarization dependence of heavy-hole and light-hole quantum beats. Phys. Rev. B 46, 10460–10463 (1992).
Sénès, M. et al. Exciton spin manipulation in InAs/GaAs quantum dots: exchange interaction and magnetic field effects. Phys. Rev. B 71, 115334 (2005).
Tongay, S. et al. Monolayer behaviour in bulk ReS2 due to electronic and vibrational decoupling. Nat. Commun. 5, 3252 (2014).
Liu, E. et al. Integrated digital inverters based on two-dimensional anisotropic ReS2 field-effect transistors. Nat. Commun. 6, 6991 (2015).
Rahman, M., Davey, K. & Qiao, S. Z. Advent of 2D rhenium disulfide (ReS2): fundamentals to applications. Adv. Funct. Mater. 27, 1606129 (2017).
Ovchinnikov, D. et al. Disorder engineering and conductivity dome in ReS2 with electrolyte gating. Nat. Commun. 7, 12391 (2016).
Aslan, O. B., Chenet, Da, van der Zande, A. M., Hone, J. C. & Heinz, T. F. Linearly polarized excitons in single- and few-layer ReS2 crystals. ACS Photonics 3, 96–101 (2016).
Sim, S. et al. Selectively tunable optical Stark effect of anisotropic excitons in atomically thin ReS2. Nat. Commun. 7, 13569 (2016).
Arora, A. et al. Highly anisotropic in-plane excitons in atomically thin and bulklike 1T′-ReSe2. Nano Lett. 17, 3202–3207 (2017).
Cui, Q. et al. Transient absorption measurements on anisotropic monolayer ReS2. Small 11, 5565 (2015).
Wu, S. et al. Phase-engineering-induced generation and control of highly anisotropic and robust excitons in few-layer ReS2. J. Phys. Chem. Lett. 8, 2719–2724 (2017).
Liu, F. et al. Highly sensitive detection of polarized light using anistropic 2D ReS2. Adv. Funct. Mater. 26, 1169–1177 (2015).
Zhang, E. et al. Tunable ambipolar polarization-sensitive photodetectors based on high-anisotropy ReSe2 nanosheets. ACS Nano 10, 8067–8077 (2016).
Ho, C. H., Liao, P. C., Huang, Y. S. & Tiong, K. K. Temperature dependence of energies and broadening parameters of the band-edge excitons of ReS2 and ReSe2. Phys. Rev. B 55, 15608–15613 (1997).
Koch, M. et al. Quantum beats versus polarization interference: an experimental di. Phys. Rev. Lett. 69, 3631–3634 (1992).
Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 1, 011002 (2014).
Kojima, O., Mizoguchi, K. & Nakayama, M. Coupling of coherent longitudinal optical phonons to excitonic quantum beats in GaAs/AlAs multiple quantum wells. Phys. Rev. B 68, 155325 (2003).
Dass, C. K. et al. Quantum beats in hybrid metal–semiconductor nanostructures. ACS Photonics 2, 1341–1347 (2015).
Chenet, D. A. et al. In-plane anisotropy in mono- and few-layer ReS2 probed by Raman spectroscopy and scanning transmission electron microscopy. Nano Lett. 15, 5667–5672 (2015).
Trifonov, A. V. et al. Multiple-frequency quantum beats of quantum confined exciton states. Phys. Rev. B 92, 201301 (2015).
Ohta, S., Kojima, O., Kita, T. & Isu, T. Observation of quantum beat oscillations and ultrafast relaxation of excitons confined in GaAs thin films by controlling probe laser pulses. J. Appl. Phys. 111, 023505 (2012).
Lambert, L. Q., Compaan, A. & Abella, I. D. Effects of nearly degenerate states on photon-echo behavior. Phys. Rev. A 4, 2022 (1971).
Lyssenko, V. G. et al. Nature of nonlinear four-wave-mixing beats in semiconductors. Phys. Rev. B 48, 5720–5723 (1993).
Joschko, M. et al. Heavy–light hole quantum beats in the band-to-band continuum of GaAs observed in 20 femtosecond pump-probe experiments. Phys. Rev. Lett. 78, 737–740 (1997).
Kojima, O., Iwasaki, Y., Kita, T. & Akahane, K. Effects of non-exciton components excited by broadband pulses on quantum beats in a GaAs/AlAs multiple quantum well. Sci. Rep. 7, 41496 (2017).
Mitsunaga, M. & Tang, C. L. Theory of quantum beats in optical transmission-correlation and pump-probe measurements. Phys. Rev. A 35, 1720–1728 (1987).
Zhong, H. X., Gao, S., Shi, J. J. & Yang, L. Quasiparticle band gaps, excitonic effects, and anisotropic optical properties of the monolayer distorted 1T diamond-chain structures ReS2 and ReSe2. Phys. Rev. B 92, 115438 (2015).
Acknowledgements
S.S., D.L., T.K., S.Cha., and H.C. were supported by the National Research Foundation of Korea (NRF) through the government of Korea (MSIP) (Grant Nos NRF-2015R1A2A1A10052520, NRF-2016R1A4A1012929), Global Frontier Program (2014M3A6B3063709). A.V.T. acknowledges Saint Petersburg State University for a research grant 11.34.2.2012. S.S., J.H.S. and M.-H.J. were supported by Institute for Basic Science (IBS), Korea, under the Project Code (IBS-R014-G1-2016-a00).
Author information
Authors and Affiliations
Contributions
H.C. and S.S. conceived the experimental idea. S.S., D.L., T.K., and S.Cha. performed experiments and data analysis. A.V.T. performed theoretical analysis. D.L., S.Cho., and W.S. prepared and characterized the sample. S.S., D.L., A.V.T., J.H.S., W.S., M.-H.J., and H.C. contributed to interpretation of the measured data. S.S., A.V.T., and H.C. wrote the manuscript with inputs from the other authors. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A correction to this article is available online at https://doi.org/10.1038/s41467-018-03558-5.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sim, S., Lee, D., Trifonov, A.V. et al. Ultrafast quantum beats of anisotropic excitons in atomically thin ReS2. Nat Commun 9, 351 (2018). https://doi.org/10.1038/s41467-017-02802-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-02802-8
This article is cited by
-
Anisotropic charge transport at the metallic edge contact of ReS2 field effect transistors
Communications Materials (2024)
-
Anisotropic excitons in 2D rhenium dichalcogenides: a mini-review
Journal of the Korean Physical Society (2022)
-
Adsorption of Re(VII) by coated solvent-impregnated resins containing Alamine 304-1 from sulfuric acid solutions
Rare Metals (2020)
-
Strong One-Dimensional Characteristics of Hole-Carriers in ReS2 and ReSe2
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.