Abstract
Harnessing the spin–momentum locking of topological surface states in conjunction with magnetic materials is the first step to realize novel topological insulator-based devices. Here, we report strong interfacial coupling in Bi2Se3/yttrium iron garnet (YIG) bilayers manifested as large interfacial in-plane magnetic anisotropy (IMA) and enhancement of damping probed by ferromagnetic resonance. The interfacial IMA and damping enhancement reaches a maximum when the Bi2Se3 film approaches its two-dimensional limit, indicating that topological surface states play an important role in the magnetization dynamics of YIG. Temperature-dependent ferromagnetic resonance of Bi2Se3/YIG reveals signatures of the magnetic proximity effect of TC as high as 180 K, an emerging low-temperature perpendicular magnetic anisotropy competing the high-temperature IMA, and an increasing exchange effective field of YIG steadily increasing toward low temperature. Our study sheds light on the effects of topological insulators on magnetization dynamics, essential for the development of topological insulator-based spintronic devices.
Similar content being viewed by others
Introduction
The development of spintronics relies crucially on control of spin-polarized currents, which carry spin angular momenta that can be utilized to manipulate magnetic moments through spin-transfer processes. Spin currents can be generated by the spin Hall effect1 in a heavy metal, or by exploiting the spin structure of some two-dimensional (2D) electron systems. A promising candidate of such a 2D system is the surface state of topological insulators (TIs). TIs are emergent quantum materials hosting topologically protected surface states, with dissipationless transport prohibiting backscattering2,3. Strong spin–orbit coupling (SOC) along with time reversal symmetry (TRS) ensures that the electrons in the topological surface states (TSSs) have their direction of motion and spin locked to each other2,4,5. The spin–momentum locking permits efficient interconversion between spin and charge currents. To date, several methods have been adopted to estimate the spin-charge conversion efficiency of TIs, either by using microwave-excited dynamical method6,7,8,9,10 (e.g., spin pumping and spin–torque ferromagnetic resonance (ST-FMR)) or thermally induced spin injection11. Very large values of spin-charge conversion ratio have been reported7,9,10. Recently, TIs are shown to be excellent sources of spin–orbit torques (SOT) for efficient magnetization switching12.
When a TI is interfaced with a magnetic layer, the interfacial exchange coupling can induce magnetic order in TIs by the magnetic proximity effect (MPE) and break the TRS13,14,15,16. The resulting gap opening of the Dirac state is necessary to realize novel phenomena such as topological magneto-electric effect17 and quantum anomalous Hall effect18,19. Since the MPE and spin-transfer process rely on interfacial exchange coupling of TI/ferromagnet, understanding the magnetism at the interface has attracted strong interests in recent years. Several techniques have been adopted to investigate the interfacial static magnetic properties, including spin-polarized neutron reflectivity15,20, second harmonic generation21, electrical transport14,22, and magneto-optical Kerr effect14. All these studies clearly indicate the existence of MPE resulting from exchange coupling and strong SOC in TIs. Specifically, a room-temperature magnetic order induced by MPE in EuS/Bi2Se3 has been reported recently15. Through exchange coupling between the TSS and EuS layer, the induced magnetic moments exhibited perpendicular magnetic anisotropy (PMA) that can potentially open a gap of TSS. For TI/yttrium iron garnet (YIG) bilayer, however, the interfacial magnetic anisotropy and the resulting magnetization dynamics under the influence of TSS are still largely unknown. It is equally important to understand how the interfacial exchange coupling affects the magnetization dynamics of Bi2Se3/YIG because of the wide applications of YIG. For example, TIs can enhance the magnetic anisotropy, introduce additional magnetic damping, and greatly alter the dynamical properties of the ferromagnetic layer, as commonly observed in ferromagnet/heavy metals systems23,24,25. The enhanced damping is visualized as larger linewidth of FMR spectra23,24,25. Given the volatile surface band structure depending on the TI thickness26, the adjacent materials27, and the magnetism at the interfaces28, experimental study on how the magnetization dynamically responds to the TSS is still lacking, which is a topic not only important for spintronics but also fundamental for physics.
In this work, we have investigated the magnetization dynamics via FMR in ferrimagnetic insulator YIG under the influence of the prototypical three-dimensional (3D) TI Bi2Se329. We choose YIG as the ferromagnetic layer because of its technological importance, with high TC ~550 K and extremely low damping coefficient α30. When YIG is interfaced with TIs, its good thermal stability minimizes the interdiffusion of materials. Through the Bi2Se3 thickness dependence study, we observed a strong modulation of FMR properties attributed to the TSS of Bi2Se3. The temperature-dependent study unraveled an effective field parallel to the magnetization direction existing in Bi2Se3/YIG. Such an effective field built up as the temperature decreased, which was utilized to demonstrate the zero-applied-field FMR of YIG. Furthermore, we identified a possible signature of MPE of TC as high as 180 K manifested as enhanced spin pumping in a fluctuating spin system, as well as a small emerging PMA at low temperature in competition with in-plane magnetic anisotropy (IMA) extending to high temperature.
Results
Interfacial IMA in Bi2Se3/YIG
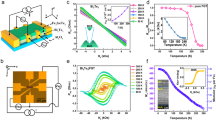
The room-temperature FMR measurements were performed using a microwave cavity of frequency 9.76 GHz (Fig. 1a) and a broadband coplanar waveguide (Fig. 1b). The FMR spectra in Fig. 1c are compared for single layer YIG(12) and Bi2Se3(25)/YIG(12) bilayer (digits denote thickness in nanometer), showing a large shift of resonance field (Hres) ~317 Oe after the Bi2Se3 growth plus a markedly broadened peak-to-peak width ΔH for Bi2Se3/YIG. Figure 1d shows Hres vs. applied field angle with respect to the surface normal θH for YIG(12) and Bi2Se3(25)/YIG(12). Larger variation of Hres with θH in the bilayer sample was observed. When the applied field was directed in the film plane, clear negative Hres shifts induced by Bi2Se3 were observed at all microwave frequencies f as shown in Fig. 1e. The data in Fig. 1d, e can be fitted in the scheme of magnetic thin films having uniaxial PMA, the strength of which is characterized by the effective demagnetization field 4πMeff = 4πMs − Han − Hint, where 4πMs, Han, and Hint are the demagnetization field, the magnetocrystalline anisotropy field of YIG, and the interfacial anisotropy field induced by Bi2Se3, respectively. The fitting result shows an ~60% enhancement of 4πMeff for the Bi2Se3(25)/YIG(12) bilayer sample. The large enhancement cannot be accounted for by an increase in the saturation magnetization Ms, which should amount to an additional magnetization of ~100 μB/nm2 for this sample. The MPE, even if it persists up to room temperature, is unlikely to induce the large amounts of magnetic moments. Furthermore, since the x-ray diffraction results in Supplementary Fig. 3(d) and (e) show that the YIG films did not gain additional strain after growing Bi2Se3, the enhanced anisotropy cannot result from the change of magnetocrystalline anisotropy. We thus attribute the change of anisotropy mostly to the Hint. Based on the above discussion, we obtain Hint = −926 and −1005 Oe from Fig. 1d, e, respectively (see Supplementary Note 2). The minus sign indicates the additional anisotropy points in the film plane.
Schematic diagrams and results of the angle- and frequency-dependent FMR measurements. a, b FMR using the cavity and co-planar waveguide configuration for angle- and frequency-dependent study, respectively. A dc external field Hext was applied and hrf denotes the microwave field. c FMR spectra of Bi2Se3(25)/YIG(12) and YIG(12) measured by the cavity. d, e θH and f dependence of Hres of Bi2Se3(25)/YIG(12) and YIG(12), respectively
The above observations suggested the presence of interfacial IMA in Bi2Se3/YIG. To verify this, we systematically varied the thickness of YIG, dYIG, while fixing the thickness of Bi2Se3. Figure 2a presents the dYIG dependence of 4πMeff for single and bilayer samples. The 4πMeff of single layer YIG was independent of dYIG varying from 12 to 30 nm. In sharp contrast, 4πMeff of Bi2Se3/YIG became significantly larger, especially at thinner YIG, which is a feature of an interfacial effect. The f- and θH-dependent FMR were performed independently to doubly confirm the trends. The interfacial IMA can be further characterized by defining the effective anisotropy constant Keff = (1/2)4πMeffMs = (1/2)(4πMs − Han)Ms − Ki/dYIG, with the interfacial anisotropy constant Ki = MsHintdYIG/2. The KeffdYIG vs. dYIG data in Fig. 2b are well fitted by a linear function, indicating that the dYIG dependence presented in Fig. 2a is suitably described by the current form of Keff. The intercept obtained by extrapolating the linear function corresponds to Ki = −0.075 erg/cm2.
YIG and Bi2Se3 thickness dependence of FMR characteristics of Bi2Se3/YIG. a The dYIG dependence of 4πMeff of Bi2Se3/YIG (solid triangles) and YIG (hollow squares) obtained from θH (red) and f (blue) dependent FMR. b The KeffdYIG vs. dYIG plot for determining Ki using a linear fit. The intercept of the y-axis corresponds to the Ki value. c dBS dependence of Ki. The figure is divided into two regions. For dBS >6 nm, the Dirac cone of TSS is intact, with the Fermi level located in the bulk conduction band. For dBS <6 nm, a gap and quantum well states form. d The dBS dependence of normalized damping enhancement \(\Delta \tilde \alpha\). The inset shows ΔH as a function of f Bi2Se3(7)/YIG(13) and YIG(13) for calculating αBS/YIG − αYIG. The red dashed line shows the typical value of \(\Delta \tilde \alpha\) of Pt/YIG for comparison. The error bars indicate standard deviations of at least four samples
TSS-modulated magnetization dynamics in Bi2Se3/YIG
To further investigate the physical origin of the IMA, we next varied the thickness of Bi2Se3 (dBS) to see how Ki evolved with dBS. Figure 2c shows the dBS dependence of Ki. Starting from the dBS = 40 nm sample, the magnitude of Ki went up as dBS decreased. An extremum of Ki −0.12 ± 0.02 erg/cm−2 was reached at dBS = 7 nm. An abrupt upturn of Ki occurred in the region 3 nm < dBS < 7 nm. The Ki magnitude dropped drastically and exhibited a sign change in the interval. Furthermore, the Ki value of 0.014 erg/cm2 at dBS = 3 nm corresponds to weak interfacial PMA.
The sizable interfacial IMA can be expected given the large SOC of Bi2Se3. One possible mechanism is that the electrons at the interface re-distribute upon hybridization between the Fe d-orbital of YIG and the Dirac surface state of Bi2Se3. Recent theoretical study on EuS/Bi2Se3 bilayers indicates that in addition to the strong SOC, TSS play a crucial role in mediating the exchange coupling of the ions in the magnetic layer31. The hybridization between TSS and the magnetic layer can overall enhance the magnetic anisotropy energy that is inherent at the interface31. Although in general an interfacial magnetic anisotropy may not necessarily be related to the topological nature of materials, here we attribute the interfacial magnetic anisotropy of Bi2Se3/YIG to the TSS based on the unique dBS dependence of Ki, that cannot be accounted for by the strain or chemical mixing effects. Note that possible interdiffusion of materials at the interface can also lead to an interfacial magnetic anisotropy. As shown in Supplementary Fig. 3(c), the transmission electron microscope (TEM) image reveals an ~1 nm interfacial layer. However, the interdiffusion is unlikely to play a dominant role in the interfacial magnetic anisotropy since Ki varied significantly with dBS up to 40 nm, and cannot account for the modulated dependence of Ki with dBS, especially under 20 nm. We now consider how the Bi2Se3 band structure evolves with dBS. Based on previous investigation on surface band structure of ultrathin Bi2Se326, dBS = 6 nm was identified as the 2D quantum tunneling limit of Bi2Se3. When dBS < 6 nm, the hybridization of top and bottom TSS developed a gap in the surface states. Spin-resolved photoemission study later showed that the TSS in this 2D regime exhibited decreased in-plane spin polarization32. The modulated spin texture may lead to the weaker interfacial magnetic anisotropy than that in the 3D regime32,33. We thus divide Fig. 2c into two regions and correlate the systematic magnetic properties with the surface state band structure. The sharp change of Ki around dBS < 6 nm strongly suggests that the interfacial IMA in Bi2Se3/YIG is of topological origin.
The ΔH broadening in FMR spectra after growing Bi2Se3 on YIG indicates that Bi2Se3 introduced additional damping in YIG. Within the macrospin approximation, the damping enhancement can be normalized with respect to dYIG by defining \(\Delta \tilde \alpha ={d_{{\mathrm Y} {\mathrm I} {\mathrm G}} \left( \alpha_{{\mathrm B} {\mathrm S}/ {\mathrm Y} {\mathrm I} {\mathrm G}}-\alpha_{{\mathrm Y} {\mathrm I} {\mathrm G}} \right)}\), where αBS/YIG and αYIG are the damping coefficient of Bi2Se3/YIG and YIG, respectively. Figure 2d displays the dBS dependence of \(\Delta \tilde \alpha\). Similar to Ki in Fig. 2c, \(\Delta \tilde \alpha\) increased as dBS decreased, reached its maximum at dBS = 7 nm with a very large value of ~0.27 nm, and then dropped abruptly in the interval of 3 nm < dBS < 7 nm. For comparison, typical \(\Delta \tilde \alpha\) of Pt/YIG, in which efficient spin pumping giving rise to sizable \(\Delta \tilde \alpha\)24, is indicated by the red dashed line. The inset shows ΔH vs. f data for Bi2Se3 (7)/YIG(13) and YIG(13) fitted by linear functions. One can clearly see a significant change of slope, from which we determined αBS/YIG − αYIG to be 0.014. In general, the large damping enhancement can have multiple origins, including spin-pumping effect, interlayer exchange coupling with other magnetic layers, and chemical reactions at the interface. However, the damping arising from the static exchange coupling from the MPE or any antiferromagnetic order at the interface is not expected at room temperature. Moreover, as previously mentioned, the slight interdiffusion at the interface is unlikely to be the major root cause of \(\Delta \tilde \alpha\) varying over the wide range of dBS. Instead, considering the closed dBS dependence of Ki and \(\Delta \tilde \alpha\), it can be seen that the trend of \(\Delta \tilde \alpha\) in Fig. 2d stemmed from the strong coupling between TSS of Bi2Se3 and YIG—that is, the surface state band structure of Bi2Se3 profoundly affected the damping of YIG6. Through dynamical exchange, spin angular momenta were transferred from YIG to the TSS via the spin-pumping effect. The spin-pumping efficiency of an interface can be evaluated by the real part of spin mixing conductance g↑↓ using the following relation25:
where g and μB, are the Landé g factor and Bohr magneton, respectively. The maximum g↑↓ value (dBS = 7 nm) is calculated to be ~2.2 × 1015 cm−2, about three times larger than that of a typical Pt/YIG sample. The large g↑↓ of Bi2Se3/YIG implies an efficient spin pumping to an excellent spin sink of Bi2Se3. Note that the trend in Fig. 2d is distinct from that of the normal metal (NM)/ferromagnetic metal (FM) structures. In NM/FM, the g↑↓ increases with increasing NM thickness as a result of vanishing spin backflow in thicker NM34. It is worth noting that the conducting bulk of Bi2Se3 can dissipate the spin-pumping-induced spin accumulation at the interface6,35. In this regard, the dBS = 7 nm sample has the largest weight of surface state contribution to g↑↓. Such unconventional dBS dependence of g↑↓ implies that TSS plays a dominant role in the damping enhancement.
Spin-pumping signature of MPE and observation of the exchange effective field
Since the effects of TSS are expected to enhance at low temperature, we next performed temperature-dependent FMR on Bi2Se3/YIG. Two bilayer samples Bi2Se3(25)/YIG(15) and Bi2Se3(16)/YIG(17), and a single layer YIG(23) were measured for comparison. Figure 3a, b shows the Hres vs. f data at various temperatures T for YIG(23) and Bi2Se3(25)/YIG(15). The Hres of both samples shows negative shifts at all f with decreasing T. The data of YIG(23) can be reproduced by the Kittel equation with increasing Ms of YIG at low T. In sharp contrast, Bi2Se3(25)/YIG(15) exhibited negative intercepts at Hres, and the intercepts gained their magnitude when the sample was cooled down. This behavior of non-zero intercept is common for all of our Bi2Se3/YIG samples. Note that the Kittel equation in its original form cannot produce an intercept. To account for the behavior, a phenomenological effective field Heff is added to the Kittel equation, i.e.,
The solid lines in Fig. 3b generated by the modified Kittel equation fitted the experimental data very well.
Temperature dependence of FMR characteristics of Bi2Se3/YIG. a, b f vs. Hres data for various T for YIG(23) and Bi2Se3(25)/YIG(15), respectively. Solids lines are fitted curves using Eq. (2). c, d, e, and f T dependence of Hres, ΔH, 4πMeff, and Heff of one YIG(23) single layer and two Bi2Se3/YIG bilayer samples, Bi2Se3(25)/YIG(15) and Bi2Se3(16)/YIG(17), respectively. The arrows in c and d denote the position of the hump-like features. Solid lines are guides of the eyes obtained by properly smoothing the experimental data. The inset of e shows the T dependence of Hint. The dashed lines indicate the hump position shown in c and d
Figure 3c, d presents the T dependence of Hres and ΔH for the YIG(23) and two Bi2Se3/YIG samples. As we lowered T, all of the samples had decreasing Hres, which was viewed as the effect of the concurrently increasing Meff and Heff as seen in Fig. 3a, b. On the other hand, ΔH built up with decreasing T. We first examined ΔH of the YIG(23) single layer. The ΔH remained relatively unchanged with T decreasing from room temperature, and dramatically increased below 100 K. The pronounced T dependence of ΔH or α has been explored in various rare-earth iron garnet and was explained by the slow-relaxation process via rare-earth elements or Fe2+ impurities triggered at low T36. For sputtered YIG films, specifically, the increase in ΔH was less prominent in thicker YIG, indicating that the dominant impurities were located near the YIG surface37. Distinct from that of YIG(23), the ΔH progressively increased for the bilayer samples. We were not able to detect FMR signals with ΔH beyond 100 Oe due to the limited sensitivity of our co-planar waveguide. However, one can clearly see that, for Bi2Se3(25)/YIG(15) and Bi2Se3(16)/YIG(17), ΔH broadened owing to increased spin pumping at first. For Bi2Se3(25)/YIG(15), the ΔH curve gradually leveled off, and intersected with that of YIG(23) at T ~40 K. The seemingly antidamping by Bi2Se3 at low T may be related to the modification of the YIG surface chemistry during the Bi2Se3 deposition. Additional analyses are needed to verify the scenario, which is, however, beyond the scope of this work. For the Bi2Se3(10)/YIG and Bi2Se3(7)/YIG samples, the damping had increased to such large magnitude below 150 K, and FMR could not be easily detected.
In both Hres and ΔH curves, hump-like features located at T = 140 and 180 K (indicated by the arrows) were revealed for Bi2Se3(25)/YIG(15) and Bi2Se3(16)/YIG(17), respectively. We note that the humps are reminiscent of spin pumping into a fluctuating magnet close to its magnetic ordering temperature. As pointed out by Ohnuma et al.38, the spin-pumping efficiency is governed by the momentum sum of imaginary part of dynamical transverse spin susceptibility \(\chi _k^R\) of the spin sink:
where k is the wave vector and ωrf is the microwave angular frequency. For a ferromagnet, the \(\chi _k^R\) is known to be divergent near its TC39. Therefore, an enhancement of spin pumping is expected as the spin sink is close to its magnetic phase transition point38,40,41. In our system, a possibly newly formed magnetic phase would be the interfacial magnetization driven by the proximity effect, namely, TC = 140 and 180 K for our Bi2Se3(25)/YIG(15) and Bi2Se3(16)/YIG(17), respectively. In fact, the TC values of our samples are in good agreement with the reported TC of 130 and 150 K in TI/YIG systems14,22.
Using Eq. (2), we further determine the T dependence of 4πMeff and Heff of YIG(23) and the two bilayers samples, as shown in Fig. 3e, f. The 4πMeff of YIG(23) became larger monotonically as previously discussed, while the 4πMeff of the bilayer samples increased before reaching a maximum when T was around 150 K, and then decreased slightly at low T. We further calculate the interfacial anisotropy field Hint using \(4\pi M_{{\mathrm{eff}}}^{{\mathrm{BS}}/{\mathrm{YIG}}} - 4\pi M_{{\mathrm{eff}}}^{{\mathrm{YIG}}} \approx - H_{{\mathrm{int}}}\). The inset of Fig. 3e shows the T dependence of Hint. The magnitude of Hint increased as the samples cooled down from room temperature at first. Upon crossing the temperature regions where the hump-like features are located, Hint magnitude started to decrease with further decreasing T. Although the samples exhibit interfacial IMA (Hint < 0) within the temperature range of our measurement, further extending the trend of Bi2Se3(16)/YIG(17), specifically, leads to interfacial PMA (Hint >0) below 40 K. The turning of Hint curves around 150 K implied that a competing magnetic anisotropy was emerging, which favored perpendicular direction and effectively diminished the IMA that persisted up to room temperature. Observing that the turning of Hint curves were in the vicinity of the individual hump temperature, we thus attribute the interfacial PMA to MPE in Bi2Se3/YIG. Our scenario is further supported by a theoretical model that considers the direct exchange coupling of TSS and an adjacent magnetic layer31,42. In this model, the calculated total electronic energy in the system with MPE indicates that PMA is in favor.
To independently show the effect of strong interfacial exchange coupling in Bi2Se3/YIG, we have performed electrical transport measurements at low T. As shown in Supplementary Fig. 7, we observed a clear negative magnetoresistance (MR) of Bi2Se3/YIG, which is distinct from weak antilocalization (WAL) effect typical of Bi2Se3 films without magnetic perturbation. Detailed analyses show that the MR data can be well reproduced if we assume that the TRS is broken and electrons are magnetically scattered at the bottom surface of Bi2Se3 (see Supplementary Note 4), which may be an indication of the presence of MPE in our Bi2Se3/YIG sample. However, we did not detect anomalous Hall effect in our samples, which might be obscured by the bulk conduction of Bi2Se3 in the transport measurements.
The Heff of the bilayer samples, again, shows different T evolution than that of the bare YIG in Fig. 3f. Heff built up with decreasing T in bilayers while the Heff of the YIG single layer was T independent and close to zero. Phenomenologically, the Heff resembles the exchange bias field of interlayer exchange coupling in an antiferromagnet/ferromagnet interface. However, we would like to exclude the possibility of exchange bias for the following two reasons. First, as shown in Supplementary Fig. 6, we did not observe shifts of magnetization hysteresis loop which is characteristic of an exchange bias effect43. Secondly, extending the field sweep to reversed applied field, we found that the FMR spectrum was symmetric with respect to the zero applied field, indicating that the direction of Heff followed that of M. The observation is distinct from the magnetization pinning of exchange bias, in which the Heff direction is fixed depending on the interfacial magnetic structure. The fact that Heff existed only in FMR measurement suggests that it comes from spin-pumping-induced spin imbalance at the interface as previously reported44. Through exchange coupling to the magnetic layer, the non-equilibrium spin density 〈S〉neq of the TSS gives rise to field-like torque:
where Δex is the exchange coupling constant45. ST-FMR experiments on NiFe/Bi2Se39 and CoFeB/Bi2Se346 showed large TFL comparable to the damp-like torque owing to spin–momentum locking of TSS. Since spin pumping is the reciprocal process of ST-FMR, one can expect that the TFL appears as an exchange effective field in spin pumping. Moreover, we noticed that the T dependence of Heff in Fig. 3f resembles that of TFL in CoFeB/Bi2Se346, which implies that Heff and TFL share the same origin. Although a large TFL can originate from other systems with strong SOC such as Rashba-split quantum well state45, which is likely to coexist with the TSS in Bi2Se3/YIG47, the TFL from Rashba state is expected to decrease with decreasing Rashba coefficient at low T48. Here, we highlight that Heff monotonically increased at low T. The unique T dependence of Heff suggests that it is likely to originate from TSS.
Zero-field FMR of Bi2Se3/YIG
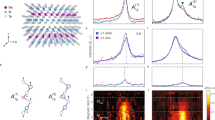
Finally, we demonstrated that the TSS-modulated magnetic anisotropy and Heff in Bi2Se3/YIG are strong enough to induce FMR without an applied field Hext, which we term zero-field FMR. Figure 4a displays T evolution of FMR first derivative spectra of Bi2Se3(25)/YIG(15) at f = 3.5 GHz. The spectral shape started to deform when the Hreswas approaching zero. The sudden twists at Hext ~ + 30 (−30) for positive (negative) field sweep arose from magnetization switching of YIG, and therefore led to hysteric spectra. The two spectra merged at 25 K and then separated again when T was further decreased. Figure 4b shows the microwave absorption intensity I spectra with positive field sweeps. We traced the peak position of I spectrum Hpeak using the red dashed line, and found it coincided with zero Hext at the zero-field FMR temperature T0 ~25 K. Below 25 K, Hpeak moved across the origin and one needed to reverse Hext to counter the internal effective field comprised of the demagnetization field 4πMs, Hint, and Heff (Fig. 4e). It should be pointed out that the presence of Hint alone would be inadequate to realize zero-field FMR. Only when Heff is finite would the system exhibit intercepts as we have seen in Fig. 3b. We further calculate T0 as a function of microwave excitation frequency f (Fig. 4f) using Eq. (2) and the extracted Heff of Fig. 3f. We obtain that, with finite Heff persisting up to room temperature, zero-field FMR can be realized at high T provided f is sufficiently low. However, we emphasize that it is advantageous for YIG to be microwave-excited above 3 GHz. When f < 3 GHz, parasitic effects such as three-magnon splitting49,50 take place and significantly decrease the microwave absorption in YIG. Here, we demonstrate that the strong exchange coupling between Bi2Se3 and YIG gave rise to zero-field FMR in the feasible high frequency operation regime of YIG. Further improvement of interface quality of Bi2Se3/YIG is expected to raise Heff and T0 for room-temperature, field free spintronic application.
Zero-field FMR of the Bi2Se3(25)/YIG(15) sample. a, b FMR first derivative and microwave absorption spectra for various T, respectively. The arrows indicate the Hext sweep direction. The dashed line in b traces the T evolution of the absorption peak Hpeak. c, d, and e Schematics of the Bi2Se3/YIG sample when T = 100, 25, and 5 K, respectively. f Zero-field FMR temperature T0 as a function of f
Discussion
Most experiments probing the spin transfer or spin–charge interconversion at TSS used FMs as the spin source/detector. The pitfall of FMs is that the constituent transition metals are chemically reactive with chalcogenides. Severe reactions can occur when an FM is deposited on a TI, forming new species that complicated the system under study. Even if an ideal TI/FM interface is achieved, theoretical study suggests that the electron doping from the FM can significantly shift the Fermi level of TIs and destroy the spin texture27. Besides, for SOT generation, current-shunting by FM reduces the current flowing in the TI and diminishes the SOT strength. Therefore, ferromagnetic insulators such as YIG is a far better platform to study the coupling mechanism between TSS and magnetic layers.
We attribute the high-temperature interfacial IMA to the enhanced exchange coupling of Fe3+ ions in YIG mediated by TSS based on the dBS dependence of Ki in Fig. 2c. We emphasize that, although the model in ref. 42 predicts a PMA originated from direct exchange coupling between TSS and a magnetic layer, in reality, other contributions of magnetic anisotropy dependent on the detailed interfacial atomic structure can arise. As illustrated in ref. 31, in addition to the PMA from MPE, the stress anisotropy energy of EuS can also be magnified by the strong SOC of Bi2Se3, which would not necessarily be PMA for a material system other than EuS/Bi2Se3. Other factors such as the Fermi energy of Bi2Se3 can have pronounced effects on the exchange coupling constant and total anisotropy energy31. Given the multiple sources of magnetic anisotropy that are possibly influenced by TSS, an in-depth theoretical study will be needed to precisely describe the high-temperature interfacial IMA and the emerging low-temperature PMA of Bi2Se3/YIG.
The TSS-modulated magnetization dynamics presented in this work have important implications. Firstly, the electronic structure of TI/ferromagnetic insulator interface has a pronounced influence on the magnetization dynamics. It should be noted that the strong coupling between the TSS and YIG can potentially modify the TSS of pure Bi2Se3. Since the spin texture of TSS is critical for spin transport, an insertion layer may be needed to decouple YIG and Bi2Se3 for spintronics devices. The interface structure, in turn, depends strongly on the sample fabrication process. For example, Wang et al.8 reported a markedly different dBS dependence of g↑↓ from the one shown in Fig. 2d. Specifically, our samples show larger \(\Delta \tilde \alpha\) when dBS was approaching the 2D limit. Note that the linewidth broadening observed in this work is overall larger than that reported in ref. 8 mainly because we have chosen thinner YIG films. The discrepancy in the dBS dependence of g↑↓ may be reconciled by the different sample characteristics by comparing the TEM images and the surface morphology of Bi2Se3, etc.
Secondly, although the interface spin structure is of great interest to investigate, it has been difficult to measure with spin-polarized photoemission techniques because of the limited probing depth. Spin pumping provides another route to resolve the problem, since it has proven to be a powerful tool to probe magnetic phase transition of ultrathin films40,41. Here, we extended the concept and used spin pumping to study the MPE in Bi2Se3/YIG. The indicators of MPE are shown in Fig. 3c, d. Further testing of the validity of this method will depend on the improvements in the sample quality, such as a sharper interface and lowering the carrier density of Bi2Se3.
Lastly, the observations of large Ki, \(\Delta \tilde \alpha\) at room temperature, and Heff at low temperature in Bi2Se3/YIG echo the theoretical predictions of the magnetization dynamics of a perpendicularly magnetized layer interacting with TSS51,52,53. According to these models, the gap opening of TSS due to broken TRS leads to topological (inverse) spin galvanic effect51,52, anisotropic shifts of FMR frequency52, and anisotropic damping53. Despite the fact that an interfacial PMA showed up at low temperature in Bi2Se3/YIG, the bilayer sample still exhibited a gross in-plane anisotropy due to the shape anisotropy of YIG. However, the notable modulation of the YIG properties presented in this work is a promising start to examine these models. We expect ferromagnetic insulators with PMA, such as strained TmIG54, will offer new opportunities to realize the phenomena.
In summary, we have investigated the magnetization dynamics of YIG in the presence of interfacial exchange coupling and TSS of Bi2Se3. The significantly modulated magnetization dynamics at room temperature are shown to be TSS-originated through the Bi2Se3 thickness dependence study. The temperature-dependent study reveals a possible signature of MPE and an emerging PMA that compensates the high-temperature IMA, with a spin-pumping-induced effective field increasing toward low temperature. The underlying mechanism of these phenomena calls for further theoretical modeling and understanding. To our knowledge, this is the first work that links the magnetization dynamics of the magnetic layer to TSS, showing that FMR and spin pumping can be effective techniques to probe the interface magnetic properties. Moreover, the TSS-modulated dynamics are a cornerstone for future investigation on novel physics such as topological inverse spin galvanic effect, and further raise several interesting topics. For example, how the Heff, a quantity that comes from the non-equilibrium process of spin pumping, depends on the spin texture of TSS and the interfacial magnetic anisotropy will be an important question to answer. Temperature-dependent FMR with out-of-plane setup should provide us with valuable information. Therefore, understanding the interplay between these phenomena and further manipulating them will be a step forward toward developing TI-based spintronics.
Methods
Sample preparation and structural properties
The YIG thin films were deposited on (111)-oriented gadolinium gallium garnet (GGG) substrates by off-axis sputtering at room temperature. The GGG(111) substrates were first ultrasonically cleaned in order of acetone, ethanol, and DI-water before being mounted in a sputtering chamber with the base pressure of 2 × 10−7 Torr. For YIG deposition, a 2-inch YIG target was sputtered with the following conditions: an applied rf power of 75 W, an Ar pressure of 50 mtorr, and a growth rate of 0.6 nm/min. The samples were then annealed at 800 °C with an O2 pressure of 11.5 mtorr for 3 h. Supplementary Fig. 1(a) displays the atomic force microscopy (AFM) image of the YIG surface, showing a flat surface with a roughness of 0.19 nm. Supplementary Fig. 1(b) shows the high-angle annular dark-field (HAADF) image of YIG/GGG. The YIG thin film was epitaxially grown on the GGG substrate with excellent crystallinity. No crystal defects were observed at the YIG bulk and YIG/GGG interface.
The YIG/GGG samples were annealed at 450 °C in the MBE growth chamber for 30 min prior to Bi2Se3 growth at 280 °C. The base pressure of the system was kept about 2 × 10−10 Torr. Elemental Bi (7N) and Se (7N) were evaporated from regular effusion cells55. As shown in Supplementary Fig. 3(a), streaky reflection high-energy electron diffraction (RHEED) patterns of Bi2Se3 were observed. Supplementary Fig. 3(b) displays the surface morphology of 7 quintuple layer (QL) Bi2Se3 taken by AFM. The image shows layer-by-layer growth of Bi2Se3 with the step heights ~1 nm, which corresponds to the thickness of 1 QL. The surface roughness of our 7 QL Bi2Se3 is ~0.28 nm within a layer. The layer structure of Bi2Se3 was also revealed by the HAADF image shown in Supplementary Fig. 3(c). Despite the high-quality growth of Bi2Se3, an amorphous interfacial layer of ~1 nm formed. The excellent crystallinity of our samples was verified by clear Pendellösung fringes of the synchrotron radiation x-ray diffraction (SR-XRD) data shown in Supplementary Fig. 3(d). The fringes of YIG(444) peak do not show clear changes before and after the growth of Bi2Se3, indicating that the lattice parameter in the normal direction of YIG remains unchanged. To check the lattice parameter of in-plane direction, we also performed in-plane radial scans of YIG/GGG(22–4) peaks. Supplementary Fig. 3(e) shows that the peaks position measured before and after growing Bi2Se3 is perfectly matched, indicating the absence of Bi2Se3-induced strains in YIG that might contribute additional magnetic anisotropy56. Supplementary Fig. 3(f) displays the x-ray reflectivity (XRR) data of our Bi2Se3(6)/YIG(50) sample. From the fit to the data, we extract the Bi2Se3 surface roughness and Bi2Se3/YIG interface roughness to be 0.16 nm and 0.22 nm, respectively. Note that the interface roughness of Bi2Se3/YIG is close to that of YIG surface (0.19 nm), which means the interdiffusion at the interface is at minimal, if any.
FMR measurement setup
To investigate the magnetic properties of Bi2Se3/YIG, room-temperature angle- and frequency-dependent FMR measurements were performed independently using a cavity and co-planar waveguide, respectively (Fig. 1a, b). For the temperature-dependent FMR, the co-planar waveguide was mounted in a cryogenic probe station (Lake Shore, CPX-HF), which enables samples to be cooled as low as 5 K. The external field is modulated for lock-in detection in all of the measurements. The modulation amplitude was kept below 1/4 of the FMR linewidth to avoid serious spectral distortions. The microwave source power was no larger than 5 dBm.
Data availability
The experimental data of this work are available from the corresponding authors upon reasonable request.
References
Sinova, J. et al. Spin Hall effects. Rev. Mod. Phys. 87, 1213–1259 (2015).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3066 (2010).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Xu, S. et al. Topological phase transition and texture inversion in a tunable topological insulator. Science 332, 560–564 (2011).
Shiomi, Y. et al. Spin-electricity conversion induced by spin injection into topological insulators. Phys. Rev. Lett. 113, 196601 (2014).
Rojas-Sánchez, J. C. et al. Spin to charge conversion at room temperature by spin pumping into a new type of topological insulator: α-Sn films. Phys. Rev. Lett. 116, 096602 (2016).
Wang, H. et al. Surface-state-dominated spin-charge current conversion in topological-insulator-ferromagnetic-insulator heterostructures. Phys. Rev. Lett. 117, 076601 (2016).
Mellnik, A. R. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Jamali, M. et al. Giant spin pumping and inverse spin hall effect in the presence of surface and bulk spin-orbit coupling of topological insulator Bi2Se3. Nano Lett. 15, 7126 (2015).
Jiang, Z. et al. Enhanced spin Seebeck effect signal due to spin-momentum locked topological surface states. Nat. Commun. 7, 11458 (2016).
Han, J. et al. Room-temperature spin-orbit torque switching induced by a topological insulator. Phys. Rev. Lett. 119, 077702 (2017).
Wei, P. et al. Exchange-coupling-induced symmetry breaking in topological insulators. Phys. Rev. Lett. 110, 186807 (2013).
Lang, M. et al. Proximity induced high-temperature magnetic order in topological insulator—ferrimagnetic insulator heterostructure. Nano Lett. 14, 3459–3465 (2014).
Katmis, F. et al. A high-temperature ferromagnetic topological insulating phase by proximity coupling. Nature 533, 513–516 (2016).
Chen, Y. L. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010).
Qi, X. L., Hughes, T. L. & Zhang, S. C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Chang, C. Z. et al. Experimental observation of the quantum anomalous hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Yu, R. et al. Quantized anomalous hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Li, M. et al. Proximity-driven enhanced magnetic order at ferromagnetic-insulator-magnetic-topological-insulator interface. Phys. Rev. Lett. 115, 087201 (2015).
Lee, C., Katmis, F., Jarillo-Herrero, P., Moodera, J. S. & Gedik, N. Direct measurement of proximity-induced magnetism at the interface between a topological insulator and a ferromagnet. Nat. Commun. 7, 12014 (2016).
Jiang, Z. et al. Independent tuning of electronic properties and induced ferromagnetism in topological insulators with heterostructure approach. Nano Lett. 15, 5835–5840 (2015).
Sun, Y. et al. Damping in yttrium iron garnet nanoscale films capped by platinum. Phys. Rev. Lett. 111, 106601 (2013).
Wang, H. L. et al. Scaling of spin hall angle in 3d, 4d, and 5d metals from Y3Fe5O12/metal spin pumping. Phys. Rev. Lett. 112, 197201 (2014).
Tserkovnyak, Y., Brataas, A. & Bauer, G. E. W. Enhanced Gilbert damping in thin ferromagnetic films. Phys. Rev. Lett. 88, 117601 (2002).
Zhang, Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 6, 584–588 (2010).
Zhang, J., Velev, J. P., Dang, X. & Tsymbal, E. Y. Band structure and spin texture of Bi2Se3 3d ferromagnetic metal interface. Phys. Rev. B 94, 014435 (2016).
Men’shov, V. N., Tugushev, V. V., Eremeev, S. V., Echenique, P. M. & Chulkov, E. V. Magnetic proximity effect in the three-dimensional topological insulator/ferromagnetic insulator heterostructure. Phys. Rev. B 88, 144430 (2013).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).
Kajiwara, Y. et al. Transmission of electrical signals by spin-wave interconversion in a magnetic insulator. Nature 464, 262–266 (2010).
Kim, J., Kim, K. W., Wang, H., Sinova, J. & Wu, R. Understanding the giant enhancement of exchange interaction in Bi2Se3-EuS heterostructures. Phys. Rev. Lett. 119, 027201 (2017).
Neupane, M. et al. Observation of quantum-tunnelling-modulated spin texture in ultrathin topological insulator Bi2Se3 films. Nat. Commun. 5, 3841 (2014).
Landolt, G. et al. Spin texture of Bi2Se3 thin films in the quantum tunneling limit. Phys. Rev. Lett. 112, 057601 (2014).
Tserkovnyak, Y., Brataas, A., Bauer, G. E. W. & Halperin, B. I. Nonlocal magnetization dynamics in ferromagnetic heterostructures. Rev. Mod. Phys. 77, 1375–1421 (2005).
Yamamoto, K. T., Shiomi, Y., Segawa, K., Ando, Y. & Saitoh, E. Universal scaling for the spin-electricity conversion on surface states of topological insulators. Phys. Rev. B 94, 204404 (2016).
Seiden, P. E. Ferrimagnetic resonance relaxation in rare-earth iron garnets. Phys. Rev. 133, A728–A736 (1964).
Jermain, C. L. et al. Increased low-temperature damping in yttrium iron garnet thin films. Phys. Rev. B 95, 174411 (2017).
Ohnuma, Y., Adachi, H., Saitoh, E. & Maekawa, S. Enhanced dc spin pumping into a fluctuating ferromagnet near TC. Phys. Rev. B 89, 174417 (2014).
Hohenberg, P. C. & Halperin, B. I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435–479 (1977).
Frangou, L. et al. Enhanced spin pumping efficiency in antiferromagnetic IrMn thin films around the magnetic phase transition. Phys. Rev. Lett. 116, 077203 (2016).
Qiu, Z. et al. Spin-current probe for phase transition in an insulator. Nat. Commun. 7, 12670 (2016).
Semenov, Y. G., Duan, X. & Kim, K. W. Electrically controlled magnetization in ferromagnet-topological insulator heterostructures. Phys. Rev. B 86, 161406(R) (2012).
Manna, P. K. & Yusuf, S. M. Two interface effects: exchange bias and magnetic proximity. Phys. Rep. 535, 61–99 (2014).
Abdulahad, F. B. et al. Spin chemical potential bias induced surface current evidenced by spin pumping into the topological insulator Bi2Te3. Phys. Rev. B 92, 241304(R) (2015).
Fischer, M. H., Vaezi, A., Manchon, A. & Kim, E. A. Spin-torque generation in topological insulator based heterostructures. Phys. Rev. B 93, 125303 (2016).
Wang, Y. et al. Topological surface states originated spin-orbit torques in Bi2Se3. Phys. Rev. Lett. 114, 257202 (2015).
Bahramy, M. S. et al. Emergent quantum confinement at topological insulator surfaces. Nat. Commun. 3, 1159 (2012).
Eldridge, P. S. et al. All-optical measurement of Rashba coefficient in quantum wells. Phys. Rev. B 77, 125344 (2008).
Suhl, S. The theory of ferromagnetic resonance at high signal power. J. Phys. Chem. Solids 1, 209–227 (1957).
Iguchi, R. et al. Spin pumping without three-magnon splitting in polycrystalline Bi1Y2Fe5O12/Pt bilayer structure. Jpn. J. Appl. Phys. 51, 103004 (2012).
Garate, I. & Franz, M. Inverse spin-galvanic effect in the interface between a topological insulator and a ferromagnet. Phys. Rev. Lett. 104, 146802 (2010).
Yokoyama, T., Zang, J. & Nagaosa, N. Theoretical study of the dynamics of magnetization on the topological surface. Phys. Rev. B 81, 241410 (2010).
Ndiaye, P. B. et al. Dirac spin-orbit torques and charge pumping at the surface of topological insulators. Phys. Rev. B 96, 014408 (2017).
Tang, C. et al. Anomalous Hall hysteresis in Tm3Fe5O12/Pt with strain-induced perpendicular magnetic anisotropy. Phys. Rev. B 94, 140403(R) (2016).
Chen, K. H. M. et al. Van der Waals epitaxy of topological insulator Bi2Se3 on single layer transition metal dichalcogenide MoS2. Appl. Phys. Lett. 111, 083106 (2017).
Wang, H. L., Du, C. H., Hammel, P. C. & Yang, F. Strain-tunable magnetocrystalline anisotropy in epitaxial Y3Fe5O12 thin films. Phys. Rev. B 89, 134404 (2014).
Acknowledgements
We would like to thank Prof. Mingzhong Wu, Dr. Hsin Lin, and Dr. Tao Liu for their helpful discussion. We would also like to thank Dr. Jauyn Grace Lin for her technical support and Dr. Chien-Ting Wu for the TEM analyses. The work is supported by MoST 105-2112-M-007-014-MY3, 106-2112-M-002-010, 106-2622-8-002-001, and 105-2112-M-001-031-MY3 of the Ministry of Science and Technology in Taiwan.
Author information
Authors and Affiliations
Contributions
Y.T.F. designed the experiment, collected the FMR data, and analyzed the data. K.H.M.C., C.C.T., C.C.C., and C.N.W. fabricated the samples. C.K.C. performed the XRD measurements and S.R.Y. performed the transport measurements. S.F.L. provided scientific supports. J.K. and M.H. supervised the project. Y.T.F. and J.K. wrote the manuscript with the comments of all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fanchiang, Y.T., Chen, K.H.M., Tseng, C.C. et al. Strongly exchange-coupled and surface-state-modulated magnetization dynamics in Bi2Se3/yttrium iron garnet heterostructures. Nat Commun 9, 223 (2018). https://doi.org/10.1038/s41467-017-02743-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-02743-2
This article is cited by
-
Energy gap of topological surface states in proximity to a magnetic insulator
Communications Physics (2023)
-
Magnetic equivalent of electric superradiance in yttrium-iron-garnet films
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.