Abstract
Magnetic two-dimensional materials have attracted considerable attention for their significant potential application in spintronics. In this study, we present a high-quality Fe-doped SnS2 monolayer exfoliated using a micromechanical cleavage method. Fe atoms were doped at the Sn atom sites, and the Fe contents are ∼2.1%, 1.5%, and 1.1%. The field-effect transistors based on the Fe0.021Sn0.979S2 monolayer show n-type behavior and exhibit high optoelectronic performance. Magnetic measurements show that pure SnS2 is diamagnetic, whereas Fe0.021Sn0.979S2 exhibits ferromagnetic behavior with a perpendicular anisotropy at 2 K and a Curie temperature of ~31 K. Density functional theory calculations show that long-range ferromagnetic ordering in the Fe-doped SnS2 monolayer is energetically stable, and the estimated Curie temperature agrees well with the results of our experiment. The results suggest that Fe-doped SnS2 has significant potential in future nanoelectronic, magnetic, and optoelectronic applications.
Similar content being viewed by others
Introduction
Two-dimensional (2D) layered transition metal dichalcogenides (TMDs), e.g., MoS2, WS2, and SnS2, are promising functional materials due to their peculiar structural and electronic properties1,2,3,4,5,6,7,8,9,10. Significant efforts, such as doping, strain, and chemical functionalization, have been used to obtain distinctive optical and electrical properties by tuning the band alignments of 2D materials11,12,13,14. Doping, which is the intentional introduction of impurities into a material, plays a significant role in functionalizing 2D materials by changing the intrinsic properties of pristine atomic layers15,16,17. For example, wolfram and selenium chemical doping of MoS2 is an effective way to engineer the optical bandgap18,19,20,21,22,23, and Nb-, Co-, and Mn-doped MoS2 few layers exhibit diverse transport properties11, 12, 24. Magnetic atom (e.g., Mn, Fe, Co, and Ni)-doped 2D TMDs are promising as 2D-diluted magnetic semiconductors (DMS)25,26,27,28,29, and many have been predicted to exhibit ferromagnetic behavior at room temperature25, 27. DMS, such as Mn-doped InAs and GaAs, have distinctive physical properties and provide the possibility of electronic control of magnetism30,31,32,33. To date, Co- and Mn-doped MoS2 nanosheets have been synthesized via the chemical vapor deposition method, and understanding their magnetic properties requires more research11, 24. Recently, Zhang et al. and Xu et al. reported the magnetic properties of Cr2Ge2Te6 and CrI3 monolayers via high-resolution and high-sensitivity magneto-optic microscopy34, 35. However, further investigation into the magnetism and functional properties of high-quality magnetic atom-doped 2D TMDs is warranted.
In this work, we synthesized different Fe-doped SnS2 (Fe0.021Sn0.979S2, Fe0.015Sn0.985S2, and Fe0.011Sn0.989S2) bulk crystals via a direct vapor-phase method, and we obtained Fe0.021Sn0.979S2 monolayer flakes via mechanical exfoliation. Monolayer Fe0.021Sn0.979S2 exhibits high-quality optoelectronic properties. Magnetic measurements show that Fe0.021Sn0.979S2 exhibits ferromagnetic behavior with a perpendicular anisotropy at 2 K and a Curie temperature of ∼31 K. The experimental results agree well with the theoretical calculations.
Results
Characterization of Fe-doped SnS2
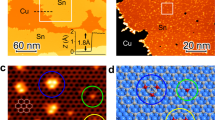
Figure 1a shows an optical image of a mechanically exfoliated Fe0.021Sn0.979S2 flake on a Si/SiO2 substrate. Atomic force microscopy (AFM) and magnetic force microscopy (MFM) were used to characterize the height and magnetism of the samples, respectively. MFM is a valuable tool that can potentially be used to detect magnetic interactions between a magnetized AFM tip and samples36. Recently, MFM has been employed to characterize the magnetic response of single- or few-layer 2D nanosheets, such as graphene and MoS2 37, 38. However, it has been reported that MFM signals have nonmagnetic contributions due to capacitive and electrostatic interactions between the nanosheets and the conductive cantilever tip38, 39. In this study, AFM and MFM images of Fe0.021Sn0.979S2 and pure SnS2 were obtained under the same test condition. The AFM images show that the obtained Fe0.021Sn0.979S2 and pure SnS2 are monolayers (Fig. 1b, Supplementary Fig. 1a). The MFM images show that the Fe0.021Sn0.979S2 monolayer has a larger negative phase shift (523 mo) than that of the pure SnS2 monolayer (51 mo) (Supplementary Fig. 1b, c) by approximately ten times, which should largely contribute to the difference in the magnetic and electrical properties between the Fe0.021Sn0.979S2 and SnS2 monolayers. Raman spectroscopy has been widely used in 2D TMD alloys, and it changes with the composition of the alloy18, 40. The Raman peaks of the Fe0.021Sn0.979S2 and pure SnS2 monolayers are located at 314 cm−1, corresponding to the A 1g mode of SnS2 3, 10. The A 1g mode of the Fe0.021Sn0.979S2 monolayer is broader than that of the pure SnS2 monolayer (Fig. 1c). This broadening behavior, which is due to the doped atoms, has also been observed in other 2D alloys20.
Characterization of the Fe0.021Sn0.979S2 flakes. a Optical image of the Fe0.021Sn0.979S2 flake. b AFM and c Raman spectra of the Fe0.021Sn0.979S2 and SnS2 monolayers. The height of the flake in b was obtained along the white dotted line. The inset in c shows the expanded view of the Raman spectra around the A 1g mode of the Fe0.021Sn0.979S2 and SnS2 monolayers. d SnS2 atomic structure. e Low-resolution HAADF-STEM image of the Fe0.021Sn0.979S2 flake. f EDS of the Fe0.021Sn0.979S2 flake. g High-resolution STEM image of the Fe0.021Sn0.979S2 flake; the red circles are Fe atoms. h Z-contrast mapping in the areas marked with yellow rectangles in g
The crystallinity of the Fe0.021Sn0.979S2 was further characterized using high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) and transmission electron microscopy (TEM). Figure 1e shows a low-resolution HAADF-STEM image of a few layers of Fe0.021Sn0.979S2. Energy-dispersive X-ray spectroscopy (EDS) of the nanosheet (Fig. 1f) shows that the nanosheet contains S, Sn, and Fe elements. Using a high-resolution STEM image and the Z-contrast intensity distribution, the Sn (Z = 50), Fe (Z = 26), and S (Z = 16) atoms were directly distinguished, as shown in Fig. 1g, h. Fe atoms were doped at the Sn atom sites. The Sn–S distance is 0.22 nm (Fig. 1h), which agrees well with the theoretical value of 0.21 nm (Fig. 1d). The low-resolution TEM image (Supplementary Fig. 2a) shows a part of the few-layer Fe0.021Sn0.979S2 flake on the holey carbon TEM grid. The selected area electron diffraction pattern and the corresponding high-resolution TEM image reveal that this flake has a high-quality hexagonal symmetry structure, and the lattice spacing of (100) plane is 0.311 nm (Supplementary Fig. 2b, c). The elemental mapping images from EDS show that Sn, S, and Fe elements are uniformly distributed throughout the entire flake (Supplementary Fig. 2d–f).
X-ray photoelectron spectroscopy (XPS) is a powerful tool for understanding the chemical states and composition of elements that exist within a material. The binding energy values obtained in the XPS analysis of Fe0.021Sn0.979S2 were corrected by referencing the C 1s peak to 284.7 eV (Supplementary Fig. 3a). The binding energies of the Sn 3d 5/2 and S 2p 3/2 electron peaks are 486.7 eV and 161.6 eV (Supplementary Fig. 3b, c), respectively, which is consistent with the previously reported values for SnS2 41. The binding energy of the Fe 2p 3/2 electron peak is 712.2 eV (Supplementary Fig. 3d), which is close to the Sn 3p electron peak (716 eV). The binding energy of the Fe 2p 3/2 electron in this instance is obviously larger than the reported values of other iron compounds (the binding energies of Fe 2p 3/2 in Fe2O3, FeCl3, and FeCl2 are 710 eV, 711.5 eV, and 710.6 eV, respectively)42. In general, the binding energy of the same electron from one atom grows with increasing oxidation state, which is related to the bonding hybridization with its nearest-neighbor atoms. In this experiment, Fe atoms were doped by substituting Sn sites (Fig. 1g), and each Fe atom is surrounded by six S atoms to form an octahedral coordination. The oxidation state of the Fe atom should be +4, leading to a high binding energy for Fe 2p 3/2 in Fe0.021Sn0.979S2. Furthermore, quantitative analysis of the XPS spectra reveals that the content of Fe is ∼2.1% in Fe0.021Sn0.979S2.
Electronic and optoelectronic properties of Fe-doped SnS2
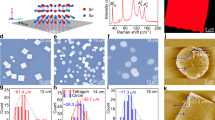
To study the electronic transport property and photoresponse of the Fe0.021Sn0.979S2 monolayer on the Al2O3/Si substrate, we fabricated field-effect transistors (FETs) from exfoliated Fe0.021Sn0.979S2 (Fig. 2a). The device characteristics of the FETs were measured at room temperature. Figure 2a, b shows the typical transfer and output characteristics of Fe0.021Sn0.979S2, respectively, achieving an excellent n-type behavior. As the gate voltage (V g) varied from −5 to 5 V, the source–drain current (I sd) changed from 1.1 × 10−12 A to 8 × 10−6 A, corresponding to a high on/off current ratio of 7.3 × 106. The field-effect mobility can be obtained using the formula
where L and W are the length and width of the device, and C(Al2O3) is the Al2O3 gate capacitance, which can be given by equation C(Al2O3)=ε 0 ε r/d. Thus, ε 0 (8.85 × 10−12 Fm−1) is the vacuum dielectric constant, and ε r (6.4) and d (30 nm) are the dielectric constant and thickness of Al2O3, respectively. Based on the transport curve (Fig. 2a), the calculated electron mobility is 8.15 cm2 V−1 s−1. Fe0.021Sn0.979S2 and Fe0.021Sn0.979S2 were also synthesized by modulating the growth conditions (Supplementary Fig. 4). The electronic transport properties of Fe0.021Sn0.979S2 (Supplementary Fig. 5) were investigated, and the calculated mobilities are larger than the values for pure SnS2 (Supplementary Table 1). The mobility increases with the Fe content in the samples. The output curves show that the I sd is linear at low V sd, and the sample had a good contact with the electrode (Fig. 2b). The mobility is related to the mean-free time (τ) and effective mass (m *) of the electron as follows:
Electrical characteristics and photoresponse of the Fe0.021Sn0.979S2 monolayer. a Transfer and b output characteristics of Fe0.021Sn0.979S2. The inset shows an optical image of one typical device and the AFM image of the corresponding sample used for fabricating the device. c Time-dependent I sd of the transistor based on Fe0.021Sn0.979S2 during the light (638 nm, 2.63 μW) switching on/off under a positive source–drain voltage, V sd, from 1 to 3 V. d Photoresponsivity (R) as a function of light power (P) with a V sd of 3 V
In 2D-doped TMDs, the mean-free time of the electron is decreased for enhanced carrier scattering, and the mobility decreases. Thus, searching for a decreased electron effective mass for 2D-doped TMDs is a feasible route to improve the mobility. The density functional theory (DFT)-calculated m * values at the conduction band bottom of monolayer SnS2 and Fe–SnS2 are listed in Supplementary Table 2. The m *of Fe–SnS2 is smaller than that of pure SnS2, which partly contributes to the higher field-effect mobility (Supplementary Fig. 6). The stability of 2D atomic layer materials is critical for their future application. The electrical property of a typical Fe0.021Sn0.979S2 monolayer FET on a SiO2/Si substrate stored in air was measured for 1 month. After 1 month, the mobility changed from 6.1 cm2 V−1 s−1 to 4.7 cm2 V−1 s−1, and the on/off ratio changed from 1.2 × 106 to 7 × 105 (Supplementary Fig. 7). The results show that Fe0.021Sn0.979S2 is very stable and has a significant potential application in optoelectronics.
Few-layer SnS2 has been demonstrated as ultrasensitive photodetectors based on previous reports3. In this study, the photoresponsive properties of the Fe0.021Sn0.979S2 monolayer were examined using a 638-nm laser at room temperature. Figure 2c shows a photo on/off ratio of ∼10, and the I sd can quickly and repetitively change between on and off states. The photoresponsivity, R, was obtained by using the formula R = I ph/P. I ph is the photocurrent defined as I ph = I light–I dark, and P is the light power. The photoresponsivity (R) shows a strong dependence on light power (P), and the experimental data are fitted by the equation R = aP α−1. In our experiment, the fitted parameters were a = 0.098 and α = 0.755 (Fig. 2d). The maximum R is 206 mA W−1 (P = 57 nW), which is larger than the reported average values of few-layer SnS2 (Supplementary Table 1). The photocurrent response time of the Fe0.021Sn0.979S2 is ∼9 ms, and the response time of pure SnS2 is ∼6 ms (Supplementary Fig. 8). Under illumination, the impurity levels will lightly promote electron–hole recombination and increase the response time. A detailed discussion of the optoelectronic properties of Fe–SnS2 is provided in Supporting Information (Supplementary Fig. 9, Supplementary Note 1).
Magnetic properties of the Fe-doped SnS2
The magnetic behaviors of the SnS2 and Fe0.021Sn0.979S2 single-crystal sheets were investigated using a vibrating sample magnetometer (VSM) from a physical properties measurement system (PPMS). The measurements were performed in two types of applied magnetic fields (H): perpendicular to the sheet, e.g., parallel to the [001] direction (H ⊥), and parallel to the sheet, e.g., perpendicular to the [001] direction (H ‖). Magnetic hysteresis loops at 2 K for SnS2 and Fe0.021Sn0.979S2 are shown in Fig. 3a, b. The pure SnS2 is diamagnetic at 2 K both in the H ⊥ and H ‖ directions because of the saturated electronic structure. The M–H curve of the Fe0.021Sn0.979S2 sheet shows remarkable anisotropy in the H ‖ and H ⊥ directions at 2 K, respectively. The saturation magnetization (M S), coercivity (H C), and remnant magnetization (M R) values in the H ⊥ and H ‖ direction for Fe0.021Sn0.979S2 are listed in Supplementary Table 3. The coercivity and remnant magnetization of H ⊥ are approximately three and five times those of H ‖, confirming that the easy axis is the [001]. The magnetism versus temperature curves show that the Curie temperature (T C) is ∼31 K (Fig. 3d). Magnetic hysteresis loops of the Fe0.021Sn0.979S2 bulk crystal were acquired under different temperatures (Supplementary Fig. 10), and the result shows that the Curie temperature is between 35 K and 30 K, which is consistent with the magnetism versus temperature curves (Fig. 3d). Fe cluster can be formed in the crystal when the content of Fe source increases during growth (Supplementary Fig. 11 and Supplementary Note 2). The resistivity of the Fe0.021Sn0.979S2 thin film as a function of different thicknesses was measured from 200 to 8 K (Supplementary Fig. 12). The temperature derivative of the measured resistivity has a transition at ∼32 K for the monolayer and 41 K for 13- and 35-nm-thick samples, which are similar to the results observed at the Curie temperature of 31 K. This resistive transition could come from the magnetic transition. Fe0.021Sn0.979S2 and Fe0.015Sn0.985S2 are ferromagnetic at 2 K, whereas Fe0.011Sn0.989S2 is paramagnetic at 2 K (Supplementary Fig. 13). The results demonstrate that the magnetic property of Fe–SnS2 varies with the Fe concentration. We discuss the detailed origin of the magnetism and the magnetic anisotropy of the Fe0.021Sn0.979S2 sheet below.
Magnetization data for SnS2 and Fe0.021Sn0.979S2. a, b Magnetic hysteresis loops for SnS2 and Fe0.021Sn0.979S2 at 2 K using VSM, respectively. c Expanded view of the loop of Fe0.021Sn0.979S2 in b. d Magnetization as a function of temperature for Fe0.021Sn0.979S2 from 2 K to 100 K. The applied magnetic field was 1000 Oe
Discussion
Wu et al. investigated the magnetism of bulk Fe-doped SnS2 in detail and observed that the ferrimagnetism originates from the exchange interaction between the doped Fe atoms at the intralayer sites27. In this study, first-principles calculations were used to further investigate the electronic and magnetic properties of the Fe–SnS2 monolayer (Fig. 4a). According to the generalized gradient approximation (GGA) calculations, the bandgaps of SnS2 and FeS2 are 1.61 eV and 0.56 eV, respectively. The bandgaps of SnS2 and FeS2 are 2.07 eV and 0.97 eV, which are larger than those determined by the calculations. We tested a group of simulations with different U values and found that the optimized bandgap of SnS2 is 2.06 eV (U = 8.0) and the bandgap of FeS2 is 0.95 eV (U = 1.8), which are consistent with the experimental values43, 44. The calculated total density of states demonstrate that the Fe–SnS2 monolayer exhibits half-metallic behavior with 100% spin-polarized carriers at the Fermi level for the down-spin channel, whereas for the up-spin channel, the monolayer exhibits a semiconducting behavior (Fig. 4b). The projected band structures of the Fe–SnS2 monolayer also confirm this behavior and clearly show that the impurity levels at the Fermi level come from the Fe atom and not from the Sn atoms (Fig. 4c, f). The total magnetic moment of the Fe atom is 1.9 μB, and the integration over all the occupied S 3p states of the S atoms bonded to the Fe dopant atom yields a magnetic moment of −0.023 μB. There are six S atoms around the Fe atom, leading to a total moment of −0.14 μB. The distribution of spin is shown in the spin density isosurface plot in Fig. 4d. The hybridization between the localized Fe 3d and the delocalized S 3p states leads to an antiferromagnetic (AFM) coupling between the Fe spin and S spins. When the S spins encounter one Fe, the antiferromagnetic coupling between S and Fe leads to an effective ferromagnetic (FM) structure for all of the Fe spins. Allowing for the delocalized feature of the S 3p states, the FM structure between the Fe spins is expected to emerge in a long range. The distribution of the outer electron of the Fe atom is 3d 64s 2 based on crystal field theory, and we can obtain the distribution of 3d electrons with the spin of Fe atoms in Fe–SnS2 (Fig. 4e). There are three 3d electrons with spin-up for the Fe atom in Fe–SnS2, and one 3d electron with spin-down. The magnetic moment is 2 μB, which is consistent with the calculated value of 1.9 μB.
Theoretical calculations of the Fe–SnS2 monolayer. a Atomic structure of the Fe–SnS2 monolayer. Red, yellow, and blue balls represent Sn, S, and Fe atoms, respectively. b Total density of states of the Fe–SnS2 monolayer. c, f Projected band structures of the Fe–SnS2 monolayer for up-spin and down-spin channels, respectively. Red and blue circles denote the contribution of Sn and Fe atoms in the total band structure, respectively. The Fermi level was set to zero. d The distribution of the spin density in real space for the Fe–SnS2 monolayer is shown. The isosurface value was taken at 0.001 eÅ−3. e Schematic of the Fe 3d electron arrangement with spin in Fe–SnS2
The magnetic anisotropy of Fe–SnS2 is due to the competition between the perpendicular and parallel spin–orbit coupling effect. The magnetic anisotropic energy (MAE) has been used to evaluate the extent of the magnetic anisotropy45. In this study, we assumed that the x and y direction are isotropic, and we took the z- and x-axes directions into account to analyze the anisotropy of the perpendicular and parallel direction, i.e., MAE = E(x)–E(z) with E(x) and E(z) denoting the total energy of the self-consistent calculations in the x and z magnetization directions, respectively46, 47. Our calculated value of MAE is 2.3 meV, confirming that the z-axis is the easy axis48. The theoretical result is consistent with the experimental result.
To further investigate the long-range FM ordering in Fe–SnS2, a 108-atom supercell was constructed with two Fe atoms (Supplementary Fig. 14a). The magnetic energy, ΔE (ΔE = E FM–E AFM), is −6.7 meV, showing an energetically more favorable FM coupling than an AFM coupling between the Fe spins. Supplementary Fig. 14b shows the long-range FM-ordering behavior of the Fe–SnS2. This behavior has also been extensively studied via theory25,26,27. The Curie temperature, T C, of the Fe–SnS2 monolayer can be estimated by the relation49:
where T b is the bulk Curie temperature, and K a is the anisotropy constant. The bulk magnetic energy, ΔE, was calculated to be −14.3 meV (Supplementary Fig. 15), and the T b was estimated to be 56 K based on the mean-field theory and Heisenberg model50. K a=K mca + K sa, where K mca is the magnetocrystalline anisotropy constant (2.3 meV), and K sa is the shape anisotropy constant (∼−0.17 meV49). Thus, K a is 2.13 meV. The calculated T C is ~33 K, which is consistent with the experimental result of 31 K.
An average magnetic moment for a Fe atom is ~0.020 μB per atom for Fe0.021Sn0.979S2 (Fig. 3b) and 0.021 μB per atom for Fe0.015Sn0.985S2 (Supplementary Fig. 13) at 2 K. The magnetic moment of the Fe atom is relatively low51, and this phenomenon should result from the AFM coupling between doped Fe atoms at the intralayer and interlayer sites. It has been reported that in magnetic atom-doped 2D TMDs, the difference in energies between FM and AFM coupling is related to the distances between magnetic atoms. When the distance between two magnetic atoms is long enough, it will be AFM coupling25, 26, 29. Wu et al. demonstrated that in Fe–SnS2, Fe atoms can have AFM coupling across the layers. In the Fe–SnS2 crystal27, Fe atoms are distributed randomly (Fig. 1g), and an AFM coupling should exist and decrease the average magnetic moment of the Fe atoms.
Field-effect transistors based on this new 2D magnetic semiconductor have a high ON/OFF ratio (>106), a high electron mobility of 8.15 cm2 V−1 s−1, and a high photoresponsivity of 206 mA W−1. Pure SnS2 is diamagnetic, and Fe–SnS2 shows remarkable magnetic perpendicular anisotropic behavior with a Curie temperature of 31 K. The DFT calculations confirmed the ferromagnetic behavior and the perpendicular anisotropy of Fe–SnS2. The experimental and theoretical results suggest that Fe–SnS2 will have excellent performance for optoelectronic devices. Magnetic atom-doped 2D materials have significant potential applications in future nanoelectronic, magnetic, and optoelectronic fields.
Methods
Synthesis of the Fe-doped SnS2 bulk crystal
Fe0.021Sn0.979S2, Fe0.015Sn0.985S2, and Fe0.011Sn0.989S2 bulk crystals were synthesized via the direct vapor transport technique. Sn, S, and FeCl3 powders were mixed in stoichiometric proportions (10:30:1, 10:30:0.8, and 10:30:0.6, respectively) and placed in an ampoule. The ampoules were pumped down to the lowest-attainable pressures in our system (10−5 Torr) and sealed immediately to avoid blasting due to the high vapor pressure that developed inside the ampoule at growth temperatures. The ampoules were inserted into a two-zone tube furnace system, and the system was heated to 610 °C at a 30 °C h−1 rate. Samples were left at a constant temperature for 1 day. During the growth phase, the temperature of the growth zone was gradually lowered to 600 °C at a rate of 2 °C h−1, and the source temperature was maintained at 610 °C. After 5 days, the system was cooled down to room temperature at a rate of 10 °C h−1.
Characterization of the Fe-doped SnS2
Raman measurements were performed using a Renishaw micro-Raman/PL system. STEM and TEM were performed using a JEOL2100F. AFM and MFM were performed using a Bruker AFM. Magnetic measurements were performed using a Quantum design PPMS.
DFT calculations
According to the GGA calculations, the bandgaps of SnS2 and FeS2 are 1.61 eV and 0.56 eV, respectively. The bandgaps of SnS2 and FeS2 are 2.07 eV and 0.97 eV, which are larger than those determined via the calculations. We tested different U values and found that the bandgap of SnS2 is 2.06 eV (U = 8.0 on the d orbital) and the bandgap of FeS2 is 0.95 eV (U = 1.8 on the d orbital), which are consistent with the experimental values. First-principles spin-polarized calculations were performed on the basis of DFT using project or augmented wave (PAW) potentials52. The exchange-correlation interactions were treated by GGA with the Perdew–Burke–Ernzerhof functional53. The plane-wave cutoff energy was 400 eV. Monkhorst–Pack meshes of 5 × 5 × 1 and 21 × 21 × 1 were employed for geometry optimization and the calculation of density of states, respectively. To obtain reliable values for the MAEs, dense k points of 21 × 21 × 1 were used for the calculations.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Najmaei, S. et al. Vapour phase growth and grain boundary structure of molybdenum disulphide atomic layers. Nat. Mater. 12, 754–759 (2013).
Duan, X. et al. Lateral epitaxial growth of two-dimensional layered semiconductor heterojunctions. Nat. Nanotechnol. 9, 1024–1030 (2014).
Su, G. et al. Chemical vapor deposition of thin crystals of layered semiconductor SnS2 for fast photodetection application. Nano Lett. 15, 506–513 (2015).
Gong, Y. et al. Two-step growth of two-dimensional WSe2/MoSe2 heterostructures. Nano Lett. 15, 6135–6141 (2015).
Tan, C. & Zhang, H. Two-dimensional transition metal dichalcogenide nanosheet-based composites. Chem. Soc. Rev. 44, 2713–2731 (2015).
Li, B. et al. Large-size 2D β-Cu2S nanosheets with giant phase transition temperature lowering (120 K) synthesized by a novel method of super-cooling chemical-vapor-deposition. Adv. Mater. 28, 8271–8276 (2016).
Xia, C. & Li, J. Recent advances in optoelectronic properties and applications of two-dimensional metal chalcogenides. J. Semicond. 37, 051001 (2016).
Li, B. et al. Direct vapor phase growth and optoelectronic application of large band offset SnS2/MoS2 vertical bilayer heterostructures with high lattice mismatch. Adv. Electron. Mater. 2, 1600298 (2016).
Zou, X. M. et al. Dielectric engineering of a boron nitride/hafnium oxide heterostructure for high-performance 2D field effect transistors. Adv. Mater. 28, 2062–2069 (2016).
Huang, Y. et al. Tin disulfide-an emerging layered metal dichalcogenide semiconductor: materials properties and device characteristics. ACS Nano 8, 10743–10755 (2014).
Li, B. et al. Synthesis and transport properties of large-scale alloy Co0.16Mo0.84S2 bilayer nanosheets. ACS Nano 9, 1257–1262 (2015).
Suh, J. et al. Doping against the native propensity of MoS2: degenerate hole doping by cation substitution. Nano Lett. 14, 6976–6982 (2014).
Liu, X. et al. P-type polar transition of chemically doped multilayer MoS2 transistor. Adv. Mater. 28, 2345–2351 (2016).
Lei, S. et al. Surface functionalization of two-dimensional metal chalcogenides by Lewis acid-base chemistry. Nat. Nanotechnol. 11, 465–472 (2016).
Erwin, S. C. et al. Doping semiconductor nanocrystals. Nature 436, 91–94 (2005).
Liu, H. T., Liu, Y. Q. & Zhu, D. B. Chemical doping of graphene. J. Mater. Chem. C. 21, 3335–3345 (2011).
Tang, K. et al. High-quality ZnO growth, doping, and polarization effect. J. Semicond. 37, 031001 (2016).
Chen, Y. et al. Tunable band gap photoluminescence from atomically thin transition-metal dichalcogenide alloys. ACS Nano 7, 4610–4616 (2013).
Li, H. et al. Growth of alloy MoS2xSe2(1-x) nanosheets with fully tunable chemical compositions and optical properties. J. Am. Chem. Soc. 136, 3756–3759 (2014).
Chen, Y. et al. Composition-dependent Raman modes of Mo1-xWxS2 monolayer alloys. Nanoscale 6, 2833–2839 (2014).
Li, H. et al. Lateral growth of composition graded atomic layer MoS2(1-x)Se2x nanosheets. J. Am. Chem. Soc. 137, 5284–5287 (2015).
Mann, J. et al. 2-dimensional transition metal dichalcogenides with tunable direct band gaps: MoS2(1-x)Se2x monolayers. Adv. Mater. 26, 1399–1404 (2014).
Mahjouri-Samani, M. et al. Patterned arrays of lateral heterojunctions within monolayer two-dimensional semiconductors. Nat. Commun. 6, 8749 (2015).
Zhang, K. et al. Manganese doping of monolayer MoS2: the substrate is critical. Nano Lett. 15, 6586–6591 (2015).
Ramasubramaniam, A. & Naveh, D. Mn-doped monolayer MoS2: An atomically thin dilute magnetic semiconductor. Phys. Rev. B 87, 195201 (2013).
Mishra, R., Zhou, W., Pennycook, S. J., Pantelides, S. T. & Idrobo, J.-C. Long-range ferromagnetic ordering in manganese-doped two-dimensional dichalcogenides. Phys. Rev. B 88, 144409 (2013).
Sun, L., Zhou, W., Liang, Y., Liu, L. & Wu, P. Magnetic properties in Fe-doped SnS2: Density functional calculations. Comput. Mater. Sci. 117, 489–495 (2016).
Seixas, L., Carvalho, A. & Castro Neto, A. H. Atomically thin dilute magnetism in Co-doped phosphorene. Phys. Rev. B 91, 155138 (2015).
Cheng, Y. C., Zhu, Z. Y., Mi, W. B., Guo, Z. B. & Schwingenschlogl, U. Prediction of two-dimensional diluted magnetic semiconductors: doped monolayer MoS2 systems. Phys. Rev. B 87, 100401 (2013).
Zhang, B. et al. Piezo voltage controlled planar Hall effect devices. Sci. Rep. 6, 28458 (2016).
Chen, L. et al. Enhancing the Curie temperature of ferromagnetic semiconductor (Ga,Mn)As to 200 K via nanostructure engineering. Nano Lett. 11, 2584–2589 (2011).
Pan, D. et al. Controlled synthesis of phase-pure InAs nanowires on Si(111) by diminishing the diameter to 10 nm. Nano Lett. 14, 1214–1220 (2014).
Ohno, H. et al. (Ga,Mn)As: a new diluted magnetic semiconductor based on GaAs. Appl. Phys. Lett. 69, 363–365 (1996).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Puntes, V. F., Gorostiza, P., Aruguete, D. M., Bastus, N. G. & Alivisatos, A. P. Collective behaviour in two-dimensional cobalt nanoparticle assemblies observed by magnetic force microscopy. Nat. Mater. 3, 263–268 (2004).
Li, H. et al. Investigation of MoS2 and graphene nanosheets by magnetic force microscopy. ACS Nano 7, 2842–2849 (2013).
Li, L. H. & Chen, Y. Electric contributions to magnetic force microscopy response from graphene and MoS2 nanosheets. J. Appl. Phys. 116, 213904 (2014).
Neves, C. S. et al. New insights into the use of magnetic force microscopy to discriminate between magnetic and nonmagnetic nanoparticles. Nanotechnology 21, 305706 (2010).
Feng, Q. et al. Growth of MoS2(1-x)Se2x (x = 0.41-1.00) monolayer alloys with controlled morphology by physical vapor deposition. ACS Nano 9, 7450–7455 (2015).
Chen, D. et al. Microwave-assisted polyol synthesis of nanoscale SnSx(x = 1,2) flakes. J. Cryst. Growth 260, 469–474 (2004).
Grosvenor, A. P., Kobe, B. A., Biesinger, M. C. & McIntyre, N. S. Investigation of multiplet splitting of Fe 2p XPS spectra and bonding in iron compounds. Surf. Interface Anal. 36, 1564–1574 (2004).
Yassin, O. A., Abdelaziz, A. A. & Jaber, A. Y. Structural and optical characterization of V- and W-doped SnS2 thin films prepared by spray pyrolysis. Mater. Sci. Semicond. Process. 38, 81–86 (2015).
Ennaoui, A. et al. Iron disulfide for solar energy conversion. Sol. Energy Mater. Sol. Cells 29, 289–370 (1993).
Wang, D.-s, Wu, R. & Freeman, A. J. First-principles theory of surface magnetocrystalline anisotropy and the diatomic-pair model. Phys. Rev. B 47, 14932–14947 (1993).
Yin, L., Wang, X. & Mi, W. Perpendicular magnetic anisotropy preserved by orbital oscillation in strained tetragonal Fe4N/BiFeO3 bilayers. ACS Appl. Mater. Interfaces 9, 15887–15892 (2017).
Yin, L., Mi, W. & Wang, X. Perpendicular magnetic anisotropy and high spin polarization in tetragonal Fe4N/BiFeO3 heterostructures. Phys. Rev. Appl. 6, 064022 (2016).
Chen, Z., He, J., Zhou, P., Na, J. & Sun, L. Z. Strain control of the electronic structures, magnetic states, and magnetic anisotropy of Fe doped single-layer MoS2. Comput. Mater. Sci. 110, 102–108 (2015).
Bander, M. & Mills, D. L. Ferromagnetism of ultrathin films. Phys. Rev. B 38, 12015–12018 (1988).
Kudrnovský, J. et al. Exchange interactions in III-V and group-IV diluted magnetic semiconductors. Phys. Rev. B 69, 115208 (2004).
Wilson, J. A. & Yoffe, A. D. Mean magnetic moments in bcc Fe–Co alloys. J. Appl. Phys. 18, 193–355 (1969).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 61622406, 11674310, 61571415, 51502283, 11574018, 11574305, and 51524701), the National Key Research and Development Program of China (Grant No. 2017YFA0207500, 2016YFB0700700, and 2016YFA0301200), the “Hundred Talents Program” of Chinese Academy of Sciences (CAS), the Strategic Priority Research Program of the CAS (Grant No. XDPB06), and the CAS/SAFEA International Partnership Program for Creative Research Teams. The authors thank Prof. Wenbo Mi (Tianjin University) and Prof. Dahai Wei (Institute of Semiconductors, CAS) for their helpful discussions.
Author information
Authors and Affiliations
Contributions
Z.W. and J.L. conceived the experiments. B.L. synthesized and characterized the single crystals. B.L. and M.Z. carried out the FET measurements. T.X. and N.L. carried out the VSM measurements. L.H. and B.L. performed ab initio calculations. J.Z. provided insightful advice. B.L. and Z.W. wrote the manuscript. All authors contributed to the scientific planning and discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commonslicense, unless indicated otherwise in a credit line to the material. If material is not included in the article’sCreative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, B., Xing, T., Zhong, M. et al. A two-dimensional Fe-doped SnS2 magnetic semiconductor. Nat Commun 8, 1958 (2017). https://doi.org/10.1038/s41467-017-02077-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-02077-z
This article is cited by
-
2D Magnetic heterostructures: spintronics and quantum future
npj Spintronics (2024)
-
Modulating p-type doping of two dimensional material palladium diselenide
Nano Research (2024)
-
Hydrothermally derived Cr-doped SnS2 layered nanoplates: investigation of their controlled structural, morphological, optical, magnetic, photo response and photocatalytic activities
Discover Applied Sciences (2024)
-
Transition metal (TM = V, Cr, Mn, Fe, Co, Ni)-doped GeSe diluted magnetic semiconductor thin films with high-temperature ferromagnetism
Science China Materials (2024)
-
First-principles calculations of physical properties of the tungsten dichalcogenides (WSe2 and WTe2)
Chemical Papers (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.