Abstract
Oxic lake surface waters are frequently oversaturated with methane (CH4). The contribution to the global CH4 cycle is significant, thus leading to an increasing number of studies and stimulating debates. Here we show, using a mass balance, on a temperate, mesotrophic lake, that ~90% of CH4 emissions to the atmosphere is due to CH4 produced within the oxic surface mixed layer (SML) during the stratified period, while the often observed CH4 maximum at the thermocline represents only a physically driven accumulation. Negligible surface CH4 oxidation suggests that the produced 110 ± 60 nmol CH4 L−1 d−1 efficiently escapes to the atmosphere. Stable carbon isotope ratios indicate that CH4 in the SML is distinct from sedimentary CH4 production, suggesting alternative pathways and precursors. Our approach reveals CH4 production in the epilimnion that is currently overlooked, and that research on possible mechanisms behind the methane paradox should additionally focus on the lake surface layer.
Similar content being viewed by others
Introduction
The appearance of methane (CH4) within oxic surface water of lakes, aka the methane paradox, is an increasingly controversial topic. Normally produced under anoxic conditions, the oversaturation of CH4 in oxic surface waters has been reported for decades in both lakes and oceans1,2. While CH4 has been monitored in hypolimnion of lakes for years, it was most often neglected in the surface layer. However, metalimnetic CH4 maxima, thought to be the most intense location for oxic water CH4 production, were found in a number of oligotrophic to mesotrophic lakes including Lake Stechlin, Germany3, Lake Lugano, Switzerland4, and Lake Biwa, Japan5, with concentrations several orders of magnitude higher than CH4 maxima reported for ocean surface oxic waters6.
While lateral transport from the littoral zone may play an important role for CH4 accumulation in the metalimnion7,8, mesocosm experiments have convincingly shown that substantial CH4 production can occur in oxic freshwaters9. Additionally, a growing number of studies have suggested several pathways leading to CH4 production under aerobic conditions10,11. In lakes, a link between the methane paradox origin and algae has been hypothesized given the often observed overlap of the metalimnetic CH4 maxima with oxygen oversaturation and chlorophyll maxima6. Other postulations for the presence of CH4 in oxygenated waters include: anoxic micro-niches12,13, algal metabolites with methionine as a possible precursor14, and CH4 as a by-product of methylphosphonate (MPn) decomposition15. It is plausible that multiple sources act to produce this phenomenon, and that these may vary from lake-to-lake and may be trophic- and/or light-dependent.
The CH4 produced anaerobically in sediments of stratified lakes is efficiently removed by oxidation processes within the lake interior, limiting its evasion to the atmosphere16,17. The occurrence of CH4 in oxic surface waters, however, bypasses diffusive limitations to a large extent as it places a CH4 source close to the water surface, intensifying fluxes to the atmosphere6,18. Furthermore, the often observed absence or inhibition of CH4 oxidizers in the epilimnion of lakes19,20 is likely to be particularly significant in this context, indirectly acting to sustain high CH4 concentrations and subsequent emissions. While there is an increasing number of publications on “oxic” methane production (OMP; in the sense of Tang et al.6, i.e., “without inferring whether the biochemical pathway itself requires oxygen”) in lakes, no studies have so far addressed the associated rates under in situ conditions.
In 2015, a distinct CH4 peak was discovered in the oxic thermocline of mesotrophic Lake Hallwil (Switzerland) along with elevated and sustained CH4 concentrations in the surface layer with no clear indications as to their origins. In this study, we quantify the CH4 bulk sources in Lake Hallwil’s oxic surface layer using a detailed mass balance approach (Fig. 1) combined with in situ incubation experiments and isotopic evaluations. We come to the unprecedented conclusion that most of the CH4 production actually takes place in the surface mixed layer (SML) (i.e., epilimnion), contrasting the often suggested metalimnetic production. This significant source of CH4 is in direct contact with the atmosphere, implying that lake surface waters may be an important but overlooked CH4 production site.
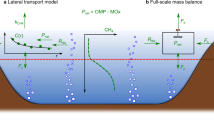
Conceptual schematic of the CH4 budget in mesotrophic Lake Hallwil. CH4 mass balance components: evasion to the atmosphere (F S), interior turbulent diffusion (F z), transport from the aeration system (F D), lateral transport (F L), and river input rate (F R = Q R × C R). The case study (Lake Hallwil, Switzerland) was divided into zone 1 (metalimnion) and zone 2 (surface mixed layer). The mass balance reveals that average dissolved CH4 concentration in the summer shows a CH4 metalimnetic maximum concentration (zone 1), however with low production rates (P net,m). The highest CH4 production rates (P net,s) are actually at the surface (zone 2). The turbulent gas exchange at the lake surface acts to mitigate the zone 2 CH4 concentrations by enhancing outgassing, while the metalimnion gas exchanges are driven by turbulent diffusion
Results
Observations
We studied Lake Hallwil (Canton Argovia, Switzerland) in 2015–2016 with the goal of isolating the key CH4 sources, sinks, and quantifying production rates as summarized in Fig. 1 (for sampling locations see Supplementary Fig. 1).
System description
Mean total phosphorous concentrations in Lake Hallwil are in the range of 10–20 mg m−3 21. After rigorous restoration measures for the past 30 years, the lake reached a mesotrophic state in 2008 (Supplementary Note 1). The re-oligotrophication process was supported since 1986 by the installation of a hypolimnetic aeration system, placed on the lake bed at ~46 m depth. The air/oxygen flow rate of the system is regulated such that, while preventing anoxic conditions in the deep water, the rising bubble plume does not affect the stratification of the water column in summer22. The aggressive restoration measures were extremely effective, resulting in a re-oligotrophication of the lake where bottom waters remain near completely oxic and preventing methane ebullition from developing in the hypolimnetic sediment (Supplementary Fig. 2).
The seasonal evolution of methane in the fully oxic water column is shown on Fig. 2a, b for the years 2015 and 2016, respectively, as well as chlorophyll a (Chl-a) (Fig. 2c, d) and temperature (Fig. 2e, f). The CH4 increase is particularly strong within the stratified metalimnion (~5–15 m depth) (0.4 µmol L−1 at 6 m in June; 0.5 µmol L−1 at 8 m in July; 0.75 µmol L−1 at 7 m in August 2016), with the buildup concomitant with the onset of summer stratification (Fig. 2e, f). CH4 concentrations between 25 and 45 m depth at the lake center were low (<0.05 µmol L−1). The presence of a double Chl-a maximum (Fig. 2c, d) is a recent phenomenon in Lake Hallwil that is particularly pronounced during the summer season. The presence of a surface chlorophyll maximum (SCM) in the epilimnion has been reported for several lakes23. In Lake Hallwil, while the SCM is associated with chrysophytes, chlorophytes, and diatoms, the deep chlorophyll maximum is associated with the filamentous cyanobacteria Planktothrix rubescens 24 (Supplementary Note 1).
Evolution of dissolved CH4 in the water column (0–40m) of Lake Hallwil. Dissolved CH4 (µmol L−1) in a and b, chlorophyll a (Chl-a; µg L−1) in c and d and temperature (°C) in e and f from June–October 2015 to April–August 2016 interpolated from measurements at the lake center (47°16.762 N, 8°12.791 E, St. A, Supplementary Fig. 1). Dashed vertical lines indicate the sampling date
Temperature-based basin scale vertical diffusivities K z (m2 s−1) were determined below 5 m depth by the heat budget method25,26 (Methods). The profiles revealed how with the onset of stratification between May and August, water column stability (N 2) between 5 and 10 m increased from 1 × 10−3 to 5 × 10−3 s−2, while at the same depths basin scale turbulent diffusion reached its minimum values (~1 × 10−6 m2 s−1) (Supplementary Fig. 3).
Methane heterogeneity
Lateral (east−west) and longitudinal (north−south) heterogeneity of the CH4 concentrations were investigated in 2015. A lateral transect (~1 km east−west) of four CH4 profiles was performed within a few hours at increasing distances from the shore toward the center (Fig. 3a). The longitudinal variability was also investigated with a south and center profile (Fig. 3b). The spatial variation of the CH4 profile (defined as the ratio of the standard deviation to the mean) is 50% smaller than the temporal variation of the profile performed at the lake center between June and August 2015. Therefore, given the spatial similarity of the metalimnetic CH4 maximum and CH4 concentrations in general, we considered the profile obtained at the center (as in Fig. 2a, b) representative for the entire lake production and transport dynamics.
Dissolved CH4 spatial heterogeneity in Lake Hallwil. Water column dissolved CH4 profiles carried out within few hours on a 10 June 2015 from the east shore toward the center of the lake at stations A, B, C, D (45, 40, 20, 2 m lake depth, respectively) and b on 21 August 2015 from center (St. A) toward south (St. E, 20 m lake depth). See Supplementary Fig. 1 for sampling locations
Oxidation rates
Stable carbon isotopes of CH4 (δ 13CCH4 values) were measured for in situ lake water incubations to investigate CH4 oxidation. Seasonally, the CH4 in the Lake Hallwil surface layer had an average δ 13CCH4 (June–August 2016) of −60‰ ± 2‰ (n = 15, all results reported in ±1 standard deviation, SD, unless otherwise indicated), and became isotopically enriched (~–40‰) below the CH4 peak and thermocline (Fig. 4a, c, e). Incubations revealed a maximum CH4 oxidation rate (MOx) of 6 nmol L−1 d−1 at 13 m depth (July–August 2016, Fig. 4d). While slight decreases of CH4 concentrations were observed in water incubations above 10 m for the period July–August 2016 (3.6 ± 0.2 and 3.2 ± 0.9 nmol L−1 d−1 at 2 and 8 m depth, respectively), no change in isotope ratio was observed after 3 weeks of incubation (Fig. 4b, d).
Water column CH4 concentration and oxidation rates. a, c, e Water column profiles of CH4, δ 13CCH4, and temperature for 17 June, 7 July, and 3 August 2016. CH4 profiles show the distinctive metalimnetic maxima, while at 25–30 m concentrations were <0.05 µmol L−1. The δ 13CCH4 profiles in the epilimnion are rather uniform with values around −62 to −60‰. b, d Average dissolved oxygen profiles and MOx rates obtained from in situ incubations for the periods June–July 2016 and July–August 2016 show maximum oxidation rates and correspondingly higher δ 13CCH4 values at 15 and 13 m depth, respectively. In the SML, oxidation rates were negligible for the period June–July 2016, and higher during the period July–August 2016 (3.6 ± 0.2 nmol L−1 d−1) although associated with no significant (2‰) change in δ 13CCH4 (*)
Benthic fluxes
Sediment porewater CH4 concentrations in Lake Hallwil measured on cores retrieved at 3 and 7 m depth (Methods) averaged 1 mmol L−1 at 5 cm b.s.s. (below sediment surface) with δ 13CCH4 of −68‰ and −66‰ in the upper 15 cm, respectively (Fig. 5). CH4 diffusive flux at these depths was calculated with Fick’s 1st law as 1.6 and 1.9 mmol m−2 d−1, respectively. CH4 diffusive fluxes at 23 and 45 m depth were estimated as 5 and 6 mmol m−2 d−1, respectively (Fig. 5). The δ 13C values of porewater CH4 at 23 and 45 m depth were about –75‰ (5 cm b.s.s.), which is 8‰ and 16‰ lower than those measured in littoral pore- and surface waters, respectively.
Porewater CH4 concentrations and δ 13CCH4 values. a Profiles of porewater CH4 concentrations (log scale) and b δ 13C values on sediment cores retrieved at deep sites (S3, 23 m and S4, 45 m) and at shallow stations (S1, 3 m and S2, 7 m) in the proximity of high lake surface CH4 concentrations: 0.8 µmol L−1 (–59‰) at the 3 m site and 1 µmol L−1 (–59‰) at the 7 m site. The 3 m site showed extensive gas voids, and some gas bubble release in the retrieved core. All profiles were performed on September 2016 except for S4, which refers to June 2015
Surface fluxes
Surface CH4 fluxes were measured with a floating chamber between June 2015 and August 2016. Average April–August 2016 evasion at the air–water interface corresponded to 0.6 ± 0.3 (1 SD, n = 28) mmol m−2 d−1, while surface CH4 concentrations averaged 0.3 ± 0.1 (1 SD, n = 5) µmol L−1. Measured CH4 emission rates were compared with flux estimates based on wind speed for May–August 2016. Chamber-based CH4 fluxes compared well with wind speed-derived diffusive fluxes calculated according to the parameterization for a stratified water column by MacIntyre et al.27 (0.8 ± 0.2 mmol m−2 d−1) (Supplementary Fig. 4). The flux estimate for negative buoyancy, typical for night convective mixing, is nearly double than what was estimated from chamber measurements as these were almost always taken during the day (Supplementary Fig. 4). Consequently, the surface flux component (F S, Fig. 1) is a conservative estimate for the summer period.
Mass balance
To determine the overall CH4 net production in the lake (P net, Fig. 1), mass balances were performed within the two defined zones using the various rates shown in Tables 1 and 2. Sources and sinks during the lake stratified period (May–October) of 2016 were determined dividing the surface layer in two key zones as shown in Fig. 1. Zone 1, between 5 and 10 m depth, includes the steep thermocline where low (basin scale) turbulent diffusion dominates (K z = 1–2 × 10−6 m2 s−1; Supplementary Fig. 3). Zone 2 is defined as the SML between 0 and 5 m depth where, on a seasonal scale, convection and wind-driven advective mixing dominates.
Metalimnion mass balance
Higher CH4 concentrations in the metalimnion diffuse toward the lower concentrations down in the hypolimnion and up to the SML. The vertical transport of dissolved CH4 from the metalimnion to the SML and hypolimnion is driven via turbulent diffusivity and the concentration gradients, where the basin scale diffusivity, K z , was determined to be ~1 × 10−6 m2 s−1. The average vertical CH4 diffusion (F Z) was determined by Fick’s 1st law (Eq. 1) as:
where C determines the CH4 concentration and z the depth. The vertical flux was calculated to be ~14 nmol L−1 d−1 (0.07 mmol m−2 d−1) both upward and downward from the peak that formed between June and August 2016.
Such small CH4 fluxes through the metalimnion are caused by low turbulent diffusivities (Supplementary Fig. 3). However, horizontal transport at the thermocline can be several orders of magnitude higher than vertical diffusion25. We therefore consider a lateral transport from the littoral sediment in the mass balance (F L = ~9 nmol L−1 d−1, see Methods and Fig. 1), with the assumption that the added mass is well-mixed horizontally across the lake over the time scale of the calculations. Bubble transport of bottom water methane facilitated by the aeration system was also considered (Discussion) as a potential contribution to CH4 concentrations in zone 1 (F D = ~3 nmol L−1 d−1, see Methods and Fig. 1).
With Fick’s 2nd law, we determined the depth-dependent CH4 production (P gross,m) in zone 1 expressed by the sum of losses by diffusion (F z, Fig. 1) and oxidation and inputs from the littoral zone and from the hypolimnion (F L and F D; Fig. 1),
with t as time. Equation 2 can be applied in both the sediment and the stratified water column28. Although only applicable below the SML, where the water column is stably stratified, this approach presents the advantage of a direct estimation of system-wide production rates (P gross,m) with high vertical resolution.
Local methane production (P net,m) was calculated by removing the estimated littoral contributions as P gross,m−(F L + F D) (Fig. 1), for both periods June–July and July–August 2016 (Fig. 6a, b), indicating an average (June–August) aerobic methane production (P net,m) of ~5.0 ± 5.0 nmol L−1 d−1 between 6 and 7 m. Yet, when net P rates are integrated over the metalimnion (zone 1 in Fig. 6), P net,m become negligible at 0.3 ± 3.0 nmol L−1 d−1 (Table 1).
High-resolution water column CH4 production and consumption rates. System-wide CH4 production rates (white bars, P gross,m) obtained by Fick’s 2nd law and local production P net,m (red bars) = [P gross,m−(F L + F D)] for the period a June–July and b July–August 2016. P net,m rates indicate an overall net CH4 production/consumption of −0.3 ± 3.0 nmol L−1 d−1 in the metalimnion (zone 1; 6–10 m), while consumption rates increase up to −20 nmol L−1 d−1 below 10 m. This analysis shows that a small net CH4 production (red bars) is observed between 7 and 8 m between June and August 2016 (~5 ± 5 nmol L−1 d−1). Note that the depth integrated production starts between 6 and 7 m; above 6 m depth (SML) the vertical diffusion (K z ) used in Fick’s 2nd law cannot be accurately inferred with the heat budget method (Methods). The dashed line indicates the lower limit of zone 1
Net production rates for both analyzed periods indicate that below 9 m, CH4 is consumed due to aerobic oxidation (MOx) at rates between 5.0 and 20 nmol L−1 d−1 (Fig. 6a, b). These estimates are in good agreement, although slightly greater than MOx rates obtained by in situ incubations at 13 and 15 m (~6.0 nmol L−1 d−1, Fig. 4b, d). However, when CH4 diffusion to the water column due to ebullitive inputs from sediments below 10 m depth is considered negligible29, the obtained consumption rate (P net,m) between 10 and 15 m is 25% lower, thus closer to the oxidation rates from incubation experiments.
Surface mass balance
Surface CH4 fluxes (0.6 ± 0.3 mmol m−2 d−1, Supplementary Fig. 4) and concentrations (0.3 ± 0.1 µmol L−1, Fig. 2a, b) exhibit relative temporal uniformity in contrast to the eight-fold CH4 accumulation between 5 and 10 m depth observed at the lake center throughout the same time period. Between June and August (both 2015 and 2016), most of the CH4 surface flux originates from the relatively well-mixed top 5 m (Fig. 2). Therefore, we assume on the seasonal scale that the surface layer can be modeled as a well-mixed reactor, and CH4 net production rates (P net,s) can be estimated as follows:
where A s and A p are the sediment surface (between 0 and 5 m) and the lake planar area, respectively. Contributions to the CH4 budget in the SML (zone 2), as shown in Fig. 1, are listed in Table 2 (see Methods for each term calculation).
As surface concentrations do not vary much seasonally (Fig. 4a, c, d), we assume steady state \((\frac{{\partial C}}{{\partial t}}\forall = 0)\) and solve the mass balance in the top 5 m revealing a source of CH4 (P net,s in Eq. 3) of 110 ± 60 nmol L−1 d−1 (73 ± 40 kg of CH4 per day during stratified periods). This rate is about a 100× higher than in the metalimnion and accounts for up to 90% of total measured CH4 evasion (Table 2). This is a conservative estimate, as it was assumed that the whole sediment surface of the lake from 0 to 5 m is subject to highest rates of ebullition (1.2 ± 0.8 mmol CH4 m−2 d−1 dissolved in water, representing 1.2% of the lake area according to Flury et al.30). The mass balance includes MOx rates from in situ incubations (Table 2), although these are negligible compared to the surface losses of CH4 to the atmosphere. While our uncertainty analysis detailed in Supplementary Table 1 indicates that the error associated with P net,s (110 ± 60 nmol L−1 d−1) is largely due to air–water exchange estimates that, as described above, are conservative.
Methane sources from isotope evaluation
To assess possible similarity between water column and porewater CH4 formation, we investigate the difference between the isotope measurements of CH4 and methanogenic precursors (total and dissolved organic carbon, TOC and DOC). Based on calculations according to Bogard et al.9 (Methods), we infer a smaller difference between the isotope values of carbon source and CH4 produced in the oxic water column (−32 to −29‰) as compared to the sediment methanogenesis (−44 to −41‰, Table 3).
The apparent fractionation factor (α app) during methanogenesis was defined as in Conrad et al.31 where the isotopic signature of source CH4 was estimated by correcting the δ 13CCH4 ambient measurement for the isotopic fractionation due to diffusion and oxidation (Methods). Sediment CH4 production of Lake Hallwil exhibits an α app of 1.056–1.060, which is characteristic for environments dominated by acetate-dependent methanogenesis. Estimates for the water column SML methane production show a smaller fractionation factor (α app = 1.045). Consequently, in Lake Hallwil we observed a different isotopic fractionation between the CH4 produced in sediments and in the SML, however both characteristic for acetoclastic methanogenesis.
Discussion
This study quantifies CH4 production rates in the oxic surface layer of a mesotrophic Swiss lake by estimating the system-wide CH4 transport, dynamics, and emissions. The conservative mass balance performed for this study illustrates that, during periods of lake stratification (April–October), up to 90% of the CH4 that is emitted to the atmosphere (73 ± 40 kg d−1 or 26 ± 14 t y−1) is the product of unknown production process(es) that primarily occur in the SML (top 5 m) of Lake Hallwil. The metalimnion CH4 concentration maximum, often observed in mesotrophic lakes, does not correspond to a maximum production rate. The observed metalimnetic CH4 production rate (P gross,m) of about 10 nmol L−1 d−1 can be largely explained by lateral transport from the adjacent sediments (Table 1). Negative production rates below 10 m (Fig. 6) are explained by oxidation of CH4 as confirmed by in situ bottle incubations (~6 nmol L−1 d−1), where a CH4 stable carbon isotope ratio increase of 20‰ was observed after 1 month for both periods June–July and July–August (Fig. 4b, d).
In the SML of Lake Hallwil, the situation is vastly different. We show that during the stratified season, the most significant production rate (P net,s = 110 ± 60 nmol L−1 d−1) is mostly expressed in these upper 5 m and not in the metalimnion. Bottle incubations in the SML show either negligible CH4 oxidation (0.3 nmol L−1 d−1, June–July 2016) or higher oxidation (3.6 ± 0.2 nmol L−1 d−1, July–August 2016) with negligible change in isotope values (2‰ after 1-month incubation) (Fig. 4b, d). This may indicate oxidation is compensated by a CH4 production mechanism. The magnitude of the surface CH4 production is however masked by the relatively rapid water–air exchange. As a result of the CH4 loss to the atmosphere, the observed CH4 concentrations remain lower and fairly consistent in the surface layer vs. the metalimnion.
Surface water CH4 oversaturation has been suggested to be produced in situ under oxic conditions10,11. Current hypotheses for lakes are derived from the strong correlations observed between OMP (P net,s), photosynthesis and O2 concentration4,13. However, the characteristic CH4 peak may lead to misinterpretations when seeking correlations. Photosynthesis and O2 concentration are positively correlated to autotrophic biomass, whose distribution in the water column is strongly related to the physical water column structure32. That is, the variables listed above also tend to correlate with water column stability. Comparing CH4 to Chl-a, turbidity and water column stability (N 2) revealed that the CH4 concentration only correlates significantly with N 2 (Supplementary Table 2), suggesting a physical component behind the observed CH4 accumulation in the metalimnion. This supports that the highest production rates are expressed at the ventilated surface layer, while the CH4 in the metalimnion represents only a local accumulation that supplies very little CH4 to the surface layer. Therefore, relying on correlations of CH4 concentration with other variables alone is misleading, while using the production rates for correlations provides a clearer picture of each vertical zone’s importance in sustaining CH4 emissions.
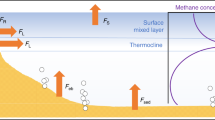
Our approach reveals for the first time that CH4 production in oxic waters (P net,s, Fig. 1) appears to decrease rapidly with water depth, where production rates in the top 5 m are 100 times greater than in the metalimnion (Fig. 7). Our mass balance-based production estimate of 110 ± 60 nmol L−1 d−1 is remarkably close to the OMP rates observed by laboratory incubations (50 nmol L−1 d−1)13 and lake enclosures (∼200 nmol L−1 d−1)9. Despite the different approaches, methane production rates lay within a surprisingly narrow range. Thus our results both support the growing body of evidence for OMP as well as better constrains the rates now reported in multiple freshwater environments.
Linking water column CH4 production oxidation and light extinction. Net CH4 production in the top 5 m as derived from mass balance (Eq. 3) and below 6 m depth from Fick’s 2nd law (Eq. 2). Light extinction curves were based on Secchi depths (Zs) of 6 m in June (blue line) and 3.5 m in August (black line). The profile of δ 13CCH4 is added to illustrate the relationship between light extinction and CH4 oxidation
Most studies on CH4 oxidation are carried out in stratified eutrophic systems, where CH4 concentrations at the thermocline are higher than in Lake Hallwil (up to 600 time higher20). In such cases, the corresponding MOx rates can be about 100 times greater than what is found in Hallwil (e.g., 1 µmol L−1 d−1). Our MOx results are however in good agreement with similar mesotrophic systems (e.g., Lake Biwa; ~5 nmol L−1 d−1 from dark incubations of 15 m deep water19) and are in the order of the lower range measured by Bogard et al.9 for Lake Cromwell (60 nmol L−1 d−1). Methane oxidizing bacteria favor isotopically lighter CH4, leaving a residual CH4 with a higher δ 13CCH4 value. Both high oxygen concentrations and light exposure have been shown to significantly inhibit MOx19,33,34. In Lake Hallwil, these findings are supported by negligible oxidation rates measured in situ (June–July 2016) and by the lighter δ 13CCH4 values above 6 m (Fig. 7). July–August surface water incubations showed a slight CH4 decrease with no isotope values change. With a δ 13CCH4 equal to −62‰ at Time 1, as from in situ measurements, the isotope value associated to the measured consumption rates of 3 nmol L−1 d−1 should have been in the order of −41‰ instead of the final measured −64‰ (assuming MOx with fractionation factor of 20‰). This might suggest a local compensation with production of isotopically lighter CH4.
δ 13CCH4 values at the surface (–62 to –60‰) are on average lower than those reported in other OMP studies (–50‰, Lake Stechlin3; –55‰, Lake Lugano4; –40‰, Lake Cromwell9; –62 to –21‰, Lake Biwa5) but are 5 and 15‰ higher than the measured porewater δ 13CCH4 at 7 and 45 m lake depth (–65‰ and –75‰, respectively). Interestingly, similar differences between lake surface and porewater CH4 stable carbon isotopes were reported in other meso-oligotrophic lake studies3,4,5. Biogenic methanogenesis of freshwater systems is known to be strictly anaerobic and mainly based on the fermentation of acetate, the most favorable substrate for freshwater methanogens35. The fractionation factor α during acetoclastic CH4 formation can vary between 1.009 and 1.06536,37,38,39. Yet the carbon isotope composition of CH4 can be influenced by the type of acetate precursor40, the production mechanism(s) and pathways, and relatively little is known about methanogenesis of oligotrophic lake surface sediments41. Lake Hallwil’s apparent fractionation (1.056–1.060) of sediment CH4 production indicates an acetate-dependent methanogenesis, which is in good agreement with temperate, oligotrophic lake sediments (e.g., 1.065, Lake Stechlin41).
While isotopic studies of OMP have been reported for plant-derived organic materials exposed to ultraviolet light42, virtually nothing is known about the stable carbon isotope fractionation associated to aerobic CH4 production in aquatic systems. Our estimates for the water column SML CH4 production show a smaller fractionation factor compared to the sediments (α app = 1.045), but still characteristic for acetoclastic methanogenesis and similar to what was found by Bogard et al.9 for their enclosure experiments (α app = 1.02–1.04). Furthermore, we assessed a smaller difference between isotope values of precursors (DOC, TOC) and product (CH4) from water column methanogenesis (32–29‰) as compared to the sediment methanogenesis (44–41‰, Table 3), which may indicate that water column P net derives from a distinct pathway, not linked to the sediments. However, the estimates of fractionation factors performed here, as in the majority of methanogenesis studies, are based on the assumption that there is no major methanogenic precursor other than acetate or CO2 31. Arguably, additional and perhaps novel pathways should be evaluated.
Only recently, MPn biodegradation has been indicated as a possible source of CH4 in oceans43, a theory which was confirmed to apply to mesotrophic lakes in recent work on Lake Yellowstone15. However, in the mentioned study, and contrary to our findings, laboratory efforts focused on samples taken at the metalimnetic CH4 peak that occurs during stratification. MPn can derive from anthropogenic activity (e.g., herbicide glyphosate) and is known to contribute to the phosphonate pool in lakes and their watersheds44. It was furthermore shown that, when environmentally limited, phosphate can be regenerated from semi-labile dissolved organic matter through the C-P lyase pathway with formation of CH4 45. Indeed, the expression of the C-P lyase gene found in many freshwater cyanobacteria46,47 is induced by P limitation48. This hypothesis suits Lake Hallwil mainly for two reasons: low water column P concentrations (3 µg L−1 in top 5 m, DIN:P tot > 100 in August 2015), and surface (1 m) CH4 concentrations that correlate with DOC (Supplementary Fig. 5a). Lake Hallwil is surrounded by an intense agricultural landscape which is potentially a source for MPn, although the absence of strong lateral CH4 gradients points toward the relationship with DOC (Supplementary Fig. 5b) supporting a link between the oxic water CH4 production and algal-derived organic matter substrate availability9.
An additional explanation for OMP could be the breakdown of chromophoric dissolved organic matter by solar radiation in the ultraviolet and visible range49,50 to organic compounds that serve as precursors for non-microbial CH4 production51,52. The photolysis of organic matter was shown to supply CH4 to the surface waters at relatively low rates in Saguenay River (4.36 × 10−6 mol m−2 yr−1)53. Such a process would directly relate to the trophic state (i.e., clarity)54. In Lake Hallwil, this seems supported by the light penetration/CH4 production curve relationship (Fig. 7; Supplementary Fig. 5a). While this aspect needs further investigation, we conclude that CH4 production is occurring in the SML, regardless of the source/process.
Littoral sediments are known to contribute to CH4 emissions via ebullition30. The dissolution of the rising bubbles55 and enhanced sediment CH4 diffusion from gas-charged sediments56 could contribute to the high dissolved CH4 concentrations in the littoral zone. Thus CH4 release from the littoral sediments and subsequent horizontal transport could be another source of CH4 in lake surface waters8, however these contributions are less important in the SML than at increasing depths. In Lake Hallwil’s metalimnion, we assess that lateral transport accounts for 10 ± 1 nmol CH4 L−1 d−1 (Table 1) leading to an accumulation of ~5 ± 5 nmol L−1 d−1 (Fig. 6) of which an average of 0.3 ± 3 nmol L−1 d−1 is locally produced/consumed. Contrarily, in the SML we estimate a significant and unaccounted for internal source of CH4 (P net,s, Fig. 1) of 110 ± 60 nmol L−1 d−1 that is in the same range of what was estimated by laboratory and mesocosm-based studies9,13.
Low CH4 concentrations (<0.05 µmol L−1) between 25 and 45 m depth at the lake center led to the conclusion that any CH4 diffusing from deep sediments (5 and 6 mmol m−2 d−1 at 23 and 45 m, respectively) does not reach the metalimnion or the SML. The highest oxidation rates are likely taking place within the surface sediments as reported for other studies in mesotrophic lakes5,57. However, the presence of the aeration system may favor the transport of bottom water CH4 within rising bubbles. This contribution to the bulk CH4 content at 5–10 m depth was quantified using modeling of air bubbles at equilibrium with the highest measured bottom water (46.5 m) CH4 concentration (7 µmol L−1, Methods). The maximum input to the thermocline (zone 1) was estimated as 120 mol d−1, which represents only 3–6% of the estimated P net,s. However, even such contribution to the mass balance is very conservative. In fact, if the plume was transporting CH4 from the benthic boundary layer upward, then we would see elevated concentrations below the thermocline in the area of plume detrainment (the main sampling station A, on Supplementary Fig. 1, is only ~250 m south of the aeration system diffuser ring). Here the profiles show that dissolved CH4 below the thermocline to ~40 m depth was near the detection level of the method in all cases (Fig. 4a, c, e), indicating the concentrations within the plume itself are likely near this background concentration.
During summer stratification, the SML is generally restricted to the top several meters of the lake, effectively isolating the surface CH4 from oxidation processes58. Therefore, CH4 formed in the surface layer can be continuously and rapidly delivered to the atmosphere. Consequently, longer stratification periods from a warmer climate could result in longer periods of OMP-related CH4 evasion (P net,s, Fig. 1). Similar conclusions were drawn for the marine environment, for which aerobic CH4 production is suggested to be sensitive to changes in water column stratification and P limitation10.
In the present study, we used detailed whole-lake mass balancing combined with incubation and isotopic approaches to show that in Lake Hallwil, during the stratified period, up to 90% of the emissions (26 ± 14 tons per year) result from surface layer CH4 production. The estimated production rates are in agreement with what is suggested by other laboratory and mesocosm-based studies9,13. However, with our whole-lake approach, this is the first study to determine that the highest production rates occur within the lake SML rather than within the often suggested metalimnion, and are depth-correlated with DOC and light penetration. Several oligo- and mesotrophic lakes such as Lake Stechlin13, Lake Lugano4, Lake Matano45, Lake Yellowstone15, and Lake Geneva (Supplementary Fig. 6) have been recently studied and reported the occurrence of OMP. The present findings for Lake Hallwil frame an important and underestimated contribution to atmospheric CH4, as oligo-mesotrophic systems are typically not considered as significant greenhouse gas sources.
Consequently, attention should be paid to the result of restoration programs (deeper light penetration, low phosphorous), which could indirectly lead to enhanced greenhouse gas emissions—another paradox concerning aquatic systems that has been so far overlooked.
Methods
Study site
Lake Hallwil (Canton of Argovia, Switzerland) is a mesotrophic lake with a surface area of 10.2 km2, a mean depth of 28.6 m, and a maximum depth of 46.5 m. The basin water volume is 0.29 km3 with negligible riverine inflow (2.5 m3 s−1), of which 50% flows in from upstream Lake Baldegg in the south. Dominant winds are from the west resulting in limited large-scale seasonal mixing of the north–south-oriented lake sheltered by hills24. Since 1986, Lake Hallwil has had no ice cover in winter. A restoration process was aided since autumn 1985 by the installation of a bubble plume hypolimnetic aeration system designed to prevent a complete loss of oxygen in deep water22 (Supplementary Note 1).
Limnological measurements
Monthly water column profiles at station A (45 m lake depth, 47°16.762 N, 8°12.791 E, Supplementary Fig. 1) were conducted with a multiparametric probe (6600 V2, YSI, USA until March 2016 and EXO2, YSI, USA afterward) equipped with temperature, conductivity, Chl-a, and turbidity sensors. Additionally, Secchi depth (Zs), concentrations of DOC, and total phosphorous (October, May, August) were measured (using standard methods; www.labeaux.ch) and provided by the Department of Civil Engineering, Transportation and Environment of the Canton of Argovia, Switzerland.
Values for buoyancy frequency (N 2) were calculated from temperature, salinity, and pressure data as:
where ρ, g, and c are the density, earth’s gravitational acceleration, and speed of sound, respectively. The fraction of light (I) penetrating at depth z \((I_z/I_0)\) for June and August 2016 was calculated by the Lamber Beer equation:
where the extinction coefficient k was inferred as in Wetzel et al.59 by measured Secchi depth (1.7/Zs).
Water column CH4 and CO2 concentration, and δ 13C
Monthly CH4 concentration profiles were taken at the deep Station A between June–October 2015 and April–August 2016. A 1 km long west–east transect was performed on 11 June 2015 at Stations A, B, C, D (45, 40, 20, and 2 m lake depth, Supplementary Fig. 1). A 3 km longitudinal transect (center–south) was performed on 21 August 2015 at Stations A and E (45 and 20 m depth, Supplementary Fig. 1).
For dissolved CH4 concentration, water samples were obtained with a 5-L Niskin bottle at a maximum depth resolution of 0.5 m, where the metalimnetic CH4 peak was expected.
Until October 2015, water samples for CH4 concentration were collected with 60 mL syringes (Plastipak, Becton-Dickinson). One depth at the time, 20 mL of the syringe volume was replaced with ambient air (CH4 = 1.75 ppm) and equilibrated by vigorously shaking for at least 2 min. The 20 mL gas volume was preserved in serum bottles prefilled with CH4 free saturated NaCl solution and capped with gas tight butyl rubber stoppers (GMT Inc., USA). The gas sample headspace was created by injecting the gas volume (20 mL) into the serum bottles with a needle (0.6 × 30 mm, 23 G) and simultaneously evacuating the same volume of NaCl solution through a second needle previously inserted in the septum. The headspace was analyzed on the same day on a portable greenhouse gas (GHG) analyzer (UGGA; Los Gatos Research, Inc., USA).
From April 2016 on, dissolved concentrations of both CO2, CH4, and their stable C isotope ratio were measured. Therefore, samples were gently transferred from the Niskin sampler into a 1 L glass bottle (Duran GmbH, Mainz, Germany) overflowing to replace the volume about three times. A headspace was made immediately by replacing 400 mL of the sampled water via a 2-way stopcock valve with ambient air. With the valves closed, the bottle was shaken vigorously for 2 min. The headspace was then transferred into a 1 L gas-sampling bag (Supel Inert Multi-Layer Foil) via a 2-way stopcock by gently injecting lake water back into the bottom of the bottle. The gas samples were measured within 1 day on a Cavity Ring-Down Spectrometer analyzer (Picarro G2201-i, Santa Clara, CA, USA) for immediate reading of concentrations in the gas phase (ppm) and stable isotope ratio (δ 13C in ‰ vs. VPDB standard). Instrument-specific precision at ambient concentrations (1−σ of 5 min average) is <0.16‰ for δ 13C of CO2, <1.15‰ for δ 13C of CH4, for [12CO2] is 200 ppb + 0.05% of reading and for [12CH4] is 5 ppb + 0.05% of reading. Water CH4 and CO2 concentrations were back calculated according to Wiesenburg and Guinasso60 accounting for water temperature, air concentration (assuming 1.75 and 410 ppm for CH4 and CO2 respectively), and the resulting headspace/water ratio in the bottle.
Each sample procedure from the Niskin bottle to the gas bag takes ~10 min. To prioritize a higher vertical resolution, given the time consuming procedure (a longer time would increase the uncertainty linked to the natural variability of the water column structure), we performed replicates only once and applied the determined coefficient of variation (averaging 10.0% for CH4 and 10.6% for CO2 over a set of eight replicates) to the data set as a ±range of uncertainty of the measurement.
CH4 oxidation rates
During June–August 2016, net methane oxidation rates were measured by incubating three replicates of 120 mL water from 2, 8, 13, 15, 25, and 35 m at Station M1 (Supplementary Fig. 1). The 120 mL glass bottles were previously soaked in 3 N HNO and rinsed with ultrapure water (MilliQ). The water samples from each depth were collected with a Niskin bottle sampler and immediately transferred to the incubation bottles while letting 3–4 volumes overflow prior to crimp capping the bottle headspace free. After sealing, incubations were started as soon as possible at in situ conditions by hanging the bottles along the thermistor chain at their corresponding sampling depth. Because dilutions were not made and nutrients were not added, there was no reason to expect any lag in the activity of the enclosed bacterial populations. Methane concentration was determined after 23 days in July and after 27 days in August on each of the bottles by replacing 40 mL with synthetic air (CO2- and CH4-free, Carbagas AG 2011) and analyzing the headspace on a Picarro analyser after complete equilibration by vigorous shaking (>2 min). The net rate of CH4 oxidation was calculated by the decrease from in situ concentrations at the time when incubation started. To verify that the remaining CH4 was an oxidized residue, we applied an isotope fractionation (ε) of 20‰61 to calculate isotope composition of CH4 in a Rayleigh fractionation model3:
where T0 and T1 are the beginning and end, respectively, of the incubation and ƒ represents the fraction of CH4 remaining at T1. The predicted CH4 isotope value was −36‰ for both periods June–July and July–August, and is in very good agreement with the values of −36 and −37‰ measured for the incubations at 8 m depth.
Porewater and sediment sampling
Sediment cores were taken at Stations A (45 m depth) and D (2.5 m depth) on 11 June 2016 and at S1, S2, S3, S4 (maximum water depth at the stations: 3, 7, 23, and 45 m, respectively) on 29 September 2016 (Supplementary Fig. 1). Sampling was performed with a gravity sediment corer (Uwitech, Mondsee, Austria) equipped with an acrylic liner of 100 cm in length and with an internal diameter of 6 cm. The liner had pre-drilled holes to fit either Rhizons (Rhizosphere Research Products, http://rhizosphere.com/rhizons) or 3 mL syringes at 1 cm intervals, covered with tape.
Porewater CH4 and CO2 concentrations, and δ 13C
About 3 mL of sediment was sub-sampled at 1–2 cm depth intervals with headless 3-mL syringes through the pre-drilled holes from the selected depths. The sediment sub-sample was immediately placed into 1 L glass bottle (Duran GmbH, Mainz, Germany) containing 600 mL of lake water previously bubbled to reach equilibration with atmospheric air. The subsequent procedure followed the same as for the water column headspace method. Porewater CH4 concentrations were back calculated from the headspace concentrations accounting for dilution of sediments in lake water (assuming that aerated lake water contained 1.75 ppm of CH4 and 410 ppm of CO2), temperature, headspace ratio, and assuming a porosity of 0.9.
Porewater dissolved organic carbon and δ 13C
Porewater was extracted using Rhizon technology, a hydrophilic, porous polymer tube with 2.5 mm in diameter, 50 mm in length, and 0.12–0.18 µm pore size membrane. Rhizons were inserted into the sediment at a depth resolution of 1 cm. The sample was immediately stored in 2-mL pre-evacuated vials with no headspace. DOC concentration and its stable carbon isotope composition (δ 13CDOC in ‰ vs. VPDB standard) were measured at the UNIL-IDYST by elemental analysis/isotope ratio mass spectrometry (EA/IRMS) using a Carlo Erba 1108 elemental analyzer (Fisons Instruments, Milan, Italy) coupled by a ConFlo III continuous flow open split interface to a Delta V Plus isotope ratio mass spectrometer, both of Thermo Fisher Scientific, Bremen, Germany. Aliquots (1.7 mL) of the porewater samples were freeze-dried in a combusted (480 °C, >4 h) 2 mL glass vial containing 1 mg of combusted (600 °C, >4 h) quartz wool and placed in a tin capsule for EA/IRMS analysis. The precision of the δ 13CDOC measurements by EA/IRMS was better than 0.1‰.
Sediment total organic carbon content and δ 13C
About 3 mL of sediment was sub-sampled at 1-cm depth intervals with headless 3-mL syringes through the pre-drilled holes. Total organic carbon content and its stable carbon isotope composition (δ 13CTOC in ‰ vs. VPDB standard) were measured from freeze-dried and homogenized sediment samples. The homogenized sediment was pretreated with 12.5% HCl to remove carbonates and TOC was measured using the EA/IRMS system. The DOC and TOC contents were determined from the peak areas of the major isotopes using the calibration standards for δ 13C. The precision of the δ 13CTOC measurements by EA/IRMS was better than 0.05‰.
Methane benthic fluxes
Methane fluxes at the sediment–water interface were calculated (Stations S1, S2, S3, S4) with Fick’s 1st law over the linear top 5 cm decrease of the porewater concentration profile, according to Berner et al.62
where F sed is the diffusive CH4 flux at the sediment–water interface, ϕ the porosity of the sediments (assumed as 0.9), D CH4 the diffusion coefficient for CH4 in water (1.5 × 10−5 cm2 s−1)63, θ 2 the square of tortuosity (1.2)64 and ∂C/∂z the measured vertical concentration gradient within the first 5 cm of surface sediments. Negative fluxes indicate a CH4 loss from the sediment.
Apparent isotopic fractionation of methanogenesis
The apparent fractionation factor (α app) during methanogenesis was defined as in Conrad31:
where the isotopic signature of source CH4 was estimated by correcting the δ 13CCH4 ambient measurement for the isotopic fractionation due to diffusion and oxidation, Δ, as in Bogard et al.9:
α was taken from literature as 0.9992 for evasion65 and 0.98 for MOx61. In Table 3, the methanogenic precursor is considered as the precursor of acetate, i.e., organic carbon. This derivation is possible assuming negligible isotopic fractionation during acetate formation31.
Mass balance
The mass balance for the SML (zone 2) was calculated as in Eq. 3, where the water volume (∀) is ~0.04 km3, the sediment surface area (A s) and the planar area (A p) equal ~0.1 km2 and ~8.4 km2, respectively. The individual fluxes: surface flux (F S, Fig. 1), littoral flux (F L, Fig. 1), diffusive vertical flux (F Z, F D, Fig. 1), and riverine input (F R = Q R × C R, Fig. 1) were estimated as described below.
Surface methane flux
CH4 flux at the water–air interface (F s) was measured with a floating chamber attached to a portable GHG analyzer (UGGA; Los Gatos Research, Inc.). Instrument-specific precision at ambient concentrations (1−σ of 100 s average) for [12CO2] is 40 ppb and for [12CH4] is 0.25 ppb. The floating chamber consisted of an inverted plastic container with foam elements for floatation (as in McGinnis et al.18). To minimize artificial turbulence effects, the buoyancy element was adjusted that only ~2 cm of the chamber penetrated below the water level. The chamber was painted white to minimize heating. Two gas ports (inflow and outflow) were installed at the top of the chamber via two 5-m gas-tight tubes (Tygon 2375) and connected to the GHG analyzer measuring the gaseous CH4 concentrations in the chamber every 1 s. Transects were performed with the chamber deployed from the boat (with engine shut down). The boat and chamber were allowed to freely drift to minimize artificial disturbance. Fluxes were obtained by the slopes of the resolved CH4 curves over the first ~10 min, when the slopes were approximately linear (R 2 > 0.97).
The chamber-based CH4 flux measurements were then compared to fluxes estimated based on wind speed. Wind speed-based fluxes were calculated as follows:
where pCH4 wtr is the CH4 partial pressures measured in water, pCH4 atm is the assumed partial pressures of atmospheric CH4 (1.75 ppm), kh is the Henry constant of CH4 dissolution at in situ temperature, and k CH4 is the gas transfer velocity. To compute k CH4 values, we first derived k 600 estimates using a wind speed-based relationship. Wind speed was measured at 10 m height (U 10; m s−1 at the nearby Mosen Meteo station, Meteo Group Schweiz AG). We then converted k 600 to k CH4 using:
where Sc CH4 is the dimensionless Schmidt number for CH4 (as in Engle and Maleck66), c is a wind speed-dependent conversion factor, for which we used −2/3 for U 10 < 3.7 m s−1, and −1/2 for all other wind speeds67. We further calculate fluxes based on relationships as in MacIntyre et al.27 for low turbulent regimes. Average flux (April–August 2016) is equal to 0.8 ± 0.2 mmol m−2 d−1 from McIntyre relationship for positive buoyancy and to 0.6 ± 0.3 mmol m−2 d−1 from chamber measurements. The latter, not significantly different from the wind-based relationship, was used for the mass balance (Table 2).
Littoral methane flux
Diffusion from the sediment to the water column (F L) was estimated at shallow sites characterized by reed vegetation (Stations S1 and S2 Fig. 1, surface water CH4 ~1 μmol L−1) from the CH4 porewater profiles as described above (equal to 1.6 and 1.9 mmol m−2 d−1, respectively). The contribution to dissolved CH4 by ebullition was estimated from ebullition rates determined at the same sites by Flury et al.30 assuming bubbles entirely composed by CH4 and that all of the CH4 bubble dissolve into the water (1.2 ± 0.8 mmol m−2 d−1). For mass balance purposes, the total littoral CH4 flux to the water column was conservatively assumed to be emitted from the whole-lake sediments surface between 0 and 10 m depth.
Vertical diffusive methane flux in the metalimnion
The vertical CH4 fluxes F z (mmol m−2 d−1) were obtained from K z (m2 s−1) and the CH4 (mmol m−1) concentration gradients by Fick’s 1st law of diffusion (Eq. 1). Vertical diffusivity K z was determined in the stratified water below 6 m depth by the heat budget method26 using temperature measurements from thermistor strings at Station M1 (0, 5, 7.5, 9, 11.5, 14, 17, 20, 25, 35, 46 m) and M2 (0, 5, 7.5, 9, 11.5, 14, 17, 20, 25 m—Supplementary Fig. 2). The temperature mooring was installed from 25 May 2016 to 30 September 2016. The loggers (RBR TR1060, Ottawa, Canada) at 5, 9, and 11.5 m measured temperature every 5 s with a 0.1 s response time and 5 × 10−5 °C resolution. The remaining loggers (Vemco Minilog-II-T loggers, Canada) were recording every 1 min, with a resolution of 1 × 10−2 °C and response time of <5 min.
Vertical diffusive CH4 flux from the hypolimnion
Methane transported by the aeration system from bottom water into the metalimnion (F D) was estimated after McGinnis et al.18 The used model describes gas transfer across the surface of an individual rising bubble and tracks the dissolution and stripping of CH4. According to the model, small bubbles (4 mm) released from 45 m would have lost all of their CH4 before reaching the thermocline and would thus not contribute CH4 to the metalimnetic peak. However, the aeration system may transport methane from the bottom boundary layer via released air/O2 bubbles. This was estimated as an upper end by implementing the model with the flow rate of the aeration system (180 Nm3 h−1) assuming a bubble diameter of 4 mm and a bottom CH4 concentration of 7 μmol L−1.
CH4 input from rivers
The input of CH4 from rivers (F R) was estimated by the product of the flow rate (Q R = 2.5 m3 s−1 for rivers and 1 m3 s−1 as conservative average for periodical surface runoff) and the maximum CH4 measured in front of the Aabach river mouth, 1 μmol L−1, corrected for background surface lake CH4 (C R) of 0.3 μmol L−1.
Depth-dependent CH4 production rates
Depth-dependent CH4 changes for the periods 15 June–6 July and 6 July–2 August were calculated by Fick’s 2nd law solved for the CH4 production (P gross,m) in Eq. 2, where K z (m2 d−1) is the calculated diffusivity. \(\frac{{\partial C}}{{\partial t}}\) was determined as [CH4 (Time 2)—CH4 (Time 1)] at each depth measured at Station A (mmol m−3 d−1) and \(\frac{{\partial ^2C}}{{\partial z^2}}\) is obtained calculating the second derivative of the mean CH4 profile (Time 1, Time 2) at Station A (mmol m−3 d−1). The net production P net,m (mmol m−3 d−1) was calculated as P gross,m−(F L + F D) with 1 m resolution from 7 to 15 m depth. The top 6 m are excluded as the air–water interface exchanges are dominated by advection and not diffusion.
Uncertainty assessment
The uncertainties of mass balance estimates were assessed by Monte Carlo simulations (999 iterations) (Supplementary Table 1). Each component of the mass balance calculation was randomly picked from either a normal distribution described by the mean and 1 standard deviation values, or within a range. For F S, F L, F Z, one standard deviation (1 SD) on n measurements were assessed while for P gross,m (Eq. 2) the uncertainty was taken as the coefficient of variation of the CH4 concentration profile measurements (as explained in CH4 concentration section). F R and F D uncertainties were instead determined as the potential range from 0 to an upper end value (to ensure largely conservative mass balance results) as described in the respective sections.
Data availability
All relevant data included in this manuscript are available by request from the authors.
References
Reeburgh, W. Oceanic methane biogeochemistry. Am. Chem. Soc. 107, 486–513 (2007).
Conrad, R. The global methane cycle: recent advances in understanding the microbial processes involved. Environ. Microbiol. Rep. 1, 285–292 (2009).
Tang, K. W., McGinnis, D. F., Frindte, K., Brüchert, V. & Grossart, H.-P. Paradox reconsidered: methane oversaturation in well-oxygenated lake waters. Limnol. Oceanogr. 59, 275–284 (2014).
Blees, J. et al. Spatial variations in surface water methane super-saturation and emission in Lake Lugano, southern Switzerland. Aquat. Sci. 77, 535–545 (2015).
Murase, J., Sakai, Y., Kametani, A. & Sugimoto, A. in Forest Ecosystems and Environments: Scaling up from Shoot Module to Watershed (eds Kohyama, T., Canadell, J., Ojima, D. S. & Pitelka, L. F.) 143–151 (Springer, Tokyo, 2005).
Tang, K. W., McGinnis, D. F., Ionescu, D. & Grossart, H.-P. Methane production in oxic lake waters potentially increases aquatic methane flux to air. Environ. Sci. Technol. Lett. 3, 227–233 (2016).
Hofmann, H., Federwisch, L. & Peeters, F. Wave-induced release of methane: littoral zones as source of methane in lakes. Limnol. Oceanogr. 55, 1990–2000 (2010).
Fernández, J. E., Peeters, F. & Hofmann, H. On the methane paradox: transport from shallow-water zones rather than in situ methanogenesis is the mayor source of CH4 in the open surface water of lakes. J. Geophys. Res. Biogeosci. 121, 2717–2726 (2016).
Bogard, M. J. et al. Oxic water column methanogenesis as a major component of aquatic CH4 fluxes. Nat. Commun. 5, 5350 (2014).
Karl, D. M. et al. Aerobic production of methane in the sea. Nat. Geosci. 1, 473–478 (2008).
Damm, E. et al. Methane production in aerobic oligotrophic surface water in the central Arctic Ocean. Biogeosciences 7, 1099–1108 (2010).
Oremland, R. S. Methanogenic activity in plankton samples and fish intestines: a mechanism for in situ methanogenesis in oceanic surface waters. Limnol. Oceanogr. 24, 1136–1141 (1979).
Grossart, H.-P., Frindte, K., Dziallas, C., Eckert, W. & Tang, K. W. Microbial methane production in oxygenated water column of an oligotrophic lake. Proc. Natl Acad. Sci. USA 108, 19657–19661 (2011).
Lenhart, K. et al. Evidence for methane production by marine algae (Emiliana huxleyi) and its implication for the methane paradox in oxic waters. Biogeosciences 13, 3163–3174 (2016).
Wang, Q., Dore, J. E. & McDermott, T. R. Methylphosphonate metabolism by Pseudomonas sp. populations contributes to the methane oversaturation paradox in an oxic freshwater lake. Environ. Microbiol. 19, 2366–2378 (2017).
Bastviken, D., Cole, J. J., Pace, M. L. & Van de Bogert, M. C. Fates of methane from different lake habitats: connecting whole-lake budgets and CH4 emissions. J. Geophys. Res. 113, G02024 (2008).
Peeters, F. & Hofmann, H. Importance of the autumn overturn and anoxic conditions in the hypolimnion for the annual methane emissions from a temperate lake. Environ. Sci. Technol. 48, 7297–7304 (2014).
McGinnis, D. F. et al. Enhancing surface methane fluxes from an oligotrophic lake: exploring the microbubble hypothesis. Environ. Sci. Technol. 49, 873–880 (2015).
Murase, J. & Sugimoto, A. Inhibitory effect of light on methane oxidation in the pelagic water column of a mesotrophic lake (Lake Biwa, Japan). Limnol. Oceanogr. 50, 1339–1343 (2005).
Oswald, K. et al. Light-dependent aerobic methane oxidation reduces methane emissions from seasonally stratified lakes. PLoS ONE 10, e0132574 (2015).
Stöckli, A. Hallwilersee—nachhaltige Gesundung sicherstellen. Umw. Aargau 69, 23–28 (2015).
McGinnis, D. F., Lorke, A., Wüest, A., Stöckli, A. & Little, J. C. Interaction between a bubble plume and the near field in a stratified lake. Water Resour. Res. 40, 1–11 (2004).
Mostofa, K. M., Yoshioka, T., Mottaleb, A. & Vione, D. Photobiogeochemistry of organic matter. Principles and practices in water environments. Environ. Sci. Eng. 3, 806 (2012).
Holzner, C. P., Tomonaga, Y., Stöckli, A., Denecke, N. & Kipfer, R. Using noble gases to analyze the efficiency of artificial aeration in Lake Hallwil, Switzerland. Water Resour. Res. 48, W09531 (2012).
Goudsmit, G., Peeters, F., Gloor, M. & Wüest, A. Boundary versus internal diapycnal mixing in stratified natural waters. J. Geophys. Res. 12, 27903–27914 (1997).
Powell, T. & Jassby, A. The estimation of vertical eddy diffusivities below the thermocline in lakes. Water Resour. Res. 10, 191–198 (1974).
MacIntyre, S. et al. Buoyancy flux, turbulence, and the gas transfer coefficient in a stratified lake. Geophys. Res. Lett. 37, 2–6 (2010).
Kreling, J., Bravidor, J., McGinnis, D. F., Koschorreck, M. & Lorke, A. Physical controls of oxygen fluxes at pelagic and benthic oxyclines in a lake. Limnol. Oceanogr. 59, 1637–1650 (2014).
DelSontro, T., Boutet, L., St-Pierre, A., Giorgio, P. A. & Prairie, Y. T. Methane ebullition and diffusion from northern ponds and lakes regulated by the interaction between temperature and system productivity. Limnol. Oceanogr. 61, 62–77 (2016).
Flury, S., McGinnis, D. F. & Gessner, M. O. Methane emissions from a freshwater marsh in response to experimentally simulated global warming and nitrogen enrichment. J. Geophys. Res. 115, G01007 (2010).
Conrad, R. Quantification of methanogenic pathways using stable carbon isotopic signatures: a review and a proposal. Org. Geochem. 36, 739–752 (2005).
Mellard, J. P., Yoshiyama, K., Litchman, E. & Klausmeier, C. A. The vertical distribution of phytoplankton in stratified water columns. J. Theor. Biol. 269, 16–30 (2011).
Rudd, J. W. M., Furutani, A., Flett, R. J. & Hasmilton, R. D. Factors controlling methane oxidation in shield lakes: the role of nitrogen fixation and oxygen concentration. Limnol. Oceanogr. 21, 357–364 (1976).
Dumestre, J. F. et al. Influence of light intensity on methanotrophic bacterial activity in Petit Saut reservoir, French Guiana. Appl. Environ. Microbiol. 65, 534–539 (1999).
Whiticar, M. J., Faber, E. & Schoell, M. Biogenic methane formation in marine and freshwater environments: CO2 reduction vs. acetate fermentation−isotope evidence. Geochim. Cosmochim. Acta 50, 693–709 (1986).
Gelwicks, J. T., Hayes, J. M. & Risatti, J. B. Carbon isotope effects associated with acetoclastic methanogenesis. Appl. Environ. Microbiol. 60, 467–472 (1994).
Whiticar, M. J. Carbon and hydrogen isotope systematics of bacterial formation and oxidation of methane. Chem. Geol. 161, 291–314 (1999).
Penning, H. & Conrad, R. Effect of inhibition of acetoclastic methanogenesis on growth of archaeal populations in an anoxic model environment. Appl. Environ. Microbiol. 72, 178–184 (2006).
Goevert, D. & Conrad, R. Effect of substrate concentration on carbon isotope fractionation during acetoclastic methanogenesis by Methanosarcina barkeri and M. acetivorans and in rice field soil. Appl. Environ. Microbiol. 75, 2605–2612 (2009).
Nüsslein, B., Eckert, W. & Conrad, R. Stable isotope biogeochemistry of methane formation in profundal sediments of Lake Kinneret (Israel). Limnol. Oceanogr. 48, 1439–1446 (2003).
Conrad, R., Chan, O.-C., Claus, P. & Casper, P. Characterization of methanogenic Archaea and stable isotope fractionation during methane production in the profundal sediment of an oligotrophic lake (Lake Stechlin, Germany). Limnol. Oceanogr. 52, 1393–1406 (2007).
Vigano, I. et al. The stable isotope signature of methane emitted from plant material under UV irradiation. Atmos. Environ. 43, 5637–5646 (2009).
Repeta, D. J. et al. Marine methane paradox explained by bacterial degradation of dissolved organic matter. Nat. Geosci. 9, 884–887 (2016).
Ilikchyan, I. N., Mckay, R. M. L., Zehr, J. P., Dyhrman, S. T. & Bullerjahn, G. S. Detection and expression of the phosphonate transporter gene phnD in marine and freshwater picocyanobacteria. Environ. Microbiol. 11, 1314–1324 (2009).
Yao, M. et al. Heterotrophic bacteria from an extremely phosphate-poor lake have conditionally reduced phosphorus demand and utilize diverse sources of phosphorus. Environ. Microbiol. 18, 656–667 (2016).
Huang, J., Su, Z. & Xu, Y. The evolution of microbial phosphonate degradative pathways. J. Mol. Evol. 61, 682–690 (2005).
Henny, C. & Maresca, J. A. Freshwater bacteria release methane as a byproduct of phosphorus acquisition. Appl. Environ. Microbiol. 1, 82–23 (2016).
Dyhrman, S. T. et al. Phosphonate utilization by the globally important marine diazotroph Trichodesmium. Nature 439, 2–5 (2006).
Bertilsson, S. & Tranvik, L. J. Photochemical transformation of dissolved organic matter in lakes. Limnol. Oceanogr. 45, 753–762 (2000).
Obernosterer, I., Benner, R. & Carolina, S. Competition between biological and photochemical processes in the mineralization of dissolved organic carbon. Limnol. Oceanogr. 49, 117–124 (2004).
Oba, Y. & Naraoka, H. Carbon and hydrogen isotope fractionation of acetic acid during degradation by ultraviolet light. Geochem. J. 41, 103–110 (2007).
Keppler, F. et al. Methane formation in aerobic environments. Environ. Chem. 6, 459–465 (2009).
Zhang, Y. & Xie, H. Photomineralization and photomethanification of dissolved organic matter in Saguenay River surface water. Biogeosciences 12, 6823–6836 (2015).
Toming, K., Kutser, T., Tuvikene, L., Viik, M. & Nõges, T. Dissolved organic carbon and its potential predictors in eutrophic lakes. Water Res. 102, 32–40 (2016).
McGinnis, D. F., Greinert, J., Artemov, Y., Beaubien, S. E. & Wüest, A. Fate of rising methane bubbles in stratified waters: how much methane reaches the atmosphere? J. Geophys. Res. 111, 1–15 (2006).
Flury, S., Glud, R. N., Premke, K. & McGinnis, D. F. Effect of sediment gas voids and ebullition on benthic solute exchange. Environ. Sci. Technol. 49, 10413–10420 (2015).
Frenzel, P., Thebrath, B. & Conrad, R. Oxidation of methane in the oxic surface layer of a deep lake sediment (Lake Constance). FEMS Microbiol. Ecol. 6, 149–158 (1990).
Winder, M. & Schindler, D. E. Climatic effects on the phenology of lake processes. Glob. Chang. Biol. 10, 1844–1856 (2004).
Wetzel, R. G. Limnology, 767 (Saunders College Publishing, Philadelphia, 1983).
Wiesenburg, D. A. & Guinasso, N. L. Equilibrium solubilities of methane, carbon monoxide and hydrogen in water and seawater. J. Chem. Eng. Data 24, 356–360 (1979).
Bastviken, D., Ejlertsson, J. & Tranvik, L. Measurement of methane oxidation in lakes: a comparison of methods. Environ. Sci. Technol. 36, 3354–3361 (2002).
Berner, R. A. Early Diagenesis: a Theoretical Approach, 241(Princeton Univ. Press, Princeton, 1980).
Broecker, W. S. & Peng, T. H. Gas exchange rates between air and sea. Tellus 26, 21–35 (1974).
Boudreau, B. P. Diagenetic Models and their Implication: Modelling Transport and Reactions in Aquatic Sediments, 142–159 (Springer-Verlag, New York, 1997).
Knox, M., Quay, P. D. & Wilbur, D. Kinetic isotopic fractionation during air-water gas transfer of O2, N2, CH4, and H2. J. Geophys. Res. 97, 335–343 (1992).
Engle, D. & Maleck, J. M. Methane emissions from an Amazon floodplain lake: enhanced release during episodic mixing and during falling water. Biogeochemistry 51, 71–90 (2000).
Jahne, B. et al. On parameters influencing air-water gas exchange. J. Geophys. Res. 92, 1937–1949 (1987).
De Kluijver, A., Schoon, P. L., Downing, J. A., Schouten, S. & Middelburg, J. J. Stable carbon isotope biogeochemistry of lakes along a trophic gradient. Biogeosciences 11, 6265–6276 (2014).
Acknowledgements
We would like to thank Timon Langenegger and Nicole Gallina for their help during the fieldwork and the Canton of Argovia, Department of Civil Engineering, Transportation and Environment for providing access to Lake Hallwil monitoring program database, infrastructure, and boat. Funding for this study was provided by Swiss National Science Foundation (SNSF) Grants No. 200021_160018 (Bubble Flux) and No. 200021_169899 (Methane Paradox).
Author information
Authors and Affiliations
Contributions
D.D. and D.F.M. initiated and designed the study, organized campaigns, performed sampling, and analyzed the data with significant contribution from S.F. and D.V. A.S. was responsible for the Canton Argovia support in data collection, analysis, and logistics. J.E.S. provided porewater and sediment organic carbon stable isotope data analysis and interpretation. D.D. wrote the manuscript with editorial help and conceptual contribution from all the coauthors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Donis, D., Flury, S., Stöckli, A. et al. Full-scale evaluation of methane production under oxic conditions in a mesotrophic lake. Nat Commun 8, 1661 (2017). https://doi.org/10.1038/s41467-017-01648-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-01648-4
This article is cited by
-
Hourly methane and carbon dioxide fluxes from temperate ponds
Biogeochemistry (2024)
-
Evaluation of the methane paradox in four adjacent pre-alpine lakes across a trophic gradient
Nature Communications (2023)
-
Multiple sources of aerobic methane production in aquatic ecosystems include bacterial photosynthesis
Nature Communications (2022)
-
The anaerobic oxidation of methane driven by multiple electron acceptors suppresses the release of methane from the sediments of a reservoir
Journal of Soils and Sediments (2022)
-
Detection of planktonic coenzyme factor 430 in a freshwater lake: small-scale analysis for probing archaeal methanogenesis
Progress in Earth and Planetary Science (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.