Abstract
Methane (CH4) strongly contributes to observed global warming. As natural CH4 emissions mainly originate from wet ecosystems, it is important to unravel how climate change may affect these emissions. This is especially true for ebullition (bubble flux from sediments), a pathway that has long been underestimated but generally dominates emissions. Here we show a remarkably strong relationship between CH4 ebullition and temperature across a wide range of freshwater ecosystems on different continents using multi-seasonal CH4 ebullition data from the literature. As these temperature–ebullition relationships may have been affected by seasonal variation in organic matter availability, we also conducted a controlled year-round mesocosm experiment. Here 4 °C warming led to 51% higher total annual CH4 ebullition, while diffusion was not affected. Our combined findings suggest that global warming will strongly enhance freshwater CH4 emissions through a disproportional increase in ebullition (6–20% per 1 °C increase), contributing to global warming.
Similar content being viewed by others
Introduction
Despite their small global extent (only ca. 4% of land area)1,2, freshwater ecosystems are important drivers of the global greenhouse gas (GHG) balance3. Global freshwater CH4 emissions have been estimated to correspond to at least 25% (in CO2 equivalents) of the terrestrial GHG sink4. Broad-scale emission estimates are, however, biased because most studies focus on diffusive fluxes and neglect the large emission component of ebullition4,5. Because ebullition often forms the dominant emission pathway, this may lead to a large underestimate of freshwater CH4 emissions4,5. Accurate estimates are still hampered by a scarcity of reliable ebullition data caused largely by the extremely heterogeneous occurrence of ebullition within a system, both in space and in time4,6,7,8,9.
Anaerobic mineralization of sediment organic matter, the source of ebullitive CH4 fluxes, tends to increase exponentially with temperature, forming a potential positive feedback to global warming10. Net CH4 emissions from freshwaters to the atmosphere, however, are usually the result of microbial CH4 production and consumption. CH4 consumption mainly takes place in the oxic sediment top layer and water column, and can consume up to 100% of dissolved CH4 11. Like production, consumption rates also increase with temperature12,13,14. Nonetheless, if a warming-induced increase in CH4 production is concomitant with a constant or higher fraction of CH4 escaping consumption, e.g., through plants or ebullition, an increase in CH4 emission due to global warming is to be expected. To date, a positive relationship between temperature and ebullition has been observed in a number of high-latitude systems15,16, but there is currently no general consensus that this is a global phenomenon. Also, it is not known whether this response is due to direct effects of temperature (e.g., on microbial process rates) or collinear indirect effects (e.g., enhanced substrate availability due to increased primary production and sedimentation of organic substrates).
To quantify the increase in CH4 ebullition due to temperature-induced increase in sediment CH4 production, we combined a standardized search for published data (as in ref. 17) with a mesocosm experiment. In the literature search, we only included studies with ebullition data from different types of freshwater ecosystems that covered a temperature range of at least 10 °C, and excluded short-term (<24 h), infrequent (<once per month) ebullition measurements since these likely underestimate the ebullitive flux7,9. To exclude influences of confounding factors occurring in the field, and to further unravel the relative importance of the different processes responsible for the temperature-induced increase in ebullition, we conducted an experiment in 1000 L mesocosms containing natural lake sediments and plankton communities comparing a temperate (control; n = 4) and a warming (+4 °C; n = 4) scenario (IPCC scenario RCP8.518). Since the frequency of heat waves is expected to increase over most land areas under future climate projections18, we included a midsummer 7-day heat wave (+4 °C). Day and night water-atmosphere diffusive gas fluxes were measured once every 2 weeks, using a closed chamber connected to a GHG analyzer, whereas bubbles were collected continuously by inverted funnel-type bubble traps. Our data compilation shows remarkably strong relationships between CH4 ebullition and temperature across a wide range of freshwater ecosystems, which we also observed in our mesocosm experiment. Our analysis of the experimental data further suggests that direct effects of temperature on microbial growth and metabolism are driving the increase in ebullition. These combined findings indicate a positive feedback for global warming.
Results
Temperature drives ebullition on a large spatial scale
Analysis of the field data meeting our criteria reveals strong positive relationships between CH4 ebullition and temperature for a wide range of shallow, freshwater ecosystems in Asia, North America, and Europe (Fig. 1 and Table 1). We observed large differences in the magnitude of ebullition among the different freshwater ecosystems (Fig. 1). Although methodological differences in determining ebullition rates play a role here, differences in quantity and quality of sediment organic matter19,20,21,22,23,24, sediment structure25, and differences in the availability of nutrients, oxygen, and alternative electron acceptors19 are also known to affect the magnitude of ebullition. Freshwaters showing high primary production and those that receive substantial loads of allochthonous carbon are more likely to have high CH4 ebullition rates15,23,25,26,27, while systems with low primary production tend to have low ebullition rates and also may have an obscured temperature effect on ebullition rates, likely due to substrate limitation15.
Relationships between temperature and CH4 ebullition found in different types of freshwater ecosystems. Regression lines represent the fitted modified Arrhenius expression; see Eq. (2). Error bars denote 95% confidence intervals (Post-glacial lakes). Graphs with thin border lines represent field data. Graph with thick border line represents experimental data. For the latter, black and red dots represent control and warm treatment, respectively. For studies with multiple data sets, the location with the longest data record is depicted. See Table 1 and Supplementary Table 1 for info on all data sets. Details on the origin and acquisition of data are described in the “Methods” section
The temperature–ebullition relationships from field measurements are likely to be influenced by differences in sampling methods as well. The available temperature data, for instance, was measured in air, water, or sediment. Also the period of sampling varied (year-round versus spring–summer or summer–autumn), which may have influenced the temperature coefficient in multiple ways. For one, a decrease in CH4 solubility in the pore water with rising temperatures will lead to a stronger increase in ebullition during the spring–summer period, whereas the opposite may occur when temperatures drop (see below for a quantitative analysis). Second, seasonal variations in organic carbon supply and oxygen availability alter CH4 production19,21,28,29. Finally, fluctuations in forcing mechanisms such as shear stress, atmospheric pressure, and hydrostatic pressure7,30 (such as the passage of ships in the River Saar7) may have weakened the temperature–ebullition relationship. Still, despite these putative confounding factors, ebullition was strongly related to temperature in the systems we analyzed (Table 1).
Drivers of increased ebullition under warming
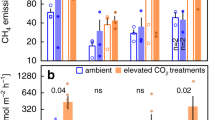
CH4 ebullition showed a strong relationship with temperature in our mesocosm experiment (Supplementary Fig. 1), which fits our analyses of data from field measurements (Fig. 1 and Table 1). We found that cumulative annual ebullition was 51% higher in the warm treatment (P = 0.009; Fig. 2), substantiating that enhanced CH4 ebullition in temperate regions is a realistic future scenario. Warming may affect CH4 ebullition in different ways. System productivity, for example, may be affected by warming31,32,33, altering the availability of substrate for methanogenesis. We found, however, no significant differences in gross primary production nor in sedimented carbon between our control and warm treatment (Supplementary Fig. 2), indicating that substrate supply was not responsible for the large increase in CH4 ebullition with warming. We estimate that the effect of temperature-dependent changes in CH4 solubility during the spring–midsummer period (period with increasing temperature) contributed 14% (control) and 7% (warm) to the total CH4 ebullition as a result of dissolved CH4 that turned gaseous. For the midsummer–winter period (period with decreasing temperature), CH4 ebullition was lowered by 17% (control) and 13% (warm) as a result of increased pore water solubility (Supplementary Fig. 3). However, effects of changes in CH4 solubility were negligible for cumulative annual ebullitive fluxes. The negligible difference in organic carbon supply as well as the negligible effect of changes in CH4 solubility strongly suggests that temperature dependency of CH4 ebullition in our experiment was mostly driven by enhanced microbial metabolism and growth.
Effects of increased temperature on diffusive CH4 emissions
Besides emission by ebullition, CH4 may also diffuse from the water column into the atmosphere. Diffusive CH4 emissions in our experiment only accounted for 10% (control) and 5% (warm) of total CH4 emissions (Fig. 2), and correlated significantly with temperature during the year (Supplementary Fig. 4). This positive correlation corroborates findings for diffusive CH4 emissions from another mesocosm experiment33 as well as from an analysis of data from globally distributed wetland and freshwater ecosystems34. In part, this may be due to gas dissolution during bubble rise35. Interestingly, however, cumulative annual diffusive CH4 fluxes in our experiment show that year-round warming did not enhance the diffusive emission pathway (Fig. 2). This clearly shows that increased CH4 production with warming (as indicated by increased ebullition) does not necessarily result in increased diffusive CH4 emissions over a longer period of time (e.g., a year), likely because of (over)compensation by increased CH4 consumption rates in the sediment top layer and water column12. This further substantiates the key role of the ebullitive pathway in total CH4 emissions.
Increased dominance of ebullition under climate change
The existence of a threshold temperature marking the onset—or a strong increase—of ebullition is a major concern for sudden shifts in global GHG emissions with climate warming. We found that above a sediment temperature of ~10 °C (Fig. 3) ebullition strongly increases with temperature, which coincides with findings in another study35. However, despite this similarity, the threshold temperature varies among systems (Fig. 1), likely depending on the physical structure of the sediment25, forcing mechanisms7, and the methanogenesis rate at a certain temperature. The latter is ultimately determined by the microbial community36,37 and environmental factors including quality and quantity of available organic substrate19,24. With increasing substrate availability, CH4 ebullition shows a stronger temperature dependence than diffusive CH4 emission in northern ponds and lakes15. Also, for our experiment, we see that CH4 ebullition becomes the dominant flux above sediment temperatures of ~10 °C (Fig. 3). Our findings thus suggest that climate warming may change diffusion-dominated systems in colder areas into higher-emission, ebullition-dominated ones. This is particularly relevant for boreal and Arctic waters where >50% of the studied systems (with available data on both CH4 ebullition and diffusion) show that diffusion is the most important emission pathway5. These cold systems already have an important share in global freshwater GHG emissions as their surface area accounts for almost half of the area of the world’s lakes and ponds4,5. Many of these systems are small and shallow38 and will therefore rapidly warm as a consequence of the predicted increase in air temperature, which is expected to be stronger than the global average in the boreal and Arctic region18,39. In addition, many of the high northern latitude lakes are formed in permafrost soils. An increase in temperature should therefore not only enhance microbial metabolism of existing substrates, but also lead to more permafrost thaw, which increases substrate availability and methanogenesis per square meter of lake on decadal to century time scales40, though the process may be limited by widespread thaw lake drainage41. The resulting increase in ebullition in these high-latitude systems may greatly amplify their share in freshwater GHG emissions.
Diffusive and ebullitive CH4 emissions expressed against water temperature. Dif refers to diffusive CH4 emissions and Ebu refers to ebullitive CH4 emissions. The dashed vertical line represents the onset of strongly increased ebullition and a transition to ebullition-dominated flux. Open and closed symbols denote control (C) and warm (W) treatment, respectively
Discussion
In the long term, ebullition rates are primarily driven by the interaction between temperature and substrate supply for methanogenesis15,20,42. In systems with low organic matter production and low allochthonous input, CH4 emission may therefore become substrate-limited as a result of global warming. However, eutrophication and the associated increase in organic matter production may preclude substrate limitation and effectively fuel ebullition15,27,43−45. Ongoing eutrophication46 enhanced by climate change-related increases in sediment nutrient release and organic carbon and nutrient loading from catchments47,48,49 will therefore likely boost CH4 ebullition at a global scale. Yet, the strongest increase in ebullition can be expected in shallow waters15,45,50,51,52 due to limited stratification, sediment temperature being strongly related to atmospheric temperature53, and direct solar warming of the sediments16,54. Small ponds and shallow lakes, which are the most abundant freshwaters globally2, are therefore expected to become hot spots of ebullition. They are also among the systems that receive relatively large terrestrial carbon inputs due to their high perimeter-to-volume ratio17. The growing number of impoundments55 also accumulate organic sediments at high rates and are already characterized as ebullition hot spots20,22.
The high spatiotemporal heterogeneity of ebullition together with paucity of data currently challenge accurate predictions of the absolute increase in emissions as a result of global warming9. If the availability of suitable organic matter is not limiting, both the temperature–ebullition relationships fitted on the field data and our experimental manipulation indicate that climate warming will increase CH4 ebullition by 6–20% per 1 °C warming (Fig. 1 and Table 1). It is currently unknown whether relative increases in ebullition will differ among certain climate regions. Microbial communities in the Arctic, for example, are well adapted to low temperatures56. However, optimum growth temperatures of cold-adapted methanogens are often much higher than in situ temperatures56 and CH4 production in permanently cold sediments has been shown to adapt when exposed to higher than in situ temperatures through changes in community composition and metabolic rates36,57. Additionally, the temperature dependence of sediment CH4 production does not seem to differ between cold and warm climate regions10. Therefore, there is no a priori reason to assume that it would be different for CH4 ebullition. The exponential nature of the empirical relationships in Fig. 1 points out that the absolute effects of warming on ebullition are largest in warmer areas and during the warmest months. Exponential increases in methanogenesis rates have been found up to temperatures of 40 °C10.
Overall, our experimental results combined with the analysis of field data provide evidence that temperature drives CH4 ebullition in different types of freshwater ecosystems in different parts of the world. This strongly suggests that climate change will substantially increase freshwater CH4 emissions through a disproportional increase in ebullition, forming a positive feedback between climate change and freshwater GHG emissions. Our study is the first to show that a strong relationship between temperature and ebullition exists on a large geographical scale and provides estimates of the increase in CH4 ebullition with climate warming. However, the limited availability of data sets (both globally and per system type) hampers accurate predictions about the relative and absolute increase of this important GHG emission pathway. Hence, to be able to extrapolate our findings to global freshwater CH4 emissions, as well as to better predict changes in future emissions, we stress the need for more measurements including ebullition with high spatiotemporal coverage.
Methods
Experimental setup
Experiments were conducted in eight metal cylindrical 988L indoor mesocosms called limnotrons with an average depth of 1.35 m and an inner diameter (ID) of 0.97 m (for more information see ref. 58). The limnotrons were filled with ~70 L of pre-sieved (5 mm mesh size), soft, muddy sediment, and subsequently filled to the top with tap water. Sediment was collected from a mesotrophic shallow pond in Wageningen, The Netherlands (coordinates in DMS: 51°59′16.0″N 5°40′06.1″E) on 13 February 2014. Sediment contained 69 ± 4% (mean ± s.d.) water (% fresh weight) and 6.6 ± 1.1% (mean ± s.d.) organic matter (% dry weight; loss on ignition method). To promote a more diverse initial benthic community, an extra portion of sediment (<8 L) was collected from a nearby eutrophic pond (coordinates in DMS: 51°58′56.7″N 5°43′34.5″E). Water was circulated among limnotrons for 2 days to promote similar starting conditions. Subsequently, nutrients and a phytoplankton inoculum (see below) were added in order to mimic phytoplankton-dominated shallow lakes. The phytoplankton inoculum was obtained by concentrating water from the two ponds mentioned before.
To mimic open water turbulence, we installed two compact axial fans (AC axial compact fan 4850 Z, ebm-papst St. Georgen GmbH & Co. KG, Georgen, Germany) set to an air flow rate of 100 m3 h−1, as well as an aquarium pump (EHEIM compact 300, EHEIM GmbH & Co. KG, Deizisau, Germany) at a depth of 6 cm set at a rate of 150 L h−1, which resulted in a piston velocity (k 600) of 0.44 ± 0.01 (mean ± s.d.) m d−1 (k O2 determined in deoxygenated water, after ref. 59). This k 600 is typical for small lakes and ponds (0.001–0.01 km2)17. The limnotrons were carefully filled with demineralized water twice a week to compensate for evaporative losses.
The incident light intensity was constant throughout the experiment with 175 ± 25 (PAR; mean ± s.d.) μmol photons m−2 s−1, provided by two HPS/MH lamps (CDM-TP Elite MW 315–400 W, AGRILIGHT B.V., Monster, The Netherlands). The light:dark cycle followed Dutch seasonality, varying from 8 h of light at midwinter to 17 h at midsummer. Nutrients were added in a way that start concentrations were achieved of 86 ± 19, 2.4 ± 0.8, and 152 ± 37 μM (mean ± s.d.), for nitrate (NO3 −), phosphate (PO4 3−), and total silicon (Si), respectively. Nutrient losses by sampling were compensated by weekly additions of nitrate and phosphate. Control mesoscoms (n = 4) were subjected to a natural seasonal temperature cycle based on temperature data of Dutch lakes. The warm mesocosms (n = 4) followed the same temperature cycle + 4 °C. From 3 to 10 August, a heat wave of an additional +4 °C was simulated in both treatments (Supplementary Fig. 1). Temperature was measured at depths of 0.5 and 1.0 m using PT100 electrodes and logged at 1 min intervals (Specview 32/859, SpecView Ltd., Uckfield, UK). The experiment started on 3 March 2014 and ended on 1 February 2015. Additional information on phytoplankton, zooplankton, and bacterial dynamics in this experiment can be found in refs. 60 , 61.
Gross primary production
Rates of gross primary production (GPP) were determined every week for each mesocosm using the diel oxygen technique62. DO and temperature were measured every 15 min for 24 h at a depth of 0.4 m, using a multi-parameter meter (HQ40d, Hach, Loveland, CO, USA) equipped with a luminescent/optical dissolved oxygen (LDO) probe (IntelliCAL LDO101). Probes contain a factory calibration of which its accuracy was checked each week by measurements of 0 and 100% O2-saturated water as well as by comparing readings of the two oxygen probes in a single mesocosm. GPP was calculated following the equations in Table 2 of ref. 62, in which the piston velocity (k) was determined in deoxygenated water as mentioned before.
Sedimented carbon
The amount of sedimented carbon was calculated by fortnightly (until heat wave) and monthly (after heat wave) analyses, where sedimentation rates were determined by hanging sedimentation traps (9 cm diameter, 18 cm height, and 1.1 L volume) at 1 m depth for a period of 3 days in each limnotron. The contents of the sediment trap were filtered over pre-washed GF/F filters (Whatman, Maidstone, UK), dried at 60 °C overnight and analyzed for carbon on a NC analyser (FLASH 2000 NC elemental analyser, Brechbuehler Incorporated, Interscience B.V., Breda, The Netherlands). To correct for seston particulate organic carbon (POC) in the overlaying water in the sedimentation traps, water samples were taken with a tube-sampler in the middle of the limnotron on the same day as the sedimentation traps were taken out. These seston samples were handled and analyzed in the same manner as the sedimentation samples. Sedimentation rates were calculated by substracting seston POC from the total amount of POC captured in the sediment trap. The cumulative annual sedimented carbon was calculated as the area under the curve of these sedimentation rates.
Diffusive fluxes
Diffusive fluxes of CH4 were measured once every 2 weeks (until heat wave) and once every 4 weeks (after heat wave) at the end of the light and the end of the dark period. Additional measurements were performed in the week before, during, and after the heat wave. Diffusive CH4 fluxes were measured over a 3-min period using a cylindrical-shaped transparent acrylic top chamber (ID 29.2 cm; headspace height 18 cm) connected in a closed loop to Greenhouse Gas Analyzers (model GGA-24EP, Los Gatos Research, Santa Clara, CA, USA, and model G2508 CRDS Analyzer, Picarro, Santa Clara, CA, USA). Both devices yielded similar results in a post-experiment comparative test, ensuring consistency of measurements. Fluxes were calculated as described by ref. 63. Flux measurements were performed in triplicate. During data analysis, replicates influenced by ebullition (causing a sudden increase in CH4 concentration) were removed and the average flux of the (remaining) replicates was calculated for each limnotron. The diel flux was determined as a weighted average of the light and dark period fluxes, based on day length. Limnotrons were always measured in random order to avoid any time or order effects.
Ebullitive fluxes
CH4 release via ebullition (bubble flux from sediment) was estimated by continuously collecting bubbles throughout the experiment, using two bubble traps in each limnotron. Bubble traps consisted of an inverted funnel (ID 15.2 cm) connected to a 120 mL infusion bottle via an 80 cm long tube (ID 10 mm). Funnels were installed ~50 cm below the water surface and tubes and infusion bottles were completely filled with limnotron water. Gas-filled infusion bottles were collected (and immediately replaced) 13 times during the experiment, always before completely being filled with gas. The number of days before collecting depended on the ebullition rate—determined by visual inspection of the gas volume in the bottles—and ranged from 8 to 65 days (median: 21). After collection, the volume of gas was determined by subtracting the weight of each bottle from the pre-determined full-filled weight (i.e., completely filled with water) of the bottle. CH4 concentrations in the gas were measured on an HP 5890 gas chromatograph equipped with a Porapak Q column (80/100 mesh) and a flame ionization detector (Hewlett Packard, Palo Alto, CA, USA). The CH4 content of the collected ebullitive gas ranged from 0 to 95% with a mean of 57 ± 3% (95% confidence interval). The amount of gaseous CH4 in each bottle was determined by multiplying the CH4 concentration (C gas) by the volume of gas (V gas). The CH4 in the bottles was assumed to be in equilibrium with the water phase. Hence, the amount of CH4 dissolved in the water (C water × V water) was calculated using Henry’s law and its solubility constant for CH4, taking the respective water temperature into account64. The total amount of CH4 in each bottle was calculated by summing the aqueous and gaseous content and divided by funnel surface (A) and time (Δt) to calculate CH4 ebullition per square meter:
Ebullitive gas samples were analyzed for O2, CO2, N2O, and N2 once during the experiment, using a gas chromatograph coupled to a mass spectrometer (Agilent 5975C; Agilent, Santa Clara, CA, USA). O2 and CO2 each typically formed less than 1% of total gas volume, while N2O could not be detected. N2 was the second main component of the gas, together with CH4 composing about 99% of ebullitive gas volume. On several occasions, gas volume in bubble traps was visually inspected before and after diffusive flux measurements to assess whether possible disturbance during this measurement would trigger bubble release. We observed no effect. Between 9 and 15 September, bubble traps were not in use due to maintenance.
Model approach
To describe the temperature dependency of CH4 ebullition for each system, we used a modified Arrhenius equation65:
Where E T is the ebullition rate in mg CH4 m−2 d−1, at temperature T (°C), E 20 is the ebullition rate in mg CH4 m−2 d−1 at 20 °C, and θ s is the overall system temperature coefficient (dimensionless)65,66.
The modified Arrhenius expression was fitted on the data using nonlinear regression analysis in IBM SPSS 21 (IBM, Armonk, NY, USA) that uses the Marquardt–Levenberg algorithm, an iterative procedure to find model parameters that minimize the residual sum of squares. Despite its limitations at the lower and upper end of the temperature range, the modified Arrhenius expression is a useful and often applied method of determining temperature dependencies of ecological and microbiological processes65,66.
Effect of changing CH4 solubility on CH4 ebullition
Solubility-adjusted ebullition rates (Supplementary Fig. 3), i.e., the ebullition rates that would have occurred if CH4 solubility in sediment pore water remained constant, were estimated as follows:
Where, V S is total sediment volume (95 L m−2), W S is sediment water content (as a fraction; 0.69), ΔS CH4 is the change in CH4 solubility (mg CH4 L−1) at a depth of 1.3 m due to changes in temperature67 between moment of bubble trap deployment and harvest, Δt is amount of days between trap deployment and harvest, and E CH4 is the ebullition rate (mg CH4 m−2 d−1) in that period. For these calculations, we assumed year-round CH4-saturated pore waters.
Literature data acquisition
We performed a standardized literature search on data on Google Scholar and the Data Observation Network for Earth (DataONE) using the keywords CH4, methane, ebullition, bubbling, and bubble flux in all possible combinations in August 2016, similar to ref. 17. We further expanded our literature collection by adding the relevant references indicated in studies we found. From all the papers that were collected, we selected those that contained ebullition data from open waters such as ponds, lakes, reservoirs, and rivers within an air/water/sediment temperature range of at least 10 °C to quantitatively model the relationship between ebullition and temperature. Due to the temporal heterogeneity of ebullition, data from short measurements (<24 h) can seriously under- or overestimate ebullitive fluxes and were therefore excluded7,9. We excluded saline and brackish waters since their biogeochemistry strongly deviates from freshwater ecosystems. Five papers fulfilled our requisites15,42,68,69,70. We also included unpublished data from a temperate eutrophic city pond, obtained directly from the authors.
For the post-glacial lakes (Sweden)70, boreal meso-eutrophic forest ponds (Canada)15, temperate river Saar (Germany)42, and temperate eutrophic city pond (Netherlands), data were obtained directly from the authors. Raw data from the temperate farm ponds (USA) were obtained from Table 1 of ref. 68. Data of the subtropical eutrophic city pond (China) was extracted from ref. 69, using WebPlotDigitizer (http://arohatgi.info/WebPlotDigitizer), a web-based tool to obtain high-precision numerical data from plots.
Ebullition data for all studies were obtained by multi-seasonal ebullition measurements, using funnel-type bubble traps. Ebullition was calculated considering the volume of the captured gas and a constant (average) CH4 concentration (refs. 15 , 42 , 69) or the CH4 concentration of each individual gas sample (refs. 68 , 70, this study, and the unpublished data set). The published data of temperate river Saar was based on an average bubble CH4 content of 80%, which was the average of several measurements42. The high-resolution temperature and ebullition data (continuous logging by automated bubble traps42) of this system were averaged over 24 h intervals to produce the dots in Fig. 1. For the subtropical eutrophic city pond, a constant CH4 concentration of 43.3% was used, which was based on the concentration in a nearby eutrophic pond69. For the boreal meso-eutrophic forest ponds15, a CH4 concentration of 57.6% was used, which was the average of all gas samples. Measured CH4 concentration ranges for the post-glacial lake data are provided in ref. 39. The unpublished data of a temperate eutrophic city pond consist of six (three in the littoral (<1 m deep) and three in the central part of the pond (max. 2 m deep)) bubble traps (ID 35 cm), measured over 24 h for each month of the year. Each time for each bubble trap, the collected gas volume was measured and the CH4 concentration was analyzed on a HP 5890 gas chromatograph equipped with a Porapak Q column (80/100 mesh) and a flame ionization detector (GC-FID, Hewlett Packard, Palo Alto, CA, USA). The temperature used in the regression model is the 24-h average water temperature measured with a multi-parameter portable meter (HQ40d, Hach, Loveland, CO, USA) equipped with a luminescent/optical dissolved oxygen (LDO) probe (IntelliCAL LDO101) at the littoral and at the deep station, at ~0.5 m depth. Temperature was recorded every 15 min. Because of the strong variation in methods used in the different studies (e.g., using different measurement frequency and duration, and assuming a fixed CH4 concentration versus accounting for temporal variations in CH4 concentrations of bubbles), we refrained from statistically comparing the different temperature–ebullition models.
Two studies contained separate ebullition data sets of multiple locations42,69. The temperature–ebullition relationships of all individual locations are described in Table 1 and the ebullition data from the location with the longest data record was included in Fig. 1. The post-glacial lake data in Fig. 1 is replotted from ref. 70. It is based on a 6-year data set (2009–2014; total of 10,227 individual flux measurements from multiple locations and depths) from lakes in Stordalen, northern Sweden. Note that it is an extended version of a figure with 4 years of data from the same lakes published in ref. 16. Because of the vast amount of individual flux measurements, data of post-glacial lakes were binned in 1 °C intervals for plotting in Fig. 1. The modified Arrhenius expression was fitted on the raw data.
Statistical analysis
To test for monotonic relationships between water temperature and CH4 diffusion, we used Spearman’s rank correlations. Temperature values for CH4 ebullition were obtained by averaging water temperature over each bubble collection period, while for CH4 diffusion; the average daily temperature at day of flux measurement was used. Cumulative annual CH4 ebullition, sedimentation, GPP, and diffusion data were tested for normal distribution using the Shapiro–Wilk’s test (P > 0.05) and a visual inspection of histograms, normal Q–Q plots and box plots. The Brown–Forsythe test was used to assess homogeneity of variances. Differences between treatments were tested with a Student’s t test or—in case assumptions for normality and homogeneity of variance were violated—with a Mann–Whitney U test. All P values mentioned are two-tailed. Statistical analyses were carried out using IBM SPSS 21 (IBM, Armonk, NY, USA).
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Downing, J. A. et al. Global abundance and size distribution of streams and rivers. Inland Waters 2, 229–236 (2012).
Verpoorter, C., Kutser, T., Seekell, D. A. & Tranvik, L. J. A global inventory of lakes based on high‐resolution satellite imagery. Geophys. Res. Lett. 41, 6396–6402 (2014).
Tranvik, L. J. et al. Lakes and reservoirs as regulators of carbon cycling and climate. Limnol. Oceanogr. 54, 2298–2314 (2009).
Bastviken, D., Tranvik, L. J., Downing, J. A., Crill, P. M. & Enrich-Prast, A. Freshwater methane emissions offset the continental carbon sink. Science 331, 50 (2011).
Wik, M., Varner, R. K., Anthony, K. W., MacIntyre, S. & Bastviken, D. Climate-sensitive northern lakes and ponds are critical components of methane release. Nat. Geosci. 9, 99–105 (2016).
Anthony, W. et al. Estimating methane emissions from northern lakes using ice‐bubble surveys. Limnol. Oceanogr. 8, 592–609 (2010).
Maeck, A., Hofmann, H. & Lorke, A. Pumping methane out of aquatic sediments: ebullition forcing mechanisms in an impounded river. Biogeosciences 11, 2925–2938 (2014).
Scandella, B. P., Delwiche, K., Hemond, H. F. & Juanes, R. Persistence of bubble outlets in soft, methane-generating sediments. J. Geophys. Res. Biogeosci. 122, 1298–1320 (2017).
Wik, M., Thornton, B. F., Bastviken, D., Uhlbäck, J. & Crill, P. M. Biased sampling of methane release from northern lakes: a problem for extrapolation. Geophys. Res. Lett. 43, 1256–1262 (2016).
Marotta, H. et al. Greenhouse gas production in low-latitude lake sediments responds strongly to warming. Nat. Clim. Change 4, 467–470 (2014).
Bastviken, D. in Encyclopedia of Inland Waters Vol. 2 (ed. Gene E. Likens) (Elsevier, Oxford, 2009).
Fuchs, A., Lyautey, E., Montuelle, B. & Casper, P. Effects of increasing temperatures on methane concentrations and methanogenesis during experimental incubation of sediments from oligotrophic and mesotrophic lakes. J. Geophys. Res. Biogeosci. 121, 1394–1406 (2016).
Lofton, D. D., Whalen, S. C. & Hershey, A. E. Effect of temperature on methane dynamics and evaluation of methane oxidation kinetics in shallow Arctic Alaskan lakes. Hydrobiologia 721, 209–222 (2014).
Shelley, F., Abdullahi, F., Grey, J. & Trimmer, M. Microbial methane cycling in the bed of a chalk river: oxidation has the potential to match methanogenesis enhanced by warming. Freshw. Biol. 60, 150–160 (2015).
DelSontro, T., Boutet, L., St‐Pierre, A., del Giorgio, P. A. & Prairie, Y. T. Methane ebullition and diffusion from northern ponds and lakes regulated by the interaction between temperature and system productivity. Limnol. Oceanogr. 61, S62–S77 (2016).
Wik, M. et al. Energy input is primary controller of methane bubbling in subarctic lakes. Geophys. Res. Lett. 41, 555–560 (2014).
Holgerson, M. A. & Raymond, P. A. Large contribution to inland water CO2 and CH4 emissions from very small ponds. Nat. Geosci. 9, 222–226 (2016).
IPCC. in Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T. F. et al.) (Cambridge University Press, Cambridge, UK and New York, NY, USA, 2013).
Duc, N. T., Crill, P. & Bastviken, D. Implications of temperature and sediment characteristics on methane formation and oxidation in lake sediments. Biogeochemistry 100, 185–196 (2010).
Maeck, A. et al. Sediment trapping by dams creates methane emission hot spots. Environ. Sci. Technol. 47, 8130–8137 (2013).
Schwarz, J. I., Eckert, W. & Conrad, R. Response of the methanogenic microbial community of a profundal lake sediment (Lake Kinneret, Israel) to algal deposition. Limnol. Oceanogr. 53, 113 (2008).
Sobek, S., DelSontro, T., Wongfun, N. & Wehrli, B. Extreme organic carbon burial fuels intense methane bubbling in a temperate reservoir. Geophys. Res. Lett. 39, L01401 (2012).
West, W. E., Coloso, J. J. & Jones, S. E. Effects of algal and terrestrial carbon on methane production rates and methanogen community structure in a temperate lake sediment. Freshw. Biol. 57, 949–955 (2012).
West, W. E., McCarthy, S. M. & Jones, S. E. Phytoplankton lipid content influences freshwater lake methanogenesis. Freshw. Biol. 60, 2261–2269 (2015).
Liu, L., Wilkinson, J., Koca, K., Buchmann, C. & Lorke, A. The role of sediment structure in gas bubble storage and release. J. Geophys. Res. Biogeosci. 121, 1992–2005 (2016).
Crenshaw, C., Valett, H. & Webster, J. Effects of augmentation of coarse particulate organic matter on metabolism and nutrient retention in hyporheic sediments. Freshw. Biol. 47, 1820–1831 (2002).
Grasset, C., Abril, G., Guillard, L., Delolme, C. & Bornette, G. Carbon emission along a eutrophication gradient in temperate riverine wetlands: effect of primary productivity and plant community composition. Freshw. Biol. 61, 1405–1420 (2016).
Kelly, C. A. & Chynoweth, D. P. The contributions of temperature and of the input of organic matter in controlling rates of sediment methanogenesis. Limnol. Oceanogr. 26, 891–897 (1981).
Schulz, S. & Conrad, R. Effect of algal deposition on acetate and methane concentrations in the profundal sediment of a deep lake (Lake Constance). FEMS Microbiol. Ecol. 16, 251–259 (1995).
Casper, P., Maberly, S. C., Hall, G. H. & Finlay, B. J. Fluxes of methane and carbon dioxide from a small productive lake to the atmosphere. Biogeochemistry 49, 1–19 (2000).
Davidson, T. A. et al. Eutrophication effects on greenhouse gas fluxes from shallow‐lake mesocosms override those of climate warming. Glob. Change Biol. 21, 4449–4463 (2015).
Yvon-Durocher, G. et al. Five years of experimental warming increases the biodiversity and productivity of phytoplankton. PLoS Biol. 13, 1002324 (2015).
Yvon-Durocher, G., Hulatt, C. J., Woodward, G. & Trimmer, M. Long-term warming amplifies shifts in the carbon cycle of experimental ponds. Nat. Clim. Change 7, 209–213 (2017).
Yvon-Durocher, G. et al. Methane fluxes show consistent temperature dependence across microbial to ecosystem scales. Nature 507, 488–491 (2014).
DelSontro, T., McGinnis, D. F., Sobek, S., Ostrovsky, I. & Wehrli, B. Extreme methane emissions from a Swiss hydropower reservoir: contribution from bubbling sediments. Environ. Sci. Technol. 44, 2419–2425 (2010).
Nozhevnikova, A. N., Holliger, C., Ammann, A. & Zehnder, A. Methanogenesis in sediments from deep lakes at different temperatures (2–70 C). Water Sci. Technol. 36, 57–64 (1997).
Segers, R. Methane production and methane consumption: a review of processes underlying wetland methane fluxes. Biogeochemistry 41, 23–51 (1998).
Lehner, B. & Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 296, 1–22 (2004).
Wik, M., Crill, P. M., Varner, R. K. & Bastviken, D. Multiyear measurements of ebullitive methane flux from three subarctic lakes. J. Geophys. Res. Biogeosci. 118, 1307–1321 (2013).
Kessler, M. A., Plug, L. J. & Anthony, K. M. W. Simulating the decadal- to millennial-scale dynamics of morphology and sequestered carbon mobilization of two thermokarst lakes in NW Alaska. J. Geophys. Res. Biogeosci. 117, G00M07 (2012).
van Huissteden, J. et al. Methane emissions from permafrost thaw lakes limited by lake drainage. Nat. Clim. Change 1, 119–123 (2011).
Wilkinson, J., Maeck, A., Alshboul, Z. & Lorke, A. Continuous seasonal river ebullition measurements linked to sediment methane formation. Environ. Sci. Technol. 49, 13121–13129 (2015).
Deemer, B. R. et al. Greenhouse gas emissions from reservoir water surfaces: a new global synthesis. Bioscience 66, 949–964 (2016).
Harrison, J. A., Deemer, B. R., Birchfield, M. K. & O’Malley, M. T. Reservoir water-level drawdowns accelerate and amplify methane emission. Environ. Sci. Technol. 51, 1267–1277 (2017).
West, W. E., Creamer, K. P. & Jones, S. E. Productivity and depth regulate lake contributions to atmospheric methane. Limnol. Oceanogr. 61, S51–S61 (2015).
Tilman, D. et al. Forecasting agriculturally driven global environmental change. Science 292, 281–284 (2001).
Dhillon, G. S. & Inamdar, S. Extreme storms and changes in particulate and dissolved organic carbon in runoff: entering uncharted waters? Geophys. Res. Lett. 40, 1322–1327 (2013).
Jeppesen, E. et al. Climate change effects on runoff, catchment phosphorus loading and lake ecological state, and potential adaptations. J. Environ. Qual. 38, 1930–1941 (2009).
Moss, B. et al. Allied attack: climate change and eutrophication. Inland Waters 1, 101–105 (2011).
Joyce, J. & Jewell, P. W. Physical controls on methane ebullition from reservoirs and lakes. Environ. Eng. Geosci. 9, 167–178 (2003).
McGinnis, D. F., Greinert, J., Artemov, Y., Beaubien, S. E. & Wüest, A. Fate of rising methane bubbles in stratified waters: how much methane reaches the atmosphere? J. Geophys. Res. 111, C09007 (2006).
Natchimuthu, S. et al. Spatio‐temporal variability of lake CH4 fluxes and its influence on annual whole lake emission estimates. Limnol. Oceanogr. 61, S13–S26 (2015).
O’Reilly, C. M. et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 42, 10773–10781 (2015).
Thornton, B. F., Wik, M. & Crill, P. M. Climate-forced changes in available energy and methane bubbling from subarctic lakes. Geophys. Res. Lett. 42, 1936–1942 (2015).
Zarfl, C., Lumsdon, A. E., Berlekamp, J., Tydecks, L. & Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 77, 161–170 (2015).
Cavicchioli, R. Cold-adapted archaea. Nat. Rev. Microbiol. 4, 331–343 (2006).
Schulz, S., Matsuyama, H. & Conrad, R. Temperature dependence of methane production from different precursors in a profundal sediment (Lake Constance). FEMS Microbiol. Ecol. 22, 207–213 (1997).
Verschoor, A. M., Takken, J., Massieux, B. & Vijverberg, J. The Limnotrons: a facility for experimental community and food web research. Hydrobiologia 491, 357–377 (2003).
Tribe, L., Briens, C. & Margaritis, A. Determination of the volumetric mass transfer coefficient (kLa) using the dynamic “gas out–gas in” method: analysis of errors caused by dissolved oxygen probes. Biotechnol. Bioeng. 46, 388-392 (1995).
Frenken, T. et al. Warming accelerates termination of a phytoplankton spring bloom by fungal parasites. Glob. Change Biol. 22, 299–309 (2016).
Velthuis, M. et al. Warming advances top-down control and reduces producer biomass in a freshwater plankton community. Ecosphere 8, 1–6 (2017).
Staehr, P. A. et al. Lake metabolism and the diel oxygen technique: state of the science. Limnol. Oceanogr. 8, 628–644 (2010).
Almeida, R. M. et al. High primary production contrasts with intense carbon emission in a eutrophic tropical reservoir. Front. Microbiol. 7, 717 (2016).
Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 15, 4399–4981 (2015).
Kadlec, R. H. & Reddy, K. Temperature effects in treatment wetlands. Water Environ. Res. 73, 543–557 (2001).
Veraart, A. J., De Klein, J. J. & Scheffer, M. Warming can boost denitrification disproportionately due to altered oxygen dynamics. PLoS ONE. 6, e18508 (2011).
Duan, Z. & Mao, S. A thermodynamic model for calculating methane solubility, density and gas phase composition of methane-bearing aqueous fluids from 273 to 523 K and from 1 to 2000 bar. Geochim. Cosmochim. Acta 70, 3369–3386 (2006).
Baker-Blocker, A., Donahue, T. M. & Mancy, K. H. Methane flux from wetlands areas. Tellus 29, 245–250 (1977).
Gao, Y. et al. Estimation of N2 and N2O ebullition from eutrophic water using an improved bubble trap device. Ecol. Eng. 57, 403–412 (2013).
Wik, M. Emission of Methane From Northern Lakes and Ponds. PhD dissertation, Stockholm Univ. (2016).
Acknowledgements
We thank R. Mendonça and T. van Bergen for their advice and discussions, as well as for providing their unpublished ebullition data set. We also thank F. Rust de Carvalho, F. Xue, and N. Helmsing for their assistance during the mesocosm experiment. The vector map of Fig. 1 was designed by Freepik (www.freepik.com). N.B. was supported by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) process number 3934-13-6 and CAPES (Brazil)/NUFFIC (The Netherlands) project 045/2012. GK's funding was provided by the Leibniz Association - project Landscales. The work of M.V. was funded by the Gieskes-Strijbis Foundation. M.W. and B.F.T. acknowledge funding from Vetenskapsrådet Grant 2007–2547 and Nordic Center of Excellence DEFROST under the Nordic Top-Level Research Initiative. The work of J.W. was financially supported by the German Research Foundation (Grant numbers LO1150/5-2 and LO1150/9-1). T.D. was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Swiss National Science Foundation. S.K. was supported by Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) Veni Grant 86312012.
Author information
Authors and Affiliations
Contributions
S.K. originally formulated the idea. R.C.H.A. conducted the measurements, collected data from published literature, and analyzed the data. R.C.H.A. and S.K. wrote the manuscript. R.C.H.A., M.V., S.S., G.K. and T.F. mainly took care of the experimental units. M.W., B.F.T., J.W. and T.D. contributed original data. N.B. contributed original, unpublished ebullition data and helped with discussions and advice. L.N.d.S.D. and E.T.H.M.P. provided advice for statistical analyses. N.B., E.v.D., T.F., S.H., G.K., L.P.M.L., E.T.H.M.P., J.G.M.R., L.N.d.S.D., S.S., M.V., D.B.V.d.W., M.W., B.F.T., J.W. and T.D. contributed to revisions of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aben, R.C.H., Barros, N., van Donk, E. et al. Cross continental increase in methane ebullition under climate change. Nat Commun 8, 1682 (2017). https://doi.org/10.1038/s41467-017-01535-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-01535-y
This article is cited by
-
High methane ebullition throughout one year in a regulated central European stream
Scientific Reports (2024)
-
Wetland hydrological dynamics and methane emissions
Communications Earth & Environment (2024)
-
Sustained and intensified lacustrine methane cycling during Early Permian climate warming
Nature Communications (2022)
-
Post-depositional alteration of stable isotope signals by preferential degradation of algae-derived organic matter in reservoir sediments
Biogeochemistry (2022)
-
Carbon fluxes in subtropical shallow lakes: contrasting regimes differ in CH4 emissions
Hydrobiologia (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.