Abstract
Superconductivity appears in the cuprates when a spin order is destroyed, while the role of charge is less known. Recently, charge density wave (CDW) was found below the superconducting dome in YBa2Cu3O y when a high magnetic field is applied perpendicular to the CuO2 plane, which was suggested to arise from incipient CDW in the vortex cores that becomes overlapped. Here by 63Cu-nuclear magnetic resonance, we report the discovery of CDW induced by an in-plane field, setting in above the dome in single-layered Bi2Sr2−x La x CuO6. The onset temperature T CDW takes over the antiferromagnetic order temperature T N beyond a critical doping level at which superconductivity starts to emerge, and scales with the pseudogap temperature T*. These results provide important insights into the relationship between spin order, CDW and the pseudogap, and their connections to high-temperature superconductivity.
Similar content being viewed by others
Introduction
High transition-temperature (T c) superconductivity is obtained by doping carriers to destroy an antiferromagnetic (AF) spin ordered Mott insulating phase. Although it is generally believed that the interaction responsible for the spin order is important for the superconductivity1, the electron pairing mechanism is still elusive. This is because the nature of the normal state is still unclear2,3. For example, in the region with low carrier concentration p (0 < p < 0.2), a pseudogap state emerges where partial density of states (DOS) is lost below a characteristic temperature T* well above T c 4 or even T N 5. Although the nature of the strange metallic state is still under debate, it is likely connected to both spin and change fluctuations or even orders. In fact, experimental progress suggests that the spin and charge degrees of freedom are highly entangled.
For example, a striped spin/charge order was found around x ~ 1/8 in La1.6−x Nd0.4Sr x CuO4 (LSCO) two decades ago6. More recently, various forms of charge order were reported in many other systems. Scanning tunneling microscopy (STM) in Bi2Sr2CaCu2O8+δ′ found a modulation of local DOS in the vortex cores where superconductivity is destroyed7, which was interpreted as due to halos of incipient CDW localized within the cores8,9. Resonant elastic and inelastic x-ray spectroscopy (RXS) measurements found a short-range CDW with ordering vectors along the in-plane Cu-O bond directions, q = (~0.3, 0) and (0, ~0.3). The correlation length is \(\xi _{a,b}\) ~ 50 Å for YBa2Cu3O7−y (YBCO)10,11 and \(\xi _{a,b}\) ~ 20 Å for the other systems12,13,14,15,16. Quite recently, it was suggested by 17O nuclear magnetic resonance (NMR) in YBCO that such CDW is of static origin17. In Bi2Sr2−x La x CuO6+δ (Bi2201), most intriguingly, the onset temperature of the short-range CDW was found to coincide12,16 with T* that is far above T c or T N 5,18.
Application of a high magnetic field is useful to diagnose the interplay between various orders in the cuprates. When a high magnetic field is applied perpendicular to the CuO2 plane, superconductivity can be suppressed substantially. In YBCO, 63Cu NMR at H = 28.5 T revealed a long-range charge density modulation perpendicular to the CuO-chain in the sample with p = 0.10819. RXS also indicated that a high field induces a correlation along the CuO-chain direction and modifies the coupling between CuO2 bilayers, thus causes a three-dimensional CDW20,21. These observations are consistent with early discovery of a Fermi-surface reconstruction by quantum oscillations22 and a recent report of a thermodynamic phase transition23.
These findings have arisen much interests, but the origin of the CDW and its connection to superconductivity is yet unknown. As the long-range CDW onsets below T c(H = 0) and only emerges when the field is applied perpendicular to the CuO2 plane, a wide-spread speculation is that it is due to incipient CDW in the vortex cores7 that becomes overlapped as the field gets stronger11,13,24. In fact, a field as large as 28.5 T applied in the CuO2—plane of YBCO did not bring about any long-range CDW19. Also, the role of the CuO chain is unclear; in Bi2Sr2CaCu2O8+δ without a CuO chain, no long-range CDW was found25.
In order to clarify the relationship between the intertwined AF spin order, CDW, pseudogap and superconductivity, we apply high magnetic fields up to 42.5 T parallel to the Cu−O bond direction (H||a or b axis) in Bi2Sr2−x La x CuO6+δ where the pseudogap spans from the parent AF insulating phase to the overdoped superconducting regime5,18. This material has no CuO chain and the application of an in-plane field does not create vortex cores in the CuO2 plane. Surprisingly, we discover a long-range CDW that emerges far above the superconducting dome for H || > 10 T. We find that such CDW order becomes the successor of the AF order beyond p = 0.107 at which superconductivity starts to emerge. The T CDW takes over T N, but disappears well before the pseudogap closes. Our results indicate that CDW can be well disentangled from other orders.
Results
Evidence for a field-induced CDW in underdoped Bi2201
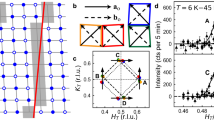
Figure 1a–d shows the 63Cu-NMR satellite (3/2 ↔ 1/2 transition) lines for four compounds of Bi2Sr2−x La x CuO6+δ at two representative temperatures at H || = 14.5 or 20.1 T. As seen in Fig. 1a, no change between T = 100 and 4.2 K is observed for the optimally doped compound (p = 0.162). However, the spectrum is broadened at T = 4.2 K for p = 0.135 (Fig. 1b), and a splitting ±δf of the spectrum is observed at T = 4.2 K for p = 0.128 and 0.114, as seen in Fig. 1c, d. The spectra at T = 4.2 K for p = 0.128 and 0.114 can be reproduced by a sum of two Gaussian functions. It is noted that at low fields below 10 T, the spectrum shows no appreciable temperature dependence in the whole temperature range. The NMR line splitting indicates a long-range order, as it measures an assemble of nuclear spins over the sample.
Field and temperature evolution of NMR satellite line for underdoped Bi2201. a–d The NMR satellite (3/2 ↔ 1/2 transition) lines for Bi2Sr2−x La x CuO6+δ with x = 0.4 (p = 0.162), x = 0.6 (p = 0.135), x = 0.65 (p = 0.128), and x = 0.75 (p = 0.114). The curves for p = 0.135, 0.128, and 0.114 at T = 4.2 K are the sum of two Gaussian functions (shaded area). f peak is the peak frequency. The intensity is normalized by the area of the spectrum. e Field evolution of the line splitting δf for p = 0.114 at T = 4.2 K. f Temperature evolution of δf for p = 0.114 under various fields. The solid arrows indicate T CDW. The dotted arrows indicate T c(H). Error bars represent the uncertainty in estimating δf
Figure 1e shows the field evolution of δf for p = 0.114. The δf grows steeply at H || = 10.4 T and saturates above H || ~ 14.5 T. Figure 1f shows the temperature dependence of δf for p = 0.114 under various fields. The δf grows rapidly below T ~ 30, 55, and 60 K at H || = 11, 13, and above 14.5 T, respectively. These results indicate that a field-induced phase transition occurs in the underdoped Bi2201. The results are qualitatively similar to the results found in YBCO where the same transition line splits into two peaks due to the spatial modulation of the NQR frequency ν Q 19.
Next we show that the field-induced phase transition is due to a charge order, but not spin order. Figure 2a, b, respectively, shows the temperature dependence of the satellite and the center lines for the sample with the lowest doping p = 0.114. A spectrum broadening is also found in the center line (1/2 ↔ −1/2 transition) at T = 4.2 K, but it is much smaller than the satellite line. Figure 2c shows the temperature dependence of the NMR intensity obtained by integrating the spectrum at each temperature. The intensity has no anomaly above T c, indicating that there is no spin order. For antiferromagnetic insulator p = 0.107 (x = 0.8), the intensity decreases below T N = 66 K because an internal field shifts the peak frequency far away5. Furthermore, a possibility of striped phase formation leading to a wipe out effect found in LSCO26 can also be ruled out. It is noted that the possibility of a field-induced spin-density-wave order has already been ruled out previously for p = 0.16227.
Evidence for the CDW without a spin order. Temperature dependence of the NMR satellite a and center b lines for p = 0.114 at H = 14.5 T. Solid curves are the results of Gaussian fittings. The curves at T = 4.2 K are the sum of two Gaussian functions (shaded area). c Temperature dependence of NMR signal intensity for the satellite line (open circles) and the center line (crosses). The intensity is corrected by taking into account the 1/T factor and the T 2 effect. The absence of any intensity loss across T CDW rules out the presence of any kinds of spin order. The intensity loss below T c is due to the Meissner effect. The temperature dependencies of 1/T 1 T d and 1/T 2 e at different fields
Therefore, the splitting of the satellite line (Fig. 2a) and the broadening of the center line (Fig. 2b) is due to a distribution of the Knight shift \(K_\parallel \pm \delta K_\parallel \) and the NQR frequency as ν Q ± δν as observed in YBCO. Furthermore, the splitting δf satellite = 1.22 MHz is much larger than δf center = 0.271 MHz, indicating that the ν Q change is the main contributor to the observed line splitting. By a simple calculation (Supplementary Note 1), we find that \(\delta K_\parallel \sim 0.05 \pm 0.01\% \) and δν = 2.5 ± 0.2 MHz can reproduce both the satellite and the center lines at the same time (shaded areas in Fig. 2a, b). The relation ν Q = 22.0 + 39.6 p (Supplementary Fig. 1) then yields a hole-concentration distribution \(\delta p\sim 0.06 \pm 0.01\) at the Cu site. Since there is no spin order here (Fig. 2c) as mentioned already, the splitting of the satellite line δf (∝ δp) indicates a field-induced long-range charge distribution, i.e., a formation of CDW at low temperature in underdoped Bi2201.
Figure 2d, e shows the temperature dependence of the nuclear spin-lattice relaxation rate divided by T, 1/T 1 T and spin-spin relaxation rate 1/T 2 for p = 0.114 obtained at two different fields. At H = 9 T, both quantities decrease monotonically below T* = 230 K. At H = 13 T, however, a pronounced peak was found in 1/T 1 T at T CDW = 55 K. Such a peak in 1/T 1 T is a characteristic of a CDW order28. The 1/T 2 also shows a sharp decrease at T CDW = 55 K. These results provide further evidence for a field-induced CDW phase transition.
H-T phase diagram for underdoped Bi2201
To obtain the CDW onset temperature (T CDW) and the threshold field (H CDW) for p = 0.114, we study the temperature dependence of the NMR spectra at various magnetic fields (Fig. 1e, f).
Figure 3 shows the H−T phase diagram for p = 0.114. Remarkably, the long-range CDW state in Bi2201 emerges at a temperature far above T c, in contrast to that in YBCO where CDW appears below T c(H = 0)19,24.
Relationship between CDW and superconductivity
Figure 4a, b shows the H-dependence and T-dependence of the satellite splitting δf which allow us to obtain H CDW and T CDW for various doping levels. Figure 5 shows the hole concentration dependence of H c2, H CDW, and T CDW. The H c2 ~ 60 T for p = 0.162 (Supplementary Fig. 5) decreases with decreasing doping level but increasing again at p = 0.114. Although the previous Nernst effect study on three Bi2201 samples (p = 0.12, 0.16, and 0.19) did not take a closer look into the doping range as we did here29, our result is consistent with the results of YBCO24 and La1.8−x Eu0.2Sr x CuO4 29.
Doping dependence of H CDW and T CDW. a H dependence of δf at T = 4.2 K. From fitting (solid curves) the data to a mean field model, δf ∝ (H−H CDW)0.5, the threshold field for H-induced CDW, H CDW = 10.4, 11.0, and 11.8 T for p = 0.114, 0.128, and 0.135, respectively, was determined. b Temperature dependence of δf for the three samples, from which the CDW onset temperature T CDW = 60, 50, and 35 K for p = 0.114, 0.128, and 0.135, respectively, was determined. The curves are fits to a mean field model, δf ∝ (T CDW−T)0.5. The dotted horizontal lines are guides to the eyes. Error bars represent the uncertainty in estimating δf
The relationship between superconductivity and the CDW in underdoped Bi2201. Doped hole concentration dependence of the upper critical field H c2, H CDW (left axis) and T CDW (right axis). Error bars represent the uncertainty in the fit using WHH formula to obtain H c2 (Supplementary Fig. 5) and in defining the onset field H CDW and temperature T CDW
The H CDW is slightly lower than that in YBCO, suggesting that CDW has a similar energy scale across different class of cuprates. However, the relationship between H CDW and H c2 is completely different from that seen in YBCO where H CDW scaled with H c2. Namely, H CDW was the lowest at the doping concentration where H c2 was the smallest there24, which led to the suggestion that CDW can only be seen when the superconducting state is suppressed as the vortex cores become overlapped. In the present case, however, no vortex cores are created in the CuO2 plane. In fact, H CDW and T CDW are more related with doping concentration itself as can be seen in Fig. 5, rather than with H c2. Namely, the long-range CDW order is induced more easily closer to the AF phase boundary.
Discussion
In this section, we discuss possible CDW form and the implication of the phase diagram we found. First, the result can be understood by an incommensurate 1-dimensional (1D) long-range CDW as follows, as the situation is similar to that observed at the in-plane Cu2F-site located below the oxygen-filled CuO chain in YBCO19. For an unidirectional CDW state, the wave modulation causes a spatial distribution in the electric field gradient (EFG) and thus the NQR frequency so that ν = ν Q + δνcos(ϕ(X))28,30, where X ( = a or b axis) is the modulation direction. The NMR spectral intensity (I(ν)) depends on the spatial variation of ϕ(X) as I(ν) = 1/(2πdν/dϕ). For an incommensurate order, ϕ(X) is proportional to X, so that the NMR spectrum shows an edge singularity at ν = ν Q ± δν, as \(I(\nu ) = 1/\left( {2\pi \delta \nu \sqrt {1 - \left( {\left( {\nu - \nu _Q} \right)/\delta \nu } \right)^2} } \right)\) 28,30. By convoluting a broadening function, a two-peak structure can be reproduced. In such case, the quantity 2δν corresponds to the CDW order parameter28. We emphasize that the value of δp is twice larger than that observed in YBCO19, indicating that a larger CDW amplitude is realized in Bi2201. This difference may arise from the different crystal structure between the two systems. YBCO is a bi-layer system while Bi2201 is single layered. When CDW has a different phase between two CuO2 planes, the ordering effect would be weakened or even canceled out.
It has been known that magnetic field works to induce a correlation along the CuO-chain direction and modifies the coupling between CuO2 bilayers in YBCO20,21. In the present case, the short-range CDW at zero magnetic field12,16 could also be modified by H || > 10 T to be a long ranged 1D CDW along the Cu−O direction.
Second, how about a 2D-CDW case? Recent resonant X-ray scattering measurement on Bi2201 p ~ 0.11 found a perfect 2D but local (ξ ~ 20 Å) CDW formation along the Cu−O bond direction with the wave vector (Q*, 0) and (0, Q*) (Q* ~ 0.26)16,31. On the other hand, STM measurement suggested a commensurate density-wave with the ordering vectors q DW = (0.25, 0) and (0, 0.25)32. In either case, if such a local CDW becomes long ranged with the same ordering vectors, a spatial distribution of the NQR frequency can be written as ν = ν Q + δν X cos(ϕ(X)) + δν Y cos(ϕ(Y)), where X = a-axis and Y = b-axis are the modulation directions30. As suggested by RXS and STM measurements, when the CDW amplitudes are equivalent δν X = δν Y , such CDWs yield \(I(\nu )\sim - {\mathrm{ln}}[(\nu - \nu _{\mathrm{Q}})/\delta \nu ]/\delta \nu \) 30. In this case, the logarithmic singularity appears at δν = 030, which is different from the 1D case. It is obvious that we can not explain our experimental results with such 2D CDW. However, if the amplitude for each directions is different, \(\delta \nu _{X(Y)} \gg \delta \nu _{Y(X)}\), two edge-singularities will appear30. It is also interesting to note that if there are CDW domains with modulations ν X = ν Q + δν X cos(ϕ(X)) and ν Y = ν Q + δν Y cos(ϕ(Y)) in each domain, the NMR lineshape will be the same as in the 1D case.
Third, a 3D CDW will not show two edge singularities in ν Q distribution in any case30. Therefore, we may exclude the possibility of a 3D CDW because, being different from the bilayer YBCO, the long distance between CuO2 planes produces no CDW correlation along the c-axis in Bi220116 and in our case the magnetic field is applied parallel to the CuO2 plane.
We now show in Fig. 6 how the long-range CDW emerges as the magnetic field is increased. As seen in the H-p plane at T = 4.2 K, the field-induced CDW emerges for H || > 10 T in the underdoped regime. At such high fields, upon increasing doping, the AF state with T N = 66 K at p = 0.107 changes to a CDW ordered state with T CDW ~ 60 K at p = 0.114. Upon further doping to p = 0.162 where the pseudogap persists; however, the CDW order disappears. Although a detailed analysis is difficult, a similar field-induced CDW is also found when the magnetic field is applied perpendicular to the CuO2 plane (Supplementary Fig. 6). Figure 7 compares the phase diagram with that for YBCO. In YBCO, the short-range CDW sets in far below T* and the field-induced CDW (FICDW) occurs inside the superconducting dome forming a dome-like shape19, while in Bi2201 the short-range CDW sets in right at T* and the FICDW emerges far above the superconducting dome and coexists with superconductivity.
Magnetic-field evolution of the phase diagram. Hole concentration (p) dependence of the pseudogap temperature T*, T N, and T c, and the p- and H-dependence of T CDW for Bi2Sr2−x La x CuO6+δ . Magnetic field is applied along the Cu-O bond direction (\(H\parallel a(b)\)). T CDW(p,H) (green and gray curves) is obtained from the results on Fig. 1f and Fig. 4. T* (yellow curve) and T N (red curve) are from the previous works5,18. T c(p,H) (blue curve) is determined by the ac-susceptibility measurements using the NMR coil
Phase diagram of Bi2201 compared with YBCO. Doping dependence of the short-range CDW reported by the X-ray measurements2,12,16 and the field-induced CDW (FICDW) for Bi2201 a and YBCO b. For both cases, T c is the zero-field value. Error bars represent the uncertainty in defining T CDW. The schematic phase diagram for YBCO is from the literatures2,19
Figure 6 reveals several important things. First and most remarkably, down-shifting the T* curve in temperature coincides with the T CDW curve. As can be seen more directly in Fig. 8, T CDW scales with T*. This may suggest that the pseudogap is a fluctuating form of the long-range order found in this work, but more work is needed. Very recently, a polar Kerr effect33 and an optical rotational anisotropy measurements34 suggested that a possible phase transition takes place at T*. However, we note that the probes used are ultrafast in time scale. In NMR measurements, the time scale is in the 10−8 s range which is much slower than the optical measurements33,34, and it is reasonable that T* is seen as a fluctuating crossover temperature. Second, T N is succeeded by T CDW beyond a critical doping level at which superconductivity emerges, pointing to the important role of charge degree of freedom in high-temperature superconductivity. However, the detailed evolution from AF to CDW order under high magnetic fields is unclear at the moment. It is a future task to clarify whether the evolution is a first-order phase transition or not. The result also calls for further scrutinies of the AF insulating phase. In fact, the entanglement of the spin and charge freedoms3,35 was recently found to occur already in the insulating phase itself36. In any case, our results show that CDW order is another outstanding quantum phenomenon that needs to be addressed on the same footing as the AF spin order. Finally, the first demonstration of the ability of using an in-plane field to tune the electronic state should stimulate more works that will eventually help to solve the problem of high-T c superconductivity.
Methods
Samples
The single crystals of Bi2Sr2−x La x CuO6+δ (Bi2201, p = 0.114 (x = 0.75), 0.128 (0.65), 0.135 (0.60), and 0.162 (0.40)) were grown by the traveling solvent floating zone method37,38. The hole concentration (p) were estimated previously39. Small and thin single-crystal platelets, typically sized up to 2 mm−2 mm−0.1 mm, cleaved from an as-grown ingot, were used. The in-plane Cu−O bond direction (a or b axis) was determined by Laue reflection. T c(H) is defined at the onset temperature of diamagnetism observed by ac-susceptibility measurement using NMR coil. H c2 is determined by fitting T c(H) to the WHH formula40.
NMR
The 63Cu-NMR spectra were taken by sweeping the rf frequency at a fixed field below H = 15 T but they were taken by sweeping the field at a fixed frequency above H = 15 T. Measurements at H = 14.5 T were conducted at Institute of Physics, CAS, Beijing, and those below H = 14.5 T were conducted at Okayama University. High magnetic fields above H = 15 T are generated by the Hybrid magnet in the National High Magnetic Field Laboratory, Tallahassee, Florida. For 63,65Cu, the nuclear spin Hamiltonian is expressed as the sum of the Zeeman and nuclear quadrupole interaction terms, \({\cal H} = {\cal H}_{\mathrm{z}} + {\cal H}_{\mathrm{Q}} = - ^{63,65}\gamma \hbar {\mathbf{I}} \cdot {\mathbf{H}}_0(1 + K) + (h\nu _{\mathrm{Q}}/6)[3I_z^2 - I(I + 1) + \eta (I_x^2 - I_y^2)]\), where 63 γ = 11.285 MHz/T and 65 γ = 12.089 MHz/T, K is the Knight shift, and I = 3/2 is the 63,65Cu nuclear spin. The NQR frequency ν Q and the asymmetry parameter η are defined as \(v_{\mathrm{Q}} = \frac{{3eQV_{{\mathrm{zz}}}}}{{2I(2I - 1)h}}\), \(\eta = \frac{{V_{{\mathrm{xx}}} - V_{{\mathrm{yy}}}}}{{V_{{\mathrm{zz}}}}}\), with Q and V αβ being the nuclear quadrupole moment and the electric field gradient (EFG) tensor41. The principal axis z of the EFG is along the c axis and η = 042. Due to \({\cal H}_{\mathrm{Q}}\), one obtains the NMR center line and the two satellite transition lines between \(\left| m \right\rangle \) and \(\left| {m - 1} \right\rangle \), (m = 3/2, 1/2, −1/2), at \(\nu _{m \leftrightarrow m - 1} = ^{63,65}\gamma H_0(1 + K) + (\nu _{\mathrm{Q}}/2)(3\mathop {{cos}}\nolimits^2 \theta - 1)(m - 1/2)\) + second-order correction. The second term of the right side is the first order term in the presence of quadrupole interaction. Here, θ is the angle between H and EFG. The T 1 and T 2 were measured at the frequencies in the center peak (m = 1/2 ↔ −1/2 transition). The T 1 values were measured by using a single saturating pulse and were determined by standard fits to the recovery curve of the nuclear magnetization to the theoretical function for the nuclear spin I = 3/218. The T 2 values were obtained by fits to the spin-echo decay curve of the nuclear magnetization I(t) to I(t) = I(0)exp(−2t/T 2)5.
Data availability
The data that support the findings of this study are available on reasonable request.
References
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Timusk, T. & Statt, B. The pseudogap in high-temperature superconductors: an experimental survey. Rep. Prog. Phys. 62, 61–122 (1999).
Kawasaki, S., Lin, C. T., Kuhns, P. L., Reyes, A. P. & Zheng, G.-q Carrier-concentration dependence of the pseudogap ground state of superconducting Bi2Sr2−x La x CuO6+δ revealed by 63,65Cu-nuclear magnetic resonance in very high magnetic fields. Phys. Rev. Lett. 105, 137002 (2010).
Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y. & Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 375, 561–563 (1995).
Hoffman, J. E. J. E. et al. A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi2Sr2CaCu2O8+δ . Science 295, 466–469 (2002).
Zhang, T., Demler, E. & Sachdev, S. Competing orders in a magnetic field: spin and charge order in the cuprate superconductors. Phys. Rev. B 66, 094501 (2002).
Kivelson, S. A., Lee, D.-H., Fradkin, E. & Oganesyan, V. Competing order in the mixed state of high-temperature superconductors. Phys. Rev. B 66, 144516 (2002).
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x . Science 337, 821–825 (2012).
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67. Nat. Phys. 8, 871–876 (2012).
Comin, R. et al. Charge order driven by Fermi-arc instability in Bi2Sr2−x La x CuO6+δ . Science 343, 390–392 (2014).
da Silva Neto, E. H. et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science 343, 393–396 (2014).
Hashimoto, M. et al. Direct observation of bulk charge modulations in optimally doped Bi1.5Pb0.6Sr1.54CaCu2O8+δ . Phys. Rev. B 89, 220511(R) (2014).
Tabis, W. et al. Charge order and its connection with Fermi-liquid charge transport in a pristine high-T c cuprate. Nat. Commun. 5, 5875 (2014).
Peng, Y. Y. et al. Direct observation of charge order in underdoped and optimally doped Bi2(Sr,La)2CuO6 by resonant inelastic x-ray scattering. Phys. Rev. B 94, 184511 (2016).
Wu, T. et al. Incipient charge order observed by NMR in the normal state of YBa2Cu3O y . Nat. Commun. 6, 6438 (2015).
Zheng, G.-q, Kuhns, P. L., Reyes, A. P., Liang, B. & Lin, C. T. Critical point and the nature of the pseudogap of single-layered copper-oxide Bi2Sr2−x La x CuO6+δ superconductors. Phys. Rev. Lett. 94, 047006 (2005).
Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3O y . Nature 477, 191–194 (2011).
Gerber, S. et al. Three-dimensional charge density wave order in YBa2Cu3O6.67 at high magnetic fields. Science 350, 949–952 (2015).
Chang, J. et al. Magnetic field controlled charge density wave coupling in underdoped YBa2Cu3O6+x . Nat. Commun. 7, 11494 (2016).
Doiron-Leyraud, N. et al. Quantum oscillations and the Fermi surface in an underdoped high-T c superconductor. Nature 447, 565–568 (2007).
LeBoeuf, D. D. et al. Thermodynamic phase diagram of static charge order in underdoped YBa2Cu3O y . Nat. Phys. 9, 79–83 (2013).
Wu, T. et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nat. Commun. 4, 2113 (2013).
Crocker, J. et al. NMR studies of pseudogap and electronic inhomogeneity in Bi2Sr2CaCu2O8+δ . Phys. Rev. B 84, 224502 (2011).
Hunt, A. W., Singer, P. M., Cederström, A. F. & Imai, T. Glassy slowing of stripe modulation in „(La,Eu,Nd)2−x Â…(Sr,Ba) x CuO4: A 63Cu and 139La NQR study down to 350 mK. Phys. Rev. B 64, 134525 (2001).
Mei, J.-W., Kawasaki, S., Zheng, G.-q, Weng, Z.-Y. & Wen, X.-G. Luttinger-volume violating Fermi liquid in the pseudogap phase of the cuprate superconductors. Phys. Rev. B 85, 134519 (2012).
Kawasaki, S. et al. Coexistence of multiple charge-density waves and superconductivity in SrPt2As2 revealed by 75As-NMR/NQR and 195Pt-NMR. Phys. Rev. B 91, 060510(R) (2015).
Chang, J. et al. Decrease of upper critical field with underdoping in cuprate superconductors. Nat. Phys. 8, 751–756 (2012).
Blinc, R. & Apih, T. NMR in multidimensionally modulated incommensurate and CDW systems. Prog. Nucl. Magn. Reson. Spectrosc. 41, 49–82 (2002).
Comin, R. et al. Symmetry of charge order in cuprates. Nat. Mater. 14, 796–800 (2015).
Fujita, K. et al. Direct phase-sensitive identification of a d-form factordensity wave in underdoped cuprates. PNAS 111, E3026–E3032 (2014).
He, R.-H. et al. From a single-band metal to a high-temperature superconductor via two thermal phase transitions. Science 331, 1579–1583 (2011).
Zhao, L. et al. A global inversion-symmetry-broken phase inside the pseudogap region of YBa2Cu3O y . Nat. Phys. 13, 250–254 (2017).
Tu, W. L. & Lee, T. K. Genesis of charge orders in high temperature superconductors. Sci. Rep. 6, 18675 (2016).
Cai, P. et al. Visualizing the evolution from the Mott insulator to a charge-ordered insulator in lightly doped cuprates. Nat. Phys. 12, 1047–1051 (2016).
Peng, J. B. & Lin, C. T. Growth and accurate characterization of Bi2Sr2−x La x CuO6+δ single crystals. J. Supercond. Nov. Magn. 23, 591–596 (2010).
Liang, B. & Lin, C. T. Floating-zone growth and characterization of high-quality Bi2Sr2−x La x CuO6+δ single crystals. J. Cryst. Growth 267, 510–516 (2004).
Ono, S. S. et al. Metal-to-insulator crossover in the low-temperature normal state of Bi2Sr2−x La x CuO6+δ . Phys. Rev. Lett. 85, 638–641 (2000).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, Hc2. III. electron spin and spin-orbit effects. Phys. Rev. 147, 295–302 (1966).
Abragam, A., The Principles of Nuclear Magnetism (Oxford University Press, London, 1961).
Zheng, G.-q, Kitaoka, Y., Ishida, K. & Asayama, K. Local hole distribution in the CuO2 plane of high-T cCu-oxides studied by Cu and oxygen NQR/NMR. J. Phys. Soc. Jpn 64, 2524–2532 (1995).
Acknowledgements
We thank D.-H. Lee, S. Uchida, L. Taillefer, T. K. Lee, M.-H. Julien, and S. Onari for useful discussion, and S. Maeda and D. Kamijima for experimental assistance. A portion of this work was performed at National High Magnetic Field Laboratory, which is supported by NSF Cooperative Agreement No. DMR-1157490 and the State of Florida. Support by research grants from Japan MEXT (No. 25400374 and 16H04016), China NSF (No. 11634015), and MOST of China (No. 2016YFA0300502 and No. 2015CB921304) is acknowledged.
Author information
Authors and Affiliations
Contributions
G.-q.Z. planned the project. C.T.L. synthesized the single crystals. S.K., Z.L., M.K., P.L.K., A.P.R., and G.-q.Z. performed NMR measurements. G.-q.Z. wrote the manuscript with inputs from S.K. All authors discussed the results and interpretation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kawasaki, S., Li, Z., Kitahashi, M. et al. Charge-density-wave order takes over antiferromagnetism in Bi2Sr2−x La x CuO6 superconductors. Nat Commun 8, 1267 (2017). https://doi.org/10.1038/s41467-017-01465-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-01465-9
This article is cited by
-
Atomic-scale visualization of a cascade of magnetic orders in the layered antiferromagnet GdTe3
npj Quantum Materials (2024)
-
Strain-induced long-range charge-density wave order in the optimally doped Bi2Sr2−xLaxCuO6 superconductor
Nature Communications (2024)
-
Possible star-of-David pattern charge density wave with additional modulation in the kagome superconductor CsV3Sb5
npj Quantum Materials (2022)
-
Unified energy law for fluctuating density wave orders in cuprate pseudogap phase
Communications Physics (2022)
-
Locally commensurate charge-density wave with three-unit-cell periodicity in YBa2Cu3Oy
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.