Abstract
Monolayer transition metal dichalcogenides, such as MoS2 and WSe2, have been known as direct gap semiconductors and emerged as new optically active materials for novel device applications. Here we reexamine their direct gap properties by investigating the strain effects on the photoluminescence of monolayer MoS2 and WSe2. Instead of applying stress, we investigate the strain effects by imaging the direct exciton populations in monolayer WSe2–MoS2 and MoSe2–WSe2 lateral heterojunctions with inherent strain inhomogeneity. We find that unstrained monolayer WSe2 is actually an indirect gap material, as manifested in the observed photoluminescence intensity–energy correlation, from which the difference between the direct and indirect optical gaps can be extracted by analyzing the exciton thermal populations. Our findings combined with the estimated exciton binding energy further indicate that monolayer WSe2 exhibits an indirect quasiparticle gap, which has to be reconsidered in further studies for its fundamental properties and device applications.
Similar content being viewed by others
Introduction
Two-dimensional (2D) transition metal dichalcogenides (TMDs) in the family of MX2 (M:Mo, W; X:S, Se) have been discovered as a new class of semiconductors for atomically thin electronics and optoelectronics1,2,3,4,5,6. Of particular interest are monolayer MX2, which have been identified as direct gap semiconductors and emerged as new optically active materials for developing novel 2D light emitters and absorbers5, 6. Experimental evidence of direct gap in monolayer MX2 was obtained from the observation of strongly enhanced photoluminescence (PL) caused by the indirect to direct gap transition when MX2 were thinned to one monolayer7, 8. Although most theoretical calculations have also shown a direct gap at K-valley in all monolayer MX2 9,10,11,12, subtle differences have been found in some calculations for monolayer WSe2 13, where the conduction band (CB) minimum lies at Q-valley (about midway between K and Γ). Indeed, recent scanning tunneling spectroscopy (STS) suggested that the Q-valley is about 80 meV below the K-valley in the CB of monolayer WSe2 14, indicative of an indirect quasiparticle gap. However, due to the unusually strong Coulomb interactions and the lack of knowledge on the binding energy of indirect excitons, it remains unclear whether the optical gap (i.e., quasiparticle gap minus exciton binding energy) is also indirect. While efficient PL is invariably observed in monolayer WSe2, the indirect quasiparticle gap observed by STS suggested that the direct/indirect nature of optical gap in monolayer WSe2 has not been settled thus far.
Strain is an effective perturbation that can modulate not only the direct gap of MX2, but also the indirect gap with a different trend11, 15,16,17,18. As the indirect gap energy is pushed away from or brought closer to the direct gap by strain, the exciton population participating in the direct-gap recombination will be affected by the presence of nearly degenerated indirect gap, leading to a modulation in the energy and intensity of direct exciton PL.
In this work, instead of applying external stress, we investigate the spatially resolved PL from monolayer WSe2–MoS2 and MoSe2–WSe2 lateral heterojunctions (HJs) with inherent nonuniform strain distribution19. The built-in local strain inhomogeneity exhibited in lateral HJs provides a unique platform to study the strain effects on MX2 without the need of applying strain. Here we first demonstrate PL from strained MoS2 in WSe2–MoS2 lateral HJs as a model system to extract the energy difference between the direct and indirect gaps in monolayer MoS2. Then we demonstrate the study of MoSe2–WSe2 lateral HJs and show that unstrained monolayer WSe2 is actually an indirect gap material.
Results
PL inhomogeneity in strained WSe2–MoS2 lateral HJs
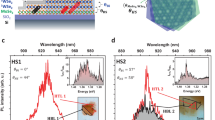
Figure 1a shows the optical image of a typical WSe2–MoS2 lateral HJs. Raman analysis (Fig. 1b) reveals that the inner and outer regions are monolayer WSe2 and MoS2, respectively. The typical size of the HJ flakes is ~ 15–25 μm. According to ref. 19, the outer MoS2 exhibits nonuniform strain distribution due to the lattice mismatch between two materials, leading to considerable spatial variations in local PL spectra in the outer MoS2. Figure 1c shows five selected PL spectra, of which the PL energy variation is ~ 100 meV, corresponding to a strain variation up to ~ 2% in the monolayer MoS2 (based on the reported linear PL energy shift rate of ~ 45 meV/% strain)16. As shown in Fig. 1d and e, the spatial distributions of PL intensity and energy in outer MoS2 show a “positive” correlation, i.e., the site with a higher PL energy always exhibited a higher intensity. The PL intensity–energy correlation can be seen clearly in Fig. 1f, where the integrated intensities and peak energies collected from all local PL spectra of the outer MoS2 are plotted together.
PL inhomogeneity in strained WSe2–MoS2 lateral HJs. a, b Optical image (a) and the corresponding contour color map of the E2g Raman peak position (b) of a monolayer WSe2–MoS2 lateral HJ flake. c Five selected PL spectra from different positions in the MoS2 region. d, e Contour color maps of the PL intensity (d) and peak energy (e) of the MoS2 region. f Integrated PL intensity as a function of peak energy obtained from all PL spectra (black dots). Solid line is the model fitting curve. The top axis is the PL peak energy shift with respect to the unstrained MoS2 (vertical line). g Schematics for the band structures of monolayer MoS2 without (black) and with (gray) tensile strain. h Schematics for the direct (K-K) and indirect (K-Γ) excitonic states with energies of E X,D and E X,I, respectively
The PL intensity–energy correlation arises from the variation of direct exciton populations caused by the strain-induced changes in the direct and indirect gap energies. For monolayer MoS2, the indirect gap (K-Γ) is higher in energy than the direct gap at K-valley (Fig. 1g)20,21,22. Since the K-Γ indirect gap (E KΓ) reduces with tensile strain faster than the K-K direct gap (E KK)11, 15,16,17, the direct and indirect exciton states will be brought closer in energy by tensile strain, leading to a marked change in direct exciton population and hence the PL intensity. We analyze the steady-state PL intensity by modeling the exciton populations in a simple two-level system (Supplementary Fig. 1 and Supplementary Note 1). In thermal equilibrium, the populations of direct N X,D and indirect N X,I excitons follow the Boltzmann distribution N X,I = N X,Dexp(−Δ/k B T), and
where Δ = E X,I−E X,D is the energy difference between the indirect (E X,I) and direct (E X,D) exciton energies (Fig. 1h), and N 0 = N X,D + N X,I is the total exciton population. The energy difference Δ is strain dependent, which can be expressed as \(\Delta = ( {E_{{\rm{X}},{\rm{I}}}^0 + {\rm{\delta }}{E_{{\rm{X}},{\rm{I}}}}} ) - ( {E_{{\rm{X}},{\rm{D}}}^0 + {\rm{\delta }}{E_{{\rm{X}},{\rm{D}}}}} ) = {\Delta _0} + (\gamma - 1)\delta {E_{{\rm{X}},{\rm{D}}}}\), where \(E_{{\rm{X}},{\rm{D}}}^0\) and \(E_{{\rm{X}},{\rm{I}}}^0\) (δE X,D and δE X,I) are the unstrained (strain-induced changes in) energies of the direct and indirect excitons, respectively, \({\Delta _0} = E_{{\rm{X}},{\rm{I}}}^0 - E_{{\rm{X}},{\rm{D}}}^0\) is the unstrained value of Δ, and γ = δE X,I/δE X,D, which is related to the ratio of deformation potential of the K-Γ and K-K quasiparticle gaps. The strain-induced shift in the direct exciton energy, i.e., \({\rm{\delta }}{E_{{\rm{X}},{\rm{D}}}} = {E_{{\rm{X}},{\rm{D}}}} - E_{{\rm{X}},{\rm{D}}}^0\), can be obtained from the difference between PL peak energies of strained and unstrained monolayer MoS2. In our analysis, we assumed the PL peak energy of transferred MoS2 monolayers on sapphire substrates (1.881 eV; vertical line in Fig. 1f) as the direct exciton energy of unstrained monolayer MoS2 (Supplementary Fig. 2). By fitting Eq. (1) to the experimental data and considering Δ0 and γ as fitting parameters, we obtain a very good fit (solid curve in Fig. 1f) and determine Δ0 = 0.08 eV and γ = 1.95 ± 0.14 (see Supplementary Figs. 3 and 4), indicative of a direct optical gap in unstrained MoS2 monolayer, consistent with past understandings7, 8, 20,21,22.
PL inhomogeneity in strained MoSe2–WSe2 lateral HJs
We now turn to the study of strained WSe2. Figure 2a shows the optical image of a typical MoSe2–WSe2 lateral HJs, where the inner and outer regions have been identified as MoSe2 and WSe2 monolayers, respectively, by PL measurements (Fig. 2b). As shown in the spatially resolved PL measurements (Fig. 2c, d) and the selected PL spectra from different areas (Fig. 2e), the outer WSe2 region also exhibits remarkable variations in local PL intensity and energy due to the spatial strain inhomogeneity. Since the lattice mismatch between MoSe2 and WSe2 is small (<0.2%)23, the strain inhomogeneity is likely to arise from the cooling process after high-temperature growth owing to the mismatch in thermal expansion coefficients between TMDs and substrates24,25,26,27. In contrary to strained MoS2, the PL intensity and energy of the strained WSe2 shows a “negative” correlation, i.e., the site with a higher PL energy exhibited a lower PL intensity (Fig. 2f). The negative intensity–energy correlation suggests that the strain-induced change in the indirect gap is very different from that in MoS2. In monolayer WSe2 (Fig. 2g), the Q-K indirect gap is very close to K-K direct gap. Under tensile strain, the K-K direct gap reduces, while the Q-K indirect gap increases18, leading to the increasing PL intensity with tensile strain.
PL inhomogeneity in strained MoSe2–WSe2 lateral HJs. a Optical image of a monolayer MoSe2–WSe2 HJ. b The PL spectra of the inner MoSe2 and the outer WSe2. c, d Contour color maps of the PL peak energy (c) and intensity (d) of outer WSe2. e Five selected PL spectra from the outer WSe2. (f) Integrated PL intensity as a function of peak energy (black dots). Solid line is the model fitting curve. The top axis is the PL peak energy shift with respect to the unstrained WSe2. g Schematics for the band structures of monolayer WSe2 without (black) and with (gray) tensile strain. h Schematics for the direct (K-K) and indirect (Q-K) excitonic states with energies of E X,D and E X,I, respectively
We use the same model to analyze the PL intensity–energy correlation of strained WSe2, but now the indirect exciton represent that formed at the Q-K indirect gap (Fig. 2h). We have also determined \(E_{{\rm{X}},{\rm{D}}}^0 = 1.661\,{\rm{eV}}\) for unstrained monolayer WSe2 (vertical line in Fig. 2f) according to PL measurements on transferred WSe2 monolayers (Supplementary Fig. 2). As shown by the solid curve in Fig. 2f, the model fits the data very well, yielding Δ0 = −0.07 eV and γ = −0.32 ± 0.05 (Supplementary Fig. 5). Interestingly, both Δ0 and γ for monolayer WSe2 are negative, in stark contrast to monolayer MoS2. The negative γ arises from the opposite energy evolutions of Q and K valleys with strain18, while the negative Δ0 is a direct evidence of indirect optical gap in unstrained monolayer WSe2. The indirect gap of monolayer WSe2 also manifested itself in the large variation in PL intensity (up to a factor of ~ 5) shown in Fig. 2f, because, according to Eq. (1), the increase in PL intensity by tensile strain should be less than a factor of two if monolayer WSe2 is initially a direct gap material.
Calculated strain-induced bandgap shifts in MoS2 and WSe2 monolayers
Band structure calculations based on density functional theory (DFT) have been performed and compared to our experimental results. As shown in Fig. 3a, the calculated band structure for unstrained monolayer MoS2 exhibits a direct gap at the K valleys. The calculated energies of the K-K and K-Γ gaps as a function of strain (Fig. 3c) show a faster decrease in E KΓ with tensile strain than E KK. If we ignore the strain-induced change in exciton binding energy, the ratio of strain-induced changes in the K-Γ and K-K gaps (i.e., δE KΓ/δE KK) thus represents the ratio of strain-induced changes in the optical gaps γ = δE X,I/δE X,D. From the calculations, we determine δE KΓ/δE KK = 2.13, consistent with our experimentally obtained γ = 1.95 ± 0.14 for monolayer MoS2. On the contrary, our calculations show that unstrained monolayer WSe2 exhibits an indirect gap between the Q-valley in the CB and the K point in the valence band (VB), as shown in Fig. 3b. Applying tensile strain (Fig. 3d) tends to shrink the K-K gap, but expand the Q-K gap. We determine δE QK/δE KK = −0.28, in good agreement with our experimental value of γ = −0.32 ± 0.05 for monolayer WSe2.
DFT calculations of strained MoS2 and WSe2 monolayers. a, b The calculated band structures for monolayer MoS2 (a) and WSe2 (b) based on DFT. E KK and E KΓ (E QK) denote the direct and the indirect gaps in MoS2 (WSe2), respectively. c, d Strain-induced energy shifts in the direct and indirect gaps in monolayer MoS2 (c) and WSe2 (d). The calculations show that unstrained WSe2 is an indirect gap material, which can be turned into a direct-gap material by applying tensile strain
We emphasize that the experimentally determined Δ0 does not reflect the actual energy difference between the direct and indirect quasiparticle gaps. Due to the strong exciton binding energy caused by reduced dielectric screening in monolayer TMDs6, 28, 29, the difference in binding energies of direct and indirect excitons has to be taken into account. We first calculate the direct exciton binding energy E B,D based on the effective 2D Coulomb potential (Supplementary Fig. 6 and Supplementary Note 2). The indirect exciton binding energy E B,I is then estimated by scaling with the effective reduced masses deduced from band structure calculations. We obtain E B,D = 0.23 eV (K-K) and E B,I = 0.26 eV (K-Γ) for monolayer MoS2. The higher E B,I by 0.03 eV, originating from the heavier hole effective mass at Γ-valley, implies that the experimentally determined ΔeV = 0.08 eV underestimates the actual energy difference between the K- and Γ-valleys in the VB, yielding ΔK−Γ = E KΓ−E KK≈0.11 eV, in good agreement with the value in the range of 0.13–0.30 eV determined by angle-resolved photoemission spectroscopy20,21,22. For monolayer WSe2, due to the similar effective mass of electrons at K- and Q-valleys in the CB, the deduced E B,D = 0.19 eV (K-K) and E B,I = 0.20 eV (Q-K) are also similar, yielding ΔK−Q = E QK−E KK≈−0.06 eV. It demonstrates that monolayer WSe2 exhibits not only an indirect optical gap, but also an indirect quasiparticle gap with a CB minimum at the Q-valley, which is ~ 60 meV lower than the K-valley, consistent with STS measurements14.
Temperature dependence of PL intensity–energy correlation
We noted that the direct exciton populations in the simple two-level model depend sensitively on temperature. To attest the validity of our model analysis, we have performed the same measurements of spatial PL mapping on another MoSe2–WSe2 HJ flake at T = 150 and 300 K, as shown in Fig. 4a–d. The corresponding PL intensity–energy correlations of the outer monolayer WSe2 at 150 and 300 K are shown in Fig. 4e. Apart from a rigid shift in PL energy, the PL intensity measured at T = 150 K exhibits a sharper change with energy due to the reduced thermal energy k B T at a lower temperature. The simple two-level model can fit the two data sets with the same Δ0 and γ-values (solid curves in Fig. 4e) by simply changing the sample temperature and the unstrained PL peak energy. The temperature dependent measurements thus further confirm that the observed PL intensity–energy correlation is governed by the interplay of direct and indirect exciton populations. The nonuniform distribution of nonradiative defects or inhomogeneous alloy mixing can thus be excluded from the origin of the observed PL intensity–energy correlation.
PL intensity–energy correlations at different temperatures. a–d Contour color maps of PL intensity (a, c) and peak energy (b, d) in the WSe2 region of a MoSe2–WSe2 lateral HJ measured at different temperatures: (a, b) T = 150 K and (c, d) T = 300 K. e Integrated PL intensity as a function of peak energy measured at 150 K (blue dots) and 300 K (red dots). Black lines are model fitting curves
Discussion
In our analysis, we neglect the influence of dark exciton states at K valleys arising from the spin splitting in the CB. In particular, the spin-forbidden K-K dark exciton state is lower in energy by ~ 30 meV in monolayer WSe2 30, which also affects the bright (direct) exciton populations and hence the PL intensity at different temperatures. However, because the strain-induced change in the CB spin splitting is very small (<0.5 meV/%)31, including the dark exciton states will not change the analysis of Δ0 and γ-values from the PL intensity–energy correlation measured at a given temperature.
Strain could also impact the radiative lifetime and the binding energy of the K-K direct exciton through modifications in wave functions, optical matrix element and band curvatures. However, according to the range of PL shifts in our samples and recent theoretical calculations32, we estimated that the strain-induced changes in the radiative lifetime and the binding energy are small (<5%), which is within our experimental uncertainty.
Spatial variation of the unintentional doping in the sample could also lead to PL shifts due to the charged exciton (trion) emissions. We have performed line-shape analysis for the selected PL spectra shown in Fig. 2e and found that no spectral signature can be attributed to the trion emissions (Supplementary Fig. 7). Therefore, spatial variation in doping level can be excluded from the observed PL shift and the intensity–energy correlation.
Alloy inhomogeneity caused by material intermixing could be another source of the observed PL inhomogeneity. We have measured the PL inhomogeneity for HJ flakes after ultrasonic treatments. Interestingly, we found that the spatial distributions of PL intensity and energy are changed, but still exhibit a similar negative correlation (Supplementary Fig. 8). Since the strain inhomogeneity is likely to form during the fast-cooling process caused by the contraction mismatch, the local interactions between TMD and the substrate could be loosen and redistributed by ultrasonic treatments, and thereby changing the pattern of strain inhomogeneity. This result thus excludes the possibility that the PL inhomogeneity is caused by local variation of doping, defect distribution or alloy composition, since they are unlikely to be altered by ultrasonic treatments.
The indirect optical gap in unstrained monolayer WSe2 identified in this work has important implications. As a light emitter, monolayer WSe2 is far from ideal as compared with other MX2 with a direct gap, since a majority of photogenerated carriers will form indirect excitons even at room temperature, which considerably limits the quantum yield of light emissions. On the other hand, the efficient light absorption through the direct optical gap, together with the suppressed radiative recombination efficiency for the indirect excitons, makes monolayer WSe2 very ideal for photovoltaic applications. The indirect Q-K exciton in WSe2 is essentially dark and inaccessible optically. Recent theoretical work predicted that non-covalently attached molecules with a strong dipole moment can turn the indirect dark exciton bright, implicating its applications in molecule sensing33. Nevertheless, applying a moderate tensile strain (~ 1% uniaxial or ~ 0.5% biaxial) can tune the bandgap from indirect to direct, which can improve drastically the emission efficiency by nearly an order of magnitude. Based on the simple two-level model, we estimated that the crossover of the direct and indirect optical gaps occurs at 1.607 eV (1.797 eV) for monolayer WSe2 (MoS2), as indicated by the vertical dash line in Fig. 2f (Fig. 1f). For the strained MoSe2–WSe2 lateral HJs investigated here, the PL peak energy of the WSe2 region spans from 1.58 to 1.64 eV, which covers the crossover energy of direct and direct optical gap at 1.607 eV. This means that local strain variation also gives rise to a spatial modulation of direct and indirect gap, which forms a very unique platform with nonuniform potential modulations for studying exciton diffusions and localizations. Finally, we point out that the indirect gap nature of monolayer WSe2 must to be taken into account in further studies of its fundamental properties (e.g., exciton spin valley dynamics) and device applications for light emissions and harvesting.
Methods
Growth of monolayer lateral heterojunctions
High-quality single-crystal TMD HJs were synthesized on sapphire substrates by chemical vapor deposition (CVD) in horizontal hot-wall chambers. The monolayer WSe2–MoS2 lateral HJs were grown using the two-step growth method (see ref. 19 for details), while MoSe2–WSe2 lateral HJs were grown using the conventional one-pot synthesis process. For WSe2–MoS2 HJs, we used high-purity WO3, MoO3, Se and S powders as the source precursors. The growth temperatures for WSe2 and MoS2 are 925 and 755°C, respectively. For MoSe2–WSe2 HJs, high-purity MoO2, WO3, and Se powder were used as the initial reactants, and the HJs were grown at 880°C. All growths were performed in Ar/H2 flowing gas at low pressure (5–40 Torr).
Optical measurements
PL and Raman measurements were performed using a home-built optical microscope in the back-scattering configuration. A 532 nm solid-state laser was used as the excitation source. The laser were focused on the sample by a 100 × objective lens (NA = 0.9). The PL and Raman signals were collected by the same objective, analyzed by a 0.75-m monochromator and detected by a nitrogen-cooled CCD camera. For confocal measurements, the sample image was projected onto a 50 μm pinhole before entering the monochromator, yielding an overall spatial resolution of ~ 0.5 μm. Room temperature spatial mappings of PL spectra were performed using a fast motorized x–y stage with a step size of 0.25 μm. Low-temperature measurements were performed in a cryogen-free and vibration-free cryostat equipped with a 3-axis piezo-positioner, an x-y scanner and an objective lens (N.A. = 0.82) in the low-temperature chamber.
DFT calculations
The first-principle calculations were based on the generalized gradient approximation (GGA)34 using the full-potential projected augmented wave method35, 36 as implemented in the Vienna ab initio simulation (VASP) package37, 38. The electronic structures of monolayer MoS2 and WSe2 were calculated using a 30 × 30 × 1 Monkhorst-Pack k-mesh over the Brillouin zone with a cutoff energy of 500 eV under geometry optimization. The spin-orbit coupling was included in a self-consistent manner. Slabs with vacuum thickness larger than 30 Å were used to model the thin films. For the strain effects, the atomic positions were relaxed until the residual forces were less than 0.001 eV/Å.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Jariwala, D., Sangwan, V. K., Lauhon, L. J., Marks, T. J. & Hersam, M. C. Emerging device applications for semiconducting two-dimensional transition metal dichalcogenides. ACS Nano 8, 1102–1120 (2014).
Fiori, G. et al. Electronics based on two-dimensional materials. Nat. Nanotechnol. 9, 768–779 (2014).
Akinwande, D., Petrone, N. & Hone, J. Two-dimensional flexible nanoelectronics. Nat. Commun. 5, 5678 (2014).
Xia, F., Wang, H., Xiao, D., Dubey, M. & Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photon 8, 899–907 (2014).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photon 10, 216–226 (2016).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Ding, Y. et al. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M = Mo, Nb, W, Ta; X = S, Se, Te) monolayers. Phys. B 406, 2254–2260 (2011).
Zhu, Z. Y., Cheng, Y. C. & Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 84, 153402 (2011).
Yun, W. S., Han, S. W., Hong, S. C., Kim, I. G. & Lee, J. D. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-MX2 semiconductors (M = Mo, W; X = S, Se, Te). Phys. Rev. B 85, 033305 (2012).
Liang, Y., Huang, S., Soklaski, R. & Yang, L. Quasiparticle band-edge energy and band offsets of monolayer of molybdenum and tungsten chalcogenides. Appl. Phys. Lett. 103, 042106 (2013).
Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012).
Zhang, C. et al. Probing critical point energies of transition metal dichalcogenides: Surprising indirect gap of single layer WSe2. Nano Lett. 15, 6494–6500 (2015).
He, K., Poole, C., Mak, K. F. & Shan, J. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2. Nano Lett. 13, 2931–2936 (2013).
Conley, H. J. et al. Bandgap engineering of strained monolayer and bilayer MoS2. Nano Lett. 13, 3626–3630 (2013).
Zhu, C. R. et al. Strain tuning of optical emission energy and polarization in monolayer and bilayer MoS2. Phys. Rev. B 88, 121301(R) (2013).
Desai, S. B. et al. Strain-induced indirect to direct bandgap transition in multilayer WSe2. Nano Lett. 14, 4592–4597 (2014).
Li, M.-Y. et al. Epitaxial growth of a monolayer WSe2-MoS2 lateral p-n junction with an atomically sharp interface. Science 349, 524–528 (2015).
Jin, W. et al. Direct measurement of the thickness-dependent electronic band structure of MoS2 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 111, 106801 (2013).
Chiu, M.-H. et al. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 6, 7666 (2015).
Yuan, H. et al. Evolution of the valley position in bulk transition-metal chalcogenides and their monolayer limit. Nano Lett. 16, 4738–4745 (2016).
Brixner, L. H. Preparation and properties of the single crystalline AB2-type selenides and tellurides of niobium, tantalum, molybdenum and tungsten. J. Inorg. Nucl. Chem 24, 257–263 (1962).
Amani, M. et al. Growth-substrate induced performance degradation in chemically synthesized monolayer MoS2 field effect transistors. Appl. Phys. Lett. 104, 203506 (2014).
Liu, Z. et al. Strain and structure heterogeneity in MoS2 atomic layers grown by chemical vapour deposition. Nat. Commun. 5, 5246 (2014).
Park, K.-D. et al. Hybrid tip-enhanced nanospectroscopy and nanoimaging of monolayer WSe2 with local strain control. Nano Lett. 16, 2621–2627 (2016).
Amani, M. et al. High luminescence efficiency in MoS2 grown by chemical vapor deposition. ACS Nano 10, 6535–6541 (2016).
Zhang, C., Johnson, A., Hsu, C.-L., Li, L.-J. & Shih, C.-K. Direct imaging of band profile in single layer MoS2 on graphite: Quasiparticle energy gap, metallic edge states, and edge band bending. Nano Lett. 14, 2443–2447 (2014).
He, K. et al. Tightly bound excitons in monolayer WSe2. Phys. Rev. Lett. 113, 026803 (2014).
Zhang, X.-X., You, Y., Zhao, S. Y. F. & Heinz, T. F. Experimental evidence for dark excitons in monolayer WSe2. Phys. Rev. Lett. 115, 257403 (2015).
Cheiwchanchamnangij, T. & Lambrecht, W. R. L. Strain effects on the spin-orbit-induced band structure splittings in monolayer MoS2 and graphene. Phys. Rev. B 88, 155404 (2013).
Feierabend, M., Morlet, A., Berghäuser, G. & Malic, E. Impact of strain on the optical fingerprint of monolayer transition metal dichalcogenides. Phys. Rev. B 96, 045245 (2017)
Feierabend, M., Berghäuser, G., Knorr, A. & Malic, E. Proposal for dark exciton based chemical sensors. Nat. Commun. 8, 14776 (2017).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Acknowledgements
This work was supported by the Ministry of Science and Technology (MOST) of Taiwan (MOST-104-2628-M-009-002-MY3, MOST-105-2119-M-009-014-MY3) and AOARD (FA2386-16-1-4035). W.-H.C. acknowledges the supports from the Center for Interdisciplinary Science of NCTU. T.-R.C. acknowledges the supports from MOST and NCKU. H.-T.J. acknowledges the supports from MOST, NTHU and Academia Sinica. T.-R.C. and H.-T.J. also thank NCHC, CINC-NTU and NCTS for technical supports.
Author information
Authors and Affiliations
Contributions
W.-H.C. and W.-T.H. conceived the idea and designed the experiment. W.-T.H and D.W. performed the spectroscopy measurements. The samples were grown and characterized by L.-S.L, J.-K.H and M.-Y.L., and assisted by Z.-Y.J., Y.-C.C and L.-J.L. T.-R.C. and H.-T.J. performed DFT calculations. W.-H.C. and W.-T.H. wrote the paper. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hsu, WT., Lu, LS., Wang, D. et al. Evidence of indirect gap in monolayer WSe2 . Nat Commun 8, 929 (2017). https://doi.org/10.1038/s41467-017-01012-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-01012-6
This article is cited by
-
The study of spin- and valley-dependent electron transport properties in silicene modulated by metallic gates
Indian Journal of Physics (2024)
-
p-Type Two-Dimensional Semiconductors: From Materials Preparation to Electronic Applications
Nano-Micro Letters (2023)
-
Strain engineering of electronic properties and anomalous valley hall conductivity of transition metal dichalcogenide nanoribbons
Scientific Reports (2022)
-
Regulation of electronic structure of monolayer MoS2 by pressure
Rare Metals (2022)
-
Electric field induced giant valley polarization in two dimensional ferromagnetic WSe2/CrSnSe3 heterostructure
npj 2D Materials and Applications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.