Abstract
Since their initiation in the 1950s, worldwide selective tree breeding programs followed the recurrent selection scheme of repeated cycles of selection, breeding (mating), and testing phases and essentially remained unchanged to accelerate this process or address environmental contingencies and concerns. Here, we introduce an “end-to-end” selective tree breeding framework that: (1) leverages strategically preselected GWAS-based sequence data capturing trait architecture information, (2) generates unprecedented resolution of genealogical relationships among tested individuals, and (3) leads to the elimination of the breeding phase through the utilization of readily available wind-pollinated (OP) families. Individuals’ breeding values generated from multi-trait multi-site analysis were also used in an optimum contribution selection protocol to effectively manage genetic gain/co-ancestry trade-offs and traits’ correlated response to selection. The proof-of-concept study involved a 40-year-old spruce OP testing population growing on three sites in British Columbia, Canada, clearly demonstrating our method’s superiority in capturing most of the available genetic gains in a substantially reduced timeline relative to the traditional approach. The proposed framework is expected to increase the efficiency of existing selective breeding programs, accelerate the start of new programs for ecologically and environmentally important tree species, and address climate-change caused biotic and abiotic stress concerns more effectively.
Similar content being viewed by others
Introduction
Forest tree selective breeding programs follow the recurrent selection scheme, involving repeated cycles of selection, breeding, and testing (Allard 1960; White et al. 2007) along with a product development phase for improved seed production (El-Kassaby 1995). While this process has successfully delivered substantial gains worldwide, it is highly structured and long-term, thus less responsive to addressing the pressing environmental contingencies (Wheeler et al. 2015; Matallana-Ramirez et al. 2021). In particular, climate change-induced biotic and abiotic stresses (Surówka et al. 2020) with their cascading biological consequences affecting populations’ survival and recruitment. These challenges require faster genetic evaluation methods that traditional selective breeding cannot provide. Thus, developing agile evaluation methods to address these new challenges necessitates efficient approaches that leverage advanced genomic capabilities and their integration into traditional selective breeding programs (Grattapaglia et al. 2018). Most tree selective breeding programs are protracted as they require creating structured pedigree (half- (HS) and full-sib (FS) families) during the breeding phase and necessitate long-term evaluation phases as most sought-after target traits (e.g., volume and wood density) are expressed at an advanced age (White et al. 2014). However, certain innovations have been effective in shortening the breeding cycle length to some extent. These include: (i) reliance on juvenile-mature correlations where early age performance serves as proxy to advanced age (Lambeth 1980), (ii) utilizing open-pollinated (OP) families to bypass the structured pedigree requirement (Stonecypher et al. 1964), and (iii) applying pedigree reconstruction to assemble a “structured pedigree” from naturally produced offspring (a.k.a., “Breeding without Breeding”), thereby eliminating the breeding phase (El-Kassaby and Lstibůrek 2009; also see Grattapaglia et al. 2004).
Pedigree-dependent quantitative genetics analyses utilize the average numerator relationship (A-matrix), reflecting the contemporary genealogical relationships among the structured pedigree members (Wright 1922). This matrix is then used to estimate the genetic variance components using Restricted Maximum Likelihood (Gilmour et al. 1995) for predicting individuals’ breeding value using the Best Linear Unbiased Prediction algorithms (BLUP) (Henderson 1975). For monoecious species, when OP families are used, a half-sib family structure is assumed, with members of each OP family sired by different males, an inconceivable assumption considering trees’ pollination biology and ecology. In reality, OP families’ offspring often represent a mixture of self-sibs (progeny from self-pollination), half-sibs, and full-sibs with varying proportions, resulting in inflated additive genetic variance and heritability estimates (Namkoong 1966; Squillace 1971; Askew and El-Kassaby 1994). Another drawback of the average numerator relationship is its inability to differentiate among siblings within HS or FS families as it applies global relationship estimates without considering the Mendelian sampling term, which represents relatedness variation among FS and HS family members that cannot be determined by traditional pedigree analyses (Avendaño et al. 2005).
The availability of DNA sequence data has facilitated the accurate determination of the actual fraction of alleles shared between individuals (identity-by-state), enabling the estimation of their realized genomic pairwise kinship (G-matrix) (VanRaden 2008; also see Ritland 1996). The strength of the G-matrix lies in its ability to capture genetic information from both contemporary and ancestral pedigrees, accurately accounting for hidden relationships that cannot be ascertained through the traditional contemporary pedigree analysis (Powell et al. 2010). This understanding has enabled the integration of DNA sequences into quantitative genetics where the pedigree-based relationship (A-matrix) is replaced by the genomic-based relationship (G-matrix). It is important to note that the G-matrix application in OP families has successfully addressed the aforementioned drawbacks, resulting in accurate estimates of additive, dominance, and epistatic genetic variances (Gamal El-Dien et al. 2016).
Complex traits, following Fisher’s infinitesimal model, are often theorized to be controlled by a large number of genes, each explaining a small fraction of the trait’s variance (Fisher 1918). To harness the linkage disequilibrium (LD) between the traits’ causal genes and the genotypic data (genome-wide SNPs), genome-wide association studies (GWAS) have been used to unravel complex traits architectures and identify their underpinning causal genes (Visscher and Goddard 2019). However, the GWAS approach is statistically burdened by the multiple testing threshold, leading to failure in detecting many potentially causal genes with smaller effects as they do not meet the predetermined significance threshold (Tam et al. 2019).
Here, we present the genomic version of the “Breeding without Breeding” conceptualized by El-Kassaby and Lstibůrek (2009). This version represents a unified and all-encompassing selective breeding framework in a holistic “end-to-end” process that: (1) quantifies all the advantages of combining genomic data with the simple OP family structure, (2) generates reliable genetic information in a substantially reduced timeframe, (3) includes genetic evaluation and ranking, and (4) culminates in selecting the best individuals for further utilization. To illustrate this, we utilized phenotypic (tree height, diameter, and wood density) and genotypic (≈9 K SNPs) data from a 40-year-old spruce OP testing population growing on three sites in British Columbia, Canada (Gamal El-Dien et al. 2016). We then compared the results to those obtained using the traditional selective breeding scheme (i.e., A-matrix).
Materials and methods
Genetic material, evaluated traits, DNA fingerprinting
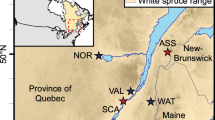
A total of 1126, 40-year-old “Interior spruce” (Picea glauca (Moench) Voss × P. engelmannii Parry ex Engelm.) trees representing 25 open-pollinated (OP) families growing on three sites in Interior British Columbia, Canada (Aleza Lake: lat. 54° 03′ 15.7″ N, long. 122° 06′ 35.4″ W, elev. 700 m asl; Prince George Tree Improvement Station: lat. 53° 46′ 17.9″ N, long. 122° 43′ 07.6″ W, elev. 610 m asl; and Quesnel: lat. 52° 59′ 27.2″ N, long. 122° 12′ 30.6″ W, elev. 915 m asl). The field trial was established by the British Columbia Ministry of Forests, Forest Improvement and Research Management Branch, following a complete randomized block design with five to ten blocks and ten or fifteen tree-row-plots planted at 2.5 × 2.5 m spacing with a total of 181 OP families.
The OP family testing method is the mass selection of individuals based on their desired phenotypic attributes, without prior knowledge of either their performance or pedigree. This selection method is conducted within a wide geographic area known as “breeding zone,” thus necessitating genetic testing to determine individuals’ genetic superiority (White et al. 2007). Offspring within OP families share a common parent (the seed donor) and are pollinated by the surrounding “local” pollen pool (male donors), often resulting in some detectable paternal relationships. Typically, OP family selection lacks a well-defined population structure, as only a limited number of individuals (seed donors) are selected from a specific location, as illustrated in Fig. 1 that depicts family structure and demonstrates the ancestral relationships among the entire test population.
It is essential to recognize that pedigree errors are often found in most breeding program (Adams et al. 1988; Devey et al. 2002; Doerksen and Herbinger 2008). Therefore, we leveraged the available genomic data to verify the pedigree in our genetic materials. This verification process led to several outcomes: (1) removal of 25 individual with low diagonal elements of the G-matrix, (2) reassignment of 15 to different pedigree families as their genomic relatedness was found to be low, (3) creation of a new OP family consisting of 9 individuals, and (4) the identification of 13 individuals who did not belong to any of the initially studied 25 OP families (see genomic network below). As a result, the initial count of OP families of 25 increased by one, while the total number of individuals was reduced from 1126 to 1101. Pedigree errors are a commonly occurring issue during development and establishment of progeny testing materials that include processes such as seed-cone collection, seed extraction, seedling production, and progeny tests planting. Additionally, as the selected 25 families represent a subset of the initial 181 OP family test, it is reasonable to expect that the detected pedigree errors are part of the overall test.
From each site, four replications representing each of the originally studied 25 OP family were sampled and measured for: (1) total tree height (HT, in meters), (2) diameter at breast height (DBH, in centimeters), and (3) wood density (WD, g·cm−3) determined using X-ray densitometry (WD) from 5-mm bark-to-bark wood cores extracted at breast height in the north-south direction of each tree by increment borers (El-Kassaby et al. 2011). DNA extraction and Genotyping-by-Sequencing (GBS) (Elshire et al. 2011), details are available elsewhere (Gamal El-Dien et al. 2018). Here, we utilized a subset of the GBS-generated SNP data from the original file with 30% missing data (Ratcliffe et al. 2015) and selected those SNPs with the least missing data, then implemented mean imputation using the ‘A.mat’ function in the ‘rrBLUP’ R package (Endelman, 2011), resulting in a total of 8767 SNPs for quantitative genetic analyses (https://doi.org/10.5061/dryad.7h44j101d).
Quantitative genetics/genomics analyses
For computational efficiency, the statistical analyses were conducted in two stages. First, each trait was analyzed separately in each site using a pedigree-based classical a priori design model, where replications were fitted as a random effect. In the second stage, the phenotypic data adjusted for the design effects were obtained for each tree and trait and at each site by subtracting the estimated replication effects from the raw phenotype. Thereafter, the additive average-numerator (ABLUP) and genomic (GBLUP-A) best linear unbiased prediction analyses were performed for each of the three traits using the following additive multi-site individual-tree mixed model:
where \({\boldsymbol{y}}{\boldsymbol{=}}\left[{{\boldsymbol{y}}}_{1}^{{\prime} }{\boldsymbol{,}}{{\boldsymbol{y}}}_{2}^{{\prime} }{\boldsymbol{,}}{{\boldsymbol{y}}}_{3}^{{\prime} }\right]\) is the vector of individual tree adjusted-phenotypes for the three sites; \({\boldsymbol{\beta }}=[{{\boldsymbol{\beta }}}_{1}^{{\prime} },{{{\boldsymbol{\beta }}}_{2}^{{\prime} }{\boldsymbol{,}}{\boldsymbol{\beta }}}_{3}^{{\prime} }]\) is the vector of site fixed effects (i.e., overall mean for each site); the additive genetic effects random vector of \({\boldsymbol{a}}=[{{\boldsymbol{a}}}_{1}^{{\prime} },{{{\boldsymbol{a}}}_{2}^{{\prime} }{\boldsymbol{,}}{\boldsymbol{a}}}_{3}^{{\prime} }]\) is distributed as \({\boldsymbol{a}}{\boldsymbol{ \sim }}{\boldsymbol{N}}\left({\boldsymbol{0}}{\boldsymbol{,}}{{\boldsymbol{\Sigma }}}_{{\boldsymbol{a}}}{\boldsymbol{\bigotimes }}{\boldsymbol{A}}\right)\), where \({{\boldsymbol{\Sigma }}}_{{\boldsymbol{a}}}\) is the genetic effects (co)variance matrix and \({\boldsymbol{A}}\) is the additive average-numerator relationship matrix containing the additive relationships among all trees (26 mothers without records plus 1101 offspring). Finally, \({\boldsymbol{e}}=[{{\boldsymbol{e}}}_{1}^{{\prime} },{{\boldsymbol{e}}}_{2}^{{\prime} },{{\boldsymbol{e}}}_{3}^{{\prime} }]\) is the vector of random residuals distributed as \({\boldsymbol{e}}{\boldsymbol{ \sim }}{\boldsymbol{N}}{\boldsymbol{(}}{\boldsymbol{0}}{\boldsymbol{,}}{{\boldsymbol{R}}}_{{\boldsymbol{0}}}{\boldsymbol{\bigotimes }}{\boldsymbol{I}}{\boldsymbol{)}}\) where R0 is the residual (co)variance matrix for the three sites with dimension 3 × 3. We assumed an unstructured (co)variance matrix for the genetic effects (\({{\boldsymbol{\Sigma }}}_{{\boldsymbol{a}}}\)). The column vector of 1s X1, X2 and X3, and the matrices \({{\boldsymbol{Z}}}_{{a}_{1}}\), \({{\boldsymbol{Z}}}_{{a}_{2}}\) and \({{\boldsymbol{Z}}}_{{a}_{3}}\) relate the observation to the means of the site effects in β, and the additive genetic effects for each tree in a. The symbol (´) indicates the transpose operation.
The additive multi-trait multi-site individual-tree ABLUP-A model and the GBLUP models, which used a G-matrix calculated using all available SNPs (8767; GBLUP-ALL) and 5628 SNPs selected by GWAS (based on their SNP absolute effect without imposing any variance contribution limits) (GBLUP-GWAS) (see below), respectively, were fitted as:
where \({\boldsymbol{y}}{\boldsymbol{=}}[{{\boldsymbol{y}}}_{11}^{{\prime} }{\boldsymbol{,}}{\boldsymbol{\cdots }}{\boldsymbol{,}}{{\boldsymbol{y}}}_{{ij}}^{{\prime} }]\) is the vector of adjusted-phenotypes for each i trait (i = DBH, HT and WD) and j site (j = 1, 2, 3); \({\boldsymbol{\beta }}=[{{\boldsymbol{\beta }}}_{11}^{{\prime} },{{\boldsymbol{\cdots }}{\boldsymbol{,}}{\boldsymbol{\beta }}}_{{ij}}^{{\prime} }]\) is the vector of trait-site combination fixed effects (i.e., overall mean for each trait-site combination); \({\boldsymbol{a}}=[{{\boldsymbol{a}}}_{11}^{{\prime} },{{\boldsymbol{\cdots }}{\boldsymbol{,}}{\boldsymbol{a}}}_{{ij}}^{{\prime} }]\) is the random vector of additive genetic effects distributed as \({\boldsymbol{a}}{\boldsymbol{ \sim }}{\boldsymbol{N}}\left({\boldsymbol{0}}{\boldsymbol{,}}{{\boldsymbol{\Omega }}}_{{\boldsymbol{a}}}{\boldsymbol{\bigotimes }}{\boldsymbol{A}}\right)\), where \({{\boldsymbol{\Omega }}}_{{\boldsymbol{a}}}\) is the unstructured genetic (co)variance matrix for each of combination of the three traits and the three sites with dimension 9 × 9. Finally, \({\boldsymbol{e}}=[{{\boldsymbol{e}}}_{11}^{{\prime} },{\boldsymbol{\cdots }},{{\boldsymbol{e}}}_{{ij}}^{{\prime} }]\) is the vector of random residuals distributed as \({\boldsymbol{e}}{\boldsymbol{ \sim }}{\boldsymbol{N}}{\boldsymbol{(}}{\boldsymbol{0}}{\boldsymbol{,}}{\boldsymbol{R}}{\boldsymbol{\bigotimes }}{\boldsymbol{I}}{\boldsymbol{)}}\) where \({\boldsymbol{R}}\) is the residual (co)variance matrix with dimension 9 × 9 between traits within sites; the residual (co)variance between traits across sites is assumed to be zero for the three sites, given that the sites were assessed separately. The matrices \({{\boldsymbol{X}}}_{{ij}}\) and \({{\boldsymbol{Z}}}_{{a}_{{ij}}}\) related the adjusted-phenotypes to the means of the trait-site combinations in \({{\boldsymbol{\beta }}}_{{ij}}^{{\prime} }\) and the genetic effects in \({{\boldsymbol{a}}}_{{ij}}^{{\prime} }\). In order to fit the GBLUP-A model, the pedigree-based relationship A-matrix of the multi-site model [1] and the multi-trait multi-site model [2] was replaced by the G-matrix (VanRaden 2008):
where, \({\boldsymbol{W}}\) is the centered matrix of SNP covariates, and \({p}_{k}\) is the current (or observed) allele frequency of the genotyped trees for marker k.
Finally, the extended multi-site GBLUP model that included the dominance \(\left({\boldsymbol{d}}=[{{\boldsymbol{d}}}_{1}^{{\prime} },{{{\boldsymbol{d}}}_{2}^{{\prime} }{\boldsymbol{,}}{\boldsymbol{d}}}_{3}^{{\prime} }]\right)\) and the additive by dominance epistatic \(\left({\boldsymbol{p}}=[{{\boldsymbol{p}}}_{1}^{{\prime} },{{{\boldsymbol{p}}}_{2}^{{\prime} }{\boldsymbol{,}}{\boldsymbol{p}}}_{3}^{{\prime} }]\right)\) genetic effects (GBLUP-ADE) were fitted for each trait. These dominance and epistatic genetic effects are distributed as \({\boldsymbol{d}}{\boldsymbol{ \sim }}{\boldsymbol{N}}\left({\boldsymbol{0}}{\boldsymbol{,}}{{\boldsymbol{\Sigma }}}_{{\boldsymbol{d}}}{\boldsymbol{\bigotimes }}{\boldsymbol{D}}\right)\) and \({\boldsymbol{p}}{\boldsymbol{ \sim }}{\boldsymbol{N}}\left({\boldsymbol{0}}{\boldsymbol{,}}{{\boldsymbol{\Sigma }}}_{{\boldsymbol{p}}}{\boldsymbol{\bigotimes }}{\boldsymbol{E}}\right)\), respectively, where \({{\boldsymbol{\Sigma }}}_{{\boldsymbol{d}}}\) and \({{\boldsymbol{\Sigma }}}_{{\boldsymbol{p}}}\) are the (co)variance matrices of dominance and additive by dominance (epistatic) genetic effects, and \({\boldsymbol{D}}\) and \({\boldsymbol{E}}\) are the average dominance and additive by dominance relationship matrices, respectively. Following Gamal El-Dien et al. (2016), the average dominance relationship matrix \({\boldsymbol{D}}\) was computed using the R function Gmatrix from the R-package (http://www.r-project.org) “AGHmatrix” (Amadeu et al. 2016) using Vitezica et al. (2013)’s method. The average relationship matrix for the additive by dominance epistatic effects was computed using the Hadamard product of the additive and dominance average relationship matrices (Muñoz et al. 2014).
Pedigree network
We generated network visualization for the A- and G-matrices (Rincent et al. 2012) in which two individuals are either linked, when their estimated pairwise relationship coefficient is larger than 0.05 and 0.10 or else unlinked. The observed difference in networks topology between the 0.05 and 0.10 thresholds highlights the role of ancestral pedigree. We used the R-package (http://www.r-project.org) “network” (Butts 2008) to generate the network representation.
Heritability estimates
Average across-site pedigree- and genomic-based narrow-sense individual heritability values for each trait ith, \({h}_{i}^{2}\), were estimated as: \({\hat{h}}_{i}^{2}={\hat{\sigma }}_{{a}_{i}}^{2}/({{\hat{\sigma }}_{{a}_{i}}^{2}+\hat{\sigma }}_{{e}_{i}}^{2})\), where \({\hat{\sigma }}_{{a}_{i}}^{2}\) is the estimated genetic variance for the ith trait, and \({\hat{\sigma }}_{{e}_{i}}^{2}\) is the estimated residual variance for the ith trait from the multi-site model [1] and multi-trait multi-site model [2]. For the GBLUP-ADE models, the denominator of the above equation also included the estimated variance of dominance and epistatic effects.
Variance components and their respective heritability estimates for the ABLUP and GBLUP-based SNP selection methods were estimated in R (www.r-project.org), with the function remlf90 from the ‘breedR’ package (Muñoz and Sanchez 2020) using the Expectation-Maximization (EM) algorithm followed by one round of an Average Information (AI) algorithm to compute the standard deviations (Chateigner et al. 2020) for the variance components and heritability estimates. The remlf90 function in R-package ‘breedR’ is based on REMLF90 (for the EM algorithm) and AIREMLF90 (for the AI algorithm) of the BLUPF90 family (Misztal et al. 2018). The program postGSF90 from the BLUPF90 family (Aguilar et al. 2019) was also used to estimate SNP effects.
SNP selection protocol
We examined the impact of SNP-marker number on the estimated genomic-based narrow-sense heritability and the theoretical accuracies of breeding values (equation [3] below) using the multi-site model [1]. To that end, subsets of 1096, 2192, 3288, 4384, 5479, 6575, 7671, and 8767 SNPs (increments of ≈1000) were randomly selected from all available SNP data and were used to build the corresponding genomic additive relationship matrices. In addition, the impact of SNP-marker type and number on heritability and theoretical accuracy was studied using additional two SNP selection strategies; namely, (1) based on their minor allele frequency (MAF) with increasing order from the rarest to the most common, and (2) based on their GWAS absolute value effect ranked from the largest to the smallest and averaged across sites using a single-step multi-site genome-wide association analysis (ssGWAS) (Aguilar et al. 2019; Uffelmann et al. 2021), using the same SNP increments as above (i.e., ≈1000).
To unravel the overlap of SNPs across traits selected by their effects, a Venn Diagram was built using subsets of 3288 SNPs each. Thereafter, the total of 5628 SNPs (Supplementary Information, Fig. S1) was used to generate a combined G-matrix associated with the three studied traits.
Genetic parameters theoretical accuracy
Estimates of the theoretical accuracy (TA) of the additive genetic variance were used to compare different genomic- and pedigree-based analytical methods. Therefore, the TA of tree i was calculated across all traits and ABLUP and GBLUP models using the following equation:
where PEVi (prediction error variance) that corresponds to individual i is obtained from the diagonal entry of the inverse of the coefficient matrix derived from the mixed model equations (MME).
Optimum contribution selection (OCS)
To select the top 30 individuals for the product development phase (i.e., seed orchard establishment), we implemented OCS to optimize the trade-off between the genetic gain (ΔG) and the degree of co-ancestry (ΔF) build-up. We conducted two optimizations with ΔF ≤ 0.25 and 0.125. Additionally, the observed negative correlation between both height and diameter and wood density required the implementation of an additional constraint in which we maintained the wood density of the selected individuals to be similar to the base population (i.e., no wood density loss). The optimizations were conducted using Gurobi 10.0 (https://www.gurobi.com) (Gurobi Optimization 2023).
Availability of R code
Software code(s) used in the present study are posted in the Dryad Digital Repository, https://datadryad.org/stash/dataset/doi:10.5061/dryad.7h44j101d.
Results
One of the most critical aspects of using the G-matrix in quantitative genomic analyses is the selection of a subset of SNPs that provide the most informative pairwise kinship information among individuals (Bernardo 2014). To address this, we implemented three SNP sampling approaches to construct the G-matrix and compared the results to those obtained using the entire SNP sample (≈9 K). These SNP sampling methods consecutively selected subsets of ≈1000 SNPs based on: (i) random sampling (with 10 replications), (ii) rare allele frequency (ranking SNPs from rarest to most common), and (iii) GWAS-based selection (ranking SNPs based on their GWAS absolute value regardless of their statistical significance threshold to circumvent the statistical threshold limitations of GWAS and leverage potential LD between SNPs and causal genes). In this context, GWAS-SNPs were incorporated in a sequential manner without imposing specific lower inclusion criteria, aside from considering their absolute effect. To evaluate the proposed framework, we compared pedigree- vs. genomic-based approaches in terms of pedigree network and theoretical breeding value accuracy and heritability estimates.
Pedigree networks
When genomic pairwise kinship threshold of 0.05 is considered, the comparison yielded astonishing results insofar as the pedigree-based approach produced 26 (the original 25 as well as the added small 9-member family (see pedigree verification above)) independent entities representing the tested HS families, along with 13 mislabelled individuals, while the genomic-based showed complete connectedness among all individuals, including the mislabelled, and generated a complete pairwise kinship matrix leveraging both contemporary and ancestral pedigrees (Fig. 2A, B). Naturally, the degree of connectedness among individuals is dependent on the set minimum kinship level used. It is interesting to note that the network topology between the 0.05 and 0.10 thresholds resulted in a different degree of connectedness among individuals with lower connectedness for the 0.10 threshold (Fig. 2C); however, the G-matrix used in our quantitative genomics analyses considered all possible pairwise relationships irrespective of the threshold. To leverage both contemporary and ancestral pedigree, we did not impose any pairwise kinship lower limit and used the complete set of 8767 SNPs or subsets (3288 for single trait and 5628 for multi-traits) in our analyses. As indicated above, mislabelling is common in traditional tree breeding, leading to erroneous genetic parameters, ranking, and gain estimates (Muñoz et al. 2014).
Single-trait multi-site analyses
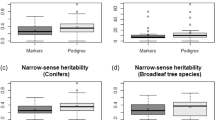
As expected, the theoretical accuracies of ABLUP derived additive genetic variances were higher than their GBLUP counterparts. However, the DBH-ABLUP estimates overlapped with those from the different SNP sampling methods and sample sizes (Fig. 3). Generally, the GWAS additive genetic variance theoretical accuracies were better compared to random and rare allele sampling. Plateaued accuracy was observed between 3000 and 4000 SNPs, indicating that selecting GWAS-informative SNPs added significant value to the resultant G-matrix (Fig. 3). Furthermore, the difference in theoretical accuracy between the two GBLUP models (additive (GBLUP-A) vs. additive, dominance and epistatic (GBLUP-ADE)) was negligible, suggesting minimal dominance and epistatic variance of these traits (Fig. 3). Notably, the additive genetic variance theoretical accuracy of the complete SNP set (8767) was lower than that obtained from the reduced GWAS-SNP set, suggesting that adding more SNPs after reaching the optimal number is detrimental to the resulting G-matrix (Fig. 3).
Estimates are shown with SNP-marker increments ranging from 1096 to 8767. Boxplots illustrate results for 10 replications of random SNP selection; black circles indicate SNPs ranked by minor allele frequency from rarest to most common; red and orange circles represent SNPs selected based on their GWAS absolute values ranked from largest to smallest effects for additive and additive, dominance, and epistatic genomic-based GBLUP models, respectively; dashed black line indicates the theoretical accuracy and narrow-sense heritability estimates for the average breeding values from the conventional pedigree-based ABLUP model; red and orange “x” marks show theoretical accuracy and narrow-sense heritability estimates for the breeding values using the additive and additive, dominance, and epistatic genomic-based GBLUP models with the full set of 8767 SNPs.
Heritability estimates
The heritability estimates exhibited a trend similar to the additive genetic variance theoretical accuracies. Importantly, the GWAS-SNP sampling yielded higher estimates compared to random and rare allele sampling (Fig. 3). Overall, ABLUP produced higher heritability estimates than GBLUP, primarily due to the ABLUP inflated additive genetic variance (Beaulieu et al. 2022). Our results showed no significant differences between the GBLUP-A and GBLUP-ADE models, further supporting minimal dominance and epistatic genetic variances (Table 1).
Multi-trait multi-site analysis
Breeding programs select for multiple traits while considering the “correlated response” among traits. Our data revealed negative genetic correlations between wood density and both height (−0.53) and diameter (−0.72) (Supplemental Fig. S2). Furthermore, the GWAS-SNP single-trait multi-site analyses indicated that 3000 to 4000 was the optimal number of SNPs needed for obtaining reliable genetic parameters (Fig. 3) and a SNP overlap existed among the studied traits (Supplemental Fig. S1). Thus, we constructed a new G-matrix from each trait’s top 3288, resulting in a total of 5628 SNPs that were subsequently used for further analyses. Overall, the ABLUP multi-trait multi-site heritability estimates were comparable to those of the single-trait multi-site, and the GWAS-SNP approach yielded better estimates than the entire SNP sample (Table 1). The superiority of the GBLUP-GWAS heritability estimates can be attributed to the refinement of residual variances, which removed the influence of dominance and epistatic genetic variances as well as their interactions with environments, from the “error” term. This refinement reduced their respective denominators and produced higher estimates and thus enhanced the expected genetic gain as compared to those from the ABLUP models (Table 1). Ignoring the inflated additive genetic variance and hereditability estimates produced and the time saving associated with use of OP families, we compared the percentage of expected genetic gain between the ABLUP and GBLUP models after selecting the top 30 individuals for improved seed production (El-Kassaby 1995). The results showed greater gains from the GBLUP compared to ABLUP for two traits (diameter: 8.18 vs. 4.35% and wood density: 14.91 vs. 10.77%), while height gain remained consistent (10.77 vs. 10.88%), supporting our proposed framework.
Optimum contribution selection (OCS)
The translational component of breeding programs is the production of improved seed, which in forestry is achieved through establishing seed orchards comprising the highest genetic worth individuals. We implemented OCS (Woolliams et al. 2015) to select the top 30 individuals and optimized genetic gain (ΔG)/co-ancestry (ΔF) trade-off, with an additional constraint to prevent wood density loss. Regardless of the analytical method used (ABLUP or GBLUP), the highest relative gains of 0.83 (diameter) and 1.10 (height) were achieved under no co-ancestry constrain (i.e., individuals were selected irrespective of their family affiliation) (Fig. 4). Compared to the unconstrained co-ancestry approach, the unrelated ABLUP resulted in diameter (0.83: 100%) and height (0.42: 35%) gains with only seven individuals, an insufficient number to maintain broad genetic diversity (Fig. 4). Under ΔF ≤ 0.25 constraint, the GBLUP-GWAS produced gains comparable to those under no constraint, yielding diameter (0.80: 96%) and height (1.04: 92%) gains with 30 carefully selected individuals. Under ΔF ≤ 0.125 constraint, reduced gains in diameter (0.22: 27%) and height (0.35: 32%) were obtained with only 24 individuals (Fig. 4). The superiority of OCS was clearly demonstrated in successfully capturing a significant portion of the available gains without compromising co-ancestry, specifically for ΔF ≤ 0.25. It should be noted that the implementation of OCS was critical in avoiding the pitfalls of exclusive genomic selection (GBLUP-GWAS), which tends to select related individuals, resulting in the accumulation of co-ancestry and depletion of genetic variation (Sonesson et al. 2012).
ABLUP is represented by ‘All_pedigree’, including all individuals in the pedigree and reflecting no co-ancestry constraint, and by ‘Unrelated’ having only unrelated individuals. Results of GBLUB-GWAS show the gains under ΔF ≤ 0.25 (ΔF ≤ 0.25) and ΔF ≤ 0.125 (ΔF ≤ 0.125) for diameter (DBH) and height.
Discussion
During the 1950s, large-scale selective tree breeding programs were initiated worldwide (White et al. 2007). Despite variation in geography, species, and breeding strategies, most programs followed the recurrent selection, with some reaching their fourth generations (Jing et al. 2023), yet limited pragmatic changes have been implemented (Cotterill 1986). These breeding programs involve thousands of parents and their crosses, and the resulting offspring are evaluated over multiple test sites located within expansive geographic areas known as breeding zones (White et al. 2007). These test sites exhibit considerable heterogeneity, requiring innovative experimental designs (Libby and Cockerham 1980) and statistical analyses that account for spatial and competition effects (Cappa et al. 2017) to separate genetic and non-genetic effects. Historically, these breeding zones were considered “static”, and the focus was on identifying individuals for future breeding or inclusion in seed orchard populations. However, due to climate change, these breeding zones are now in constant state of flux (Cortés et al. 2020). The existing traditional test sites, with their confounding factors and evolving environmental heterogeneity, are inadequate for addressing crucial climate change questions, such as identifying genotypes that are resilient to abiotic and biotic stresses (Surówka et al. 2020). Additionally, conventional breeding methods necessitate using structured pedigree (White et al. 2007), which is time-consuming and impractical and can be overcome using the proposed framework.
The effectiveness of the proposed selective breeding framework can be illustrated within the context of the breeder equation (ΔG = i r σa / L), where ΔG, i, r, σa, and L represent the genetic gain, selection intensity, accuracy of selection, additive genetic variance estimate, and breeding cycle length, respectively (Lush 1937). When considering equal i for ABLUP and GBLUP, the GBLUP yields higher estimates for r and σa. Furthermore, if OP families are utilized, the breeding cycle length (L) would be significantly shortened for bypassing the structured pedigree requirement, confirming the superiority of our approach. Additionally, traditional tree breeding programs required extensive pedigree control to mitigate the adverse effects of inbreeding depression (Williams and Savolainen 1996). Our results showed pedigree errors (A-matrix); thus, it is suggested that the G-matrix information should be employed for effective pedigree and genetic diversity management (El-Kassaby et al. 2019).
Despite the considerable size of the spruce genome (20 Gb; Birol et al. 2013) and the “limited” likelihood of our ≈9000 SNPs being in linkage disequilibrium (LD) with the studied traits, we have confidence in the efficacy of our method for the following reasons: (1) it is widely recognized that 3000 to 4000 SNPs are generally sufficient for resolving relatedness (Thistlethwaite et al. 2020), and our SNP count falls within this range and (2) the selected SNPs have been established to exert an effect on the studied attributes through GWAS, even if these effects are modest. Collectively, they still contribute to explaining a portion of the variance in the studied traits. Therefore, we believe that despite the relatively small number of SNPs (≈9000) used in our study, these selected SNPs effectively capture some of the variance in the traits, with the added advantage of elucidating the pedigree.
Comparing the proposed genomic-based approach with the two previously used “time-saving” testing and evaluation methods (i.e., OP testing and pedigree reconstruction (Breeding without Breeding)) can be summarized as follows: (1) while both methods capitalize on the readily available natural matings and invoke either half-sib (OP families) or full-sib (pedigree reconstruction) family structure and thus avoiding the creation of structured pedigree (i.e., the breeding phase), the OP testing produces inflated additive genetic vicariance and heritability estimates (Askew and El-Kassaby 1994) which the pedigree reconstruction considers (El-Kassaby and Lstibůrek 2009) and (2) both OP testing and pedigree reconstruction are anchored on the use of the A-matrix and therefore both do not benefit from the information gained from ancestral pedigree (VanRaden 2008) and thus hidden relationships and inbreeding are not accounted for.
Lastly, it is essential to underscore that the presented framework is exceptionally well-suited for evaluating climate change-related adaptive attributes. These attributes can be conveniently assessed at a very young age owing to their notably high heritability values. Examples of such attributes include vegetative phenology (Guo et al. 2021), drought tolerance (Moran et al. 2017), frost tolerance (Gomory et al. 2010), salt tolerance (Khasa et al. 2002), and insect resistance (Klápště et al. 2022).
Conclusions
Tree selective breeding methods have remained static since their inception, with no pragmatic changes implemented to expedite the process or to address environmental contingences. Here, we introduced an innovative approach that integrates genomic data and optimization protocols for evaluating and selecting superior individuals. The proposed framework leverages the existing OP families, eliminating the need for the traditional breeding phase and resulting in greater gains with a shorter timeline.
Data availability
All data sets used are available in the Dryad Digital Repository, https://doi.org/10.5061/dryad.7h44j101d.
Code availability
Software code(s) used in the present study are posted in the Dryad Digital Repository, https://datadryad.org/stash/dataset/doi:10.5061/dryad.7h44j101d.
References
Adams WT, Neale DB, Loopstra CA (1988) Verifying controlled crosses in conifer tree-improvement programs. Silvae Genet 37:147–152
Aguilar I, Legarra A, Cardoso F, Masuda Y, Lourenco D, Misztal I (2019) Frequentist p‑values for large‑scale‑single step genome‑wide association, with an application to birth weight in American Angus cattle. Genet Sel Evol 51:28
Allard RW (1960) Principles of plant breeding. J. Wiley & Sons, Inc, NY
Amadeu RR, Cellon C, Olmstead JW, Garcia AAF, Resende Jr MFR, Muñoz PR (2016) AGHmatrix: R Package to construct relationship matrices for autotetraploid and diploid species: a blueberry example. Plant Genom 9:1–10
Askew GR, El-Kassaby YA (1994) Estimation of relationship coefficients among progeny derived from wind-pollinated orchard seeds. Theor Appl Genet 88:267–272
Avendaño S, Woolliams JA, Villanueva B (2005) Prediction of accuracy of estimated Mendelian sampling terms. J Anim Breed Genet 122:302–308
Beaulieu J, Lenz P, Bousquet J (2022) Metatdata analysis indicates biased estimation of genetic parameters and gains using conventional pedigree information instead of genomic-based approaches in tree breeding. Sci Rep. 12:3933
Bernardo R (2014) Genomewide selection when major genes are known. Crop Sci 54:68–75
Birol I, Raymond A, Jackman SD, Pleasance S, Coope R, Taylor GA et al. (2013) Assembling the 20 Gb white spruce (Picea glauca) genome from whole-genome shotgun sequencing data. Bioinformatics 29:1492–1497
Butts C (2008) network: a package for managing relational data in R. J Stat Softw 24:1–36
Cappa EP, El-Kassaby YA, Muñoz F, Garcia MN, Villalba PV, Klápště J et al. (2017) Improving accuracy of breeding values by incorporating genomic information in spatial-competition mixed models. Mol Breed 37:125
Chateigner A, Lesage-Descauses M-C, Rogier O, Jorge V, Leplé J-C, Brunaud V et al. (2020) Gene expression predictions and networks in natural populations supports the omnigenic theory. BMC Genom 21:416
Cortés AJ, Restrepo-Montoya M, Bedoya-Canas LE (2020) Modern strategies to assess and breed forest tree adaptation to changing climate. Front Plant Sci 11:583323
Cotterill PP (1986) Genetic gains expected from alternative breeding strategies including low cost options. Silvae Genet 35:212–223
Devey ME, Bell JC, Uren TL, Moran GF (2002) A set of microsatellite markers for fingerprinting and breeding applications in Pinus radiata. Genome 45:984–989
Doerksen TK, Herbinger CM (2008) Male reproductive success and pedigree error in red spruce openpollinated and polycross mating systems. Can J Res 38:1742–1749
El-Kassaby YA (1995) Evaluation of the tree-improvement delivery system: factors affecting genetic potential. Tree Physiol 15:545–550
El-Kassaby YA, Lstibůrek M (2009) Breeding without breeding. Genet Res 91:111–120
El-Kassaby YA, Mansfield S, Isik F, Stoehr M (2011) In situ wood quality assessment in Douglas-fir. Tree Genet Genom 7:553–561
El-Kassaby YA, Wang Q, Wang T, Ratcliffe B, Bi Q-X, Wang Z et al. (2019) Concept for gene conservation strategy for the endangered Chinese yellowhorn, Xanthoceras sorbifolium, based on simulation of pairwise kinship coefficient. Ecol Manag 432:976–982
Elshire RJ, Glaubitz JC, Sun Q, Poland JA, Kawamoto K, Buckler ES et al. (2011) A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS One 6:e19379
Endelman JB (2011) Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 4:250–255
Fisher RA (1918) The correlation between relatives under the supposition of Mendelian inheritance. Trans R Soc Edinb 52:399–433
Gamal El-Dien O, Ratcliffe B, Klápště J, Porth I, Chen C, El-Kassaby YA (2016) Implementation of the realized genomic relationship matrix to open-pollinated white spruce family testing for disentangling additive from nonadditive genetic effects. G3 6:743–753
Gamal El-Dien O, Ratcliffe B, Klápště J, Porth I, Chen C, El-Kassaby YA (2018) Multi-environment genomic variance decomposition analysis of open-pollinated interior spruce (Picea glauca x engelmannii). Mol Breed 38:26
Guo X, Klisz M, Puchałka P, Silvestro R, Faubert P, Belien E et al. (2021) Common-garden experiment reveals clinal trends of bud phenology in black spruce populations from a latitudinal gradient in the boreal forest. J Ecol 110:1043–1053
Gilmour AR, Thompson R, Cullis BR (1995) Average information REML: an efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51:1140–1450
Gomory D, Foffova E, Kme J, Longauer R, Romsakova I (2010) Norway spruce (Picea abies [L.] Karst.) provenance variation in autumn cold hardiness: adaptation or acclimation? Acta Biol 52:42–49
Grattapaglia D, Ribeiro VJ, Rezende GDSP (2004) Retrospective selection of elite parent trees using paternity testing with microsatellite markers: an alternative short term breeding tactic for Eucalyptus. Theor Appl Genet 109:192–199
Grattapaglia D, Silva-Junior OB, Resende RT, Cappa EP, Müller BSF, Tan B et al. (2018) Quantitative genetics and genomics converge to accelerate forest tree breeding. Front Plant Sci 9:1693
Gurobi Optimization, LLC (2023) https://www.gurobi.com
Henderson CR (1975) Best linear unbiased estimation and prediction under a selection model. Biometrics 31:423–447
Jing Y, Bain L, Zhang X, Zhao B, Zheng R, Su S et al. (2023) Genetic diversity and structure of the 4th cycle breeding population of Chinese fir (Cunninghamia lanceolata (lamb.) hook). Front Plant Sci 14:1106615
Khasa D, Hambling B, Kernaghan G, Fung M, Ngimbi E (2002) Genetic variability in salt tolerance of selected boreal woody seedlings. Ecol Manag 165:257–269
Klápště J, Jaquish B, Porth I (2022) Building resiliency in conifer forests: interior spruce crosses among weevil resistant and susceptible parents produce hybrids appropriate for multi-trait selection. PLoS ONE 17:e0263488
Lambeth CC (1980) Juvenile-mature correlations in Pinaceae and implications for early selection. For Sci 26:571–580
Libby WJ, Cockerham CC (1980) Random non-contiguous plots in interlocking field layouts. Silvae Gene 29:183–190
Lush J (1937) Animal Breeding Plans. Iowa State College Press, Ames, Iowa
Matallana-Ramirez LP, Whetten RW, Sanchez GM, Payn KG (2021) Breeding for climate change resilience: a case study of loblolly pine (Pinus taeda L.) in North America. Front Plant Sci 12:606908
Misztal I, Tsuruta S, Lourenco D, Aguilar I, Legarra A, Vitezica Z (2018) Manual for BLUPF90 family of programs. University of Georgia, Athens, USA, 125
Moran E, Lauder J, Musser C, Stathos A, Shu M (2017) The genetics of drought tolerance in conifers. N. Phytol 216:1034–1048
Muñoz F, Sanchez I (2020) breedR: statistical methods for forest genetic resources analysts. R package version 0.12-4. https://github.com/famuvie/breedR
Muñoz PR, Resende Jr MFR, Huber DA, Quesada T, Resende MDV, Neale DB et al. (2014) Genomic relationship matrix for correcting pedigree errors in breeding populations: impact on genetic parameters and genomic selection accuracy. Crop Sci 54:1115–1123
Muñoz PR, Resende Jr MFR, Gezan SA, Resende MDV, de los Campos G, Kirst M et al. (2014) Unraveling additive from nonadditive effects using genomic relationship matrices. Genetics 198:1759–1768
Namkoong G (1966) Inbreeding effects on estimation of genetic additive variance. Sci 12:8–13
Powell JE, Visscher PM, Goddard ME (2010) Reconciling the analysis of IBD and IBS in complex trait studies. Na Rev Genet 11:800–805
Ratcliffe B, Gamal El-Dien O, Klápště J, Porth I, Chen C, Jaquish B et al. (2015) A comparison of genomic selection models across time in Interior Spruce (Picea engelmannii × glauca) using high density SNP imputation methods. Heredity 115:547–555
Rincent R, Laloë D, Nicolas S, Altmann T, Brunel D, Revilla P et al. (2012) Maximizing the reliability of genomic selection by optimizing the calibration set of reference individuals: comparison of methods in two diverse groups of maize inbreds (Zea mays L.). Genetics 192:715–728
Ritland K (1996) Estimators for pairwise relatedness and individual inbreeding coefficients. Genet Res 67:175–185
Sonesson AK, Woolliams JA, Meuwissen THE (2012) Genomic selection requires genomic control of inbreeding. Genet Sel Evol 44:27
Squillace AE (1971) Average genetic correlations among offspring from open-pollinated forest trees. Silvae Genet 23:149–156
Stonecypher RW, Cech FC, Zobel BJ (1964) Inheritance of specific gravity in two and three-year-old seedlings of loblolly pine. Tappi 47:405–406
Surówka E, Rapacz M, Janowiak F (2020) Climate change influences the interactive effects of simultaneous impact of abiotic and biotic stresses on plants. In: M. Hasanuzzaman (ed.) Plant ecophysiology and adaptation under climate change: mechanisms and perspectives I. Springer Nature Singapore, p 1-49
Tam V, Patel N, Turcotte M, Bossé Y, Paré G, Meyre D (2019) Benefits and limitations of genome-wide association studies. Nat Rev Genet 20:467–484
Thistlethwaite FR, Gamal El-Dien O, Ratcliffe B, Klapstě J, Porth I, Chen C et al. (2020) Linkage disequilibrium vs. pedigree: genomic selection prediction accuracy in conifer species. PLoS ONE 15:e0232201
Uffelmann E, Huang QQ, Munung NS, de Vries J, Okada Y, Martin AR et al. (2021) Genome-wide association studies. Nat Rev 1:59
VanRaden PM (2008) Efficient methos to compute genomic predictions. J Dairy Sci 91:4414–4423
Visscher PM, Goddard ME (2019) From R.A. Fisher’s 1918 paper to GWAS a century later. Genetics 211:1125–1130
Vitezica ZG, Varona L, Legarra A (2013) On the additive and dominant variance and covariance of individuals within the genomic selection scope. Genetics 195:1223–1230
Wheeler NC, Steiner KC, Schlarbaum SE, Neale DB (2015) The evolution of forest genetics and tree improvement research in the United States. J 113:500–510
White TL, Adams WT, Neale DB (2007) Forest Genetics. CAB International, Oxfordshire, U.K.
White T, Davis J, Gezan S, Hulcr J, Jokela E, Kirst M et al. (2014) Breeding for value in a changing world: past achievements and future prospects. New 45:301–309
Williams CC, Savolainen O (1996) Inbreeding depression in conifers: implications for breeding strategy. For Sci 42:102–117
Woolliams JA, Berg P, Dagnachew BS, Meuwissen THE (2015) Genetic contributions and their optimizations. J Anim Breed 132:89–99
Wright S (1922) Coefficients of inbreeding and relationship. Am Nat 56:330–338
Acknowledgements
We thank the British Columbia Ministry of Forests, Forest Improvement and Research Management Branch for trials access. Funding: This work was supported by a NSERC Discovery Grant and the Johnson’s Family Forest Biotechnology Endowment to YAE. The optimization work was completed using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF (ACI-1548562) under the resource allocation to CC (MCB-180177).
Author information
Authors and Affiliations
Contributions
Conceptualization: YAEK. Methodology: YAEK, EPC, CC, BR, IMP. Writing: YAEK – original draft. Review and editing: YAEK, EPC, CC, BR, IMP.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Associate editor Chenwu Xu
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
El-Kassaby, Y.A., Cappa, E.P., Chen, C. et al. Efficient genomics-based ‘end-to-end’ selective tree breeding framework. Heredity 132, 98–105 (2024). https://doi.org/10.1038/s41437-023-00667-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41437-023-00667-w