Abstract
Many species are structured in social groups (SGs) where individuals exhibit complex mating strategies. Yet, most population genetic studies ignore SGs either treating them as small random-mating units or focusing on a higher hierarchical level (the population). Empirical studies acknowledging SGs have found an overall excess of heterozygotes within SGs and usually invoke inbreeding avoidance strategies to explain this finding. However, there is a lack of null models against which ecological theories can be tested and inbreeding avoidance quantified. Here, we investigate inbreeding (deviation from random mating) in an endangered forest-dwelling pair-living lemur species (Propithecus tattersalli). In particular, we measure the inbreeding coefficient (FIS) in empirical data at different scales: SGs, sampling sites and forest patches. We observe high excess of heterozygotes within SGs. The magnitude of this excess is highly dependent on the sampling scheme: while offspring are characterised by a high excess of heterozygotes (FIS < 0), the reproductive pair does not show dramatic departures from Hardy–Weinberg expectations. Moreover, the heterozygosity excess disappears at larger geographic scales (sites and forests). We use a modelling framework that incorporates details of the sifaka mating system but does not include active inbreeding avoidance mechanisms. The simulated data show that, although apparent “random mating” or even inbreeding may occur at the “population” level, outbreeding is maintained within SGs. Altogether our results suggest that social structure leads to high levels of outbreeding without the need for active inbreeding avoidance mechanisms. Thus, demonstrating and measuring the existence of active inbreeding avoidance mechanisms may be more difficult than usually assumed.
Similar content being viewed by others
Introduction
In many vertebrate species, individuals live in social groups (SGs) with variable kinship structure, complex mating strategies, and sex-biased dispersal (Clutton-Brock 2016). The large variety of species that live in groups include many non-humans primates, rodents, bats, cetaceans, fish and birds (Clutton-Brock 2016; Rubenstein and Abbot 2017). Within these, social organisations can range from temporary pair-bounded aggregations to stable complex societies, exhibiting cooperative breeding or complex dominance hierarchies for example (Clutton-Brock 2016). Sociality has been mostly interpreted as an adaptive mechanism (Silk 2007; Clutton-Brock 2009, 2016) within the context of the kin selection theoretical paradigm. According to this paradigm, individuals may gain indirect (inclusive) fitness benefits by enhancing the fitness of others through helping and cooperating with relatives (that carry copies of the same genes; Hamilton 1964). Several studies propose that, at low population inbreeding loads, inclusive fitness benefits should induce individuals to prefer mating with relatives (Lehmann and Perrin 2003; Kokko and Ots 2006). Indeed, in some species animals do prefer to mate with kin rather than with unrelated individuals (Rioux-Paquette et al. 2010; Olson et al. 2012; Szulkin et al. 2013; Jacob et al. 2016). From a population genetics perspective, the consequence of mating among related individuals is increased homozygosity, which can expose recessive deleterious alleles causing inbreeding depression (Charlesworth and Charlesworth 1999). Inbreeding avoidance is thus seen as an important evolutionary mechanism (Szulkin et al. 2013). Sex-biased dispersal and differences in dispersal distances between sexes are often invoked as inbreeding avoidance mechanisms (Greenwood 1980; Lawson Handley and Perrin 2007). However, this usually relies on verbal arguments that make a link between behavioural observations and outbreeding without quantifying kin recognition and dispersal as means of inbreeding avoidance (see Perrin and Mazalov 1999; Roze and Rousset 2005 for theoretical discussions on inbreeding avoidance as the reason for dispersal). Although inbreeding avoidance and inbreeding preference are typically envisioned in a selective context (Silk 2007; Lukas and Clutton-Brock 2011; Clutton-Brock 2016), there is an increasing number of studies challenging this view, highlighting the limitations of current inbreeding theories and models and thus calling for new neutral models (Szulkin et al. 2013; Parreira and Chikhi 2015).
Inbreeding is often estimated through Wright’s inbreeding coefficient (FIS), a parameter that was developed under the classical population genetics framework (Wright 1951). In practice, F-statistics are a tool for describing the partitioning of genetic diversity within and among (sub) populations. FIS measures the deviation from Hardy–Weinberg proportions within demes. Negative values indicate an excess of heterozygotes while positive values indicate a deficit. Under this framework, the latter means that mating occurs more often between more closely related individuals than between individuals drawn at random from the (sub)population. FST measures the genetic variance in allelic frequencies among demes, describing the mean reduction in heterozygosity of a deme relative to the total due to genetic drift. This framework ignores social structure and envisions structured populations as a network of panmitic demes, which are considered the smallest level of population structure. When species are socially structured, the smallest unit of population structure is the SG. SGs typically comprise individuals of several overlapping generations, with complex mating strategies and often sex-biased dispersal. Social structure was addressed in a theoretical mathematical framework by Chesser (1991a, b) and Chesser et al. (1993), who extended Wright’s F–statistics to describe the apportionment of genetic diversity in populations subdivided in SGs. Under this framework, F-statistics are derived as a function of co-ancestries of genes in individuals within and among SGs. Chesser (1991a, b) and Chesser et al. (1993) have shown that FIS is expected to be negative within SGs. This means that we expect to observe a negative FIS within SGs even in the absence of inbreeding avoidance mechanisms, either those that are active (such as kin recognition and extra-group copulations) or those interpreted as “passive inbreeding avoidance” (e.g. sex-biased dispersal; Chesser 1991b; Sugg and Chesser 1994; Sugg et al. 1996; Di Fiore 2012; Parreira and Chikhi 2015). The fact that negative FIS values are expected within SGs also shows that, despite the fact that individuals within SGs are highly related (through co-ancestry maintained by the pedigree), a high relatedness may not be translated into a loss of genetic diversity (inbreeding measured by drift as change in heterozygosity). This is highly counterintuitive because under the classical population genetics framework small units (demes) are expected to lose genetic diversity by drift and accumulate inbreeding (co-ancestry by drift; see Wakeley and Wilson 2016 for a review on the several concepts of identity-by-descent).
We have proposed a new framework that explicitly models the subdivision of species into SGs, incorporates mating systems, and can be used as a null-model to test inbreeding avoidance strategies (Parreira and Chikhi 2015). Under this framework, populations are modelled as a network of SGs, which are age-structured units where individuals mate according to different strategies (e.g. monogamy, polygyny) without any mating bias against kin (Parreira and Chikhi 2015). Our previous findings based on this framework were purely theoretical and based on an n-island type of structure that incorporates structure but ignores space (i.e., every SG is connected to all others in the overall population and thus all SGs are at the same “distance” from each other). Previous results were based on simulated scenarios and no real species ecological and genetic data were used.
The aim of the present study is to understand the role of the social structure in the genetic diversity of an endangered primate species, the golden-crowned sifaka (Propithecus tattersalli, Simons 1988). Previous genetic studies have focused on the patterns of genetic differentiation across the landscape or on the demographic history of the species (Quéméré et al. 2010a, b, 2012). Quéméré et al. (2010a) reported a bias towards negative FIS values (ranging from −0.01 to −0.18) at the level of forest fragments. However, the origin of this pattern has not been investigated. Here, we ask whether outbreeding is a consequence of population structure in the form of SGs and dispersal. In this study we apply our previously developed modelling framework to the golden-crowned sifaka (Parreira and Chikhi 2015). We use the simulations as a null model to predict FIS values for a population subdivided in SGs where mating occurs according to monogamy (P. tattersalli mating system) and without inbreeding avoidance by mate choice through kin recognition. As such, if sifakas have developed mechanisms to avoid inbreeding, we expect FIS values to be more negative in the real population than in the simulated one. Our aim is to understand the effect of social structure on the levels of inbreeding in this species and to provide hints for its biological interpretation.
Materials and methods
Study population and sampling strategy
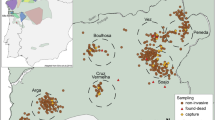
The golden-crowned sifaka is a social lemur species from the Indriidae family (Simons 1988). It is only found in a restricted and fragmented forest habitat in the Loky-Manambato region of northeastern Madagascar (Quéméré et al. 2010a, b, Fig. 1) and has been classified as critically endangered in IUCN’s last assessments (e.g. Andriaholinirina et al. 2014, Semel et al. 2020). Studies on the ecology and social structure of sifakas are still limited, but there is a long-term study on Propithecus verreauxi that describes sifakas as diurnal animals living in SGs that contain from two to ten individuals (Lawler et al. 2003; Lewis 2008). One single male and one single female are thought to monopolise reproduction, although groups may include other (sub)adults which are thought to be pre-dispersal natal individuals (Meyers 1993). Females are more philopatric than males; within groups adult females can relate to each other as mother–daughter or as sisters, while males are thought to leave the natal group once they reach sexual maturity (Meyers 1993).
Faecal material from 224 individuals belonging to 104 SGs was collected during two field missions in 2006 and 2008 at 19 sites in the nine main forest fragments of the species’ distribution range (Quéméré et al. 2010a, b, Fig. 1). These data were already published and are available at the Dryad Digital Repository (doi.org/10.5061/dryad.8f45n). The geographic location of all samples was recorded by GPS and is presented in Fig. 1. The sample collection, faecal DNA extraction and genotyping procedures were performed by Quéméré et al. (2010a, b) and protocols are extensively described therein. In short, faecal extraction was performed using a protocol adapted from Vallet et al. (2008) and all individuals were genotyped for 13 microsatellite loci. Samples were genotyped using a sequential replicate-based approach according to which, in order to ensure the reliability of the genotyping, an allele is recorded only if amplification is unambiguous at least twice for heterozygous genotypes and at least three times for homozygous genotypes (Frantz et al. 2003). Two amplifications are initially performed and, if necessary, further amplifications are sequentially added (up to seven successful PCRs) until a consensus genotype is reached. Genotyping error rates (allele dropout and false error rates) and mean quality index for each locus across individuals (QI) were calculated following Miquel et al. (2006) and are provided in Quéméré et al. (2010b).
The number of sampled individuals within SGs varied from one (25 out of the 104 SGs) to four, but only groups composed of two or more individuals were included in the analysis performed at the SG level (see below). Within the largest forest fragments, SGs were sampled in several sites (Fig. 1). Although the geographic limits of these “sites” are somewhat arbitrary, they consist of an agglomeration of SGs geographically close to each other, and would correspond to how a “sampling location” is usually defined in other empirical population genetics studies.
Simulation approach
We used a framework previously developed by us (Parreira and Chikhi 2015, where a detailed explanation of the model can be found). In a few words, individuals are not modelled as members of populations but as members of a network of SGs. SGs are age-structured units wherein diploid dioceous individuals reproduce according to specific mating strategies (e.g. monogamy, polygyny, etc., see below) and among which individuals can disperse (Fig. 2). This framework is an individual-based forward time model where each individual is explicitly characterised by its sex, reproductive status, age and genotype. Individuals undergo a simplified life-cycle involving different age classes: new borns, juveniles, and adults (reproductive status—RS or non-reproductive status—non-RS, see below). This allows for a great flexibility in simulating attributes of primate social systems, such as long living, slow reproduction, strong variance in reproductive success, dominance hierarchies, etc. Under this framework, SGs are units in which generations overlap. This is thus fundamentally different from the classical Wright–Fisher (WF) approach that envisions populations as a network of random-mating units (demes) with non-overlapping generations that exchange migrants according to a pre-defined rate (Wright 1943). Reproduction occurs among individuals living in the same SG according to different strategies such as monogamy, polygyny, etc., without any active kin discrimination behaviour. Only a limited number of adult individuals take part in reproduction and these are identified as RS individuals. RS individuals are a fixed number of males and females within each SG and the ratio RS males to RS females characterises the mating system. In the simulations performed here, we set RS individuals to one in both males and females so that there is only one mating pair per SG — monogamy as in the golden-crowned sifaka. Male–female mating pairs are formed without taking relatedness into account, i.e., no inbreeding or outbreeding.
a The simulated population consists of a large network of 22 × 22 SGs. Individuals can move to their four neighbouring SGs. Grey squares identify the position of SGs from where individuals were sampled in order to calculate F-statistics. b Each SG is simulated as being composed of two reproductive status individuals (RS) identified by large figures (red females and black males), offspring and juveniles, identified by small figures, and non-RS adult individuals identified by grey figures. For Propithecus tattersalli the number of RS individuals is fixed to one male and one female. Within SGs individuals undergo a simplified life-cycle including aging (b.1) and reproduction (b.2). Individuals colonize and disperse to neighbouring SGs (b.3). This simplified life-cycle is repeated over a pre-defined number of time intervals. See supplementary material for further details.
To account for spatial structure, we simulated a geographical area, represented as a grid of 22 by 22 SGs (total of 484 SGs with bounded edges). This grid is equivalent to a stepping-stone model except that the units are SGs instead of demes (Fig. 2a). In practice, this set of interconnected groups can be seen as a single forest fragment. We considered that individuals could disperse to the closest neighbouring SGs in agreement to what has previously been suggested for this species. Quéméré et al. (2010a) have found significant isolation-by-distance and spatial autocorrelation at a small spatial scale (<1.5 km), which suggested dispersal is most likely to be restricted among neighbouring groups, a finding that is in agreement with behavioural observations for this species (Meyers 1993). In the model, dispersal will only occur if the individuals can become RS and reproduce in a neighbouring SG. That is, we considered actual dispersal events rather than applying a constant dispersal rate. Since RS individuals maintain their status until death, breeding vacancies within a SG only become available due to death events. When all RS individuals from one sex die, RS individuals of the remaining sex lose the reproductive status (becoming non-RS) and the SG virtually vanishes. A new SG will be founded by individuals that move from a neighbouring SG in order to establish themselves as new RS. New RS individuals are chosen at random among non-RS according to the predefined connections in the network. A SG may include adults that were not yet able to disperse (non-RS) and that may eventually not disperse at all during their life if no such opportunity appears. In nature, sifaka males disperse or are evicted from their natal group once they reach adulthood, and thus adult non-breeding males (non-RS individuals) are usually not part of a SG. A flow chart summarizing the main assumptions of the modelling framework is displayed in Fig. 2.
There is scarce information on the life-history traits of the golden-crowned sifaka, but it is known that females usually give birth to a single offspring once every two years (Garbutt 2007) and that individuals can live up to 20 years in captivity (Weigl 2005). Age of sexual maturity is not known with precision but females of a closely related sifaka species (P. verreauxi) are known to become sexually mature two or three years after birth (Richard et al. 2006). These ecological data were used as a starting point to define the most likely values for the birth interval, number of offspring, and age of first reproduction in the model. Because values for many demographic parameters reported in literature (lifespan, sexual maturity, weaning age, etc.) are uncertain for the golden-crowned sifaka, we tested 1800 different parameter combinations in a number of exploratory simulations by considering a realistic range of values for each parameter (Table S1). For each parameter combination we produced 100 replicates. We retained the parameter combination that led to a demographically stable population (not causing population crash) and that, at the same time, resulted in group sizes similar to those observed in nature (up to ten individuals, see above). Specifically, we selected a parameter combination that led to two up to 20 individuals per SG, including the reproductive pair, their offspring, juveniles, and non-reproductive adults (which usually do not stay in real sifaka SGs).
In order to measure genetic variation within and among SGs, we randomly sampled 22 social units along the main diagonal of the simulation matrix (Fig. 2a). This sampling design incorporates the full range of possible distances among SGs, allowing us to account for the effect of isolation-by-distance (Wright 1943). We sampled four individuals per SG whenever possible. Individuals were randomly sampled according to different sampling schemes: (1) among juveniles, RS, and non-RS females (hereafter denominated as random sampling), (2) juveniles, (3) RS individuals only (only two individuals were sampled in this case). We chose to ignore non-RS male adults because in nature these individuals disperse as soon as they reach adulthood and are usually not found within SGs. A modelling framework that incorporates ecological data for a specific social species allows obtaining the expected (null) FIS distribution for a given species of interest. Differences between empirical and theoretical distributions provide us with information on the amount of inbreeding/outbreeding generated by matings among related/unrelated individuals beyond that generated by the subdivision of populations in SGs.
Assessment of population subdivision and genetic structure
The genetic diversity and structure were described using the heterozygosities estimated according to Nei (1978) and the F-statistics estimators calculated according to Weir and Cockerham (1984). We used two F-statistics: FIS, which measures for deviations from Hardy–Weinberg equilibrium as the correlation of alleles within individuals in relation to that of the sub-population unit considered (SG, “site” and forest fragment); and FST, which measures for genetic differentiation. In the empirical study F-statistics and heterozygosities were measured using the GENETIX 4.05.2 software (Belkhir et al. 1996). Statistics were measured at three different scales: the SG (N = 76, only groups where two or more individuals have been sampled were considered), the sampling site (N = 19 locations comprising several neighbouring SGs), and the forest fragment (N = 9 areas comprising several sites that are separated by unsuitable habitat; see Fig. 1). Statistics measured at the “site” and fragment scales, as usually done in population genetics studies, ignore the information about the SG of origin of each individual and pool together individuals sampled from the same “site” and fragment. In the simulation study, F-statistics were estimated within SGs and at the fragment scale by pooling a different number of SGs (from two to 22). These SGs were randomly chosen among all the sampled SGs in the matrix. F-statistics were calculated using R scripts developed by us in the R© software version 3.3.2 (R Core Team 2014). Also, in the simulation study, F-statistics were calculated either by distinguishing the age/reproductive status of individuals or by sampling at random as in the empirical study (where the status of individuals was not always identifiable).
The geographic distance among neighbouring SGs (within sites in the real dataset) was calculated by the euclidean distance based on GPS coordinates using the Landscape Genetics Toolbox in ArcGis (Etherington 2011).
Results
Deviations from Hardy–Weinberg equilibrium within SGs
We found highly negative FIS values within SGs both in the empirical and simulation studies, indicating an excess of heterozygotes in relation to what was expected under random mating. In the empirical study, the mean FIS was −0.235 (SE = 0.022, range = −0.733 to 0.158) with 86% of SGs (N = 65 out of 76) showing negative FIS values, out of which 71% (N = 46) showed significantly negative FIS values (p < 0.05). Only 14% (N = 11 out of 76) showed null or non-significant positive FIS values (Fig. 3). A strong excess of heterozygotes was also found within SGs in the simulation study (Fig. 4). The mean simulated FIS per SG was −0.079 (SE = 0.004; range = –0.810 to 0.455) when individuals were sampled at random within SGs (i.e., ignoring their age / reproductive status). This mean FIS was measured across 100 repetitions within sampled SGs using SGs where n > 1 [\({\rm{sample}}\;{\rm{size}} = {\rm{SG}}\left( {n \,>\, 1} \right) \times {{nb.} \rm{repetitions}} = 2200\)]. The age/reproductive status of the sampled individuals greatly influenced FIS measures: FIS were highly negative when sampling only offspring (mean ± SE = −0.288 ± 0.005, range = −0.833 to 0.44; n = 1755) indicating a great excess of heterozygotes in the progeny, whereas it was close to zero when only reproductive adults where sampled (mean ± SE = −0.016 ± 0.004, range = −0.793 to 0.773; n = 2197; Fig. 4) indicating only a small deficit of heterozygotes in parents. Within SGs, the increase in FIS in parents (RS) in comparison to FIS in offspring was due to differences in the expected (HE) rather than observed heterozygosity (HO), that is HO in RS and offspring was quite similar, while HE in parents was higher than in offspring (Fig. S1). Altogether, simulations were thus able to recover FIS values obtained in the empirical study. We also found that the empirical distribution of FIS values was intermediate between the juveniles and the random sample distributions obtained from the simulated dataset (Fig. 4, see also Fig. S2).
Circles are FIS values measured within SGs; each dashed horizontal line corresponds to a sampling site (see Fig. 1 for a correspondence between names and geographic locations). Colours correspond to p-value significance: white—non-significant, light grey—p < 0.05, dark grey—p < 0.01 and black—p < 0.001. FIS were calculated according to Weir and Cockerham (1984) and only SGs where more than one individual was sampled were considered (thus N = 76, instead of 103).
Coloured lines show FIS distributions measured in the simulated datasets according to Wright (1951). Different colours represent different sampling schemes—juveniles in green (mean = −0.288; 95% CI: [−0.34, −0.16]), RS in red (mean = −0.016; 95% CI: [−0.06, 0.06]) and random sample in blue (mean = −0.079; 95% CI: [−0.12, 0.01]). Each density curve was obtained using FIS values measured at the last time step and from nSG ≥ 2 at 100 independent simulations. This corresponds to 2197 data points when RS individuals are sampled, 1755 data points when only juveniles are sampled, and 2200 points when a random sample was taken. The black curve shows the distribution of FIS values obtained from the golden-crowned sifaka real dataset (mean = −0.235; note that these are the same as values shown in Fig. 3). Density curves were fitted using the locfit function in the R software. This function estimates the density of a set of values (FIS) having as limits the minimum and maximum frequencies observed in the dataset and for this reason the density curves shown do not necessarily extent towards zero in the y axis.
Excess of heterozygotes at different spatial scales
Even though sifaka SGs taken individually showed a strong excess of heterozygotes (FIS < 0), the magnitude of this markedly decreased at the “site” and fragment scales (significant FIS at eight out of 19 sites and significant FIS at four out of nine fragments, Tables 1 and S2). In other words, FIS values tended to become less negative as the hierarchical scale at which samples were analysed increased: mean FIS values increased from −0.236 (SGs) to −0.069 (sites, n = 19) and −0.044 (fragments, n = 9; see Table 1 legend). We found a positive correlation between the increase in FIS and the distance between SGs (Figs. 5 and S3): the increase in FIS was larger when pooled SGs were located further away from each other, as expected when there is isolation-by-distance (Wright 1943). However, at the scale of the fragment, most SGs are located close to each other and we could not detect any significant correlation between geographic distance and FST. Also, our results showed that the magnitude of increase in FIS values with changing hierarchical scales depends on the number of SGs pooled at sites and fragments—the larger the number of groups pooled, the greater the increase in FIS values (Fig. 5). This was also observed in the simulated dataset, where pooling an increasing number of SGs increased FIS towards positive values. In this case, mean FIS values were slightly positive when six or ten SGs were pooled and markedly positive only when 22 SGs were pooled together (Fig. S4). This is in agreement with the real dataset results where the largest increase (from −0.137 to 0.025) was found in the BEK site (G1, N = 21 pooled SGs). This increase in FIS values (SGs to sites and sites to fragments) is consistent with the Wahlund effect and mostly determined by an increase in the expected heterozygosity (both in RS and offspring), rather than by a change in the observed heterozygosity, which was more or less constant among the different hierarchical levels (Table S2 and Fig. S5).
FIS measured within sampling sites (Fig. 1). FIS within sites (N = 19) were measured by pooling neighbouring SGs that belong to a given forest fragment. Black symbols show FIS as a function of the number of SGs, whereas grey symbols show FIS as a function of the mean geographic distance among the pooled SGs (measured in meters). FST is largely determined by geographically limited dispersal resulting in isolation-by-distance (Wright 1943). Because male sifakas predominantly disperse to neighbouring groups, the observed increase in FIS with mean geographic distance was expected (see also Fig. S3).
Discussion
The genetic diversity of a population is influenced by its spatial distribution and also by several aspects of population dynamics and behavioural ecology, such as dispersal and mating tactics (Chesser 1991a, b; Sugg et al. 1996; Di Fiore 2012; Parreira and Chikhi 2015). When populations are subdivided in SGs, many individuals are related through parents or through the philopatric sex (thus sharing alleles identical-by-descent through the pedigree). SGs are thus often seen as potentially inbred units that need to evolve active or “passive” mechanisms to counteract potential inbreeding depression effects, such as kin recognition and sex-biased dispersal. However, the subdivision of populations in SGs, while maintaining identity-by-descent sharing through the pedigree, can result in outbreeding (excess in heterozygotes; Chesser 1991a, b; Chesser et al. 1993; Sugg and Chesser 1994; Sugg et al. 1996). Here we show that strongly negative FIS values can be the result of social structure driven by age structure (offspring) but that it does not require inbreeding avoidance strategies. Although dispersal is often seen as an inbreeding avoidance mechanism, the fact is that the number of theoretical studies on the relationship between inbreeding and dispersal (Gandon 1999; Perrin and Mazalov 1999; Lehmann and Perrin 2003; Roze and Rousset 2005; Guillaume and Perrin 2006) contrasts with the few empirical studies where dispersal as a means of inbreeding avoidance has actually been quantified (Greenwood et al. 1978; Schiegg et al. 2006; Szulkin and Sheldon 2008). When populations are structured, they are subdivided into distinct units (demes or SGs) among which individuals can move. Thus, dispersal is by definition part of population structure. The fact that individuals move away from their natal unit (deme or SG) and mate elsewhere decreases the chances of mating with close kin thereby decreasing inbreeding.
Negative FIS have been reported in various social species, such as in Indian fruit bats (Cynopterus sphinx, Storz et al. 2001), yellow-bellied marmots (Marmota flaviventris, Schwartz and Armitage 1980) and alpine marmots (Marmota marmota, Goossens et al. 2001), black-tailed prairie dogs (Cynomys ludovicianus, Winterrowd et al. 2009), and white sifakas (P. verreauxi verreauxi, Lawler et al. 2003). The consistent excess of heterozygotes found within SGs of the golden-crowned sifaka is considerably higher than comparable estimates for other mammals, suggesting that this species exhibits uncommonly large levels of outbreeding. For instance, the lowest reported FIS values were −0.16 in Indian fruit bats and −0.20 in white sifakas, whereas in the present study the most extreme FIS value was −0.733 (Fig. 3). We have recently shown in a theoretical study that the negative FIS expectation is maximised under a monogamous mating system (Parreira and Chikhi 2015), as seen in golden-crowned sifakas (Meyers 1993). The natural organisation of this species in SGs and the monogamic matings may explain the highly negative values found in the present golden-crowed sifaka study.
Possible evolutionary consequences of the subdivision into SGs
The simulated datasets revealed differences between FIS measured in parents (RS) and offspring meaning that in practice, inbreeding is highly dependent on the sampling scheme (Figs. 4 and S2). The difference between inbreeding levels measured in RS and offspring individuals is probably because most RS pairs are composed of individuals that differ in origin and thus carry different alleles. As a consequence, sampling RS individuals increases FIS towards zero within SGs (due to the higher HE in RS; see Fig. S1).
The effect of age and reproductive status can also be interpreted in respect to dispersal timing. Basset et al. (2001) have noted that FIS measured in offspring corresponds to sampling individuals before dispersal and thus measures the genetic product of mating (distribution of genes in the next generation), whereas measuring FIS in RS individuals corresponds to sampling individuals after dispersal and measures the redistribution of genotypes across the population. For some authors, such as Storz et al. (2001), SGs are transient units from which individuals eventually disperse at some point in their lives. As a consequence, genetic estimates measured at the SG level are quite ephemeral snapshots of the genetic and genotypic diversity of a specific life-cycle time point and are not important on an evolutionary scale. Other authors do not reject the idea that mating and dispersal systems may have an evolutionary importance and SGs have been used to explain fast evolutionary rates supposedly found in mammal genera where most species are social (Bush-Wilson theory; Bush et al. 1977; Wilson 1992). However, this latter argument rests on the assumption that SGs can be treated under the Wright–Fisher framework as small demes. Under the classical framework, SGs are characterised by small effective sizes, high genetic drift and increased homozygosity. This is expected to increase the probability of fixation of new mutations, including chromosomal rearrangements, and accelerate rates of evolution. Our results, and those obtained for other social species exhibiting high levels of individual heterozygosity (consistent with lower drift; Schwartz and Armitage 1980; Pope 1992; Coltman et al. 2003; Lawler et al. 2003), contradict the Bush–Wilson theory. In addition, several recent studies have noted that social structure may influence rates of molecular evolution not because SGs behave as demes but because mating systems may influence the number of DNA replications per generation (Bromham 2009, 2011).
We argue that SGs have a significant effect on instantaneous patterns of genotypic diversity and also that they may have an evolutionary significance different from that predicted by the Bush–Wilson theory. For instance, social structure may have important evolutionary consequences by decreasing the frequency of homozygotes (and maintaining a high genotypic diversity, HO), thus influencing the fitness and survival of individuals and populations.
Differences in F-statistics across geographic scales
We found an excess of heterozygotes in P. tattersalli not only within SGs but also in most sites and fragments (Table 1). Although the estimated FIS was still negative at several levels of subdivision above the SG, the magnitude of excess of heterozygotes decreased when pooling different SGs (i.e., FIS SG < FIS site < FIS fragment). Importantly, this increase in FIS is due to the increase in HE mainly determined by offspring but also by the classical effect of population structure (Wahlund effect). The Wahlund effect consists in an increase in FIS due to the pooling of distinct units of population subdivision (Wahlund 1928) resulting in a heterozygote deficit (FIS > 0) when units of population subdivision are panmitic (FIS = 0). However, when these units are not at Hardy–Weinberg equilibrium, as observed in SGs of sifakas (FIS < 0), the “Wahlund-like” effect may not necessarily result in positive FIS and will rather increase FIS towards zero. In the golden-crowned sifaka, FIS values were highly negative within most SGs (Fig. 3 and Table 1) and that explains why these were still negative at most sites and fragments. Also, the magnitude of the Wahlund effect depends on the number of SGs pooled (Figs. 5 and S4; Table S2) and on the degree of population differentiation. Because (1 − FIT) = (1 − FST)(1 − FIS), FST values constrain the possible FIS and FIT values (Wright 1951). SGs are highly complex systems, structured both demographically (composed of individuals with different ages and sexes) and spatially (subdivision into subunits and their spatial arrangement). Observed genetic diversity appears to be influenced by factors intrinsic to the life histories of the organism, such as the mating system and the age structure, and by demographic factors, such as distribution ranges and levels of gene flow. For instance, the increase in FIS at the site and fragment scales is determined by the increase in HE caused by offspring but also depends on a Wahlund effect whose magnitude is largely determined by population structure and levels of subdivision. The several layers of structure interact among each other and quantifying the effect of each level is not easy and calls for more theoretical studies.
Concluding remarks
In the last decades, there has been an increasing number of studies addressing the fine-scale genetic structure of populations (Lawler et al. 2003; Di Fiore and Fleisher 2005; Fredsted et al. 2005; Archie et al. 2008; Di Fiore 2012; Di Fiore and Valencia 2014; van Djik et al. 2015). Still, compared to the number of studies focusing on the species or “population” scale, there are considerably less studies focusing on the social group. At the “population” and sub-population scales, deviations from random mating are usually not detected. That may be because in population level studies, samples usually consist of an agglomeration of individuals from different SGs and that leads, as we have shown, to an increase in FIS towards zero (random mating).
For many population genetics questions, the fact that individuals do not mate at random at finer levels of population structure does not seem problematic if one can still assume that the overall population is, or behaves as if it were, panmitic. This may be true for questions which depend on coalescences (shared common ancestry) occurring in the distant past. In other words, for questions at the level of the population, it may still be possible to use classical coalescent theoretical treatments to infer key evolutionary parameters, such as effective population sizes (Ne), despite the fact that species do not mate at random. However, for questions depending on shared ancestry at the very recent past, such as dispersal or inbreeding, deviations from random mating caused by social structure may be important. Deviations from random mating may also be important when conducting analyses that rely on Hardy–Weinberg equilibrium assumptions, such as STRUCTURE or genotype calling (Peterman et al. 2016; Waples and Anderson 2017).
The consequences of social structure can also be studied through the effect of sampling siblings and family clusters for estimates of genetic diversity, such as effective population sizes, allele frequencies and population differentiation (Peterman et al. 2016, Waples and Anderson 2017). For instance, Waples and Anderson (2017) have shown that, under a non-structured population model, Ne can be biased upwardly when siblings are removed and one single representative per family is kept in the sample but downwardly when some families are over-represented. These authors have shown that unbiased estimates of Ne can eventually be obtained if an “optimal” proportion of siblings is removed; however, this “optimal” number varies according to the mating system. These results may be related to the fact that when sampling siblings, we mostly recover coalescences occurring in the very recent past (with shared ancestry depending also on the mating system), whereas when sampling one individual per family (social group), one mostly recovers coalescences occurring at the more distant past.
Finally, our findings are particularly relevant in the context of Madagascar where habitats are increasingly fragmented and many species have been losing genetic diversity (Craul et al. 2009; Bailey et al. 2016; Hawkins et al. 2018; Vieilledent et al. 2018). The effect of ecological disturbance on social structure in Malagasy species is not well studied. However, studies in Australian social mammals suggest that habitat disruption may affect the structure and function of SGs (Banks et al. 2007). For instance, habitat loss and fragmentation may alter group size and mate availability causing changes in mating and dispersal behaviours. Unfortunately, it may be difficult to fully elucidate certain features of social systems, such as dispersal patterns, kinship structure, and mating system from observational data. In this context, simulation tools, as the one used in the present study, can be applied to other social species of interest. One could for instance, simulate alternative scenarios (using different ecological and life-history parameters and SGs network topology) to identify some of the most important factors affecting genetic and genotypic diversity.
Data accessibility
The complete genotype microsatellite dataset and the geographic coordinates of all individuals are available in the Dryad Digital Repository: https://doi.org/10.5061/dryad.8f45n. We have excluded six individuals from the original dataset deposited in the Dryad as for these samples analysis could not be performed at the site and fragment scales (ANALABE and AMBORONARIVO). Results for the computer simulations and R-scripts for the analysis can be provided upon request.
References
Andriaholinirina N, Baden A, Blanco M, Chikhi L, Cooke A, Davies N, et al. (2014) Propithecus tattersalli. The IUCN red list of threatened species. https://doi.org/10.2305/IUCN.UK.2014RLTS.T18352A16116567.en
Archie EA, Maldonado JE, Hollister-Smith JA, Poole JH, Moss CJ, Fleischer RC, Alberts SC (2008) Fine-scale population genetic structure in a fission-fusion society. Mol Ecol 17:2666–2679
Bailey CA, McLain AT, Paquette SR, McGuire SM, Shore GD, Lei R, Randriamanana JC et al. (2016) Evaluating the genetic diversity of three endangered lemur species (Genus: Propithecus) from Northern Madagascar. J Primatol 5:132
Banks SC, Maxine PP, Adam JS, Andrea CT (2007) Sex and sociality in a disconnected world: a review of the impacts of habitat fragmentation on animal social interactions. Can J Zool 85:1065–1079
Basset P, Balloux F, Perrin N (2001) Testing demographic models of effective population size. Proc R Soc Lond B, Biol Sci 268:311–317
Belkhir K, Borsa P, Chikhi L, Raufaste N, Bonhomme F (1996) GENETIX, logiciel sous Windows TM pour la génétique des populations. Montpellier: Laboratoire Génome, Populations, Interactions, CNRS UMR 5171, Université de Montpellier II. https://kimura.univ-montp2.fr/genetix/
Bromham L (2009) Why do species vary in their rate of molecular evolution? Biol Lett 5:401–404
Bromham L (2011) The genome as a life-history character: why rate of molecular evolution varies between mammal species. Philos Trans R Soc B 366:2503–2513
Bush GL, Case SM, Wilson AC, Patton JL (1977) Rapid speciation and chromosomal evolution in mammals. PNAS 74:3942–3946
Charlesworth B, Charlesworth D (1999) The genetic basis of inbreeding depression. Genet Res 74:329–340
Chesser RK (1991a) Gene diversity and female philopatry. Genetics 127:437–447
Chesser RK (1991b) Influence of gene flow and breeding tactics on gene diversity within populations. Genetics 129:573–583
Chesser RK, Rhodes OE, Sugg DW, Schnabel A (1993) Effective sizes for subdivided populations. Genetics 135:1221–1232
Clutton-Brock T (2009) Structure and function in mammalian societies. Philos Trans R Soc B 364:3229–3242
Clutton-Brock T (2016) Mammal societies. John Wiley and Sons, Chichester, West Sussex
Coltman DW, Pilkington JG, Pemberton JM (2003) Fine-scale genetic structure in a free-living ungulate population. Mol Ecol 12:733–742
Craul M, Chikhi L, Sousa V, Olivieri GL, Rabesandratana A, Zimmermann E, Radespiel U (2009) Influence of forest fragmentation on an endangered large-bodied lemur in northwestern Madagascar. Biol Conserv 142:2862–2871
Di Fiore A (2012) Genetic consequences of primate social organization. In: Mitani JC, Call J, Kappeler PM, Palombit RA, Silk JB (eds) The evolution of primate societies. The University of Chicago Press, Chicado and London, pp 269–292
Di Fiore A, Fleisher RC (2005) Social behavior, reproductive strategies, and population genetic structure of Lagothrix poeppiggi. Int J Primatol 26:1137–1173
Di Fiore A, Valencia LM (2014) The interpaly of landscape features and social system on the genetic structure of a primate population: an gent-based simulation study using “Tamarins”. Int J Primatol 35:226–257
Etherington TR (2011) Python based GIS tools for landscape genetics: visualising genetic relatedness and measuring landscape connectivity. Methods Ecol Evol 2:52–55
Frantz AC, Pope LC, Carpenter PJ, Roper TJ, Wilson GJ, Delahay RJ et al. (2003) Reliable microsatellite genotyping of the Eurasian badger (Meles meles) using faecal DNA. Mol Ecol 12:1649–1661
Fredsted T, Pertoldi C, Schierup C, Kappeler PM (2005) Microsatellite analyses reveal fine-scale genetic structure in grey mouse lemurs (Microcebus murinus). Mol Ecol 14:2363–2372
Gandon S (1999) Kin competition, the cost of inbreeding and the evolution of dispersal. J Theor Biol 200:345–364
Garbutt N (2007) Mammals of Madagascar: a complete guide. Yale University Press, New Haven
Goossens B, Chikhi L, Taberlet P, Waits LP, Allain ED (2001) Microsatellite analysis of genetic variation among and within Alpine marmot populations in the French Alps. Mol Ecol 10:41–52
Greenwood PJ, Harvey PH, Perrins CM (1978) Inbreeding and dispersal in the great tit. Nature 271:52–54
Greenwood PJ (1980) Mating systems, philopatry and dispersal in birds and mammals. Anim Behav 2:1140–1162
Guillaume F, Perrin N (2006) Joint evolution of dispersal and inbreeding load. Genetics 173:497–509
Hamilton WD (1964) The genetical evolution of social behaviour. I. II. J Theor Biol 7:1–52
Hawkins MTR, Culligan RR, Frasier CL, Dikow RB, Hagenson R, Lei R, Louis Jr EE (2018) Genome sequence and population declines in the critically endangered greater bamboo lemur (Prolemur simus) and implications for conservation. BMC Genom 19:445
Jacob G, Prévot A-C, Baudry E (2016) Feral pigeons (Columba Livia) prefer genetically similar mates despite inbreeding depression. PLoS ONE 11:e0162451
Kokko H, Ots I (2006) When not to avoid inbreeding. Evolution 60:467–475
Lawler RR, Richard AF, Riley MA (2003) Genetic population structure of the white sifaka (Propithecus verreauxi verreauxi) at Beza Mahafaly Special Reserve, southwest Madagascar (1992–2001). Mol Ecol 12:2307–2317
Lawson Handley LJ, Perrin N (2007) Advances in our understanding of mammalian sex-biased dispersal. Mol Ecol 16:1559–1578
Lehmann L, Perrin N (2003) Inbreeding avoidance through kin recognition: choosy females boost male dispersal. Am Nat 162:638–652
Lewis RJ (2008) Social Influences on group membership in Propithecus verreauxi verreauxi. Int J Primatol 29:1249–1270
Lukas D, Clutton-Brock TH (2011) Group structure, kinship, inbreeding risk and habitual female dispersal in plural‐breeding mammals. J Evol Biol 24:2624–2630
Meyers DM (1993) The effects of resource seasonality on behavior and reproduction in the golden-crowned Sifaka (Propithecus Tattersalli, Simons, 1988) in three Malagasy forests. Ph.D. thesis, Duke University
Miquel C, Bellemain E, Poillot C, Bessière J, Durand A, Taberlet P (2006) Quality indexes to assess the reliability of genotypes in studies using noninvasive sampling and multiple-tube approach. Mol Ecol Notes 6:985–988
Nei M (1978) Estimation of average heterozygosity and genetic distance from a small number of individuals. Genetics 89:583–590
Olson LE, Blumstein DT, Pollinger JR, Wayne RK (2012) No evidence of inbreeding avoidance despite demonstrated survival costs in a polygynous rodent. Mol Ecol 21:562–571
Parreira B, Chikhi L (2015) On some genetic consequences of social structure, mating systems, dispersal, and sampling. PNAS 112:E3318–E3326
Perrin N, Mazalov V (1999) Dispersal and inbreeding avoidance. Am Nat 154:282–292
Peterman W, Brocato ER, Semlitsch RD, Eggert LS (2016) Reducing bias in population and landscape genetic inferences: the effects of sampling related individuals and multiple life stages. Peer J 4:e1813
Pope TR (1992) The influence of dispersal patterns and mating system of genetic differentiation within and between populations of the red howler monkey (Alouatta seniculus). Evolution 46:1112–1128
Quéméré E, Amelot X, Pierson J, Crouau-Roy B, Chikhi L (2012) Genetic data suggest a natural prehuman origin of open habitats in northern Madagascar and question the deforestation narrative in this region. PNAS 109:13028–13033
Quéméré E, Crouau-Roy B, Rabarivola C, Louis Jr EE, Chikhi L (2010a) Landscape genetics of an endangered lemur (Propithecus tattersalli) within its entire fragmented range. Mol Ecol 19:1606–1621
Quéméré E, Louis EE, Ribéron A, Chikhi L, Crouau-Roy B (2010b) Non-invasive conservation genetics of the critically endangered golden-crowned sifaka (Propithecus tattersalli): high diversity and significant genetic differentiation over a small range. Conserv Genet 11:675–87
R Core Team (2014) R: a language and environment for statistical computing. Vienna. http://www.R-project.org/
Richard AF, Dewar RE, Schwartz M, Ratsirarson J (2006) Life in the slow lane? Demography and life histories of male and female sifaka (Propithecus verreauxi verreauxi). J Zool 256:421–36
Rioux-Paquette E, Festa-Bianchet M, Coltman DW (2010) No inbreeding avoidance in an isolated population of bighorn sheep. Anim Behav 80:865–871
Roze D, Rousset F (2005) Inbreeding depression and the evolution of dispersal rates: a Multilocus Model. Am Nat 166:708–721
Rubenstein DR, Abbot P (2017) Comparative social evolution. Cambridge University Press, Cambridge
Schiegg K, Daniels SJ, Walters JR, Priddy JA, Pasinelli G (2006) Inbreeding in red-cockaded woodpeckers: effects of natal dispersal distance and territory location. Biol Conserv 131:544–552
Schwartz OA, Armitage KB (1980) Genetic variation in social mammals: The Marmot Model. Science 207:665–667
Semel B, Semel M, Salmona J, Heriniaina, R (2020) Propithecus tattersalli. The IUCN Red List of Threatened Species 2020: e.T18352A115571806. https://doi.org/10.2305/IUCN.UK.2020-2.RLTS.T18352A115571806.en
Silk JB (2007) The adaptive value of sociality in mammalian groups. Philos Trans R Soc B 362:539–559
Simons EL (1988) A new species of Propithecus (Primates) from Northeast Madagascar. Folia Primatol 50:143–151
Storz JF, Bhat HR, Kunz TH (2001) Genetic consequences of polygyny and social structure in an indian fruit bat, Cynopterus sphinx. II. Variance in male mating success and effective population size. Evolution 55:1224–1232
Sugg DW, Chesser RK (1994) Effective population sizes with multiple paternity. Genetics 137:1147–1155
Sugg DW, Chesser RK, Stephen Dobson F, Hoogland JL (1996) Population genetics meets behavioral ecology. TREE 11:338–342
Szulkin M, Sheldon BC (2008) Dispersal as a means of inbreeding avoidance in a wild bird population. Proc R Soc B 275:703–711
Szulkin M, Stopher KV, Pemberton JM, Reid JM (2013) Inbreeding avoidance, tolerance, or preference in animals? TREE 28:205–211
Vallet D, Petit EJ, Gatti S, Levréro F, Ménard N (2008) A new 2CTAB/PCI method improves DNA amplification success from faeces of Mediterranean (Barbary macaques) and tropical (lowland gorillas) primates. Conserv Genet 9:677–680
van Djik EE, Covas R, Doutrelant C, Spottiswoode C, Hatchwell BJ (2015) Fine-scale genetic structure reflects sex-specific dispersal strategies in a population of social weavers (Philetairus socius). Mol Ecol 24:4296–4311
Vieilledent G, Grinand C, Rakotomalala FA, Ranaivosoa R, Rakotoarijaona J-R, Allnut TF, Achard F (2018) Combining global tree cover loss data with historical national forest cover maps to look at six decades of deforestation and forest fragmentation in Madagascar. Biol Conserv 222:189–197
Wahlund S (1928) Zusammensetzung von populationen und korrelationserscheinungen vom standpunkt der vererbungslwhre aus betrachtet. Hereditas 11:65–106. [English translation In: Weiss KM, Ballonof PA (eds.) (1975) Demographic genetics. Dowden, Hutchinson and Ross, Stroudsburg: 224–263
Wakeley J, Wilson PR (2016) Coalescent and models of identity-by-descent. In: Kliman RM (ed) Encycopedia of evolutionary biology, vol 1. Academic Press, Oxford, pp 287–292
Waples RS, Anderson EC (2017) Purging putative siblings from population genetic data sets: a cautionary view. Mol Ecol 26:1211–1224
Weigl R (2005) Longevity of mammals in captivity: from the living collections of the world: a list of mammalian longevity in captivity. Schweizerbart Science Publishers, Stuttgart
Weir BS, Cockerham CC (1984) Estimating F-Statistics for the analysis of population structure. Evolution 38:1358–1370
Wilson EO (1992) The effects of complex social life on evolution and biodiversity. Oikos 63:47–56
Winterrowd MF, Dobson FS, Hoogland JL, Foltz DW (2009) Social subdivision influences effective population size in the colonial-breeding black-tailed prairie dog. J Mammal 90:380–387
Wright S (1943) Isolation by distance. Genetics 28:114–138
Wright S (1951) The genetical structure of populations. Ann Eugen 15:323–354
Acknowledgements
We thank V. Sousa for very useful comments on several drafts of this manuscript, F. Borges for generous reading of the final version and A. Branquinho for the artwork of Fig. 2. We also thank to the editor and two anonymous reviewers for detailed reading and constructive comments that helped us to improve the clarity of the text. We are grateful to the government of Madagascar for permission to perform this research and to the Direction Générale du Ministère de l’Environnement et des Forêts de Madagascar (Région Sava), Madagascar’s Ad Hoc Committee for Fauna and Flora and Organizational Committee for Environmental Research (CAFF/CORE), and the Fanamby NGO. This study benefited from the continuous support of the Department of Animal Biology and Ecology, University of Mahajanga, and the Department of Animal Biology, University of Antananarivo. This work was supported by the Fundação para a Ciência e Tecnologia (ref. SFRH/BPD/118783/2016 to BP, ref. SFRH/BPD/97566/2013 and IGC-DL57NT-32 to IC, ref. PTDC/BIA-BIC/4476/2012, PTDC/BIA-BEC/100176/2008 and PTDC-BIA-EVL/30815/2017 to LC), the 2015-2016 BiodivERsA COFUND call for research proposals, with the national funders ANR (ANR-16-EBI3-0014) and the Fundação para a Ciência e Tecnologia ref. Biodiversa/0003/2015 and PT-DLR (01LC1617A). It was also funded by the LABEX entitled TULIP (ANR-10-LABX-41 and ANR-11-IDEX-0002-02) as well as the the LIA BEEG-B (Laboratoire International Associé–Bioinformatics, Ecology, Evolution, Genomics and Behaviour). We acknowledge an Investissement d’Avenir grant of the Agence Nationale de la Recherche (CEBA: ANR-10-LABX-25-01).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Associate editor: Armando Caballero
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Parreira, B., Quéméré, E., Vanpé, C. et al. Genetic consequences of social structure in the golden-crowned sifaka. Heredity 125, 328–339 (2020). https://doi.org/10.1038/s41437-020-0345-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41437-020-0345-5
This article is cited by
-
Past volcanic activity predisposes an endemic threatened seabird to negative anthropogenic impacts
Scientific Reports (2024)
-
Relatedness-based mate choice and female philopatry: inbreeding trends of wolf packs in a human-dominated landscape
Heredity (2024)
-
Polyandry and non-random fertilisation maintain long-term genetic diversity in an isolated island population of adders (Vipera berus)
Heredity (2023)
-
The persistence of the critically endangered Asiatic cheetah relies upon urgent connectivity protection: a landscape genetics perspective
Conservation Genetics (2023)
-
Searching for genetic evidence of demographic decline in an arctic seabird: beware of overlapping generations
Heredity (2022)