Abstract
Objectives
This comparative study aimed to determine if total keratometry (TK) from IOLMaster 700 could be applied to conventional formulas to perform IOL power calculation in eyes with previous myopic laser refractive surgery, and to evaluate their accuracy with known post-laser refractive surgery formulas.
Methods
Sixty-four eyes of 49 patients with previous myopic laser refractive surgery were evaluated 1 month after cataract surgery. A comparison of the prediction error was made between no clinical history post-laser refractive surgery formulas (Barrett True-K, Haigis-L, Shammas-PL) and conventional formulas (EVO, Haigis, Hoffer Q, Holladay I, and SRK/T) using TK values obtained with the optical biometer IOLMaster 700 (Carl Zeiss Meditec), as well as Barrett True-K with TK.
Results
The mean prediction error was statistically different from zero for Barrett True-K, Barrett True-K with TK, Haigis-L, Shammas-PL, and Holladay I with TK. The mean absolute error (MAE) was 0.424, 0.671, 0.638, 0.439, 0.408, 0.424, 0.479, 0.647, and 0.524, and median absolute error (MedAE) was 0.388, 0.586, 0.605, 0.298, 0.294, 0.324, 0.333, 0.438, and 0.377 for Barrett True-K, Haigis-L, Shammas-PL, Barrett True-K TK, EVO with TK, Haigis with TK, Hoffer Q with TK, Holladay I with TK, and SRK/T with TK, respectively. EVO TK followed by Barrett True-K TK and Haigis TK achieved the highest percentages of patients with absolute prediction error within 0.50 and 1.00 D (68.75%, 92.19%, and 64.06%, 92.19%, respectively)
Conclusions
Formulas combined with TK achieve similar or better results compared to existing no-history post-myopic laser refractive surgery formulas.
Similar content being viewed by others
Introduction
Intraocular lens (IOL) power calculation for cataract surgery in eyes with previous laser refractive surgery has been a challenge for many years [1]. Indeed, a great variety of formulas and algorithms have been described and validated for IOL power calculation in this type of eyes, with some requiring previous laser refractive surgery clinical history [2,3,4,5,6] and some without [2, 7,8,9]. No clinical history methods are popular due to their ease of use, the difficulty in patients obtaining their previous clinical history, and the variability in the accuracy of the clinical data. The Haigis-L [7] and Shammas-PL [8] formulas are examples of commonly used no-history methods. Recently, the Barrett True-K no-history formula has also been shown to be accurate [2, 10, 11].
Two of the main sources of errors in IOL power calculation in eyes with previous laser refractive surgery are the keratometric index error and effective lens position (ELP) error in formulas that utilize keratometry (K) to predict their ELP [7]. The use of standard K readings in conventional formulas results in overestimation of the corneal power and an erroneously anterior ELP, leading to hyperopic refractive surprises [12]. A potential solution to the keratometric index error would be the direct measurement of total corneal power.
One of the latest technologies for measurement of the total corneal power is the combination of a telecentric 3-zone K and swept-source optical coherence tomography technology from the IOLMaster 700 version 1.70 (Carl Zeiss Meditec AG, Jena, Germany) [13]. Specifically, this system provides a parameter called total keratometry (TK) which considers measured anterior and posterior corneal curvatures together with corneal thickness [14]. This may therefore be advantageous for patients whose anterior to posterior corneal relationships are altered, such as in post-laser in situ keratomileusis (LASIK) and keratoconus eyes [15]. Posterior corneal astigmatism has also been reported to be important in the implantation of toric IOLs [16]. Previously, total corneal power estimates have also been performed with measured anterior and posterior corneal curvatures and corneal thickness using Scheimpflug technology [9, 17].
The aims of this study were to determine if TK from IOLMaster 700 could be applied to conventional formulas to perform IOL power calculation in eyes with previous myopic laser refractive surgery, and to compare their results with known formulas specifically developed for this kind of eyes. It also aims to determine the accuracy of Barrett True-K with TK.
Methods
Patients
This comparative study enrolled eyes that underwent uneventful cataract surgery with previous laser corneal refractive surgery, either photorefractive keratectomy (PRK) or LASIK. All cataract surgeries were performed by four experienced surgeons at Tan Tock Seng Hospital, Singapore between 9 September 2017 and 8 March 2019. Inclusion criteria for the study were patients with uneventful cataract surgery, corrected distance visual acuity (CDVA) of 6/12 or better after cataract surgery, previous uneventful myopic PRK or LASIK, and successful biometric measurements with the IOLMaster 700 including TK (software version 1.70). Exclusion criteria included previous ocular surgery except PRK or LASIK, corneal pathology, retinal disorders or optic neuropathies with postoperative CDVA worse than 6/12, amblyopia, strabismus, and pupil abnormalities. This study conformed to ethics codes based on the tenets of the Declaration of Helsinki and was approved by the institution review board of the National Healthcare Group, Singapore.
Clinical examination and surgical protocol
A complete pre-operative ophthalmological examination was performed in all cases, which included measurements of distance visual acuity, optical biometry (IOLMaster 700, Carl Zeiss Meditec AG, Germany), slit-lamp biomicroscopy, Goldmann applanation tonometry, corneal topography, and dilated fundoscopy. Cataract surgery was performed by four experienced surgeons (TKY, WJH, DP, HBF) using standard phacoemulsification through a temporal clear corneal incision. Postoperative pharmacological treatment consisted of a combination of antibiotic and steroidal anti-inflammatory drops. Patients were examined postoperatively at 1 day, 1 week, and 1 month after surgery. Manifest refraction was performed at the 1-month follow-up visit.
Formula comparison
As the majority of patients did not have their previous refractive surgery history, comparison was made between the no-history post-refractive surgery formulas, namely the Barrett True-K (no history), Haigis-L, and Shammas-PL formulas, found on the American Society of Cataract and Refractive Surgeons (ASCRS) website, to conventional formulas not specifically developed for post-refractive surgery eyes, using TK values obtained with the IOLMaster 700, as well as the new Barrett True-K TK formula. The Barrett True-K TK formula, which utilizes measured posterior corneal power values from TK, is found on the Asia-Pacific Association of Cataract and Refractive Surgeons (APACRS) website. The conventional formulas were the Emmetropia Verifying Optical (EVO), Haigis [18], Hoffer Q [19], Holladay I [20], and SRK/T [21] formulas. The EVO formula is a new unpublished formula developed by the author (TKY) found at www.evoiolcalculator.com that has been recently compared favorably to other conventional formulas [22, 23].
As the Haigis formula does not use K or corneal power to predict its ELP, TK can be directly incorporated into the formula for its prediction. The EVO, Hoffer Q, Holladay I, and SRK/T formulas, however, all utilize K to predict their respective ELPs. Therefore, to avoid an error in ELP prediction, a novel “reverse double-K” method was applied using the equations shown below. (1) The mean posterior keratometry (PK) was converted to posterior radius. (2) Assuming that the posterior radius was not significantly altered by previous PRK or LASIK, the pre-refractive surgery anterior radius could then be calculated by dividing the measured posterior radius with the Gullstrand ratio of 0.883. This presumed pre-refractive surgery anterior radius obtained was then used to generate the ELP for each formula. (3) The measured TK value was converted to a composite radius based on the machine keratometric index. This is because IOLMaster 700 adjust TK values depending on the preset machine keratometric index (1.3375 for all eyes in this study) to ensure lens constants remain the same when using TK. The composite radius was then applied into each formula to generate their respective corneal powers.
(1) Pos r = (1376 − 1336)/PK = 40/PK
(2) Pre Ant r = −Pos r/0.883
(3) Comp r = 337.5/TK
Pos r = posterior radius
Pre Ant r = pre-refractive surgery anterior radius
Comp r = composite radius
TK = total keratometry
User Group for Laser Interference Biometry (ULIB) lens constants were used for the EVO, Haigis, Hoffer Q, Holladay I, and SRK/T formulas. The APACRS website recommended lens constants, if available, were used for the Barrett True-K and Barrett True-K TK formulas, otherwise the ULIB value was used (Table 1). Lens constant optimization was not performed for any of the formulas, to elicit any myopic or hyperopic bias. The predicted refraction was generated for each eye for each formula and deducted from the actual post-cataract surgery refraction to obtain the error in prediction. The mean error (ME) in prediction, mean absolute error (MAE), median absolute error (MedAE), standard deviation (SD), and percentages of eyes with absolute error <0.50, 0.75, and 1.00 D were then calculated. A box and whiskers plot of the prediction errors was also generated for each formula. For ease of reporting, all conventional formulas using TK were denoted with “TK” added to the formula name as a suffix (e.g., EVO TK = EVO using TK).
Statistical analysis
Data analysis was performed using statistical software SPSS version 26.0 (IBM, Armonk, NY, USA). The means of standard K and TK were compared using the two-tailed t-test. Normality of data samples was evaluated by means of the Shapiro–Wilk test. The one sample t-test was used to determine if there was any significant deviation from zero in the mean prediction error obtained with each formula. For pair-wise comparison of absolute errors, the nonparametric Friedman’s test with Bonferroni correction was used. A p value < 0.05 was considered to be statistically significant.
Results
A total of 64 eyes of 49 patients with age ranging from 45 to 74 years old (average 56 years old) were included in the study. Three eyes (4.69%) had undergone previous PRK, whereas the remaining 61 eyes (95.31%) had undergone previous LASIK. The study sample included 28 (43.75%) male and 36 (56.25%) female eyes, and 34 (53.13%) and 30 (46.88%) right and left eyes, respectively. The following IOL models were implanted: AT TORBI 709M (n = 5; 7.81%) (Carl Zeiss Meditec, Jena, Germany), Sensar AAB00 (n = 37; 57.81%), Sensar AR40e (n = 3; 4.69%), and Tecnis ZCB00 (n = 19; 29.69%) (Johnson & Johnson Vision, Jacksonville, USA). The mean axial length, and IOL power implanted were 27.47 mm (range 24.46–32.49 mm) and 18.14 D (range 7.50–25.00 D), respectively. The mean standard K reading was 39.25 D (range 34.99–42.83 D), while the mean TK was lower at 38.15 D (range, 33.71–42.18 D). This difference was statistically significant (p < 0.001). Table 2 shows the patient demographics.
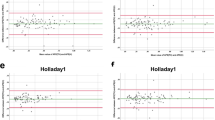
The mean refraction prediction error was significantly different from zero for the Barrett True-K (p = 0.004), Barrett True-K TK (p = 0.014), Haigis-L (p < 0.001), Shammas-PL (p < 0.001), and Holladay I TK (p < 0.001) formulas. In contrast, the mean prediction errors obtained with EVO TK (p = 0.534), Haigis TK (p = 0.203), Hoffer Q TK (p = 0.587), and SRK/T TK (p = 0.236) were not significantly different from zero. The box and whisker plot of the prediction error for each formula is detailed in Fig. 1. The EVO TK formula had the lowest interquartile range (0.626), followed by Barrett True-K TK (0.643) and Haigis TK (0.661). The highest interquartile ranges were found for the Holladay I TK (0.948) and SRK/T TK (0.780) formulas. Comparing absolute error, statistically significant differences were found between the formulas (p < 0.001). Pair-wise post hoc analysis revealed that there were significant differences in absolute prediction error for the following comparisons: EVO TK vs. Haigis-L (p < 0.001), EVO TK vs. Holladay I TK (p < 0.001), EVO TK vs. Shammas-PL (p < 0.001), Barrett True-K TK vs. Haigis-L (p < 0.001), Barrett True-K TK vs. Holladay I TK (p = 0.012), Barrett True-K TK vs. Shammas-PL (p = 0.005), Haigis TK vs. Haigis-L (p < 0.001), Haigis TK vs. Holladay I TK (p = 0.005), Haigis TK vs. Shammas-PL (p = 0.002), Hoffer Q TK vs. Haigis-L (p = 0.014), and SRK/T TK vs. Haigis-L (p = 0.044). There was statistical difference between Barrett True-K against Haigis-L (p = 0.020) but not against Shammas-PL (p = 0.827) after Bonferroni correction.
Table 3 details the mean numerical prediction error, SD of numerical error, MAE and MedAE for all formulas. The EVO TK formula had the lowest MAE (0.408), followed by Haigis TK (0.424), Barrett True-K TK (0.439), and Hoffer Q TK (0.479). The EVO TK formula also had the lowest MedAE (0.294), followed by Barrett True-K TK (0.298), Haigis TK (0.324), and Hoffer Q TK (0.333). For SD of prediction error, EVO TK was lowest at 0.535, followed by Haigis TK (0.554), Barrett True-K TK (0.590), and Shammas-PL (0.638). Figure 2 shows the percentage of eyes with absolute prediction error within 0.5, 0.75, and 1.00 D. The EVO TK formula had the highest percentage of eyes within 0.5 D error (68.75%). Its percentage of eyes within 0.75 and 1.00 D errors were 82.81 and 92.19%. This was followed by Barrett True-K TK (64.06, 82.81, 92.19%), Haigis TK (64.06, 82.81, 89.06%), Hoffer Q TK (59.38, 78.13, 85.94%), and Barrett True-K (59.38, 76.56, 85.94%).
Without the use of TK, the mean numerical prediction errors for EVO, Haigis, Hoffer Q, Holladay I, and SRK/T were all hyperopic: 0.996, 0.659, 0.754, 1.611, and 1.526, respectively. The MAEs were 1.005, 0.704, 0.786, 1.611, and 1.526, and the percentages of eyes with 0.5 D were 23.44, 51.56, 45.31, 6.25, and 6.25%.
Discussion
The use of total corneal power for IOL power calculation is crucial in patients where standard K fails, due to the significant modification of the anterior to posterior curvature ratio of the cornea in eyes with previous laser corneal refractive surgery [7]. Currently, new biometers are introducing the concept of total corneal power for IOL power calculation, such as the TK parameter integrated in the IOLMaster 700 version 1.70 [13].
In our sample of eyes with previous laser refractive surgery, the mean prediction error was not significantly different from zero for EVO TK, Haigis TK, Hoffer Q TK, and SRK/T TK. The Barrett True-K TK, Barrett True-K, Haigis-L, and Shammas-PL formulas, on the other hand, were noted to have significant myopic tendency, and the Holladay I TK significant hyperopic tendency. Similar myopic mean prediction errors have been reported for the Barrett True-K no history [2], Haigis-L [2, 11, 24,25,26], and Shammas-PL [2, 11, 26] formulas. Although Holladay I TK performed well, its significant hyperopic ME may suggest it to be less suitable for post-myopic laser refractive surgery eyes in comparison to other conventional formulas using TK. The performance of EVO TK, Barrett True-K TK, and Haigis TK was particularly encouraging. EVO TK, Barrett True-K TK, and Haigis TK all performed better than Haigis-L, Holladay I TK, and Shammas-PL, while Barrett True-K, Hoffer Q TK, and SRK/T TK performed better than Haigis-L. The Barrett True-K no-history formula outcomes were similar to what was previously reported [2] (MAE: 0.512 vs. 0.520, MedAE: 0.388 vs. 0.410, SD: 0.645 vs. 0.670). Although current no-history formulas (Barrett True-K, Haigis-L, Shammas-PL) found on the ASCRS website have been shown to be accurate for IOL power calculation in eyes with previous corneal refractive surgery [10, 25,26,27], the use of formulas with TK may be a better option, using measured total corneal power rather than regression-based estimation. Indeed, prediction errors of similar or lower values have been reported with other approaches for post-LASIK eyes, using adjustments of corneal power with or without requirement of pre-laser refractive surgery data [4, 28,29,30]. Cho et al. [17] reported low prediction errors, comparable to those obtained with the Haigis-L and Barrett True-K formulas, with the use of the conventional Haigis formula and total corneal power measured with a Scheimpflug imaging-based device.
In this study, Haigis-L and Shammas-PL formulas, had the highest MAE with 34.38 and 46.88% of eyes having <0.50 D of absolute prediction error. In contrast, the EVO TK and Barrett True-K TK formulas achieved 68.75 and 64.06% of eyes with absolute prediction error of <0.50 D. Similarly, Wong et al. [24] found that the predictability of achieving a target within ±0.50 and ±1.00 D was 35.7% and 63.1%, respectively, when using the Haigis-L formula for IOL power calculation in eyes with previous myopic laser refractive surgery.
The use of a novel reverse double-K method as described above was validated with the results of the EVO TK, Hoffer TK, Holladay I TK, and SRK/T TK formulas. It is similar in concept to the Aramberri double-K method [5], but without the need for clinical history, instead using the PK value from TK to derive the pre-refractive surgery K. Therefore, the use of conventional formulas in combination with TK via a reverse double-K method, has been shown to be a valid option for calculating IOL power for eyes with previous myopic laser refractive surgery, comparable to or better than existing no-history methods. It would also be of interest to compare conventional formulas using TK to clinical history methods of IOL calculation for post-myopic laser refractive surgery eyes in the future. Further studies are also needed to confirm the utility of TK in eyes with previous laser refractive surgery for the correction of hyperopia and radial keratotomy, although some recommendations have been recently reported [24]. Mainly monofocal IOLs were studied in the majority of published studies on post-corneal refractive surgery IOL power calculations. Further research may include the assessment of TK formulas in eyes implanted with multifocal IOLs. A recent study has shown that the Shammas formula provided the least accuracy in predicting IOL power in eyes with multifocal IOL implantation after previous laser refractive surgery for myopia [11].
This study enrolled 64 eyes with previous corneal refractive surgery. This number is comparable or more than previous published studies [3, 4, 7, 8, 24]. Future studies of larger numbers would likely further support the findings of this initial pilot study. ULIB or website recommended lens constants were used rather than optimized constants for each IOL for each formula. This is because optimization should not be performed for post-refractive surgery formula comparisons as it would mask hyperopic or myopic tendencies of the formulas, and also does not represent the real clinical scenario where surgeons do not usually optimize lens constants for such patients. Four different types of IOLs were included in this study, each in fair numbers. Other similar studies have reported combinations of different IOL models [2, 23], because corneal refractive surgery patients are relatively uncommon.
In conclusion, the use of TK especially in conjunction with the Barrett True-K, EVO, and Haigis formulas is an accurate option for IOL power calculations in eyes with previous myopic laser refractive surgery.
Summary
What was known before
-
IOL power calculation errors in eyes with previous refractive surgery include the keratometric index error and ELP error.
What this study adds
-
TK improves accuracy of the Barrett True-K and Haigis formulas, and together with the reverse double-K method enabled conventional formulas to predict for eyes with previous refractive surgery.
References
Savini G, Hoffer KJ. Intraocular lens power calculation in eyes with previous corneal refractive surgery. Eye Vis. 2018;5:18.
Abulafia A, Hill WE, Koch DD, Wang L, Barrett GD. Accuracy of the BarrettTrue-K formula for intraocular lens power prediction after laser in situkeratomileusis or photorefractive keratectomy for myopia. J Cataract Refract Surg. 2016;42:363–9.
Masket S, Masket SE. Simple regression formula for intraocular lens poweradjustment in eyes requiring cataract surgery after excimer laser photoablation. J Cataract Refract Surg. 2006;32:430–4.
Savini G, Hoffer KJ, Carbonelli M, Barboni P. Intraocular lens powercalculation after myopic excimer laser surgery: clinical comparison of publishedmethods. J Cataract Refract Surg. 2010;36:1455–65.
Aramberri J. Intraocular lens power calculation after corneal refractivesurgery: double-K method. J Cataract Refract Surg. 2003;29:2063–8.
Borasio E, Stevens J, Smith GT. Estimation of true corneal power afterkeratorefractive surgery in eyes requiring cataract surgery: BESSt formula. J Cataract Refract Surg. 2006;32:2004–14.
Haigis W. Intraocular lens calculation after refractive surgery for myopia:Haigis-L formula. J Cataract Refract Surg. 2008;34:1658–63.
Shammas HJ, Shammas MC. No-history method of intraocular lens powercalculation for cataract surgery after myopic laser in situ keratomileusis. J Cataract Refract Surg. 2007;33:31–6.
Potvin R, Hill W. New algorithm for intraocular lens power calculations aftermyopic laser in situ keratomileusis based on rotating Scheimpflug camera data. J Cataract Refract Surg. 2015;41:339–47.
Wang L, Tang M, Huang D, Weikert MP, Koch DD. Comparison of newer intraocular lens power calculation methods for eyes after corneal refractive surgery. Ophthalmology. 2015;122:2443–9.
Vrijman V, Abulafia A, van der Linden JW, van der Meulen IJE, Mourits MP, Lapid-Gortzak R. Evaluation of different IOL calculation formulas of the ASCRScalculator in eyes after corneal refractive laser surgery for myopia withmultifocal IOL implantation. J Refract Surg. 2019;35:54–9.
Gimbel H, Sun R, Kaye GB. Refractive error in cataract surgery after previous refractive surgery. J Cataract Refract Surg. 2000;26:142–4.
LaHood BR, Goggin M. Measurement of posterior corneal astigmatism by the IOLMaster 700. J Refract Surg. 2018;34:331–6.
Akman A, Asena L, Gungor SG. Evaluation and comparison of the new swept source OCT-based IOLMaster 700 with the IOLMaster 500. Br J Ophthalmol. 2016;100:1201–5.
Savini G, Abbate R, Hoffer KJ, Mularoni A, Imburgia A, Avoni L, et al. Intraocular lens power calculation in eyes with keratoconus. J Cataract Refract Surg. 2019;45:576–81.
Koch DD, Ali SF, Weikert MP, Shirayama M, Jenkins R, Wang L. Contribution of posterior corneal astigmatism to total corneal astigmatism. J Cataract Refract Surg. 2012;38:2080–7.
Cho K, Lim DH, Yang CM, Chung ES, Chung TY. Comparison of intraocular lens power calculation methods following myopic laser refractive surgery: new options using a rotating Scheimpflug camera. Korean J Ophthalmol. 2018;32:497–505.
Haigis W, Lege B, Miller N, Schneider B. Comparison of immersion ultrasound biometry and partial coherence interferometry for intraocular lens calculation according to Haigis. Graefes Arch Clin Exp Ophthalmol. 2000;238:765–73.
Hoffer KJ. The Hoffer Q formula: a comparison of theoretic and regression formulas. J Cataract Refract Surg. 1993;19:700–12.
Holladay JT, Prager TC, Chandler TY, Musgrove KH, Lewis JW, Ruiz RS. A three-part system for refining intraocular lens power calculations. J Cataract Refract Surg. 1988;14:17–24.
Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens power calculation formula. J Cataract Refract Surg. 1990;16:333–40.
Melles RB, Kane JX, Olsen T, Chang WJ. Update on intraocular lens calculation formulas. Ophthalmology. 2019;126:1334–5.
Savini G, Hoffer KJ, Balducci N, Barboni P, Schiano-Lomoriello D. Comparisonof formula accuracy for intraocular lens power calculation based on measurementsby a swept-source optical coherence tomography optical biometer. J Cataract Refract Surg. 2020;46:27–33.
Wang L, Spektor T, de Souza RG, Koch DD. Evaluation of total keratometry and its accuracy for IOL power calculation in eyes following corneal refractive surgery. J Cataract Refract Surg. 2019;45:1416–21.
Wong CW, Yuen L, Tseng P, Han DC. Outcomes of the Haigis-L formula for calculating intraocular lens power in Asian eyes after refractive surgery. J Cataract Refract Surg. 2015;41:607–12.
McCarthy M, Gavanski GM, Paton KE, Holland SP. Intraocular lens power calculations after myopic laser refractive surgery: a comparison of methods in 173 eyes. Ophthalmology. 2011;118:940–4.
Wang L, Hill WE, Koch DD. Evaluation of intraocular lens power prediction methods using the American Society of Cataract and Refractive Surgeons post-keratorefractive intraocular lens power calculator. J Cataract Refract Surg. 2010;36:1466–73.
Chen X, Yuan F, Wu L. Metaanalysis of intraocular lens power calculation after laser refractive surgery in myopic eyes. J Cataract Refract Surg. 2016;42:163–70.
Camps VJ, Piñero DP, Mateo V, Ribera D, de Fez D, Blanes-Mompó FJ, et al. Algorithm for correcting the keratometric error in the estimation of the corneal power in eyes with previous myopic laser refractive surgery. Cornea. 2013;32:1454–9.
Saiki M, Negishi K, Kato N, Ogino R, Arai H, Toda I, et al. Modified double-K method for intraocular lens power calculation after excimer laser corneal refractive surgery. J Cataract Refract Surg. 2013;39:556–62.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yeo, T.K., Heng, W.J., Pek, D. et al. Accuracy of intraocular lens formulas using total keratometry in eyes with previous myopic laser refractive surgery. Eye 35, 1705–1711 (2021). https://doi.org/10.1038/s41433-020-01159-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41433-020-01159-5
This article is cited by
-
Differences in anterior chamber depth in keratoconus patients with binocular very asymmetry ectasia
BMC Ophthalmology (2024)
-
Accuracy of refractive outcomes using standard or total keratometry for intraocular lens power formulas in conventional cataract surgery
BMC Ophthalmology (2023)
-
Comparison of the accuracy of 9 intraocular lens power calculation formulas after SMILE in Chinese myopic eyes
Scientific Reports (2023)
-
Lower refractive prediction accuracy of total keratometry using intraocular lens formulas loaded onto a swept-source optical biometer
Graefe's Archive for Clinical and Experimental Ophthalmology (2023)
-
Application of total keratometry in ten intraocular lens power calculation formulas in highly myopic eyes
Eye and Vision (2022)