Abstract
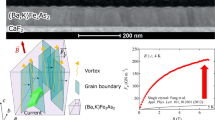
The addition of artificial pinning centers has led to an impressive increase in the critical current density (Jc) of superconductors, enabling record-breaking all-superconducting magnets and other applications. The Jc of superconductors has reached ~0.2–0.3 Jd, where Jd is the depairing current density, and the numerical factor depends on the pinning optimization. By modifying λ and/or ξ, the penetration depth and coherence length, respectively, we can increase Jd. For (Y0.77Gd0.23)Ba2Cu3Oy ((Y,Gd)123), we can achieve this by controlling the carrier density, which is related to λ and ξ. We can also tune λ and ξ by controlling the chemical pressure in Fe-based superconductors, i.e., BaFe2(As1−xPx)2 films. The variation in λ and ξ leads to an intrinsic improvement in Jc via Jd, allowing extremely high values of Jc of 130 MA/cm2 and 8.0 MA/cm2 at 4.2 K, consistent with an enhancement in Jd of a factor of 2 for both incoherent nanoparticle-doped (Y,Gd)123 coated conductors (CCs) and BaFe2(As1−xPx)2 films, showing that this new material design is useful for achieving high critical current densities in a wide array of superconductors. The remarkably high vortex-pinning force in combination with this thermodynamic and pinning optimization route for the (Y,Gd)123 CCs reached ~3.17 TN/m3 at 4.2 K and 18 T (H||c), the highest values ever reported for any superconductor.
Similar content being viewed by others
Introduction
High-temperature superconductors are attractive because their high critical temperature (Tc) enables them to be used at high temperature and outperform standard superconductors in terms of magnetic field performance1,2. However, the limiting factor is the ability to arrest the motion of Abrikosov vortices at a very high critical current. The dissipative motion of vortices can be reduced or eliminated by pinning at nonsuperconducting defects. There are several possible approaches for enhancing the critical current density. Over the last three decades, enormous improvements in the properties of the oxide high-temperature superconductors (HTSs) of the REBa2Cu3Oy family (RE123) have mostly been achieved by adding and tailoring pinning centers to immobilize vortices. The number of routes for engineering the pinning landscape to increase Jc is too large to describe and continues to be fruitful3,4,5,6,7,8,9,10,11,12. The creep-free Jc, \(J_{{{{\mathrm{c}}}}0,{{{\mathrm{cal}}}}}^{{{{\mathrm{NPs}}}}}\left( {T,H} \right)\), for strong pinning by nanoparticles (Dnp ≥ 2ξab) is expressed as11
where Nnp is the density of the nanoparticles (NPs), D is the mean size of the NPs, ξab is the coherence length, λab is the London penetration depth, and Hc is the thermodynamic critical field (see SI, Section 1). How close Jc can be to the upper limit of Jc, i.e., the depairing current density (Jd), by the addition of pinning centers is still an open question. The Jd within the Ginzburg-Landau theory13 is
where ϕ0 is the flux quantum.
Experimentally, the enhancement in Jc by tuning the carrier density, especially in standard RE123 films, i.e., without artificial pinning centers (APCs), has been reported14,15,16. Recently, A. Stangl et al. reported that overdoped standard Y123 films grown by pulsed laser deposition (PLD) attained 18% Jd at 5 K, which is a consequence of the increase in condensation energy with charge carrier density17. On the other hand, by adding and tailoring APCs, the highest Jc achieved for RE123 and Fe-based films is in the range of 10–20% Jd4,5,6,8,9,10,11,12,13. Most of the studies introducing APCs into RE123 are on coherent BaMO3 (BMO, M = Zr, Hf, Sn, etc.) nanorods4,6,7,9,13 and coherent Y2BaCuO5 precipitates5,10. The c axis of the RE123 matrix is expanded by coherent APCs7,11, resulting in a reduced carrier density due to strain-induced oxygen-vacancy formation and decreased crystallinity6,7,11. On the other hand, we have succeeded in introducing incoherent BMO NPs into not only (Y0.77Gd0.23)Ba2Cu3Oy ((Y,Gd)123) films11 but also Fe-based pnictide BaFe2(As1−xPx)2 (Ba122:P) films8, which leaves the matrix unaltered with just slightly decreased superconducting properties. The BaHfO3 (BHO) NPs in RE123 films and BrZrO3 (BZO) NPs in Ba122:P films have an average size (Dave.) of 7 nm with a density Nnp ∼ 80 × 1021 m−3 and Dave. of 8 nm with Nnp ∼ 68 × 1021 m−3, respectively. For both nanocomposite materials, we have shown a large enhancement in Jc at not only self-field but also in-field by introducing a high density of incoherent NPs of a tailored size8,11. Theoretically, using the time-dependent Ginzburg-Landau equations (TDGL) and a targeted evolution approach, Sadovskyy et al.17 explored the optimization of Jc, showing that a level of 30–40% Jd could be attained.
Now, in addition to focusing on improving the pinning morphology, we can increase Jd. Considering Formulas (1) and (2), we see that Jc ∝ \(\left( {\frac{1}{{{\uplambda }}^2\xi }} \right)\) ∝ Jd. Therefore, reducing ξ or λ would improve Jd and consequently Jc. However, these parameters are material-specific and have not been thoroughly studied for improving the Jc of APC-doped cuprates and Fe-based superconducting films. If both these characteristic lengths can be changed, in addition to the enhancement in the flux pinning, Jc can be dramatically improved through the enhancement in Jd. Increasing Tc has been the empirical method for increasing Jd; however, this depends on discovering new superconductors, and even in the cases where this has been achieved (e.g., HgBa2Ca2Cu3O8+δ and Bi2Sr2Ca2Cu3O10+δ), it has not led to improved performance, as the gains have been negated by the enhancement in thermal fluctuations that grow, since3,18
where Gi is the Ginzburg number.
Herein, we present a novel route for improving the performance of superconductors by increasing Jd. Unlike the increase in pinning, which is extrinsic, this route is thermodynamic: Jd is raised by decreasing λ and/or increasing Hc ∝ (λξ)−1 14. This method is general and applicable to any superconductor; herein, we show results for RE123 and Ba122:P films both with and without incoherent BMO NPs. The method works in conjunction with any pinning landscape improvement that has already been achieved, facilitating a method for increasing performance independent from the microstructure. As a concomitant advantage, the decrease in λ also reduces the deleterious effects of thermal fluctuations by reducing Gi. In the RE123 compounds, we achieve this by increasing the carrier concentration, and thus decreasing λ; we also detect an increase in Hc and a decrease in γ observed through the increased Hc2 (i.e., decrease in ξ) with a consequent reduction in γ. When we combine this new strategy with our previously developed methods to incorporate a large density Nnp of incoherent BHO NPs of a tailored size, we obtain Jc ∼ 150 MA/cm2 (~32.4% of Jd) and Jc ∼ 130 MA/cm2 (~28% of Jd) at 4.2 K and self-field for nanocomposite (Y,Gd)123 films on single-crystal substrates and metallic substrates (coated conductors), respectively. These improvements carry over to the in-field properties. We also apply this route in Ba122:P films with incoherent BZO NPs, where we can increase Jd and Jc by controlling λ and γ through the tuning of the chemical pressure. This coordinated strategy can inform the improvement efforts in the newly discovered hydrogen-based superconductors.
We start by increasing Jd by decreasing λ and ξ for RE123. The Cu-O planes containing chains in RE123 are an exception among other cuprates (La2-xSrxCuO419, Y1–xCuxSr2Cu2Tl0.5Pb0.5O720, Tl2Ba2CuO6+x21,22) or Fe-pnictides18. This allows a unique opportunity for λ to be decreased23 and Hc to be increased24 up to the highest possible overdoping, unlike other cuprates21,25 and Fe-pnictides26 for which λ is minimized at the optimum Tc doping. An indication of the possible gain in terms of enhancing Jd by tuning the carrier concentration is observed in the specific heat jump (directly related to Hc) that for y = 7 (p = 0.19) is 45% higher than for optimum doping. These beneficial effects outweigh the negative effects of the 4% decrease in Tc. Thus, we proceed to change the oxygen content y and modify the carrier concentration p to ultimately change λ and ξ for RE123 with two very different pinning landscapes. In Table 1, we summarize the main experimental results for the RE123 compounds. To avoid changes stemming from different Tc values, we compare two samples with similar Tc (89.2 and 90.2 K) that are on either side of the optimal doping, i.e., p = 0.18 and 0.144. A comparison of these samples leads to Jd values of 498 and 230 MA/cm2, respectively, almost an increase by a factor of two with decreases in λ and ξ.
Materials and methods
Film growth
The epitaxially grown Y123 nanocomposite films of standard (Y,Gd)123 and BHO NP-doped (Y,Gd)123 ((Y,Gd)123 + BHO) films were grown from metal organic solutions including Y-, Gd-, and Ba-trifluoroacetates and Cu-naphthenate with a cation ratio of 0.77:0.23:1.5:3 on buffered tapes of CeO2 (grain-boundary angles, Δϕceo2 = 3.0°)/Y2O3/LaMnO3/ion-beam-assisted deposition (IBAD)-MgO/Gd2Zr2O7/Hastelloy C276 (Haynes International Inc., Kokomo, IN, USA). We added Hf-naphthenate into the (Y,Gd)123 solutions; the volume percent of BHO was 12, and the concentration of the starting solution was 0.45 mol/L with a coating thickness (dcoat) of 30 nm, resulting in small-size (7 nm) and high-density (7.5 × 1022 m−3) nanoparticles while maintaining the crystallinity and Tc of the RE123 matrix. Moreover, nanocomposite ((Y,Gd)123 + BHO) films were also fabricated on CeO2(ΔϕCeO2(220) = 1.0°)/R-Al2O3 single-crystals. For comparison, we also fabricated 10 mol.% BHO-doped Eu123 (Eu123 + BHO) films on buffered tapes of CeO2 (ΔϕCeO2(220) = 3.0°)/Y2O3/LaMnO3/ion-beam-assisted deposition (IBAD)-MgO/Gd2Zr2O7/Hastelloy C276. The Eu123 + BHO film exhibited coherent BHO nanorods of 5 nm diameter, not incoherent BHO NPs, which are obtained with metal organic deposition (MOD). The details of the PLD film preparation have been published elsewhere27. The total thickness of the RE123 layer for all samples was 600 nm to 1000 nm, which was confirmed by cross-sectional transmission electron microscopy (TEM, JEM-F200, JEOL Ltd., Tokyo, Japan). The standard BaFe2(As1−xPx)2 and 3 mol. % BaZrO3 (BZO)-doped epitaxial films were deposited on MgO (100) single-crystal substrates by ablating the polycrystalline pulsed laser deposition targets using the second harmonic (wavelength: 532 nm) of a pulsed Nd:YAG laser at a repetition rate of 10 Hz in a vacuum of 10−4 Pa at a substrate temperature of 850 °C. In this work, the amount of P substitution x in the target was selected as 0.33, 0.40, and 0.50. The total thickness of the (Ba122:P) films with and without BZO was 80 nm.
Oxygenation treatments for cuprate films
The oxygenation treatments were precisely controlled to tune the carrier concentration for the (Y,Gd)123 + BHO coated conductors (CCs). The oxygenation process is reversible, as confirmed by the ability to recover Tc,zero and Jcs.f. after varying the oxygen content (SI, Fig. S1 and Table S1). In an investigation of bulk RE123 (RE = Nd, Sm, Eu, Gd Dy, Ho and Y), the optimum doping annealing temperature (TAopt.) was found to depend on the RE element28. For maximum Tc, RE123 with larger RE3+ ions required lower O2 annealing temperatures compared to RE123 with smaller RE3+ ions (at the same O2 pressure). TAopt. (the temperature for the highest Tc,zero and smallest ΔT (= Tc,onset − Tc,zero) for each RE123 material) for our RE123 CCs prepared by different growth methods (MOD and PLD) is consistent with that of bulk studies28, at TAopt. = 500, 450 and 350 °C for Y123, (Y,Gd)123 and Eu123 CCs, respectively (See SI, Fig. S2). In this work, for the oxygenation of the RE123 films prepared from different fabrication processes (MOD and PLD), we annealed in an O2 environment of 1.1 atm, and each annealing temperature (TA = 300–550 °C) was held for 3 h and then rapidly quenched to room temperature. From the c-axis length measured by XRD (RINT2100 and ATX-G (Rigaku Co., Tokyo, Japan)) and Tc,zero, annealing at 300 °C for 3 h was sufficient to oxygenate the RE123 films.
Transport properties in magnetic fields
The films were patterned using a pulsed fiber laser (1095 nm, 20 W) into bridges of ∼50 μm width. The crystalline quality was examined by X-ray diffraction (XRD). The temperature dependence of the resistivity (ρ) was measured by a four-probe method in the temperature range of 4–300 K using a physical property measurement system (PPMS, Quantum Design, Inc., San Diego, CA, USA) with a superconducting magnet generating a field H up to 14 T and in an 18 T-superconducting magnet at Tohoku University. In the PPMS, a rotational stage was used to rotate the samples with respect to H. The critical current was determined using a 1 μV cm−1 criterion. Hc2 and Hirr were determined using 0.90 ρN and 0.01ρN criteria, respectively, where ρN is the normal-state resistivity. Hall measurements were conducted in a magnetic field of 9 T. The six electrical contacts used silver paste on silver pads deposited on the film by sputtering. The magnetization studies were performed using a SQUID (Quantum Design, Inc., San Diego, CA, USA) magnetometer to characterize the temperature and field dependence of Jc and S.
Results
Controlling the carrier density of the superconducting films
First, to investigate the effects of introducing coherent BHO nanorods on the Tc,zero, c-axis length and self-field Jc (Jcs.f.), we measured the hole concentration (nH, determined from the Hall effect at 300 K) dependence of these properties for both standard Eu123 and Eu123 with coherent BHO nanorod (Eu123 + coherent BHO) CCs grown by PLD (Fig. 1a, b). Tc,zero is determined using a 0.01ρN criterion. As shown in the inset of Fig. 1a, the Eu123 + coherent BHO CC has coherent BHO nanorods with a diameter of 5 nm. As shown in Fig. 1a, the Tc,zero and c-axis length of the standard Eu123 CCs decrease systematically with decreasing oxygenation temperature (TA) from nH300K = 9.4 × 1021/cm3 (optimum doped) to 15.3 × 1021/cm3, confirming that the samples are in the overdoped regime. On the other hand, although the Eu123 + coherent BHO CCs are treated under the same O2 annealing conditions as the overdoped standard CCs, Tc,zero is not reached even for the optimum doping level (i.e., underdoped regime), and the c-axis length is longer than that in standard Eu123 CCs. Figure 1b shows Jcs.f. as a function of carrier concentration (doping level) in the CuO2 layer (p) for both the standard Eu123 and Eu123 + coherent BHO CCs. The variation in p is determined by following Tc,zero on the universal doping curve29, where Tc,zero reaches its maximum at optimum doping (p = 0.16) (see Supplementary Information, Fig. S3). As a result, although the Eu123 + coherent BHO films have strong pinning, the Jcs.f. of the nanocomposite CCs is not enhanced compared to that of the standard ones because the carrier concentration p is lower due to the strain-induced oxygen-vacancy formation, leading to a reduction in the carrier doping level7. There are no reports of overdoped RE123 with coherent APCs because it is generally difficult to overdope coherent APC-doped RE123 films, although overdoping is easily achieved in standard films (with no APCs).
a Dependence of Tc (top panel) and c-axis length (bottom panel) on nH at 300 K and b p dependence of Jcs.f. at 77 K for standard Eu123 and Eu123 + BHO CCs grown by PLD. c Dependence of Tc and c-axis length on nH at 300 K (d) p dependence of Jcs.f. for standard (Y,Gd)123 and (Y,Gd)123 + BHO CCs grown by MOD. The insets of Fig.1a and c are cross-sectional TEM images of the Eu123 + BHO and (Y,Gd)123 + BHO CCs, where BHO NPs are colored. The error bars of Jc were determined from the uncertainty in the in-plane crystallinity, natural defects, and film thickness.
Now, we focus on our incoherent BHO NP-doped (Y,Gd)123 CCs. As shown in Fig. 1c, although the (Y,Gd)123 + BHO CCs have a high density of NPs (see inset of Fig. 1c), Tc,zero and the c-axis length systematically decrease with decreasing oxygenation temperature (TA) from nH300K = 9.4 × 1021/cm3 (optimum doped) to 21 × 1021/cm3, attaining overdoped status. However, the Jcs.f. at 77 K (see Fig. 1d) increases monotonically with increasing p beyond optimum doping. Even though the (Y,Gd)123 and (Y,Gd)123 + BHO CCs have almost the same Tc,zero-nH broad peak (because the superconducting matrix remains intact11), the Jcs.f. of the (Y,Gd)123 + BHO CC is over two times higher than that of the (Y,Gd)123 CC. It is worth noting that even though Tc,zero ∼ 90 K is almost the same for the (Y,Gd)123 + BHO CCs with nH300K = 7 × 1021/cm3 and nH300K = 21 × 1021/cm3, as shown in Fig. 1c, the overdoped CC shows a Jcs.f. 1.8 times higher at 77 K. It is worth noting that we achieved an overdoped doping level up to p = 0.18 for our incoherent BHO NP-doped (Y,Gd)123 CCs but not for the standard one (without APCs).
Influence of grain boundaries in carrier density-controlled films
To clarify that the enhancement in Jc (Fig. 1d) for our overdoped (Y,Gd)123 + BHO CCs, which are fabricated on oxide-buffered metallic substrates (in-plane crystallinity (ΔϕCeO2 = 3°)), is not due to doping-induced improved grain-boundary properties (similar to the improvement in the intergrain-Jc for Ca-doped Y123 films on bicrystal substrates30), we investigated the in-plane crystallinity of CeO2 (ΔϕCeO2) buffered metallic substrates with respect to the self-field Jc at 77 K of underdoped (Y,Gd)123, underdoped (Y,Gd)123 + BaHfO3 and overdoped (Y,Gd)123 + BaHfO3 films (Fig. 2a). For ΔϕCeO2 > 3°, the Jcs.f. of all films decreases exponentially with increasing boundary angle. However, for ΔϕCeO2 < 3°, the Jcs.f. of all films decreases by just 10% when changing ΔϕCeO2 from 0.6° to 3° independent of p and of the pinning landscape. As shown in Fig. 2b, although the ratio of Jcs.f. (Δϕ)/Jcs.f. (0.6°) for ΔϕCeO2 > 3° of the two underdoped films is lower than that of the overdoped film, the ratio for ΔϕCeO2 < 3° clearly shows exactly the same trend even for different p-values (underdoped and overdoped) and for different microstructures (without and with BHO NPs). To investigate the GB misorientation angles in our MOD CCs, we studied the plan-view TEM images of (Y,Gd)123 CCs on ΔϕCeO2 = 3° buffered metallic substrates (see inset of Fig. 2b). The chain of edge dislocation distances (D) is 13.5–15.3 nm for a film on ΔϕCeO2 = 3°, which represents the misorientation angles of 1.5–1.7° calculated using D = (|b|/2)/sin(θGB/2), where |b| is the norm of the corresponding Burgers vector. Because the crystal growth of MOD films is meandering and passes over the substrate grain boundaries (differing from that in PLD), the value of the misorientation angle is almost half that of ΔϕCeO2, which is the same as the in-plane crystallinity of (Y,Gd)123 (Δϕ(Y,Gd)123(103) = 1.5°), as evaluated by XRD. It is clear that the GBs of (Y,Gd)123 and (Y,Gd)123 + BaHfO3 CCs grown on ΔϕCeO2 = 3° of CeO2 buffered metallic substrate are not Josephson weakly linked (i.e., with a locally suppressed order parameter). Based on Fig. 2a, b, we conclude that our Jcs.f. properties for films grown on ΔϕCeO2 = 3° of CeO2 buffered metallic substrates mainly depend on the value of the intragrain Jc, not the intergrain-Jc, as is the case for large misorientation angles of the GBs30.
a Jcs.f. and b the ratio Jcs.f./Jcs.f. (Δϕceo2 = 0°) at 77 K for the underdoped (Y,Gd)123, underdoped (Y,Gd)123 + BaHfO3 and overdoped (Y,Gd)123 + BaHfO3 films grown on CeO2-buffered metallic substrates (2.5° < Δϕceo2 < 8.5°) and on CeO2 buffered R-Al2O3 substrates (0.6° < Δϕceo2 < 2°). The inset of Fig. 2b shows the plane-view TEM image of the (a Y,Gd)123 film on a CeO2 buffered metallic substrate with ΔϕCeO2 = 3.0°. White and yellow indicate the twin boundaries (TBs) and dislocations, respectively. The error bars of Jc were determined from the uncertainty in the in-plane crystallinity, natural defects and film thickness.
Penetration depth and coherence length in carrier-controlled films
In Fig. 3, we show that λ and ξ vary with carrier concentration (p). We observed changes consistent with those found in the literature for single-crystal samples. The upper panel of Fig. 3a presents the measured λab as a function of p for Y12323,31 and (Y,Ca)12332 single-crystals. For refs. 23,31, we calculated the penetration depth using λab = [λaλb]1/2. For the extraction of λab(0) for our (Y,Gd)123 + BHO film, we use the temperature dependence of the resonant frequency of the coplanar waveguide resonators based on the equations derived by K. Watanabe et al.33 (measurement details are shown in SI, Figs. S4 and S5). Indeed, for λab(0), the decrease with increasing p for (Y,Gd)123 + BHO films is similar to that of Y123 and (Y,Ca)123 single-crystals23,31,32.
a λab (upper panel) and Hc2(0) estimated by using WHH (lower panel) as a function of carrier concentration (p) for the (Y,Gd)123 + BHO films. b Calculated Hc(0) from Formula (3) (upper panel) and estimated superfluid density (lower panel) as a function of p for our (Y,Gd)123 + BHO CCs. For reference, values for Y12323,31,35 and (Y,Ca)12332 single-crystals are also shown. The error bars of Hc2(0) for the Y123 single-crystal35 are reported values, which represent the uncertainty in extrapolating Hc2(T) to T = 0.
The Hc2(0) for H||c for the (Y,Gd)123 + BHO CCs with different p-values are shown in the lower panel of Fig. 3a. The values for (Y,Gd)123 + BHO CCs and Gd123 single-crystals are estimated by using the Werthamer–Helfand–Hohenberg (WHH) formula34 (detailed data in SI, Figs. S6 and S7). The (Y,Gd)123 + BHO CCs with p = 0.144, 0.168 and 0.180 exhibit an upward trend in Hc2(0) similar to that of Gd123 single-crystals (measured) and Y123 single-crystals from ref. 35. The μ0Hc2c(0) vs. p trend for our (Y,Gd)123 + BHO CCs and the Gd123 single-crystal is consistent with Y123 single-crystal studies, showing that Hc2 increases with p up to p = 0.18.
Using λab (upper panel of Fig. 3a) and ξab, we calculated Hc(0) using \(\mu _0H_{{{\mathrm{c}}}}(0) = \frac{{\phi _0}}{{2\sqrt 2 \pi \lambda _{{{{\mathrm{ab}}}}}(0)\xi _{{{{\mathrm{ab}}}}}(0)}}\) for our (Y,Gd)123 + BHO films and Y123 single-crystals23,31,35 with various p-values, as shown in the upper panel of Fig. 3b. These results are consistent with the calculated Hc(0) values based on Hc2 and Hc1 for the Gd123 single-crystal (detailed data in SI, Fig. S7). The Hc(0) values for the (Y,Gd)123 + BHO CCs increase with increasing p, which is a similar trend to that for the Gd123 and Y123 single-crystals.
In view of the changes in ξ and λ, summarized in Table 1, we can use Jd \(\propto\) \(\left( {\frac{1}{{{\uplambda }}^2\xi }} \right)\) and assert that the variation in λ is more important for Jd than the variation in ξ, as λ also affects Hc. The enhanced Hc is one of the main reasons for the higher Jc of our most overdoped (Y,Gd)123 + BHO film with p = 0.18 and the Jc calculated for strong pinning nanoparticle-doped films, \(J_{{{{\mathrm{c0,cal}}}}}^{{{{\mathrm{NPs}}}}} \propto \left( {\frac{1}{{{\uplambda }}^2\xi }} \right)\) (see Supplementary Information, Section 9). The monotonic increase in Hc(0) with p shown in the upper panel of Fig. 3b, consistent with previous studies in single-crystal36 and polycrystalline24 Y123, confirms the different behavior of Y123 compared to other HTS cuprate materials where Hc(0) and ΔC/Tc coincide with the maximum of Tc20,22.
To investigate the ns dependence of the normal-state carrier density for Y123, we calculated ns for (Y,Gd)123 + BHO CCs with different p. The dependence of the effective mass (m*) in Y123 single-crystals on the hole doping level was recently measured37. To calculate the ns for our (Y,Gd)123 + BHO CCs, we used the relationship \(\lambda _{ab}\left( 0 \right) = \sqrt {\frac{{m^\ast }}{{\mu _0n_s(0)e^2}}}\) and m* from reference37 (no m* data above p = 0.152 was reported, so we extrapolated from the available curve). The ns for our (Y,Gd)123 + BHO CCs increases monotonically with the hole concentration, as shown in the lower panel of Fig. 3b. This is consistent with the Y123 single-crystal data, also shown for comparison23,31.
As shown in Fig. 3, the overdoped (Y,Gd)123 + BHO CCs have larger Hc and smaller λab than the under—and optimally doped CCs, indicating an increase with p of Jc (∝ λ−2ξ−1) and Jd (∝λ−2ξ−1). From Formula (1), the (Y,Gd)123 + BHO CCs with p = 0.144, 0.168 and 0.180 yield Jd(0) = 230, 368 and 498 MA/cm2, respectively. This remarkable enhancement in the Jd(0) of the overdoped sample is due to the reduced ξab(0) and λab(0) achieved by controlling the carrier density.
Substantially higher J c at all temperatures
Consistent with the enhancements in Jc being induced by the changes in Jd, we observed the same enhancement at all temperatures over a wide range of applied magnetic fields. The upper panel of Fig. 4a shows the calculated Jd(T) with different p based on the parameters in Table 1. The overdoped (Y,Gd)123 + BHO CC (p = 0.18) has a higher Jd(T) than films with p = 0.168 and 0.144. As seen in the lower panel of Fig. 4a, the Jd(T) for p = 0.18 is ~2 times higher than that for p = 0.144 over a wide temperature range. Figure 4b shows Jcs.f.(T) for the (Y,Gd)123 + BHO CCs with different p. Even though all the CCs have the same high density of BHO nanoparticles, Jcs.f. for p = 0.18 is the highest at all temperatures. Although CCs with p = 0.18 and p = 0.144 have almost the same Tc, slightly lower than that for the optimum doped one, the Jcs.f. of the p = 0.18 film is almost twice that of p = 0.144. At p = 0.18, the Jcs.f. for the (Y,Gd)123 + BHO CC achieves a maximum value of 130 MA/cm2 at 4.2 K. This is higher than that previously reported for any superconducting material6,9,11,13,17,38 except nanowires and ultrathin films (where the flux pinning mechanism is different)39,40,41. The Jcs.f. results are independent of the sample’s width (W) and length (L), as demonstrated by the results at 77 K (SI, Fig. S8), indicating very uniform superconducting films. If we apply our finding to a film on a CeO2 (Δϕceo2 = 1°) buffered R-Al2O3 single-crystal (shown in the inset of Fig. 4b), we achieve a Jcs.f. of ∼150 MA/cm2 at 4.2 K, which is also the highest value ever reported for any superconducting material with a thickness >> λab. The enhancement of 1.15 in Jcs.f. at 4.2 K for the film on a single-crystal substrate compared to the film on an oxide-buffered metallic substrate (all other parameters being the same) is almost the same enhancement of 1.1 at 77 K (compared to the Jcs.f. of films on Δϕceo2 = 1° and Δϕceo2 = 1° of substrates in Fig. 2b) due to the slightly higher in-plane crystallinity of the former.
a Calculated Jd(T) for different p for the (Y,Gd)123 + BHO CCs based on the parameters in Table 1. b Jcs.f.(T) for the (Y,Gd)123 + BHO CCs with different p-values. The inset of Fig. 4b shows the Jcs.f.(T) for the (Y,Gd)123 + BHO (p = 0.18) film on CeO2 buffered R-Al2O3 single-crystal substrate. c In-field Jc(T) at μ0H = 0.3 T and H||c for the (Y,Gd)123 + BHO CCs at various p. A comparison of transport Jc and Jc calculated from magnetization using the Bean model for the (Y,Gd)123 + BHO CCs is shown in the inset of Fig. 4c.
Insights into the benefit of further controlling Jd by changing the hole doping level are given by the in-field Jc(T) at μ0H = 0.3 T and H||c in Fig. 4c. The overdoped (Y,Gd)123 + BHO CC (p = 0.18) shows the highest in-field Jc, approximately twice the value for p = 0.145. As shown in the inset of Fig. 4c, the transport Jc coincides very well with the Jc calculated from magnetization (measured on a different piece) using the Bean model42, indicating that our Jc values are highly uniform and reproducible. The solid lines in the upper panel of Fig. 4c are the calculated Jc (\(J_{{{{\mathrm{c}}}}0,{{{\mathrm{cal}}}}}^{{{{\mathrm{NPs}}}}}\))3, and the solid symbols are the experimentally obtained parameters (calculation details are shown in Supplementary Information, Table S2), indicating that \(J_{{{{\mathrm{c}}}}0,{{{\mathrm{cal}}}}}^{{{{\mathrm{NPs}}}}}\) for (Y,Gd)123 + BHO CCs with different p are in good agreement with the experimental Jc. This agreement confirms the critical role of the decrease in λ and increase in Hc. The most interesting and important feature of the data presented here is that the enhancement ratios in Jd-T and Jc-T in both the self and in-field are identical (see lower panels of Fig. 4). This confirms that we can enhance Jc by enhancing Jd by changing Hc and λ while keeping the pinning enhancement intact.
Ginzburg number of carrier-controlled films
The top panel of Fig. 5a shows the γ values for (Y,Gd)123 and (Y, Gd)123 + BHO CCs with various hole concentrations measured at 300 K. The γ is calculated from the angular dependence of Hc2 (see Supplementary Information, Fig. S9 and ref. 43 for details). For CCs both with and without BHO, the c-axis length (Fig. 1c) and mass anisotropy decrease with increasing nH, i.e., hole doping level. These dependences follow the same trend observed in the c-axis length vs. p characteristics of the Y123 SC44 and in the γ vs. p characteristics of the (Y,Ca)123 SC45. We also observed a systematic reduction in the c-axis length and smaller mass anisotropy for the samples with nanoparticles. The origin of this effect is under investigation and will be the focus of future publications.
As indicated above, the reduction in γ also diminishes the effect of thermal fluctuations, as characterized by Gi ~ γ 2 (see Formula (3)). While Jc increases by increasing Jd, it can also increase by reducing the effect of flux creep. The effect of flux creep is characterized by the creep rate, S, with which pinned vortices escape from the pinning centers under thermal agitation. It was found that there is a universal lower limit of the creep rate Smin ~ Gi1/2(T/Tc)18, which demonstrates that the creep rate can be essentially reduced by reducing the anisotropy of the superconductor. In addition, S can also be reduced to its limit Smin by adding pinning.
The bottom panel of Fig. 5a shows S(T = 50 K, μ0H = 0.3 T) vs. nH for our CCs, as a representative example of S(T,H) over a wide range of conditions outside the Anderson-Kim (A‒K) regime. This relationship can also be replotted as that of S(T = Tc/4, μ0H = 1 T) (i.e., inside the A‒K regime) vs. Gi1/2. as shown in Fig. 5b. Thus, reducing the anisotropy is a new way to reduce S. In addition, the introduction of nanoparticles is effective, as seen from the comparison between (Y,Gd)123 + BHO CCs and (Y,Gd)123 CCs.
Discussion
The effect of Jd on Jc is general and apparent for different superconductors with varied pinning landscapes (see Fig. 6). Herein, we display Jcs.f. as a function of Jd at 4.2 K43,44,45,46,47,48,49,50,51,52. Details of the calculation parameters for Jd and experimentally obtained Jc are shown in SI, Table S3. First, we see that there is a general trend for several superconductors in which Jc is proportional to Jd (clearly seen in the inset of Fig. 6). Second, as shown in Fig. 6 for standard (Y,Gd)123 CCs, we can tune Jcs.f. at 4.2 K from 23.5 to 44.5 MA/cm2 by changing Jd. We note that the relation of Jc~0.1Jd remains unchanged. Enhancements in Jd and Jc by tuning the carrier concentration are also observed for Ca-doped Y123 SC50. Third, the combination of controlling Jd by tuning the carrier concentration in a film with a high density of nanoparticles leads to the highest Jcs.f.(4.2 K) = 130 MA/cm2 for (Y,Gd)123 + BHO CCs, which is 28.0% Jd. Moreover, a (Y,Gd)123 + BHO film on a single-crystal achieved 32.4% Jd (Jcs.f.(4.2 K) = 150 MA/cm2) because of the further improvement obtained by the higher in-plane crystallinity. This value is close to the 33% achievement predicted by Gurevich53 for a superconductor with NP pinning centers similar to the actual conditions in our (Y,Gd)123 + BHO films and CCs.
Jcs.f. at 4.2 K as a function of Jd at 4.2 K for different superconductors with varied pinning landscapes43,44,45,46,47,48,49,50,51,52. Open and solid symbols indicate the Jc for pristine and superconductors with introduced pinning centers. The inset of Fig. 6 shows Jc vs. Jd for chemical–pressure-controlled Fe-based pnictide Ba122:P films with and without nanoparticles.
As shown in the inset of Fig. 6, increasing Jd is an effective method for enhancing Jc for not only Y123 cuprate CCs but also Fe-based pnictide Ba122:P films. In the Ba122:P system, the isovalent substitution of P for As induces chemical pressure, suppressing magnetism and inducing superconductivity, which is different from the effect of electron doping or hole doping54,55,56. For standard Ba122:P films, by tuning x, the Jcs.f. at 4.2 K increases from 1.0 to 3.6 MA/cm2 due to the increase in Jd from 23 to 74 MA/cm2. Moreover, Ba122:P + BZO films with different x show that Jc increases (up to 8 MA/cm2 at 4.2 K) with increasing Jd, indicating that the combined approach of tuning Jd and enhancing flux pinning (i.e., adding NPs) can also be used to improve the performance of superconductors of different families. In this regard, it is important to note that although the method for controlling Jd (Hc and λab) is different for the cuprate and the pnictide (changing carrier concentration (p) and the chemical pressure (x), respectively), the end result is the same, thus highlighting the general applicability of our strategy.
Further insight into the effects of the combination of increasing Jd and enhancing flux pinning can be obtained from the field dependence of Jc. Figure 7a shows the Jc(H||c) at 4.2 K for our overdoped (Y,Gd)123 + BHO CC compared with that of several RE123 films and CCs16,57,58,59. As seen for up to 18 T, the Jc(H||c) of overdoped (Y,Gd)123 + BHO CC is the highest among all superconductors. Compared with overdoped standard Y123 at 5 K16, the enhancement of our overdoped (Y,Gd)123 + BHO CC is 144% at the self-field and 199% at 5 T. Moreover, compared to that of coherent BHO-doped CCs59, the Jc(H||c) of our CC shows a 254% increase at 1 T and 175% increase at 18 T. The remarkable in-field performance of overdoped (Y,Gd)123 + BHO CC is highlighted in Fig. 7b, where the pinning force, Fp = Jc(H) × μ0H, is compared with that of several RE123 materials16,57,58,59. The Fp at 4.2 K of our overdoped (Y,Gd)123 + BHO CC reaches ~3.17 TN/m3 at 18 T (H||c), which is the highest reported value for any superconductor material. Please note that because the anisotropy of RE123 materials is ~5 (Fig. 5a), the Fp measured along the c axis is the minimum value for a RE123 superconductor.
Conclusions
In summary, we have succeeded in combining this thermodynamic route (increasing Jd by decreasing λ and/or increasing Hc) with our previously developed methods to tailor the size and incorporate large densities of incoherent nanoparticles. We obtain Jc ∼ 150 MA/cm2 (~32.4% of Jd) and Jc ∼ 130 MA/cm2 (~28.0% of Jd) at 4.2 K and in the self-field for nanocomposite RE123 films on single-crystal substrates and metallic substrates (CCs), respectively. Moreover, for films of chemical–pressure-controlled Ba122:P with incoherent BZO NPs, the Jcs.f. at 4.2 K increases from 1.0 to 8.0 MA/cm2 due to the increase in Jd in combination with the introduction of high densities of incoherent BZO NPs. To our knowledge, the Jc values attained for our CC of overdoped (Y,Gd)123 in not only the self-field but also the high field are the highest reported to date for any superconductor. This highlights that thermodynamic improvements of superconductors can work in parallel with already successful artificial pinning centers and that a maximum Jc ~ 0.3 Jd appears to be the current upper limit for the enhancement in Jc.
References
Hahn, S. et al. 45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet. Nature 570, 496–499 (2019).
Wang, Q. et al. Progress of ultra-high-field superconducting magnets in China. Supercond. Sci. Technol. 35, 023001 (2022).
Blatter, G., Feigl’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125–1388 (1994).
MacManus-Driscoll, J. L. et al. Strongly enhanced current densities in superconducting coated conductors of YBa2Cu3O7-x+BaZrO3. Nat. Mater. 3, 439–443 (2004).
Haugan, T., Barnes, P. N., Wheeler, R., Meisenkothen, F. & Sumption, M. Addition of nanoparticle dispersions to enhance flux pinning of the YBa2Cu3O7-x superconductor. Nature 430, 867–870 (2004).
Selvamanickam, V., Gharahcheshmeh, M. H., Xu, A., Zhang, Y. & Galstyan, E. Critical current density above 15MAcm2 at 30K, 3T in 2.2μm thick heavily-doped (Gd,Y)Ba2Cu3Ox superconductor tapes. Supercond. Sci. Technol. 28, 072002 (2015).
Horide, T., Kametani, F., Yoshioka, S., Kitamura, T. & Matsumoto, K. Structural evolution induced by interfacial lattice mismatch in self-organized YBa2Cu3O7-δ nanocomposite film. ACS Nano 11, 1780–1788 (2017).
Miura, M. et al. Strongly enhanced flux pinning in one-step deposition of BaFe2(As0.66P0.33)2 superconductor films with uniformly dispersed BaZrO3 nanoparticles. Nat. Commun. 4, 2499 (2013).
Xu, A. et al. Je(4.2 K, 31.2 T) beyond 1 kA/mm2 of a ~3.2 μm thick, 20 mol% Zr-added MOCVD REBCO coated conductor. Sci. Rep. 7, 6853 (2017).
Sebastian, M. A. P. et al. Study of the flux pinning landscape of YBCO thin films with single and mixed phase additions BaMO3 + Z: M = Hf, Sn, Zr and Z = Y2O3, Y211. IEEE Trans. Appl. Supercond. 27, 7500805 (2017).
Miura, M. et al. Tuning nanoparticle size for enhanced functionality in perovskite thin films deposited by metal organic deposition. npg Asia Mater. 9, e447 (2017).
Li, Z. et al. Control of nanostructure and pinning properties in solution deposited YBa2Cu3O7−x nanocomposites with preformed perovskite nanoparticles. Sci. Rep. 9, 5828 (2019).
Tinkham, M. Introduction of Superconductivity 2nd edn (McGraw-Hill, New York, 1996).
Claus, H. et al. Critical current of grain boundaries in YBa2Cu3Ox bicrystal films as a function of oxygen concentration. Phys. Rev. B 76, 014529 (2007).
Strickland, N. M., Semwal, A., Williams, G. V. M., Verebelyi, D. T. & Zhang, W. Optimizing the doping state of YBCO coated conductors. Supercond. Sci. Technol. 17, S473–S476 (2004).
Stangl, A., Palau, A., Deutscher, G., Obradors, X. & Puig, T. Ultra‑high critical current densities of superconducting YBa2Cu3O7-δ thin films in the overdoped state. Sci. Rep. 11, 8176 (2021).
Sadovskyy, I. A., Koshelev, A. E., Kwok, W., Welp, U. & Glatz, A. Targeted evolution of pinning landscapes for large superconducting critical currents. Proc. Natl Acad. Sci. USA 116, 10291–10296 (2019).
Eley, S., Miura, M., Maiorov, B. & Civale, L. Universal lower limit on vortex creep in superconductors. Nat. Mater. 16, 409–413 (2017).
Loram, J. W., Mirza, K. A., Liang, W. Y. & Osborne, J. A systematic study of the specific heat anomaly in La2-xSrxCuO4. Phys. C. 162–164, 498–499 (1989).
Loram, J. W., Mirza, K. A. & Liuet, R. S. Specific heat anomalies in the 108 K superconducting system Y1-xCaxSr2Cu2Tl.5Pb.5O7. Supercond. Sci. Technol. 4, S286 (1991).
Niedermayer, C. et al. Muon spin rotation study of the correlation between Tc and ns/m* in overdoped Tl2Ba2CuO6+δ. Phys. Rev. Lett. 71, 1764 (1993).
Wade, J. M., Loram, J. W., Mirza, K. A., Cooper, J. R. & Tallon, J. L. Electronic specific heat of Tl2Ba2CuO6+δ from 2 K to 300 K for 0 ≤ δ ≤ 0.1. J. Supercond. 7, 261 (1994).
Pereg-Barnea, T. et al. Absolute values of the London penetration depth in YBa2Cu3O6+y measured by zero field ESR spectroscopy on Gd doped single crystals. Phys. Rev. B 69, 184513 (2004).
Breit, V. et al. Evidence for chain superconductivity in near-stoichiometric YBa2Cu3Ox single crystals. Phys. Rev. B 52, R15727(R) (1995).
Li, Y. et al. Hole pocket–driven superconductivity and its universal features in the electron-doped cuprates. Sci. Adv. 5, eaap7349 (2019).
Kurokawa, H. et al. Relationship between superconductivity and nematicity in FeSe1−xTex (x = 0−0.5) films studied by complex conductivity measurements. Phys. Rev. B 104, 014505 (2021).
Ibi, A. et al. Improvement of in-field performance for EuBCO with heavily doped BHO coated conductors by PLD method with high temperature deposition and low temperature annealing. IOP Conf. Ser. Mater. Sci. Eng. 756, 012024 (2020).
Shimoyama, J., Horii, S., Otzschi, K. & Kishio, K. How to optimize critical current performance of RE123 materials by controlling oxygen content. Mat. Res. Soc. Symp. Proc. 689, 265 (2002).
Presland, M. R., Tallon, J. L., Buckley, R. G., Liu, R. S. & Flower, N. E. General trends in oxygen stoichiometry effects on Tc in Bi and Tl superconductors. Phys. C. 176, 95–105 (1991).
Song, X., Daniels, G. A., Feldmann, D. M., Gurevich, A. & Larbalestier, D. C. Electromagnetic, atomic-structure and chemistry changes induced by Ca-doping of low angle YBCO grain boundaries. Nat. Mater. 4, 470–475 (2005).
Sonier, J. E., Brewer, J. H. & Kiefl, R. F. μSR studies of the vortex state in type-II superconductors. Rev. Mod. Phys. 72, 769 (2000).
Tallon, J. L. et al. In-Plane anisotropy of the penetration depth due to superconductivity on the Cu-O Chains in YBa2Cu3O7-δ, Y2Ba4Cu7O15-δ, and YBa2Cu4O8. Phys. Rev. Lett. 74, 1008 (1995).
Watanabe, K., Yoshida, K., Aoki, T. & Kohjiro, S. Kinetic inductance of superconducting coplanar waveguides. Jpn. J. Appl. Phys. 33, 5708 (1994).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, Hc2. III. electron spin and spin-orbit effects. Phys. Rev. 147, 295 (1966).
Grissonnanche, G. et al. Direct measurement of the upper critical field in cuprate superconductors. Nat. Commun. 5, 3280 (2014).
Daumling, M. The reversible magnetization of oxygen deficient YBa2Cu3O7-δ. Phys. C. 183, 293–302 (1991).
Ramshaw, B. J. et al. Quasiparticle mass enhancement approaching optimal doping in a high-Tc superconductor. Science 348, 317–320 (2015).
Zhang, C. et al. Hybrid physical chemical vapor deposition of ultrathin MgB2 films on MgO substrate with high Tc and Jc. IEEE Trans. Appl. Supercond. 23, 7500204 (2013).
Nawaz, S., Arpaia, R., Bauch, T. & Lombardi, F. Approaching the theoretical depairing current in YBa2Cu3O7-δ nanowires. Phys. C. 495, 33–38 (2013).
Nawaz, S., Arpaia, R., Lombardi, F. & Bauch, T. Microwave response of superconducting YBa2Cu3O7-δ nanowire bridges sustaining the critical depairing current: evidence of Josephson-like behavior. Phys. Rev. Lett. 110, 167004 (2013).
Zhang, C. et al. Fabrication of superconducting nanowires from ultrathin MgB2 films via focused ion beam milling. AIP Adv. 5, 027139 (2015).
Bean, C. P. Magnetization of high-field superconductors. Rev. Mod. Phys. 36, 31–39 (1964).
Miura, M. et al. Upward shift of the vortex solid phase in high-temperature superconducting wires through high density nanoparticle addition. Sci. Rep. 6, 20436 (2016).
Liang, R., Bonn, D. A. & Hardy, W. N. Evaluation of CuO2 plane hole doping in YBa2Cu3O6+x single crystals. Phys. Rev. B 73, 180505(R) (2006).
Nagasao, K., Masui, T. & Tajima, S. Rapid change of electronic anisotropy in overdoped (Y, Ca)Ba2Cu3O7-δ. Phys. C. 468, 1188–1191 (2008).
Civale, L. et al. Vortex confinement by columnar defects in YBa2Cu3O7 crystals: enhanced pinning at high fields and temperatures. Phys. Rev. Lett. 67, 648 (1991).
Matsushita, T. et al. Condensation energy density in Bi-2212 superconductors. Supercond. Sci. Technol. 19, 200–205 (2006).
Krusin-Elbaum, L., Tsuei, C. C. & Gupta, A. High current densities above 100 K in the high-temperature superconductor HgBa2CaCu2O6+δ. Nature 373, 679–681 (1995).
Balachandran, S. et al. Beneficial influence of Hf and Zr additions to Nb4at%Ta on the vortex pinning of Nb3Sn with and without an O source. Supercond. Sci. Technol. 32, 044006 (2019).
Tallon, J. L. Thermodynamics and critical current density in high-Tc superconductors. IEEE Trans. Appl. Supercond. 25, 8000806 (2015).
Miura, M. et al. Enhanced critical current density in BaFe2(As0.66P0.33)2 nanocomposite superconducting films. Supercond. Sci. Technol. 32, 064005 (2019).
Barua, S. et al. Critical current distributions of recent Bi-2212 round wires. IEEE Trans. Appl. Supercond. 31, 6400406 (2021).
Gurevich, A. Pinning size effects in critical currents of superconducting films. Supercond. Sci. Technol. 20, S128–S135 (2007).
Chaparro, C. et al. Doping dependence of the specific heat of single-crystal BaFe2(As1-xPx)2. Phys. Rev. B 85, 184525 (2012).
Miura, M. et al. Anisotropy and superconducting properties of BaFe2(As1-xPx)2 films with various phosphorus contents. Appl. Phys. Express 6, 093101 (2013).
Hashimoto, K. et al. A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe2(As1-xPx)2. Science 336, 1554–1557 (2012).
Miura, S. et al. Characteristics of high-performance BaHfO3-doped SmBa2Cu3Oy superconducting films fabricated with a seed layer and low temperature growth. Supercond. Sci. Technol. 28, 065013 (2015).
Xu, A. et al. Strongly enhanced vortex pinning from 4 to 77 K in magnetic fields up to 31 T in 15 mol.% Zr-added (Gd, Y)-Ba-Cu-O superconducting tapes. APL Mater. 2, 046111 (2014).
Majkic, G. et al. In-field critical current performance of 4.0 μm thick film REBCO conductor with Hf addition at 4.2 K and fields up to 31.2 T. Supercond. Sci. Technol. 33, 07LT03 (2020).
Acknowledgements
This work at Seikei University was supported by JST-FOREST (Grant Number JPMJFR202G, Japan). A part of this work at Seikei University was supported by JSPS KAKENHI (18KK0414 and 20H02184) and Promotion, Mutual Aid Corporation for Private Schools of Japan (Science Research Promotion Fund). This work at Los Alamos National Laboratory was supported by the LDRD office 20210320ER (B.M.) and the US DOE, Office of Basic Energy Sciences, Materials Sciences and Engineering Division (L.C.). This work at AIST was supported by the New Energy and Industrial Technology Development Organization (NEDO). We thank Jeffrey O Willis (LANL) for the helpful discussions and critical reading of the manuscript. M.M. also thanks Akira Ibi for the sample fabrication of PLD-EuBCO films.
Author information
Authors and Affiliations
Contributions
M.M. and B.M. carried out the experimental design. M.M., G.T., and T.H. grew the films and carried out transport measurements. B.M. carried out the data analysis and provided advice and consultation on the flux pinning and manuscript preparation. R.Y. and T.K. carried out microstructural studies. Y.K. carried out the analysis for Hc2. T.I. contributed to the discussion on the film preparation. H.K., F.N., and A.M. contributed to the discussion on the penetration depth analysis. K.S. and N.S. carried out the analysis for the resonance frequency. T.O. and S.A. contributed to the discussion on the analysis for the transport measurement at high field. L.C. contributed to the discussion and manuscript preparation. All authors discussed the results and implications and commented on the manuscript. M.M. and B.M. wrote the manuscript with contributions from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miura, M., Tsuchiya, G., Harada, T. et al. Thermodynamic approach for enhancing superconducting critical current performance. NPG Asia Mater 14, 85 (2022). https://doi.org/10.1038/s41427-022-00432-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-022-00432-1
This article is cited by
-
Significantly enhanced critical current density and pinning force in nanostructured, (RE)BCO-based, coated conductor
Nature Communications (2024)
-
Quadrupling the depairing current density in the iron-based superconductor SmFeAsO1–xHx
Nature Materials (2024)
-
Impact of high growth rates on the microstructure and vortex pinning of high-temperature superconducting coated conductors
Nature Reviews Physics (2023)