Introduction

The introduction of magnetic elements into a protected topological insulator breaks the time-reversal symmetry, and the magnetic interaction can open a gap in the otherwise gapless topological Dirac surface states (DSSs)1. This allows various novel topological quantum states to be generated, such as magnetic topological insulators1,2,3, magnetic Weyl semimetals4,5 and axion insulators6. A plethora of magnetoelectric effects are predicted from the topological invariants of these novel materials, such as the quantum anomalous Hall effects (QAHE)7,8,9, with the appearance of chiral dissipationless edge channels, half-quantized surface anomalous Hall conductivity6, nonlinear effects such as multiple harmonic generation10,11 and the circular photogalvanic effect12,13.

Doping with magnetic elements is the usual means for exploring the interaction between topology and magnetism14. However, doping inhomogeneity leads to complex magnetic ordering and small exchange gaps15. Consequently, various topological quantum effects appear at very low temperatures. Therefore, intrinsic magnetic topological insulators are highly desirable for increasing those temperatures and for investigating topological quantum phenomena.

MnBi2Te4 (MBT) is a novel intrinsic magnetic topological insulator where an additional layer of Mn atoms is inserted into the tetradymite structure of Bi2Te3, creating a septuple-layer (SL) of atoms with a Te-Bi-Te-Mn-Te-Bi-Te sequence16,17. The layers are then stacked through van der Waals (vdW) forces, crystallizing in a rhombohedral layered structure with the space group R-3m and creating a layered magnet similar to transition metal halides such as CrI318,19,20. In MBT, the distance between the Mn layers causes weak magnetic interlayer coupling21, resulting in an A-type antiferromagnetic ground state with a Néel temperature of 24 K while preserving a ferromagnetic long-range order in the single SLs22,23,24,25. Therefore, magnetism and topology are structurally separated in MBT, with Mn layers inducing magnetism and Bi-Te layers generating topological states. This structural separation makes MBT a case study for investigating quantum topological phenomena26,27,28.

The nontrivial topology results in the presence of electronic DSSs at the Γ point in the Brillouin zone, which have been observed both in single crystals29,30 and thin films31 by angle-resolved photoemission spectroscopy (ARPES). Below the Néel temperature, the time-reversal symmetry is broken by the magnetic ordering, causing the system to enter a magnetic topological phase. In this magnetic phase, the surface Dirac states lose their protection, causing the opening of an energy gap at the Dirac point whose properties, however, are still under debate28,32.

Although many MBT properties have already been measured in single crystals or thin flakes, it is known that topological insulator crystals can be strongly affected by impurities and stoichiometric defects33. Therefore, the growth of MBT thin films with well-controlled properties may remove defects and impurities, which negatively affect the single-crystal properties, to a considerable extent11,33,34,35,36. Indeed, nearly pure DSSs are expected at the Fermi level for thin films31, differing from the flakes cleaved by single crystals, which have been shown to host additional electronic contributions from bulk states29,30. Moreover, due to the antiferromagnetic coupling between the Mn layers, the magnetic properties of MBT films can be tuned through the thin film geometry by simply changing the number of SLs, with a QAHE and an axion insulator state predicted for odd and even numbers of layers, respectively37.

In this manuscript, we investigate the electrodynamics of high-quality MnBi2Te4 thin films deposited on high-resistivity floating-zone (HRFZ)-silicon substrates over a very broad spectral range, from terahertz (THz) to ultraviolet (UV), as a function of thickness (from 7 to 40 SLs) and temperature. The electronic response in the thinnest sample (7 SLs) is dominated by mobile Dirac surface states generating Drude behavior in the THz and infrared (IR) spectral range. Therefore, we investigate the low energy behavior of the 7 SL film at various temperatures above and below the magnetic transition (~24 K). We observe that the broken time reversal symmetry affects the Dirac surface states at the Fermi level, opening a magnetic gap at the Dirac point of ~80 meV, in good agreement with theoretical calculations.

Results

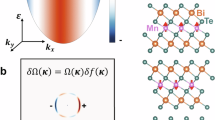
MnBi2Te4 thin films were synthesized at different thicknesses through an evaporation process on an HRFZ-Si(111) substrate (see Methods). The rhombohedral crystal structure of MnBi2Te4 (R-3m space group) is shown in Fig. 1a. Bismuth (Bi) and tellurium (Te) atoms are bonded to form an ordered structure with a manganese (Mn) additional layer, forming a septuple layer structure, Te-Bi-Te-Mn-Te-Bi-Te and yielding intrinsic magnetic properties. The black arrows indicate the a, b, and c crystal axes, while the red arrows indicate the antiferromagnetic coupling between the Mn layers that are stacked and linked through van der Waals forces.

Fig. 1: Optical spectroscopy of MBT thin films.
figure 1

a View of the crystal structure of MnBi2Te4. The Bi, Te and Mn atoms are bonded to form a septuple layer structure, with an antiferromagnetic exchange between the Mn layers. The arrows indicate the crystal axes. The dotted lines highlight the unit cell. b Schematic description of the thin film samples over an HRFZ-Si(111) substrate. The two surfaces are expected to host Dirac states due to the nontrivial topology of the bulk gapped bands. c Experimental transmittance of MBT films over a silicon substrate. The black curves correspond to a Drude-Lorentz fitting (see main text) on the transmittance of the bare Si substrate (black points) and on the 7 SL film (black dashed line).

Full size image

Reflectance (R) and transmittance (T) measurements on films at different thicknesses were performed across a broad spectral range from THz (≃30 cm−1) to UV (30,000 cm−1) frequencies. The spectroscopy setup is discussed in the Methods section and shown in Fig. 1b. Figure 1c shows the measured optical transmittance of all films and the Si substrate. Figure 2a shows the real part of the extracted optical conductivity σ1(ω) of MBT films with different thicknesses across the whole measured spectrum. σ1(ω) is obtained through a Kramers-Kronig constrained simultaneous fitting of reflectance and transmittance data, described through a multilayer model using the RefFIT software38. Examples of the transmittance fit are shown as black lines in Fig. 1c. The measured HRFZ-Si(111) optical parameters are used as inputs in the RefFIT procedure. The optical conductivity for all thicknesses is dominated by a broad absorption band located between 15,000 and 20,000 cm−1, which can be associated with bulk interband transitions, in good agreement with data for single crystals39. This broad peak is well separated from a low-energy metallic contribution appearing for all films below 1000 cm−1 (see Fig. 2b).

Fig. 2: Room temperature optical conductivity at different thicknesses for MBT thin films.
figure 2

a Optical conductivity of MBT films from THz to UV, as extracted for each thickness through the reflectance and transmittance measurements. The inset shows the fit of the MBT film bulk transitions. An electronic gap Eg ∼ 5000 cm−1 (0.62 eV) is extracted for the three thicker samples. Eg softens to 3000 cm−1 (0.37 eV) in the 7 SL film. b THz conductivity of the five films with different thicknesses. c Drude spectral weight (SW) times the thickness (SW·thickness) as a function of thickness. The free carrier response of MBT shows monotonic linear decreasing behavior with thickness, reaching a plateau below 25 nm due to the presence of DSSs.

Full size image

Discussion

An estimation of the electronic gap Eg can be obtained by taking the zero crossing of a linear fitting curve for the interband conductivity onset. This fitting is plotted for all films in the inset of Fig. 2a through dashed black lines. Their intersections with the frequency axis provide an estimation for the energy gap. Eg is on the order of 5000 cm−1 (0.62 eV) for the three (20, 30 and 40 SL) thicker films. The gap is subjected to a redshift with decreasing thickness, reaching nearly 3000 cm−1 (0.37 eV) in the 7 SL film. Although the gap values estimated from our optical measurements are higher than the absorption edge obtained from bulk MBT22,29,39,40 (nearly 200 meV), they are in good agreement with ARPES studies on the same films31. Moreover, near 2500 cm−1 (0.3 eV), an additional absorption feature appears for the 7 and 12 SL films at variance with the results of the thicker films, which instead exhibit a smooth decreasing behavior. Given its energy range, this extra peak could be associated with transitions from the lower energy Dirac cone to the upper one, analogous to the Pauli blocking transitions in graphene.

Figure 2b shows the real part of the optical conductivity in the terahertz spectral range, highlighting the metallic absorption edge coming from the low energy states. Strong thickness-dependent changes can be observed, with the thinner 7 SL sample exhibiting a conductivity almost 4 times higher than that of the 40 SL film. To highlight the contribution of the surface states to the low-energy electrodynamics of MBT, we fit the low-energy optical conductivity with a Drude term characterized by a scattering rate Γ and a spectral weight \(SW = \omega _p^2/8\), where ωp is the plasma frequency. To understand the surface contributions to the Drude response, the spectral weight is multiplied by the thickness d of the films. This result is plotted in Fig. 2c as a function of d. Here, the metallic contribution is nearly constant for the 7, 12 and 20 SL films and grows in a roughly linear way at larger thicknesses. The nearly constant value of SW × d for films between 7 and 20 SLs suggests that in those films, the free-charge contribution mainly comes from Dirac surface states. This result also supports a surface-related origin for the Eg redshift and the increase in strength of the oscillator near 2500 cm−1 (see Fig. 2a), both found in the thinner films, where the topological surface states are expected to contribute strongly to the optical conductivity.

Supposing the conductivity of the 7 SL film fully originates from the 2D surface states, it is possible to link its Drude spectral weight to the density of carriers n2D as41

$$\omega _p^2d = \frac{{n_{2D}e^2}}{{m^ \ast {\it{\epsilon }}_0}}$$
(1)

where m* is the mass for the Dirac fermions of the surface states, obtained as the ratio of the Fermi momentum kF and velocity νF: m* = ℏkF/νF. Considering the surface state dispersion as purely linear near the Fermi level31, the right part of Eq. (1) can be written as41

$$\omega _p^2d = \frac{{G_0}}{\hbar }\frac{{E_F}}{{{\it{\epsilon }}_0}}$$
(2)

where G0 is the quantum of conductance (\(G_0 = 2e^2/h \simeq 7.75 \times 10^{ - 5}\) S) and \(E_F = \hbar k_F\nu _F\) is the Fermi energy. From the Drude fitting, we can thus determine \(E_F \sim 120\;meV\), and using the constant Fermi velocity νF = vF = 5.5 × 105 m/s extracted by ARPES measurements31, a Fermi wavevector kF ∼ 0.04 Å−1 is estimated, which can be compared to the result kF ∼ 0.07 Å−1 obtained by ARPES31.

Temperature-dependent optical conductivity

As shown in the previous section, the optical conductivity of the 7 SL thin film is dominated by Dirac surface states. Therefore, we investigate its optical behavior as a function of temperature to study the effect of the magnetic order and then of the time-reversal breaking on the Dirac surface states. In this regard, optical transmittance measurements were performed between 20 and 10,000 cm−1 from 300 K to 5 K, crossing the Néel temperature at ~24 K. The real part of the optical conductivity is shown in Fig. 3a, as extracted from transmittance measurements through the RefFit program. The optical conductivity from 300 to 50 K (above the Néel temperature) is nearly constant, showing a Drude term (associated with mobile Dirac surface states) below 1000 cm−1, an absorption band in the mid-infrared (MIR) at ~2500 cm−1 (310 meV) and, at higher frequency, the absorption tail related to interband bulk transitions, whose linear extrapolation to the frequency axis provides an electronic gap of ~3000 cm−1 (see above). The inset in Fig. 3a schematically describes these electronic transitions. Below TN ≃ 24 K, the optical conductivity decreases over the whole spectral range with respect to that at all other temperatures. More specifically, the electronic gap hardens to ~4000 cm−1, the Drude term is reduced in intensity, and the MIR absorption band nearly disappears. This is at variance with single-crystal measurements, where an increase in the optical conductivity with decreasing temperature is observed, as given by the reduced scattering of the bulk electrons22,39.

Fig. 3: Temperature dependence of the optical conductivity of the 7 SL MBT film.
figure 3

a Real optical conductivity at different temperatures. The inset shows the electronic transitions accounting for the optical conductivity features. b Drude spectral weight (SW) as a function of temperature. The inset shows the ratio of the SW at different temperatures with respect to the SW at 50 K over the same ratio for the film resistance.

Full size image

The effect of magnetism on the DSSs can be quantified by plotting the Drude spectral weight SW as a function of temperature (see Fig. 3b). Here, the SW is approximately constant above 30 K, while it decreases rapidly without disappearing down to 5 K, i.e., well below the Néel temperature. Our optical conductivity measurements reproduce the DC behavior of the resistance R on a film of the same batch well, as shown in the inset of Fig. 3b. Here, we plot the ratio R(T)/R(50K) vs. T (black line) in comparison to the zero-frequency extrapolation of the optical resistivity (ρDC = 1/σ1(ω = 0)) normalized at 50 K (ρDC(T)/ρDC(50 K)). In addition to some discrepancies observed at approximately room temperature (probably caused by an extra temperature dependence of the silicon substrate), the two ratios behave in a very similar way, indicating that the increase of the resistance below the Néel temperature can be linked to the reduction of the Drude spectral weight as induced by the breaking of the time-reversal symmetry. Indeed, broken time-reversal symmetry is expected to remove the topological protection of DSSs2, inducing the formation of a gap at the Dirac node. In this framework, the gap opening modifies the linear (Dirac) energy-momentum dispersion which, in the magnetic phase, should become \(E(k) = \pm \sqrt {\hbar {^2}v_F^2k^2 + {\Delta}^2}\), where 2Δ is the gap value2. Since in MBT the Dirac node is located well below the Fermi level (≃−0.12 eV), the gap opening should only partially affect the electronic transitions near the Fermi level, such as the Drude term, whose spectral weight is dampened due to the modified energy-momentum dispersion. In other words, the gap opening corresponds to the Dirac quasiparticles acquiring an effective mass, thus decreasing their mobility and conductivity contribution. An estimate of the gap value can be obtained from the Drude SW reduction below TN, again using Eq. (1), as explained in the methods section. From this calculation, a gap value 2Δ ≃ 80 meV is extracted. Our results are at variance with recent high-resolution ARPES data on single crystals29, highlighting an unperturbed Dirac node even below TN. However, they are in good agreement with recent ARPES results obtained on MBT thin films grown via MBE42, which evidence a large energy gap (>70 meV) below the Néel temperature for a 5 SL film on silicon. This result confirms the importance of thin film geometry in highlighting the magnetic gap opening and as a platform where topological surface states, overcoming bulk contribution, can be used for device applications. Moreover, our results are in good agreement with theoretical calculations28 and point contact tunneling spectroscopy results43. These results suggest a magnetic gap of ~50–60 meV (∼400–500 cm−1), slightly lower than the value extracted in this work, 2∆ ≃ 80 meV. Therefore, the evidence of a gap opening below TN, along with the dominant surface state behavior at the Fermi level, highlights the intrinsic topological character of MBT thin films, in stark contrast with single crystals and thin flakes.

Conclusions

In this work, we investigated the optical properties of intrinsic magnetic topological MnBi2Te4 material over a broad spectral range from terahertz to ultraviolet. High-quality MBT thin films were studied at room temperature with different thicknesses, from 7 to 40 septuple layers, allowing us to separate the contribution of Dirac surface free-electron states in the optical conductivity from bulk electronic transitions. In the 7 SLs (where the Dirac surface states provide the major contribution to the low-energy conductivity), we further studied the behavior of these states crossing the Néel critical temperature at nearly 24 K and entering the magnetically time-reversal broken state. The temperature-dependent optical conductivity measurements indicate the opening of a gap at the Dirac node, as induced by the broken time-reversal symmetry, in stark contrast to ARPES measurements in both single crystals and thin flakes, where contradictory results have been obtained. From the reduction of the Drude spectral weight below TN, we estimated a gap on the order of 80 meV, which is in good agreement with calculation and tunneling measurements. This optical study indicates that an intrinsic topological behavior is observed in MnBi2Te4 thin films, paving the road for exploring the interaction between magnetism and topology and the appearance of novel electrodynamics effects31,40,44,45.

Methods

Thin film growth

The Si(111) substrates (resistivity 10000 Ohm cm) were cleaned by flashing to 1200 °C in an ultrahigh vacuum chamber for MBE growth (base pressure 10−9 mbar). The treated Si(111) substrates showed sharp 7 × 7 reconstruction patterns from reflection high energy election diffraction. High purity Bi (99.9999%), Mn (99.9999%) and Te (99.9999%) were coevaporated onto the substrates, which were kept at a certain temperature of 230 °C. The growth was carried out under Te-rich conditions, and the flux ratio between Mn and Bi was kept at nominally 1:2. The growth rate was 1 SL/7 min. Postannealing at 250 °C was carried out to improve the crystalline quality46.

Optical characterization

Transmission and reflection measurements were taken through a Vertex 70 v FTIR broadband interferometer coupled with different detection systems to scan the spectral range from THz (20 cm−1) to NIR (10,000 cm−1). Reflectivity measurements were collected at higher frequencies up to ultraviolet wavelengths (30,000 cm−1) by a JASCO V770 spectrometer. The MBT thin films were measured at various temperatures through a He-cooled Helitran cryostat. The optical properties of the Si substrate were measured under the same experimental conditions, and the real (n) and imaginary (k) parts of the refraction index were determined by the Refit program. n and k were used as input parameters in a film/substrate bilayer model38 to extract the real and imaginary parts of the film optical conductivity.

The transport data of the 7 SL MnBi2Te4 film were measured from a film grown under the same growth conditions as the sample used for the optical conductivity measurements. The low-temperature transport measurements were taken in a closed-cycle system (Oxford Instruments TelatronPT). Freshly cut indium cubes were cold pressed onto the sample as contacts. Standard lock-in techniques were employed to determine the sample resistance in a four-terminal configuration.

Calculation of the gap at the dirac node

Using Eq. (1), the ratio between the SW of the film at two different temperatures, T1 and T2, can be linked with the change in the effective mass m* and the 2D surface electron density n2D as follows:

$$\frac{{SW_{T_1}}}{{SW_{T_2}}} = \frac{{m_{T_2}^ \ast }}{{m_{T_1}^ \ast }}\frac{{n_{2D,T_1}}}{{n_{2D,T_2}}}$$
(3)

To understand the effect of the magnetic phase transition on the spectral weight, we choose the experimental temperatures T1 = T> > TN and T2 = T< < TN, respectively, above and below the Néel temperature TN. The 2D electron density for a single surface takes the form \(n_{2D} = k_F^2/4\pi 41\), while the effective mass is m* = ℏkF/νF, where \(\nu _F = (1/\hbar )\partial E_F/\partial k_F\) is the Fermi velocity. By using the gapped energy-momentum dispersion \(E_F = \sqrt {(\hbar v_Fk_F)^2 + {\Delta}^2}\) for T<, where 2Δ is the gap2, Eq. (3) can be written as

$$\frac{{SW_{T_ > }}}{{SW_{T_ < }}} = \sqrt {\frac{{E_F^2 + {\Delta}^2}}{{E_F^2 - {\Delta}^2}}}$$
(4)

which describes a reduction of the Drude spectral weight in the magnetic ordered state, quantified by the gap value. Using the experimental data, i.e., T< = 5 K, T> = 50 K, and EF, as obtained by Eq. (2) (the Fermi energy is approximately constant across the transition), a gap value of 2Δ ≃ 80 meV is obtained.